Algoritmo de optimización del comportamiento social adaptativo (ASBO): — Adaptive Social Behavior Optimization (ASBO): Evolución en dos fases

Índice

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

1. Introducción

En el artículo anterior, analizamos un ejemplo del concepto de Schwefel, que incluía una distribución normal, el uso de tasas de mutación autoadaptativas y una función de vecino más próximo basada en la aptitud. Ahora nuestro camino nos lleva a una nueva etapa de investigación, donde nos sumergiremos en un proceso de dos fases, completando el entrenamiento del algoritmo como modelo matemático, con el ASBO (Adaptive Social Behavior Optimization). Asimismo, realizaremos una prueba exhaustiva de este interesante modelo con las funciones de prueba que ya nos son familiares y sacaremos conclusiones sobre su eficacia. En este artículo, descubriremos nuevas aplicaciones del comportamiento social en organismos vivos en el campo de la optimización y presentaremos resultados únicos que nos ayudarán a comprender y usar mejor los principios del comportamiento colectivo para resolver problemas complejos.

2. Implementación del algoritmo

Comenzaremos formando el pseudocódigo del algoritmo ABSO (las ecuaciones utilizadas se presentan a continuación):

Parámetros de entrada: tamaño de la población PZ, número de poblaciones M, número de épocas P' para cada población. f(x) será la función objetivo.

Inicialización:

1. Crear M poblaciones, cada una de tamaño PZ
2. Para cada población:

• Inicializamos las soluciones xi aleatoriamente
• Calculamos los valores de la función objetivo f(xi) para cada solución
• Definimos al líder global Gb como la solución con f(xi) máxima
• Para cada solución xi determinamos el grupo de vecinos más próximos Nc
• Inicializamos las mejores soluciones personales Sb = xi
• Inicializamos los parámetros adaptativos Cg, Cs, Cn aleatoriamente en el rango [-1.0; 1.0]
  

Fase 1 : Procesamiento independiente de poblaciones.
3. Para cada una de las poblaciones M:

•  Para cada solución xi:
  

• Aplicamos la mutación autoadaptativa para actualizar los coeficientes Cg, Cs y Cn según las ecuaciones (3) y (4)
  
• Calculamos el cambio de posición ΔX (i + 1) utilizando la ecuación (1)
• Actualizamos la posición de xi utilizando la ecuación (2)
• Calculamos el nuevo valor de f(xi)
• Actualizamos la mejor solución personal Sb si f(xi) > f(Sb)
• Actualizamos el líder global Gb si f(xi) > f(Gb)

• Repetimos hasta alcanzar las épocas P'

4. Guardamos poblaciones finales, valores f(xi) y los parámetros Cg, Cs, Cn

Fase 2 : Procesamiento de la población combinada.
5. De todas las poblaciones finales, seleccionamos las mejores soluciones PZ para f (xi)
6. Utilizamos los parámetros guardados Cg, Cs y Cn para estas soluciones PZ
7. Aplicamos el algoritmo ASBO a una población combinada de tamaño PZ
8. Repetimos los pasos 6 y 7 hasta alcanzar el criterio de detención.

Conclusión: Óptimo global Gb

Ecuaciones clave:

• ΔX (i + 1) = Cg * R1 * (Gb - xi) + Cs * R2 * (Sb - xi) + Cn * R3 * (Nc - xi)  (1)
• x (i + 1) = xi + ΔX (i + 1)                                                                           (2)
• p'i (j) = pi (j) + σi (j) * N (0, 1)                                                                  (3)
• σ'i (j) = σi (j) * exp (τ' * N (0, 1) + τ * Nj (0, 1))                                        (4)

Donde:

• Gb - líder global
• Sb - mejor solución personal
• Nc - centro del grupo de vecinos por aptitud
  
• R1, R2, R3 - números aleatorios en el rango [0, 1]
• Cg, Cs y Cn - parámetros adaptativos
• N(0,1) - número aleatorio de una distribución normal
• Nj (0,1) - número aleatorio de la distribución normal para cada dimensión j
• τ, τ' - factores de escala para la mutación autoadaptativa

Por el pseudocódigo presentado se puede ver que el algoritmo implementa una evolución en dos fases del desarrollo del modelo social. Podemos describir brevemente la lógica del algoritmo por fases:

1. Primera fase:

• Inicialmente tomamos M poblaciones del mismo tamaño PZ.
• Para cada una de estas M poblaciones, aplicamos el algoritmo ASBO independientemente durante un número fijo de iteraciones P'.
• Al final de esta fase, guardamos los valores de las funciones de aptitud y los parámetros de mutación adaptativa para cada individuo de todas las poblaciones finales.

2. Segunda fase:

• De todas las poblaciones finales de la primera fase, se seleccionan los PZ de los mejores individuos según el valor de la función de aptitud.
• Para estos PZ de los mejores individuos, se utilizan sus parámetros de mutación adaptativa almacenados.
• Luego aplicamos el algoritmo ASBO a esta nueva población de tamaño PZ para obtener la solución final.

Sentido de la evolución en dos fases:

1. La primera fase ofrece una amplia diversidad de soluciones y una mejor localización de la región óptima global gracias a la evolución independiente de varias poblaciones.
2. La segunda fase usa las mejores soluciones de las poblaciones de la primera fase y sus parámetros adaptativos para lograr una convergencia acelerada hacia el óptimo global.

De esta forma, la evolución en dos fases, en teoría, permite combinar la búsqueda global en la primera etapa con una optimización local más eficiente en la segunda etapa, lo que en última instancia, presumiblemente, mejora el rendimiento del algoritmo en su conjunto.

La versión clásica del algoritmo ASBO de dos fases y múltiples poblaciones implica el uso de varias poblaciones en paralelo e independientemente en la primera fase. En la segunda fase se toman las mejores soluciones de las poblaciones y se crea una nueva población. No obstante, el uso de nuestra plantilla única para todos los algoritmos de población nos plantea la pregunta de cómo manejar poblaciones múltiples.

La primera solución podría consistir en dividir una población normal, digamos de 50 individuos, en varias poblaciones, digamos 5. En este caso, cada una de las 5 poblaciones contendrá 10 individuos. Podemos usar múltiples poblaciones de la forma habitual, como si fueran una sola población, pero en la segunda fase surge un problema: necesitamos tomar las mejores soluciones de estas cinco poblaciones y colocarlas en una nueva población. Sin embargo, no podremos obtener el número requerido porque tendríamos que ponerlas todas al completo, lo cual significaría, de hecho, crear una copia de la población original.

La segunda solución a este problema es crear 5 poblaciones con tamaños iguales al tamaño de nuestra población, es decir, con 50 individuos. Para cada una de estas poblaciones asignamos un número fijo de épocas, por ejemplo 20. En este caso, en la primera fase procesaremos secuencialmente estas 5 poblaciones con un número fijo de épocas para cada población, es decir, 5 * 20 = gastaremos 100 épocas. Las 100 eras restantes (de un total de 200 eras) constituirán la segunda fase. En esta segunda fase, pondremos estas 5 poblaciones en una gran población de 250 individuos, las clasificaremos y tomaremos los mejores 50 individuos y crearemos una nueva población. A continuación, realizaremos operaciones con esta nueva población de la forma habitual según las fórmulas. En cuanto a su sentido, esto resulta completamente consecuente con el algoritmo original, y además nos ceñiremos a nuestro concepto de trabajo con algoritmos de población. Ya hemos tenido que aplicar enfoques innovadores en otros algoritmos con anterioridad, como el Nelder-Mead, el CRO químico, los algoritmos evolutivos y otros, para garantizar que todos los algoritmos resulten compatibles y puedan intercambiarse sin problemas.

Vamos a imaginar que ya hemos discutido todo, todos los métodos y acciones lógicas del algoritmo, y a pasar directamente a escribir el código.

Escribiremos la estructura "S_ASBO_Agent ", que en el algoritmo ASBO de dos fases de población múltiple describirá al agente de búsqueda. La estructura definirá las variables y el método "Init", que inicializa el agente.

Variables:

• c - array de coordenadas
• cBest - array de mejores coordenadas
• f - valor de aptitud
• fBest - mejor relación de aptitud
• Cg, Cs y Cn - parámetros adaptativos
• u - objeto de la clase "C_AO_Utilities"

El método "Init" inicializa el agente:

• Toma un número de coordenadas "coords" y arrays "rangeMin" y "rangeMax" que representan los valores mínimo y máximo para cada coordenada.
• Asigna memoria para los arrays "c" y "cBest" con el número de coordenadas "coords".
• Establece el valor inicial "fBest" en "-DBL_MAX ".
• Genera valores aleatorios para los parámetros adaptativos "Cg", "Cs", "Cn".
• Llena el array "c " con valores aleatorios en el rango entre "rangeMin" y "rangeMax".
• Asigna los valores de "c" al array "cBest ".
  

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Agent
{
    double c     [];   //coordinates
    double cBest [];   //best coordinates
    double f;          //fitness
    double fBest;      //best fitness

    double Cg, Cs, Cn; //adaptive parameters
    C_AO_Utilities u;

    void Init (int coords, double &rangeMin [], double &rangeMax [])
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
      Cg = u.RNDprobab ();
      Cs = u.RNDprobab ();
      Cn = u.RNDprobab ();

      for (int i = 0; i < coords; i++)
      {
        c     [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]);
        cBest [i] = c [i];
      }

    }
};
//——————————————————————————————————————————————————————————————————————————————

Para trabajar con varias poblaciones una a una, nos será más cómodo utilizar un array de poblaciones. Para ello, escribiremos la estructura “S_ASBO_Population”, que contiene solo un campo:

• agent - array de objetos del tipo "S_ASBO_Agent" que representan agentes en la población.

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Population
{
    S_ASBO_Agent agent [];
};
//——————————————————————————————————————————————————————————————————————————————

Luego declararemos la clase "C_AO_ASBO", un descendiente de la clase "C_AO". La clase contiene una serie de métodos y variables para trabajar con la optimización:

1. Constructor y destructor:

• El constructor inicializa los parámetros del algoritmo, tales como el tamaño de la población, el número de poblaciones, el número de épocas para cada población y las referencias a la descripción del algoritmo.
• El destructor se encuentra vacío.
  

2. Métodos:

• SetParams - establece los parámetros del algoritmo del array "params".
• Init - inicializa el algoritmo con los parámetros dados: rango de búsqueda, paso de búsqueda y número de épocas.
• Moving - realiza operaciones de desplazamiento de agentes en el espacio de búsqueda.
• Revision - realiza operaciones de revisión de agentes en el espacio de búsqueda y actualiza la mejor solución global.

3. Variables:

• numPop, epochsForPop-: número de poblaciones y número de épocas para cada población.
• epochs, epochNow, currPop, isPhase2, popEpochs, tau, tau_prime - variables adicionales utilizadas en el algoritmo.
• allAgentsForSortPhase2, allAgentsTemp, agentsPhase2, agentsTemp - arrays de agentes utilizados en el algoritmo.
• pop - conjunto de poblaciones.
  

4. Métodos auxiliares:

• AdaptiveMutation - realiza una mutación adaptativa en el agente.
• UpdatePosition - actualiza la posición del agente.
• FindNeighborCenter - encuentra el centro vecino para el agente.
• Sorting - realiza la clasificación de agentes.

Así, la clase "C_AO_ASBO" representa una implementación del algoritmo ASBO utilizando varios métodos y operaciones para desplazar y revisar agentes en el espacio de búsqueda.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ASBO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASBO () { }
  C_AO_ASBO ()
  {
    ao_name = "ASBO";
    ao_desc = "Adaptive Social Behavior Optimization";
    ao_link = "https://www.mql5.com/es/articles/15283";

    popSize       = 50;   //population size
    numPop        = 5;    //number of populations
    epochsForPop  = 10;   //number of epochs for each population

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "numPop";       params [1].val = numPop;
    params [2].name = "epochsForPop"; params [2].val = epochsForPop;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    numPop       = (int)params [1].val;
    epochsForPop = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPop;       //number of populations
  int epochsForPop; //number of epochs for each population

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  currPop;
  bool isPhase2;
  int  popEpochs;

  double tau;
  double tau_prime;

  S_ASBO_Agent      allAgentsForSortPhase2 [];
  S_ASBO_Agent      allAgentsTemp          [];
  S_ASBO_Agent      agentsPhase2           [];
  S_ASBO_Agent      agentsTemp             [];
  S_ASBO_Population pop                    []; //M populations

  void   AdaptiveMutation   (S_ASBO_Agent &agent);
  void   UpdatePosition     (int ind, S_ASBO_Agent &ag []);
  void   FindNeighborCenter (int ind, S_ASBO_Agent &ag [], double &center []);
  void   Sorting (S_ASBO_Agent &p [], S_ASBO_Agent &pTemp [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

El método "Init" realiza una función importante de la clase "C_AO_ASBO": inicializa los parámetros y las estructuras de datos para el algoritmo, necesarios para que el algoritmo ASBO funcione antes de que comience la optimización. Los principales pasos de inicialización en el método "Init" son:

1. Comprobación e inicialización de parámetros básicos:

• El método llama a "StandardInit" para inicializar parámetros básicos como los rangos de búsqueda mínimo y máximo y el paso de búsqueda. Si la inicialización falla, el método retornará "false".

2. Inicialización de variables adicionales:

• Se establecen los valores de las variables "epochs", "epochNow", "currPop", "isPhase2" y "popEpochs".
• Los valores de las variables "tau" y "tau_prime" se calculan en función de la dimensionalidad del espacio de búsqueda "coords".

3. Creación e inicialización de poblaciones y agentes:

• Se crea el array "pop" para almacenar las poblaciones y se inicializa cada población. Para cada agente de la población, se llama al método "Init" para inicializar sus coordenadas en el rango dado.
• Se crea el array "agentsPhase2" para los agentes de la fase 2 y se inicializa de manera similar a las poblaciones.
• Los arrays "allAgentsForSortPhase2" y "allAgentsTemp" se crean para almacenar temporalmente agentes durante el proceso de clasificación, y cada agente se inicializa.

4. Retorno del resultado:

•    El método retorna "true" si la inicialización ha tenido éxito.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASBO::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  currPop   = 0;
  isPhase2  = false;
  popEpochs = 0;

  tau       = 1.0 / MathSqrt (2.0 * coords);
  tau_prime = 1.0 / MathSqrt (2.0 * MathSqrt (coords));

  ArrayResize (pop, numPop);
  for (int i = 0; i < numPop; i++)
  {
    ArrayResize (pop [i].agent, popSize);

    for (int j = 0; j < popSize; j++) pop [i].agent [j].Init (coords, rangeMin, rangeMax);
  }

  ArrayResize (agentsPhase2, popSize);
  ArrayResize (agentsTemp,   popSize);
  for (int i = 0; i < popSize; i++) agentsPhase2 [i].Init (coords, rangeMin, rangeMax);

  ArrayResize (allAgentsForSortPhase2, popSize * numPop);
  ArrayResize (allAgentsTemp,          popSize * numPop);

  for (int i = 0; i < popSize * numPop; i++)
  {
    allAgentsForSortPhase2 [i].Init (coords, rangeMin, rangeMax);
    allAgentsTemp          [i].Init (coords, rangeMin, rangeMax);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método “Moving” de la clase “C_AO_ASBO” representa el proceso básico de desplazamiento del agente dentro del algoritmo ASBO, incluyendo la transición entre fases y la ejecución de las operaciones correspondientes para cada fase. Pasos principales del método "Moving":

1. Se aumenta el valor "epochNow":

• Se incrementa el 1 el valor de la variable "epochNow", lo que refleja el comienzo de una nueva época de optimización.

2. Fase 1:

• Si el algoritmo no está en la fase 2, entonces se hará lo siguiente:
• Si el número de épocas de la población actual ha alcanzado el límite "epochsForPop", entonces se reiniciará el contador "popEpochs", incrementaremos el contador "currPop" y se reiniciará el valor "fB".
• Si se alcanza el número máximo de poblaciones "numPop", el algoritmo pasará a la fase 2. En este caso, los agentes de todas las poblaciones se combinarán en un única array, se clasificarán y los mejores agentes se copiarán en el array "agentsPhase2".
• De lo contrario, para cada agente de la población actual, se realizarán operaciones de mutación adaptativa y actualización de posición, así como copiado de coordenadas.

3. Fase 2:

• En la fase 2, para cada agente del array "agentsPhase2", también se realizan operaciones de mutación adaptativa y actualización de posición, así como copiado de coordenadas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Moving ()
{
  epochNow++;

  //Фаза 1----------------------------------------------------------------------
  if (!isPhase2)
  {
    if (popEpochs >= epochsForPop)
    {
      popEpochs = 0;
      currPop++;

      fB = -DBL_MAX;
    }

    if (currPop >= numPop)
    {
      isPhase2 = true;

      int cnt = 0;
      for (int i = 0; i < numPop; i++)
      {
        for (int j = 0; j < popSize; j++)
        {
          allAgentsForSortPhase2 [cnt] = pop [i].agent [j];
          cnt++;
        }
      }

      u.Sorting (allAgentsForSortPhase2, allAgentsTemp, popSize * numPop);

      for (int j = 0; j < popSize; j++) agentsPhase2 [j] = allAgentsForSortPhase2 [j];
    }
    else
    {
      for (int i = 1; i < popSize; i++)
      {
        AdaptiveMutation (pop [currPop].agent [i]);
        UpdatePosition   (i, pop [currPop].agent);

        ArrayCopy (a [i].c, pop [currPop].agent [i].c);
      }

      popEpochs++;
      return;
    }
  }

  //Фаза 2----------------------------------------------------------------------
  for (int i = 1; i < popSize; i++)
  {
    AdaptiveMutation (agentsPhase2 [i]);
    UpdatePosition   (i, agentsPhase2);

    ArrayCopy (a [i].c, agentsPhase2 [i].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_ASBO" representa el proceso de revisión de los resultados de optimización, incluida la actualización del valor "fB" y la actualización de los resultados de optimización para cada fase del algoritmo ASBO. Los componentes principales del código son:

1. Variables y su inicialización:

• int ind = -1 ; — variable para almacenar el índice del elemento con el mejor valor de la función "f".
• fB — variable que representa el mejor valor de la función "f" encontrado en la etapa actual.

2. Búsqueda del mejor agente:

• En el primer ciclo "for", se iteran todos los agentes (objetos que representan decisiones) en el array "a" de tamaño "popSize".
• Si el valor de la función "f" del agente actual es mayor que el mejor valor actual "fB", entonces "fB" y el índice "ind" se actualizarán.

3. Copiado de datos:

• Si se encuentra un agente con el mejor valor de la función "ind != -1", entonces el array "cB" (que representa los parámetros de la mejor solución) se actualiza con los valores del array "a".

4. Fase 1:

• Si la población actual "currPop" es menor que el número total de poblaciones "numPop", los valores de la función "f" se actualizarán para los agentes de la población actual.
• Si el valor de "f" de un agente en el array "a" es mayor que su mejor valor "fBest", entonces "fBest" se actualiza y las características correspondientes se copian a "cBest".
• Luego, los agentes de la población actual se clasifican utilizando el método "u.Sorting".

5. Fase 2:

• Si la población actual es igual o mayor que el número total de poblaciones, entonces se realizan acciones similares para el array "agentsPhase2".
• Se actualizan los valores de la función "f", se comprueban y actualizan los mejores valores "fBest" y se realiza la clasificación.

Lógica general de funcionamiento:

• El método "Revision" ejecuta dos pasos principales: la búsqueda del mejor agente y la actualización de los datos de los agentes según la fase actual (fase 1 o fase 2).
• El objetivo principal consiste en monitorear y actualizar las mejores soluciones encontradas durante el proceso de optimización y mantener la clasificación de los agentes para su uso posterior.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  //фаза 1
  if (currPop < numPop)
  {
    for (int i = 0; i < popSize; i++)
    {
      pop [currPop].agent [i].f = a [i].f;

      if (a [i].f > pop [currPop].agent [i].fBest)
      {
        pop [currPop].agent [i].fBest = a [i].f;
        ArrayCopy (pop [currPop].agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (pop [currPop].agent, agentsTemp, popSize);
  }
  //фаза 2
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      agentsPhase2 [i].f = a [i].f;

      if (a [i].f > agentsPhase2 [i].fBest)
      {
        agentsPhase2 [i].fBest = a [i].f;
        ArrayCopy (agentsPhase2 [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (agentsPhase2, agentsTemp, popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "AdaptiveMutation" de la clase "C_AO_ASBO" representa el proceso de mutación adaptativa de los coeficientes del agente "ag" dentro del algoritmo ASBO, incluyendo la aplicación de la distribución Gaussiana y el cálculo de nuevos valores de coeficientes basados en variables aleatorias. Los pasos principales del método “AdaptiveMutation” son:

1. Mutación adaptativa de coeficientes:

• Los coeficientes "Cg", "Cs" y "Cn" del agente "ag" se mutan utilizando una distribución gaussiana.
• Para cada coeficiente, se calcula un nuevo valor usando la función exponencial de la suma de dos variables aleatorias gaussianas, cada una de las cuales se multiplica por el coeficiente correspondiente "tau_prime" y "tau".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::AdaptiveMutation (S_ASBO_Agent &ag)
{
  ag.Cg *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cs *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cn *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
}
//——————————————————————————————————————————————————————————————————————————————

El método "UpdatePosition" de la clase "C_AO_ASBO" representa el proceso de actualización de la posición del agente dentro del algoritmo ASBO, incluido el cálculo del cambio de posición según varios coeficientes y la actualización de la posición dentro de los rangos especificados. Los pasos principales del método "UpdatePosition" son:

1. Se calcula el cambio de posición:

• El cambio de posición del agente "ag[ind]" en cada dimensión "j" se calcula utilizando varios coeficientes y valores como "cB", "cBest", "deltaX", "rangeMin", "rangeMax" y "rangeStep".

2. Se actualiza la posición del agente:

• Para cada dimensión "j", se calcula un nuevo valor de la posición del agente "ag[ind].c[j]" sumando el cambio "deltaX[j]" y luego ajustando el valor dentro de los rangos dados.

La parte comentada del código "1)" es la versión original de los autores, "3)" es mi versión sin considerar los coeficientes "Cg", "Cs", "Cn"; en lugar de ellos se ha utilizado la distribución normal. La opción "2)", que es mi opción, ha mostrado los mejores resultados de estas tres opciones.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::UpdatePosition (int ind, S_ASBO_Agent &ag [])
{
  double deltaX [];
  ArrayResize (deltaX, coords);

  FindNeighborCenter (ind, ag, deltaX);

  for (int j = 0; j < coords; j++)
  {
    /*
    //1)
    deltaX [j] = ag [ind].Cg * u.RNDfromCI (-1, 1) * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * u.RNDfromCI (-1, 1) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * u.RNDfromCI (-1, 1) * (deltaX         [j] - ag [ind].c [j]);
    */
    
    //2)
    deltaX [j] = ag [ind].Cg * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * (deltaX         [j] - ag [ind].c [j]);


    /*
    //3)
    deltaX [j] = u.GaussDistribution (0, -1, 1, 8) * (cB             [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (deltaX         [j] - ag [ind].c [j]);
    */

    ag [ind].c [j] += deltaX [j];
    ag [ind].c [j] = u.SeInDiSp (ag [ind].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados de las pruebas

La impresión del algoritmo ASBO revela una serie de características interesantes que lo hacen verdaderamente único. Una de sus características clave es su extraordinaria escalabilidad, lo cual permite que el algoritmo gestione eficazmente problemas de alta dimensionalidad. Resultan especialmente destacables los resultados obtenidos al probar las funciones Forest y Megacity con 1 000 parámetros. En estos casos, el ASBO demuestra un rendimiento impresionante, comparable a los resultados de los algoritmos líderes en la tabla de clasificación. Estos logros resaltan no solo la eficiencia del algoritmo, sino también su potencial de aplicación en una amplia variedad de áreas que requieren optimización de alta calidad.

ASBO|Optimización del comportamiento social adaptativo|50.0|5.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0,7633114189858913
25 Hilly's; Func runs: 10000; result: 0,4925279738997658
500 Hilly's; Func runs: 10000; result: 0,3261850685263711
=============================
5 Forest's; Func runs: 10000; result: 0,7954558091769679
25 Forest's; Func runs: 10000; result: 0,4003462752027551
500 Forest's; Func runs: 10000; result: 0,26096981234192485
=============================
5 Megacity's; Func runs: 10000; result: 0,2646153846153846
25 Megacity's; Func runs: 10000; result: 0,1716923076923077
500 Megacity's; Func runs: 10000; result: 0,18200000000000044
=============================
All score: 3.65710 (40.63%)

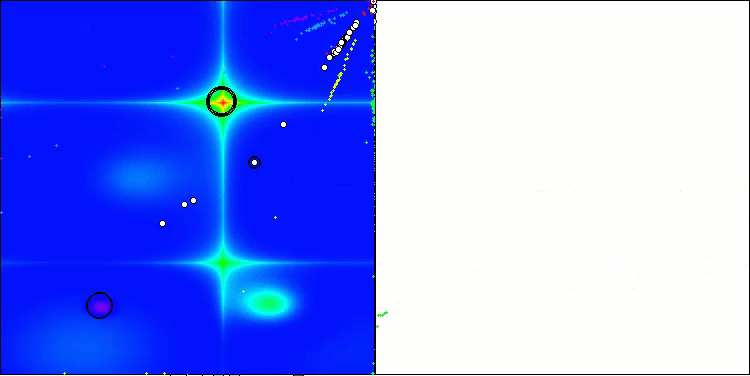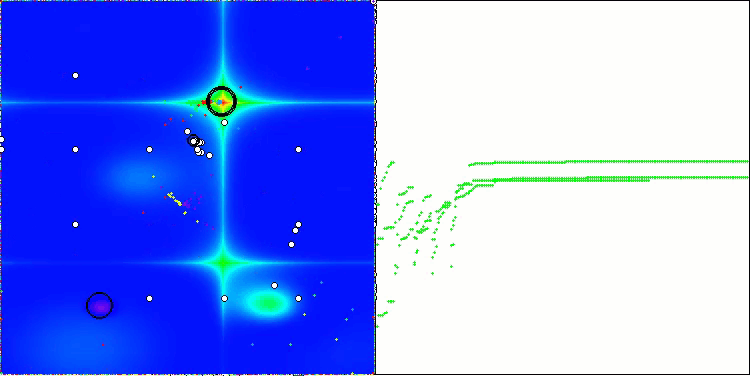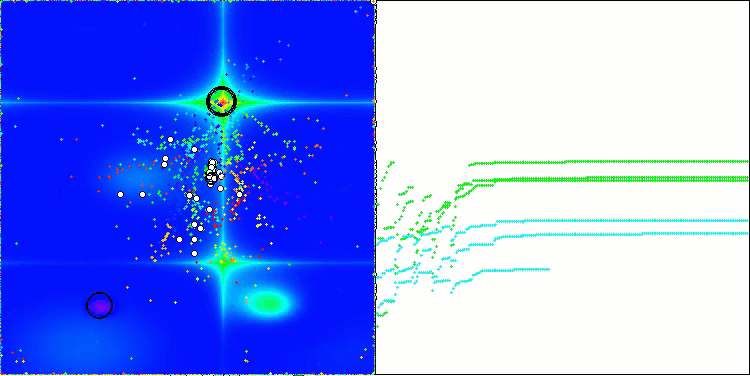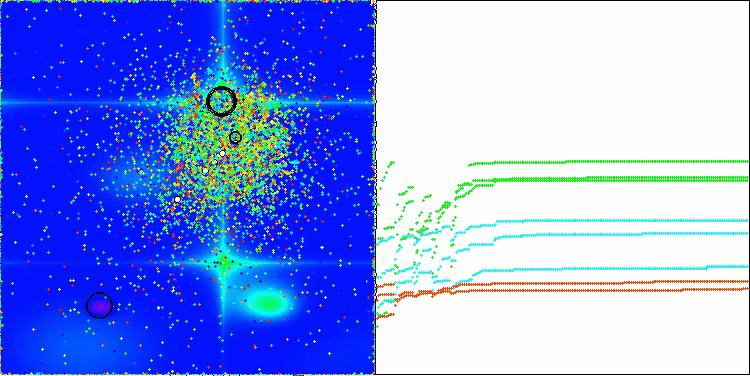
La visualización de los resultados del algoritmo ASBO revela una serie de características interesantes que merecen nuestra atención. Desde el comienzo mismo del funcionamiento del algoritmo, podemos observar cómo identifica con éxito regiones significativas de la solución, lo cual demuestra su capacidad para explorar eficazmente el espacio de parámetros.

El gráfico de convergencia muestra rupturas características en la línea, causadas por el funcionamiento secuencial de varias poblaciones en la primera fase. Estas rupturas indican que cada población contribuye al proceso de optimización explorando diferentes partes del espacio. No obstante, en la segunda fase, el gráfico adquiere una forma sólida, lo cual significa que se combinan las mejores soluciones de todas las poblaciones recopiladas después de la primera fase. Esta unificación permite que el algoritmo se centre en mejorar áreas prometedoras.

De esta forma, la visualización no solo ilustra la dinámica del algoritmo, sino que también resalta sus mecanismos adaptativos y cooperativos.

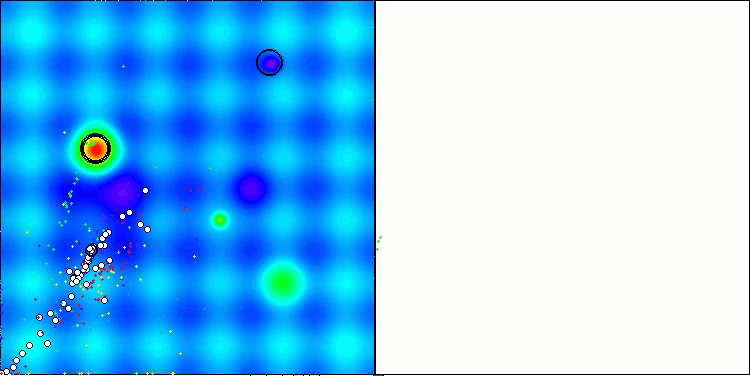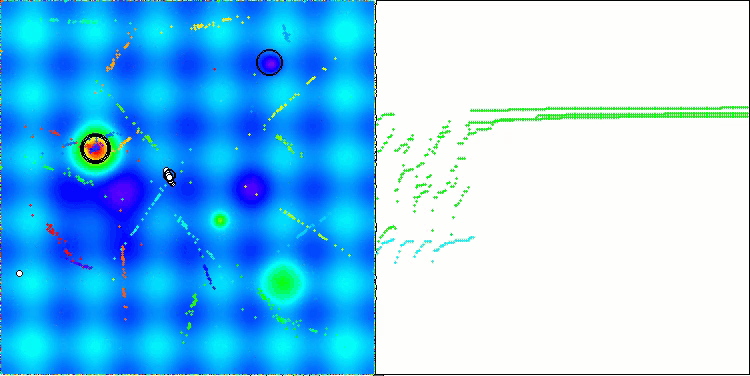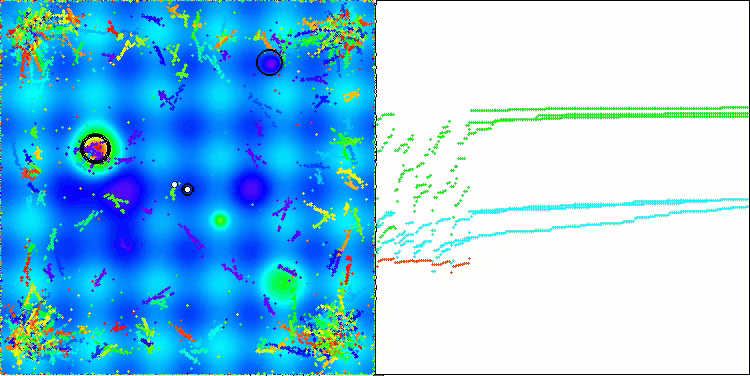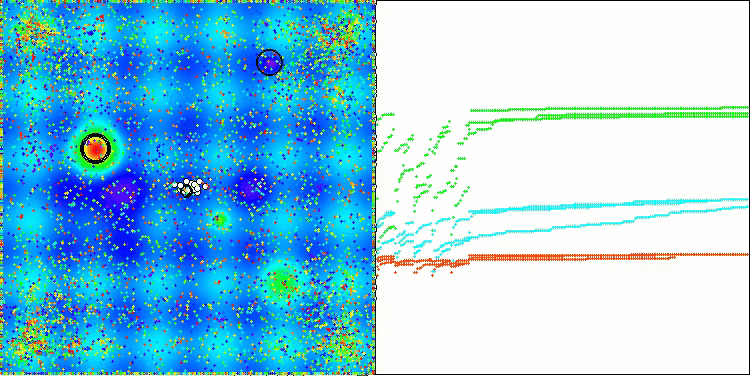
  ASBO en la función de prueba Hilly.

ASBO en la función de prueba Forest.

ASBO en la función de prueba de Megacity.

Según los resultados de la investigación, vemos que el algoritmo ocupa un lugar seguro en la parte media de la tabla de clasificación.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
4	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
5	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
6	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
7	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
8	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
9	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
10	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
11	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
12	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
13	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
14	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
15	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
16	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
17	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
18	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
19	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
20	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
21	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3.657	40,63
22	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
23	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
24	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
25	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
26	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
27	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
28	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
29	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
30	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
31	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
32	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
33	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
34	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
35	PSO	particle swarm Optimization	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
36	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
37	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
38	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
39	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
40	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
41	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
42	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
43	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Conclusiones

El algoritmo destaca por su originalidad y comportamiento no estándar, lo cual hace que su visualización resulte única y diferente a cualquier método conocido anteriormente. Esto atrae la atención y despierta el interés por sus mecanismos internos.

Cabe señalar que, a pesar de los resultados generales promedio y la convergencia al resolver problemas de pequeña dimensionalidad, el algoritmo demuestra su verdadero potencial al trabajar con problemas más complejos y en condiciones de un gran espacio de búsqueda. El algoritmo usa múltiples poblaciones que se ejecutan secuencialmente en la primera fase, lo cual plantea la cuestión de la conveniencia de dividir un número limitado de épocas en cálculos previos de poblaciones independientes. Los experimentos realizados usando solo una población en la primera fase muestran resultados significativamente peores, lo que confirma la utilidad de recopilar previamente información sobre el espacio de búsqueda circundante. Esto permite que el algoritmo use de forma más efectiva los individuos líderes: las soluciones más exitosas en la segunda fase de la búsqueda.

Además, el algoritmo tiene un gran potencial para futuras investigaciones. Creo que sus capacidades aún no se han aprovechado plenamente y se necesita más experimentación y análisis para entender cómo usar mejor sus beneficios algorítmicos.

Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados mayores o iguales a 0.99 se resaltan en blanco. Los nombres resaltados en verde son mis propios algoritmos.

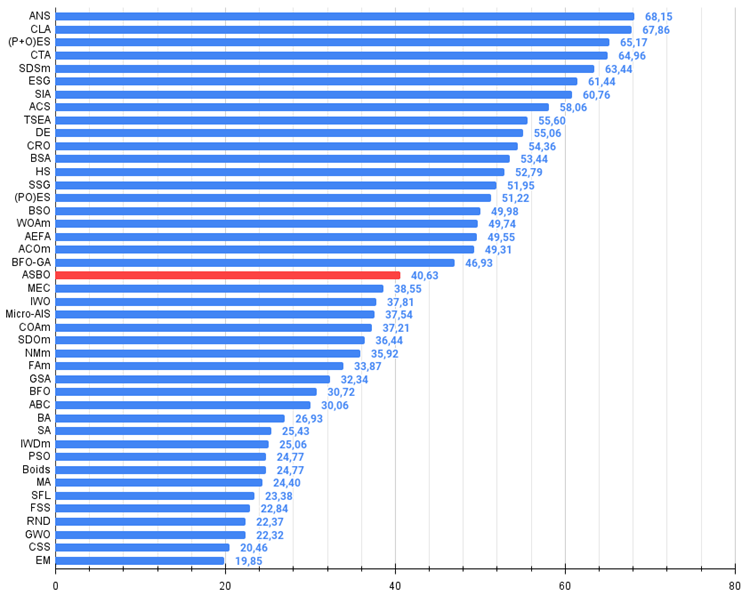
Figura 3. Histograma de los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),

donde 100 es el máximo resultado teórico posible; el script para calcular la tabla de clasificación está en el archivo)

Ventajas y desventajas del algoritmo de comportamiento social adaptativo (ASBO):

Ventajas:

1. Tiene un número reducido de parámetros externos.
   
2. Buenos resultados en problemas complejos y de alta dimensionalidad.
   

Desventajas:

1. Baja convergencia en problemas de baja dimensionalidad.
   

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/es/code/49355

Resumimos los resultados provisionales del trabajo realizado

Durante nuestra investigación, hemos analizado más de cuarenta algoritmos de optimización, cada uno de los cuales representa un enfoque único para resolver problemas complejos. Este proceso no solo ha sido divertido, sino también extremadamente educativo, revelando la riqueza y diversidad de métodos en el campo de la optimización.

Recreación y modificación de algoritmos. Para la gran mayoría de los algoritmos considerados, no había un código fuente ampliamente disponible. Esto me impulsó a adoptar un enfoque creativo: recreé el código basándome únicamente en las descripciones textuales de los autores, tomadas de varias publicaciones. Este enfoque no solo nos ha permitido comprender mejor los principios de funcionamiento de cada algoritmo, sino que también ha hecho posible adaptarlos a nuestras necesidades específicas.
Los pocos algoritmos que eran de código abierto no podían aplicarse al resolver problemas de optimización en general. Esto ha requerido una modificación significativa para hacerlos de propósito general y fácilmente aplicables a una amplia gama de tareas.

Innovaciones y mejoras. Algunos algoritmos, como el ACO (algoritmos de colonias de hormigas para resolver problemas en gráficos), no fueron pensados originalmente por sus autores para trabajar con problemas en el espacio continuo y han requerido modificaciones para ampliar su ámbito de aplicación. Otros algoritmos han mejorado su estrategia de búsqueda, aumentando su eficacia. A estas versiones modificadas les hemos dado el sufijo "m" en sus nombres, lo cual refleja su evolución. Además, hemos analizado con detalle muchas técnicas diferentes para procesar poblaciones, generar nuevas soluciones y métodos de selección.

Como demostración de las nuevas ideas y enfoques de optimización, hemos desarrollado más de cinco nuevos algoritmos con propiedad intelectual, que hemos presentado exclusivamente en los artículos.

Aplicación y estudio posterior. Debemos señalar que cualquiera de los algoritmos presentados se puede aplicar para resolver problemas de optimización sin necesidad de realizar modificaciones o mejoras adicionales. Esto los hace accesibles y cómodos para una amplia gama de investigadores y profesionales.

Para aquellos que buscan lograr los mejores resultados en tareas individuales específicas, ofrecemos tablas comparativas e histogramas que permiten estudiar las propiedades individuales de cada algoritmo. Esto descubre nuevas oportunidades a la hora de realizar ajustes más precisos, permitiendo optimizar estos para satisfacer requisitos específicos.

Y en conclusión : ambos enfoques (el uso de algoritmos ya preparados y su estudio profundo y adaptación) tienen su razón de ser. Comprender las sutilezas y técnicas de las estrategias de búsqueda de diferentes algoritmos abre nuevos horizontes que permiten a los investigadores lograr resultados sobresalientes.

Deseo sinceramente que todos los lectores tengan éxito en la búsqueda de las mejores soluciones y logren sus objetivos. ¡Que su viaje en el mundo de la optimización y el trading algorítmico sea emocionante y fructífero!