Algoritmo de comportamento social adaptativo — Adaptive Social Behavior Optimization (ASBO): Evolução em duas fases

Conteúdo

1. Introdução
2. Implementação do algoritmo
3. Resultados dos testes

1. Introdução

No artigo anterior, analisamos o conceito de Schwefel, incluindo a distribuição normal, a aplicação de coeficientes de mutação autoadaptativos e a função de determinação dos vizinhos mais próximos com base em sua adaptabilidade. Agora, avançamos para uma nova etapa de pesquisa, na qual nos aprofundamos no processo em duas fases, completando a formação do algoritmo como um modelo matemático — ASBO (Adaptive Social Behavior Optimization). Realizaremos testes abrangentes nesse modelo interessante em funções de teste já conhecidas e tiraremos conclusões sobre sua eficácia. Neste artigo, exploraremos novas aplicações do comportamento social dos organismos vivos no campo da otimização e apresentaremos resultados únicos que nos ajudarão a compreender e utilizar melhor os princípios do comportamento coletivo para resolver problemas complexos.

2. Implementação do algoritmo

Iniciaremos pela formação do pseudocódigo do algoritmo ASBO (as equações utilizadas estão apresentadas abaixo):

Parâmetros de entrada: tamanho das populações PZ, número de populações M, número de épocas P' para cada população e função objetivo f(x).

Inicialização:

1. Criar M populações, cada uma com tamanho PZ
2. Para cada população:

• Inicializar soluções xi aleatoriamente
• Calcular os valores da função objetivo f (xi) para cada solução
• Determinar o líder global Gb como a solução com f (xi) máximo
• Para cada solução xi, determinar o grupo de vizinhos mais próximos Nc
• Inicializar as melhores soluções individuais Sb = xi
• Inicializar parâmetros adaptativos Cg, Cs, Cn aleatoriamente no intervalo [-1.0; 1.0]
  

Fase 1: Processamento independente das populações.
3. Para cada uma das M populações:

•  Para cada solução xi:
  

• Aplicar mutação auto-adaptativa para atualizar os coeficientes Cg, Cs, Cn pelas equações (3) e (4)
  
• Calcular a mudança de posição ΔX (i + 1) pela equação (1)
• Atualizar a posição xi pela equação (2)
• Calcular o novo valor de f (xi)
• Atualizar a melhor solução individual Sb, se f (xi) > f (Sb)
• Atualizar o líder global Gb, se f (xi) > f (Gb

• Repetir até atingir P' épocas

4. Salvar as populações finais, os valores de f (xi) e os parâmetros Cg, Cs, Cn

Fase 2: Processamento da população unificada.
5. De todas as populações finais, selecionar os PZ melhores soluções com base em f (xi)
6. Utilizar os parâmetros Cg, Cs, Cn salvos para essas PZ soluções
7. Aplicar o algoritmo ASBO à população unificada de tamanho PZ
8. Repetir os passos 6-7 até que o critério de parada seja atendido

Resultado: Ótimo global Gb

Equações principais:

• ΔX (i + 1) = Cg * R1 * (Gb - xi) + Cs * R2 * (Sb - xi) + Cn * R3 * (Nc - xi)  (1)
• x (i + 1) = xi + ΔX (i + 1)                                                                           (2)
• p'i (j) = pi (j) + σi (j) * N (0, 1)                                                                  (3)
• σ'i (j) = σi (j) * exp (τ' * N (0, 1) + τ * Nj (0, 1))                                        (4)

Onde:

• Gb - líder global
• Sb - melhor solução individual
• Nc - centro do grupo de vizinhos baseado em adaptabilidade
  
• R1, R2, R3 - números aleatórios no intervalo [0, 1]
• Cg, Cs, Cn - parâmetros adaptativos
• N (0, 1) - número aleatório de distribuição normal
• Nj (0,1) - número aleatório de distribuição normal para cada dimensão j
• τ, τ' - fatores de escala para a mutação auto-adaptativa

Com base no pseudocódigo apresentado, observa-se que o algoritmo realiza uma evolução em duas fases no desenvolvimento do modelo social. Em resumo, a lógica do algoritmo pode ser descrita por fases:

1. Primeira fase:

• Inicialmente, são consideradas M populações de tamanho igual a PZ.
• Para cada uma dessas M populações, o algoritmo ASBO é aplicado independentemente durante um número fixo de iterações P'.
• No final desta fase, os valores da função fitness e os parâmetros de mutação adaptativa de cada indivíduo em todas as populações finais são armazenados.

2. Segunda fase:

• Das populações finais da primeira fase, são selecionados os PZ melhores indivíduos com base no valor da função fitness.
• Para esses PZ melhores indivíduos, utilizam-se os parâmetros de mutação adaptativa previamente armazenados.
• Nesta nova população de tamanho PZ, o algoritmo ASBO é aplicado para obter a solução final.

Propósito da evolução em duas fases:

1. A primeira fase garante a diversidade das soluções e uma melhor localização da região do ótimo global por meio da evolução independente de várias populações.
2. A segunda fase utiliza as melhores soluções das populações da primeira fase e seus parâmetros adaptativos para uma convergência mais rápida ao ótimo global.

Assim, a evolução em duas fases permite, teoricamente, combinar uma busca global na primeira etapa com uma otimização local mais eficiente na segunda, o que, presumivelmente, aumenta o desempenho geral do algoritmo.

A versão clássica do algoritmo ASBO em múltiplas populações e duas fases pressupõe o uso de várias populações de maneira paralela e independente na primeira fase. Na segunda fase, as melhores soluções dessas populações são selecionadas para formar uma nova população. No entanto, ao utilizar nosso modelo unificado para todos os algoritmos populacionais, surge a questão de como gerenciar várias populações.

A primeira solução seria dividir uma população padrão, por exemplo, de 50 indivíduos, em várias populações menores, como uma de 5 indivíduos. Nesse caso, cada uma dessas populações conteria 10 indivíduos. Podemos tratar essas populações como uma única população em seu funcionamento. Porém, na segunda fase, enfrentamos um problema: precisamos selecionar as melhores soluções dessas cinco populações e colocá-las em uma população nova. No entanto, não será possível reunir o número necessário de soluções, pois precisaríamos incluir todas elas, o que, na prática, significa criar uma cópia da população original.

A segunda solução para essa questão é criar cinco populações, cada uma com o mesmo tamanho da população original, ou seja, cinquenta indivíduos. A cada uma dessas populações será atribuído um número fixo de épocas, por exemplo, 20. Nesse caso, na primeira fase, processaremos essas cinco populações sequencialmente, cada uma por um número fixo de épocas, ou seja, serão consumidas 100 épocas no total. As 100 épocas restantes (de um total de 200) serão utilizadas na segunda fase. Nesta segunda fase, combinaremos essas cinco populações em uma única população maior, com 250 indivíduos. Em seguida, faremos uma ordenação e selecionaremos os 50 melhores indivíduos para formar uma nova população. Em seguida, realizaremos operações com essa nova população, de acordo com as fórmulas. Em essência, isso é consistente com o algoritmo original, enquanto mantemos nossa abordagem para algoritmos populacionais. Já implementamos abordagens inovadoras anteriormente em outros algoritmos, como Nelder-Mead, CRO químico, algoritmos evolutivos e outros, para garantir a compatibilidade entre todos os algoritmos e sua substituição sem inconvenientes.

Parece que discutimos tudo, todos os métodos e ações lógicas no algoritmo; agora, passamos diretamente à escrita do código.

Vamos escrever a estrutura "S_ASBO_Agent", que descreverá o agente de busca no algoritmo ASBO em múltiplas populações e duas fases. Ela contém variáveis e o método "Init", que inicializa o agente.

Variáveis:

• c - matriz de coordenadas
• cBest - matriz das melhores coordenadas
• f - valor de adaptabilidade (fitness)
• fBest - melhor valor de adaptabilidade
• Cg, Cs, Cn - parâmetros adaptativos
• u - objeto da classe "C_AO_Utilities"

O método "Init" inicializa o agente:

• Recebe o número de coordenadas "coords" e as matrizes "rangeMin" e "rangeMax", que representam os valores mínimo e máximo para cada coordenada.
• Aloca memória para as matrizes "c" e "cBest" com o número de coordenadas "coords".
• Define o valor inicial de "fBest" como "-DBL_MAX".
• Gera valores aleatórios para os parâmetros adaptativos "Cg", "Cs" e "Cn".
• Preenche a matriz "c" com valores aleatórios dentro do intervalo entre "rangeMin" e "rangeMax".
• Atribui os valores da matriz "c" à matriz "cBest".
  

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Agent
{
    double c     [];   //coordinates
    double cBest [];   //best coordinates
    double f;          //fitness
    double fBest;      //best fitness

    double Cg, Cs, Cn; //adaptive parameters
    C_AO_Utilities u;

    void Init (int coords, double &rangeMin [], double &rangeMax [])
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
      Cg = u.RNDprobab ();
      Cs = u.RNDprobab ();
      Cn = u.RNDprobab ();

      for (int i = 0; i < coords; i++)
      {
        c     [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]);
        cBest [i] = c [i];
      }

    }
};
//——————————————————————————————————————————————————————————————————————————————

Para lidar sequencialmente com várias populações, é conveniente usar uma matriz de populações. Para isso, escreveremos a estrutura "S_ASBO_Population", que contém apenas um campo:

• agent - matriz de objetos do tipo "S_ASBO_Agent", representando agentes dentro da população.

//——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Population
{
    S_ASBO_Agent agent [];
};
//——————————————————————————————————————————————————————————————————————————————

Declararemos a classe "C_AO_ASBO" como herdeira da classe "C_AO". A classe contém uma série de métodos e variáveis para trabalhar com a otimização:

1. Construtor e destrutor:

• O construtor inicializa os parâmetros do algoritmo, como o tamanho da população, o número de populações, o número de épocas para cada população e as referências à sua descrição.
• O destrutor é vazio.
  

2. Métodos:

• SetParams - define os parâmetros do algoritmo a partir da matriz "params".
• Init - inicializa o algoritmo com os parâmetros fornecidos: intervalo de busca, passo de busca e número de épocas.
• Moving - realiza operações de movimentação dos agentes no espaço de busca.
• Revision - realiza operações de revisão dos agentes no espaço de busca e atualiza a melhor solução global.

3. Variáveis:

• numPop, epochsForPop - número de populações e número de épocas para cada população.
• epochs, epochNow, currPop, isPhase2, popEpochs, tau, tau_prime - variáveis adicionais usadas no algoritmo.
• allAgentsForSortPhase2, allAgentsTemp, agentsPhase2, agentsTemp - matrizes de agentes utilizadas no algoritmo.
• pop - matriz de populações.
  

4. Métodos auxiliares:

• AdaptiveMutation - realiza a mutação adaptativa para um agente.
• UpdatePosition - atualiza a posição do agente.
• FindNeighborCenter - encontra o centro dos vizinhos de um agente.
• Sorting - realiza a ordenação dos agentes.

Assim, a classe "C_AO_ASBO" representa a implementação do algoritmo ASBO, utilizando diversos métodos e operações para movimentação e revisão dos agentes no espaço de busca

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ASBO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASBO () { }
  C_AO_ASBO ()
  {
    ao_name = "ASBO";
    ao_desc = "Adaptive Social Behavior Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15283";

    popSize       = 50;   //population size
    numPop        = 5;    //number of populations
    epochsForPop  = 10;   //number of epochs for each population

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "numPop";       params [1].val = numPop;
    params [2].name = "epochsForPop"; params [2].val = epochsForPop;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    numPop       = (int)params [1].val;
    epochsForPop = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPop;       //number of populations
  int epochsForPop; //number of epochs for each population

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  currPop;
  bool isPhase2;
  int  popEpochs;

  double tau;
  double tau_prime;

  S_ASBO_Agent      allAgentsForSortPhase2 [];
  S_ASBO_Agent      allAgentsTemp          [];
  S_ASBO_Agent      agentsPhase2           [];
  S_ASBO_Agent      agentsTemp             [];
  S_ASBO_Population pop                    []; //M populations

  void   AdaptiveMutation   (S_ASBO_Agent &agent);
  void   UpdatePosition     (int ind, S_ASBO_Agent &ag []);
  void   FindNeighborCenter (int ind, S_ASBO_Agent &ag [], double &center []);
  void   Sorting (S_ASBO_Agent &p [], S_ASBO_Agent &pTemp [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" é fundamental para a classe "C_AO_ASBO", pois inicializa os parâmetros e as estruturas de dados necessários para o funcionamento do algoritmo ASBO antes do início do processo de otimização. Os principais passos de inicialização nesse método são:

1. Verificação e inicialização de parâmetros básicos:

• O método chama "StandardInit" para inicializar parâmetros básicos, como os intervalos mínimos e máximos de busca e o passo de busca. Se a inicialização falhar, o método retorna "false".

2. Inicialização de variáveis adicionais:

• São definidos os valores das variáveis "epochs", "epochNow", "currPop", "isPhase2" e "popEpochs".
• Os valores de "tau" e "tau_prime" são calculados com base na dimensionalidade do espaço de busca "coords".

3. Criação e inicialização de populações e agentes:

• Um array "pop" é criado para armazenar populações, e cada população é inicializada. Para cada agente dentro da população, o método "Init" é chamado para inicializar suas coordenadas dentro do intervalo especificado.
• Um array "agentsPhase2" é criado para os agentes da fase 2 e é inicializado de forma semelhante às populações.
• Arrays "allAgentsForSortPhase2" e "allAgentsTemp" são criados para armazenar temporariamente os agentes durante o processo de ordenação, e cada agente é inicializado.

4. Retorno do resultado:

•    O método retorna "true" se a inicialização for bem-sucedida.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASBO::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  currPop   = 0;
  isPhase2  = false;
  popEpochs = 0;

  tau       = 1.0 / MathSqrt (2.0 * coords);
  tau_prime = 1.0 / MathSqrt (2.0 * MathSqrt (coords));

  ArrayResize (pop, numPop);
  for (int i = 0; i < numPop; i++)
  {
    ArrayResize (pop [i].agent, popSize);

    for (int j = 0; j < popSize; j++) pop [i].agent [j].Init (coords, rangeMin, rangeMax);
  }

  ArrayResize (agentsPhase2, popSize);
  ArrayResize (agentsTemp,   popSize);
  for (int i = 0; i < popSize; i++) agentsPhase2 [i].Init (coords, rangeMin, rangeMax);

  ArrayResize (allAgentsForSortPhase2, popSize * numPop);
  ArrayResize (allAgentsTemp,          popSize * numPop);

  for (int i = 0; i < popSize * numPop; i++)
  {
    allAgentsForSortPhase2 [i].Init (coords, rangeMin, rangeMax);
    allAgentsTemp          [i].Init (coords, rangeMin, rangeMax);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" da classe "C_AO_ASBO" representa o principal processo de movimentação dos agentes dentro do algoritmo ASBO, incluindo a transição entre as fases e a execução de operações específicas para cada fase. Os principais passos no método "Moving" são:

1. Incremento do valor de "epochNow":

• O valor da variável "epochNow" é incrementado em 1, indicando o início de uma nova época de otimização.

2. Fase 1:

• Se o algoritmo não estiver na fase 2, são executados os seguintes passos:
• Se o número de épocas para a população atual atingir o limite "epochsForPop", o contador "popEpochs" é reiniciado, o contador "currPop" é incrementado e o valor de "fB" é redefinido.
• Se o número máximo de populações "numPop" for atingido, o algoritmo transita para a fase. Nesse caso, os agentes de todas as populações são reunidos em um único array, ordenados, e os melhores agentes são copiados para o array "agentsPhase2".
• Caso contrário, para cada agente na população atual, são realizadas as operações de mutação adaptativa, atualização de posição e cópia das coordenadas.

3. Fase 2:

• Na fase 2, para cada agente no array "agentsPhase2", também são realizadas as operações de mutação adaptativa, atualização de posição e cópia das coordenadas

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Moving ()
{
  epochNow++;

  //Фаза 1----------------------------------------------------------------------
  if (!isPhase2)
  {
    if (popEpochs >= epochsForPop)
    {
      popEpochs = 0;
      currPop++;

      fB = -DBL_MAX;
    }

    if (currPop >= numPop)
    {
      isPhase2 = true;

      int cnt = 0;
      for (int i = 0; i < numPop; i++)
      {
        for (int j = 0; j < popSize; j++)
        {
          allAgentsForSortPhase2 [cnt] = pop [i].agent [j];
          cnt++;
        }
      }

      u.Sorting (allAgentsForSortPhase2, allAgentsTemp, popSize * numPop);

      for (int j = 0; j < popSize; j++) agentsPhase2 [j] = allAgentsForSortPhase2 [j];
    }
    else
    {
      for (int i = 1; i < popSize; i++)
      {
        AdaptiveMutation (pop [currPop].agent [i]);
        UpdatePosition   (i, pop [currPop].agent);

        ArrayCopy (a [i].c, pop [currPop].agent [i].c);
      }

      popEpochs++;
      return;
    }
  }

  //Фаза 2----------------------------------------------------------------------
  for (int i = 1; i < popSize; i++)
  {
    AdaptiveMutation (agentsPhase2 [i]);
    UpdatePosition   (i, agentsPhase2);

    ArrayCopy (a [i].c, agentsPhase2 [i].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" da classe "C_AO_ASBO" representa o processo de revisão dos resultados da otimização, incluindo a atualização do valor de "fB" e a otimização dos resultados para cada fase do algoritmo ASBO. Componentes principais do código:

1. Variáveis e inicialização:

• int ind = -1; — variável para armazenar o índice do elemento com o melhor valor da função "f".
• fB — variável que representa o melhor valor da função "f" encontrado na etapa atual.

2. Busca pelo melhor agente:

• No primeiro laço "for", todos os agentes (objetos que representam soluções) no array "a" com tamanho "popSize" são iterados.
• Se o valor da função "f" do agente atual for maior que o valor atual de "fB", então "fB" e o índice "ind" são atualizados.

3. Cópia de dados:

• Se um agente com o melhor valor de função foi encontrado ("ind != -1"), o array "cB" (que representa os parâmetros da melhor solução) é atualizado com os valores do array "a".

4. Fase 1:

• Se a população atual "currPop" for menor que o número total de populações "numPop", os valores da função "f" dos agentes na população atual são atualizados.
• Se o valor de "f" do agente no array "a" for maior que o seu melhor valor "fBest", "fBest" é atualizado, e as características correspondentes são copiadas para "cBest".
• Em seguida, os agentes da população atual são ordenados utilizando o método "u.Sorting".

5. Fase 2:

• Se a população atual for igual ou maior que o número total de populações, ações similares são realizadas no array "agentsPhase2".
• Os valores da função "f" são atualizados, os melhores valores "fBest" são verificados e atualizados, e a ordenação é realizada.

Lógica geral do método:

• O método "Revision" realiza dois passos principais: identificar o melhor agente e atualizar os dados dos agentes dependendo da fase atual (fase 1 ou fase 2).
• O objetivo principal é monitorar e atualizar as melhores soluções encontradas durante o processo de otimização, além de manter os agentes ordenados para uso posterior.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  //фаза 1
  if (currPop < numPop)
  {
    for (int i = 0; i < popSize; i++)
    {
      pop [currPop].agent [i].f = a [i].f;

      if (a [i].f > pop [currPop].agent [i].fBest)
      {
        pop [currPop].agent [i].fBest = a [i].f;
        ArrayCopy (pop [currPop].agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (pop [currPop].agent, agentsTemp, popSize);
  }
  //фаза 2
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      agentsPhase2 [i].f = a [i].f;

      if (a [i].f > agentsPhase2 [i].fBest)
      {
        agentsPhase2 [i].fBest = a [i].f;
        ArrayCopy (agentsPhase2 [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (agentsPhase2, agentsTemp, popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "AdaptiveMutation" da classe "C_AO_ASBO" representa o processo de mutação adaptativa dos coeficientes do agente "ag" dentro do algoritmo ASBO, incluindo a aplicação da distribuição gaussiana e o cálculo de novos valores para os coeficientes com base em variáveis aleatórias. Essas são as etapas básicas do método "AdaptiveMutation":

1. Mutação adaptativa dos coeficientes:

• Os coeficientes "Cg", "Cs" e "Cn" do agente "ag" são mutados utilizando a distribuição gaussiana.
• Para cada coeficiente, um novo valor é calculado utilizando a função exponencial da soma de duas variáveis aleatórias gaussianas, cada uma multiplicada pelos respectivos coeficientes "tau_prime" e "tau".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::AdaptiveMutation (S_ASBO_Agent &ag)
{
  ag.Cg *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cs *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cn *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
}
//——————————————————————————————————————————————————————————————————————————————

O método "UpdatePosition" da classe "C_AO_ASBO" representa o processo de atualização da posição de um agente dentro do algoritmo ASBO, envolvendo o cálculo da mudança na posição com base em vários coeficientes e a atualização da posição dentro dos intervalos definidos. Os passos principais no método "UpdatePosition" são:

1. Cálculo da mudança de posição:

• A mudança na posição do agente "ag[ind]" é calculada em cada dimensão "j" usando diferentes coeficientes e valores, como "cB", "cBest", "deltaX", "rangeMin", "rangeMax" e "rangeStep".

2. Atualização da posição do agente:

• Para cada dimensão "j", um novo valor de posição para o agente "ag[ind].c[j]" é calculado adicionando a mudança "deltaX[j]" e corrigindo o valor para mantê-lo dentro dos intervalos definidos.

A seção comentada do código apresenta três versões do cálculo de posição: A versão "1)" reflete a abordagem original dos autores. A versão "3)" é uma modificação que substitui os coeficientes "Cg", "Cs" e "Cn" por valores de uma distribuição normal. A versão "2)", segundo o autor, apresentou os melhores resultados entre as três abordagens testadas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::UpdatePosition (int ind, S_ASBO_Agent &ag [])
{
  double deltaX [];
  ArrayResize (deltaX, coords);

  FindNeighborCenter (ind, ag, deltaX);

  for (int j = 0; j < coords; j++)
  {
    /*
    //1)
    deltaX [j] = ag [ind].Cg * u.RNDfromCI (-1, 1) * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * u.RNDfromCI (-1, 1) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * u.RNDfromCI (-1, 1) * (deltaX         [j] - ag [ind].c [j]);
    */
    
    //2)
    deltaX [j] = ag [ind].Cg * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * (deltaX         [j] - ag [ind].c [j]);


    /*
    //3)
    deltaX [j] = u.GaussDistribution (0, -1, 1, 8) * (cB             [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (deltaX         [j] - ag [ind].c [j]);
    */

    ag [ind].c [j] += deltaX [j];
    ag [ind].c [j] = u.SeInDiSp (ag [ind].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados dos testes

Os testes do algoritmo ASBO revelaram diversas características interessantes que o tornam único. Uma das principais é sua excepcional capacidade de escalabilidade, que permite que o algoritmo lide eficientemente com problemas de alta dimensionalidade. Os resultados foram particularmente notáveis nos testes realizados com as funções Forest e Megacity, envolvendo mil parâmetros. Nessas situações, o ASBO apresentou desempenhos impressionantes, comparáveis aos dos principais algoritmos nas tabelas de classificação. Tais conquistas destacam não apenas a eficiência do algoritmo, mas também seu potencial para aplicações em diversas áreas que demandam otimização de alta qualidade.

ASBO|Adaptive Social Behavior Optimization|50.0|5.0|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7633114189858913
25 Hilly's; Func runs: 10000; result: 0.4925279738997658
500 Hilly's; Func runs: 10000; result: 0.3261850685263711
=============================
5 Forest's; Func runs: 10000; result: 0.7954558091769679
25 Forest's; Func runs: 10000; result: 0.4003462752027551
500 Forest's; Func runs: 10000; result: 0.26096981234192485
=============================
5 Megacity's; Func runs: 10000; result: 0.2646153846153846
25 Megacity's; Func runs: 10000; result: 0.1716923076923077
500 Megacity's; Func runs: 10000; result: 0.18200000000000044
=============================
All score: 3.65710 (40.63%)

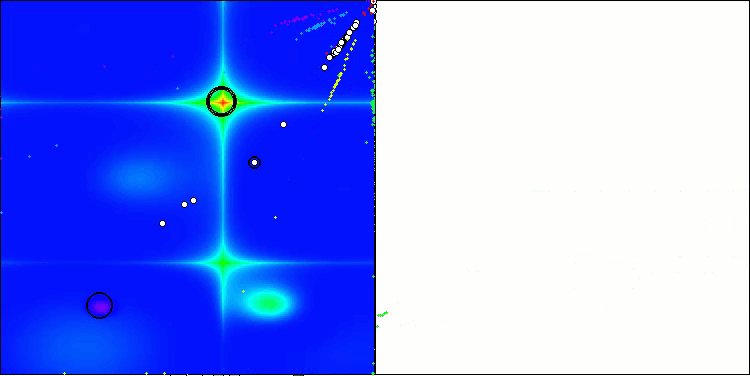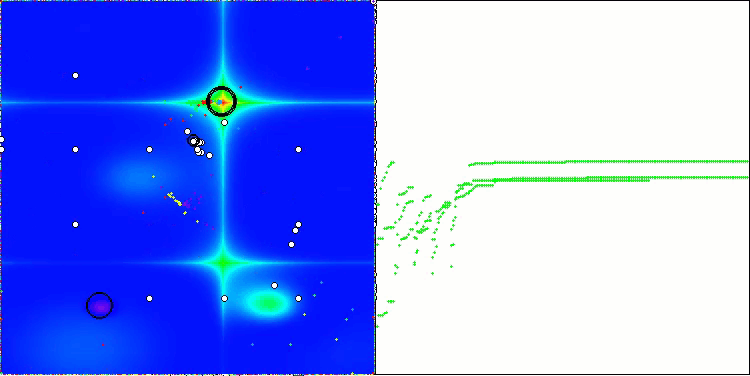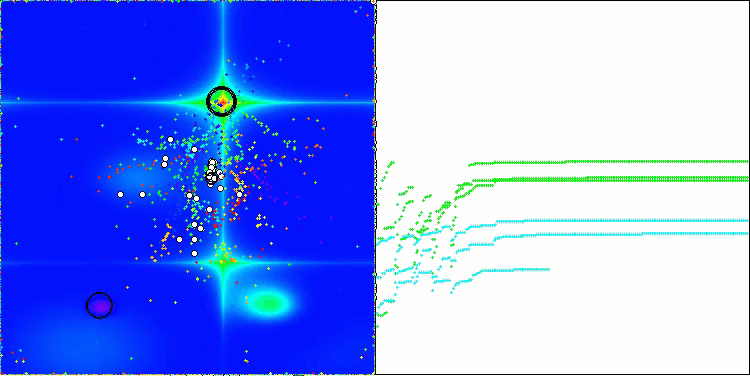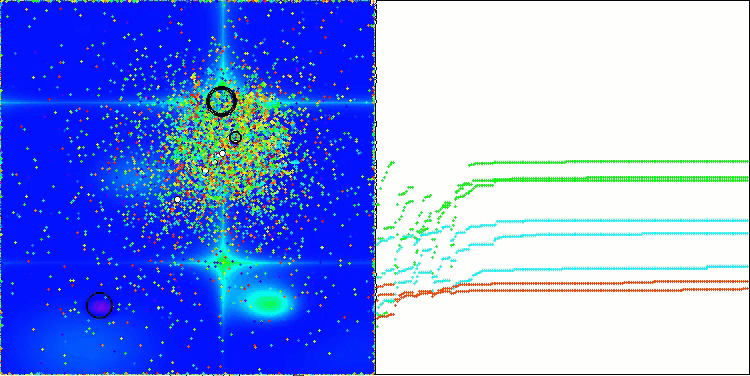
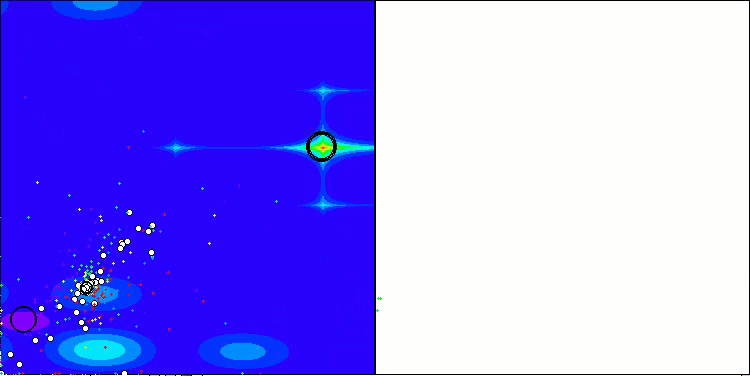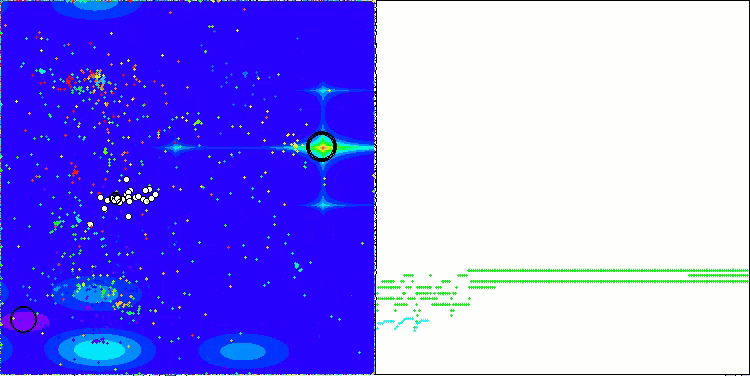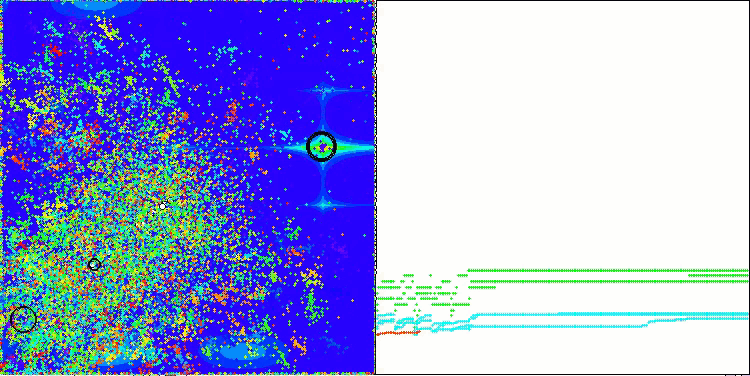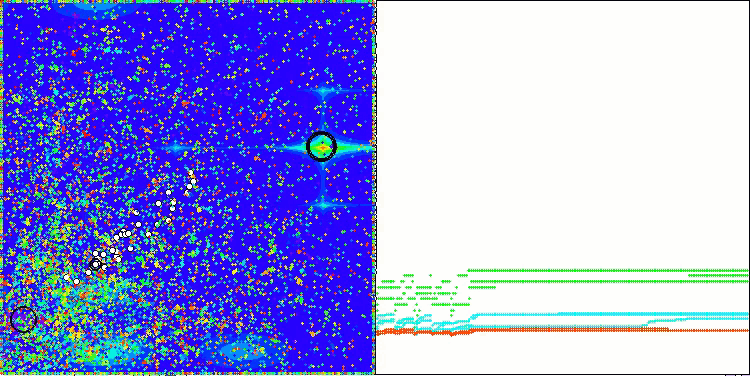
A visualização dos resultados do algoritmo ASBO revela diversas características interessantes que merecem atenção. Desde o início de sua execução, é evidente sua capacidade de destacar áreas significativas da solução, demonstrando sua eficiência na exploração do espaço de parâmetros.

O gráfico de convergência mostra rupturas características na linha, causadas pelo trabalho sequencial de várias populações durante a primeira fase. Essas rupturas indicam que cada população contribui para o processo de otimização, explorando diferentes regiões do espaço. Na segunda fase, no entanto, o gráfico adota uma forma contínua, representando a unificação das melhores soluções de todas as populações, reunidas após a primeira fase. Essa unificação permite que o algoritmo se concentre no aprimoramento de áreas promissoras.

Assim, a visualização não apenas ilustra a dinâmica do algoritmo, mas também destaca seus mecanismos adaptativos e cooperativos.

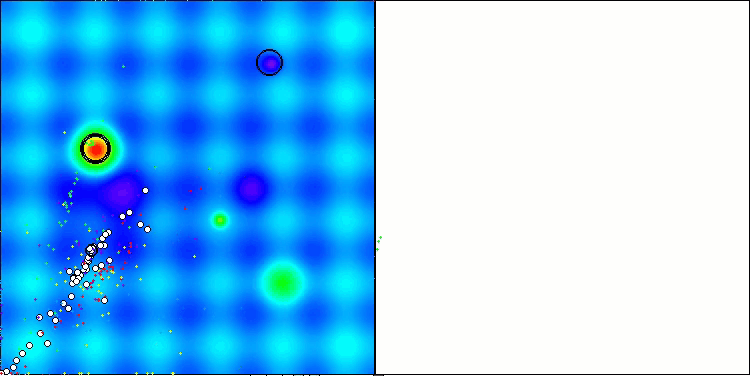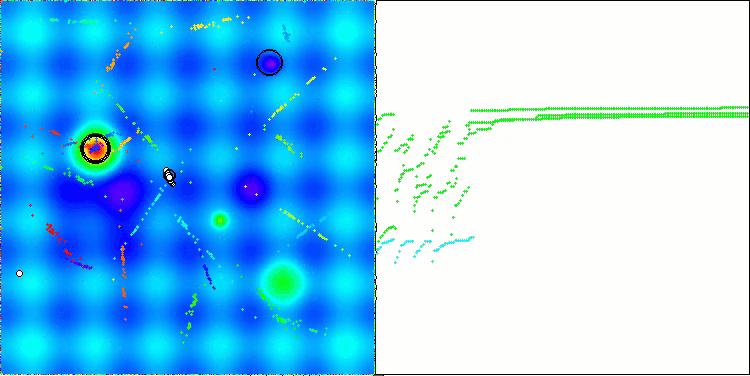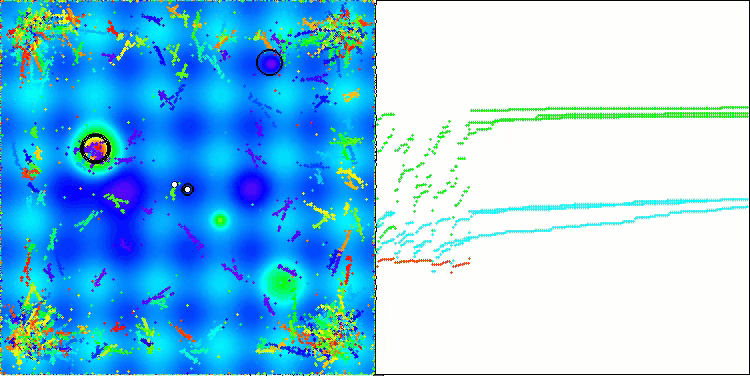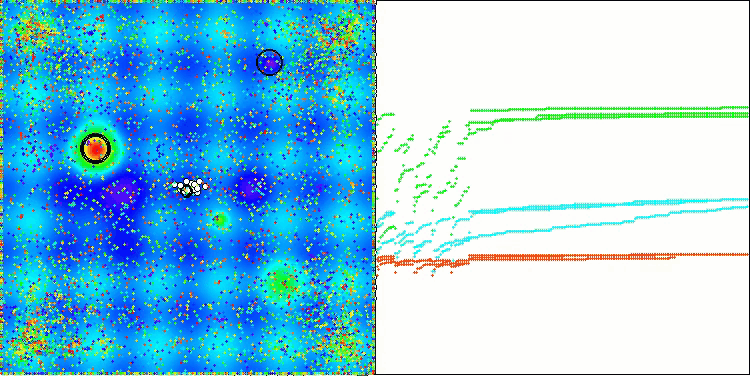
  ASBO na função de teste Hilly.

ASBO na função de teste Forest.

ASBO na função de teste Megacity.

De acordo com os resultados das pesquisas realizadas, o algoritmo ocupa uma posição sólida na parte intermediária da tabela de classificações.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
4	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
5	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
6	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
7	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
8	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
9	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
10	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
11	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
12	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
13	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
14	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
15	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
16	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
17	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
18	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
19	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
20	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
21	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
22	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
23	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
24	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
25	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
26	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
27	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
28	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
29	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
30	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
31	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
32	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
33	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
34	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
35	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
36	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
37	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
38	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
39	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
40	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
41	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
42	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
43	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Considerações finais

O algoritmo se destaca por sua originalidade e comportamento fora do padrão, tornando sua visualização única e diferente dos métodos conhecidos anteriormente. Isso atrai atenção e desperta interesse em seus mecanismos internos.

É importante salientar que, apesar de apresentar resultados medianos e boa convergência em problemas de baixa dimensionalidade, o algoritmo demonstra seu verdadeiro potencial ao lidar com problemas mais complexos e em condições de espaços de busca amplos. Ele utiliza múltiplas populações que trabalham de forma sequencial na primeira fase, levantando a questão da viabilidade de dividir um número limitado de épocas em cálculos preliminares para populações independentes. Os experimentos realizados utilizando apenas uma população na primeira fase apresentaram resultados significativamente piores, confirmando a utilidade do levantamento preliminar de informações sobre o espaço de busca. Essa abordagem permite que o algoritmo utilize de forma mais eficaz os indivíduos líderes — as soluções mais promissoras — na segunda fase de busca.

Além disso, o algoritmo tem um enorme potencial para futuras investigações. Estou convencido de que suas capacidades ainda não foram completamente exploradas, sendo necessários mais experimentos e análises para entender como aproveitar ao máximo suas vantagens algorítmicas.

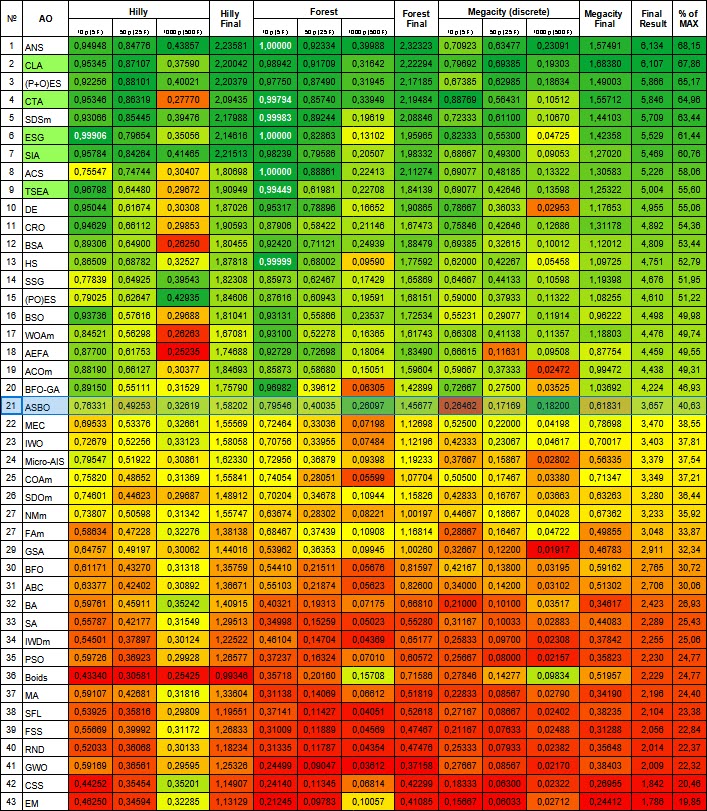
Figura 2. Graduação de cores dos algoritmos para os respectivos testes. Resultados maiores ou iguais a 0,99 estão destacados em branco. Os nomes destacados em verde correspondem aos algoritmos desenvolvidos pelos autores.

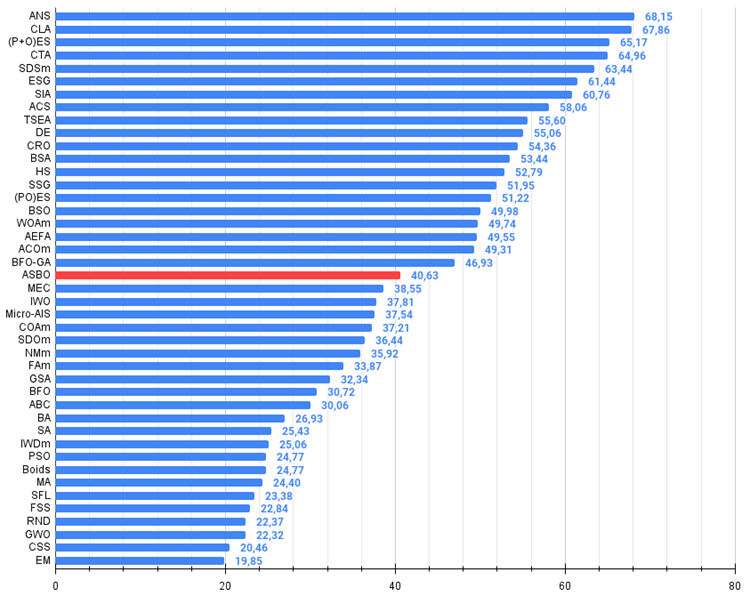
Figura 3. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,

onde 100 é o resultado teórico máximo possível; o arquivo inclui um script para calcular a tabela de classificações).

Prós e contras do algoritmo de comportamento social adaptativo (ASBO):

Prós:

1. Poucos parâmetros externos.
   
2. Resultados satisfatórios em problemas complexos de alta dimensionalidade.
   

Contras:

1. Convergência limitada em problemas de baixa dimensionalidade.
   

O artigo é acompanhado de um arquivo contendo as versões atualizadas dos códigos dos algoritmos. O autor não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, já que muitos deles foram modificados para aprimorar suas capacidades de busca. As conclusões e interpretações apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/pt/code/49355

Conclusão preliminar do trabalho realizado

Analisamos mais de quarenta algoritmos de otimização durante nossas pesquisas, cada um apresentando uma abordagem única para resolver problemas complexos. Esse processo não apenas foi fascinante, mas também extremamente educativo, revelando a riqueza e a diversidade dos métodos na área de otimização.

Reconstrução e modificação de algoritmos. Para a grande maioria dos algoritmos analisados, os códigos-fonte não estavam disponíveis publicamente. Por isso, optei por uma abordagem criativa: reconstruí os códigos exclusivamente com base nas descrições textuais dos autores em diversas publicações. Essa abordagem não apenas proporcionou uma compreensão mais profunda dos princípios de funcionamento de cada algoritmo, mas também permitiu adaptá-los às nossas necessidades específicas.
Os poucos algoritmos com código-fonte aberto não estavam prontos para resolver problemas de otimização de maneira genérica. Por isso, foram necessárias modificações substanciais para torná-los universais e facilmente aplicáveis a uma ampla variedade de problemas.

Inovações e melhorias. Alguns algoritmos, como o ACO (colônias de formigas, voltados para resolver problemas em grafos), originalmente não foram projetados por seus autores para trabalhar em espaços contínuos e exigiram modificações para ampliar seu campo de aplicação. Em outros algoritmos, melhorias foram incorporadas às estratégias de busca, aumentando sua eficiência. Essas versões modificadas receberam o sufixo "m" no nome, refletindo sua evolução. Além disso, examinamos em detalhes diversas técnicas de processamento de populações, geração de novas soluções e métodos de seleção.

Como demonstração de novas ideias e abordagens para otimização, foram desenvolvidos mais de cinco novos algoritmos autorais, apresentados exclusivamente nos artigos.

Aplicação e estudos futuros. Vale ressaltar que qualquer um dos algoritmos apresentados pode ser utilizado para resolver problemas de otimização sem a necessidade de modificações ou ajustes adicionais. Isso os torna acessíveis e convenientes para uma ampla gama de pesquisadores e profissionais.

Para aqueles que buscam os melhores resultados em problemas específicos, são fornecidas tabelas comparativas e histogramas que permitem explorar as propriedades individuais de cada algoritmo. Isso possibilita ajustes mais detalhados e otimizações adaptadas às demandas específicas.

Por fim, tanto o uso de algoritmos prontos quanto seu estudo aprofundado e adaptação são igualmente válidos. Compreender os detalhes e as técnicas das estratégias de busca de diferentes algoritmos oferece aos pesquisadores novas possibilidades para alcançar resultados extraordinários.

Desejo sinceramente a todos os leitores sucesso na busca pelas melhores soluções e na realização de seus objetivos. Que sua jornada no mundo da otimização e do trading algorítmico seja emocionante e frutífera!