
Otimização em estilo Battle Royale — Battle Royale Optimizer (BRO)
Conteúdo
Introdução
Na otimização meta-heurística, onde os algoritmos frequentemente se inspiram em processos naturais, fenômenos físicos e mecanismos evolutivos, surgiu uma nova e surpreendente fonte de inspiração, os jogos eletrônicos. O Battle Royale Optimizer (BRO), desenvolvido por Taymaz Rahkar Farshi, representa um algoritmo de otimização inovador baseado na mecânica dos populares jogos do gênero "Battle Royale", como o PlayerUnknown's Battlegrounds (PUBG).
O algoritmo BRO inaugura uma nova categoria de métodos de otimização — os "game-based" (baseados em jogos) — complementando o já consolidado trio de abordagens de otimização, que inclui os algoritmos evolucionários, os algoritmos de inteligência de enxame e os algoritmos baseados em fenômenos físicos, todos pertencentes ao vasto grupo dos algoritmos populacionais de otimização. Diferente dos algoritmos de inteligência de enxame, onde os agentes cooperam para alcançar um objetivo comum, no BRO os indivíduos competem entre si, buscando sobreviver e ocupar a melhor posição no espaço de busca.
A principal característica do BRO é o seu mecanismo singular de competição e “dano” entre soluções. Cada solução é comparada com seu vizinho mais próximo, e a que perde recebe um “dano”, enquanto a vencedora recomeça do zero. As soluções que acumulam dano excessivo são removidas da população e substituídas por novas soluções geradas aleatoriamente, de forma análoga à eliminação de jogadores no PUBG após sofrerem dano crítico. Esse processo garante o mecanismo de exploração do espaço de busca.
Implementação do algoritmo
O algoritmo Battle Royale Optimizer (BRO) pode ser visualizado como um mundo virtual, onde vários jogadores são lançados em um campo de batalha e apenas um deve permanecer vivo, este é o princípio essencial do jogo que serviu de inspiração. Agora, vamos transferir esse conceito para a resolução de problemas de otimização.
No início da execução do algoritmo, é criada uma população de soluções distribuídas aleatoriamente pelo espaço de busca. Cada solução representa um tipo de “jogador” que possui uma posição específica e uma qualidade associada (fitness) a essa posição. Em seguida, tem início o ciclo principal de competições, no qual cada solução é comparada com seu vizinho mais próximo, de forma semelhante a como os jogadores em uma batalha se enfrentam diretamente.
Quando duas soluções “se encontram”, elas são comparadas de acordo com sua qualidade. A melhor solução é declarada vencedora e recebe zero de dano, enquanto a pior torna-se a perdedora e acumula um ponto de dano. Esse contador de dano é um elemento fundamental do algoritmo. A solução perdedora não apenas sofre dano, mas também tenta melhorar sua posição, movendo-se na direção da melhor solução conhecida na população. Esse movimento simula o instinto de sobrevivência, buscando um local mais seguro e vantajoso.
Se uma solução acumular dano em excesso (ultrapassando um limite predefinido), ela é “eliminada do jogo”, ou seja, removida da população e substituída por uma nova solução gerada aleatoriamente. Isso se assemelha à eliminação de um jogador em uma partida battle royale e à entrada de um novo competidor no próximo confronto. Esse mecanismo garante a renovação constante da população e mantém a diversidade entre as soluções.
Periodicamente, o algoritmo realiza o estreitamento do espaço de busca, um análogo à zona de jogo que se reduz nas partidas battle royale, forçando os jogadores a se aproximarem. As fronteiras do espaço de busca se contraem em torno da melhor solução encontrada, o que leva a população a se concentrar nas regiões mais promissoras.
Graças a essa abordagem, o algoritmo BRO mantém um equilíbrio entre a exploração de novas áreas e o aproveitamento das soluções já descobertas. As soluções perdedoras se movem em direção às melhores, preservando a tendência de melhoria, enquanto as que são completamente eliminadas são substituídas por novas, proporcionando uma nova perspectiva sobre o espaço de busca. Ao mesmo tempo, o estreitamento periódico das fronteiras intensifica a busca local ao redor das soluções mais promissoras.
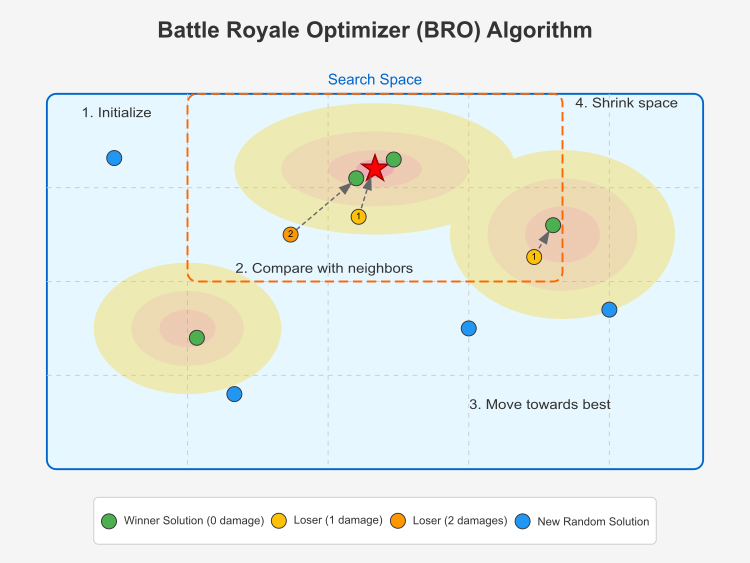
Figura 1. Ilustração do funcionamento do algoritmo BRO.
Esta ilustração mostra os principais componentes do funcionamento do algoritmo Battle Royale Optimizer (BRO). O espaço de busca é representado como uma área 2D com contornos que simbolizam a função de otimização (as regiões mais brilhantes representam as melhores soluções). A melhor solução global é marcada por uma estrela vermelha no centro do pico mais alto. As soluções vencedoras são marcadas por pontos verdes — representam soluções com zero dano (aquelas que venceram suas comparações com os vizinhos). As soluções perdedoras são indicadas por pontos amarelos (com 1 dano) e laranja (com 2 danos). As novas soluções geradas aleatoriamente são mostradas como pontos azuis, surgindo quando uma solução acumula dano em excesso. As soluções perdedoras movem-se em direção à melhor solução (representadas por setas tracejadas). O estreitamento do espaço de busca é ilustrado por uma moldura tracejada laranja, centralizada na melhor solução.
As etapas fundamentais do algoritmo são: inicialização, comparação com os vizinhos, movimento em direção à melhor solução e estreitamento do espaço de busca.As soluções no algoritmo BRO competem entre si, e as perdedoras recebem “dano”. As soluções que acumulam dano em excesso são substituídas por novas soluções geradas aleatoriamente. Agora que o princípio de funcionamento do algoritmo está claro, podemos passar à escrita do pseudocódigo.
Inicialização:
- Criar uma população de soluções de tamanho popSize
- Para cada solução, definir o contador de dano como 0
- Definir o limite máximo de dano maxDamage
- Definir o número de épocas epochs
- Calcular o valor inicial de delta para o estreitamento periódico do espaço de busca
Algoritmo principal:
- Criação da população inicial:
- Para cada solução na população:
- Gerar coordenadas aleatórias em um determinado espaço de busca
- Para cada solução na população:
- Para cada época, executar:
- Atualizar a melhor solução global, se for encontrada uma melhor
- Realização de “disputas” entre decisões:
- Para cada solução na população:
- Encontrar o vizinho mais próximo (a solução com a menor distância)
- Comparar a qualidade da solução atual com a de seu vizinho:
- Se a solução atual for melhor:
- Zerar o contador de dano da solução atual
- Aumentar o contador de dano do vizinho
- A solução perdedora (o vizinho) move-se em direção à melhor solução
- Caso contrário:
- Aumentar o contador de dano da solução atual
- Zerar o contador de dano do vizinho
- A solução perdedora (a atual) move-se em direção à melhor solução
- Se a solução atual for melhor:
- Para cada solução na população:
- Tratamento das soluções excessivamente danificadas:
- Para cada solução na população:
- Se o contador de dano ≥ maxDamage:
- Zerar o contador de dano
- Substituir a solução por uma nova gerada aleatoriamente
- Se o contador de dano ≥ maxDamage:
- Para cada solução na população:
- Estreitamento periódico do espaço de busca:
- Se o número da época atual for divisível por delta:
- Calcular o desvio padrão das coordenadas de toda a população
- Reduzir o espaço de busca em torno da melhor solução
- Atualizar o valor de delta
- Se o número da época atual for divisível por delta:
- Retornar a melhor solução encontrada
O algoritmo utiliza as seguintes fórmulas:
- Cálculo do valor inicial de delta para o estreitamento do espaço de busca: delta = ⌊epochs / log₁₀(epochs)⌋
- Cálculo da distância euclidiana entre soluções: distance = √(∑(a[idx1][c] - a[idx2][c])²)
- Movimento da solução perdedora em direção à melhor solução global: a[i][c] = a[i][c] + r × (cB[c] - a[i][c])
- Cálculo do valor médio para cada coordenada: mean[c] = (∑a[i][c]) / popSize
- Cálculo do desvio padrão para cada coordenada: sdValues[c] = √(∑(a[i][c] - mean[c])² / popSize)
- Fórmulas para o estreitamento do espaço de busca: newMin[c] = cB[c] - sdValues[c] newMax[c] = cB[c] + sdValues[c]
- Atualização do parâmetro delta após o estreitamento do espaço de busca: delta = delta + ⌊delta / 2⌉
Para o estreitamento periódico do espaço de busca, o autor propõe a seguinte fórmula: Δ (delta) = maxEpochs / log₁₀(maxEpochs), cujo gráfico é apresentado abaixo:
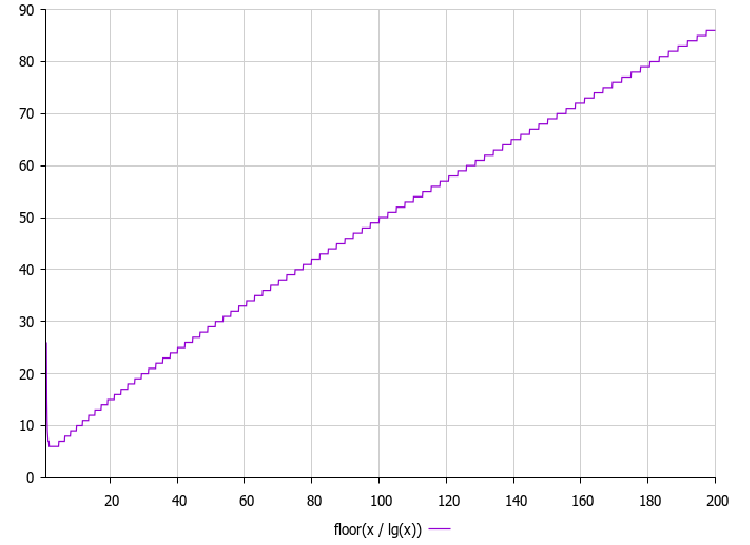
Figura 2. Gráfico da função de dependência do parâmetro delta em relação ao número de épocas
O gráfico da função delta = epochs/log₁₀(epochs) tem grande importância no funcionamento do algoritmo BRO, pois determina a quantidade de iterações após as quais ocorrerá o estreitamento do espaço de busca. Como se pode observar no gráfico, o valor de delta aumenta com o número de épocas, mas não tão rapidamente quanto as próprias épocas, devido à divisão pelo logaritmo. Isso cria uma dependência não linear, que oferece as seguintes vantagens: nas etapas iniciais da otimização (quando o número de épocas é pequeno), o estreitamento ocorre com maior frequência, ajudando o algoritmo a se concentrar mais rapidamente nas regiões promissoras, já nas etapas posteriores (com número elevado de épocas), o estreitamento ocorre com menor frequência, permitindo uma exploração mais detalhada das regiões já identificadas como favoráveis.
Durante meus experimentos, modifiquei a fórmula de dependência do parâmetro delta, aplicando o logaritmo duas vezes, e o algoritmo apresentou desempenho superior.
// Вычисление начального delta для сужения пространства поиска delta = (int)MathFloor(epochs / MathLog(MathLog(epochs)));
Vamos agora à implementação do código, criando a classe "C_AO_BRO", que herda da classe base "C_AO", ou seja, herda todos os membros públicos e protegidos da classe "C_AO" e pode redefinir seu comportamento. Essa classe representará a implementação do algoritmo de otimização baseado no conceito de "Battle Royale".
1. Membros públicos da classe:
- popSize — define o tamanho da população.
- maxDamage — define o limite máximo de dano, ou seja, quantas “derrotas” uma solução pode sofrer antes de ser eliminada.
- SetParams() — método que atualiza os valores de "popSize" e "maxDamage" com base nos valores armazenados no array "params", permitindo ajustar os parâmetros do algoritmo durante a execução.
- Init() — método de inicialização do algoritmo. Recebe os seguintes parâmetros:
- rangeMinP[] — valores mínimos do intervalo de busca para cada variável.
- rangeMaxP[] — valores máximos do intervalo de busca.
- rangeStepP[] — passo de busca para cada variável.
- epochsP — número de épocas (iterações) do algoritmo. O valor padrão é 0.
- Moving() — método que implementa a lógica principal de movimento ou atualização das soluções no espaço de busca.
- Revision() — método que implementa a lógica de revisão das soluções atuais, realizando a avaliação dos “danos” recebidos por cada solução.
- maxDamage — membro público que armazena o limite máximo de dano.
2. Campos privados da classe:
- delta — intervalo para o estreitamento (shrink) do espaço de busca. É usado para adaptar o tamanho do passo de busca durante o processo de otimização.
- damages[] — array que armazena a quantidade de “danos” recebidos por cada solução na população.
- epoch — época atual (número da iteração) do algoritmo.
- epochs — número máximo de épocas (iterações) do algoritmo.
3. Métodos auxiliares:
- FindNearestNeighbor() — encontra o vizinho mais próximo de uma solução com base em seu índice, sendo usado para a interação entre soluções.
- CalculateDistance() — calcula a distância entre duas soluções identificadas por seus respectivos índices.
- CalculateStandardDeviations() — calcula o desvio padrão dos valores das soluções da população, usado para avaliar a diversidade da população e adaptar os parâmetros de busca.
- ShrinkSearchSpace() — método que realiza o estreitamento do espaço de busca. Trata-se de uma técnica padrão para auxiliar a convergência do algoritmo em direção à solução ótima.
Visão geral:
C_AO_BRO representa a classe do algoritmo de otimização Battle Royale, cuja ideia central, em resumo, é a seguinte:
- Inicialização: cria-se uma população de soluções aleatórias dentro de um espaço de busca definido.
- Avaliação: cada solução é avaliada por meio de uma função objetivo (fitness function).
- Battle Royale: as soluções “batalham” entre si (são comparadas com base nos valores da função objetivo).
- Dano: algumas soluções recebem “danos”, de acordo com os resultados das “batalhas”.
- Eliminação: soluções que acumulam um número de “damage” superior a “maxDamage” são removidas da população.
- Reprodução/substituição: as soluções removidas são substituídas por novas soluções aleatórias.
- Estreitamento do espaço de busca: o espaço de busca é reduzido para concentrar a busca nas regiões mais promissoras.
- Repetição: os passos 2 a 7 se repetem durante o número de épocas definido.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BRO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BRO () { } C_AO_BRO () { ao_name = "BRO"; ao_desc = "Battle Royale Optimizer"; ao_link = "https://www.mql5.com/ru/articles/17688"; popSize = 100; // размер популяции maxDamage = 3; // максимальный порог повреждений ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "maxDamage"; params [1].val = maxDamage; } void SetParams () { popSize = (int)params [0].val; maxDamage = (int)params [1].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int maxDamage; // максимальный порог повреждений private: //------------------------------------------------------------------- int delta; // интервал для сужения пространства поиска int damages []; // количество повреждений для каждого решения int epoch; // текущая эпоха int epochs; // максимальное количество эпох // Вспомогательные методы int FindNearestNeighbor (int index); double CalculateDistance (int idx1, int idx2); void CalculateStandardDeviations (double &sdValues []); void ShrinkSearchSpace (); }; //——————————————————————————————————————————————————————————————————————————————
O método Init() inicializa o algoritmo BRO, chamando StandardInit() para realizar a inicialização padrão, utilizando os intervalos e passos de busca fornecidos. Se StandardInit retornar “false”, o método Init() também retorna “false”, indicando uma falha na inicialização. Ele inicializa o array damages, alocando memória para cada solução da população (popSize) e define o número inicial de “danos” de todas as soluções como 0. Define o número total de épocas (epochs) e zera a época atual (epoch = 0).
O valor de delta é calculado com base no número total de épocas, de modo que o espaço de busca seja estreitado gradualmente. Caso delta seja menor ou igual a 0, seu valor é ajustado para 1. Em resumo, esse método prepara o algoritmo para execução, inicializando seus principais parâmetros e estruturas de dados.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BRO::Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Инициализация счетчиков повреждений для каждого решения ArrayResize (damages, popSize); ArrayInitialize (damages, 0); // Установка эпох epochs = epochsP; epoch = 0; // Вычисление начального delta для сужения пространства поиска delta = (int)MathFloor (epochs / MathLog10 (epochs)); if (delta <= 0) delta = 1; return true; } //——————————————————————————————————————————————————————————————————————————————
O método Moving() implementa a lógica de inicialização da população de soluções, em que cada coordenada de cada solução é gerada aleatoriamente entre os limites mínimo e máximo definidos por rangeMin e rangeMax, sendo discretizada de acordo com o passo rangeStep. Esse método garante que a população seja inicializada apenas uma vez.
/—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::Moving () { if (!revision) { // Инициализация популяции случайными решениями for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double coordinate = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; } } //——————————————————————————————————————————————————————————————————————————————
O método Revision() é uma etapa fundamental no algoritmo de otimização BRO. A cada iteração, ele atualiza a melhor solução: se alguma solução da população atual for melhor que a solução global até então, essa melhor solução global é atualizada.
O método compara as soluções com seus vizinhos: para cada solução na população, é identificado o vizinho mais próximo. Em seguida, os valores da função objetivo são comparados. A melhor solução do par é “recompensada” com a redefinição de seu contador de dano, enquanto o contador da solução pior é incrementado. A solução com pior desempenho na comparação é deslocada em direção à melhor solução global.
Em seguida, as soluções “danificadas” são substituídas: se uma solução acumular dano suficiente (atingindo o valor máximo definido por maxDamage), ela é substituída por uma nova solução gerada aleatoriamente. Periodicamente, de acordo com o valor da variável delta, ocorre o estreitamento da área de busca. Esse processo se repete ao longo de várias iterações do algoritmo. Através das comparações com vizinhos, as soluções se deslocam progressivamente em direção a regiões mais vantajosas do espaço de busca.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::Revision () { epoch++; // Обновление глобального наилучшего решения for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Сравнение каждого решения с его ближайшим соседом и обновление счетчиков повреждений for (int i = 0; i < popSize; i++) { int neighbor = FindNearestNeighbor (i); if (neighbor != -1) { if (a [i].f >= a [neighbor].f) { // Решение i побеждает damages [i] = 0; damages [neighbor]++; // Проигравший (сосед) движется к наилучшему решению for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0, 1); a [neighbor].c [c] = a [neighbor].c [c] + r * (cB [c] - a [neighbor].c [c]); a [neighbor].c [c] = u.SeInDiSp (a [neighbor].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } else { // Решение i проигрывает damages [i]++; damages [neighbor] = 0; // Проигравший (i) движется к наилучшему решению for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0, 1); a [i].c [c] = a [i].c [c] + r * (cB [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } // Проверка, достигло ли какое-либо решение максимального повреждения, и его замена for (int i = 0; i < popSize; i++) { if (damages [i] >= maxDamage) { // Сброс счетчика повреждений damages [i] = 0; // Генерация нового случайного решения for (int c = 0; c < coords; c++) { double coordinate = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]); } } } // Периодическое сужение пространства поиска if (epochs > 0 && epoch % delta == 0) { ShrinkSearchSpace (); // Обновление delta delta = delta + (int)MathRound (delta / 2); } } //——————————————————————————————————————————————————————————————————————————————
O método FindNearestNeighbor() encontra o índice do vizinho mais próximo para uma solução de índice index dentro da população. Ele percorre todas as soluções, calcula a distância até cada uma delas (exceto até si própria, representada por index) e retorna o índice da solução com a menor distância. Se não for possível encontrar um vizinho (por exemplo, se existir apenas uma solução na população), o método retorna -1. Em resumo, esse método identifica o vizinho mais próximo para uma solução específica.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_BRO::FindNearestNeighbor (int index) { double minDistance = DBL_MAX; int nearestIndex = -1; for (int i = 0; i < popSize; i++) { if (i == index) continue; double distance = CalculateDistance (index, i); if (distance < minDistance) { minDistance = distance; nearestIndex = i; } } return nearestIndex; } //——————————————————————————————————————————————————————————————————————————————
O método CalculateDistance() calcula a distância euclidiana entre duas soluções da população, identificadas pelos índices idx1 e idx2. O processo inicia com a variável distanceSum igual a zero. Essa variável acumula a soma dos quadrados das diferenças entre as coordenadas correspondentes das duas soluções. O loop for percorre todas as coordenadas das soluções. A cada iteração, calcula a diferença entre as coordenadas de idx1 e idx2. O quadrado dessa diferença é adicionado a distanceSum.
Após a conclusão do loop, o método retorna a raiz quadrada de distanceSum, que representa a distância euclidiana entre as duas soluções. Assim, o método retorna um valor numérico que reflete a “distância” entre duas soluções no espaço de busca. Quanto maior esse valor, mais distantes entre si estão as soluções.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_BRO::CalculateDistance (int idx1, int idx2) { double distanceSum = 0.0; for (int c = 0; c < coords; c++) { double diff = a [idx1].c [c] - a [idx2].c [c]; distanceSum += diff * diff; } return MathSqrt (distanceSum); } //——————————————————————————————————————————————————————————————————————————————
O método CalculateStandardDeviations() calcula o desvio padrão de cada coordenada das soluções da população e armazena os resultados no array sdValues. O tamanho do array de entrada sdValues é ajustado para comportar o valor do desvio padrão de cada uma das coordenadas (coords). Em seguida, o loop percorre cada coordenada das soluções e realiza o cálculo do desvio padrão. O método zera a soma dos quadrados dos desvios para a coordenada atual e também reinicia seu valor médio. O loop soma os valores da coordenada “c” de todas as soluções da população. Em seguida, calcula o valor médio dessa coordenada.
Para calcular a soma dos quadrados dos desvios, o loop percorre todas as soluções da população e computa a soma dos quadrados das diferenças em relação ao valor médio da coordenada atual. Ele calcula a diferença entre o valor da coordenada “c” da solução “i” e o valor médio dessa coordenada. Adiciona o quadrado dessa diferença à soma total dos desvios. O desvio padrão é então obtido como a raiz quadrada da soma dos quadrados dos desvios dividida pelo tamanho da população. O resultado é armazenado no elemento correspondente do array sdValues.
Assim, o método calcula uma medida de dispersão dos valores de cada coordenada das soluções na população e armazena esses valores no array sdValues. O desvio padrão mostra o quanto os valores de uma determinada coordenada variam em torno do valor médio.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::CalculateStandardDeviations (double &sdValues []) { ArrayResize (sdValues, coords); for (int c = 0; c < coords; c++) { double sum = 0.0; double mean = 0.0; // Вычисление среднего for (int i = 0; i < popSize; i++) mean += a [i].c [c]; mean /= popSize; // Вычисление суммы квадратов отклонений for (int i = 0; i < popSize; i++) { double diff = a [i].c [c] - mean; sum += diff * diff; } sdValues [c] = MathSqrt (sum / popSize); } } //——————————————————————————————————————————————————————————————————————————————
O método ShrinkSearchSpace() realiza o estreitamento do espaço de busca com base nos desvios padrão das coordenadas e na posição da melhor solução encontrada. Ele atua como uma forma de concentrar a busca na região mais promissora, onde já foi identificado um bom resultado.
Primeiramente, são calculados os desvios padrão por meio do método CalculateStandardDeviations(), que avalia o grau de variação de cada coordenada das soluções da população e armazena os valores obtidos em sdValues. O cálculo das novas fronteiras do espaço de busca é então realizado: essas fronteiras são centralizadas em torno da melhor solução encontrada, e sua largura é determinada pelo desvio padrão. Se o desvio padrão for pequeno, o espaço de busca é estreitado ao redor da melhor solução. Se for grande, a busca permanece mais ampla. É feita uma verificação de validade para garantir que o novo espaço de busca não ultrapasse os limites originalmente definidos como permitidos.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BRO::ShrinkSearchSpace () { double sdValues []; CalculateStandardDeviations (sdValues); for (int c = 0; c < coords; c++) { // Новые границы центрированы вокруг наилучшего решения с шириной стандартного отклонения double newMin = cB [c] - sdValues [c]; double newMax = cB [c] + sdValues [c]; // Убедитесь, что новые границы находятся в пределах исходных ограничений if (newMin < rangeMin [c]) newMin = rangeMin [c]; if (newMax > rangeMax [c]) newMax = rangeMax [c]; // Обновление границ rangeMin [c] = newMin; rangeMax [c] = newMax; } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Após a realização dos testes, observou-se que o algoritmo apresentou um bom desempenho nas funções Hilly e Forest. No entanto, em relação à função discreta Megacity, os indicadores de convergência mostraram-se significativamente mais fracos.
BRO|Battle Royale Optimizer|50.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7494493002235458
25 Hilly's; Func runs: 10000; result: 0.4983307394255448
500 Hilly's; Func runs: 10000; result: 0.27994639979348446
=============================
5 Forest's; Func runs: 10000; result: 0.6962444245506945
25 Forest's; Func runs: 10000; result: 0.3845619185097379
500 Forest's; Func runs: 10000; result: 0.20427058729050862
=============================
5 Megacity's; Func runs: 10000; result: 0.3815384615384616
25 Megacity's; Func runs: 10000; result: 0.21107692307692308
500 Megacity's; Func runs: 10000; result: 0.10607692307692404
=============================
All score: 3.51150 (39.02%)
Na visualização, é possível observar a dispersão dos valores dos resultados e as capacidades de busca mais fracas na última função discreta, Megacity.
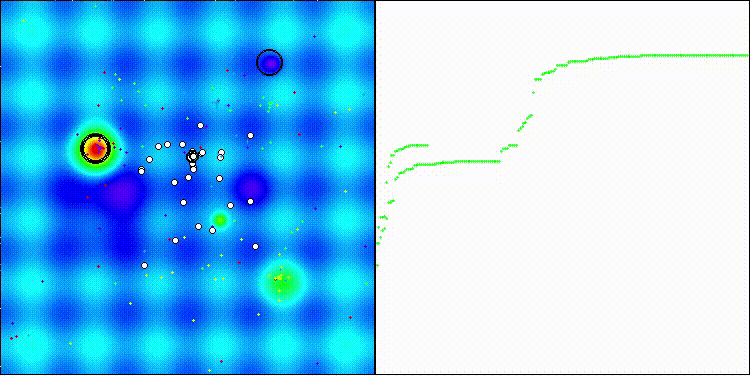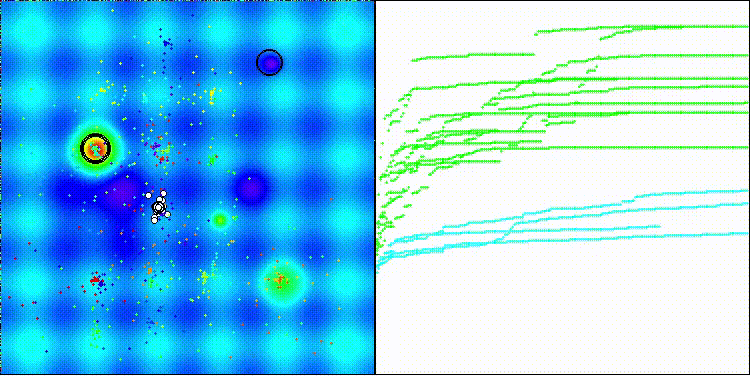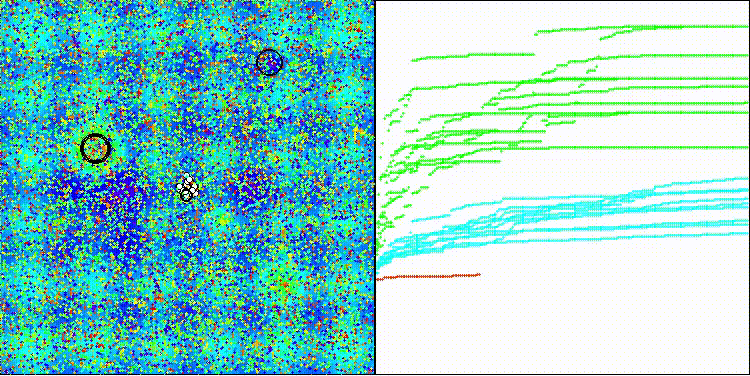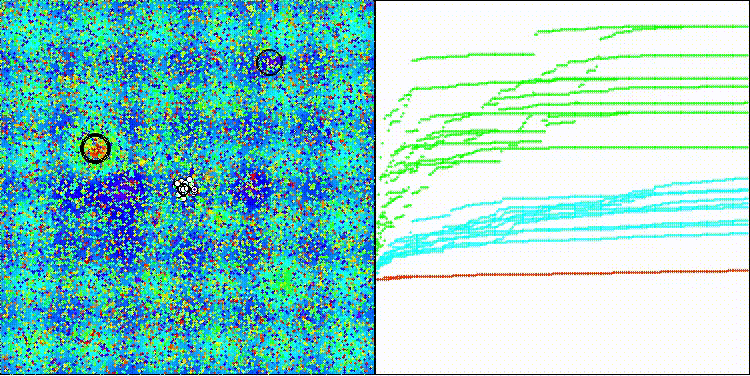
BRO na função de teste Hilly
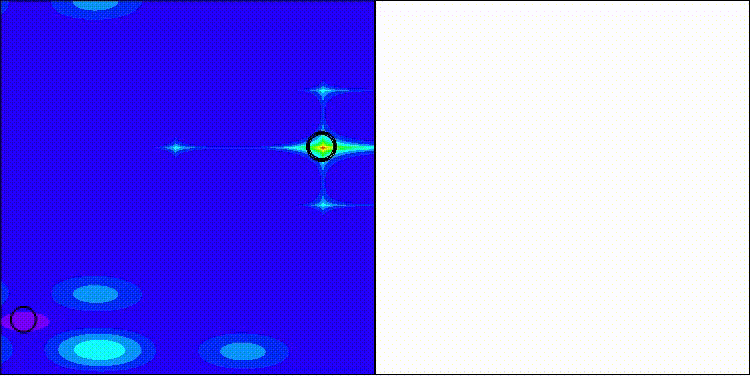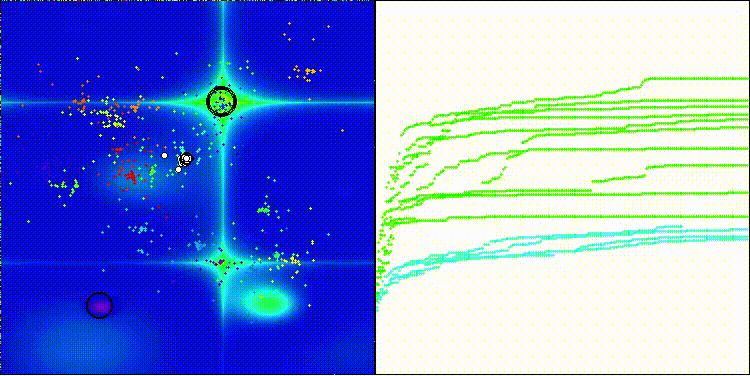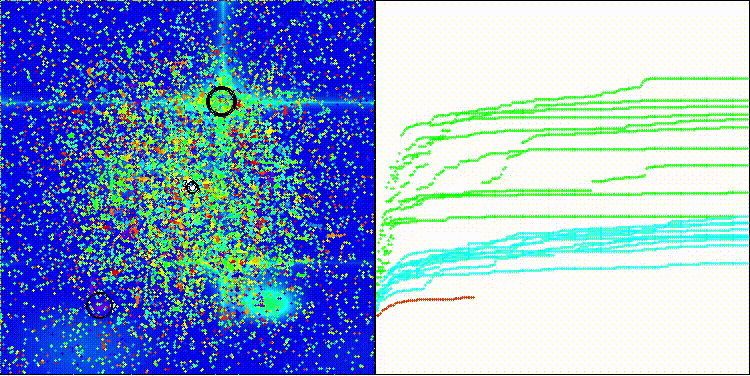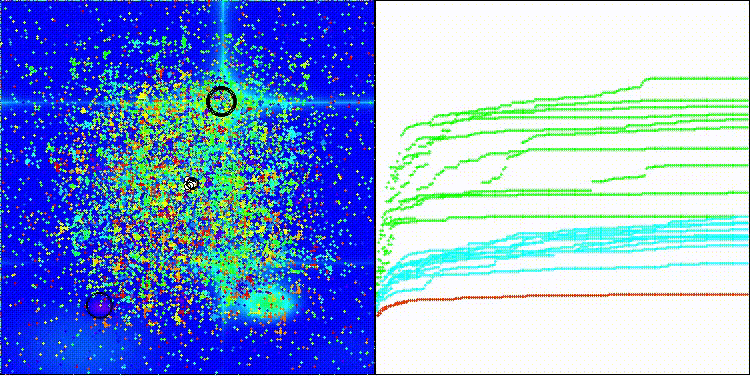
BRO na função de teste Forest
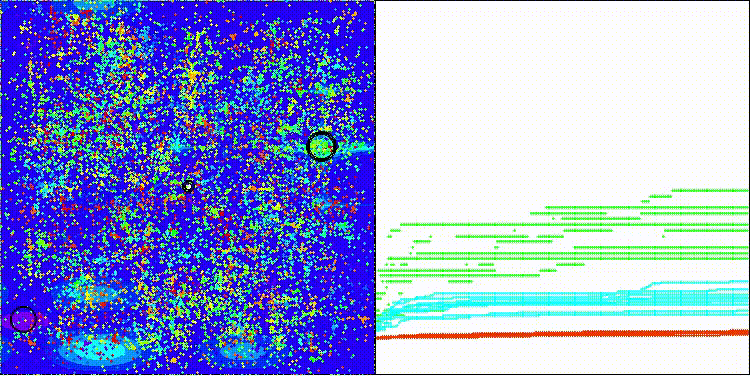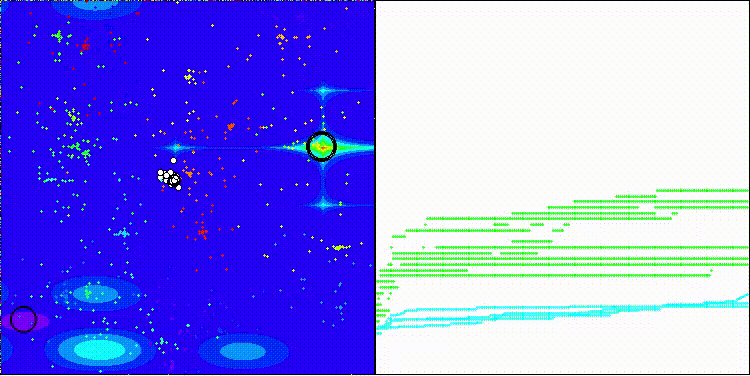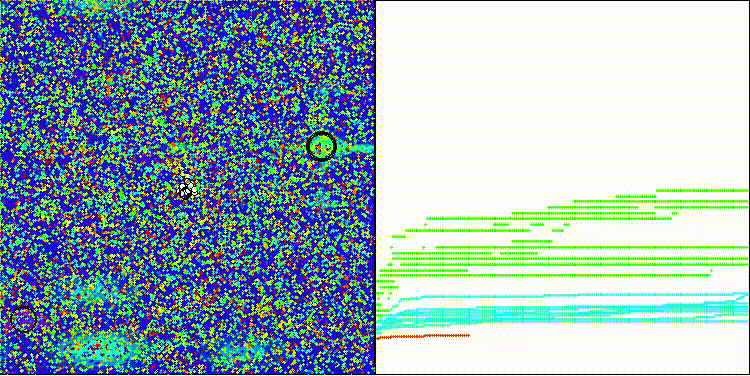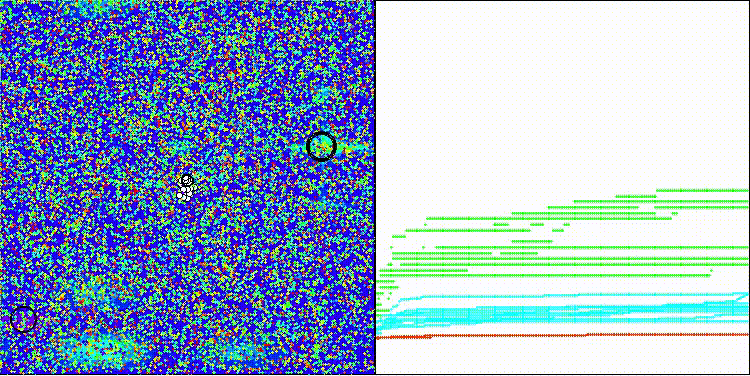
BRO na função de teste Megacity
Com base nos resultados dos testes, o algoritmo BRO ocupa a última posição no ranking dos algoritmos populacionais de otimização.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 30 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 31 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 32 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 33 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 34 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 35 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 36 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 37 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 38 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 39 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 40 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 41 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 42 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| 43 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 44 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 45 | BRO | battle royale optimizer | 0,74945 | 0,49833 | 0,27995 | 1,52773 | 0,69624 | 0,38456 | 0,20427 | 1,28507 | 0,38154 | 0,21108 | 0,10608 | 0,69870 | 3,512 | 39,02 |
| RW | neuroboids optimization algorithm 2(joo) | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O algoritmo BRO demonstra uma abordagem interessante para a otimização meta-heurística, abrindo caminho para métodos “baseados em jogos”, utilizando a metáfora de um “Battle Royale”, em que as soluções competem entre si. Os pontos fortes do algoritmo incluem sua simplicidade conceitual, o fato de ser intuitivo e relativamente fácil de implementar, o estreitamento automático do espaço de busca baseado em características estatísticas da população, e o uso do conceito de vizinhos mais próximos para competições locais. O algoritmo BRO é um método de otimização muito promissor, cujo potencial ainda está longe de ser totalmente explorado.
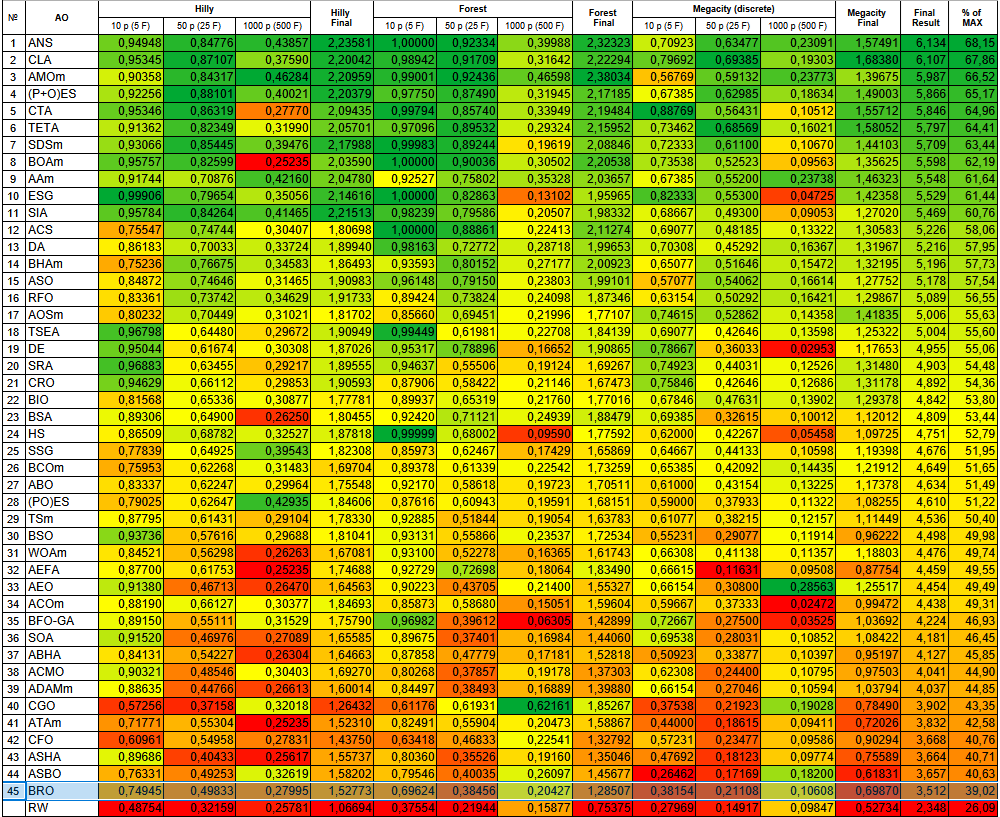
Figura 3. Graduação de cores dos algoritmos conforme os respectivos testes
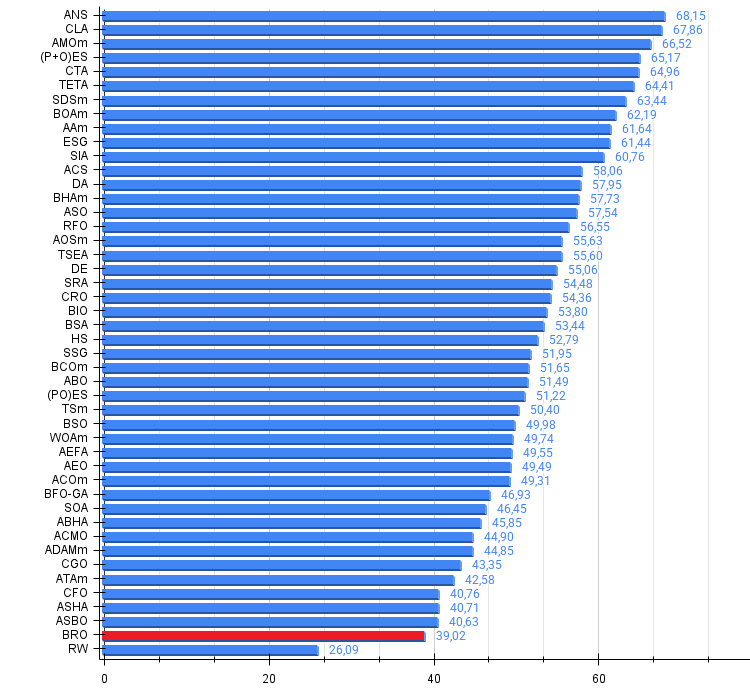
Figura 4. Histograma dos resultados dos testes dos algoritmos (em escala de 0 a 100, quanto maior melhor, onde 100 é o resultado teórico máximo possível, no arquivo compactado há um script para calcular a tabela de classificação)
Prós e contras do algoritmo BRO:
Prós:
- Ideia inovadora.
- Implementação simples.
- Desenvolvimento promissor.
Contras:
- Desempenho fraco em funções discretas.
O artigo inclui um arquivo com as versões mais recentes dos códigos dos algoritmos. O autor não assume responsabilidade pela precisão absoluta das descrições dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e considerações apresentadas neste texto baseiam-se exclusivamente nos resultados experimentais obtidos.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções para o ambiente de teste |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados e geração da tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente unificado de teste para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_BRO.mq5 | Script | Ambiente de teste específico para o BRO |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17688
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais em trading: Hierarquia de habilidades para comportamento adaptativo de agentes (Conclusão)
Redes neurais em trading: Hierarquia de habilidades para comportamento adaptativo de agentes (Conclusão)
 Simulação de mercado: Position View (XVIII)
Simulação de mercado: Position View (XVIII)
 Definição de sobrecompra e sobrevenda segundo a teoria do caos
Definição de sobrecompra e sobrevenda segundo a teoria do caos
 Do básico ao intermediário: Filas, Listas e Árvores (VII)
Do básico ao intermediário: Filas, Listas e Árvores (VII)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso