MetaTrader 5 / Тестер
preview
Оптимизация Королевской Битвой — Battle Royale Optimizer (BRO)

Оптимизация Королевской Битвой — Battle Royale Optimizer (BRO)

MetaTrader 5 — Тестер |
458 0
Andrey Dik
Andrey Dik

Содержание

  1. Введение
  2. Реализация алгоритма
  3. Результаты тестов


Введение

В метаэвристической оптимизации, где алгоритмы часто черпают вдохновение из природных процессов, физических явлений и эволюционных механизмов, появился принципиально новый источник вдохновения — компьютерные игры. Battle Royale Optimizer (BRO), разработанный Таймазом Раххаром Фарши, представляет собой инновационный алгоритм оптимизации, основанный на механике популярных игр жанра "Battle Royale", таких, как PlayerUnknown's Battlegrounds (PUBG).

Алгоритм BRO открывает новую категорию оптимизационных методов — "game-based" (основанных на играх), дополняя устоявшийся тройственный ландшафт алгоритмов оптимизации, включающий эволюционные алгоритмы, алгоритмы роевого интеллекта и алгоритмы, основанные на физических явлениях, относящихся к обширной группе популяционных алгоритмов оптимизации. В отличие от алгоритмов роевого интеллекта, где агенты сотрудничают для достижения общей цели, в BRO особи конкурируют между собой, стремясь выжить и занять наилучшее положение в пространстве поиска.

Ключевой особенностью BRO является уникальный механизм соревнования и "повреждения" решений. Каждое решение сравнивается с ближайшим соседом, и проигравший получает "урон", в то время как победитель начинает с чистого листа. Решения, накопившие слишком много повреждений, устраняются из популяции и заменяются новыми случайными решениями — точно так же, как игроки в PUBG выбывают из матча после получения критического урона. Этим обеспечивается механизм исследования пространства поиска.


Реализация алгоритма

Алгоритм Battle Royale Optimizer (BRO) образно представляет собой виртуальный мир, где множество игроков высаживаются на поле боя, и только один должен остаться в живых, и это является сутью игры-прототипа. Теперь перенесем эту концепцию на решение оптимизационных задач.

В начале работы алгоритма мы создаем популяцию решений, случайно распределенных по пространству поиска. Каждое решение — это своеобразный "игрок", который имеет определенную позицию и качество (фитнес) этой позиции. Затем начинается основной цикл соревнований, где каждое решение сравнивается со своим ближайшим соседом — примерно как игроки в битве сталкиваются друг с другом.

Когда два решения "встречаются", они сравниваются по своему качеству. Лучшее решение объявляется победителем и получает нулевой урон, а худшее становится проигравшим и получает одно повреждение. Этот счетчик повреждений — ключевая особенность алгоритма. Проигравшее решение не просто получает урон, оно также пытается улучшить свою позицию, двигаясь в направлении лучшего известного решения в популяции. Это движение имитирует стремление выжить, найдя более безопасное и выгодное место.

Если какое-то решение накапливает слишком много повреждений (превышает заданный порог), оно "исключается из игры" — удаляется из популяции и заменяется новым случайным решением. Это напоминает выбывание игрока в battle royale и появление нового в следующем матче. Такой механизм обеспечивает постоянное обновление популяции и поддерживает разнообразие решений.

Периодически в алгоритме происходит сужение пространства поиска — аналог уменьшающейся игровой зоны в battle royale, которая заставляет игроков сближаться. Границы поиска сужаются вокруг лучшего найденного решения, что заставляет популяцию концентрироваться в более перспективных областях.

Благодаря такому подходу, алгоритм BRO балансирует между исследованием новых областей и использованием уже найденных хороших решений. Проигравшие решения стремятся к лучшим, сохраняя тенденцию к улучшению, а полностью проигравшие заменяются новыми, обеспечивая свежий взгляд на пространство поиска. В то же время, периодическое сужение границ усиливает локальный поиск вокруг перспективных решений.

bro-algorithm

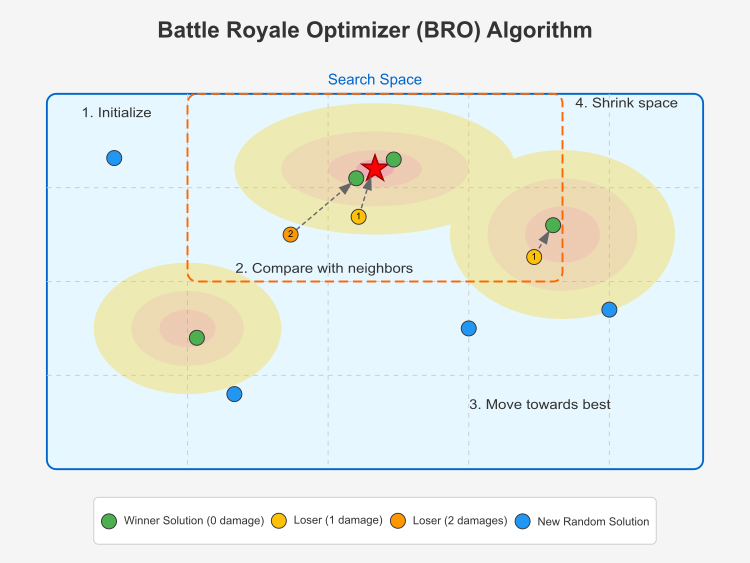
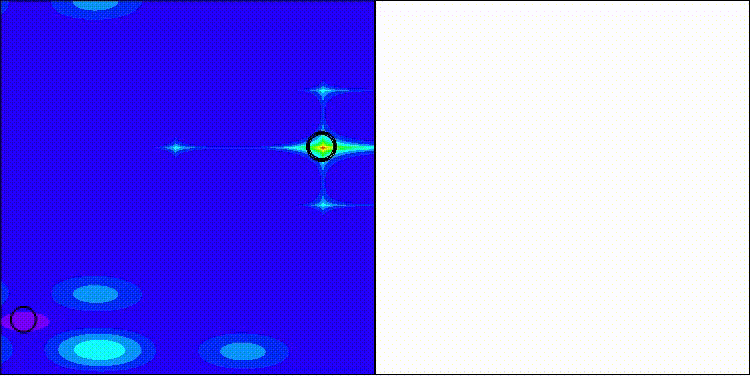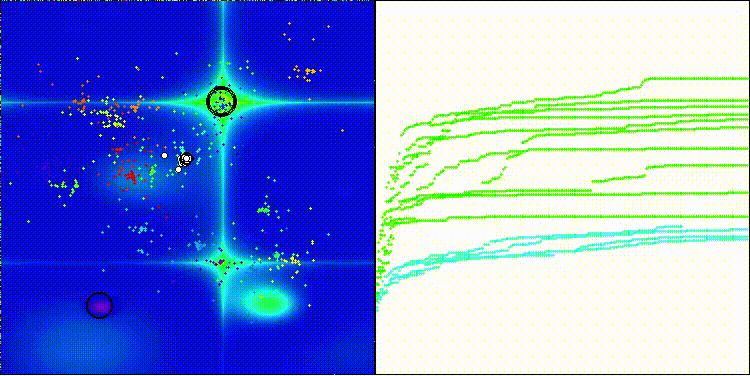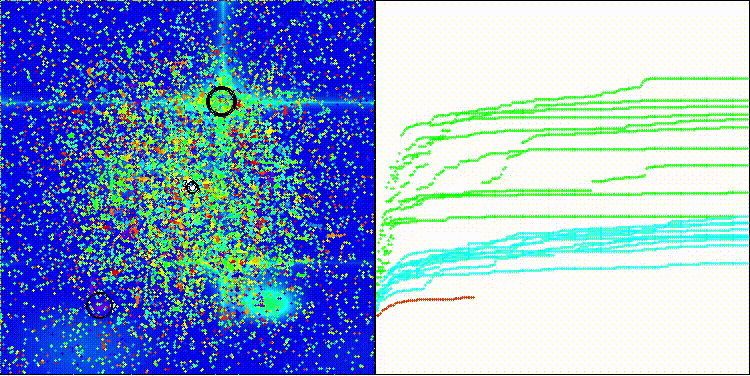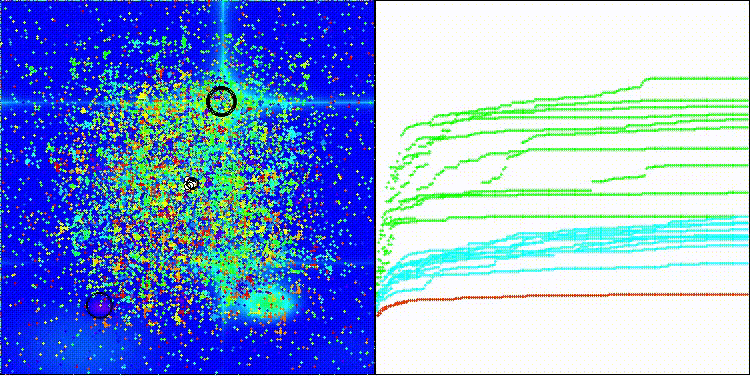
Рисунок 1. Иллюстрация работы алгоритма BRO.

Данная иллюстрация показывает основные компоненты работы алгоритма Battle Royale Optimizer (BRO). Пространство поиска представлено в виде 2D-области с контурами, которые символизируют функцию оптимизации (более яркие области представляют лучшие решения). Глобальное лучшее решение отмечено красной звездой в центре самой высокой "горы". Решения-победители отмечены зелеными точками — это решения с нулевым уроном (выигравшие в сравнении с соседями). Решения-проигравшие — желтые (с 1 повреждением) и оранжевые (с 2 повреждениями) точки. Новые случайные решения — это синие точки, которые появляются, когда решение накапливает слишком много повреждений. Проигравшие решения перемещаются к лучшему решению (показано пунктирными стрелками). Сужение пространства поиска изображено оранжевой пунктирной рамкой, которая центрируется вокруг лучшего решения.

Ключевыми этапами алгоритма являются: инициализация, сравнение с соседями, движение в сторону лучшего решения и сужение пространства поиска.

    Решения в алгоритме BRO конкурируют друг с другом, и проигравшие получают "повреждения". Решения со слишком большим количеством повреждений заменяются новыми случайными. Теперь, когда понятен принцип работы алгоритма, можем перейти к написанию псевдокода.

    Инициализация:

    1. Создать популяцию решений размером popSize
    2. Для каждого решения установить счетчик повреждений в 0
    3. Установить максимальный порог повреждений maxDamage
    4. Определить количество эпох epochs
    5. Вычислить начальное значение delta для периодического сужения пространства поиска

    Основной алгоритм:

    1. Создание начальной популяции:
      • Для каждого решения в популяции:
        • Сгенерировать случайные координаты в пределах заданного пространства поиска
    2. Для каждой эпохи выполнить:
      • Обновить глобальное наилучшее решение, если найдено лучшее
      • Проведение "сражений" между решениями:
        • Для каждого решения в популяции:
          • Найти ближайшего соседа (решение с минимальным расстоянием)
          • Сравнить качество текущего решения с соседом:
            • Если текущее решение лучше:
              • Сбросить счетчик повреждений текущего решения
              • Увеличить счетчик повреждений соседа
              • Проигравший (сосед) двигается к наилучшему решению
            • Иначе:
              • Увеличить счетчик повреждений текущего решения
              • Сбросить счетчик повреждений соседа
              • Проигравший (текущее решение) двигается к наилучшему решению
      • Обработка сильно поврежденных решений:
        • Для каждого решения в популяции:
          • Если счетчик повреждений ≥ maxDamage :
            • Сбросить счетчик повреждений
            • Заменить решение на новое случайное
      • Периодическое сужение пространства поиска:
        • Если номер текущей эпохи делится на delta :
          • Вычислить стандартные отклонения координат по всей популяции
          • Сузить пространство поиска вокруг наилучшего решения
          • Обновить значение delta
    3. Возвращение наилучшего найденного решения

    В алгоритме задействованы следующие формулы:

    • Расчет начального значения дельты для сужения пространства поиска: delta = ⌊epochs / log₁₀(epochs)⌋
    • Расчет евклидова расстояния между решениями: distance = √(∑(a[idx1][c] - a[idx2][c])²)
    • Движение проигравшего решения к глобальному лучшему: a[i][c] = a[i][c] + r × (cB[c] - a[i][c])
    • Расчет среднего значения для каждой координаты: mean[c] = (∑a[i][c]) / popSize
    • Расчет стандартного отклонения для каждой координаты: sdValues[c] = √(∑(a[i][c] - mean[c])² / popSize)
    • Формулы для сужения пространства поиска: newMin[c] = cB[c] - sdValues[c] newMax[c] = cB[c] + sdValues[c]
    • Обновление параметра delta после сужения пространства: delta = delta + ⌊delta / 2⌉

    Для периодического сужения пространства поиска автор предлагает следующую формулу: Δ (delta) = maxEpochs / log₁₀(maxEpochs), график которой представлен ниже:

    func

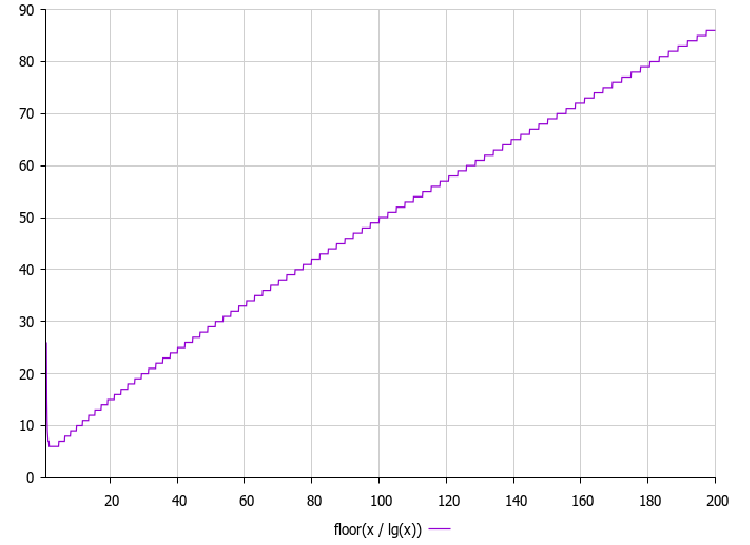
    Рисунок 2. График функции зависимости параметра delta от количества эпох

    График функции delta = epochs/log₁₀(epochs)  имеет важное значение в работе алгоритма BRO, так как определяет, через какое количество итераций будет происходить сужение пространства поиска. Как видно из графика, значение delta растет с увеличением числа эпох, но не так быстро, как сами эпохи, благодаря делению на логарифм. Это создает нелинейную зависимость, которая обеспечивает следующие преимущества: на ранних этапах оптимизации (при малом количестве эпох) сужение происходит относительно часто, что помогает алгоритму быстрее сфокусироваться на перспективных областях, а на поздних этапах (при большом количестве эпох) сужение происходит реже, что дает возможность более тщательно исследовать уже найденные перспективные зоны.

    В ходе моих экспериментов, я преобразовал формулу зависимости параметра delta, логарифмом применяется дважды, алгоритм работает лучше.

    // Вычисление начального delta для сужения пространства поиска
  delta = (int)MathFloor(epochs / MathLog(MathLog(epochs)));

    Перейдем к формированию кода, напишем пользовательский класс "C_AO_BRO", который наследуется от базового класса "C_AO", т.е. наследует все публичные и защищенные члены класса "C_AO" и может переопределять их поведение. Этот класс и будет представлять собой реализацию оптимизационного алгоритма, основанного на концепции "Battle Royale".

    1. Публичные члены класса:

    • popSize — устанавливает размер популяции.
    • maxDamage — устанавливает максимальный порог повреждений, сколько "поражений" решение может выдержать, прежде чем будет устранено.
    • SetParams () — метод обновляет значения "popSize" и "maxDamage" на основе значений, хранящихся в массиве "params", что позволяет изменять параметры алгоритма во время выполнения.
    • Init () — метод инициализации алгоритма. Принимает следующие параметры:
      • rangeMinP [] — минимальные значения диапазона поиска для каждой переменной.
      • rangeMaxP [] — максимальные значения диапазона поиска.
      • rangeStepP [] — шаг поиска для каждой переменной.
      • epochsP — количество эпох (итераций) алгоритма. Значение по умолчанию - 0.
    • Moving () — метод реализует основную логику движения или обновления решений в пространстве поиска.
    • Revision () — метод реализует логику пересмотра текущих решений, здесь происходит оценка "ущерба", полученного каждым решением.
    • maxDamage — публичный член, хранящий максимальный порог повреждений.

    2. Приватные поля класса:

    • delta — интервал для сужения (shrink) пространства поиска. Используется для адаптации размера шага поиска в процессе оптимизации.
    • damages [] — массив хранит количество "повреждений" для каждого решения в популяции. 
    • epoch — текущая эпоха (номер итерации) алгоритма.
    • epoch — максимальное количество эпох (итераций) алгоритма.

    3. Вспомогательные методы:

    • FindNearestNeighbor () — находит ближайшего соседа для решения по заданному индексу, используется для взаимодействия между решениями.
    • CalculateDistance () — вычисляет расстояние между двумя решениями, идентифицируемыми по их индексам.
    • CalculateStandardDeviations () — вычисляет стандартные отклонения значений решений популяции, используется для оценки разнообразия популяции и адаптации параметров поиска.
    • ShrinkSearchSpace () — метод сужает пространство поиска. Это стандартная техника для сходимости алгоритма к оптимальному решению.

    Общее представление:

    C_AO_BRO  представляет собой класс для алгоритма оптимизации Battle Royale и основная идея алгоритма, если говорить кратко, заключается в следующем:

    1. Инициализация: создается популяция случайных решений в определенном пространстве поиска.
    2. Оценка: каждое решение оценивается с помощью целевой функции (fitness function).
    3. Battle Royale: решения "сражаются" друг с другом (сравниваются по значениям целевой функции).
    4. Повреждения: некоторые решения получают "повреждения", в зависимости от результатов "сражений".
    5. Устранение: решения, получившие количество "damage", превышающее "maxDamage", удаляются из популяции.
    6. Воспроизводство/замена: удаленные решения заменяются новыми случайными решениями.
    7. Сужение пространства поиска: пространство поиска может быть сужено, чтобы сосредоточиться на наиболее перспективных областях.
    8. Повторение: шаги 2-7 повторяются в течение заданного количества эпох.
    //——————————————————————————————————————————————————————————————————————————————
class C_AO_BRO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BRO () { }
  C_AO_BRO ()
  {
    ao_name = "BRO";
    ao_desc = "Battle Royale Optimizer";
    ao_link = "https://www.mql5.com/ru/articles/17688";

    popSize   = 100;    // размер популяции
    maxDamage = 3;      // максимальный порог повреждений

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "maxDamage"; params [1].val = maxDamage;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    maxDamage = (int)params [1].val;
  }

  bool Init (const double &rangeMinP [],  // минимальный диапазон поиска
             const double &rangeMaxP [],  // максимальный диапазон поиска
             const double &rangeStepP [], // шаг поиска
             const int     epochsP = 0);  // количество эпох

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  int maxDamage;    // максимальный порог повреждений

  private: //-------------------------------------------------------------------
  int    delta;      // интервал для сужения пространства поиска
  int    damages []; // количество повреждений для каждого решения
  int    epoch;      // текущая эпоха
  int    epochs;     // максимальное количество эпох

  // Вспомогательные методы
  int    FindNearestNeighbor (int index);
  double CalculateDistance (int idx1, int idx2);
  void   CalculateStandardDeviations (double &sdValues []);
  void   ShrinkSearchSpace ();
};
//——————————————————————————————————————————————————————————————————————————————

    Метод "Init ()" инициализирует алгоритм BRO, вызывает "StandardInit ()" для стандартной инициализации, используя переданные диапазоны поиска и шаги. Если "StandardInit" возвращает "false", метод "Init ()" также возвращает "false", сигнализируя об ошибке инициализации. Инициализирует массив "damages", выделяя память для каждого решения в популяции "popSize" и устанавливая начальное количество "повреждений" каждого решения в 0. Устанавливает общее количество эпох "epochs" и сбрасывает текущую эпоху "epoch" на 0.

    Значение "delta" вычисляется на основе общего количества эпох, чтобы пространство поиска сужалось постепенно. Если "delta" получается меньше или равно 0, устанавливается значение 1. В целом, этот метод подготавливает алгоритм к работе, инициализируя его основные параметры и структуры данных.

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_BRO::Init (const double &rangeMinP  [],  // минимальный диапазон поиска
                     const double &rangeMaxP  [],  // максимальный диапазон поиска
                     const double &rangeStepP [],  // шаг поиска
                     const int     epochsP = 0)    // количество эпох
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  // Инициализация счетчиков повреждений для каждого решения
  ArrayResize (damages, popSize);
  ArrayInitialize (damages, 0);

  // Установка эпох
  epochs = epochsP;
  epoch  = 0;

  // Вычисление начального delta для сужения пространства поиска
  delta = (int)MathFloor (epochs / MathLog10 (epochs));
  if (delta <= 0) delta = 1;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    Метод "Moving ()" реализует логику инициализации популяции решений, при этом каждая координата каждого решения генерируется случайно между заданными минимальным и максимальным диапазоном "rangeMin" и "rangeMax" и дискретизируется с определенным шагом "rangeStep". Этот метод гарантирует, что популяция инициализируется только один раз. 

    /——————————————————————————————————————————————————————————————————————————————
void C_AO_BRO::Moving ()
{
  if (!revision)
  {
    // Инициализация популяции случайными решениями
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        double coordinate = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Метод "Revision ()", является ключевым шагом в оптимизационном алгоритме BRO. Каждая итерация метода обновляет лучшее решение: если какое-то решение в текущей популяции лучше, чем текущее лучшее глобальное решение, то лучшее глобальное решение обновляется.

    Метод сравнивает решения с соседями: для каждого решения в популяции находится ближайший сосед. Затем их значения функции сравниваются. Лучшее решение в паре "награждается" сбросом счетчика повреждений, а счетчик повреждений худшего решения увеличивается. Худшее решение в паре смещается в сторону глобально лучшего решения.

    Далее заменяются "поврежденные" решения: если какое-либо решение накопило достаточно "повреждений" (достигло значения "maxDamage"), оно заменяется новым, сгенерированным случайным образом. Периодически, в зависимости от переменной "delta", происходит сужение поисковой области. Этот процесс повторяется на протяжении нескольких итераций алгоритма. За счет сравнения с соседями, происходит перемещение решений в более выгодные области для поиска.

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BRO::Revision ()
{
  epoch++;

  // Обновление глобального наилучшего решения
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  // Сравнение каждого решения с его ближайшим соседом и обновление счетчиков повреждений
  for (int i = 0; i < popSize; i++)
  {
    int neighbor = FindNearestNeighbor (i);

    if (neighbor != -1)
    {
      if (a [i].f >= a [neighbor].f)
      {
        // Решение i побеждает
        damages [i] = 0;
        damages [neighbor]++;

        // Проигравший (сосед) движется к наилучшему решению
        for (int c = 0; c < coords; c++)
        {
          double r = u.RNDfromCI (0, 1);
          a [neighbor].c [c] = a [neighbor].c [c] + r * (cB [c] - a [neighbor].c [c]);
          a [neighbor].c [c] = u.SeInDiSp (a [neighbor].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
      else
      {
        // Решение i проигрывает
        damages [i]++;
        damages [neighbor] = 0;

        // Проигравший (i) движется к наилучшему решению
        for (int c = 0; c < coords; c++)
        {
          double r = u.RNDfromCI (0, 1);
          a [i].c [c] = a [i].c [c] + r * (cB [c] - a [i].c [c]);
          a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }
  }

  // Проверка, достигло ли какое-либо решение максимального повреждения, и его замена
  for (int i = 0; i < popSize; i++)
  {
    if (damages [i] >= maxDamage)
    {
      // Сброс счетчика повреждений
      damages [i] = 0;

      // Генерация нового случайного решения
      for (int c = 0; c < coords; c++)
      {
        double coordinate = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (coordinate, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }

  // Периодическое сужение пространства поиска
  if (epochs > 0 && epoch % delta == 0)
  {
    ShrinkSearchSpace ();
    // Обновление delta
    delta = delta + (int)MathRound (delta / 2);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Метод "FindNearestNeighbor ()" находит индекс ближайшего соседа для решения с индексом "index" в популяции. Он перебирает все решения, вычисляет расстояние до каждого из них (исключая само решение "index"), и возвращает индекс решения с минимальным расстоянием. Если ближайшего соседа найти не удалось (например, в популяции только одно решение), то возвращает -1. В двух словах, метод находит ближайшего соседа для заданного решения.

    //——————————————————————————————————————————————————————————————————————————————
int C_AO_BRO::FindNearestNeighbor (int index)
{
  double minDistance = DBL_MAX;
  int nearestIndex = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (i == index) continue;

    double distance = CalculateDistance (index, i);
    if (distance < minDistance)
    {
      minDistance = distance;
      nearestIndex = i;
    }
  }

  return nearestIndex;
}
//——————————————————————————————————————————————————————————————————————————————

    Метод "CalculateDistance ()" вычисляет евклидово расстояние между двумя решениями в популяции, заданными их индексами "idx1" и "idx2". Начинается с инициализации переменной "distanceSum" нулем. Эта переменная будет накапливать сумму квадратов разностей координат. Цикл "for" перебирает все координаты решений. На каждой итерации цикла вычисляется разность между соответствующими координатами решений "idx1" и "idx2". Квадрат этой разности добавляется к "distanceSum".

    После завершения цикла, метод возвращает квадратный корень из "distanceSum", что представляет собой евклидово расстояние между двумя решениями. В итоге, метод возвращает численное значение, отражающее "расстояние" между двумя решениями в пространстве поиска. Чем больше это значение, тем дальше друг от друга находятся решения.

    //——————————————————————————————————————————————————————————————————————————————
double C_AO_BRO::CalculateDistance (int idx1, int idx2)
{
  double distanceSum = 0.0;

  for (int c = 0; c < coords; c++)
  {
    double diff = a [idx1].c [c] - a [idx2].c [c];
    distanceSum += diff * diff;
  }

  return MathSqrt (distanceSum);
}
//——————————————————————————————————————————————————————————————————————————————

    Метод "CalculateStandardDeviations ()" вычисляет стандартное отклонение для каждой координаты решений в популяции и сохраняет результаты в массиве "sdValues". Изменяется размер входного массива "sdValues" таким образом, чтобы он мог хранить стандартное отклонение для каждой из "coords" координат. Далее, цикл перебирает каждую координату решений и вычисляется стандартное отклонение. Метод обнуляет сумму квадратов отклонений для текущей координаты, затем, также обнуляет ее среднее значение. Цикл суммирует значения текущей координаты "c" для всех решений в популяции. Затем, вычисляет среднее значение этой координаты. 

    Вычисление суммы квадратов отклонений: цикл перебирает все решения в популяции и вычисляет сумму квадратов отклонений от среднего значения для текущей координаты. Вычисляет разницу между значением координаты "c" для решения "i" и ее средним значением. Добавляет квадрат разницы к сумме квадратов отклонений. Вычисляет стандартное отклонение, как квадратный корень из суммы квадратов отклонений, деленный на размер популяции. Результат сохраняется в соответствующий элемент массива "sdValues".

    В итоге, метод вычисляет меру разброса значений для каждой координаты решений в популяции и сохраняет её в переданном массиве  "sdValues", а стандартное отклонение показывает, насколько сильно значения координаты варьируются вокруг среднего значения.

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BRO::CalculateStandardDeviations (double &sdValues [])
{
  ArrayResize (sdValues, coords);

  for (int c = 0; c < coords; c++)
  {
    double sum = 0.0;
    double mean = 0.0;

    // Вычисление среднего
    for (int i = 0; i < popSize; i++) mean += a [i].c [c];

    mean /= popSize;

    // Вычисление суммы квадратов отклонений
    for (int i = 0; i < popSize; i++)
    {
      double diff = a [i].c [c] - mean;
      sum += diff * diff;
    }

    sdValues [c] = MathSqrt (sum / popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Метод "ShrinkSearchSpace ()"  сужает пространство поиска, основываясь на стандартных отклонениях координат и местоположении лучшего найденного решения. Он как бы фокусирует поиск в более перспективной области, где уже есть хорошее решение.

    Сначала идет вычисление стандартных отклонений, для этого вызывается метод "CalculateStandardDeviations ()", который вычисляет стандартные отклонения для каждой координаты решений в популяции и сохраняет их в массиве "sdValues", или другими словами, насколько сильно значения каждой координаты различаются в популяции. Вычисление новых границ: новые границы центрируются вокруг наилучшего найденного решения, а их ширина определяется стандартным отклонением. Если стандартное отклонение мало, то поиск сужается вокруг лучшего решения. Если стандартное отклонение велико, то поиск остается более широким. Проверка на допустимость: поиск не выйдет за пределы исходного допустимого пространства решений.

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BRO::ShrinkSearchSpace ()
{
  double sdValues [];
  CalculateStandardDeviations (sdValues);

  for (int c = 0; c < coords; c++)
  {
    // Новые границы центрированы вокруг наилучшего решения с шириной стандартного отклонения
    double newMin = cB [c] - sdValues [c];
    double newMax = cB [c] + sdValues [c];

    // Убедитесь, что новые границы находятся в пределах исходных ограничений
    if (newMin < rangeMin [c]) newMin = rangeMin [c];
    if (newMax > rangeMax [c]) newMax = rangeMax [c];

    // Обновление границ
    rangeMin [c] = newMin;
    rangeMax [c] = newMax;
  }
}
//——————————————————————————————————————————————————————————————————————————————


    Результаты тестов

    После проведенных тестов видно, что алгоритм работает достаточно хорошо на функциях Hilly и Forest, однако, на дискретной Megacity показатели сходимости гораздо слабее.

    BRO|Battle Royale Optimizer|50.0|3.0|
    =============================
    5 Hilly's; Func runs: 10000; result: 0.7494493002235458
    25 Hilly's; Func runs: 10000; result: 0.4983307394255448
    500 Hilly's; Func runs: 10000; result: 0.27994639979348446
    =============================
    5 Forest's; Func runs: 10000; result: 0.6962444245506945
    25 Forest's; Func runs: 10000; result: 0.3845619185097379
    500 Forest's; Func runs: 10000; result: 0.20427058729050862
    =============================
    5 Megacity's; Func runs: 10000; result: 0.3815384615384616
    25 Megacity's; Func runs: 10000; result: 0.21107692307692308
    500 Megacity's; Func runs: 10000; result: 0.10607692307692404
    =============================
    All score: 3.51150 (39.02%)

    На визуализации можно заметить разброс значений результатов и более слабые поисковые способности на последней дискретной функции Megacity.

    Hilly

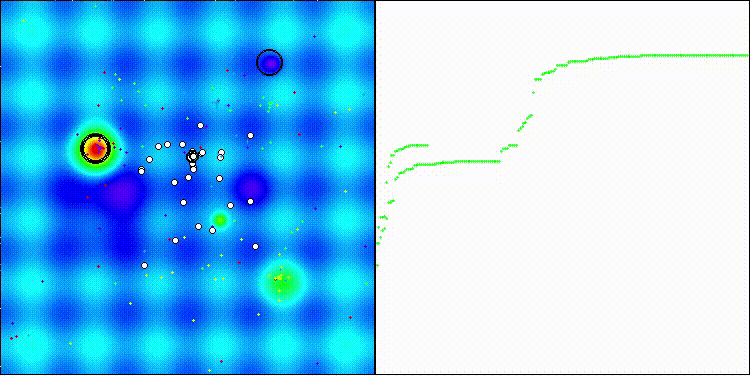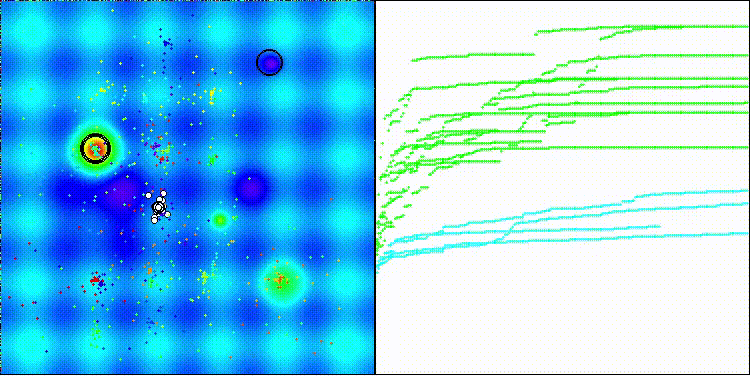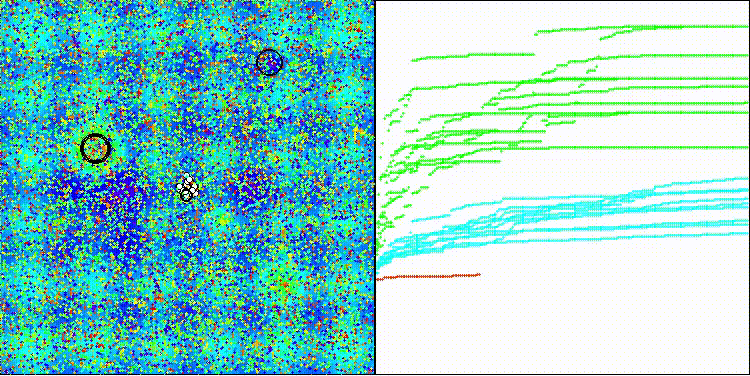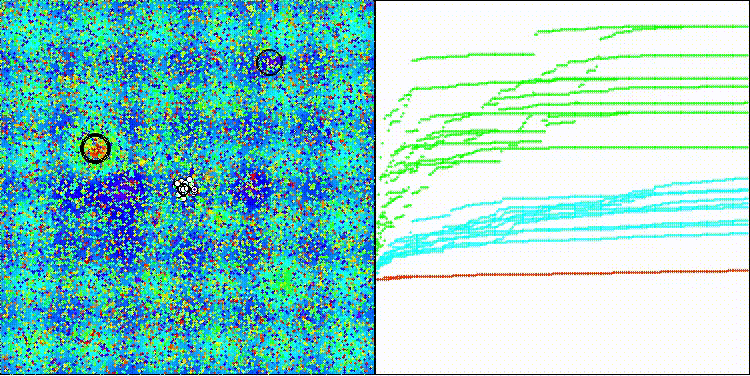
    BRO на тестовой функции Hilly

    Forest

    BRO на тестовой функции Forest

    Megacity

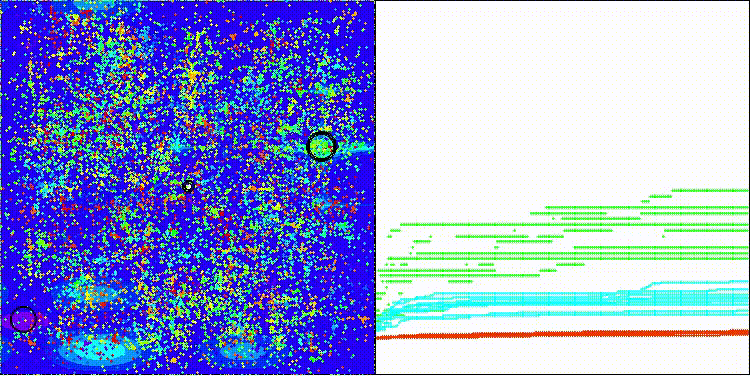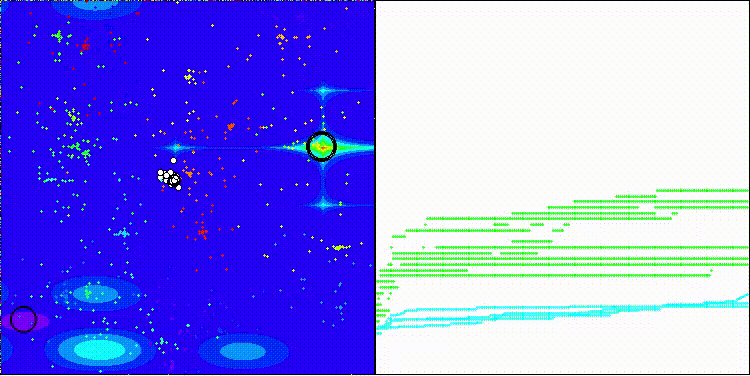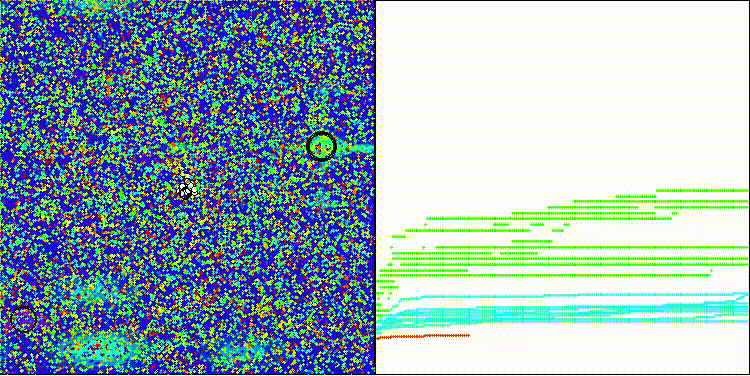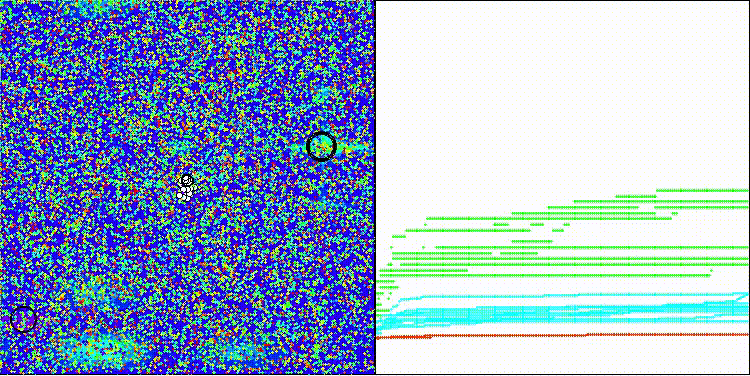
    BRO на тестовой функции Megacity

    По результатам тестирования алгоритм BRO замыкает рейтинговую таблицу популяционных алгоритмов оптимизации.

    № AO Description Hilly Hilly
    Final     		Forest Forest
    Final     		Megacity (discrete) Megacity
    Final     		Final
    Result     		% of
    MAX
    10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)
    1ANSacross neighbourhood search0,949480,847760,438572,235811,000000,923340,399882,323230,709230,634770,230911,574916,13468,15
    2CLAcode lock algorithm (joo)0,953450,871070,375902,200420,989420,917090,316422,222940,796920,693850,193031,683806,10767,86
    3AMOmanimal migration ptimization M0,903580,843170,462842,209590,990010,924360,465982,380340,567690,591320,237731,396755,98766,52
    4(P+O)ES(P+O) evolution strategies0,922560,881010,400212,203790,977500,874900,319452,171850,673850,629850,186341,490035,86665,17
    5CTAcomet tail algorithm (joo)0,953460,863190,277702,094350,997940,857400,339492,194840,887690,564310,105121,557125,84664,96
    6TETAtime evolution travel algorithm (joo)0,913620,823490,319902,057010,970960,895320,293242,159520,734620,685690,160211,580525,79764,41
    7SDSmstochastic diffusion search M0,930660,854450,394762,179880,999830,892440,196192,088460,723330,611000,106701,441035,70963,44
    8BOAmbilliards optimization algorithm M0,957570,825990,252352,035901,000000,900360,305022,205380,735380,525230,095631,356255,59862,19
    9AAmarchery algorithm M0,917440,708760,421602,047800,925270,758020,353282,036570,673850,552000,237381,463235,54861,64
    10ESGevolution of social groups (joo)0,999060,796540,350562,146161,000000,828630,131021,959650,823330,553000,047251,423585,52961,44
    11SIAsimulated isotropic annealing (joo)0,957840,842640,414652,215130,982390,795860,205071,983320,686670,493000,090531,270205,46960,76
    12ACSartificial cooperative search0,755470,747440,304071,806981,000000,888610,224132,112740,690770,481850,133221,305835,22658,06
    13DAdialectical algorithm0,861830,700330,337241,899400,981630,727720,287181,996530,703080,452920,163671,319675,21657,95
    14BHAmblack hole algorithm M0,752360,766750,345831,864930,935930,801520,271772,009230,650770,516460,154721,321955,19657,73
    15ASOanarchy society optimization0,848720,746460,314651,909830,961480,791500,238031,991010,570770,540620,166141,277525,17857,54
    16RFOroyal flush optimization (joo)0,833610,737420,346291,917330,894240,738240,240981,873460,631540,502920,164211,298675,08956,55
    17AOSmatomic orbital search M0,802320,704490,310211,817020,856600,694510,219961,771070,746150,528620,143581,418355,00655,63
    18TSEAturtle shell evolution algorithm (joo)0,967980,644800,296721,909490,994490,619810,227081,841390,690770,426460,135981,253225,00455,60
    19DEdifferential evolution0,950440,616740,303081,870260,953170,788960,166521,908650,786670,360330,029531,176534,95555,06
    20SRAsuccessful restaurateur algorithm (joo)0,968830,634550,292171,895550,946370,555060,191241,692670,749230,440310,125261,314804,90354,48
    21CROchemical reaction optimisation0,946290,661120,298531,905930,879060,584220,211461,674730,758460,426460,126861,311784,89254,36
    22BIOblood inheritance optimization (joo)0,815680,653360,308771,777810,899370,653190,217601,770160,678460,476310,139021,293784,84253,80
    23BSAbird swarm algorithm0,893060,649000,262501,804550,924200,711210,249391,884790,693850,326150,100121,120124,80953,44
    24HSharmony search0,865090,687820,325271,878180,999990,680020,095901,775920,620000,422670,054581,097254,75152,79
    25SSGsaplings sowing and growing0,778390,649250,395431,823080,859730,624670,174291,658690,646670,441330,105981,193984,67651,95
    26BCOmbacterial chemotaxis optimization M0,759530,622680,314831,697040,893780,613390,225421,732590,653850,420920,144351,219124,64951,65
    27ABOafrican buffalo optimization0,833370,622470,299641,755480,921700,586180,197231,705110,610000,431540,132251,173784,63451,49
    28(PO)ES(PO) evolution strategies0,790250,626470,429351,846060,876160,609430,195911,681510,590000,379330,113221,082554,61051,22
    29TSmtabu search M0,877950,614310,291041,783300,928850,518440,190541,637830,610770,382150,121571,114494,53650,40
    30BSObrain storm optimization0,937360,576160,296881,810410,931310,558660,235371,725340,552310,290770,119140,962224,49849,98
    31WOAmwale optimization algorithm M0,845210,562980,262631,670810,931000,522780,163651,617430,663080,411380,113571,188034,47649,74
    32AEFAartificial electric field algorithm0,877000,617530,252351,746880,927290,726980,180641,834900,666150,116310,095080,877544,45949,55
    33AEOartificial ecosystem-based optimization algorithm0,913800,467130,264701,645630,902230,437050,214001,553270,661540,308000,285631,255174,45449,49
    34ACOmant colony optimization M0,881900,661270,303771,846930,858730,586800,150511,596040,596670,373330,024720,994724,43849,31
    35BFO-GAbacterial foraging optimization - ga0,891500,551110,315291,757900,969820,396120,063051,428990,726670,275000,035251,036924,22446,93
    36SOAsimple optimization algorithm0,915200,469760,270891,655850,896750,374010,169841,440600,695380,280310,108521,084224,18146,45
    37ABHAartificial bee hive algorithm0,841310,542270,263041,646630,878580,477790,171811,528180,509230,338770,103970,951974,12745,85
    38ACMOatmospheric cloud model optimization0,903210,485460,304031,692700,802680,378570,191781,373030,623080,244000,107950,975034,04144,90
    39ADAMmadaptive moment estimation M0,886350,447660,266131,600140,844970,384930,168891,398800,661540,270460,105941,037944,03744,85
    40CGOchaos game optimization0,572560,371580,320181,264320,611760,619310,621611,852670,375380,219230,190280,784903,90243,35
    41ATAmartificial tribe algorithm M0,717710,553040,252351,523100,824910,559040,204731,588670,440000,186150,094110,720263,83242,58
    42CFOcentral force optimization0,609610,549580,278311,437500,634180,468330,225411,327920,572310,234770,095860,902943,66840,76
    43ASHAartificial showering algorithm0,896860,404330,256171,557370,803600,355260,191601,350460,476920,181230,097740,755893,66440,71
    44ASBOadaptive social behavior optimization0,763310,492530,326191,582020,795460,400350,260971,456770,264620,171690,182000,618313,65740,63
    45BRObattle royale optimizer0,749450,498330,279951,527730,696240,384560,204271,285070,381540,211080,106080,698703,51239,02
    RWneuroboids optimization algorithm 2(joo)0,487540,321590,257811,066940,375540,219440,158770,753750,279690,149170,098470,527342,34826,09


    Выводы

    Алгоритм BRO демонстрирует интересный подход к метаэвристической оптимизации, открывая путь "игровых" методов, используя метафору "Battle Royale", где решения соревнуются между собой. Сильными сторонами алгоритма являются концептуальная простота, алгоритм интуитивно понятен и относительно прост в реализации, автоматическое сужение пространства поиска на основе статистических характеристик популяции, использование концепции ближайших соседей для локальных соревнований. Алгоритм BRO является очень перспективным методом оптимизации, потенциал которого далеко не раскрыт.

    Tab

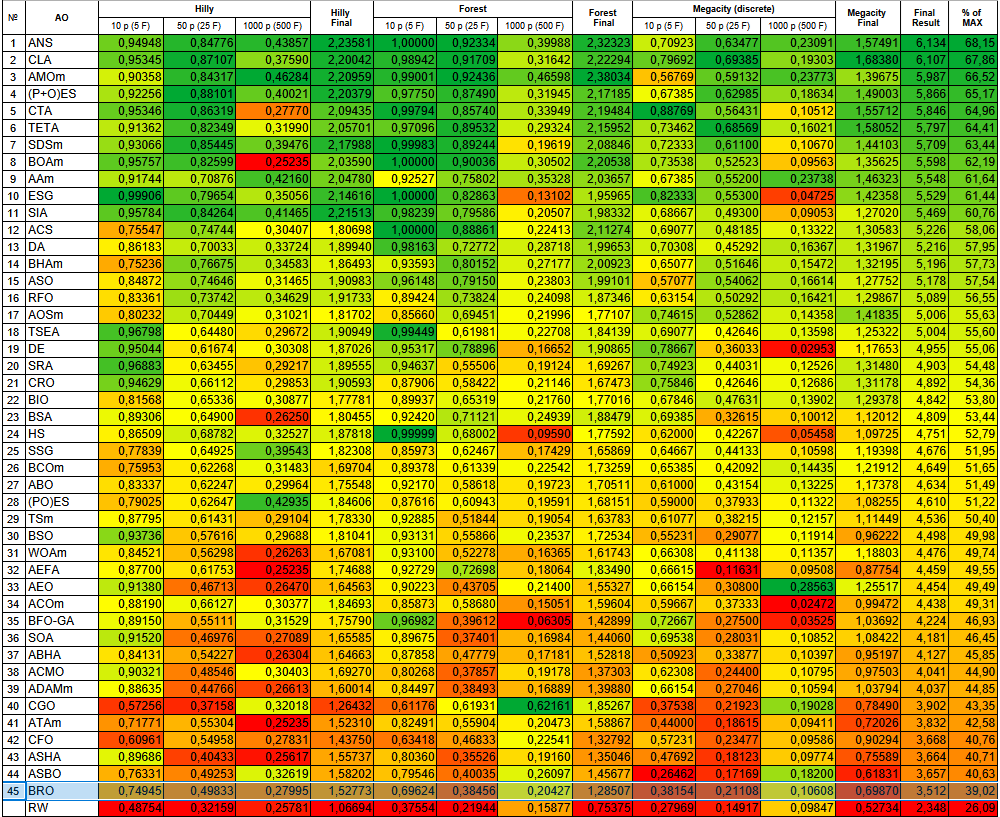
    Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам

    chart

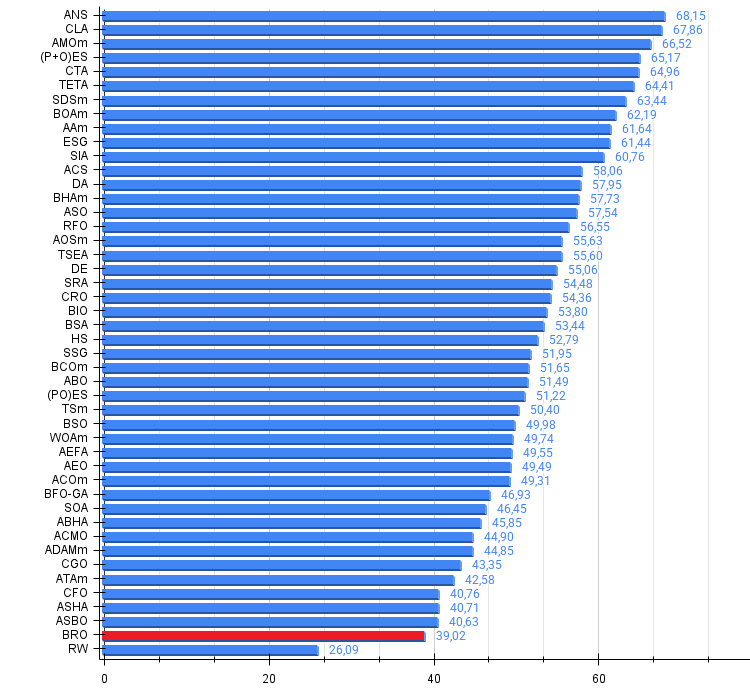
    Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

    Плюсы и минусы алгоритма BRO:

    Плюсы:

    1. Интересная идея.
    2. Простая реализация.
    3. Перспективная разработка.

    Минусы:

    1. Слабые результаты на дискретных функциях.

    К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.


    Программы, используемые в статье

    #ИмяТипОписание
    1#C_AO.mqh
    		Включаемый файл
    		Родительский класс популяционных алгоритмов оптимизации
    2#C_AO_enum.mqh
    		Включаемый файл
    		Перечисление популяционных алгоритмов оптимизации
    3TestFunctions.mqh
    		Включаемый файл
    		Библиотека тестовых функций
    4
    		TestStandFunctions.mqh
    		Включаемый файл
    		Библиотека функций тестового стенда
    5
    		Utilities.mqh
    		Включаемый файл
    		Библиотека вспомогательных функций
    6
    		CalculationTestResults.mqh
    		Включаемый файл
    		Скрипт для расчета результатов в сравнительную таблицу
    7
    		Testing AOs.mq5
    		СкриптЕдиный испытательный стенд для всех популяционных алгоритмов оптимизации
    8
    		Simple use of population optimization algorithms.mq5
    		Скрипт
    		Простой пример использования популяционных алгоритмов оптимизации без визуализации
    9
    		Test_AO_BRO.mq5
    		СкриптИспытательный стенд для BRO

    Прикрепленные файлы |
    Загрузить ZIP
    BRO.ZIP (423.38 KB)
    Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

    Другие статьи автора

    Перейти к обсуждению на форуме трейдеров
    Возможности Мастера MQL5, которые вам нужно знать (Часть 39): Индекс относительной силы Возможности Мастера MQL5, которые вам нужно знать (Часть 39): Индекс относительной силы
    RSI — популярный импульсный осциллятор, который измеряет темп и размер недавнего изменения цены ценной бумаги для оценки ситуаций переоценки или недооценки ее цены. Эти знания о скорости и масштабах имеют ключевое значение для определения точек разворота. Мы применим этот осциллятор в работе очередного пользовательского класса сигналов и изучим особенности некоторых из его сигналов. Однако начнем мы с того, что подведем итог нашему разговору о полосах Боллинджера.
    Введение в MQL5 (часть 9): Использование объектов на графике Введение в MQL5 (часть 9): Использование объектов на графике
    В этой статье мы научимся создавать и настраивать объекты графиков в MQL5, используя текущие и исторические данные. Здесь также представлено практическое руководство, с которым вы сможете отображать сделки на графике и использовать другие объекты MQL5 на практике.
    Пример CNA (сетевого анализа причинно-следственных связей), SMOC (оптимального управления стохастической моделью) и теории игр Нэша с Глубоким обучением Пример CNA (сетевого анализа причинно-следственных связей), SMOC (оптимального управления стохастической моделью) и теории игр Нэша с Глубоким обучением
    Мы добавим Глубокое обучение к тем трем примерам, которые были опубликованы в предыдущих статьях, и сравним результаты с предыдущими. Цель состоит в том, чтобы научиться каким образом добавлять Глубокое обучение (DL) в другие советники.
    Нейросети в трейдинге: Иерархия навыков для адаптивного поведения агентов (Окончание) Нейросети в трейдинге: Иерархия навыков для адаптивного поведения агентов (Окончание)
    В статье рассматривается практическая реализация фреймворка HiSSD в задачах алгоритмического трейдинга. Показано, как иерархия навыков и адаптивная архитектура могут быть использованы для построения устойчивых торговых стратегий.