Mecanismos de compuertas en el aprendizaje en conjuntos

Los métodos de compuertas ajustan dinámicamente la influencia de los modelos individuales basándose en información contextual utilizando variables de compuerta. Estas variables actúan como mecanismos de supervisión, ponderando estratégicamente los resultados del modelo para lograr un rendimiento predictivo superior en comparación con cualquier modelo individual.

A diferencia de los métodos de conjunto tradicionales que se basan en promedios, votaciones o apilamiento, el método de compuertas utiliza explícitamente variables de compuerta para la combinación de modelos. Este enfoque resulta especialmente valioso en escenarios con un rendimiento variable de los modelos, como las previsiones financieras, en los que las tendencias económicas influyen en la precisión de las predicciones. Al ponderar los modelos de forma adaptativa en función del contexto, las compuertas mejoran la precisión y la adaptabilidad en entornos complejos.

Las técnicas de compuertas se dividen generalmente en dos categorías: seleccionar un único modelo basado en variables de compuerta o combinar los resultados de todos los modelos con ponderaciones dependientes del contexto. Este último suele ser más robusto, aprovechando las fortalezas de múltiples modelos. Las siguientes secciones exploran ejemplos de ambos enfoques: especialización preordenada y aprendida.

Especialización predestinada

La especialización preordenada constituye una forma fundamental de control, en la que una sola variable actúa como factor decisivo para elegir entre dos o más modelos especialistas preentrenados. Este enfoque divide eficazmente el espacio de entrada, dirigiendo las instancias al modelo más adecuado en función del valor de la variable de control. Para ilustrar este concepto, considere un problema de clasificación binaria representado en un espacio de características bidimensional, con las variables A y B. En este escenario hipotético, la variable B exhibe un poder discriminativo insignificante entre las dos clases, mientras que la variable A demuestra una capacidad predictiva moderada, logrando clasificaciones precisas para algunos casos pero arrojando resultados ambiguos para otros.

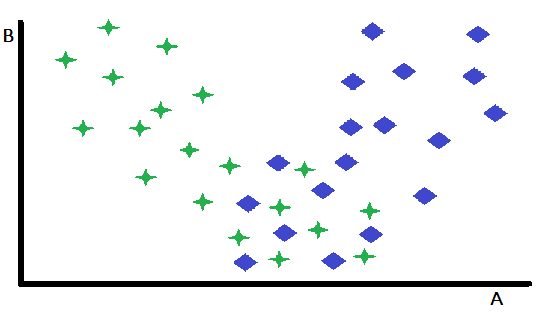
Un análisis detallado de un diagrama de dispersión de las características revela que la variable B delimita eficazmente los casos en los que A actúa como un clasificador robusto de aquellos en los que su poder predictivo disminuye. Específicamente, los casos caracterizados por altos valores de B muestran una precisión de clasificación superior cuando se utiliza A como predictor principal. Esta observación sugiere una estrategia de partición natural: dividir el conjunto de datos en función de un valor umbral de B. Esta partición permite el desarrollo de dos modelos de clasificación distintos: uno optimizado para instancias con valores altos de B (donde A es un predictor fuerte) y otro para instancias con valores bajos de B (donde A puede ser menos fiable).

Si bien este ejemplo simplificado demuestra el principio fundamental, es importante reconocer que los beneficios de dicha partición pueden ser limitados cuando el subconjunto restante de instancias resulta inherentemente difícil de clasificar. Una ventaja clave de este enfoque radica en su capacidad para aislar y abordar eficazmente los casos más fácilmente clasificables. Esta simplificación también ayuda en el desarrollo de modelos más eficientes para el subconjunto de datos restante, que resulta más complejo. Aunque el ejemplo descrito se centró en una sola variable para aclarar el concepto, en las aplicaciones prácticas, la selección del modelo apropiado puede depender de los valores de múltiples variables, que pueden o no estar incluidas en el conjunto principal de predictores utilizados por los modelos individuales.

Especialización aprendida

La especialización aprendida representa un enfoque más sofisticado para la segmentación, donde la variable de división óptima y su umbral correspondiente no se determinan a priori, sino que se aprenden a partir de los propios datos. Si bien la inspección visual de los diagramas de dispersión puede proporcionar ocasionalmente información preliminar sobre posibles variables de división y sus umbrales, estos enfoques intuitivos a menudo resultan insuficientes en aplicaciones del mundo real.

En la práctica, es necesario un enfoque más sistemático y basado en datos. Esto suele implicar un proceso de búsqueda riguroso, que explora una amplia gama de posibles variables de división y sus umbrales asociados. Para cada variable de división y umbral candidato, el conjunto de datos se divide y se entrenan y evalúan modelos separados en los subconjuntos resultantes. Este proceso iterativo de exploración, entrenamiento y evaluación puede ser computacionalmente exigente, especialmente cuando se trabaja con grandes conjuntos de datos o modelos complejos. Sin embargo, las posibles mejoras en el rendimiento del modelo a menudo justifican el mayor coste computacional.

Además, la búsqueda de variables de división óptimas no debe limitarse a un único candidato. En cambio, una evaluación exhaustiva de múltiples variables potenciales es esencial para identificar la estrategia de control más eficaz. Esto requiere una exploración sistemática del espacio de características para identificar las variables que exhiben un fuerte poder predictivo a la hora de determinar el modelo óptimo para cada subconjunto de los datos. La búsqueda de las variables de puerta óptimas se puede realizar empleando redes neuronales u otros algoritmos de aprendizaje para determinar la relación entre las entradas y los modelos de componentes.

Especialización aprendida utilizando las salidas del modelo como variables de control

Una variante de la especialización aprendida adopta un enfoque único para la selección de modelos, basándose en el análisis de las predicciones generadas por todos los modelos competidores. A diferencia de los métodos de selección que requieren variables predefinidas para seleccionar un modelo, este enfoque aprovecha las propias predicciones de los modelos como factores de toma de decisiones. En esencia, esta forma de especialización aprendida implica un análisis de meta-nivel de los resultados del modelo. Primero se invocan todos los modelos que compiten entre sí para generar predicciones para una entrada determinada. Posteriormente, estas predicciones se analizan para determinar el modelo más fiable para ese caso específico. Este enfoque transforma de manera efectiva las propias salidas del modelo en "variables de control" dinámicas que guían el proceso de selección.

Un ejemplo simplificado puede ilustrarse en un escenario de clasificación binaria con dos modelos que compiten entre sí. Cuando ambos modelos coinciden en la etiqueta de clase, el proceso de selección es sencillo. Sin embargo, en caso de desacuerdo, se requiere un enfoque sistemático para resolver el conflicto.

Un método que en ocasiones resulta eficaz, aunque primitivo, consiste en analizar los datos de entrenamiento para identificar la regla de decisión más fiable para resolver predicciones contradictorias. Este análisis requiere examinar los datos de rendimiento dentro de la muestra para determinar qué modelo presenta mayor precisión en escenarios de conflicto específicos. Por ejemplo, si un modelo supera sistemáticamente a un segundo modelo cuando ambos modelos discrepan, debería priorizarse la predicción del primer modelo.

Este enfoque basado en datos permite desarrollar un conjunto de reglas de decisión que optimizan la combinación de los resultados del modelo a partir de evidencia empírica.

Existen limitaciones obvias al aplicar este método simple. Si las muestras de entrenamiento no son representativas de la mayoría de las instancias fuera de la muestra que se encontrarán en el uso del mundo real, entonces el modelo de conjunto resultante será inútil. Las metodologías más sofisticadas, como la que se analizará en la próxima sección, presentan una mayor aplicabilidad y suelen demostrar un rendimiento superior en aplicaciones prácticas. No obstante, cuando se requiere un algoritmo computacionalmente eficiente y rápido, el método aquí presentado puede resultar adecuado. Además, un análisis en profundidad de este algoritmo simplificado proporciona una base valiosa para comprender conceptos más avanzados.

El código fuente completo de esta técnica se puede encontrar en el archivo oracle.mqh, que se adjunta al final de este artículo. El siguiente código es la declaración de la clase COracle.

//+------------------------------------------------------------------+
//| Tabulated combination of component model outputs                 |
//+------------------------------------------------------------------+
class COracle
  {
private:
   ulong             m_ncases;
   ulong             m_nin;
   ulong             m_ncats;
   uint              m_nmodels;
   matrix            m_thresh;
   ulong             m_tally[];
public:
                     COracle(void);
                    ~COracle(void);
   bool              fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats);
   double            predict(vector &inputs,IModel* &models[]);

  };

La clase define dos contenedores clave, m_thresh y m_tally. La matriz m_thresh almacena los umbrales de salida que dividen el conjunto de entrenamiento en subconjuntos de igual tamaño, mientras que la matriz m_tally identifica el modelo óptimo para cada uno de estos subconjuntos. Al invocar fit() se construye un modelo basado en los datos de entrenamiento proporcionados. La sección inicial de este método se muestra a continuación.

//+------------------------------------------------------------------+
//| fit an oracle                                                    |
//+------------------------------------------------------------------+
bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats)
  {
   if(predictors.Rows()!=targets.Size())
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return false;
     }

   m_ncases = predictors.Rows();
   m_nin = predictors.Cols();
   m_nmodels = models.Size();

   m_ncats = ncats;
   ulong nthresh = m_ncats - 1;
   ulong nbins = 1;

   nbins = (ulong)pow(m_ncats,m_nmodels);

   m_thresh = matrix::Zeros(m_nmodels,nthresh);

   ZeroMemory(m_tally);

   if(ArrayResize(m_tally,int(nbins))<0)
     {
      Print(__FUNCTION__," ", __LINE__," error ", GetLastError());
      return false;
     }

   matrix outputs(m_ncases,m_nmodels);
   matrix bins(nbins,m_nmodels);

   bins.Fill(0.0);

   vector inrow;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow=predictors.Row(icase);
      for(uint imodel =0; imodel<m_nmodels; imodel++)
         outputs[icase][imodel] = models[imodel].forecast(inrow);
     }

   double frac;
   for(uint imodel =0; imodel<m_nmodels; imodel++)
     {
      inrow = outputs.Col(imodel);
      qsortd(0,long(m_ncases-1),inrow);
      for(ulong i = 0; i<nthresh; i++)
        {
         frac = double(i+1)/double(ncats);
         m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))];
        }
     }

El método comienza recopilando las predicciones de cada modelo componente en la matriz de salidas. La matriz de intervalos se utiliza para contar el número de veces que cada modelo es el mejor dentro de un intervalo. A continuación, para cada columna de la matriz de salidas, el número de umbrales se determina encontrando las entradas equidistantes en el vector columna ordenado, inrow. La siguiente sección del método fit() progresa de la siguiente manera.

vector outrow;
   ulong ibin,index, klow, khigh, ibest, k;
   k = 0;
   double diff,best;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow = predictors.Row(icase);
      outrow = outputs.Row(icase);
      ibin = 0;
      index = 1;
      for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         if(outrow[imodel] <= m_thresh[imodel][0])
            k = 0;
         else
            if(outrow[imodel] > m_thresh[imodel][nthresh-1])
               k = nthresh;
            else
              {
               klow = 0;
               khigh = nthresh-1;
               while(true)
                 {
                  k = (klow+khigh)/2;
                  if(k == klow)
                    {
                     k = khigh;
                     break;
                    }
                  if(outrow[imodel]<=m_thresh[imodel][k])
                     khigh = k;
                  else
                     klow = k;
                 }
              }
         ibin += k * index;
         index *= ncats;
        }
      best = DBL_MAX;

Para cada muestra del conjunto de datos de entrenamiento, se determina el intervalo correspondiente a su predicción del modelo. Luego, se encuentra la predicción, del conjunto de predicciones del modelo de componentes, que más se aproxima al valor verdadero. Cuando se encuentra, se incrementa la combinación correspondiente de modelo y contenedor. La sección final del método fit() concluye con el siguiente código.

for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         diff = fabs(outrow[imodel] - targets[icase]);
         if(diff<best)
           {
            best = diff;
            k = imodel;
           }
        }
      bins[ibin][k]+=1.0;
     }

   for(ibin =0; ibin<nbins; ibin++)
     {
      k = 0;
      ibest = 0;
      for(uint imodel = 0; imodel<m_nmodels; imodel++)
        {
         if(bins[ibin][imodel] > double(ibest))
           {
            ibest = ulong(bins[ibin][imodel]);
            k = ulong(imodel);
           }
        }
      m_tally[ibin] = k;
     }

   return true;
  }

Los pasos finales implican recorrer la matriz de contenedores para encontrar el modelo que se seleccionó con mayor frecuencia para ese contenedor, y los índices de estos modelos se guardan en m_tally. El proceso de discretización empleado en este análisis utiliza una estructura matricial para categorizar de manera eficiente las muestras de entrenamiento en función de sus clasificaciones en múltiples modelos. La matriz puede considerarse como un vector que contiene otros vectores, de una longitud que corresponde al número de modelos que se están considerando. Cada una almacena la frecuencia con la que cada modelo fue designado como el más cercano al objetivo para la combinación específica de categorías representadas por el contenedor.

Para ilustrar esto, considere un escenario con tres modelos y cuatro categorías. Visualice un espacio tridimensional donde cada eje representa un modelo y está dividido en cuatro categorías. Esto da como resultado un cubo de 4x4x4, donde cada punto único dentro de este cubo representa una combinación distinta de asignaciones de categorías en los tres modelos.

El proceso de discretización utiliza un par de variables de indexación. El primero de este par se dirige directamente a un contenedor o fila específica de la matriz, que corresponde a la combinación única de categorías para una muestra. La segunda variable de indexación actúa como un factor de escala, asegurando que los incrementos naveguen correctamente a través del espacio multidimensional.

Este esquema de indexación garantiza que cada incremento del índice de fila posicione correctamente una muestra dentro del contenedor apropiado de la matriz, capturando de manera efectiva las asignaciones conjuntas de categorías en todos los modelos.

El método predict() ejecuta todos los modelos para encontrar el intervalo al que pertenecen las salidas. Luego se revisa la matriz m_tally para encontrar qué modelo es más probable que sea el más apropiado para aplicar a la muestra dada.

//+------------------------------------------------------------------+
//| make a prediction                                                |
//+------------------------------------------------------------------+
double COracle::predict(vector &inputs,IModel* &models[])
  {
   ulong k, klow, khigh, ibin, index, nthresh ;
   nthresh = m_ncats -1;
   k = 0;
   ibin = 0;
   index = 1;
   vector otk(m_nmodels);

   for(uint imodel = 0; imodel<m_nmodels; imodel++)
     {
      otk[imodel] = models[imodel].forecast(inputs);

      if(otk[imodel]<m_thresh[imodel][0])
         k = 0;
      else
         if(otk[imodel]>m_thresh[imodel][nthresh-1])
            k = nthresh - 1;
         else
           {
            klow=0;
            khigh = nthresh -1 ;
            while(true)
              {
               k = (klow + khigh) / 2;
               if(k == klow)
                 {
                  k = khigh;
                  break;
                 }
               if(otk[imodel] <= m_thresh[imodel][k])
                  khigh = k;
               else
                  klow = k;
              }
           }
      ibin += k*index;
      index *= m_ncats;
     }

   return otk[ulong(m_tally[ibin])];
  }

Probando el código

El script Oracle_Demo.mq5 prueba la funcionalidad de la clase COracle. Este programa permite al usuario configurar varios parámetros de simulación, incluyendo el tamaño del conjunto de datos de entrenamiento, el número de intervalos, el número de modelos y un nivel de ruido que controla la complejidad de la tarea de predicción. La siguiente salida del script presenta los resultados obtenidos en una serie de escenarios que involucran tres modelos de poder predictivo equivalente.

Dificultad de predicción fácil, 2 intervalos y tamaño de datos de entrenamiento de 10 muestras.

PF      0       13:59:15.542    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10777835
MQ      0       13:59:15.542    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835

Dificultad de predicción moderada, 2 intervalos y tamaño de datos de entrenamiento de 10 muestras.

FD      0       14:00:30.967    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38588979
KG      0       14:00:30.967    Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990

Dificultad de predicción alta, 2 intervalos y tamaño de datos de entrenamiento de 10 muestras.

ES      0       14:01:11.874    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16908710
ND      0       14:01:11.874    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689

Dificultad de predicción fácil, 2 intervalos y tamaño de datos de entrenamiento de 100 muestras.

LQ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10706090
NJ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483

Dificultad de predicción moderada, 2 intervalos y tamaño de datos de entrenamiento de 100 muestras.

LL      0       14:04:24.070    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36310507
JO      0       14:04:24.070    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485

Dificultad de predicción alta, 2 intervalos y tamaño de datos de entrenamiento de 100 muestras.

RJ      0       14:06:02.290    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12115161
PM      0       14:06:02.290    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456

Dificultad de predicción fácil, 4 intervalos y tamaño de datos de entrenamiento de 100 muestras.

FI      0       14:08:24.445    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10681953
FR      0       14:08:24.445    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329

Dificultad de predicción moderada, 4 intervalos y tamaño de datos de entrenamiento de 100 muestras.

KG      0       14:10:29.012    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36348921
LP      0       14:10:29.012    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647

Dificultad de predicción alta, 4 intervalos y tamaño de datos de entrenamiento de 100 muestras.

MR      0       14:12:16.225    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12231642
EE      0       14:12:16.225    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202

Experimentos posteriores incorporaron un cuarto modelo, diseñado para producir predicciones aleatorias, simulando así un escenario con un modelo no informativo. Los resultados, que se presentan a continuación, demuestran una alteración significativa en el comportamiento del sistema.

Dificultad de predicción fácil, 2 intervalos y tamaño de datos de entrenamiento de 10 muestras.

GH      0       14:13:47.886    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12971017
MS      0       14:13:47.886    Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652

Dificultad de predicción moderada, 2 intervalos y tamaño de datos de entrenamiento de 10 muestras.

JN      0       14:14:16.985    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.40381512
MI      0       14:14:16.985    Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764

Dificultad de predicción alta, 2 intervalos y tamaño de datos de entrenamiento de 10 muestras.

ND      0       14:14:54.040    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16720001
OG      0       14:14:54.040    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663

Dificultad de predicción fácil, 2 intervalos y tamaño de datos de entrenamiento de 100 muestras.

QJ      0       14:17:05.521    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12727773
HM      0       14:17:05.521    Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364

Dificultad de predicción moderada, 2 intervalos y tamaño de datos de entrenamiento de 100 muestras.

QP      0       14:18:26.976    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38337835
CK      0       14:18:26.976    Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874

Dificultad de predicción alta, 2 intervalos y tamaño de datos de entrenamiento de 100 muestras.

IF      0       14:20:01.925    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13780482
IQ      0       14:20:01.925    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032

Dificultad de predicción fácil, 4 intervalos y tamaño de datos de entrenamiento de 100 muestras.

HL      0       14:23:03.090    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12709947
QO      0       14:23:03.090    Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572

Dificultad de predicción moderada, 4 intervalos y tamaño de datos de entrenamiento de 100 muestras.

CR      0       14:25:25.091    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38314408
CE      0       14:25:25.091    Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436

Dificultad de predicción alta, 4 intervalos y tamaño de datos de entrenamiento de 100 muestras.

GH      0       14:27:50.024    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13828093
CS      0       14:27:50.024    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816

El análisis de ambos conjuntos de resultados muestra que, en escenarios con bajos niveles de ruido, esta técnica demuestra una eficacia excepcional, lo que resulta en una reducción sustancial de la varianza del error. Por el contrario, en escenarios con mucho ruido, la técnica no solo no proporciona mejoras significativas, sino que con frecuencia conduce a un rendimiento inferior en comparación con la utilización de un solo modelo. Este fenómeno se observa incluso cuando todos los modelos constituyentes poseen un poder predictivo equivalente, aunque las diferencias de rendimiento en tales casos son, sin duda, menores.

Las pruebas también revelan que utilizar cuatro contenedores en lugar de dos produjo diferencias de rendimiento inconsistentes e insignificantes. Este resultado no es sorprendente dado que o bien todos los modelos presentan un poder predictivo comparable o bien un modelo produce sistemáticamente predicciones inútiles. La función principal de este algoritmo, en el presente contexto, es identificar y descartar modelos no informativos cuando estén presentes. Sin embargo, es posible que existan escenarios en los que un mayor número de categorías resulte beneficioso.

Conjuntos de regresión general con compuertas

Esta sección presenta una técnica de amplia aplicación para la combinación de modelos que aprovecha las variables de control. El método se inspira en conceptos de las Redes Neuronales de Regresión General (General Regression Neural Networks, GRNN) y permite que una o más variables actúen como puertas dinámicas, modulando la influencia de cada modelo contribuyente. A diferencia de los métodos de selección anteriores, que requieren seleccionar un único modelo para producir el resultado final, la selección por regresión general integra los resultados de todos los modelos constituyentes ponderando de forma óptima cada uno en función de las variables de selección. Estas variables de control pueden incluir valores medidos externos, así como los resultados de los modelos individuales. Este enfoque se conoce como método de regresión general con compuertas.

La implementación de este método requiere al menos dos modelos de componentes entrenados y un conjunto de datos separado para entrenar el conjunto inspirado en GRNN. El conjunto de datos de entrenamiento debe contener una o más variables de puerta, predicciones de los modelos de componentes y valores objetivo correspondientes. Cabe destacar que también es posible designar ciertas salidas de los modelos de componentes como variables de control, lo que mejora aún más la flexibilidad del enfoque.

Una red neuronal de regresión general (General Regression Neural Networks, GRNN) es un tipo de red neuronal artificial diseñada para tareas de regresión, que implican la predicción de salidas continuas. GRNN funciona según los principios de la estimación de densidad kernel y se basa en un enfoque de aprendizaje basado en la memoria. Consta de cuatro capas: entrada, patrón, suma y salida.

La capa de entrada recibe las variables predictoras, que se pasan a la capa de patrones, donde cada neurona representa una muestra de entrenamiento y calcula la similitud entre la entrada y los datos de entrenamiento utilizando una función de base radial. La capa de suma agrega las salidas ponderadas de la capa de patrones, y la capa de salida produce la predicción final normalizando la suma de los pesos.

La GRNN resulta particularmente ventajosa para modelar relaciones no lineales, ya que requiere un tiempo de entrenamiento mínimo y se adapta automáticamente a la distribución de datos subyacente.

En este contexto, la distancia euclidiana ponderada entre una muestra de prueba y una muestra de entrenamiento está determinada por las variables de puerta. Específicamente, al evaluar una muestra de prueba, la puerta GRNN prioriza las muestras de entrenamiento cuyas variables de puerta se asemejan mucho a las de la muestra de prueba. Al emplear la GRNN para predecir el error cuadrático de un modelo, el error cuadrático previsto para un modelo de componente se calcula utilizando la ecuación siguiente.

Si bien existen infinitas maneras de combinar modelos de componentes para producir una predicción conjunta, el enfoque más sencillo consiste en expresar la predicción final como una combinación lineal de las salidas de los modelos. Si los modelos componentes exhiben la propiedad deseable de predicciones imparciales, esta propiedad se conserva solo si se impone la condición de que la suma de los pesos sea igual a la unidad. Incluso cuando las predicciones no son estrictamente imparciales, esta condición sigue siendo ventajosa en la mayoría de los escenarios. Para una combinación lineal de estimadores insesgados con error cuadrático medio mínimo, las ponderaciones óptimas son proporcionales al recíproco de la varianza de cada estimador. Sustituyendo la varianza por el error cuadrático previsto, los pesos se pueden calcular utilizando la siguiente fórmula.

Para generar una predicción controlada por GRNN, dados los valores apropiados para los pesos sigma, comenzamos estimando el error de predicción para cada modelo en una muestra de prueba determinada. Posteriormente, se calculan los pesos y se evalúan los modelos de componentes en la muestra de prueba. Finalmente, las predicciones individuales de los modelos componentes se combinan en una estimación final utilizando las ponderaciones calculadas.

Determinar los valores óptimos para los pesos sigma no es tarea fácil, ya que requiere una estimación utilizando los datos de entrenamiento. El método más eficaz para evaluar la calidad de un vector sigma candidato es mediante validación cruzada. Esto implica extraer una muestra del conjunto de entrenamiento para que sirva como caso de prueba, generar una predicción con puerta GRNN para esta muestra utilizando el vector sigma especificado y comparar el valor predicho con el valor verdadero. La muestra se devuelve entonces al conjunto de entrenamiento y el proceso se repite para todas las muestras del conjunto de datos. El error cuadrático medio en estas repeticiones sirve como medida de la calidad del vector sigma candidato.

Cualquier algoritmo de optimización sin derivadas puede utilizarse para determinar el conjunto de pesos sigma que minimiza el error de validación cruzada. Entre las opciones disponibles, la evolución diferencial se reconoce por su robustez y amplia aplicabilidad. Sin embargo, el método de Powell ofrece una alternativa computacionalmente eficiente, mostrando un rendimiento satisfactorio en la mayoría de las aplicaciones prácticas. Dada su eficiencia, se adopta el método de Powell para este estudio, a pesar de la superioridad ocasional de la evolución diferencial en casos raros que involucran múltiples extremos locales.

El archivo, gatedreg.mqh, contiene el código fuente de la clase CGatedReg, que implementa el método de conjunto con compuertas inspirado en GRNN que acabamos de describir. La declaración de la clase se presenta a continuación.

//+------------------------------------------------------------------+
//|  GRNN gating model combination                                   |
//+------------------------------------------------------------------+
class CGatedReg:public CPowellsMethod
  {
private:
   ulong             m_nsamples;
   ulong             m_ngates;
   ulong             m_nmodels;
   matrix            m_tset;
   vector            m_sigma;
   vector            m_errvals;
   vector            m_params;

   double            criter(vector &params);
   double            trial(vector &gates, vector &contenders,long i_exclude,long n_exclude);
   virtual double    func(vector &p) {  return criter(p); }
public:
                     CGatedReg(void);
                    ~CGatedReg(void);
   bool              fit(matrix &gates, matrix &contenders,vector &targets);
   double            predict(vector &gates, vector &contenders);
  };

Se supone que las predicciones de los modelos de componentes se han precalculado y almacenado en una matriz. Cada modelo debe haber sido entrenado previamente para predecir la variable dependiente. Se emplearán variables de puerta (a menudo una sola variable) para ponderar diferencialmente las contribuciones de estos modelos componentes en la predicción final. El método fit() se encarga de copiar los datos de entrenamiento necesarios y determinar los pesos sigma óptimos. A continuación se proporciona la implementación del método.

//+------------------------------------------------------------------+
//| fit a gated grnn model                                           |
//+------------------------------------------------------------------+
bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets)
  {
   if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size()  || gates.Rows()!=targets.Size())
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid training data ");
      return false;
     }
   m_nsamples = gates.Rows();
   m_ngates = gates.Cols();
   m_nmodels = contenders.Cols();

   m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1);
   m_sigma = vector::Zeros(m_ngates);
   m_errvals = vector::Zeros(m_nmodels);

   for(ulong i = 0; i<m_nsamples; i++)
     {
      for(ulong j = 0; j<m_ngates; j++)
         m_tset[i][j] = gates[i][j];
      for(ulong k = 0; k<m_nmodels; k++)
         m_tset[i][m_ngates+k] = contenders[i][k];
      m_tset[i][m_ngates+m_nmodels] = targets[i];
     }

   m_params = vector::Zeros(m_ngates);

   double err =  criter(m_params);
   if(err > 0.0)
      Optimize(m_params);

   criter(m_params);

   return true;

  }

Los datos de entrenamiento, que comprenden todas las entradas al método fit(), deben conservarse ya que las predicciones posteriores requieren el uso de regresión general para la predicción de errores intermedios de cada modelo. Además, se requerirá el vector m_errval para cada predicción. La técnica de optimización de Powell se utiliza para identificar los pesos sigma óptimos. La función objetivo a minimizar se define como el método privado criter().

//+------------------------------------------------------------------+
//|  function criterion                                              |
//+------------------------------------------------------------------+
double CGatedReg::criter(vector &params)
  {
   int i, ngates, nmodels, ncases;
   double  out, diff, error, penalty ;
   vector inputs1,inputs2,row;

   ngates = int(m_ngates); ;
   nmodels = int(m_nmodels) ;
   ncases = int(m_nsamples) ;

   penalty = 0.0 ;
   for(i=0 ; i<ngates ; i++)
     {
      if(params[i] > 8.0)
        {
         m_sigma[i] = exp(8.0) ;
         penalty += 10.0 * (params[i] - 8.0) ;
        }
      else
         if(params[i] < -8.0)
           {
            m_sigma[i] = exp(-8.0) ;
            penalty += 10.0 * (-params[i] - 8.0) ;
           }
         else
            m_sigma[i] = exp(params[i]) ;
     }

   error = 0.0 ;

   for(i=0 ; i<ncases ; i++)
     {
      row = m_tset.Row(i);
      inputs1 = np::sliceVector(row,0,m_ngates);
      inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels));
      out = trial(inputs1, inputs2, long(i), 0) ;
      diff = row[ngates+nmodels] - out ;
      error += diff * diff ;
     }

   return error / double(ncases) + penalty ;

  }

Este método emplea la validación cruzada para evaluar la calidad de un vector sigma de prueba. En lugar de optimizar directamente cada sigma, se optimiza el logaritmo de sigma. Esto linealiza el impacto de las variaciones, lo que resulta en una mayor estabilidad. Para mitigar los problemas asociados con la superficie de error de una puerta GRNN que presenta planitud para valores extremos. La función criterio inicialmente eleva al exponente el parámetro al tiempo que impone un rango acotado. Se introduce un término de penalización para fomentar valores sigma que no sean extremos. Para cada muestra de entrenamiento, se realiza una predicción y esta predicción se compara con el valor verdadero. El error cuadrático se acumula para servir como criterio de error.

Los elementos m_errvals se inicializan a cero para acumular el numerador de la ecuación de error. El denominador de esta ecuación no requiere cálculo explícito, ya que se cancela al considerar el factor de normalización en el denominador de la ecuación de ponderaciones. Antes de incorporar cada término a la suma, se verifica la proximidad secuencial de una muestra de prueba a una muestra de entrenamiento.

Este método puede utilizarse para realizar predicciones basadas tanto en los miembros del conjunto de entrenamiento como en muestras totalmente desconocidas. Al pasar el número de secuencia i_exclude de cada muestra de entrenamiento a la rutina trial(), se puede implementar la validación cruzada. También se pasa un límite de distancia, n_exclude. Normalmente, este valor se establece en cero, excluyendo únicamente el caso individual.

Los lectores deben tener en cuenta que el algoritmo de validación cruzada tiene una limitación importante a la hora de manejar conjuntos de entrenamiento que presentan correlación serial. Lo cual es común en los datos de series temporales. Esto se puede solucionar excluyendo las muestras que estén espacialmente próximas a la muestra de entrenamiento que se está probando.

//+------------------------------------------------------------------+
//| trial ( )                                                        |
//+------------------------------------------------------------------+
double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude)
  {
   int icase, ivar, idist, size, ncases;
   double psum, diff, dist, err, out ;

   m_errvals.Fill(0.0);
   int ngates = int(m_ngates);
   int nmodels = int(m_nmodels);
   size = ngates + nmodels + 1 ;
   ncases = int(m_nsamples);

   for(icase=0 ; icase<ncases ; icase++)
     {

      idist = (int)fabs(int(i_exclude) - icase) ;
      if(ncases - idist < idist)
         idist = ncases - idist ;

      if(idist <= int(n_exclude))
         continue ;

      dist = 0.0 ;

      for(ivar=0 ; ivar<ngates ; ivar++)
        {
         diff = gates[ivar] - m_tset[icase][ivar] ;
         diff /= m_sigma[ivar] ;
         dist += diff * diff ;
        }

      dist = exp(-dist) ;

      for(ivar=0 ; ivar<nmodels ; ivar++)
        {
         err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ;
         m_errvals[ivar] += dist * err * err ;
        }

     }

   psum = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
     {
      if(m_errvals[ivar] > 1.e-30)
         m_errvals[ivar] = 1.0 / m_errvals[ivar] ;
      else
         m_errvals[ivar] = 1.e30 ;
      psum += m_errvals[ivar] ;
     }

   for(ivar=0 ; ivar<nmodels ; ivar++)
      m_errvals[ivar] /= psum ;

   out = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
      out += m_errvals[ivar] * contenders[ivar] ;

   return out ;
  }

Si un caso de entrenamiento pasa la prueba de exclusión de validación cruzada, se calcula la distancia euclidiana ponderada entre los dos casos. Esta distancia se eleva a la potencia de la anterior para utilizarla en el cálculo del error de predicción para cada modelo de componente. Posteriormente, para cada modelo, se determina el error de predicción. El paso final consiste en utilizar la ecuación de ponderación del modelo para combinar los resultados de cada modelo candidato en una única predicción. Esto constituye el valor de retorno de la función.

//+------------------------------------------------------------------+
//|  infer                                                           |
//+------------------------------------------------------------------+
double CGatedReg::predict(vector &gates,vector &contenders)
  {
   return trial(gates,contenders,-1,0);
  }

Prueba de un conjunto GRNN con compuertas

El script Gating_Demo.mqh ofrece una comparación exhaustiva de cuatro estrategias de control distintas. Cada estrategia cumple un propósito único al demostrar diferentes aspectos de la selección y combinación de modelos. Aquí tenéis un breve resumen de las cuatro estrategias:

• Predicciones de componentes como variables de control: Este enfoque utiliza directamente las predicciones de los modelos de componentes individuales como variables de control, lo que permite una comparación directa con el método de referencia (clase COracle). Prueba el efecto de utilizar los propios resultados de los modelos como factores de decisión en la selección de modelos.

• Control de variables originales: En esta estrategia, las variables de entrada originales (las utilizadas por los modelos de componentes) sirven como variables de control. Dado que estas variables no están diseñadas para actuar como señales de activación efectivas, este enfoque ayuda a demostrar el impacto de las variables de activación deficientes o irrelevantes en el rendimiento del modelo.

• Control aleatorio: Esta estrategia emplea números generados aleatoriamente como variables de control, simulando un escenario donde no hay variables de control informativas disponibles. Sirve como punto de referencia para mostrar la caída del rendimiento al utilizar señales completamente no informativas.

• Control basado en ratios: En este enfoque, se utiliza el logaritmo del ratio entre los errores de predicción del primer y segundo modelo como variable de control. Si bien este método sería poco realista en un entorno del mundo real (ya que el verdadero error de predicción de los modelos generalmente se desconoce), sirve como un escenario idealizado para dos modelos. Para múltiples modelos, proporciona información de activación parcial pero aún valiosa.

Estas cuatro estrategias están diseñadas para probar diversas condiciones de rendimiento y ofrecer información sobre las fortalezas y limitaciones de diferentes técnicas de control para el aprendizaje conjunto. El script evalúa cómo cada estrategia de control afecta la precisión general de la predicción y la varianza del error, lo que permite una comprensión más clara de la efectividad del mecanismo de control GRNN.

Tres modelos, 100 muestras y baja dificultad de predicción.

EK      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  1000    replications completed.
GL      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10790466
JP      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Component error = 0.10790458
DF      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Original error = 0.10790458
HM      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Random error = 0.10790458
DJ      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458

Tres modelos, 100 muestras y alta dificultad de predicción.

GF      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12143040
FE      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Component error = 1.11991444
GQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Original error = 1.11991445
QI      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Random error = 1.11991443
EO      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443

Cuatro modelos, 100 muestras y baja dificultad de predicción.

IO      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LK      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12792841
RS      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Component error = 0.11516554
MK      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Original error = 0.11516373
GR      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Random error = 0.11516595
GE      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Ratio error = 0.11516595

Cuatro modelos, 100 muestras y alta dificultad de predicción.

QQ      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  1000    replications completed.
HE      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.14025014
EI      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Component error = 1.13144872
GM      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Original error = 1.13144863
QD      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Random error = 1.13144883
NL      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882

La sorprendente mejora en el rendimiento lograda mediante la activación aleatoria se puede atribuir al funcionamiento del algoritmo de activación GRNN. En escenarios típicos, cabría esperar que las señales de activación aleatorias empeoraran el rendimiento del modelo porque introducen ruido y no proporcionan información útil para la selección del modelo. Sin embargo, el mecanismo GRNN se basa en distancias euclidianas ponderadas entre muestras de entrenamiento y ajusta su predicción en función de la similitud entre la muestra de prueba y las muestras de entrenamiento.

En los casos en que la señal de activación es aleatoria, el algoritmo GRNN sigue utilizando la estructura general de los datos y los modelos para calcular un promedio ponderado de las predicciones del modelo componente. Dado que los valores de activación aleatorios no introducen un sesgo fuerte hacia ningún modelo en particular, el algoritmo puede depender más de la estructura inherente de los datos y del rendimiento de los modelos individuales, que están entrenados para predecir bien. El resultado global puede ser una combinación más robusta de modelos, donde la selección aleatoria actúa como un neutralizador, asegurando que ningún modelo individual domine el proceso de toma de decisiones.

En el caso de que tres modelos muestren una alta precisión predictiva y un modelo genere predicciones aleatorias, el enfoque de selección aleatoria podría actuar inadvertidamente como un método para descartar el modelo aleatorio al reducir su influencia en el conjunto. Esto conduce a una situación en la que el rendimiento del modelo de conjunto mejora significativamente, ya que se minimiza la influencia del modelo aleatorio no informativo.

Así, aunque la selección aleatoria de variables pueda no parecer intuitivamente beneficiosa, el proceso de selección de variables de GRNN puede aprovechar la estructura del conjunto de datos y los modelos de maneras que resulten en mejoras inesperadas, especialmente en problemas de predicción "fáciles" donde los modelos ya son muy precisos. Este comportamiento subraya el poder de la técnica de compuerta GRNN, que, incluso en situaciones subóptimas, puede aprovechar el potencial de múltiples modelos para ofrecer predicciones mejoradas al ponderar eficazmente la contribución de cada modelo.

El algoritmo estima de forma efectiva el error de predicción de cada modelo. En presencia de un modelo con errores de predicción consistentemente altos, como en el caso del modelo de predicción aleatoria, el error de predicción generará consistentemente estimaciones de error grandes para ese modelo. Lo cual da como resultado que el esquema de ponderación del conjunto asigne un peso correspondientemente bajo a este modelo dentro de la combinación ponderada.

Esta observación subraya la ventaja clave de la segmentación GRNN. Puede identificar y reducir eficazmente la ponderación de modelos con un rendimiento predictivo deficiente, incluso cuando las propias variables de control carecen de poder predictivo inherente. En consecuencia, incluso en situaciones en las que las señales de activación proporcionan información limitada o nula, la activación de GRNN aún puede generar mejoras de rendimiento significativas, particularmente cuando el conjunto incluye modelos con diferentes niveles de precisión predictiva.

Conclusión

Estas técnicas demuestran la adaptabilidad de los mecanismos de control para mejorar la interpretabilidad y el poder predictivo de los algoritmos de aprendizaje. La elección de la técnica depende del contexto específico, incluyendo la complejidad de la tarea, la naturaleza de los datos y las limitaciones computacionales. Con frecuencia, una combinación de métodos, como técnicas de optimización combinadas con conocimientos del dominio, produce los resultados más eficaces e interpretables. Todo el código al que se hace referencia en el artículo se adjunta al final. La tabla siguiente describe todos los archivos fuente adjuntos.

Nombre del archivo	Descripción
MQL5/include/gatedreg.mqh	Contiene la definición de la clase CGatedReg que implementa un conjunto GRNN con compuertas.
MQL5/include/imodel.mqh	Contiene la definición de interfaces que encapsulan un modelo entrenado.
MQL5/include/minimize.mqh	Proporciona la definición del método CPowellsMethod, que implementa la minimización de funciones utilizando el método de Powell.
MQL5/include/multilayerperceptron.mqh	Proporciona la definición de una clase CMlp, que es una implementación de un perceptrón multicapa.
MQL5/include/np.mqh	Una colección de funciones auxiliares genéricas para manipular vectores y matrices.
MQL5/include/oracle.mqh	Proporciona la definición de la clase COracle y permite la selección de modelos a partir de un conjunto de modelos de componentes especializados.
MQL5/include/qsort.mqh	Proporciona funciones sencillas para ordenar vectores.
Mql5/scripts/Gating_Demo.mq5	Un script que demuestra la funcionalidad proporcionada por la clase CGatedReg.
Mql5/scripts/Oracle_Demo.mq5	Otro script que demuestra el uso de la clase COracle.