Population optimization algorithms: Artificial Bee Colony (ABC)

Contents

1. Introduction
2. Algorithm description
3. Modified version
4. Test results
   

1. Introduction

Social insects are highly evolved creatures that perform many complex tasks not performed by many single insects. Communication, complex nest building, environmental control, protection and division of labor are just a few of the behaviors that honey bees have evolved to thrive in social colonies.
Bees belong to swarm beings and demonstrate extraordinary abilities in finding optimal solutions. In nature, they find clusters of flowers to collect nectar and pollen near the hive. Sometimes the search radius can increase up to several kilometers. Returning bees report their findings using an improvised dance.

At first glance, it seems that this is impossible, but they are able to transmit information about the geographical position to each other through rhythmic movements. Depending on the intensity of the dance of their brethren, the bees draw conclusions about the number of flowers and the estimated amount of nectar at a specified point. The more potential food, the more actively the dance takes place. This unusual phenomenon was discovered in the middle of the 20th century by insect researcher Karl von Frisch.

For many years, the bee search methods were researched exclusively by biologists. However, the interest in applying swarm behavior in the development of new optimization algorithms was growing. In 2005, professor Dervis Karaboga became interested in the research results. He published a scientific article and was the first to describe the model of swarm intelligence mostly inspired by bee dance. The model was called the artificial bee colony.

2. Algorithm description

There are many implementations of an artificial bee colony, differing in the principles of managing bees in a hive and in area exploration rules. In this article, I will talk about my interpretation of the classic version of the algorithm.

The idea of the algorithm is based on the bee behavior when searching for places where they can get as much nectar as possible. First, all the bees fly out of the hive in a random direction, acting as scouts and trying to find areas where there is nectar. After that, the bees return to the hive and in a special way tell the others where and how much nectar they found.

Worker bees are sent to the found areas. The more nectar is supposed to be found in this area, the more bees fly in that direction. The scouts again fly away to look for other areas, but already in the vicinity of the areas found. Thus, all bees are divided into two types: worker bees collecting nectar and scout bees exploring new areas. Nectar collection areas have a value corresponding to the amount of nectar in them. Regions of a lower rank are displaced relative to a region of a higher rank along a line passing through the centers of the regions.

Schematically, the distribution of worker bees by region can be visualized in Figure 1.

Fig. 1. The number of bees in areas depending on the area ranks

Area 1 has a higher rank, it contains the most nectar, so more bees tend to fly there. By the number of bees, we can visually determine that area 4 has the lowest rank (value). Information about the value of each area is reported by bees in the form of a special dance. Each hive has its own dance, in which the direction and amount of nectar in the area is programmed.

Suppose that the location of the global extremum is the area where there is the most nectar, and there is only one such area. There is nectar in other places, albeit in less amount. Bees live in multidimensional space, where each coordinate represents one parameter of the function that needs to be optimized. The found amount of nectar is the value of the objective function at this point if we are looking for a global maximum. If we are looking for a global minimum, then it is enough to multiply the objective function by -1.

Since the nectar collection areas have a certain value, only the area with the highest rank has the right to move (center shift) to the point with the highest concentration of nectar. Areas of a lower rank will be shifted to the center of the highest concentration and checked for the intersection with an area of a higher rank. In this way, the concentration of bees in some narrow small area is not allowed, and the search space is served by worker bees as efficiently as possible, thereby preventing the depletion of the food source. In terms of optimization, this eliminates or minimizes getting stuck in local extrema. After the areas are dispersed and shifted relative to each other along the chain of rank towards their optimums, their neighborhoods will be additionally investigated by bee scouts.

Many beekeepers recommend sending scout bees to random areas of the search space, but my experience shows that the practical value of such "scouting" is close to zero and is only useful for one and two dimensions. In other words, if we are talking about multidimensional spaces, then the degrees of freedom increase geometrically, and it is incredibly difficult to accidentally stumble upon a more valuable source of nectar. The resources of the hive will only be wasted. It is much more useful to send scouts to the neighborhoods of the already known search areas, so that the coordinates are not scattered, but are concentrated specifically in the zones of possible sources of nectar.

If the areas intersect, it is necessary to shift the center so that the areas touch only the borders. This is shown in Figure 2.

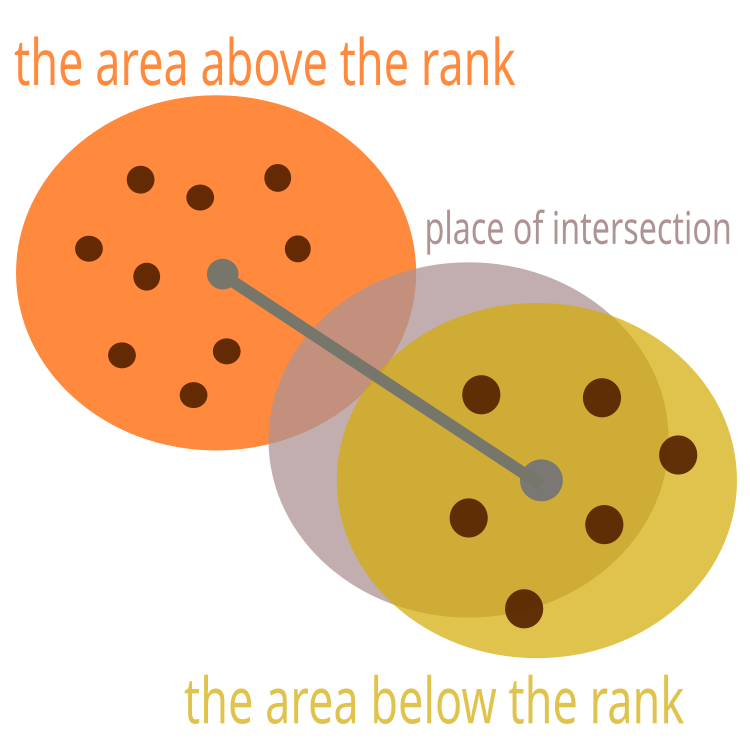
Fig 2. The area having a lower rank should be shifted

The rank of areas is not rigidly set, but is formed dynamically. The finds of scout bees will be assigned to the area, in the vicinity of which they flew. In case more valuable food source is discovered, the center of the area will be shifted there. It may even become the new best nectar collection center. The remaining areas will now be shifted relative to it. In other words, they will be shifted relative to it along the rank chain.

The method of transmitting information, which is called the dance of the bees, is an essential element of the strategy of the hive as a whole. It is necessary to most rationally distribute the available resources of the hive for processing areas, so the number of sent bees should be proportional to the value of the area. This means an equal number of bees will be sent to areas of equal value.

Let's move on to the algorithm itself. The execution steps are listed below:

1. All bees fly randomly along the search space as scouts.
2. Measure the amount of nectar received from each bee.
3. Sorting bees.
4. Assign areas according to the nectar amount information obtained from bees.
5. Sending worker bees to the area. The more nectar in the area, the more bees will be sent.
6. Sending scout bees in the vicinity of a randomly selected area.
   
7. Measuring the amount of nectar received from each bee.
8. Ranking the areas by the amount of nectar.
   
9. Repeating p. 4 until the stop criterion is met.

For ease of visual perception, let's make a block diagram of the algorithm in Figure 3.

Fig. 3. Algorithm block diagram

Let's describe the Bee Colony algorithm code in more detail.

A bee is an elementary and basic logical unit of the algorithm. It can be described by a structure. As you might remember, a bee location is set by coordinates, affiliation with the area nectar was collected in and the amount of nectar. The bees of the hive will then be represented by an array. Each one can be accessed by its index.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bee
{
  double c []; //coordinates
  int    aInd; //area index
  double n;    //nectar
};
//——————————————————————————————————————————————————————————————————————————————

The second, larger logical unit is the area of nectar collection. It is defined by the center and point of the greatest concentration of nectar and the amount of nectar that determines the value of the area. In the area of the highest rank (the first in the list), the coordinates of the center and the highest concentration of nectar coincide. For areas of the second and lower ranks in the list, they may not match, since they have been shifted. The initialization of the area concludes with resetting the nectar amount indicator and distributing the coordinates to the corresponding number of parameters of the optimized function.

//——————————————————————————————————————————————————————————————————————————————
struct S_Area
{
  void Init (int coordinatesNumber)
  {
    n = -DBL_MAX;

    ArrayResize (cC, coordinatesNumber);
    ArrayResize (cB, coordinatesNumber);
  }

  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

Let's describe the dance of the bees as a structure, the array of which will correspond to the number of areas.

//——————————————————————————————————————————————————————————————————————————————
struct S_BeeDance
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

I will describe the hive as a class setting search areas, bees, best coordinates and the largest amount of nectar found in all iterations. Also, all the necessary methods for sorting bees and areas, as well as moving bees and areas relative to each other will be defined here. Here we can see the already familiar function declarations for the previous algorithms: generating random evenly distributed numbers, scaling to a range and choosing a number from a range with a step.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABC //Bees Hive
{
  //============================================================================
  public: S_Area areas     []; //nectar collection areas
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Bee  bees      []; //all the bees of the hive
  public: double cB        []; //best coordinates
  public: double nB;           //nectar of the best coordinates

  public: void InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP); //scout area radius

  public: void TasksForBees ();
  public: void CollectingNectar ();

  //============================================================================
  private: void   BeeFlight      (double &cC [] , S_Bee &bee);
  private: void   ScoutBeeFlight (double &cC [] , S_Bee &bee);
  private: void   MarkUpAreas    ();
  private: void   SortingBees    ();
  private: void   SortingAreas   ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: int    coordinates;      //coordinates number
  private: int    beesNumber;       //the number of all bees
  private: int    workerBeesNumber; //worker bees number
  private: int    areasNumber;      //areas number
  private: S_Bee  beesT       [];   //temporary, for sorting
  private: S_Area areasT      [];   //temporary, for sorting
  private: int    indA        [];   //array for indexes when sorting
  private: double valA        [];   //array for nectar values when sorting
  private: int    indB        [];   //array for indexes when sorting
  private: double valB        [];   //array for nectar values when sorting
  private: double areasRadius [];   //radius for each coordinate
  private: double scoutRadius [];   //scout radius for each coordinate

  private: double collectionRadius;   //collection radius
  private: double scoutAreaRadius;    //scout area radius
  private: double hypersphereRadius;  //hypersphere radius
  private: double distHyperspCenters; //distance hyperspheres centers
  private: double scoutHyperspRadius; //scout hypersphere radius
  private: bool   scouting;           //scouting flag

  private: S_BeeDance beeDance [];    //bee dance
};
//——————————————————————————————————————————————————————————————————————————————

Each new optimization should necessarily begin with class initialization. The value of the amount of nectar is reset for the entire hive and for individual bees, as well as for areas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP)  //scout area radius
{
  MathSrand (GetTickCount ());
  scouting = false;
  nB       = -DBL_MAX;

  coordinates      = coordinatesP;
  beesNumber       = beesNumberP;
  workerBeesNumber = workerBeesNumberP;
  areasNumber      = areasNumberP < 3 ? 3 : areasNumberP;

  collectionRadius = collectionRadiusP; //collection radius
  scoutAreaRadius  = scoutAreaRadiusP;  //scout area radius

  ArrayResize (areas,  areasNumber);
  ArrayResize (areasT, areasNumber);
  for (int i = 0; i < areasNumber; i++)
  {
    areas  [i].Init (coordinates);
    areasT [i].Init (coordinates);
  }

  ArrayResize (beeDance, areasNumber);

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (indA, areasNumber);
  ArrayResize (valA, areasNumber);

  ArrayResize (areasRadius, coordinates);
  ArrayResize (scoutRadius, coordinates);
  for (int i = 0; i < coordinates; i++)
  {
    areasRadius [i] = (rangeMax [i] - rangeMin [i]) * collectionRadius;
    scoutRadius [i] = (rangeMax [i] - rangeMin [i]) * scoutAreaRadius;
  }

  double sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += areasRadius [i] * areasRadius [i];
  hypersphereRadius  = MathSqrt (sqr) * collectionRadius;

  distHyperspCenters = hypersphereRadius * 2.0;

  sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += scoutRadius [i] * scoutRadius [i];
  scoutHyperspRadius = MathSqrt (sqr) * scoutAreaRadius;

  ArrayResize (indB, beesNumber);
  ArrayResize (valB, beesNumber);

  ArrayResize (bees,  beesNumber);
  ArrayResize (beesT, beesNumber);
  for (int i = 0; i < beesNumber; i++)
  {
    ArrayResize (bees  [i].c, coordinates);
    ArrayResize (beesT [i].c, coordinates);
    bees  [i].n = -DBL_MAX;
    beesT [i].n = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

The simplest and also open class method is the distribution of tasks to bees. Everything is simple here. If the areas have not yet been explored, then we reset the nectar value for the entire hive and launch the area marking. We call the method on each epoch until the value of the fitness function is obtained.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::TasksForBees ()
{
  if (!scouting)
  {
    nB = -DBL_MAX;
  }
  MarkUpAreas ();
}
//——————————————————————————————————————————————————————————————————————————————

The second public method called on every epoch. The launch should be performed after getting the value of the fitness function. In this case, if exploration has not yet been carried out, we sort the bees by the value of the nectar and copy the coordinates and the amount of nectar of the first bees in the list into the corresponding areas. If exploration has already taken place, then we copy the coordinates and the amount of nectar in the area the nectar was collected from provided that the results have improved. Also, update the best results for the entire hive.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::CollectingNectar ()
{
  if (!scouting)
  {
    SortingBees ();

    for (int a = 0; a <areasNumber; a++)
    {
      ArrayCopy (areas [a].cB, bees [a].c, 0, 0, WHOLE_ARRAY);
      areas [a].n = bees [a].n;
    }

    scouting = true;
  }
  else
  {
    //transfer the nectar to the hive---------------------------------------------
    for (int b = 0; b < beesNumber; b++)
    {
      if (bees [b].n > areas [bees [b].aInd].n)
      {
        ArrayCopy (areas [bees [b].aInd].cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        areas [bees [b].aInd].n = bees [b].n;
      }

      if (bees [b].n > nB)
      {
        ArrayCopy (cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        nB = bees [b].n;
      }
    }

    SortingAreas ();
  }
}
//——————————————————————————————————————————————————————————————————————————————

The MarkUpAreas () method is worthy of being considered in detail. Let's break the code into parts.

Before the areas are explored and there is no information about finding flowers to collect nectar, we will send all the bees to perform preliminary exploration. At this stage, all the bees play the role of scouts. Since there is no information about the nectar, we send scouts in a random direction, generating random numbers evenly distributed over the range of coordinates.

//if the areas is not scouting - send all the bees to scouting----------------
if (!scouting)
{
  for (int b = 0; b < beesNumber; b++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      bees [b].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      bees [b].c [c] = SeInDiSp  (bees [b].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

After the areas are explored, it is necessary to copy the coordinates of the maximum concentration of nectar to the center of the area. In other words, it is necessary to move the area to a better place. Having performed this action, we need to make sure that the area does not intersect the area of a higher rank. We can check the intersection of areas by measuring the distance between their centers. Areas intersect if the distance between centers is less than two radii (one of the algorithm parameters). If an intersection is detected, then the area is transferred to a point at a distance of two radii, while the coordinates of the best result achieved (the coordinates of the maximum nectar concentration) remain in the same place. Thus, the areas are constantly in motion. The best areas force the rest to shift. The rest areas, while shifting, can get to a richer food source, becoming the best after sorting, which occurs in the next method.

for (int s = 0; s < areasNumber; s++)
{
  //move the center of the area to the best point in with more nectar-------
  ArrayCopy (areas [s].cC, areas [s].cB, 0, 0, WHOLE_ARRAY);

  //ordinary area-----------------------------------------------------------
  if (s != 0)
  {
    //check if there is no intersection of a region with a region of higher rank
    //measure the distance from the centers of the regions
    double centersDistance = 0.0;

    for (int c = 0; c < coordinates; c++) centersDistance += pow (areas [s].cC [c] - areas [s - 1].cC [c], 2.0);
    centersDistance = MathSqrt (centersDistance);

    //the areas intersect, then need to move the current area
    if (centersDistance < distHyperspCenters)
    {
      double incrementFactor = (distHyperspCenters - centersDistance) / centersDistance;
      double coordDistance   = 0.0;

      for (int c = 0; c < coordinates; c++)
      {
        coordDistance = areas [s].cC [c] - areas [s - 1].cC [c];
        areas [s].cC [c] = areas [s].cC [c] + (coordDistance * incrementFactor);

        areas [s].cC [c] = SeInDiSp (areas [s].cC [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}

This is where the dance of the bees takes place. Using information about the direction and amount of nectar in the regions and applying a random component, we mark the distribution area of a random number in such a way that the probability of a bee choosing an area at the next iteration is proportional to the amount of nectar in this area. In simple words, on the number line, we plot segments whose lengths correspond to the difference between the nectar value of each area with the worst area.

//send bees to the marked areas-----------------------------------------------
double r = 0.0;

beeDance [0].start = bees [0].n;
beeDance [0].end   = beeDance [0].start + (bees [0].n - bees [areasNumber - 1].n);

for (int a = 1; a < areasNumber; a++)
{
  if (a != areasNumber - 1)
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a].n - bees [areasNumber - 1].n);
  }
  else
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a - 1].n - bees [a].n) * 0.1;
  }
}

In this part of the method code, a random selection of the area occurs with the probability transmitted by the dance of the worker bees. To do this, we generate a random number in the range made by marking on the number line with a dance. For scouts, dance does not matter, since they fly with an equal degree of probability in the vicinity of any of the areas, thereby expanding the search capabilities of the bee strategy. As in nature, each hive participant has a certain value while playing a role.

for (int b = 0; b < beesNumber; b++)
{
  if (b < workerBeesNumber)
  {
    r = RNDfromCI(beeDance [0].start, beeDance [areasNumber - 1].end);
        
    for (int a = 0; a < areasNumber; a++)
    {
      if (beeDance [a].start <= r && r < beeDance [a].end)
      {
        bees [b].aInd = a;
        break;
      }
    }

    BeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
  else
  {
    //choose the area to send the bees there
    r = RNDfromCI (0.0, areasNumber - 1);

    bees [b].aInd = (int)r; //area index

    ScoutBeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
}

This private method implements the flight of a bee. Everything is simple here, although at first glance it looks incomprehensible and complicated. The bee flies to an area with a cubic probability shift closer to the center. Thus, the probability decreases from the area center to its borders. Keep in mind that this is the center of the area, and not the best position found earlier. Even in this simple action, the bee's strategy can be traced, ensuring a continuous search for new food sources.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::BeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (0.0, 1.0);
    r  = r * r * r;
    r = Scale (r, 0.0, 1.0, 0.0, areasRadius [c], false);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Unlike the previous method, the flight of the scout bee is described here. The bee flies outside the area within the radius specified in the algorithm settings. Despite the fact that the setting is the same, the radii are calculated beforehand when the class is initialized, because the coordinate ranges may differ, so the radii should be appropriate. To launch a scout bee in flight, we need to generate a random number in the range from the radius of the area to the sum of the radius of the area and the radius of the exploration, and then simply add the resulting value to the center of the area. In such a simple way, the scout bee will be in the vicinity of the area by chance, while the coordinates will not be scattered throughout the search space.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::ScoutBeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (areasRadius [c], areasRadius [c] + scoutRadius [c]);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

There are two specific methods in the algorithm - bee sorting and area sorting. It makes no sense to describe them, it's just a simple bubble sort. I use it in almost all optimization algorithms (where sorting is required at all), because this method is simple and easily modified for specific tasks, while providing one of the best speeds among all sorting methods.

//——————————————————————————————————————————————————————————————————————————————
//Sorting of bees
void C_AO_ABC::SortingBees ()
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Sorting of areas
void C_AO_ABC::SortingAreas ()
//——————————————————————————————————————————————————————————————————————————————

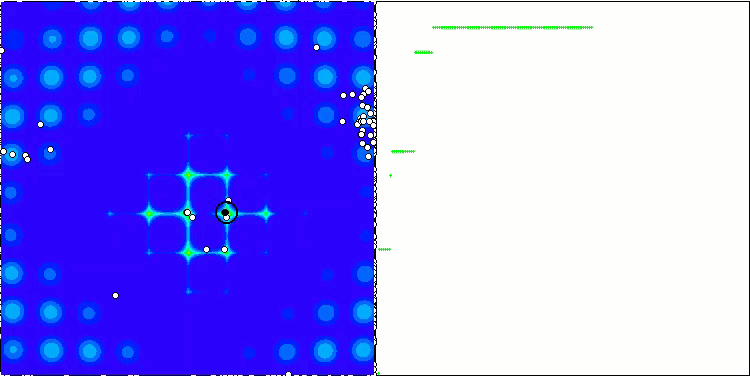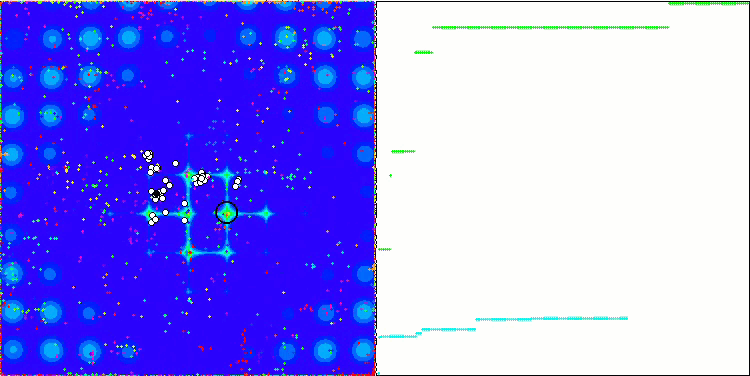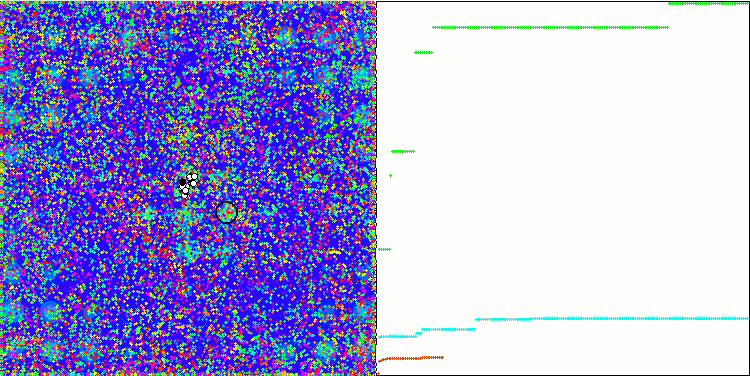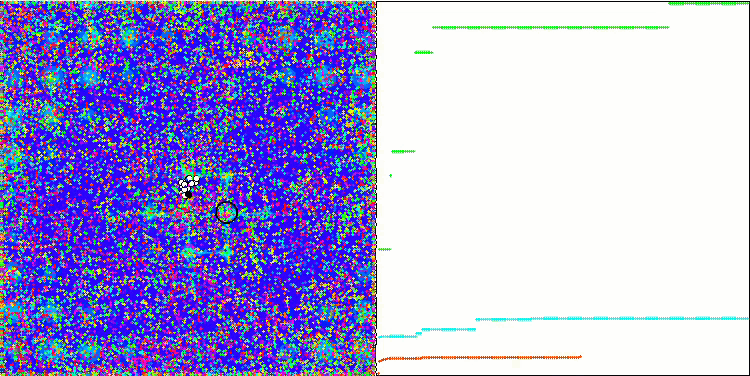
It's time to collect all the considered code and compile it. After running the test stand, we can see the following animations, which show the behavior of the bee algorithm. Bees are clearly observed in separate areas. We can see how the areas are displaced replacing one another. Accuracy and the number of peculiar "swarms" depend on the algorithm settings.

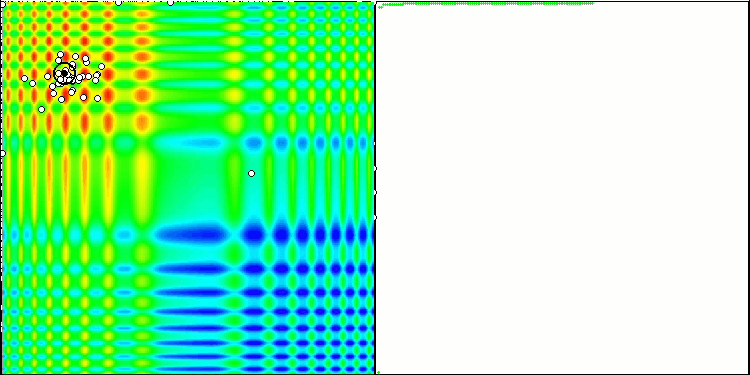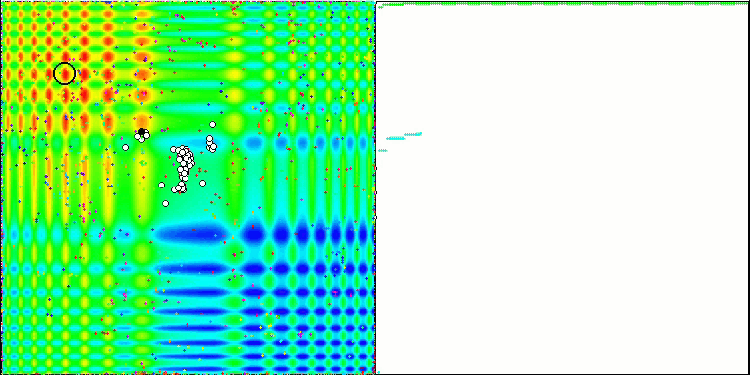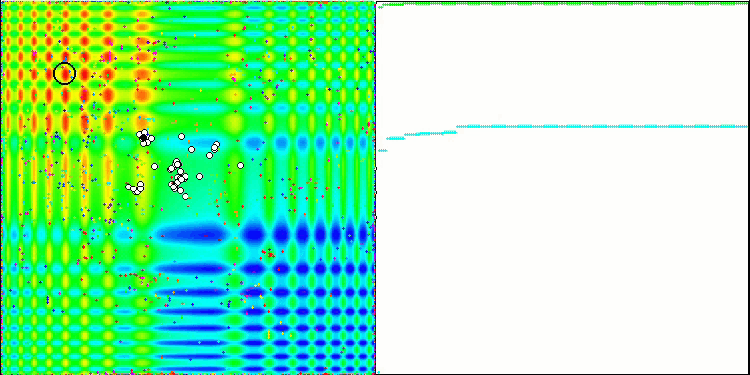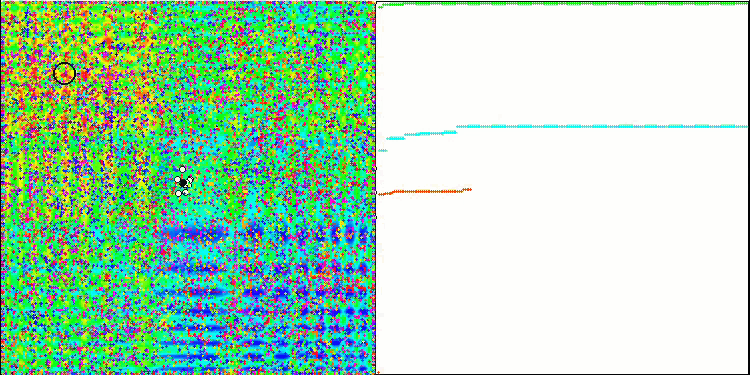
ABC on the Skin test function

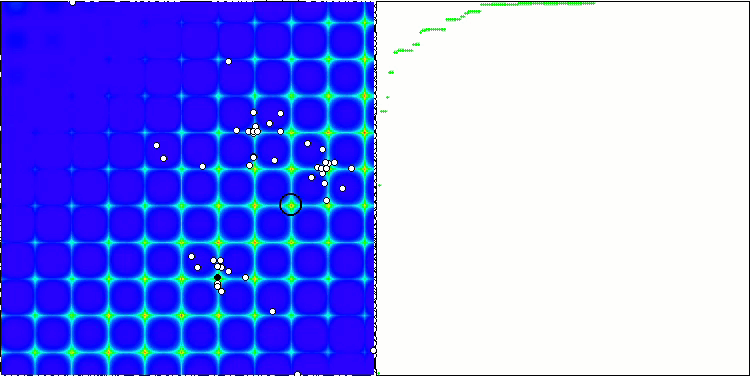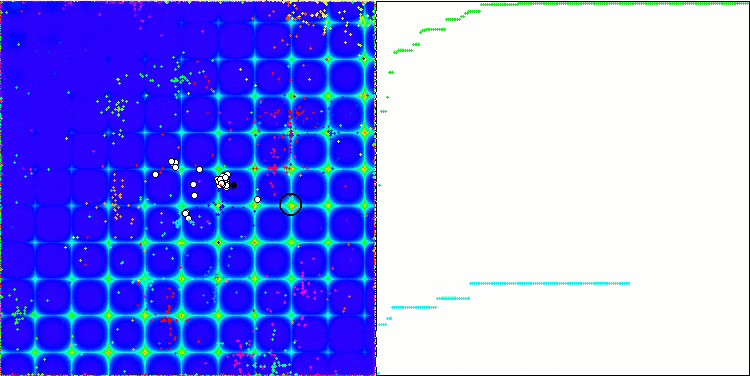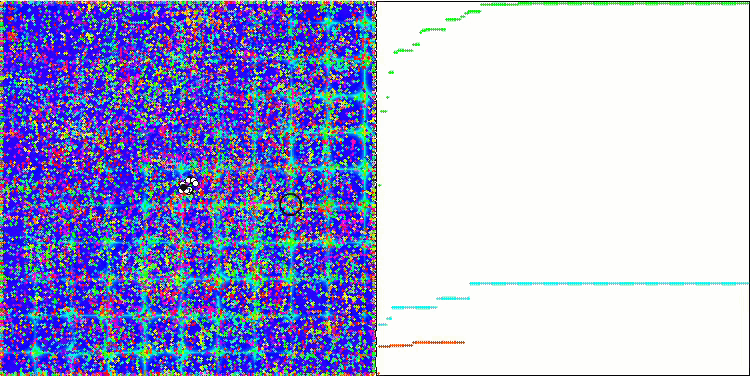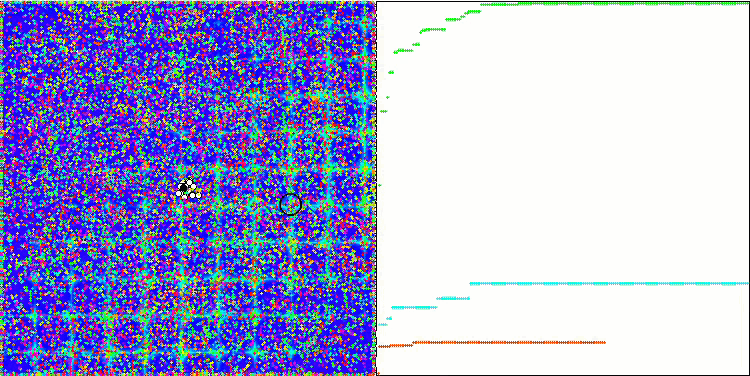
ABC on the Forest test function

ABC on the Megacity test function

Here are the algorithm results on the test functions:

2022.11.21 13:14:06.669    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    1 Skin's; Func runs 1000 result: 14.018634225602678; Func runs 10000 result: 14.06060189007221
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.99772; Score2: 1.00000
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    20 Skin's; Func runs 1000 result: 7.459929501115262; Func runs 10000 result: 8.320771456653533
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.64085; Score2: 0.68769
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.69267387794685; Func runs 10000 result: 4.838631770950824
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.49029; Score2: 0.49823
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.063567301715784; Func runs 10000 result: 15.912087696850861
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.94435; Score2: 0.99755
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.0207584941876133; Func runs 10000 result: 4.1918977577943295
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.18937; Score2: 0.26279
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.2004991531402736; Func runs 10000 result: 1.288357831462411
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.07526; Score2: 0.08077
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 10.4; Func runs 10000 result: 15.0
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.69333; Score2: 1.00000
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.5499999999999998; Func runs 10000 result: 2.31
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.10333; Score2: 0.15400
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    500 Megacity's; Func runs 1000 result: 0.6180000000000001; Func runs 10000 result: 0.6568
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.04120; Score2: 0.04379
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    All score for C_AO_ABC: 0.49447371765340953

The algorithm has fully converged for the two two-variable test functions, which is an excellent indicator of convergence. Evaluating the remaining results would be premature. It is better to put the results in a table and draw conclusions in comparison with other optimization algorithms.

3. Modified version

When developing and designing any optimization algorithm, the question always arises: "Does the algorithm work as intended or is there an error somewhere in the code?" The stochastic search process is random by its very nature, hence it is not clear whether the optimization results were obtained by the algorithm or there was an error somewhere and the result is really non-random? When developing the bee colony algorithm, I encountered a similar phenomenon. During the first test out of five in the test set, the algorithm obviously got stuck at th points it started the search from not trying to converge at all. This bug was solved in a completely incredible way from the point of view of logic. All I had to do was initialize the hive class an additional second time on the first epoch despite the fact that the class had already been pre-initialized before the start of the epochs (string 142 in Test_AO_ABC.mq5). If someone manages to unravel this mystery, then I will be glad to hear the solution in the comments.

Partly because of the above, and partly because of the not entirely satisfactory results of the first tests (although later it became clear that I needed to experiment with the algorithm settings), I came up with the idea to change the bee search strategy. In the original version, bees fly in proportion to the area value. In the new algorithm, there should be a fixed number of bees in each area. In other words, regardless of the area rank, each of them always has the same number of bees. Therefore, the area was logically transformed into the concept of "Swarm of bees".

Now, instead of the area structure, there will be the following structure:

//——————————————————————————————————————————————————————————————————————————————
struct S_BeesSwarm
{
  void Init (int coordinatesNumber, int beesNumber)
  {
    ArrayResize (bees, beesNumber);

    for (int i = 0; i < beesNumber; i++)
    {
      ArrayResize (bees [i].c, coordinatesNumber);
      bees [i].n = -DBL_MAX;
    }

    n = -DBL_MAX;

    ArrayResize     (cC, coordinatesNumber);
    ArrayInitialize (cC, -DBL_MAX);
  }

  S_Bee  bees []; //bees
  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

This structure also has an initialization function, but additionally there is the bees[] array.

In general, the rest of the code is very similar to the classic version and you should not focus on it too much. The code is attached in the archive below. It is worth paying special attention to the differences in the logic of the algorithms. In step-by-step form, it looks like this:

1. Create a center for the first swarm and place the bees around the center.
2. Create a center for subsequent swarms and check that the distance from the center to the previous swarms is greater than or equal to R*2 (two radii), place the bees in the vicinity of the center.
3. Send scout bees so that each of the bees is farther than the other swarms by a distance greater than or equal to R (radius).
4. Get the value of the fitness function for all bees.
5. Sort the swarms.
6. Place the bees around the center of each swarm.
7. Repeat from p.4 until the stop criterion is met.

As you might have noticed, there is a fundamental difference in the search strategy. Whereas in the classic version, each area can have a different number of bees, here the swarms are always the same size. This is done to ensure that areas continue to be explored even if the food source dries up, thus providing a more thorough exploration of the surface in hyperspace. The tests confirm the legitimacy of this approach. The results are improving. Scout bees do not fly in the vicinity of areas, but fall into free areas of space, moreover, following the rules of the areas, as in the classic version. In the classic version of the bees, the scouts do not behave as described, because they scatter in a completely random direction without caring that they can get into previously explored areas, thus losing their most basic exploration. The last swarm in the array is the scout swarm. For this swarm, the rule "do not enter someone else's space" also applies, but not for the swarm as a whole, but for the scout bees personally.

Below are the results of the modified version:

2022.11.21 21:53:19.695    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    1 Skin's; Func runs 1000 result: 14.009060385607679; Func runs 10000 result: 14.060603974847265
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    Score1: 0.99720; Score2: 1.00000
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    20 Skin's; Func runs 1000 result: 7.826824877236677; Func runs 10000 result: 8.735832346695558
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    Score1: 0.66082; Score2: 0.71028
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.645933304640949; Func runs 10000 result: 4.844246724239038
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    Score1: 0.48774; Score2: 0.49853
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.44507700105064; Func runs 10000 result: 15.662273922787355
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    Score1: 0.96827; Score2: 0.98188
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.6397442648278924; Func runs 10000 result: 4.759146560755886
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    Score1: 0.22818; Score2: 0.29836
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.2349621811342104; Func runs 10000 result: 1.4191098624570897
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    Score1: 0.07742; Score2: 0.08897
2022.11.21 21:54:01.112    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 12.0; Func runs 10000 result: 15.0
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    Score1: 0.80000; Score2: 1.00000
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.7; Func runs 10000 result: 2.35
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    Score1: 0.11333; Score2: 0.15667
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    500 Megacity's; Func runs 1000 result: 0.572; Func runs 10000 result: 0.67
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    Score1: 0.03813; Score2: 0.04467
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    All score for C_AO_ABCm: 0.508357869056105

We can see that the modified algorithm repeated the success on two functions with two variables showing 100% convergence. In general, the results have improved, the final score has become higher: 0.50836. Unfortunately, this is not a significant improvement in results. Convergence problems on functions with a large number of variables are comparable to the classical version of the algorithm implementation.

By the way, there is no bug requiring re-initialization of the hive in the modified version.

4. Test results

AO	Runs	Skin			Forest			Megacity (discrete)			Final result
		2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)
ACOm	1000	0.99502	0.69826	0.50498	0.99087	0.22374	0.08408	0.78667	0.11667	0.04224	0.54688
	10,000	0.99599	0.86403	0.58800	0.99302	0.65571	0.17442	0.78667	0.26133	0.08208
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
	10,000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283
ABCm	1000	0.99720	0.66082	0.48774	0.96827	0.22818	0.07742	0.80000	0.11333	0.03813	0.50836
	10,000	1.00000	0.71028	0.49853	0.98188	0.29836	0.08897	1.00000	0.15667	0.04467
ABC	1000	0.99772	0.64085	0.49029	0.94435	0.18937	0.07526	0.69333	0.10333	0.04120	0.49447
	10,000	1.00000	0.68769	0.49823	0.99755	0.26279	0.08077	1.00000	0.15400	0.04379
PSO	1000	0.98436	0.72243	0.65483	0.71122	0.15603	0.08727	0.53333	0.08000	0.04085	0.47695
	10,000	0.99836	0.72329	0.65483	0.97615	0.19640	0.09219	0.82667	0.10600	0.04085

Let's sum up. Surprisingly, the bee colony algorithm showed 100% convergence in all five tests on two test functions, smooth Skin and discrete Megacity, thus demonstrating phenomenal speed and quality of convergence. However, this only applies to functions with two variables. In terms of scalability, the algorithm is inferior to other members of the rating table. Functions with multiple variables are definitely not a strong point of a bee colony. This can be seen both in the animation of the test stand and in the results provided in the table.

The ABC algorithm requires the user to fiddle with several parametric settings such as swarm size, number of scouts and area radii. If these settings are not chosen appropriately for a particular application, the algorithm may converge prematurely or not converge at all. In addition, ABC has disadvantages such as slow convergence on complex functions, local solution capture and mediocre search properties.

Pros:
1. Relatively fast.
2. Phenomenal convergence for smooth and discrete functions with few variables.

Cons:
1. Strong influence of algorithm parameters on the result.
2. Non-universatility.
3. Getting stuck in local extremes.
4. Average scalability.