Artificial Algae Algorithm (AAA)

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

Introduction

Algae, some of the most ancient organisms on Earth, play a key role in aquatic ecosystems. There are over 45,000 species of algae, which can vary greatly in color, shape, size, and habitat. They provide life to aquatic environments as they are the basis of the diet of many animal species, and they also produce oxygen through photosynthesis, making them important for maintaining life on the planet. These living organisms can be either unicellular or multicellular, and often form colonies that function as a single unit.

Unicellular algae can divide by mitosis, creating new cells that remain connected to each other to form a colony. Multicellular algae can reproduce using spores that spread in water and germinate into new organisms, also forming colonies. These amazing organisms demonstrate how biological processes can be used to create innovative solutions in mathematical modeling and optimization.

The Artificial Algae Algorithm (AAA), proposed by Uymaz, Tezel, and Yel in 2015, is a combination of biological natural phenomenon and mathematical elegance. This metaheuristic optimization algorithm draws its inspiration from the fascinating world of microalgae, whose colonial habits and adaptive capabilities served as the basis for the creation of an algorithmic optimization model. Inspired by the ability of microalgae to move toward a light source, adapt to changing environmental conditions, and reproduce by mitosis to improve photosynthesis, AAA was developed to mathematically model these unique properties.

The algorithm includes three key processes: spiral movement, evolutionary process and adaptation. Spiral movement simulates the three-dimensional movement of algae in a nutrient solution, allowing them to find optimal conditions for growth. Evolutionary process ensures the reproduction of algae colonies in the most suitable conditions promoting their development and improving solutions. Adaptation helps less successful colonies to become more like the largest colony, ensuring their survival and further development.

Implementation of the algorithm

The Artificial Algae Algorithm (AAA) was developed to mathematically model the properties of algae, such as their spiral motion, adaptation and evolutionary process. Each algae colony represents a possible candidate solution to the optimization problem (and each cell in the colony is a separate coordinate), and these colonies combine to form an algae population. Each colony is characterized by its size, which reflects the quality of the solution presented.

In the evolutionary process, algae colonies that reach more suitable environmental conditions are able to develop and grow. Colonies that cannot obtain suitable conditions do not develop and die. After the spiral movement is complete, the algae colonies are ranked according to their size. A randomly chosen cell from the largest colony is copied into the same cell from the smallest colony, completing the evolutionary process.

Algae colonies perform spiral movement in water to achieve better environmental conditions. Their energy is proportional to the colony size. During the movement they lose energy, but if they reach a better environment, they restore half of the lost energy. The energy of a colony is directly proportional to the concentration of nutrients, so the more energy a colony has, the higher its movement frequency.

Friction force is another important factor that influences movement in water. Colonies with a smaller surface area have a greater range of movement because their friction surface is smaller. Colonies that achieve better conditions have a larger friction surface area due to their size, so the colonies slow down their movements, which helps them explore the vicinity of the found solution and increase their local search capabilities.

Adaptation occurs when algae colonies that have not reached sufficient development during spiral movement try to imitate the largest colony. The colony with the highest hunger value undergoes this process. At the beginning of the optimization, the hunger value of all colonies is zero. During the spiral movement, the hunger value of colonies that have not found a better solution increases by one. After the spiral movement and evolutionary process, the colony with the highest hunger value enters the adaptation period. However, the adaptation process does not occur at every iteration. First, a random value between 0 and 1 is selected. If this value is less than the adaptation parameter, the adaptation is performed.

Let's move on to writing the AAA pseudocode:

Initialization:
    Create a population of agents
    For each agent:
        Initialize a random position in the search space
        Initialize parameters (size, energy, hunger, etc.)

Main loop:
    Until the stopping criterion is reached:
        For each agent:
            Perform the Movement
            Rate the fitness function
        
        Update the best solution found
        
        For each agent:
            Update energy
            Update size
            Update hunger
        
        Perform evolution
        Perform adaptation

Movement Function:
    For each agent:
        Select another agent using tournament selection
        For each coordinate:
            Update agent position using spiral trigonometric movement equation
            and friction ratio

EvolutionProcess function:
    Find the agent with the smallest size
    Replace its coordinates with the coordinates of a randomly selected agent

AdaptationProcess function:
    Find the agent with the greatest hunger
    With a certain probability:
        Find the agent with the largest size
        Update the starving agent's coordinates to bring them closer to the coordinates
        of the large agent
        Reset starving agent parameters

EnergyCalculation function:
    Calculate energy based on colony size, nutrient concentration
    and current growth rate

TournamentSelection function:
    Select two random agents
    Return the agent with the best fitness function value

Let's list the equations used in the algorithm. Equations 1-5 relate directly to the implementation of the basic logic of the algorithm.

1. Population initialization: population = [[x1_1, x1_2, ..., x1_D], [x2_1, x2_2, ..., x2_D], [xN_1, xN_2, ..., xN_D]], where xj_i  — i th cell of the j th algae colony, D — colony dimension and N — population size.

2. Spiral movement: x'i_j = xi_j + α * cos (θ) * τ (Xi) * p; y'i_j = yi_j + α * sin (θ) * τ (Xi) * p; z'i_j = zi_j + r * v, where (x'i_j, y'i_j, z'i_j) — new coordinates of the i th colony, α, θ ∈ [0, 2π], p ∈ [-1, 1], r ∈ [-1, 1], v ∈ [-1, 1], τ (Xi)  — friction area of the i th colony.

3. Evolutionary process: biggest = max (Gi), m = randomly selected cell, smallest.xm = biggest.xm

4. Adaptation: starving = max (Ai); starving.x = starving.x + (biggest.x - starving.x) * rand

5. Monod model of algae growth: μt = μtmax * St / (St + Kt), where μt is the growth rate of algae at a given time t, μtmax  is a maximum growth rate, St — colony size at a given t time and Kt is a half-saturation constant.

6. Friction area: τ (Xi) = 2π * (3√ (3*Gi) / (4π))^2, where τ (Xi)  is a friction area of the i th colony and Gi is a size of the i th colony.

7. Colony selection for spiral movement: tournament selection is used to select the colony that will move. We will consider this in more detail below.

8. Selecting random dimensions for spiral motion: p, r, v  are randomly selected measurement indices that are different from each other.

9. Selecting a neighboring colony for spiral movement: Xj is a colony selected by tournament selection the Xi colony will move to.

10. Initial hunger of all colonies: Ai = 0 for all i.

11. Increased hunger in colonies that did not improve the solution: Ai = Ai + 1, if the colony has not found a better solution.

12. Selecting a colony with maximum hunger: starving = max (Ai).

13. Adaptation probability: rand < Ap, where Ap is an adaptation parameter.

Equations 6-13 describe additional details of the algorithm implementation, such as the calculation of the friction area, selection of colonies for movement, management of colony starvation, and the adaptation probability.

Monod model is quite often used to describe the growth and behavior of populations in biological systems. It is based on the works of Jacques Monod, a French biochemist who studied the growth kinetics of microorganisms. The rate of population growth depends on the concentration of the substrate (nutrient). At low substrate concentrations, the growth rate is proportional to the concentration, and at high concentrations it reaches its maximum. In optimization algorithms, the Monod model is used to model the growth and adaptation of populations in evolutionary algorithms. During the optimization, the population parameters change depending on the available resources, which allows for more accurate modeling of real biological processes.

I would like to draw your attention to the tournament selection for choosing a colony. We have not used this method before in the algorithms. Let's write a script and print out the results in order to clearly see the distribution of probabilities of selection of individuals in the population using this selection method. The code section highlighted in blue is directly involved in the distribution formation during selection.

input int      PopSize = 50;
input int      Count   = 1000000;
input int      BarWidth = 50; // Histogram width in characters

void OnStart()
{
  int pop[];
  ArrayResize(pop, PopSize);

  for(int i = 0; i < PopSize; i++) pop[i] = PopSize - i;

  Print("Original population:");
  ArrayPrint(pop);

  int tur[];
  ArrayResize(tur, PopSize);
  ArrayInitialize(tur, 0);

  int ind1 = 0, ind2 = 0;

  for(int i = 0; i < Count; i++)
  {
    ind1 = MathRand() % PopSize;
    ind2 = MathRand() % PopSize;

    if(pop[ind1] > pop[ind2]) tur[ind1]++;
    else                      tur[ind2]++;
  }

  Print("Probability distribution (in %):");

  double maxPercentage = 0;
  double percentages[];
  ArrayResize(percentages, PopSize);

  for(int i = 0; i < PopSize; i++)
  {
    percentages[i] = (double)tur[i] / Count * 100;
    if(percentages[i] > maxPercentage) maxPercentage = percentages[i];
  }

  for(int i = 0; i < PopSize; i++)
  {
    int barLength = (int)((percentages[i] / maxPercentage) * BarWidth);
    string bar = "";
    for(int j = 0; j < barLength; j++) bar += "|";

    PrintFormat("%2d: %5.2f%% %s", i, percentages[i], bar);
  }
}

Below is the result of running a script to visualize the probability distribution of choosing each individual in the population:

Original population:
20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1
Probability distribution (in %):
 0:  9.76% ||||||||||||||||||||||||||||||||||||||||||||||||||
 1:  9.24% |||||||||||||||||||||||||||||||||||||||||||||||
 2:  8.74% ||||||||||||||||||||||||||||||||||||||||||||
 3:  8.22% ||||||||||||||||||||||||||||||||||||||||||
 4:  7.77% |||||||||||||||||||||||||||||||||||||||
 5:  7.27% |||||||||||||||||||||||||||||||||||||
 6:  6.74% ||||||||||||||||||||||||||||||||||
 7:  6.26% ||||||||||||||||||||||||||||||||
 8:  5.78% |||||||||||||||||||||||||||||
 9:  5.25% ||||||||||||||||||||||||||
10:  4.75% ||||||||||||||||||||||||
11:  4.22% |||||||||||||||||||||
12:  3.73% |||||||||||||||||||
13:  3.25% ||||||||||||||||
14:  2.75% ||||||||||||||
15:  2.25% |||||||||||
16:  1.75% ||||||||
17:  1.25% ||||||
18:  0.77% |||
19:  0.25% |

The probability distribution decreases linearly, allowing colonies with higher chances of good solutions to be selected, but less efficient options also have a chance of being selected. This approach to selection does not depend on the absolute values of the fitness of individuals, which provides a wide range of solution diversity.

In previous articles, we have already considered equations for changing the probability distribution during selection, but with the ability to provide both linear and non-linear decrease in probabilities, and with less computational costs (for tournament selection, a double call to the MathRand() function is required).

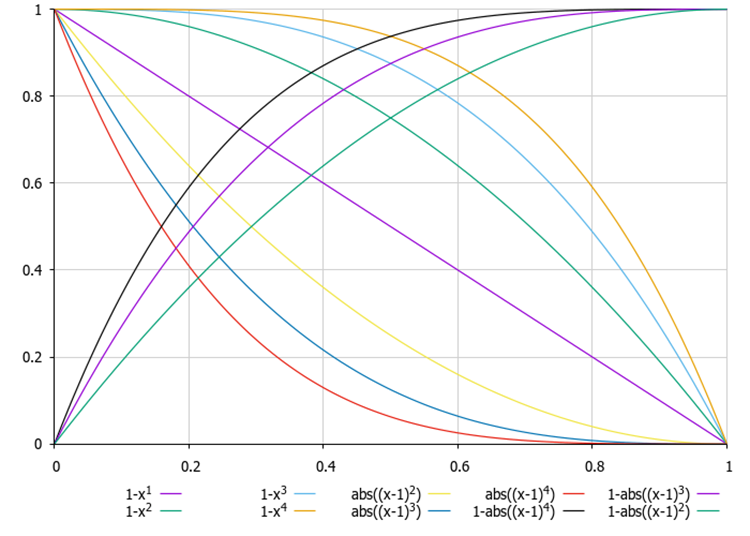
Figure 1. Examples of equations for changing the shape of a probability distribution, where x is a uniformly distributed random number in the range [0.0, 1.0]

Now that we have covered all the intricacies of the algorithm in detail, we can begin writing the code itself.

Let's describe the S_AAA_Agent structure, which will be used to simulate the algae colony (agent) in the algorithm. The structure contains four fields:

• energy — agent's energy level.
• hunger — agent's hunger level.
• size — agent size (algae height and length).
  
• friction — friction ratio affecting the agent movement.

Init — the method initializes the structure members with default values. 

Thus, the S_AAA_Agent structure is a simple agent model with basic characteristics.

//——————————————————————————————————————————————————————————————————————————————
struct S_AAA_Agent
{
  double energy;
  int    hunger;
  double size;
  double friction;

  void Init ()
  {
    energy   = 1.0;
    hunger   = 0;
    size     = 1.0;
    friction = 0.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Let's write the definition of the C_AO_AAA class inherited from the C_AO base class. This means that it will inherit all the members and methods of the base class and can extend or override them.

1. In the class constructor, values are set for various parameters related to the algorithm and are also initialized:

• popSize  — population size.
• adaptationProbability  — adaptation probability.
• energyLoss — energy loss.
• maxGrowthRate — maximum growth rate.
• halfSaturationConstant — half-absorption constant.

All these parameters are stored in the params array.

2. The SetParams method updates the values of the algorithm parameters from the params array.

3. The options available are:

• Init () — initialization method accepts arrays for the minimum and maximum parameter values, as well as steps and the number of epochs.
• Moving () — method is responsible for moving or updating the state of agents.
• Revision ()  — method for reviewing or assessing a state.
• EvolutionProcess (), AdaptationProcess (), CalculateEnergy (), TournamentSelection () — private methods are responsible for the evolutionary process, adaptation, calculation of algae energy and tournament selection, respectively.
  

Class fields:

• adaptationProbability, energyLoss, maxGrowthRate, halfSaturationConstant — variables for storing parameter values.
• S_AAA_Agent agent []  — array of agents.
  
• fMin, fMax — fitness values (algae size) for a population.

C_AO_AAA class is a structure that allows convenient management of the parameters and agents' states, as well as integration into a wider system based on inheriting from the C_AO class.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAA : public C_AO
{
  public: //--------------------------------------------------------------------

  ~C_AO_AAA () { }

  C_AO_AAA ()
  {
    ao_name = "AAA";
    ao_desc = "Algae Adaptive Algorithm";
    ao_link = "https://www.mql5.com/en/articles/15565";

    popSize                = 200;
    adaptationProbability  = 0.2;
    energyLoss             = 0.05;
    maxGrowthRate          = 0.1;
    halfSaturationConstant = 1.0;

    ArrayResize (params, 5);

    params [0].name = "popSize";                params [0].val = popSize;
    params [1].name = "adaptationProbability";  params [1].val = adaptationProbability;
    params [2].name = "energyLoss";             params [2].val = energyLoss;
    params [3].name = "maxGrowthRate";          params [3].val = maxGrowthRate;
    params [4].name = "halfSaturationConstant"; params [4].val = halfSaturationConstant;
  }

  void SetParams ()
  {
    popSize                = (int)params [0].val;
    adaptationProbability  = params      [1].val;
    energyLoss             = params      [2].val;
    maxGrowthRate          = params      [3].val;
    halfSaturationConstant = params      [4].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double adaptationProbability;
  double energyLoss;
  double maxGrowthRate;
  double halfSaturationConstant;

  S_AAA_Agent agent [];

  private: //-------------------------------------------------------------------
  void   EvolutionProcess    ();
  void   AdaptationProcess   ();
  double CalculateEnergy     (int index);
  int    TournamentSelection ();
  double fMin, fMax;
};
//——————————————————————————————————————————————————————————————————————————————

Let's look at the following Init method of the C_AO_AAA class in detail:

• rangeMinP — array of minimum values for each parameter.
• rangeMaxP — array of maximum values for each parameter.
• rangeStepP — array of change steps for each parameter.
• epochsP — number of epochs (default - 0).

Method fields:

1. The StandardInit method performs standard initialization with the passed parameters. 

2. Changes the agent array size to popSize. This allows us to prepare an array for storing agents.

3. Sets the minimum and maximum values for functions used during operation.

4. The loop goes through each agent, initializing it using the Init method.

5. The inner loop initializes the coordinates of each agent:

• first, the c coordinate is set randomly in the range from rangeMin [c] to rangeMax [c] using the RNDfromCI method.
• Next, the coordinate is changed using the SeInDiSp, which normalizes the values.

If all operations are successful, the method returns true. Thus, the Init method initializes the array of agents with given ranges and steps for their coordinates. It includes standard initialization, setting the bounds for the function, and random assignment of coordinate values.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  ArrayResize (agent, popSize);

  fMin = -DBL_MAX;
  fMax =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init ();

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Let's consider the code of the Moving method of the C_AO_AAA class. General structure and functionality:

1. If the revision variable is false, it is set to true, and the function terminates. This means that the basic logic of the Moving method is not executed on the first iteration.

2. The loop goes through all popSize population elements.

3. Tournament selection is performed in the TournamentSelection function, which returns the index of one of the agents (algae) for further use.

4. The inner loop iterates over each coordinate (the dimension of space specified by the coords variable).

5. Three random values are generated: α and β (angles) and ρ (the value in the range from -1 to 1) using the u.RNDfromCI method.

6. Depending on the variant value (which varies from 0 to 2), a [i].c [c] coordinates are updated:

• if variant is 0, the cosine of the α angle is used.
• if variant is 1, the sine of the β angle is used.
• if variant is 2, ρ value is used.

Using the variant variable allows to simulate three-dimensional spiral movement of algae in multidimensional space. The coordinate update takes into account the friction specified as agent[i].friction.

7. The a [i].c [c] coordinates are limited using the u.SeInDiSp function, which sets a value within a given range and with a given step.

The Moving function implements the process using random changes in the coordinates of agents based on their current state and the state of other agents. Using friction and random values allows us to create dynamics that simulate the behavior of agents in the search space. The code includes mechanisms that prevent going beyond the specified ranges, which is important for maintaining valid coordinate values.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int variant = 0;

    int j = TournamentSelection ();

    for (int c = 0; c < coords; c++)
    {
      double α = u.RNDfromCI (0.0, 2 * M_PI);
      double β = u.RNDfromCI (0.0, 2 * M_PI);
      double ρ = u.RNDfromCI (-1.0, 1.0);

      if (variant == 0) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathCos (α);
      if (variant == 1) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathSin (β);
      if (variant == 2) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * ρ;

      variant++;

      if (variant > 2) variant = 0;

      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

After the Moving method, move on to the Revision method of the C_AO_AAA class. This method is responsible for updating the state of agents in a population based on their characteristics and interactions. General structure:

1. The ind variable is initialized with the value of -1. It will be used to store the index of the agent with the best function value.

2. The loop goes through all agents in the popSize population. Inside the loop: if the a [i].f function value exceeds the current fB maximum, 

• the fB maximum value is updated.
• the index of the agent with the best value is stored in the ind variable.
• the agent [i].size agent size is updated according to its a [i].f fitness function value.
• minimum fMin and maximum fMax values of the fitness function for the current agent are updated.

3. If an agent with the maximum fitness value f has been found, its coordinates are copied to the cB array using the ArrayCopy function.

4. Updating energy and other agent parameters:

• its energy is calculated using the CalculateEnergy function.
• friction is calculated, normalized by fMin and fMax.
• agent's energy is decreased by energyLoss.
• If the new energy is greater than the current one, then the energy increases by half the loss, and the agent's hunger is reset. Otherwise, the level of hunger increases.
• a growth factor is calculated based on the agent's current size and satiety, and the agent's size is updated.

5. Calling processes: at the end of the function, the EvolutionProcess and AdaptationProcess methods are called. The methods are responsible for the further evolution and adaptation of agents based on their current state.

In general, the Revision function is responsible for updating the state of agents in a population based on their characteristics and interactions. It includes analysis, as well as updating and calling additional processes, which allows modeling population dynamics.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;

      ind = i;
    }

    agent [i].size = a [i].f;

    if (a [i].f < fMin) fMin = a [i].f;
    if (a [i].f > fMax) fMax = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].energy   = CalculateEnergy (i);

    agent [i].friction = u.Scale (a [i].f, fMin, fMax, 0.1, 1.0, false);

    agent [i].energy -= energyLoss;

    double newEnergy = CalculateEnergy (i);

    if (newEnergy > agent [i].energy)
    {
      agent [i].energy += energyLoss / 2;
      agent [i].hunger = 0;
    }
    else
    {
      agent [i].hunger++;
    }

    double growthRate = maxGrowthRate * agent [i].size / (agent [i].size + halfSaturationConstant);

    agent [i].size *= (1 + growthRate);
  }

  //----------------------------------------------------------------------------
  EvolutionProcess  ();
  AdaptationProcess ();
}
//——————————————————————————————————————————————————————————————————————————————

Let's describe the EvolutionProcess () function. It is responsible for the evolution of agents in the population. The main purpose of this function is to find the least fit agent (the lowest algae) and replace its coordinates with the coordinates of random more fit agents (higher algae).

1. Finding the most unfit agent:

• the smallestIndex variable is initialized. It will store the index of the most unfit agent. Initially set to 0.
• the loop goes through all agents (starting with the first) and compares their fitness. If the fitness of the current agent is less than the fitness of the agent with the smallestIndex index, smallestIndex is updated.

2. Copying coordinates:

• the m variable for storing a random agent index is initialized.
• the loop iterates through all coordinates from 0 to coords.
• inside the loop, the u.RNDminusOne (popSize) method is called. It generates the m random index in the range from 0 to popSize 1.
• then the coordinates of the most unfit agent by smallestIndex index are replaced with the coordinates of a random agent by m index.

The EvolutionProcess function implements a simple evolution mechanism, in which the least fit agent in the population receives the coordinates of a random agent. This operation is part of the adaptation mechanism, allowing agents to improve their characteristics by selecting more successful coordinates from other agents. In general, it performs the combinatorial functions of the algorithm.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::EvolutionProcess ()
{
  int smallestIndex = 0;

  for (int i = 1; i < popSize; i++)
  {
    if (agent [i].size < agent [smallestIndex].size) smallestIndex = i;
  }

  int m = 0;

  for (int c = 0; c < coords; c++)
  {
    m = u.RNDminusOne (popSize);

    a [smallestIndex].c [c] = a [m].c [c];
  }
}
//——————————————————————————————————————————————————————————————————————————————

Let's take a closer look at the AdaptationProcess () function code. It is responsible for the adaptation of agents in the population, based on their hunger and size. The main goal of the function is to change the coordinates of the hungriest agent if a certain condition of adaptation probability is met.

1. Search for the hungriest agent (algae):

• the starvingIndex variable, storing the index of the hungriest agent, is initialized. Initially set to 0.
• the loop iterates through all agents (starting from the first one) and compares the hunger level. If the hunger level of the current agent is greater than that of the agent with the index of starvingIndex, starvingIndex is updated.

2. Checking adaptation probability:

• the u.RNDprobab () method, which generates a random number (probability), is used. If this number is less than the given adaptation probability (adaptationProbability), the following code block is executed.

3. Finding the highest algae - agent:

• similar to the first step, the index of the highest agent in the population is sought here. Initially, biggestIndex is set to 0.
• the loop goes through all agents and updates BiggestIndex if the current agent is higher.

4. Adaptation of coordinates:

• the loop iterates through all coordinates.
• coordinates of the agent with the index of starvingIndex are updated by adding the value calculated as the difference between the coordinates of the highest agent and the hungriest agent, multiplied by a random probability.
• then the coordinates are normalized using the u.SeInDiSp () method, which checks and adjusts coordinates within the specified limits rangeMin, rangeMax and rangeStep.

5. Agent status update:

• he agent's size is updated by the fitness value f from the a array.
• the hunger level is set to 0, which means that the agent is full.
• agent's energy is set to 1.0. This is the maximum value.

The AdaptationProcess function implements the adaptation mechanism that allows the hungriest agent to improve its coordinates by borrowing them from the highest agent if the probability condition is met. This is part of a system that mimics natural selection, where agents adapt to the environment to improve their chances of survival.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::AdaptationProcess ()
{
  int starvingIndex = 0;

  for (int i = 1; i < popSize; i++) if (agent [i].hunger > agent [starvingIndex].hunger) starvingIndex = i;
  
  if (u.RNDprobab () < adaptationProbability)
  {
    int biggestIndex = 0;

    for (int i = 1; i < popSize; i++) if (agent [i].size > agent [biggestIndex].size) biggestIndex = i;

    for (int j = 0; j < coords; j++)
    {
      a [starvingIndex].c [j] += (a [biggestIndex].c [j] - a [starvingIndex].c [j]) * u.RNDprobab ();

      a [starvingIndex].c [j] = u.SeInDiSp (a [starvingIndex].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }

    agent [starvingIndex].size   = a [starvingIndex].f;
    agent [starvingIndex].hunger = 0;
    agent [starvingIndex].energy = 1.0;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Next, we have the code of the CalculateEnergy function. It is designed to calculate the energy of a given agent based on its characteristics, such as colony size, energy level and nutrient concentration. The function returns the energy value used in other parts of the algorithm.

1. Initialization of variables:

• colony_size — get the height of the algae using index.
• max_growth_rate — maximum growth rate.
• half_saturation_constant — half of the saturation constant.

2. Fitness function normalization: the normalized value of nutrient concentration is calculated. It is calculated as the ratio of the difference between f (from the a array) and the minimum value of fMin to the range between fMax and fMin. Adding 1e-10 prevents zero divide.

3. Getting the current growth rate: current_growth_rate — get the current value of the agent's energy, which is also interpreted as the current growth rate.

4. Calculating growth rate: growth_rate — calculated based on maximum growth rate, normalized nutrient concentration and current growth rate. The equation takes into account the saturation effect, where the growth rate decreases as the current growth rate increases.

5. Energy calculation: energy is calculated as the difference between growth_rate and some energy losses (energyLoss). This value shows how much energy the agent receives after taking into account losses.

6. If the calculated energy is negative, it is set to 0. This prevents negative energy values.

7. The function returns the calculated energy value.

The CalculateEnergy function models a process, in which an agent gains energy based on its growth rate, colony size, and nutrient concentration. It also takes into account energy losses to ensure realistic behavior of agents in the simulation. 

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AAA::CalculateEnergy (int index)
{
  double colony_size              = agent [index].size;
  double max_growth_rate          = maxGrowthRate;
  double half_saturation_constant = halfSaturationConstant;

  // Use the normalized value of the fitness function
  double nutrient_concentration = (a [index].f - fMin) / (fMax - fMin + 1e-10);

  double current_growth_rate = agent [index].energy;

  double growth_rate = max_growth_rate * nutrient_concentration / (half_saturation_constant + current_growth_rate) * colony_size;

  double energy = growth_rate - energyLoss;

  if (energy < 0) energy = 0;

  return energy;
}
//——————————————————————————————————————————————————————————————————————————————

The last method is to implement the tournament selection mechanism. The TournamentSelection method selects one of the two candidates from the population based on their fitness function values. It returns the index of the candidate that has the best fitness value. Tournament selection provides selection. We have already considered above its probability distributions among agents in the population.

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AAA::TournamentSelection ()
{
  int candidate1 = u.RNDminusOne (popSize);
  int candidate2 = u.RNDminusOne (popSize);

  return (a [candidate1].f > a [candidate2].f) ? candidate1 : candidate2;
}
//——————————————————————————————————————————————————————————————————————————————

Test results

AAA test stand results:

AAA|Algae Adaptive Algorithm|200.0|0.2|0.05|0.1|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.5000717048088521
25 Hilly's; Func runs: 10000; result: 0.3203956013467087
500 Hilly's; Func runs: 10000; result: 0.25525273777603685
=============================
5 Forest's; Func runs: 10000; result: 0.37021025883379577
25 Forest's; Func runs: 10000; result: 0.2228350161785575
500 Forest's; Func runs: 10000; result: 0.16784823154308887
=============================
5 Megacity's; Func runs: 10000; result: 0.2784615384615384
25 Megacity's; Func runs: 10000; result: 0.14800000000000005
500 Megacity's; Func runs: 10000; result: 0.097553846153847
=============================
All score: 2.36063 (26.23%)

Both the printout and the visualization of the algorithm's operation show weak convergence, which is confirmed by the test results. Unfortunately, my expectations for high results were not met. Considering a complex search strategy for an algorithm, it is difficult to determine the reasons for its inefficiency, since it weakly localizes the global optimum. However, despite these shortcomings, the algorithm still has its advantages.

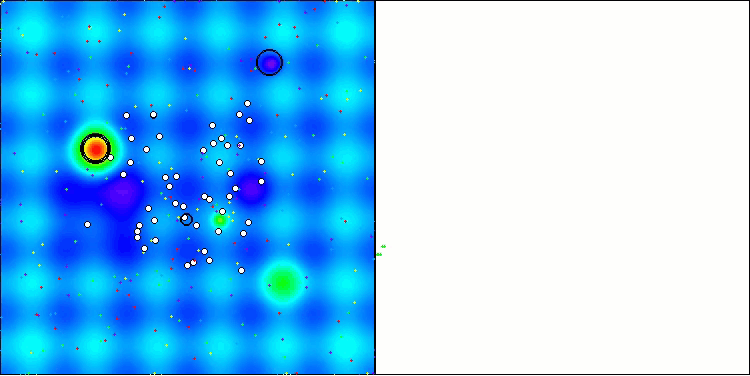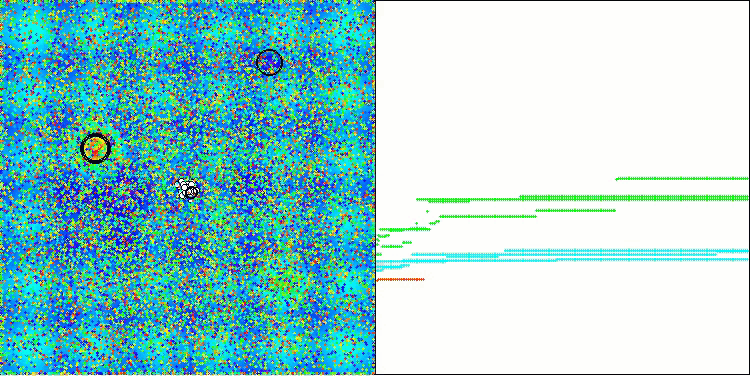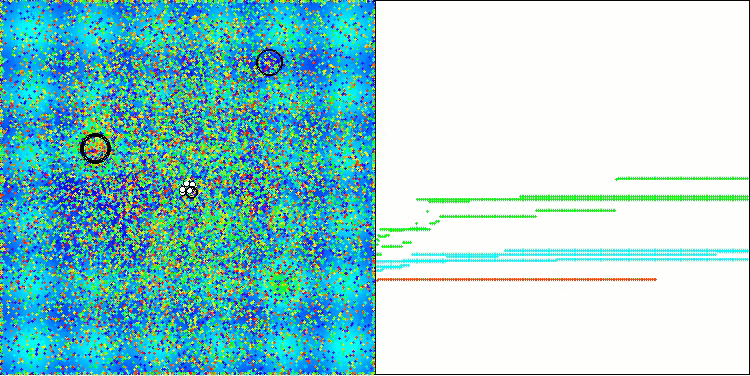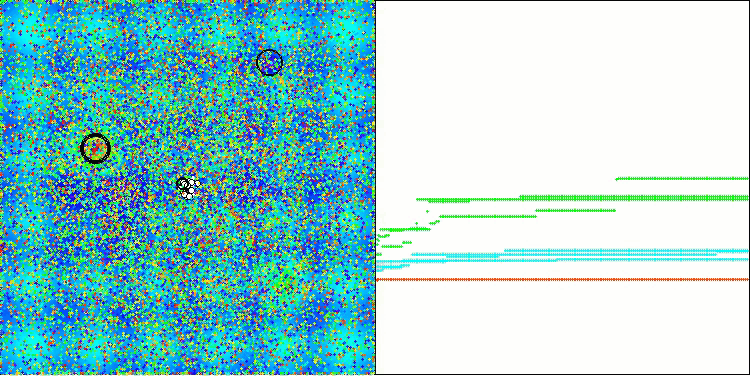
AAA on the Hilly test function

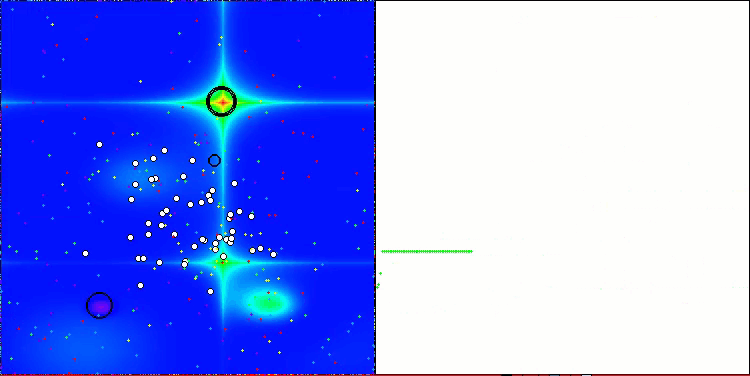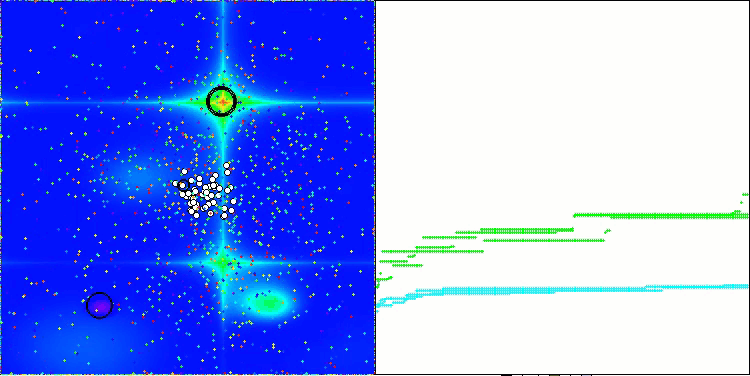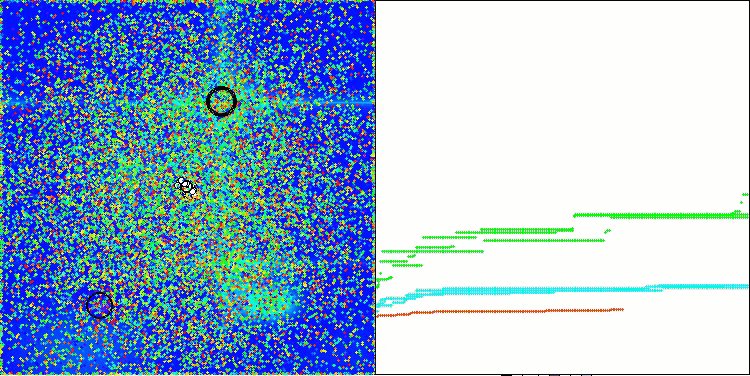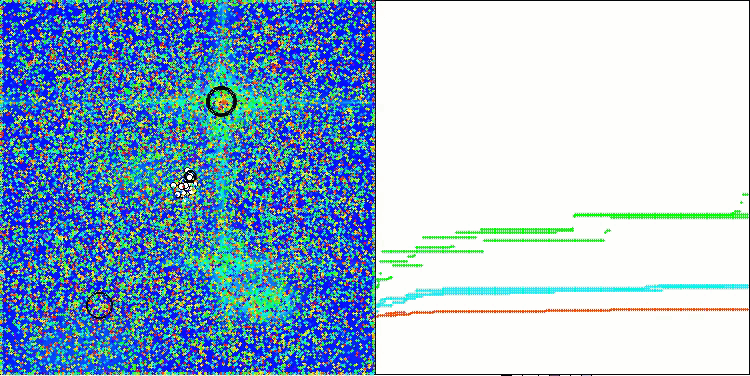
AAA on the Forest test function

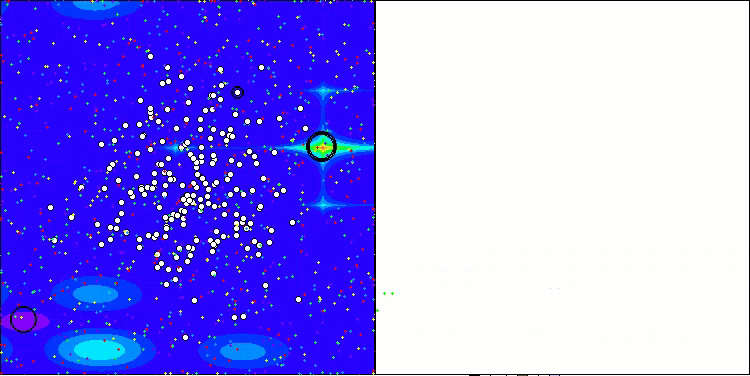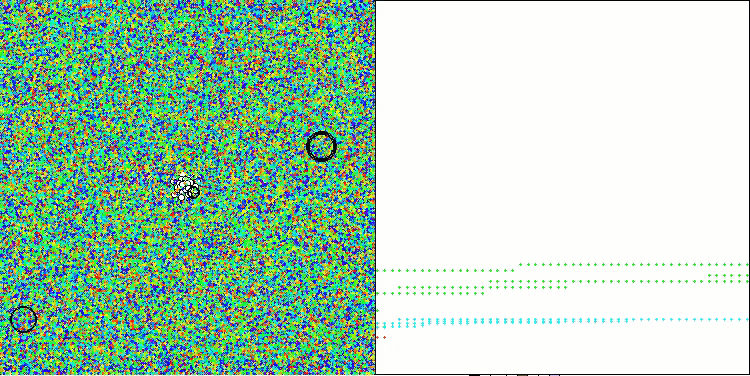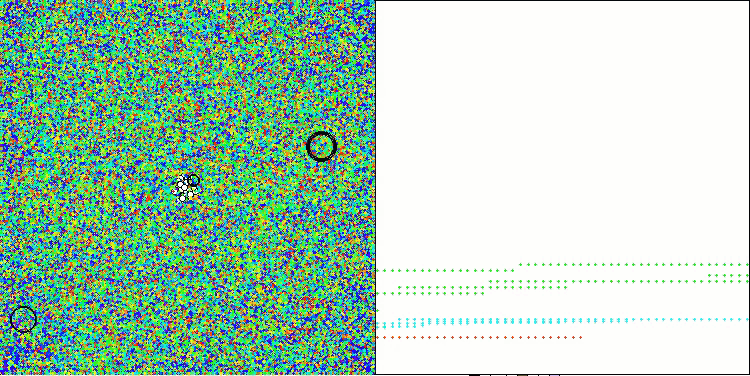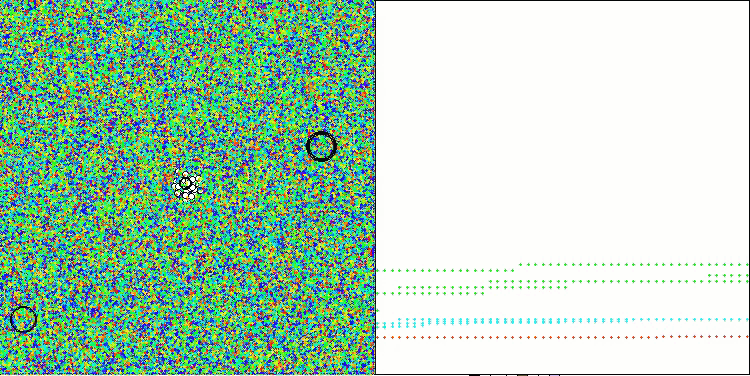
AAA on the Megacity test function

Based on the test results, the algorithm ranks 36 th in the rating table.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration ptimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	evolution of social groups	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	simulated isotropic annealing	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	turtle shell evolution algorithm	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
19	WOAm	whale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
20	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
21	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
22	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
23	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
24	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
25	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
26	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
27	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
28	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
29	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
30	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
31	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
32	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
33	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
34	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
35	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
36	AAA	algae adaptive algorithm	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
37	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
38	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
39	PSO	particle swarm optimisation	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
40	Boids	boids algorithm	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
41	MA	monkey algorithm	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
42	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
43	FSS	fish school search	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
44	RND	random	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
45	GWO	grey wolf optimizer	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32

Summary

The printout shows low convergence. I am somewhat disappointed with the algorithm capabilities: despite using multiple methods and complex step logic, it has ended up at the bottom of the table. Perhaps, it is worth paying more attention and understanding to the methods used, since their quantity does not always guarantee quality. Readers are free to experiment with it, and if the algorithm shows better results, please share them. I look forward to comments on the article.

Positive aspects of the algorithm include good results on Forest and Megacity functions with 1000 variables compared to its closest competitors. This demonstrates the potential of the algorithm in terms of scalability for problems with "sharp" extremes and discrete problems.

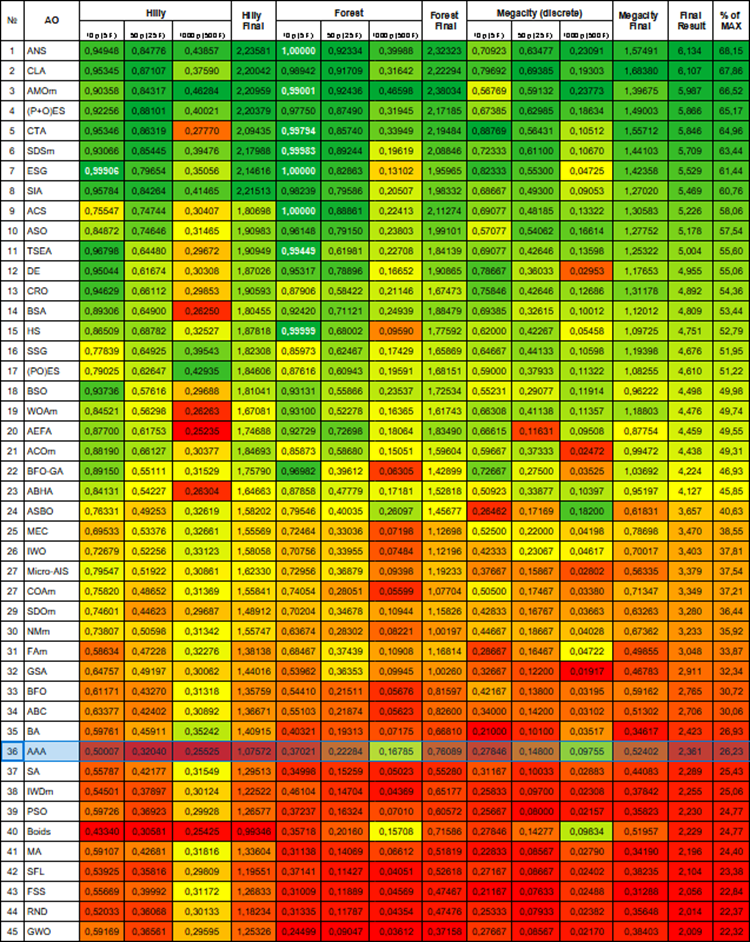
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

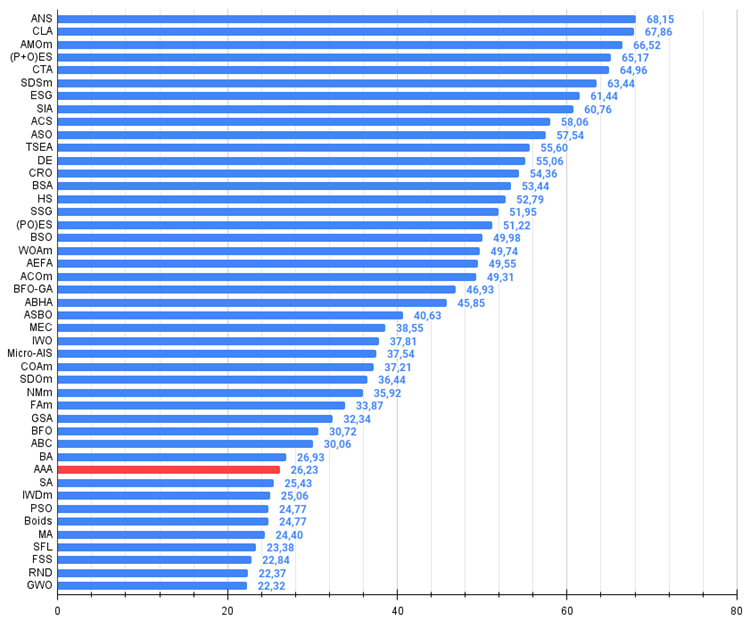
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

AAA pros and cons:

Advantages:

1. Promising idea and innovative approaches.

Disadvantages:

1. Large number of parameters (very difficult to configure).
   
2. Weak convergence.
3. Difficult to debug.

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355