ALGLIB library optimization methods (Part II)

Contents

1. Introduction
2. ALGLIB library optimization methods:
• BC (Box Constrained Optimization)
• NLC (Nonlinearly Constrained Optimization with Lagrangian Algorithm)
• LM (Levenberg-Marquardt Method)
3. Table of functions used in ALGLIB methods
4. Testing methods
   

Introduction

In the first part of our research concerning ALGLIB library optimization algorithms in MetaTrader 5 standard delivery, we thoroughly examined the following algorithms: BLEIC (Boundary, Linear Equality-Inequality Constraints), L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) and NS (Nonsmooth Nonconvex Optimization Subject to box/linear/nonlinear - Nonsmooth Constraints). We not only looked at their theoretical foundations, but also discussed a simple way to apply them to optimization problems.

In this article, we will continue to explore the remaining methods in the ALGLIB arsenal. Particular attention will be paid to testing them on complex multidimensional functions, which will allow us to form a holistic view of each method efficiency. In conclusion, we will conduct a comprehensive analysis of the results obtained and present practical recommendations for choosing the optimal algorithm for specific types of tasks.

BC (Box Constrained Optimization)

Optimization with box constraints, the subroutine minimizes the F(x) function with N arguments subject to box constraints (some of the box constraints are actually equalities). This optimizer uses an algorithm similar to the BLEIC (linear constraint optimizer) algorithm, but the presence of only box constraints allows for faster constraint activation strategies. On large-scale problems, with multiple active constraints in the solution, this optimizer can be faster than BLEIC.

Let me explain more simply what box-constrained optimization is. It is an optimization algorithm that searches for the best solution, works with box constraints (where each variable must be within certain limits) and essentially searches for the minimum of a function where all variables must be within given ranges. The main feature of the algorithm is that it is similar to BLEIC, but works faster and specially optimized for working with range constraints.

Requirements: The starting point must be feasible or close to the feasible region, and the function must be defined over the entire feasible region.

To use the BC method and others in the ALGLIB library, we will need to connect the file (the library is supplied with the MetaTrader 5 terminal, the user does not need to install anything additionally).

#include <Math\Alglib\alglib.mqh>

Let's develop a script - an example for effective work using ALGLIB methods. I will highlight the main steps that are typical when working with ALGLIB methods. Identical blocks of code are also highlighted in the appropriate color.

1. Let's define the boundary conditions of the problem, such as the number of launches of the fitness function (objective function), the ranges of the parameters to be optimized and their step. For ALGLIB methods, it is necessary to assign starting values of the "x" optimized parameters (the methods are deterministic and the results depend entirely on the initial values, so we will apply random number generation in the range of the problem parameters), as well as the "s" scale (the methods are sensitive to the scale of the parameters relative to each other, in this case we set the scale to "1").

2. Declare the objects necessary for the algorithm to work.

3. Set the external parameters of the algorithm (settings).

4. initialize the algorithm by passing the ranges and steps of the parameters to be optimized, as well as the external parameters of the algorithm, to the method.

5. Perform optimization.

6. Obtain the optimization results for further use.

Keep in mind that the user has no way to influence the optimization process or stop it at any time. The method performs all operations independently, calling the fitness function inside its process. The algorithm can call the fitness function an arbitrary number of times (although it is guided by a user-specified parameter). The user can control the maximum number of calls allowed by passing a stop command to the method.

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  // Initialization of optimization parameters---------------------------------------
  int numbTestFuncRuns = 10000;
  int params           = 1000;

  // Create and initialize arrays for range bounds---------------------
  CRowDouble rangeMin, rangeMax;
  rangeMin.Resize (params);
  rangeMax.Resize (params);
  double rangeStep;

  for (int i = 0; i < params; i++)
  {
    rangeMin.Set (i, -10);
    rangeMax.Set (i,  10);
  }
  rangeStep =  DBL_EPSILON;

  CRowDouble x; x.Resize (params);
  CRowDouble s; s.Resize (params);
  s.Fill (1);

  // Generate random initial parameter values in given ranges----
  for (int i = 0; i < params; i++)
  {
    x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0));
  }

  // Create objects for optimization------------------------------------------
  C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns);
  CObject             obj;
  CNDimensional_Rep   frep;
  CMinBCReport        rep;

  // Set the parameters of the BC optimization algorithm------------------------------
  double diffStep = 0.00001;
  double epsg     = 1e-16;
  double epsf     = 1e-16;

  CAlglib::MinBCCreateF  (x, diffStep, fFunc.state);
  CAlglib::MinBCSetBC    (fFunc.state, rangeMin, rangeMax);
  CAlglib::MinBCSetScale (fFunc.state, s);
  CAlglib::MinBCSetCond  (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns);
  CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj);
  CAlglib::MinBCResults  (fFunc.state, x, rep);

  // Output of optimization results-----------------------------------------------
  Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches);
}
//——————————————————————————————————————————————————————————————————————————————

Since the method calls the fitness function itself (and not from the user program), it will be necessary to wrap the call to the fitness function in a class that inherits from a parent class in ALGLIB (these parent classes are different for different methods). Declare the wrapper class as C_OptimizedFunction and set the following methods in the class:

1. Func () is a virtual method that is overridden in derived classes.
2. Init ()  — initialize class parameters. Inside the method:

• Variables related to the number of runs and the best value found for the function are initialized.
• The c and cB arrays are reserved for storing coordinates.

 Variables:

• state — CMinBCState type object specific to the BC method is used when calling static methods of the algorithm and calling the stop method.
  
• numberLaunches — current number of launches (necessary to prevent uncontrolled or too long execution of the fitness function).
  
• maxNumbLaunchesAllowed  — maximum permissible number of launches.
• fB — best found value of the fitness function.
  
• c []  — array of current coordinates.
• cB []  — array for storing the best search coordinates.

//——————————————————————————————————————————————————————————————————————————————
// Class for function optimization, inherits from CNDimensional_Func
class C_OptimizedFunction : public CNDimensional_Func
{
  public: //--------------------------------------------------------------------
  C_OptimizedFunction (void) { }
  ~C_OptimizedFunction (void) { }

  // A virtual function to contain the function being optimized--------
  virtual void Func (CRowDouble &x, double &func, CObject &obj);

  // Initialization of optimization parameters---------------------------------------
  void Init (int coords,
             int maxNumberLaunchesAllowed)
  {
    numberLaunches         = 0;
    maxNumbLaunchesAllowed = maxNumberLaunchesAllowed;
    fB = -DBL_MAX;

    ArrayResize (c,  coords);
    ArrayResize (cB, coords);
  }

  //----------------------------------------------------------------------------
  CMinBCState state;             // State 
  int         numberLaunches;    // Launch counter 

  double fB;                     // Best found value of the objective function (maximum)
  double cB [];                  // Coordinates of the point with the best function value

  private: //-------------------------------------------------------------------
  double c  [];                  // Array for storing current coordinates
  int    maxNumbLaunchesAllowed; // Maximum number of function calls allowed
};
//——————————————————————————————————————————————————————————————————————————————

The Func method of the C_OptimizedFunction is intended to access the user's fitness function. It takes the x vector as arguments (one of the variants of the optimized parameters of the problem, proposed by the optimization method), the func argument to accept the calculated value of the fitness function being returned and the obj object (the purpose of which is unclear to me, perhaps reserved for the ability to pass additional information to/from the method). The main stages of the method:

1. The numberLaunches counter is increased. Its objective is to track the number of Func method calls.
2. If the number of launches exceeds the permissible value of maxNumbLaunchesAllowed, the function sets the func value in DBL_MAX (the maximum value of the "double" type, ALGLIB methods are designed to minimize functions, this value means the worst possible solution). Then we call the MinBCRequestTermination function meant to signal the BC method to stop the optimization.
3. Next the values are copied from the x vector to the c array in the loop. This is necessary in order to use these values to pass to the user's fitness function.
4. The ObjectiveFunction function is called. It calculates the value of the objective function for the current values in the c array. The result is saved in ffVal, while the func value is set to the negative ffVal (we optimize an inverted paraboloid, which needs to be maximized, and BC minimizes the function, so we flip the value).
5. If the current value of ffVal exceeds the previous best value of fB, then fB is updated and the cB array copies the current state of c. This allows us to keep track of the best found value of the objective function with the corresponding parameters and refer to them later if necessary.

The Func function implements a call to a custom fitness function and tracks the number of times it has been launched, updating the best results. It also controls the stop conditions if the number of starts exceeds a set limit.

//——————————————————————————————————————————————————————————————————————————————
// Implementation of the function to be optimized
void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj)
{
  // Increase the function launch counter and limitation control----------------
  numberLaunches++;
  if (numberLaunches >= maxNumbLaunchesAllowed)
  {
    func = DBL_MAX;
    CAlglib::MinBCRequestTermination (state);
    return;
  }

  // Copy input coordinates to internal array-------------------------
  for (int i = 0; i < x.Size (); i++) c [i] = x [i];

  // Calculate objective function value----------------------------------------
  double ffVal = ObjectiveFunction (c);
  func = -ffVal;

  // Update the best solution found--------------------------------------
  if (ffVal > fB)
  {
    fB = ffVal;
    ArrayCopy (cB, c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

After running the test script with the BC algorithm to optimize the paraboloid function, we get the following result in print:

BC, best result: 0.6755436156375465, number of function launches: 84022

Unfortunately, despite requests to stop optimization using the MinBCRequestTermination method, the algorithm continued the process and attempted to access the fitness function beyond the limit of 10,000 runs.

Now let's try not to limit BC and give it the opportunity to act at its own discretion. The result is as follows:

BC, best result: 1.0, number of function launches: 56015

As we can see, BC is able to completely converge on the paraboloid function, but in this case it is impossible to estimate in advance the required number of runs of the target function.

The differentiation step is important in the algorithm. For example, if we use a very small step, for example 1e-16 instead of 0.00001, then the algorithm stops prematurely, essentially getting stuck, with the following result:

BC, best result: 0.6625662039929793, number of function launches: 4002

NLC (Nonlinearly Constrained Optimization with Preconditioned Augmented Lagrangian Algorithm)

This non-linear optimization algorithm with constraints allows minimizing a complex objective function F(x) with N variables, taking into account various constraints: constraints on the boundaries of variables (min <= x <= max), linear inequalities and equalities, non-linear equalities G(x) = 0, non-linear inequalities H(x) <= 0.

Imagine that you have some difficult goal you want to achieve, but there are some restrictions you cannot violate. For example, you want to maximize sales profits, but you cannot exceed a certain overhead cost. The ALGLIB algorithm helps to solve this kind of constrained optimization problems. Here is how it works:

1. You give the algorithm a starting point — some initial guess about how to achieve the goal. This point must satisfy all the constraints.

2. The algorithm then begins to move slowly from this starting point, step by step approaching the optimal solution. At each step, it solves some auxiliary problem to understand, in which direction to move further.

3. To speed up this process, the algorithm uses a special technique called "preconditioning". This means that it sort of adjusts its "steps" to the structure of the task in order to move faster.

4. Eventually, after several iterations, the algorithm finds a solution that minimizes your objective function (for example, minimizes overhead) while satisfying all constraints.

Users can choose from three different solvers that are suitable for problems of different scale and complexity implemented in ALGLIB:

SQP (sequential quadratic programming) is recommended for medium-sized problems with difficult objective functions.
AUL (preconditioned augmented Lagrangian method) is recommended for large-scale problems or the ones having cheap (fast) objective functions.
SLP (sequential linear programming) is slower but more robust in complex cases.

Experiments with test functions have shown the efficiency of the AUL solver, other solvers are commented out in the code.

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  // Initialization of optimization parameters---------------------------------------
  int numbTestFuncRuns = 10000;
  int params           = 1000;

  // Create and initialize arrays for range bounds---------------------
  CRowDouble rangeMin, rangeMax;
  rangeMin.Resize (params);
  rangeMax.Resize (params);
  double rangeStep;

  for (int i = 0; i < params; i++)
  {
    rangeMin.Set (i, -10);
    rangeMax.Set (i,  10);
  }
  rangeStep = DBL_EPSILON;

  CRowDouble x; x.Resize (params);
  CRowDouble s; s.Resize (params);
  s.Fill (1);

  // Generate random initial parameter values in given ranges----
  for (int i = 0; i < params; i++)
  {
    x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0));
  }

  // Create objects for optimization------------------------------------------
  C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns);
  CObject             obj;
  CNDimensional_Rep   frep;
  CMinNLCReport       rep;

  // Setting parameters of the NLC optimization algorithm-----------------------------
  double diffStep = 0.00001;
  double rho      = 1000.0;
  int    outerits = 5;

  CAlglib::MinNLCCreateF    (x, diffStep, fFunc.state);
  CAlglib::MinNLCSetBC      (fFunc.state, rangeMin, rangeMax);
  CAlglib::MinNLCSetScale   (fFunc.state, s);
  CAlglib::MinNLCSetCond    (fFunc.state, rangeStep, numbTestFuncRuns);

  //CAlglib::MinNLCSetAlgoSQP (fFunc.state);
  CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits);
  //CAlglib::MinNLCSetAlgoSLP (fFunc.state);

  CAlglib::MinNLCOptimize   (fFunc.state, fFunc, frep, obj);
  CAlglib::MinNLCResults    (fFunc.state, x, rep);

  // Output of optimization results-----------------------------------------------
  Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches);
}
//——————————————————————————————————————————————————————————————————————————————

In NLC, the "state" variable type is set to CMinNLCState.

//——————————————————————————————————————————————————————————————————————————————
// Class for function optimization, inherits from CNDimensional_FVec
class C_OptimizedFunction : public CNDimensional_FVec
{
  public: //--------------------------------------------------------------------
  C_OptimizedFunction (void) { }
  ~C_OptimizedFunction (void) { }

  // A virtual function to contain the function being optimized--------
  virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj);

  // Initialization of optimization parameters---------------------------------------
  void Init (int coords,
             int maxNumberLaunchesAllowed)
  {
    numberLaunches         = 0;
    maxNumbLaunchesAllowed = maxNumberLaunchesAllowed;
    fB = -DBL_MAX;

    ArrayResize (c,  coords);
    ArrayResize (cB, coords);
  }

  //----------------------------------------------------------------------------
  CMinNLCState state;            // State 
  int          numberLaunches;   // Launch counter 

  double fB;                     // Best found value of the objective function (maximum)
  double cB [];                  // Coordinates of the point with the best function value

  private: //-------------------------------------------------------------------
  double c  [];                  // Array for storing current coordinates
  int    maxNumbLaunchesAllowed; // Maximum number of function calls allowed
};
//——————————————————————————————————————————————————————————————————————————————

Request the stop of the optimization process using the MinNLCRequestTermination command.

//——————————————————————————————————————————————————————————————————————————————
// Implementation of the function to be optimized
void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj)
{
  // Increase the function launch counter and limitation control----------------
  numberLaunches++;
  if (numberLaunches >= maxNumbLaunchesAllowed)
  {
    fi.Set (0, DBL_MAX);
    CAlglib::MinNLCRequestTermination (state);
    return;
  }

  // Copy input coordinates to internal array-------------------------
  for (int i = 0; i < x.Size (); i++) c [i] = x [i];

  // Calculate objective function value----------------------------------------
  double ffVal = ObjectiveFunction (c);
  fi.Set (0, -ffVal);

  // Update the best solution found--------------------------------------
  if (ffVal > fB)
  {
    fB = ffVal;
    ArrayCopy (cB, c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

After running the test script with the NLC algorithm to optimize the paraboloid function, we get the following result in print:

NLC, best result: 0.8858935739350294, number of function launches: 28007

With no limits on the number of target function launches, NLC completely converges but performs over a million of iterations along the way:

NLC, best result: 1.0, number of function launches: 1092273

Using a very small step of 1e-16, the algorithm does not stop prematurely, like, for example, the BC method, but shows a result slightly worse than with the step of 0.00001.

NLC, best result: 0.8543715192632731, number of function launches: 20005

LM (Levenberg-Marquardt Method)

Levenberg-Marquardt Method (LM) is an optimization algorithm widely used to solve non-linear least squares problems. This method is effective in curve and surface fitting problems.

The basic idea of LM combines two optimization techniques: the gradient descent method and the Gauss-Newton method. This allows the algorithm to adapt to the shape of the objective function. How it works:

• At each iteration, the algorithm computes the step direction using a combination of gradient descent and second-order approximation.
• The attenuation ratio (λ) is automatically adjusted to control the step size and the balance between the two methods.

Imagine you are trying to find the lowest point in a mountainous area, but all you have is a map with fuzzy edges. The Levenberg-Marquardt method is like a smart navigator that combines two ways of finding a way:

1. The first method (Gauss-Newton method) is fast, but risky. It is like you are running straight down a slope. It works great when you are close to your target, but you might trip up if the terrain is difficult.

2. The second method (gradient descent) is slow but reliable. It is as if you are carefully descending in small steps. It is slower but safer. It works well even on difficult terrain.

The algorithm intelligently switches between these two methods. When the path is clear, it uses the fast method, but when the situation is difficult, it switches to a high alert mode. It automatically adjusts a step size.

Also, it may get stuck in a local minimum. The algorithm requires a good initial approximation (you need to know roughly where to look) and is not very effective for problems with a large number of parameters (more than 100).

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  // Initialization of optimization parameters---------------------------------------
  int numbTestFuncRuns = 10000;
  int params           = 1000;

  double rangeMin [], rangeMax [], rangeStep;
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeMax,  params);

  for (int i = 0; i < params; i++)
  {
    rangeMin  [i] = -10;
    rangeMax  [i] =  10;
  }
  rangeStep = DBL_EPSILON;

  double x [];
  double s [];
  ArrayResize (x, params);
  ArrayResize (s, params);
  ArrayInitialize (s, 1);

  // Generate random initial parameter values in given ranges----
  for (int i = 0; i < params; i++)
  {
    x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0);
  }

  // Create objects for optimization------------------------------------------
  C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns);
  CObject             obj;
  CNDimensional_Rep   frep;
  CMinLMReportShell   rep;

  // Set the parameters of the LM optimization algorithm------------------------------
  double diffStep = 1e-16;//0.00001;

  CAlglib::MinLMCreateV  (1, x, diffStep, fFunc.state);
  CAlglib::MinLMSetBC    (fFunc.state, rangeMin, rangeMax);
  CAlglib::MinLMSetScale (fFunc.state, s);
  CAlglib::MinLMSetCond  (fFunc.state, rangeStep, numbTestFuncRuns);
  CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj);
  CAlglib::MinLMResults  (fFunc.state, x, rep);

  // Output of optimization results-----------------------------------------------
  Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches);
}
//——————————————————————————————————————————————————————————————————————————————

For LM, the "state" variable type is set to CMinLMStateShell.

//——————————————————————————————————————————————————————————————————————————————
// Class for function optimization, inherits from CNDimensional_FVec
class C_OptimizedFunction : public CNDimensional_FVec
{
  public: //--------------------------------------------------------------------
  C_OptimizedFunction (void) { }
  ~C_OptimizedFunction (void) { }

  // A virtual function to contain the function being optimized--------
  virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj);

  // Initialization of optimization parameters---------------------------------------
  void Init (int coords,
             int maxNumberLaunchesAllowed)
  {
    numberLaunches         = 0;
    maxNumbLaunchesAllowed = maxNumberLaunchesAllowed;
    fB = -DBL_MAX;

    ArrayResize (c,  coords);
    ArrayResize (cB, coords);
  }

  //----------------------------------------------------------------------------
  CMinLMStateShell state;          // State 
  int              numberLaunches; // Launch counter 

  double fB;                       // Best found value of the objective function (maximum)
  double cB [];                    // Coordinates of the point with the best function value

  private: //-------------------------------------------------------------------
  double c  [];                    // Array for storing current coordinates
  int    maxNumbLaunchesAllowed;   // Maximum number of function calls allowed
};
//——————————————————————————————————————————————————————————————————————————————

As in the previous optimization methods, we limit the number of calls to the objective function, but the LM method is the only one for which a stop command is not provided. It would be logical to expect the presence of the MinLMRequestTermination function.

//——————————————————————————————————————————————————————————————————————————————
// Implementation of the function to be optimized
void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj)
{
  // Increase the function launch counter and limitation control----------------
  numberLaunches++;
  if (numberLaunches >= maxNumbLaunchesAllowed)
  {
    fi.Set (0, DBL_MAX);
    //CAlglib::MinLMRequestTermination (state); // such method does not exist
    return;
  }

  // Copy input coordinates to internal array-------------------------
  for (int i = 0; i < x.Size (); i++) c [i] = x [i];

  // Calculate objective function value----------------------------------------
  double ffVal = ObjectiveFunction (c);
  fi.Set (0, -ffVal);

  // Update the best solution found--------------------------------------
  if (ffVal > fB)
  {
    fB = ffVal;
    ArrayCopy (cB, c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

After running the test script with the LM algorithm to optimize the paraboloid function, we get the following result in print:

LM, best result: 0.6776047308612422, number of function launches: 4003

The LM method stopped at the 4003 rd run of the target function, so removing the restrictions on the number of iterations will give the same result, because the algorithm got stuck before reaching the "ceiling" of 10,000 iterations:

LM, best result: 0.6776047308612422, number of function launches: 4003

If we use a very small step size of 1e-16, the algorithm stops prematurely even earlier, at the 2001st run of the objective function:

LM, best result: 0.6670839162547625, number of function launches: 2001

Table of functions used in ALGLIB methods

ALGLIB optimization methods use different types of variables as initial values and box constraints, different types of parent classes of the objective function and sets of objects needed for optimization, and different lists of functions to call. This can make it difficult to intuitively write programs that use these methods.

To make it easier to understand and structure knowledge about ALGLIB optimization methods, I have prepared a summary table. It will help programmers quickly get their bearings and start optimizing their projects correctly.

Optimization algorithm	Type FF function	Type of variable	List of objects	List of called methods
BLEIC	Func	double	1) Cobject 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell	1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination
LBFGS	Func	double	1) Cobject 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell	1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination
NS	FVec	CRowDouble	1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState	1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination
BC	Func	CRowDouble	1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState	1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination
NLC	Fvec	CRowDouble	1) Cobject 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState	1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination
LM	FVec	double	1) Cobject 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell	1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (does not exist)

Testing methods

After studying the optimization methods of the ALGLIB library, the question naturally arises as to which of these methods to choose for specific tasks. Different types of optimization problems can be solved with different efficiency depending on the chosen method. To answer this important question, we will use complex test functions that have proven to be closest to real-world problems. These functions represent typical cases: smooth functions are represented by the Hilly test function, smooth with sharp vertices (differentiable not on their entire definition) — by Forest, while a purely discrete function is Megacity.

Tests will be performed with 50 reruns of each test and a limit of 10,000 target function calls. We will prepare a bench script for testing using the BC method as an example. This approach will allow us to obtain more accurate and representative results that will help us choose the most appropriate optimization method for each specific task.

Let's implement the FuncTests function that will perform test runs of optimization using the corresponding ALGLIB method. The function will allow us to collect data on the performance of methods and visualize their work, as well as build convergence graphs.

Let's briefly list what the FuncTests function does:

1. It accepts a test objective function, number of tests, visualization color, and variables for the overall result.
2. If video is enabled, it plots the function.
3. It sets the boundaries for testing and initializes variables for the results.
4. It generates random input data and performs optimization using the CAlglib library.
5. It keeps track of the number of calls to the target function and the best results.
6. It calculates and displays average results.
7. It updates the overall score based on current tests.

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_Function    &f,                  // Reference to the target function object
                const  int     funcCount,          // Number of functions to test
                const  color   clrConv,            // Visualization color
                double        &allScore,           // Total score of all tests
                double        &allTests)           // Total number of tests
{
  if (funcCount <= 0) return;                      // If the number of functions = 0, exit the function

  allTests++;                                      // Increase the total number of tests

  if (Video_P)                                     // If visualization is enabled
  {
    ST.DrawFunctionGraph (f);                      // Draw the function graph
    ST.SendGraphToCanvas ();                       // Send the graph to the canvas
    ST.MaxMinDr          (f);                      // Determine the maximum and minimum of the function
    ST.Update            ();                       // Update the visualization
  }

  //----------------------------------------------------------------------------
  C_AO_Utilities Ut;                               // Utilities for handling numbers
  int    xConv      = 0.0;                         // Variable for converting along the X axis
  int    yConv      = 0.0;                         // Variable for converting along the Y axis
  double aveResult  = 0.0;                         // Average test result
  int    aveRunsFF  = 0;                           // Average number of function runs
  int    params     = funcCount * 2;               // Number of parameters (2 for each function)
  int    epochCount = NumbTestFuncRuns_P / PopSize_P; // Number of epochs

  //----------------------------------------------------------------------------
  CRowDouble bndl; bndl.Resize (params);          // Array for lower bounds
  CRowDouble bndu; bndu.Resize (params);          // Array for upper bounds

  for (int i = 0; i < funcCount; i++)             // Fill the boundaries for each function
  {
    bndu.Set (i * 2, f.GetMaxRangeX ());          // Set the upper boundary by X
    bndl.Set (i * 2, f.GetMinRangeX ());          // Set the lower boundary by X

    bndu.Set (i * 2 + 1, f.GetMaxRangeY ());      // Set the upper bound by Y
    bndl.Set (i * 2 + 1, f.GetMinRangeY ());      // Set the lower boundary by Y
  }

  CRowDouble x; x.Resize (params);                // Array for parameter values
  CRowDouble s; s.Resize (params);                // Array for scaling
  s.Fill (1);                                     // Fill the array with ones

  for (int test = 0; test < NumberRepetTest_P; test++) // Run the tests
  {
    for (int i = 0; i < funcCount; i++)          // For each function
    {
      x.Set (i * 2,     Ut.RNDfromCI (bndl [i * 2],     bndu [i * 2]));     // Generate random values by X
      x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Generate random values by Y
    }

    //--------------------------------------------------------------------------
    CObject             obj;                                                                // Object for storing results
    C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Initialize the optimization function
    CNDimensional_Rep   frep;                                                               // Representation of multidimensional space
    CMinBCState         state;                                                              // State of the minimization method
    CMinBCReport        rep;                                                                // Minimization report

    double epsg = 1e-16;                                                                    // Parameter for gradient stop condition
    double epsf = 1e-16;                                                                    // Parameter for the stop condition by function value

    CAlglib::MinBCCreateF  (x, DiffStep_P, state);                                          // Create minimization state
    CAlglib::MinBCSetBC    (state, bndl, bndu);                                             // Set the boundaries
    CAlglib::MinBCSetScale (state, s);                                                      // Set scaling 
    CAlglib::MinBCSetCond  (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P);         // Set conditions
    CAlglib::MinBCOptimize (state, fFunc, frep, obj);                                       // Optimization
    CAlglib::MinBCResults  (state, x, rep);                                                 // Get results
    //--------------------------------------------------------------------------

    aveRunsFF += fFunc.numberLaunches;  // Sum up the number of function runs
    aveResult += -fFunc.bestMIN;        // Sum up the best minimum found
  }

  aveRunsFF /= NumberRepetTest_P;       // Calculate the average number of runs
  aveResult /= NumberRepetTest_P;       // Calculate the average result

  double score = aveResult;             // Estimate based on average result

  Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Output test results
  allScore += score;                    // Update the overall score
}
//——————————————————————————————————————————————————————————————————————————————

Let's run the test bench sequentially for all considered optimization methods of the ALGLIB library. Below are printouts of the test results for the respective methods, which should be read as follows:

BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8| - method abbreviation, full name, differentiation step (optionally, additional method parameters).

5 Hilly's - number of corresponding test objective functions in a multivariate problem.

Func runs: 2178(10000) - number of runs of the target function - the number of attempts to call methods to the target function and the specified desired "ceiling" for the number of runs.

result: 0.38483704535107116 - average result for 50 test runs.

Printout of the BLEIC method performance on the test objective functions:

BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|
=============================
5 Hilly's; Func runs: 2178(10000); result: 0.38483704535107116
25 Hilly's; Func runs: 10130(10000); result: 0.3572376879336238
500 Hilly's; Func runs: 11989(10000); result: 0.2676346390264618
=============================
5 Forest's; Func runs: 1757(10000); result: 0.28835869530001046
25 Forest's; Func runs: 9383(10000); result: 0.22629722977214342
500 Forest's; Func runs: 14978(10000); result: 0.16606494305819486
=============================
5 Megacity's; Func runs: 1211(10000); result: 0.13815384615384615
25 Megacity's; Func runs: 9363(10000); result: 0.12640000000000004
500 Megacity's; Func runs: 15147(10000); result: 0.09791692307692391
=============================
All score: 2.05290 (22.81%)

Printout of the L-BFGS method performance on the test objective functions:

L-BFGS|limited memory BFGS method for large scale optimization|0.9|
=============================
5 Hilly's; Func runs: 5625(10000); result: 0.38480050402327626
25 Hilly's; Func runs: 10391(10000); result: 0.2944296786579764
500 Hilly's; Func runs: 41530(10000); result: 0.25091140645623417
=============================
5 Forest's; Func runs: 3514(10000); result: 0.2508946897150378
25 Forest's; Func runs: 9105(10000); result: 0.19753907736098766
500 Forest's; Func runs: 40010(10000); result: 0.1483916309143011
=============================
5 Megacity's; Func runs: 916(10000); result: 0.12430769230769222
25 Megacity's; Func runs: 4639(10000); result: 0.10633846153846153
500 Megacity's; Func runs: 39369(10000); result: 0.09022461538461606
=============================
All score: 1.84784 (20.53%)

Printout of the NS method performance on the test objective functions:

NS|nonsmooth nonconvex optimization|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs: 10171(10000); result: 0.3716823351189392
25 Hilly's; Func runs: 11152(10000); result: 0.30271115043870767
500 Hilly's; Func runs: 1006503(10000); result: 0.2481831526729561
=============================
5 Forest's; Func runs: 10167(10000); result: 0.4432983184931045
25 Forest's; Func runs: 11221(10000); result: 0.20891527876847327
500 Forest's; Func runs: 1006503(10000); result: 0.15071828612481414
=============================
5 Megacity's; Func runs: 7530(10000); result: 0.15076923076923068
25 Megacity's; Func runs: 11069(10000); result: 0.12480000000000002
500 Megacity's; Func runs: 1006503(10000); result: 0.09143076923076995
=============================
All score: 2.09251 (23.25%)

Printout of the BC method performance on the test objective functions:

BC|box constrained optimization with fast activation of multiple box constraints|0.9|
=============================
5 Hilly's; Func runs: 1732(10000); result: 0.37512809463286956
25 Hilly's; Func runs: 9763(10000); result: 0.3542591015005374
500 Hilly's; Func runs: 22312(10000); result: 0.26434986025328294
=============================
5 Forest's; Func runs: 1564(10000); result: 0.28431712294752914
25 Forest's; Func runs: 8844(10000); result: 0.23891148588644037
500 Forest's; Func runs: 15202(10000); result: 0.16925473100070892
=============================
5 Megacity's; Func runs: 1052(10000); result: 0.12307692307692313
25 Megacity's; Func runs: 9095(10000); result: 0.12787692307692308
500 Megacity's; Func runs: 20002(10000); result: 0.09740000000000082
=============================
All score: 2.03457 (22.61%)

Printout of the NLC method performance on the test objective functions:

NLC|nonlinearly  constrained  optimization with preconditioned augmented lagrangian algorithm|0.8|1000.0|5|
=============================
5 Hilly's; Func runs: 8956(10000); result: 0.4270442612182801
25 Hilly's; Func runs: 10628(10000); result: 0.3222093696838907
500 Hilly's; Func runs: 48172(10000); result: 0.24687323917487405
=============================
5 Forest's; Func runs: 8357(10000); result: 0.3230697968403923
25 Forest's; Func runs: 10584(10000); result: 0.2340843463074393
500 Forest's; Func runs: 48572(10000); result: 0.14792910131023018
=============================
5 Megacity's; Func runs: 5673(10000); result: 0.13599999999999995
25 Megacity's; Func runs: 10560(10000); result: 0.1168615384615385
500 Megacity's; Func runs: 47611(10000); result: 0.09196923076923148
=============================
All score: 2.04604 (22.73%)

Printout of the LM method performance on the test objective functions:

LM|improved levenberg-marquardt algorithm|0.0001|
=============================
5 Hilly's; Func runs: 496(10000); result: 0.2779179366819541
25 Hilly's; Func runs: 4383(10000); result: 0.26680986645907423
500 Hilly's; Func runs: 10045(10000); result: 0.27253276065962373
=============================
5 Forest's; Func runs: 516(10000); result: 0.1549127879839302
25 Forest's; Func runs: 3727(10000); result: 0.14964009375922901
500 Forest's; Func runs: 10051(10000); result: 0.1481206726095718
=============================
5 Megacity's; Func runs: 21(10000); result: 0.0926153846153846
25 Megacity's; Func runs: 101(10000); result: 0.09040000000000001
500 Megacity's; Func runs: 2081(10000); result: 0.08909230769230835
=============================
All score: 1.54204 (17.13%)

Now we can clearly analyze the behavior of the algorithms on test functions. Most methods are characterized by premature termination of work before the limit on the number of runs of the target function is exhausted (in the parameters we specified a limit of 10,000 iterations). For example, the Levenberg-Marquardt (LM) method on the discrete Megacity problem with a dimension of 1,000 parameters stopped on average at 2,081 iterations, and with a dimension of 10 - only at 21 iterations. At the same time, on smooth Hilly functions, this method tried to find the minimum in a significantly larger number of iterations. Other methods, by contrast, made more than a million calls to the target function.

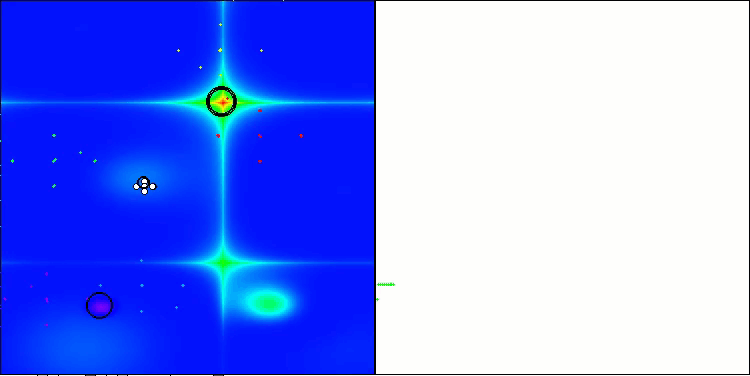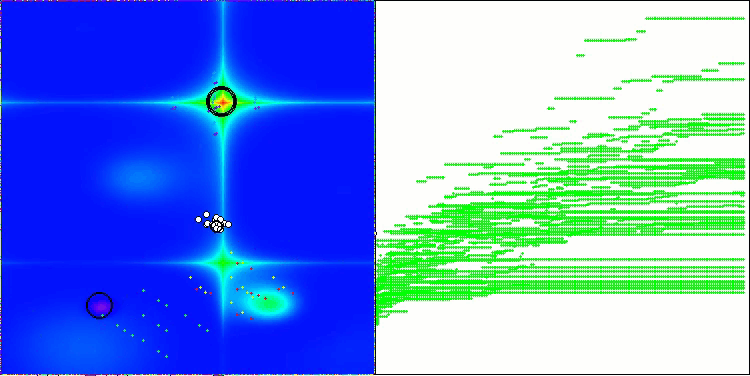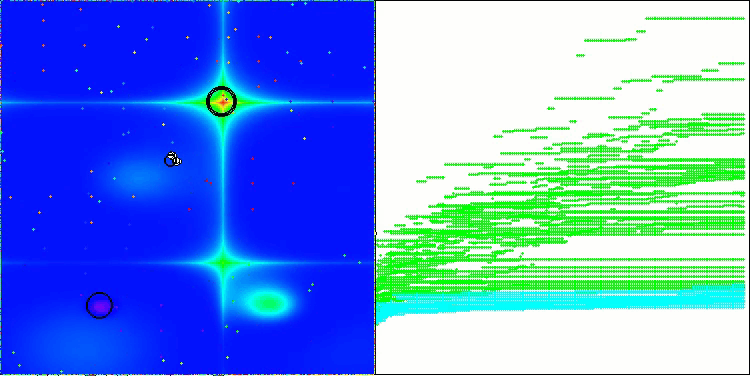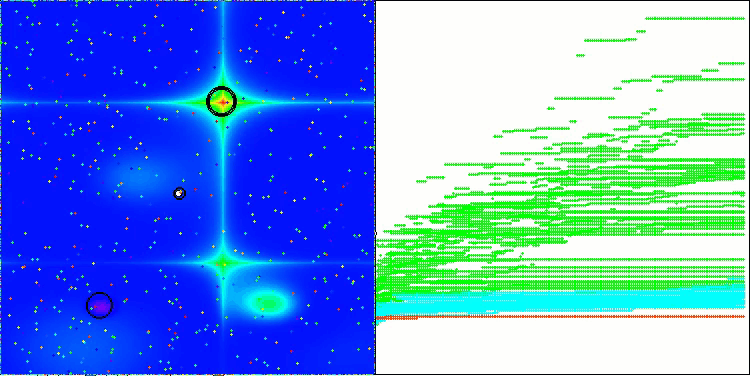
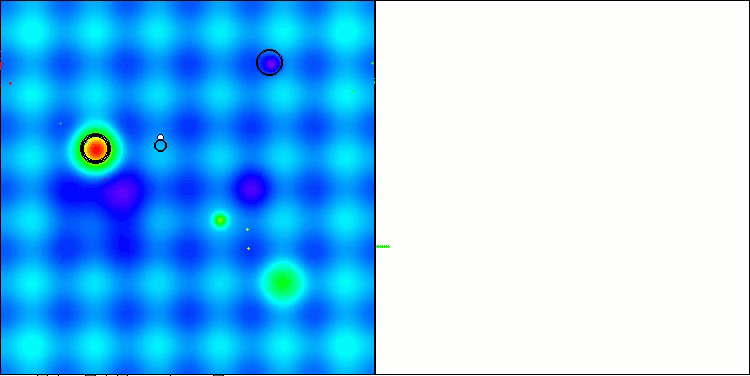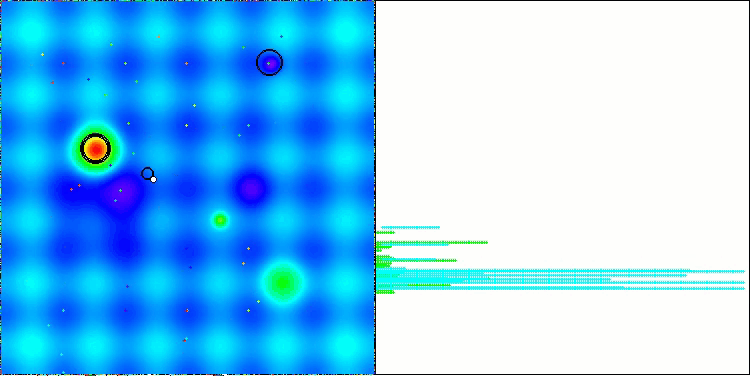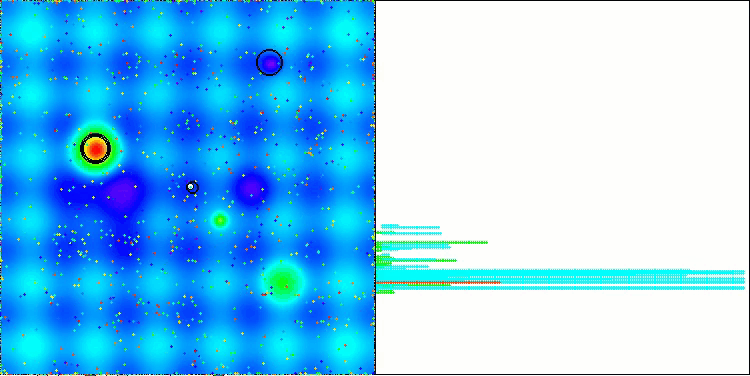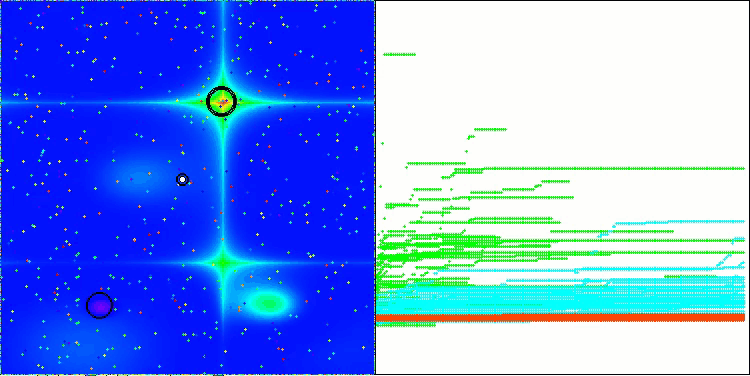
Below are visualizations of the performance of the NS method (which scored the highest) and the LM method (which scored the lowest).

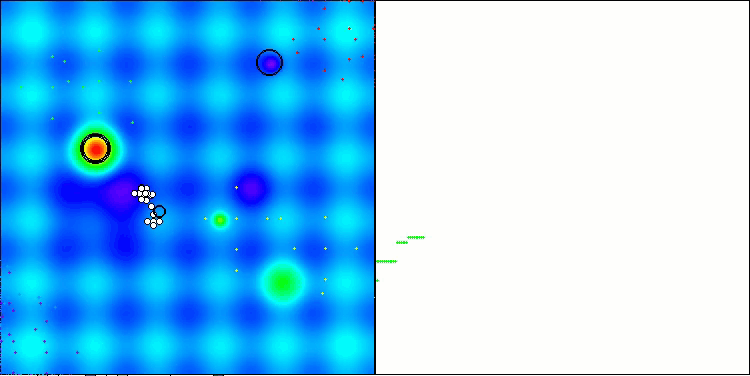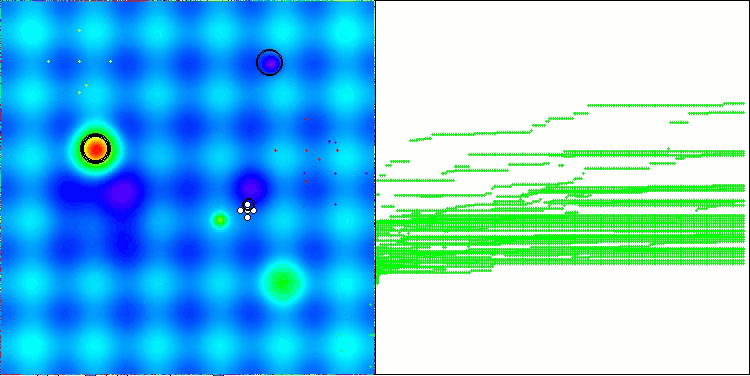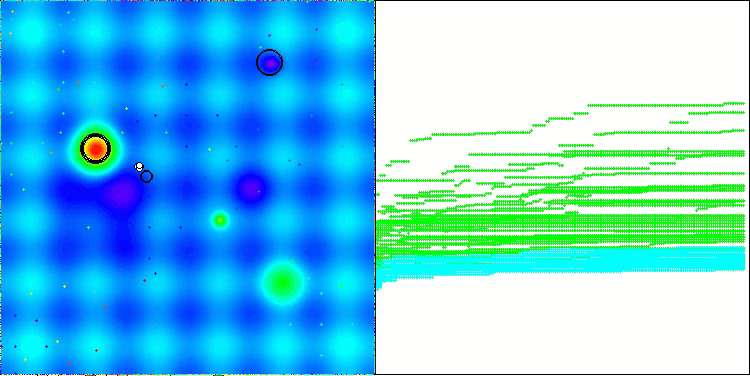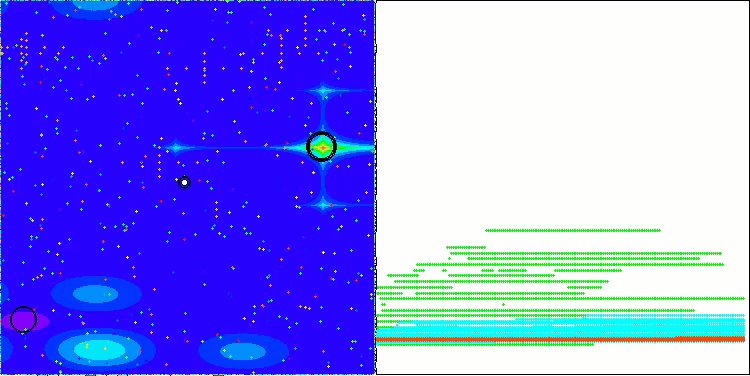
NS on the Hilly test function

NS on the Forest test function

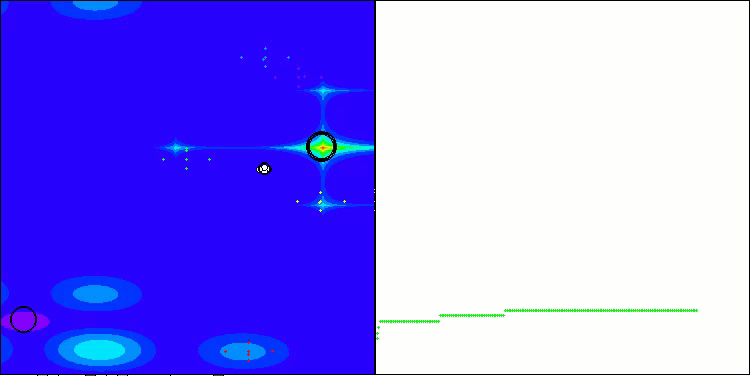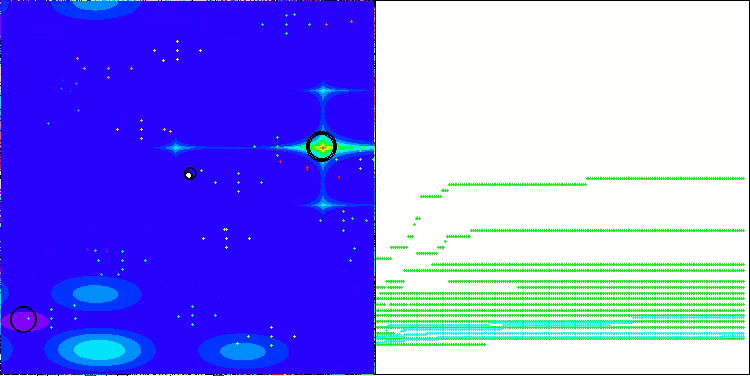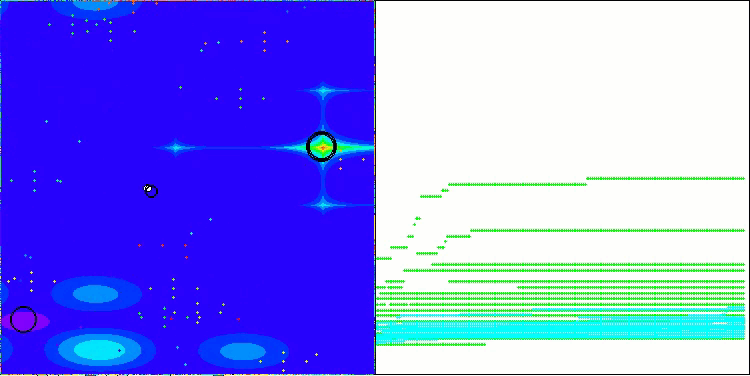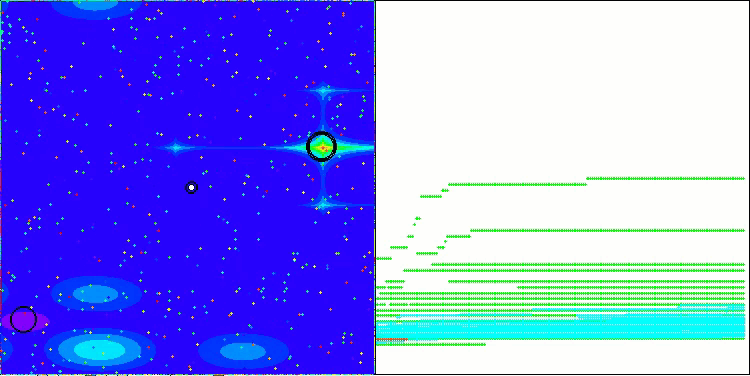
NS on the Megacity test function

  LM on the Hilly test function

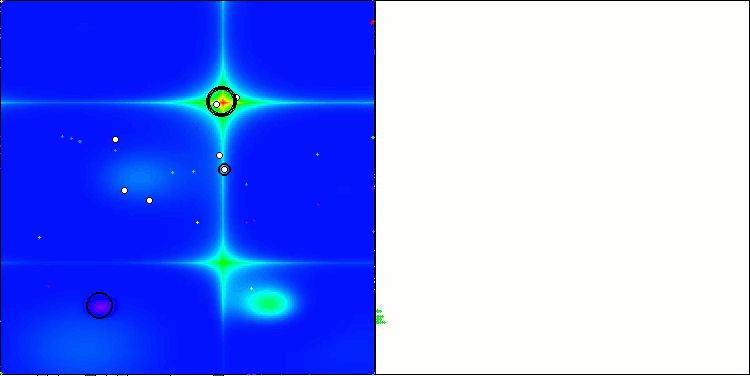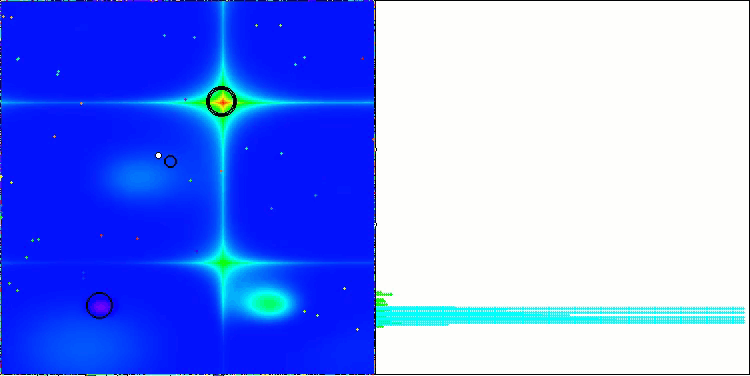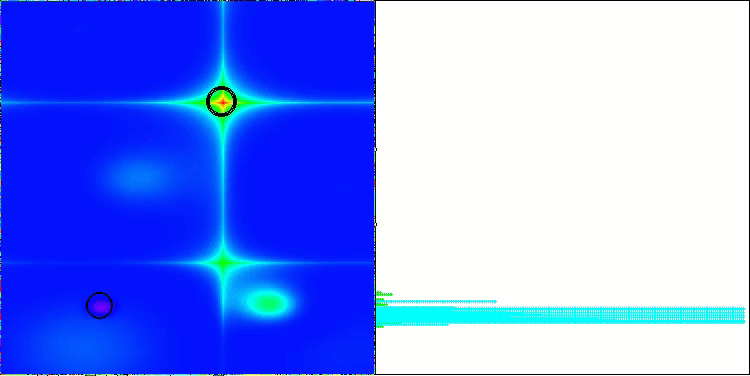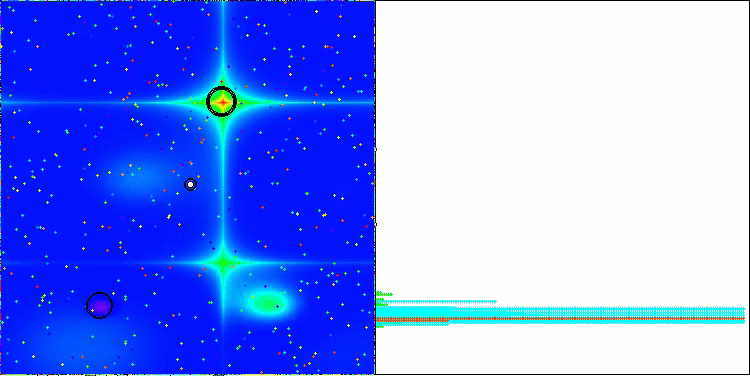
LM on the Forest test function

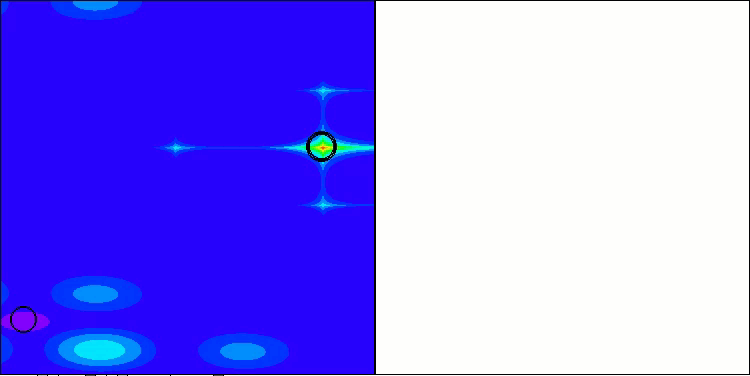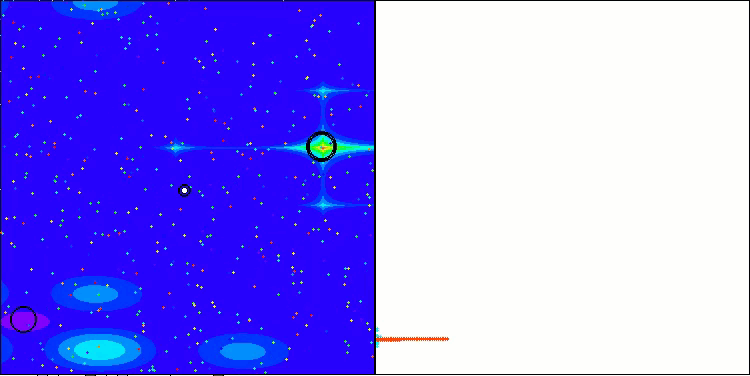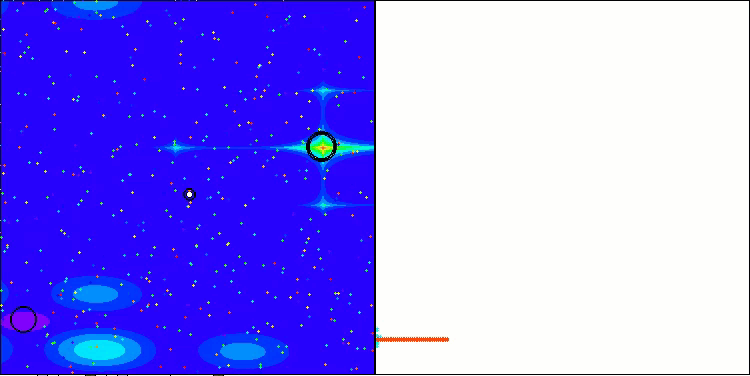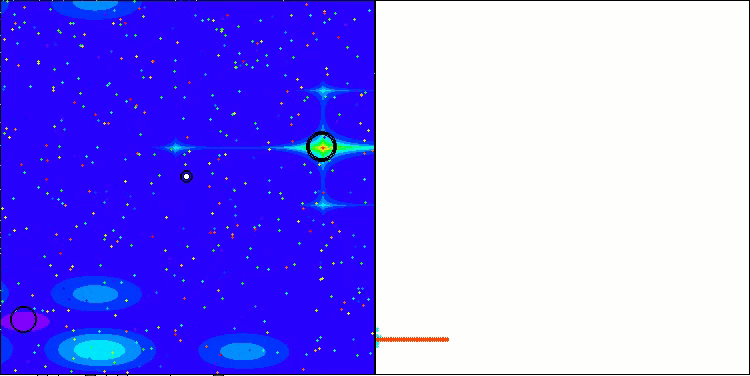
LM on the Megacity test function

Let's summarize the obtained results in a table.

Color gradation of algorithms according to the corresponding tests

Summary

In two articles, we looked at optimization methods from the ALGLIB library, studied ways to integrate them into user programs, and also the features of interaction with the method functions. In addition, we conducted tests to identify the strengths and weaknesses of the algorithms. Let's briefly summarize:

• On smooth functions (Hilly) of low dimension, the NLC method showed the best results, while on high dimensions, the LM method was in the lead.
• On smooth functions with sharp extrema (Forest) in low dimensions, the NS method demonstrated the best results, and in high dimensions, the BC method was the best.
• On the discrete Megacity problem in small dimensions the NS method took the lead, while in large dimensions the BLEIC method was the first.

The differences in the results of the methods are insignificant, the deviations are within the range of their own results, however, the NS method can be called more universal, while it is not possible to stop it forcibly.

The codes attached to the article include everything you need to start using optimization methods in your projects, as well as visually see and evaluate their capabilities.

Programs used in the article

#	Name	Type	Description
1	Simple test ALGLIB BLEIC.mq5	Script	Test script for working with BLEIC
2	Simple test ALGLIB LBFGS.mq5	Script	Test script for working with L-BFGS
3	Simple test ALGLIB NS.mq5	Script	Test script for working with NS
4	Simple test ALGLIB BC.mq5	Script	Test script for working with BC
5	Simple test ALGLIB NLC.mq5	Script	Test script for working with NLC
6	Simple test ALGLIB LM.mq5	Script	Test script for working with LM
7	Test_minBLEIC.mq5	Script	Test bench for BLEIC
8	Test_minLBFGS.mq5	Script	Test bench for L-BFGS
9	Test_minNS.mq5	Script	Test bench for NS
10	Test_minBC.mq5	Script	Test bench for BC
11	Test_minNLC.mq5	Script	Test bench for NLC
12	Test_minLM.mq5	Script	Test bench for LM
13	CalculationTestResults.mq5	Script	Script for calculating results in the comparison table
14	TestFunctions.mqh	Include	Library of test functions
15	TestStandFunctions.mqh	Include	Test stand function library
16	Utilities.mqh	Include	Library of auxiliary functions