Expert Advisor based on the universal MLP approximator

Contents

1. Introduction
2. Immersion in the problems of training
   
3. Universal approximator
4. Implementation of MLP as part of a trading EA

Introduction

When it comes to neural networks, many people imagine complex algorithms and cumbersome technical details. At its core, a neural network is a composition of functions, where each layer consists of a combination of a linear transformation and a nonlinear activation function. If we put this into an equation, it will look like this:

F(x) = f2(f1(x))

where f1 is the function of the first layer, and f2 is the function of the second one.

Many people think that neural networks are something incredibly complex and difficult to understand, but I want to explain them in simple terms so that everyone can see them from a different perspective. There are many different neural network architectures, each designed to perform specific tasks. In this article, we will focus on the simplest multilayer perceptron (MLP), which performs transformations on input information through nonlinear functions. Knowing the network architecture, we can write it in an analytical form, where each activation function in neurons serves as a nonlinear transformer.

Each layer of the network contains a group of neurons that handle information passing through many nonlinear transformations. Multilayer perceptron is capable of performing tasks such as approximation, classification and extrapolation. The general equation describing the operation of the perceptron is adjusted using weights, which allows it to be adapted to different tasks.

Interestingly, we can integrate this approximator into any trading system. If we consider a neural network without mentioning optimizers such as SGD or ADAM, MLP can be used as an information transformer. For example, it can analyze market conditions - be it flat, trend or transitional state - and apply various trading strategies based on this. We can also use a neural network to convert indicator data into trading signals.

In this article, we aim to dispel the myth about the complexity of using neural networks and show how, leaving aside the complex details of weighting and optimization, we can create a trading EA based on a neural network without having deep knowledge of machine learning. We will go through the process of creating an EA step by step, from collecting and preparing data to training the model and integrating it into a trading strategy.

Immersion in the problems of training

There are three main types of training. We are interested in the nuances of these types as they apply to market data analysis. The approach presented in this article aims to take into account the shortcomings of these types of training.

Supervised learning. The model is trained on labeled data, making predictions based on examples. Objective function: minimizing the error of the prediction matching the target value (e.g. MSE error). However, this approach has a number of disadvantages. It requires a significant amount of high-quality labeled data, which is a major challenge in the time series context. If we have clear and reliable examples to train from, such as in handwriting recognition or image content recognition tasks, then training goes smoothly. The neural network learns to recognize exactly what it was trained to recognize.

In case of time series, the situation is different: it is extremely difficult to label the data in a way that allows one to be confident in its reliability and relevance. In practice, it turns out that the network learns what we assume, and not what is actually relevant to the process under study. Many authors emphasize that successful supervised training requires the use of "good" labels, but the degree of their quality in the context of time series is often difficult to determine in advance.

As a result, other subjective assessments of the quality of training arise, such as "overfitting". The artificial concept of "noise" is also introduced, implying that an overly "overfit" network could remember noise data, and not the main patterns. You will not find clear definitions and quantifications of "noise" and "overfitting" anywhere, precisely because they are subjective when it comes to time series analysis. Therefore, it should be recognized that the application of supervised learning to time series requires taking into account many nuances that are difficult to algorithmize, which significantly affect the stability of the model on new data.

Unsupervised learning. The model itself searches for hidden structures in unlabeled data. Objective functions may vary different depending on the methods. It is difficult to assess the quality of the results obtained, since there are no clear markers for verification. The model may not find useful patterns if the data does not have a clear structure, and it is not known whether structures were actually found in the data that are directly related to the "carrier process".

Methods that are traditionally classified as unsupervised learning include: K-means, Self-Organizing Maps (SOM), and others. All these methods are trained using their specific target functions.

Let's consider some examples:

• K-means. Minimizing the intra-cluster variance, which is defined as the sum of the squares of the distances between each point and its cluster center.
• Principal component analysis (PCA). Maximizing the variance of projections of data onto new axes (principal components).
• Decision trees (DT). Minimization of entropy, Gini index, dispersion and others.
  

Reinforcement learning. Objective function: total reward. It is a machine learning technique where an agent (such as a program or a robot) learns to make decisions by interacting with its environment. The agent receives a reward or penalty depending on its actions. The agent's goal is to maximize the total reward by learning from experience.

Results may be unstable due to the random nature of training, which makes it difficult to predict the behavior of the model and is not always suitable for problems where there is no clear system of rewards and penalties, which can make learning less effective. Reinforcement learning is usually associated with many practical problems: the difficulty of representing the objective reinforcement function when using neural network learning algorithms such as ADAM and the like, since it is necessary to normalize the values of the objective function to a range close to [-1;1]. This involves calculating the derivatives of the activation function in neurons and passing the error back through the network to adjust the weights to avoid "weight explosion" and similar effects that cause the neural network to stall.

We looked at the conventional classification of training types above. As you can see, they are all based on minimization/maximization of some objective function. Then it becomes obvious that the main difference between them is only one thing - the absence or presence of a "supervisor". If it is absent, the division of types of training comes down to the specifics of the target function that needs to be optimized.

Thus, in my opinion, the classification of training types can be represented as supervised learning, when there are target values (minimization of the prediction error relative to the goal) and unsupervised learning when there are no target values. Subtypes of unsupervised learning depend on the type of objective function based on data properties (distance, density, etc.), system performance (integrated metrics, such as profit, productivity, etc.), distributions (for generative models), and other evaluation criteria.

Universal approximator

The approach I propose belongs to the second type - unsupervised learning. In this method, we do not try to "teach" the neural network how to trade correctly and do not tell it where to open or close positions, since we ourselves do not know the answer to these questions. Instead, we let the network make its own trading decisions, and our job is to evaluate its overall trading results.

In this case, we do not need to normalize the evaluation function or worry about problems such as "weight explosions" and "network stall", since they are absent in this approach. We logically separate the neural network from the optimization algorithm and give it only the task of transforming the input data into a new type of information that reflects the trader's skills. Essentially, we are simply converting one type of information into another, without any understanding of the patterns in the time series or how to trade to make a profit.

A type of neural network such as MLP (multilayer perceptron) is ideal for this role, which is confirmed by the universal approximation theorem. This theorem states that neural networks can approximate any continuous function. In our case, by "continuous function" we mean a process occurring in the analyzed time series. This approach eliminates the need to resort to artificial and subjective concepts, such as "noise" and "overfitting", which have no quantitative value.

To get an idea of how this works, just look at Figure 1. We feed MLP some information related to the current market data (these could be OHLC bar prices, indicator values, etc.), and at the output we receive ready-to-use trading signals. After running through the history of a trading symbol, we can calculate the objective function, which is an integral assessment (or complex of assessments) of trading results, and adjust the network weights with an external optimization algorithm, maximizing the objective function describing the quality of the neural network's trading results.

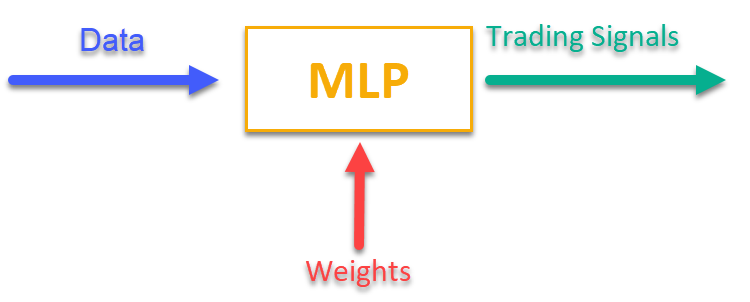
Figure 1. Transformation of one type of information into another

Implementation of MLP as part of a trading EA

First, we will write the MLP class, then we will embed the class into the EA. The articles contain many different implementations of networks of different architectures, but I will show my version of MLP, which is exactly a neural network, without an optimizer.

Let's declare a C_MLP class that implements a multilayer perceptron (MLP). Key Features:

1. Init ()  — initialization configures the network depending on the required number of layers and the number of neurons in each layer and returns the total number of weights.

2. ANN ()  — a forward pass from the first input layer to the last output layer, the method takes input data and weights, calculates the output values of the network (see Fig. 1).

3. GetWcount ()  — total number of weights in the network.

4. LayerCalc ()  — network layer calculation.

Internal elements:

• layers store the values of neurons
• weightsCNT — total number of weights
• layersCNT — total number of layers

The class allows us to create an MLP neural network with any number of hidden layers and any number of neurons in them.

//+----------------------------------------------------------------------------+
//| Multilayer Perceptron (MLP) class                                          |
//| Implement a forward pass through a fully connected neural network          |
//| Architecture: Lin -> L1 -> L2 -> ... Ln -> Lout                            |
//+----------------------------------------------------------------------------+
class C_MLP
{
  public: //--------------------------------------------------------------------

  // Initialize the network with the given configuration
  // Return the total number of weights in the network, or 0 in case of an error
  int Init (int &layerConfig []);

  // Calculate the values of all layers sequentially from input to output
  void ANN (double &inLayer  [],  // input values
            double &weights  [],  // network weights (including biases)
            double &outLayer []); // output layer values

  // Get the total number of weights in the network
  int GetWcount () { return weightsCNT; }

  int layerConf []; // Network configuration - number of neurons in each layer

  private: //-------------------------------------------------------------------
  // Structure for storing the neural network layer
  struct S_Layer
  {
      double l [];     // Neuron values
  };

  S_Layer layers [];    // Array of all network layers
  int     weightsCNT;   // Total number of weights in the network (including biases)
  int     layersCNT;    // Total number of layers (including input and output ones)
  int     cnt_W;        // Current index in the weights array when traversing the network
  double  temp;         // Temporary variable to store the sum of the weighted inputs

  // Calculate values of one layer of the network
  void LayerCalc (double   &inLayer  [], // values of neurons of the previous layer
                  double   &weights  [], // array of weights and biases of the entire network
                  double   &outLayer [], // array for writing values of the current layer
                  const int inSize,      // number of neurons in the input layer
                  const int outSize);    // outSize  - number of neurons in the output layer
};

A multilayer perceptron (MLP) is initialized with a given layer configuration. Main steps:

1. Check the configuration:

• Check that the network has at least 2 layers (input and output).
• Check that there is at least 1 neuron in each layer. If the conditions are not met, an error message is displayed and the function returns 0.

2. Saving the configuration of each layer for quick access to the layerconf array.

3. Creating arrays of layers: memory is allocated to store neurons in each layer.

4. Weight count: The total number of weights in the network is calculated, including biases for each neuron.

The function returns the total number of weights or 0 in case of an error.

//+----------------------------------------------------------------------------+
//| Initialize the network                                                     |
//| layerConfig - array with the number of neurons in each layer               |
//| Returns the total number of weights needed, or 0 in case of an error       |
//+----------------------------------------------------------------------------+
int C_MLP::Init (int &layerConfig [])
{
  // Check that the network has at least 2 layers (input and output)
  layersCNT = ArraySize (layerConfig);
  if (layersCNT < 2)
  {
    Print ("Error Net config! Layers less than 2!");
    return 0;
  }

  // Check that each layer has at least 1 neuron
  for (int i = 0; i < layersCNT; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Error Net config! Layer No." + string (i + 1) + " contains 0 neurons!");
      return 0;
    }
  }

  // Save network configuration
  ArrayCopy (layerConf, layerConfig, 0, 0, WHOLE_ARRAY);

  // Create an array of layers
  ArrayResize (layers, layersCNT);

  // Allocate memory for neurons of each layer
  for (int i = 0; i < layersCNT; i++)
  {
    ArrayResize (layers [i].l, layerConfig [i]);
  }

  // Calculate the total number of weights in the network
  weightsCNT = 0;
  for (int i = 0; i < layersCNT - 1; i++)
  {
    // For each neuron of the next layer we need:
    // - one bias value
    // - weights for connections with all neurons of the current layer
    weightsCNT += layerConf [i] * layerConf [i + 1] + layerConf [i + 1];
  }

  return weightsCNT;
}

The LayerCalc method performs computations for a single layer of a neural network using the hyperbolic tangent as the activation function. Main steps:

1. Input and output parameters:

• inLayer []  — array of input values from the previous layer
• weights []  — weights array contains offsets and weights for the links
• outLayer []  — array for storing output values of the current layer
• inSize — number of neurons in the input layer
• outSize — number of neurons in the output layer

2. Cycle through the neurons of the output layer. For each neuron in the output layer:

• starts with a bias value
• adds weighted input values (each input value is multiplied by the corresponding weight)
• the value of the activation function for a neuron is calculated

3. Applying the activation function:

• uses the hyperbolic tangent to nonlinearly transform a value into a range between -1 and 1
• the result is written to the outLayer [] output array

//+----------------------------------------------------------------------------+
//| Calculate values of one layer of the network                               |
//| Implement the equation: y = tanh(bias + w1*x1 + w2*x2 + ... + wn*xn)       |
//+----------------------------------------------------------------------------+
void C_MLP::LayerCalc (double    &inLayer  [],
                       double    &weights  [],
                       double    &outLayer [],
                       const int  inSize,
                       const int  outSize)
{
  // Calculate the value for each neuron in the output layer
  for (int i = 0; i < outSize; i++)
  {
    // Start with the bias value for the current neuron
    temp = weights [cnt_W];
    cnt_W++;

    // Add weighted inputs from each neuron in the previous layer
    for (int u = 0; u < inSize; u++)
    {
      temp += inLayer [u] * weights [cnt_W];
      cnt_W++;
    }

    // Apply the "hyperbolic tangent" activation function
    // f(x) = 2/(1 + e^(-x)) - 1
    // Range of values f(x): [-1, 1]
    outLayer [i] = 2.0 / (1.0 + exp (-temp)) - 1.0;
  }
}

We implement the work of an artificial neural network by sequentially calculating the values of all layers - from the input to the output. 

1. Input and output parameters:

• inLayer []  — array of input values fed into the neural network
• weights []  — array of weights that includes both the weights for the connections between neurons and the biases
• outLayer []  — array to contain the output values of the last layer of the neural network

2. Reset weight counter: the cnt_W variable, which keeps track of the current position in the weight array, is reset to 0 before the calculation begins.

3. Copying input data: input data from inLayer is copied to the first layer of the network using the ArrayCopy function.

4. Loop through layers:

• the loop goes through all layers of the neural network.
• for each layer, the LayerCalc function is called for calculating values for the current layer based on the output values of the previous layer, the weights, and the sizes of the layers.

5. After all layers have completed their calculations, the output values of the last layer are copied into the outLayer layer using the ArrayCopy function.

//+----------------------------------------------------------------------------+
//| Calculate the values of all layers sequentially from input to output       |
//+----------------------------------------------------------------------------+
void C_MLP::ANN (double &inLayer  [],  // input values
                 double &weights  [],  // network weights (including biases)
                 double &outLayer [])  // output layer values
{
  // Reset the weight counter before starting the pass
  cnt_W = 0;

  // Copy the input data to the first layer of the network
  ArrayCopy (layers [0].l, inLayer, 0, 0, WHOLE_ARRAY);

  // Calculate the values of each layer sequentially
  for (int i = 0; i < layersCNT - 1; i++)
  {
    LayerCalc (layers    [i].l,     // output of the previous layer
               weights,             // network weights (including bias)
               layers    [i + 1].l, // next layer
               layerConf [i],       // size of current layer
               layerConf [i + 1]);  // size of the next layer
  }

  // Copy the values of the last layer to the output array
  ArrayCopy (outLayer, layers [layersCNT - 1].l, 0, 0, WHOLE_ARRAY);
}

It is time to write an advisor for an automatic trading strategy using machine learning based on the MLP neural network.

1. We will connect libraries for trading operations, handling trading symbol information, mathematical functions, multilayer perceptron (MLP) and optimization algorithms.

2. Trading parameters - position volume, trading start and end hours. Training parameters - choosing the optimizer, neural network structure, number of bars to analyze, history depth for training, model validity period, and signal threshold.

3. Declaring classes and variables - class objects for utilities, neural network, and variables to store input data, weights, and last training time.

#include "#Symbol.mqh"
#include <Math\AOs\Utilities.mqh>
#include <Math\AOs\NeuroNets\MLP.mqh>
#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>

//------------------------------------------------------------------------------
input group    "---Trade parameters-------------------";
input double   Lot_P              = 0.01;   // Position volume
input int      StartTradeH_P      = 3;      // Trading start time
input int      EndTradeH_P        = 12;     // Trading end time

input group    "---Training parameters----------------";
input E_AO     OptimizerSelect_P  = AO_CLA; // Select optimizer
input int      NumbTestFuncRuns_P = 5000;   // Total number of function runs
input string   MLPstructure_P     = "1|1";  // Hidden layers, <4|6|2> - three hidden layers
input int      BarsAnalysis_P     = 3;      // Number of bars to analyze
input int      DepthHistoryBars_P = 10000;  // History depth for training in bars 
input int      RetrainingPeriod_P = 12;     // Duration in hours of the model's relevance
input double   SigThr_P           = 0.5;    // Signal threshold

//------------------------------------------------------------------------------
C_AO_Utilities U;
C_MLP          NN;
int            InpSigNumber;
int            WeightsNumber;
double         Inputs  [];
double         Weights [];
double         Outs    [1];
datetime       LastTrainingTime = 0;

C_Symbol       S;
C_NewBar       B;
int            HandleS;
int            HandleR;

I chose the first thing that came to mind as data passed to the neural network for handling: OHLC - bar prices (by default in the settings, 3 previous bars before the current one) and the values of the RSI and Stochastic indicators on these bars. The OnInit () function initializes a trading strategy using a neural network. 

1. Initializing indicators - objects for RSI and Stochastic are created.

2. Calculate the number of input signals for the network based on the BarsAnalysis_P input.

3. Setting up the neural network structure - the input parameter line with the network configuration is split, the validity of the number of layers and neurons is checked. The input string parameter specifies the number of hidden layers of the network and neurons in them, by default the parameter is "1|1", which means 2 hidden layers in the network with one neuron in each.

4. Initialize the neural network - the method is called to initialize the network, arrays for weights and input data are created.

5. Information output - data on the number of layers and network parameters is printed.

6. Return a successful initialization status.

The function ensures the preparation of all necessary components for the trading strategy to work.

//——————————————————————————————————————————————————————————————————————————————
int OnInit ()
{
  //----------------------------------------------------------------------------
  // Initializing indicators: Stochastic and RSI
  HandleS = iStochastic (_Symbol, PERIOD_CURRENT, 5, 3, 3, MODE_EMA, STO_LOWHIGH);
  HandleR = iRSI        (_Symbol, PERIOD_CURRENT, 14, PRICE_TYPICAL);

  // Calculate the number of inputs to the neural network based on the number of bars to analyze
  InpSigNumber = BarsAnalysis_P * 2 + BarsAnalysis_P * 4;

  // Display information about the number of inputs
  Print ("Number of network logins  : ", InpSigNumber);

  //----------------------------------------------------------------------------
  // Initialize the structure of the multilayer MLP
  string sepResult [];
  int layersNumb = StringSplit (MLPstructure_P, StringGetCharacter ("|", 0), sepResult);

  // Check if the number of hidden layers is greater than 0
  if (layersNumb < 1)
  {
    Print ("Network configuration error, hidden layers < 1...");
    return INIT_FAILED; // Return initialization error
  }

  // Increase the number of layers by 2 (input and output)
  layersNumb += 2;

  // Initialize array for neural network configuration
  int nnConf [];
  ArrayResize (nnConf, layersNumb);

  // Set the number of inputs and outputs in the network configuration
  nnConf [0] = InpSigNumber;   // Input layer
  nnConf [layersNumb - 1] = 1; // Output layer

  // Filling the hidden layers configuration
  for (int i = 1; i < layersNumb - 1; i++)
  {
    nnConf [i] = (int)StringToInteger (sepResult [i - 1]); // Convert a string value to an integer

    // Check that the number of neurons in a layer is greater than 0
    if (nnConf [i] < 1)
    {
      Print ("Network configuration error, in layer ", i, " <= 0 neurons...");
      return INIT_FAILED; // Return initialization error
    }
  }

  // Initialize the neural network and get the number of weights
  WeightsNumber = NN.Init (nnConf);
  if (WeightsNumber <= 0)
  {
    Print ("Error initializing MLP network...");
    return INIT_FAILED; // Return initialization error
  }

  // Resize the input array and weights
  ArrayResize (Inputs,  InpSigNumber);
  ArrayResize (Weights, WeightsNumber);

  // Initialize weights with random values in the range [-1, 1] (for debugging)
  for (int i = 0; i < WeightsNumber; i++)
      Weights [i] = 2 * (rand () / 32767.0) - 1;

  // Output network configuration information
  Print ("Number of all layers     : ", layersNumb);
  Print ("Number of network parameters: ", WeightsNumber);

  //----------------------------------------------------------------------------
  // Initialize the trade and bar classes
  S.Init (_Symbol);
  B.Init (_Symbol, PERIOD_CURRENT);

  return (INIT_SUCCEEDED); // Return successful initialization result
}
//——————————————————————————————————————————————————————————————————————————————

The main logic of the trading strategy is implemented in the OnTick () function. The strategy is simple: if the signal of the output layer neuron exceeds the threshold specified in the parameters, then the signal is interpreted as corresponding to the buy/sell direction, and if there are no open positions and the current time is allowed for trading, then we open a position. The position is closed if the neural network receives an opposite signal, or is forced to close if the time allowed for trading ends. Let's enumerate the main steps of the strategy:

1. Check for the need for new training. If enough time has passed since the last training, the neural network training is started. In case of an error, a message is displayed.

2. Testing the new bar. If the current tick is not the beginning of a new bar, the function execution is terminated.

3. Receiving data. The code requests price data (open, close, high, low) and indicator values (RSI and Stochastic).

4. Data normalization. The maximums and minimums are found among the received symbol price data, after which all data is normalized in the range from -1 to 1.

5. Forecasting. The normalized data is fed into a neural network to produce output signals.

6. Generating a trading signal. Based on the output data, a signal is generated to buy (1) or sell (-1).

7. Position management. If the current position contradicts the signal, it is closed. If the signal to open a new position coincides with the allowed time, the position is opened. Otherwise, if there is an open position, it is closed.

Thus, the logic in OnTick() implements the full cycle of automated trading, including training, data acquisition, normalization, forecasting and position management.

//——————————————————————————————————————————————————————————————————————————————
void OnTick ()
{
  // Check if the neural network needs to be retrained
  if (TimeCurrent () - LastTrainingTime >= RetrainingPeriod_P * 3600)
  {
    // Start the neural network training
    if (Training ()) LastTrainingTime = TimeCurrent (); // Update last training time
    else             Print ("Training error...");      // Display an error message

    return; // Complete function execution
  }

  //----------------------------------------------------------------------------
  // Check if the current tick is the start of a new bar
  if (!B.IsNewBar ()) return;

  //----------------------------------------------------------------------------
  // Declare arrays to store price and indicator data
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  // Get price data
  if (CopyRates (_Symbol, PERIOD_CURRENT, 1, BarsAnalysis_P, rates) != BarsAnalysis_P) return;

  // Get Stochastic values
  if (CopyBuffer (HandleS, 0, 1, BarsAnalysis_P, sto) != BarsAnalysis_P) return;
  // Get RSI values
  if (CopyBuffer (HandleR, 0, 1, BarsAnalysis_P, rsi) != BarsAnalysis_P) return;

  // Initialize variables to normalize data
  int wCNT   = 0;
  double max = -DBL_MAX; // Initial value for maximum
  double min =  DBL_MAX; // Initial value for minimum

  // Find the maximum and minimum among high and low
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    if (rates [b].high > max) max = rates [b].high; // Update the maximum
    if (rates [b].low  < min) min = rates [b].low;  // Update the minimum
  }

  // Normalization of input data for neural network
  for (int b = 0; b < BarsAnalysis_P; b++)
  {
    Inputs [wCNT] = U.Scale (rates [b].high,  min, max, -1, 1); wCNT++; // Normalizing high
    Inputs [wCNT] = U.Scale (rates [b].low,   min, max, -1, 1); wCNT++; // Normalizing low
    Inputs [wCNT] = U.Scale (rates [b].open,  min, max, -1, 1); wCNT++; // Normalizing open
    Inputs [wCNT] = U.Scale (rates [b].close, min, max, -1, 1); wCNT++; // Normalizing close

    Inputs [wCNT] = U.Scale (sto   [b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
    Inputs [wCNT] = U.Scale (rsi   [b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
  }

  // Convert data from Inputs to Outs
  NN.ANN (Inputs, Weights, Outs);

  //----------------------------------------------------------------------------
  // Generate a trading signal based on the output of a neural network
  int signal = 0;
  if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
  if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

  // Get the type of open position
  int posType = S.GetPosType ();
  S.GetTick ();

  if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
  {
    if (!S.PosClose ("", ORDER_FILLING_FOK) != 0) posType = 0;
    else return;
  }

  MqlDateTime time;
  TimeToStruct (TimeCurrent (), time);

  // Check the allowed time for trading
  if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P)
  {
    // Open a new position depending on the signal
    if (posType == 0 && signal != 0) S.PosOpen (signal, Lot_P, "", ORDER_FILLING_FOK, 0, 0.0, 0.0, 1);
  }
  else
  {
    if (posType != 0) S.PosClose ("", ORDER_FILLING_FOK);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Next, let's look at training a neural network on historical data:

1. Receiving data. Historical price data is loaded together with RSI and Stochastic indicator values.

2. Defining trading time. An array is created that marks which bars fall within the allowed trading time.

3. Setting up optimization parameters. The boundaries and parameter steps for optimization are initialized.

4. Selecting an optimization algorithm. Define an optimization algorithm and specify the population size.

5. The main loop of neural network weight optimization: 

• for each solution in the population, the value of the objective function is calculated, assessing its quality.
• the solution population is updated based on the results.

6. Output of results. The algorithm name, the best result are printed and the best parameters are copied to the weights array.

7. The memory occupied by the optimization algorithm object is freed.

The function carries out training the neural network to find the best parameters based on historical data.

//——————————————————————————————————————————————————————————————————————————————
bool Training ()
{
  MqlRates rates [];
  double   rsi   [];
  double   sto   [];

  int bars = CopyRates (_Symbol, PERIOD_CURRENT, 1, DepthHistoryBars_P, rates);
  Print ("Training on history of ", bars, " bars");
  if (CopyBuffer (HandleS, 0, 1, DepthHistoryBars_P, sto) != bars) return false;
  if (CopyBuffer (HandleR, 0, 1, DepthHistoryBars_P, rsi) != bars) return false;

  MqlDateTime time;
  bool truTradeTime []; ArrayResize (truTradeTime, bars); ArrayInitialize (truTradeTime, false);
  for (int i = 0; i < bars; i++)
  {
    TimeToStruct (rates [i].time, time);
    if (time.hour >= StartTradeH_P && time.hour < EndTradeH_P) truTradeTime [i] = true;
  }

  //----------------------------------------------------------------------------
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = NumbTestFuncRuns_P / popSize; // Total number of epochs (iterations) for optimization

  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps

  ArrayResize (rangeMin,  WeightsNumber);              // Resize 'min' borders array
  ArrayResize (rangeMax,  WeightsNumber);              // Resize 'max' borders array
  ArrayResize (rangeStep, WeightsNumber);              // Resize the steps array

  for (int i = 0; i < WeightsNumber; i++)
  {
    rangeMax  [i] =  5.0;
    rangeMin  [i] = -5.0;
    rangeStep [i] = 0.01;
  }

  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (OptimizerSelect_P);             // Select an optimization algorithm

  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)

  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs

  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = TargetFunction (ao.a [set].c, rates, rsi, sto, truTradeTime); //FF.CalcFunc (ao.a [set].c); //ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }

  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB);
  ArrayCopy (Weights, ao.cB);
  delete ao;                                           // Release the memory occupied by the algorithm object

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

We implement the objective function to evaluate the efficiency of a trading strategy using a neural network.

1. Initialization of variables. Set variables to track profits, losses, number of trades and other parameters.

2. Handling historical data. The loop goes through historical data and checks whether opening positions is allowed on the current bar.

3. Data normalization. For each bar, the price values (high, low, open, close) and indicators (RSI and Stochastic) are normalized for subsequent transmission to the neural network.

4. Signal prediction. The normalized data is fed into a neural network, which generates trading signals (buy or sell).

5. Virtual positions are managed according to the trading strategy in OnTick ().

6. Calculating the result. At the end of the function, the overall profit/loss ratio is calculated, multiplied by the number of trades, taking into account a reduction factor for the imbalance between buys and sells.

The function evaluates the efficiency of a trading strategy by analyzing profits and losses based on signals generated by a neural network and returns a numerical value reflecting its quality (in essence, the function performs one run through history back from the current position of the trading EA in time).

//——————————————————————————————————————————————————————————————————————————————
double TargetFunction (double &weights [], MqlRates &rates [], double &rsi [], double &sto [], bool &truTradeTime [])
{
  int bars = ArraySize (rates);

  // Initialize variables to normalize data
  int    wCNT       = 0;
  double max        = 0.0;
  double min        = 0.0;
  int    signal     = 0;
  double profit     = 0.0;
  double allProfit  = 0.0;
  double allLoss    = 0.0;
  int    dealsNumb  = 0;
  int    sells      = 0;
  int    buys       = 0;
  int    posType    = 0;
  double posOpPrice = 0.0;
  double posClPrice = 0.0;

  // Run through history
  for (int h = BarsAnalysis_P; h < bars - 1; h++)
  {
    if (!truTradeTime [h])
    {
      if (posType != 0)
      {
        posClPrice = rates [h].open;
        profit = (posClPrice - posOpPrice) * signal - 0.00003;

        if (profit > 0.0) allProfit += profit;
        else              allLoss   += -profit;

        if (posType == 1) buys++;
        else              sells++;

        allProfit += profit;
        posType = 0;
      }

      continue;
    }

    max  = -DBL_MAX; // Initial value for maximum
    min  =  DBL_MAX; // Initial value for minimum

    // Find the maximum and minimum among high and low
    for (int b = 1; b <= BarsAnalysis_P; b++)
    {
      if (rates [h - b].high > max) max = rates [h - b].high; // Update maximum
      if (rates [h - b].low  < min) min = rates [h - b].low;  // Update minimum
    }

    // Normalization of input data for neural network
    wCNT = 0;
    for (int b = BarsAnalysis_P; b >= 1; b--)
    {
      Inputs [wCNT] = U.Scale (rates [h - b].high,  min, max, -1, 1); wCNT++; // Normalizing high
      Inputs [wCNT] = U.Scale (rates [h - b].low,   min, max, -1, 1); wCNT++; // Normalizing low
      Inputs [wCNT] = U.Scale (rates [h - b].open,  min, max, -1, 1); wCNT++; // Normalizing open
      Inputs [wCNT] = U.Scale (rates [h - b].close, min, max, -1, 1); wCNT++; // Normalizing close

      Inputs [wCNT] = U.Scale (sto   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing Stochastic
      Inputs [wCNT] = U.Scale (rsi   [h - b],       0,   100, -1, 1); wCNT++; // Normalizing RSI
    }

    // Convert data from Inputs to Outs
    NN.ANN (Inputs, weights, Outs);

    //----------------------------------------------------------------------------
    // Generate a trading signal based on the output of a neural network
    signal = 0;
    if (Outs [0] >  SigThr_P) signal =  1; // Buy signal
    if (Outs [0] < -SigThr_P) signal = -1; // Sell signal

    if ((posType == 1 && signal == -1) || (posType == -1 && signal == 1))
    {
      posClPrice = rates [h].open;
      profit = (posClPrice - posOpPrice) * signal - 0.00003;

      if (profit > 0.0) allProfit += profit;
      else              allLoss   += -profit;

      if (posType == 1) buys++;
      else              sells++;

      allProfit += profit;
      posType = 0;
    }

    if (posType == 0 && signal != 0)
    {
      posType = signal;
      posOpPrice = rates [h].open;
    }
  }

  dealsNumb = buys + sells;

  double ko = 1.0;
  if (sells == 0 || buys == 0) return -DBL_MAX;
  if (sells / buys > 1.5 || buys / sells > 1.5) ko = 0.001;

  return (allProfit / (allLoss + DBL_EPSILON)) * dealsNumb;
}
//——————————————————————————————————————————————————————————————————————————————

Figure 2 shows a graph of the balance of trading results obtained using an MLP-based EA on new data unfamiliar to the neural network. The input is normalized OHLC price values, as well as RSI and Stochastic indicators calculated based on the specified number of bars. The EA trades as long as the neural network remains up-to-date; otherwise, it trains the network and then continues trading. Thus, the results shown in Figure 2 reflect the performance on OOS (out of sample).

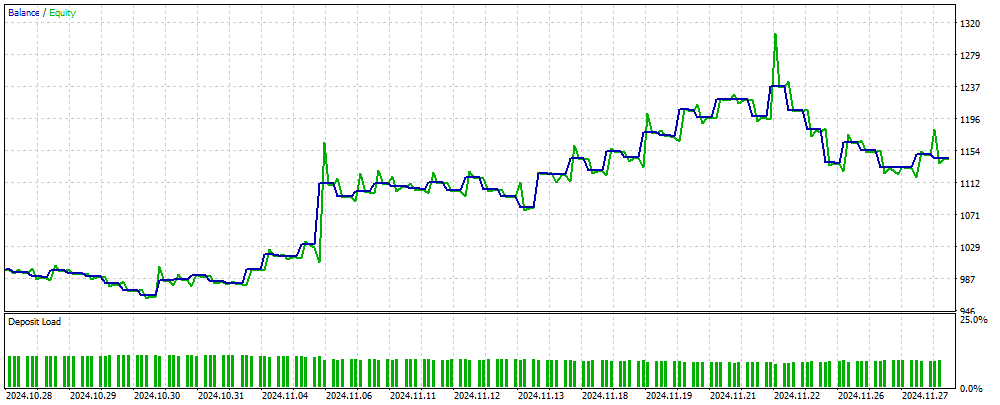
Figure 2. The result of the EA operation on data unfamiliar to MLP

Summary

The article presents a simple and accessible way to use a neural network in a trading EA, which is suitable for a wide range of traders and does not require deep knowledge in the field of machine learning. This method eliminates the need to normalize the objective function values to feed them into the neural network as an error, and also eliminates the need for methods to prevent "weight explosion". In addition, it solves the problem of "network stall" and offers intuitive training with visual control of results.

It should be noted that the EA does not have the necessary checks when performing trading operations, and it is intended for informational purposes only.

Programs used in the article

#	Name	Type	Description
1	#C_AO.mqh	Include	Parent class of population optimization algorithms
2	#C_AO_enum.mqh	Include	Enumeration of population optimization algorithms
3	Utilities.mqh	Include	Library of auxiliary functions
4	#Symbol.mqh	Include	Library of trading and auxiliary functions
5	ANN EA.mq5	Expert Advisor	EA based on MLP neural network