Population optimization algorithms: Bacterial Foraging Optimization (BFO)

Contents

1. Introduction
2. Algorithm description
3. Test results

1. Introduction

The Bacterial Foraging Optimization (BFO) algorithm is a fascinating optimization technique that can be used to find approximate solutions to extremely complex or impossible numerical function maximization/minimization problems. The algorithm is widely recognized as a global optimization algorithm for distributed optimization and control. BFO is inspired by the social foraging behavior of Escherichia coli. BFO has already attracted the attention of researchers for its effectiveness in solving real-world optimization problems that arise in several application areas. The biology behind the foraging strategy of E. coli is emulated in an original way and used as a simple optimization algorithm.

Bacteria, such as E. coli or salmonella, are among the most successful organisms on the planet. These agile bacteria have semi-rigid appendages called flagella, with which they propel themselves with a twisting motion. When all the flagella rotate counterclockwise, a propeller effect is created and the bacterium will move in a more or less rectilinear direction. In this case, the bacterium performs a movement called swimming. All flagella rotate in the same direction.

Flagella help the E. coli bacterium to tumble or swim, which are the two main operations performed by the bacterium during foraging. As they rotate the flagella clockwise, each flagellum pushes against the cell. When the flagella rotate in different directions, the bacterium tumbles. The bacterium moves with fewer tumbles in a favorable environment, while in a harmful one it tumbles frequently to find the nutrient gradient. The anticlockwise movement of the flagella helps the bacteria to swim at a very high speed.

In the above algorithm, the behavior of bacteria is determined by a mechanism called bacterial chemotaxis, which is a motor reaction of these microorganisms to a chemical stimulus in the environment. This mechanism allows the bacterium to move towards attractants (most often nutrients) and away from repellents (substances potentially harmful to the bacterium). Receptors that detect attractants and repellents are located at the poles of the bacterium.

Due to the small size of the bacterium, it is not able to catch the difference in concentrations of useful and harmful substances between the poles. Bacteria determine the gradients of these substances by measuring changes in their concentrations during movement. The speed of this movement can reach several tens of bacterium lengths per second. For example, Escherichia coli usually moves at a speed of 10-20 of its length per second.

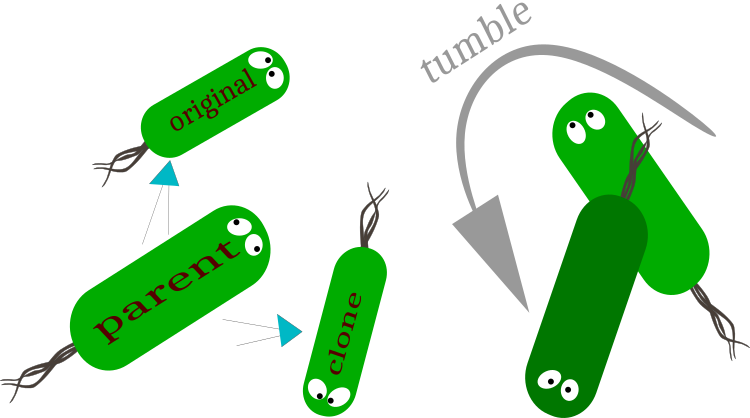
Fig. 1. Replication: division into original (preservation of the motion vector) and cloned (change in the motion vector) bacteria.
Tumble - a change in the vector of bacterium motion

If the direction of movement chosen by the bacterium corresponds to an increase in the concentration of the attractant (a decrease in the concentration of the repellent), then the time until the next tumble increases. Due to the small size of the bacterium, its movement is strongly affected by Brownian motion. As a result, the bacterium only moves on average in directions towards beneficial substances and away from harmful substances.

The considered mechanism of bacterial movement is not the only one. Some bacteria have one flagellum. Variants of bacterium movement in this case provide different modes of its rotation and stop. However, in all cases, if the bacterium moves in the right direction, then the duration of such movement increases. Thus, in general, bacterial chemotaxis can be defined as a complex combination of swimming and tumbling, which allows bacteria to stay in places of high concentration of nutrients and avoid unacceptable concentrations of harmful substances.

In the context of a search engine optimization problem, bacterial chemotaxis can also be interpreted as a mechanism for optimizing the use of known food resources by a bacterium and searching for new, potentially more valuable areas.A population of bacteria of sufficient abundance can form complex spatio-temporal structures - the effect of structure formation in bacterial populations. This effect can be caused both by chemotaxis and by many other reasons.

For some bacteria, the formation of such structures is explained by the regulatory properties of their metabolic products. A similar effect is possible based on the phenomena of magnetotaxis (sensitivity to a magnetic field), bioconvection, negative geotaxis (preferential movement of microorganisms against the direction of gravity) and other phenomena. As a rule, bacteria travel a greater distance in a friendly environment. When they get enough food, they grow in length and, given the right temperature, break in the middle, turning into an exact replica of themselves.

This phenomenon inspired Passino to introduce the reproduction event into the BFO. Due to sudden changes in the environment or an attack, the chemotactic process can be disrupted and the group of bacteria can move to some other place. This represents an elimination and dispersal event in a real bacterial population, when all the bacteria in the region die or a group of bacteria disperses to a new part of the environment. In addition, the considered procedures of chemotaxis and reproduction are generally insufficient for finding the global maximum of the multiextremal objective function, since these procedures do not allow bacteria to leave the local maxima of this function that they have found. The elimination and dispersal procedure is designed to overcome this shortcoming. According to natural selection (survival of the fittest), bacteria with poor fitness will be destroyed and bacteria with higher fitness will reproduce themselves.

2. Algorithm description

The canonical version of BFO includes the following major steps:

1. Initialize a colony of bacteria.
2. Chemotaxis.
3. Swarming.
4. Reproduction.
5. Liquidation and removal.

      
1. Initializing the parameter.
Bacteria can form complex, stable spatio-temporal patterns in some semi-solid nutrients, and they can survive in an environment if initially placed together at the center. Moreover, under certain conditions, they will secrete intercellular attractant signals so that they will cluster and protect each other.
2. Chemotaxis.
The characteristics of the movement of bacteria in search of food can be determined in two ways, i.e. swimming and tumbling together is known as chemotaxis. It is said that a bacterium "swims" if it moves in the right direction, and "tumbles" if it moves in the direction of the environment deterioration.

3. Swarming.
In order for the bacteria to get to the most food-rich place, it is desirable that the optimal bacterium, up to a point in time in the search period, tries to attract other bacteria so that they converge together more quickly at the desired place. To do this, a penalty function is added to the original cost function based on the relative distance of each bacterium from the fittest bacterium to this search duration. Finally, when all bacteria merge to the decision point, this penalty function becomes zero. The effect of swarming is that bacteria gather in groups and move in concentric patterns with a high density of bacteria.

4. Reproduction.
The initial set of bacteria, having passed several chemotactic stages, reaches the stage of reproduction. Here the best set of bacteria is divided into two groups. The healthier half is replaced by the other half of the bacteria, which are destroyed due to their lesser ability to find food. This makes the population of bacteria constant in the course of evolution.

5. Elimination and dispersal.
During evolution, a sudden unforeseen event can occur that can drastically change the smooth process of evolution and cause the elimination of many bacteria and/or their dispersal into a new environment. Ironically, instead of disrupting the normal chemotactic growth of a set of bacteria, this unknown event may place a newer set of bacteria closer to where the food is. From a broad perspective, elimination and dispersal are part of the behavior of a population over long distances. When applied to optimization, this helps reduce the stagnation often seen in such parallel search algorithms.

My implementation of BFO is slightly different from the canonical version. When considering specific sections of the code, I will dwell on the differences in addition with the rationale for the need for these changes. In general, changes in the implementation cannot be considered significant, so I will not assign the "m" (modified version) marker to the name of the algorithm. I will only note that implemented changes have improved the results.

Next, consider the algorithm and code that I have implemented.

Algorithm steps:

1. Bacterial colony initialization.
2. Measuring bacteria health (fitness).
3. Replication?
3.1. Yes. Perform replication.
3.2. No. p.4.
4. Old (life limit reached)?
4.1. Yes. Perform a tumble (change the movement vector).
4.2. No. p.5.
5. Moving in the right direction?
5.1. Yes. Continue moving with the same vector.
5.2. No. Perform a tumble (change the movement vector).
6. Measure the bacteria health (fitness).
7. Continue from p.3 until the stop criterion is met.

The logical scheme of the algorithm is shown in Fig. 1.

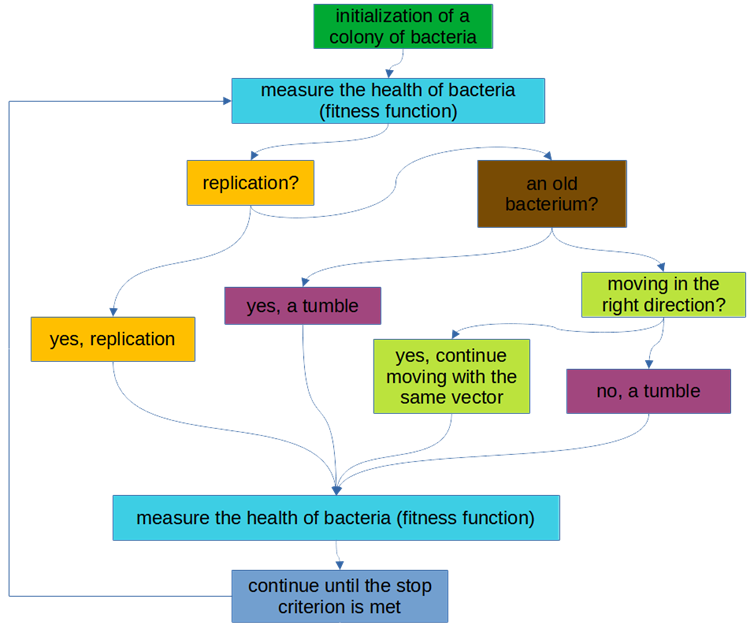
Fig. 2. BFO algorithm logic block diagram

Let's take a look at the code.

The best way to describe a bacterium is a structure containing arrays of coordinates and motion vectors. Bacteria's current and previous health values and life counter. In essence, the life counter is necessary to limit the amount of sequential movement in one direction, unlike the original version, in which, upon reaching the life limit, the bacterium will be destroyed and a new one will be created in a random place in the search space. However, since we have already touched on this topic in previous articles, creating a new agent in a random place has no practical meaning and only worsens search capabilities. In this case, it is better to either create a new agent at the location of the best solution, or continue moving from the current location, but change the direction vector. The second option showed better results.

The canonical version uses a constant motion vector. With a large number of lives, this would lead to the movement of bacteria along a straight line in the search space. If this line did not pass through any extremum better, then this process of rectilinear movement would occur infinitely, but here the counter plays the role of a forced tumble, which allows the bacterium to avoid rectilinear movement throughout its life. On functions with areas that do not have a gradient, it will eventually still lead to a place where it can begin to improve its fitness.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c  [];   //coordinates
  double v  [];   //vector
  double f;       //current health
  double fLast;   //previous health
  double lifeCNT; //life counter
};
//——————————————————————————————————————————————————————————————————————————————

Let's declare the BFO algorithm class as C_AO_BFO. The class contains the declaration of the bacteria colony, the boundaries of the search space, the value of the best solution and the array of coordinates of the best solution. Also, declare constant values of the algorithm parameters.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP);   //life counter

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];
  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: bool   evaluation;

  private: void   Sorting ();
  private: double SeInDiSp             (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

The public Init () method is meant for initializing constant variables, distributing array sizes and resetting flags and the value of the best solution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP)    //life counter
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,  parameters);
    ArrayResize (b [i].v,  parameters);
    b [i].f  = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,  parameters);
    ArrayResize (bT [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

The first public method required to be called at each iteration - Swimming (), or bacteria swimming, includes all the main logic of the algorithm.

void C_AO_BFO::Swimming ()
{}

Let's consider the method in detail. At the first iteration, when the evalution flag is set to 'false', we scatter the bacteria over the entire search space randomly with a uniform distribution. At this stage, the current health (fitness) and the previous one are unknown. Let's assign the DBL_MAX value to the corresponding variables. Check the randomly obtained coordinates for going beyond the boundaries and apply the step of changing the optimized parameters. At this iteration, it is necessary to set an individual displacement vector for each bacterium using the NewVector () private method (I will consider it below). All bacteria swim uniformly forward and in a straight line with the same individual vector until the conditions for its change are met.

//----------------------------------------------------------------------------
if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f  = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
}

On the second and subsequent iterations, operations of swimming, tumbling, replication and destruction of bacteria are performed when the limit of lives is reached. The first in the logic is the operation of reproduction (with the probability specified in the parameters). It implies that the bacterial colony is sorted at the previous iteration in descending order of health value.

Reproduction in the algorithm performs an important function: accelerating the convergence of the algorithm by improving the "gene pool" of the bacterial colony. The operation is an imaginary division of bacteria into two parts, and only the first, better half of the colony is allowed to divide. The first half of the colony is halved, the original parent version is placed in the second half of the colony. The parent bacterium will continue to move with the same vector as opposed to its clone. The clone remains in its place in the colony and a new movement vector is assigned to it. The parent and its clone will continue moving from the point in space where the division occurred.

r = RNDfromCI (0.0, 1.0);

//==========================================================================
if (r < reproduction)
{
  int st = populationSize / 2;
  for (int s = 0; s < st; s++)
  {
    //bacterium original--------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [st + s].v [k] = b [s].v [k];
      b [st + s].c [k] = b [s].c [k] + b [s].v [k];
      b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [st + s].fLast = b [s].f;
      b [st + s].lifeCNT++;
    }

    //bacterium clone-------------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT = 0;
    }
  }
}

If the probability of replication is not implemented, then a check for reaching the limit of bacterial lives is performed. In the canonical version of the algorithm, the "old" bacterium should be destroyed, and a new one should be created instead of it in a random place in the search space within the list of bacteria. In the general case, the operations of reproduction and chemotaxis are not enough to find the global maximum of the multi-extremal fitness function, since
these procedures do not allow bacteria to leave the local minima they have found. The liquidation procedure is designed to overcome this shortcoming. However, as the practice of experiments with this and other algorithms has shown, it is more efficient in this case to simply change the motion vector. The life counter is reset. The counter is a trigger for changing the direction of movement after a given number of steps (lives). The total number of bacteria as a result of replication and elimination remains constant.

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);
    b [s].c [k] = b [s].c [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    b [s].fLast = b [s].f;
    b [s].lifeCNT = 0;
  }
}

If the life limit has not been exhausted, then we will check whether the bacterium is moving towards improving the gradient of the fitness function. In other words, we check two health values - at the current iteration and at the previous one. If health has improved, then the motion vector is preserved, otherwise the bacterium should perform a tumble (change the motion vector).

In the canonical version, a strict "greater than" current and previous health check is performed, while in my version, "greater than or equal to" is applied, which allows the bacterium to continue moving even on a completely "horizontal" section of the surface under study, where there is no fitness function gradient, otherwise the bacterium would tumble endlessly in one place (there is no change in health, which means there is no swimming direction). At this stage, we also need to check for the output of the received new coordinates beyond the boundaries of the search space.

else
{
  if (b [s].f >= b [s].fLast)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
  else
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
}

NewVecror () - is a private method for changing the motion vector (tumble). The method is applied for each coordinate. The idea here is simple: the difference between the search boundaries for the corresponding coordinate v is multiplied by a random number r from the range [-1.0;1.0] and multiplied by the lambda scale factor (one of the algorithm parameters). The bacterium uses the movement vector without changes until the limit of lives is exhausted (a new bacterium is created in the same place, but with a new movement vector), during replication (the clone has a new vector) and during health deterioration (an attempt to find a new more favorable environment).  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

The second public Evaluation() method, which should be executed at each iteration, calls the sorting method, checks for updates of the global solution comparing the health of the best bacterium in the sorted colony with the best found solution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Evaluation ()
{
  Sorting ();

  if (b [0].f > fB)
  {
    fB = b [0].f;
    ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test results

BFO test stand results:

2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash,M1)    C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash,M1)    5 Rastrigin's; Func runs 10000 result: 72.94540549092933
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash,M1)    Score: 0.90383
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash,M1)    25 Rastrigin's; Func runs 10000 result: 54.75744312933767
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash,M1)    Score: 0.67848
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    500 Rastrigin's; Func runs 10000 result: 40.668487609790404
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    Score: 0.50391
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash,M1)    5 Forest's; Func runs 10000 result: 0.8569098398505888
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash,M1)    Score: 0.48471
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash,M1)    25 Forest's; Func runs 10000 result: 0.37618151461180294
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash,M1)    Score: 0.21279
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    500 Forest's; Func runs 10000 result: 0.08748190028975696
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    Score: 0.04948
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash,M1)    5 Megacity's; Func runs 10000 result: 4.8
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash,M1)    Score: 0.40000
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash,M1)    25 Megacity's; Func runs 10000 result: 2.216
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash,M1)    Score: 0.18467
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash,M1)    500 Megacity's; Func runs 10000 result: 0.4232
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash,M1)    Score: 0.03527

It is too early to draw unambiguous conclusions. It is necessary to analyze the results in relation to other test participants first.

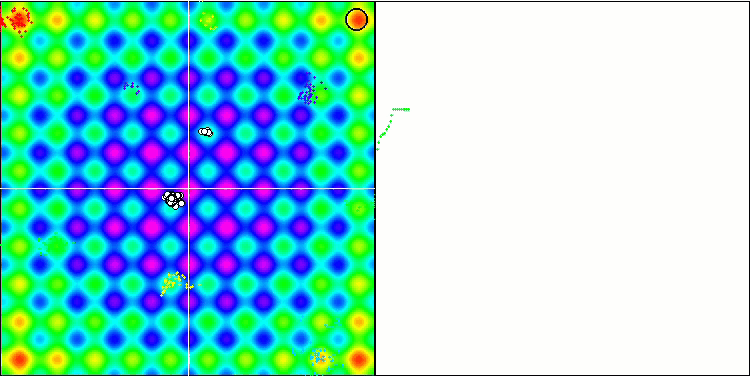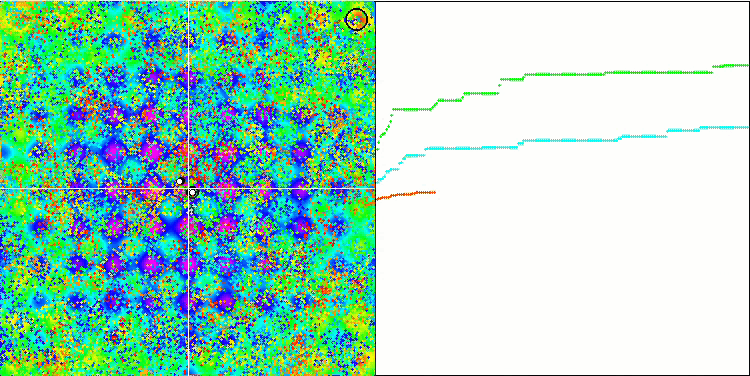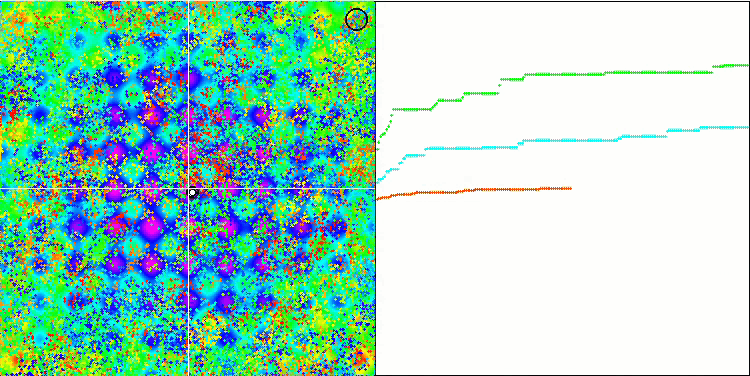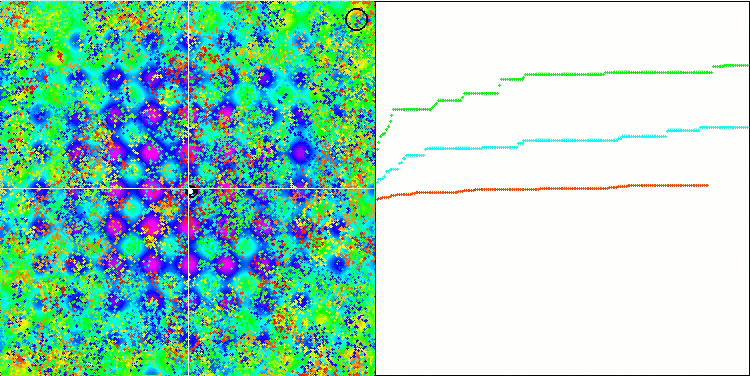
  BFO on the Rastrigin test function.

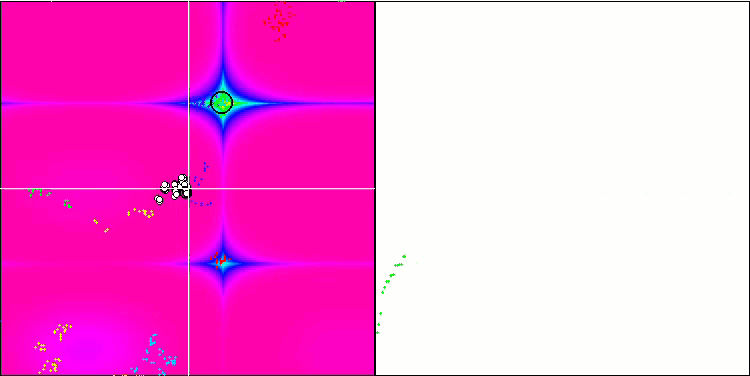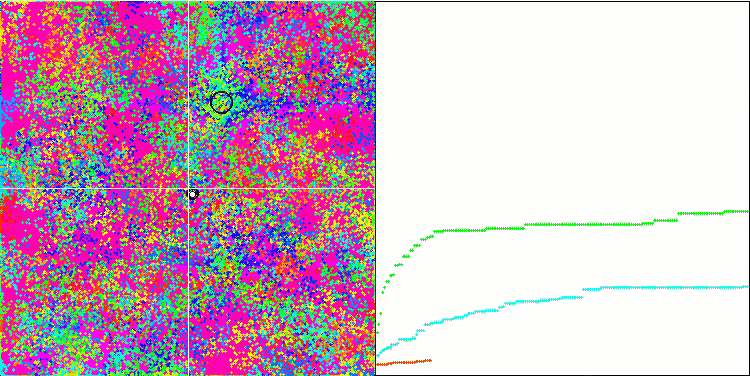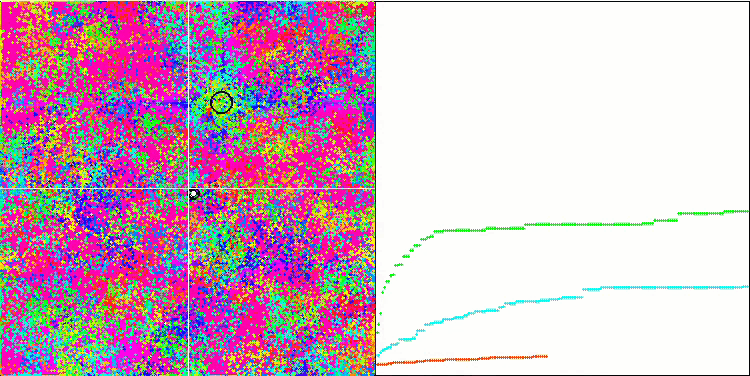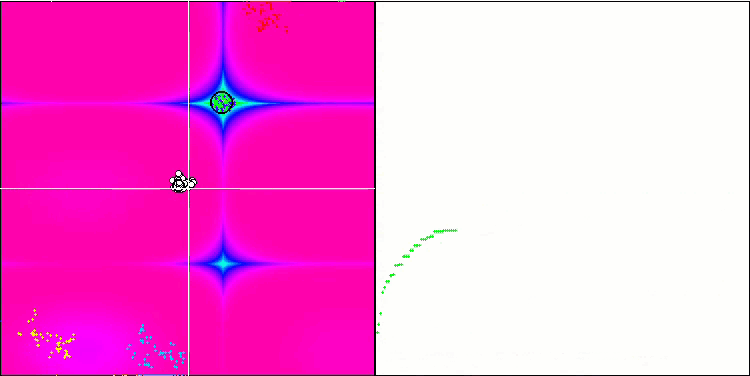
BFO on the Forest test function.

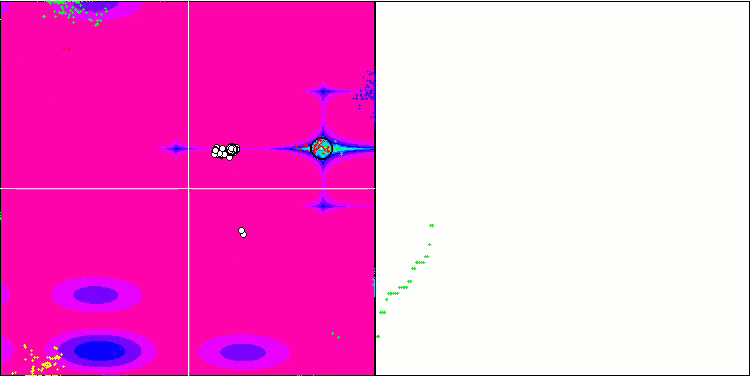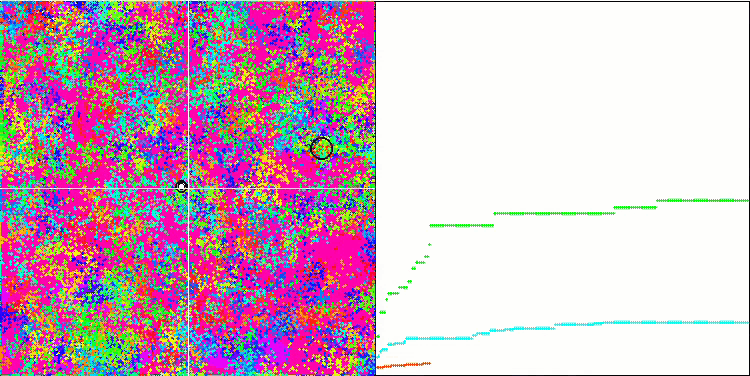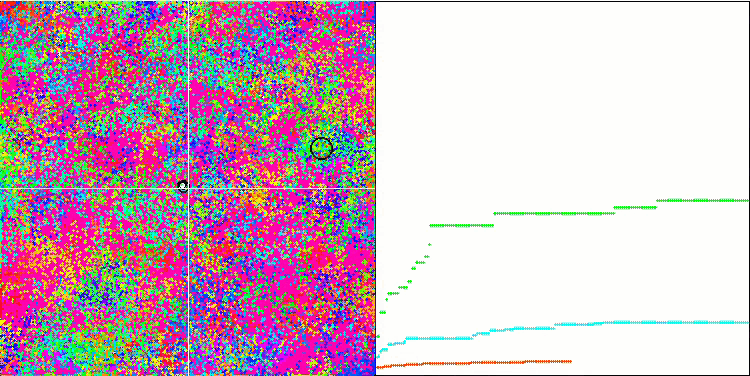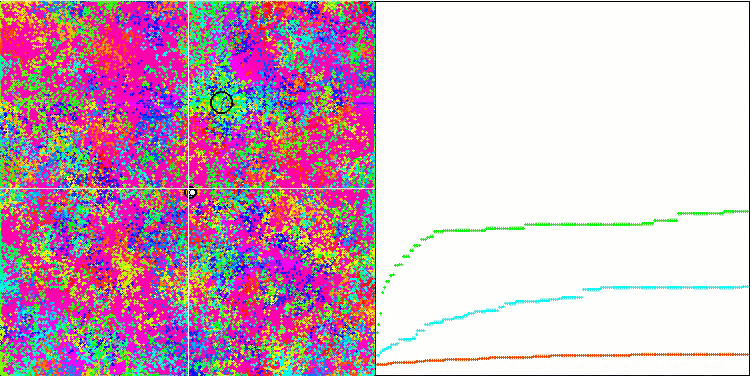
BFO on the Megacity test function.

Let's pay attention to the test visualization. The animation confirmed the correctness of the decision to replace the "greater than" sign with "greater than or equal to" in our algorithm. This allowed the bacteria to continue moving in the horizontal sections of the test functions. This is especially noticeable on the Forest and Megacity functions. The bacteria try to move on even where there is no function gradient at all. It is also necessary to note the ability of a bacterial colony to divide into several separate colonies visually divided into separate local extremes, which can be unambiguously considered a positive feature, although the algorithm does not contain any logical methods for the formation of subcolonies. In general, a uniform movement of bacteria in the search space is noticeable without attempts to make a sharp jump in any of the directions, which is explained by a uniform incremental movement - chemotaxis.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
IWO	invasive weed optimization	1.00000	1.00000	0.33519	2.33519	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94088	2.14903	100.000
ACOm	ant colony optimization M	0.36118	0.26810	0.17991	0.80919	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.10959	2.10959	95.996
COAm	cuckoo optimization algorithm M	0.96423	0.69756	0.28892	1.95071	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.45422	1.46848	74.204
FAm	firefly algorithm M	0.62430	0.50653	0.18102	1.31185	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	71.024
BA	bat algorithm	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.46287	0.68774	59.650
ABC	artificial bee colony	0.81573	0.48767	0.22588	1.52928	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.35941	1.10066	57.237
BFO	bacterial foraging optimization	0.70129	0.46155	0.11627	1.27911	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.50973	1.27800	55.516
FSS	fish school search	0.48850	0.37769	0.11006	0.97625	0.07806	0.05013	0.08423	0.21242	0.00000	0.01084	0.18998	0.20082	20.109
PSO	particle swarm optimisation	0.21339	0.12224	0.05966	0.39529	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.00000	0.10413	14.232
RND	random	0.17559	0.14524	0.07011	0.39094	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.08904	0.08904	8.142
GWO	grey wolf optimizer	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.01802	0.24898	1.000

It is time to analyze the test results. BFO is located in the middle of the rating table with an overall score of just over 55 in the current list of participating algorithms. The results are not impressive, but not bad either. In particular, good results were obtained on the Rastrigin function with 10 variables. In case of 50 and 1000 variables, the results are noticeably worse. Also, the algorithm did not perform well on the Forest function. The relatively good behavior on the discrete Megacity function is surprising, since there are no mechanisms for working on such functions in the algorithm. Besides, there is a good scalability compared to other algorithms (test with 1000 Megacity parameters).

BFO is a scientific field with a wide range of possibilities. There are a number of aspects of bacterial foraging and animal foraging in general that can be modeled to enhance optimization performance. For the BFO algorithm, automatic adaptation of the control parameters may be of particular importance, since there are a lot of parameters, and it can give improved performance, which is a reason for additional experiments.

BFO has a number of advantages, including low sensitivity to the initial values of the coordinates during initialization and choice of parameters, good reliability, simplicity of logic, ease of implementation, the possibility of parallelization and global search. Thus, the BFO algorithm is used to solve a wide range of optimization problems. However, BFO also has a number of drawbacks, including slow convergence, the inability to go beyond local optima in some cases, and a fixed step length. BFO is a metaheuristic, meaning it is simply a conceptual framework that can be used to develop algorithm modifications. The version of BFO I have presented here is just one of many possibilities and should be seen as a starting point for experimentation, rather than the last word on the topic.

The histogram of algorithm test results is provided below.

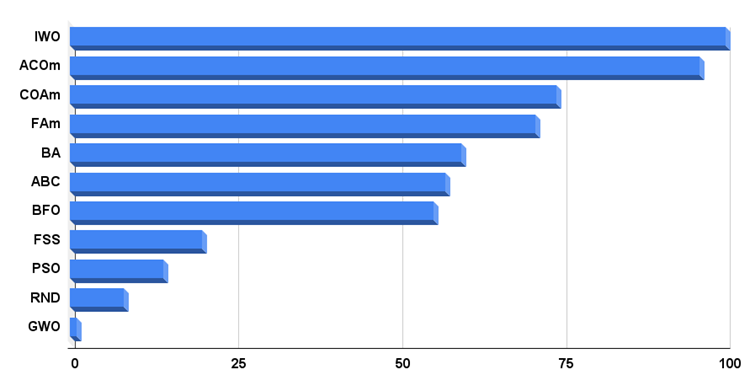
Fig. 3. Histogram of the final results of testing algorithms

Conclusions on the properties of the Bacterial Foraging Optimization (BFO) algorithm:

Pros:
1. High speed.
2. Simple logic.
3. Converging throughout all iterations, albeit slowly.

Cons:
1. Slow convergence.
2. No methods for exiting local extrema.