From Basic to Intermediate: Floating point

Introduction

In the previous article “From Basic to Intermediate: Definitions (II)”, we talked about how important macros are and how we can use them effectively to make our code even more readable.

Well, given everything we have discussed so far, we now have enough material and adequate tools to explain how floating-point numbers work. I know many people think that double or float values are the best choice in different situations. However, there is one problem with this type of value that very few people understand, especially those not being programmers.

And since such values are widely used in MQL5, and we work with information where floating point is almost a consensus, it is necessary to understand very well how this type of values is processed by the CPU.

Why say this? It is clear that fractional numbers such as 2.5 are always very easy to understand, since no one will confuse this type of values with any other. But, my dear reader, when it comes to calculations, things are not so simple. In fact, floating-point numbers are quite useful in a number of situations. However, they should not be considered or understood in the same way as integers.

Basically, many of you might be used to dealing with floating-point numbers in two types of notation: scientific one where we note values like 1-e2, and the more common arithmetic one where we note values like 0.01. Both values are equal in magnitude, but are noted differently. Likewise, there is a fractional way of noting the same value, which will be equal to 1/100.

Please note that in all cases we are talking about the same value. However, different programs or programming languages handle these values differently.

Brief history

In the early days of computing, floating-point numbers as we know them today did not exist. Or rather, there was no standardized way to handle them. Each programmer, every operating system, and even every program handled this type of numbers in a very specific and individual way.

During the 1960s and 1970s, there was no way for one program to interact with another to share and speed up the factorization of such values. Just imagine: at the very beginning of the space age, when such numbers would have been of paramount importance, it was IMPOSSIBLE to calculate floating-point values on then operating computers. And even when such capacity became available, it was impossible to divide the task among a large number of computers to speed up calculations.

Then IBM, which controlled almost the entire market at the time, started offering a way to represent these kinds of values. But the market does not always accept what it is offered. Therefore, other manufacturers have developed their own ways of representing such values. It was real CHAOS. Until, at some point, the Institute of Electrical and Electronics Engineers (IEEE) began to clean things up by establishing what is now known as IEEE 754 standard. At the end of this article, in the "Links" section, I will leave some links for those who want to delve deeper into this topic.

The first standard established was IEEE 754-1985, as an attempt to resolve this whole issue. Nowadays, we use a much more to-date standard, but it is based on the same, originally established scheme.

An important detail: despite the existence of this standard, which is intended to normalize and enable distributed factorization, there are cases where this standard is not used, and calculations - or, more precisely, the factorization - are performed according to other principles, which we will not consider here, since they are completely outside the scope of the topic. This is due to the fact that MQL5, like several other languages, uses this IEEE 754 standard.

Initially, CPU could not handle this type of calculation, so there was a separate processor, known at the time as FPU, dedicated solely to this purpose. That FPU was purchased separately, as its cost did not always justify its use. Model 80387 may serve as an example of FPU. And yes, that is not a typo. In essence, this model is very similar to the famous one 80386, commonly referred to as 386. But this was more of a marketing solution by Intel to differentiate CPU (80386) from FPU (80387). The computer could only work with the central processor unit, but not with the FPU alone, since the latter was designed only for performing floating-point calculations.

OK, but what is wrong with this floating point? Why is an entire article devoted only to this topic? The reason is that if you do not understand how the floating-point representation works, you can make a number of mistakes. Not because of poor programming, but because of the idea that the calculations performed should be taken literally, whereas the very fact of using the IEEE 754 standard already creates a potential error in the final value calculated.

This may seem absurd because computers are machines that must always provide us with accurate values. It is not serious to say that the result of the operation contains an error, moreover, it is  unacceptable. Especially when our goal is to trade on the financial market using such data. If our calculations are wrong, we can lose money, even if everything points at the probability of making a profit. And it is for this reason that this article is important.

There are a number of floating-point related aspects that are not so important within the framework of what we are going to do. But there is another thing that is very important and crucial, and that is rounding.

I know that many people say or even brag, claiming: 

I DON'T use rounding in my calculations. They are always accurate and error-free.

But this particular idea, in my opinion, demonstrates a complete and utter misunderstanding of programming, which leads people to make false assumptions, when in fact everything is different. Rounding does not necessarily have to be done by a programmer. It just exists  regardless of whether the programmer wants it or not. Therefore, it is important that you read the materials on the links that I leave at the end hereof. I am doing so since the issue of floating-point numbers cannot be explained in one article. Remember: there are experts who have been working on this topic since the very beginning of the development of computing technology.

Here we will look at another type of thing, much simpler and focused on understanding exactly what a double or float is, since all other data types are much simpler, and have already been explained in previous articles.

Representation of a floating-point number

So, here we will talk about the type that is actually used in MQL5. In this type, we basically follow the IEEE 754 specification, which provides for two formats — or, more precisely, two precisions. And yes, when we talk about floating-point numbers, it is correct to use the term "precision" rather than "format" or "number of bits involved". But in order not to complicate things, as this can be quite confusing for many people, we will use the term "number of bits" here, but only so that most readers can better understand the material and to simplify further explanations. I believe that I am not addressing engineers or specialists with extensive and comprehensive knowledge in the field of electronics and chip design, but rather people interested in programming in the MQL5 language and eager for knowledge.

Well, to start with, let us look at a very simple code. However, despite its simplicity, you will need all the knowledge gained from previous articles in the series to fully understand it. Let us get to it.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

Code 01

Well, my dear reader, this code is quite interesting, besides being quite inquisitive and fun to experiment with. Despite this, here we are implementing only the first part of what we really want and will do.

Please note: in the fourth string we specify which type of value we will use as a floating-point number. We can specify that we need a double or float type. The difference between them lies in the precision that each of them allows you to obtain. But before we go into more details, let's figure out what this code does.

So, after declaring the type, we can use a union to create a way to read memory. To do this, we use string eight. Already inside the union, we use string 10 to create a variable and string 11 to create a shared access array. Similar structures have already been discussed and explained in previous articles. Please read them for more information if you are not clear what is going on here and what the purpose of creating this union is.

For us, the most important string here is that 14, because it is in it that we set the value that we want to visualize. And string 16 just provides a way to display the contents of memory, which is our goal right now, because we want to understand how a floating-point value is represented in memory until the computer can interpret it.

So, after executing, code 01 will provide us with the result shown in the image below.

Figure 01

Hmm... What is this strange representation in hexadecimal format that we are currently seeing? Well, my dear reader, this is exactly the way the computer interprets a floating—point value, following the IEEE 754 standard. An important detail: this value is noted as a value in Little Endian format. We will talk more about what this format is later. But for now, you just need to understand the following: this hexadecimal value is noted in reverse order and must be read from right to left.

Well, in any case, you probably don't believe it. Therefore, we can use another program to clarify this. Let us use the hex editor. HxD is one of the simplest and free options. If you enter the values shown in the hexadecimal field of image 01, highlight them and see what value is represented there, you will see an image similar to what is shown below.

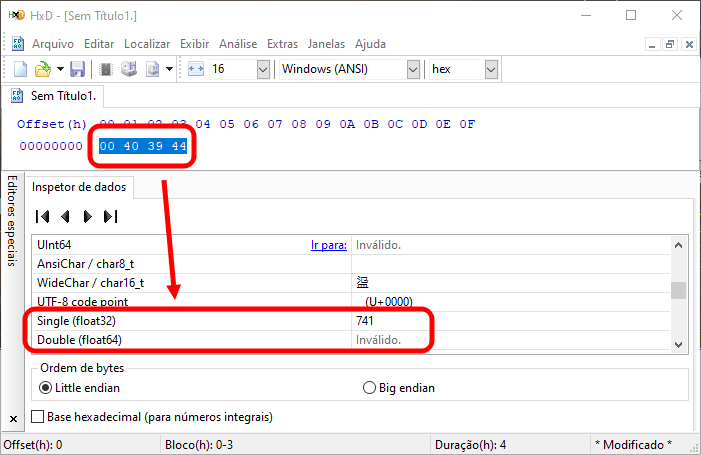
Figure 02

Note that, we actually have an expected value that can be visualized. However, I personally prefer to use the extension of my development environment to view such things which allows to avoid installing a lot of different programs on the computer. Although, to be fair, let me note that HxD does not require installation. In any case, what we can see is shown in the following figure.

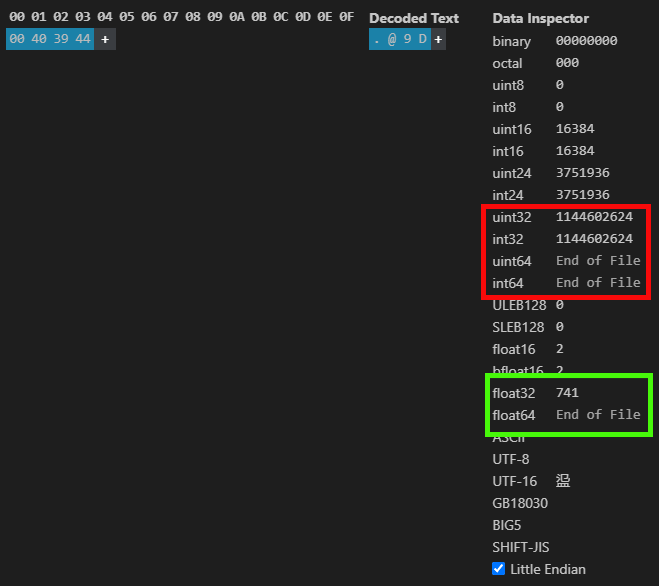
Figure 03

Such information as provided here, can be obtained in both MetaTrader 5 and HxD. But I want you to take a close look at what I am showing in image 03. Note that the same floating-point value is a different value represented as integer. But why is it so? The reason is that it does not matter to a computer whether a value is represented by an integer or any other type — it does not make any difference to it. However, for us and for the compiler, this is fundamental — the data type affects whether we get a reasonable result or something completely unexpected.

Nevertheless, the example we just considered in code 01 is just a simple case. Let us replace code 01 with a slightly different example, which can be seen just below.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

Code 02

Very well, code 02 may seem more complicated. However, it is as simple as code 01, but here we have an opportunity to discuss a few additional points regarding the display of floating-point values. This is possible thanks to string 4, where we can choose whether we want to use a type with single (float) or double precision. But when executing the code as shown above, we will get the answer shown below.

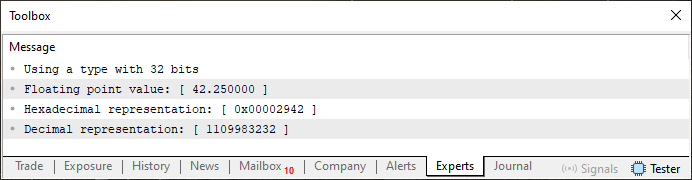
Figure 04

And just as we saw earlier, using the specified values shown in Figure 04, we get the result shown in the following image:

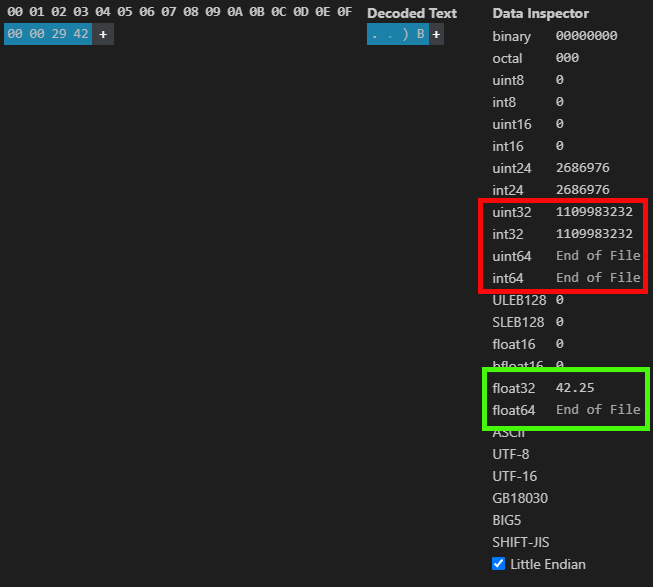
Figure 05

In other words, something is truly going on here. But how does the IEEE 754 system work? Well, dear reader, to explain this, we should look deeper into the internal structure of the system itself. I will endeavour not to complicate things too much, because in the end it can negate any attempt to explain what is happening and help to figure everything out.

Initially — and currently — there are two IEEE 754 formats: one for single precision (where 32 bits are used) and the other for double precision (where 64 bits are used). The difference between them is not that one is more precise than the other; the difference is in the range of values within which to work. Therefore, the term “precision" can often be misleading. This is the reason why I prefer not to use it, even though it is considered correct.

In the image below, you can see two types defined by the standard:

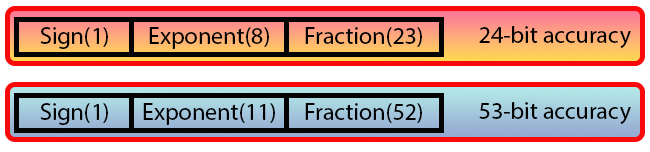
Image 06

"Wait a minute... Didn't you say that we use 32 bits for one type and 64 for the other? But it seems that something is being used here that doesn't make sense at all. What are these data and values that we see in Image 06?"

Well, this is the way a floating-point value is represented according to IEEE 754 standard. Here, each of the values you see is a BIT. Please note that we have chunks with an unusual width, different from the one we have seen so far. However, this does not prevent us from understanding the system itself. Although the explanations could be simpler if we used C or C++ languages. This is because in MQL5 we do ntt have the capacity to name bits one at a time, something that can be done in C or C++. However, we can use macros and definitions to get closer to what is being done in these languages.

Therefore, I will try to explain it already in this article. If it doesn't work out, I will make a separate article to explain everything properly. I do not want to limit myself to just a cursory explanation. I want you, dear reader, to really understand what the problem is when using floating-point values in our codes. Because I see how many people claim and even sincerely believe that it is possible to make calculations that are actually impossible. This is because there is a slight discrepancy between the expected and actual result, which can cause problems if we are not prepared for it.

Let us start with the following: if you add up the number of bits shown in image 06, you will notice that the first format contains 32 bits, and the second contains 64 bits. This is where the questions start to arise. Therefore, to simplify, let us focus on just one of the formats, since the difference between them is related to the value being used during adjustment. But we will talk about that later.

The bit indicated in image 06 as Sign  is the sign bit. That is, it indicates whether the value is negative or positive, just as it happens in integer types, where the leftmost bit tells us whether the number is negative or positive.

So, the sign bit (Sign) is followed immediately by eight bits called Exponent. This value generates a so-called bias equal to 127, which encodes the exponent. In the case of double precision (double), eleven bits are used, which creates a bias of 1023. Please note that, despite the name "double precision", the bias value is significantly higher here.

But the most important part for us is the one that goes right after the exponent. This field is called Fraction. It determines the accuracy of the value that will be presented. Note that in the case of 32 bits (single precision), this field contains 23 bits, which gives a precision of 24 bits. Whereas, in the case of double precision this field contains 52 bits, which gives a precision of 53 bits. Again, the value is more than double than the previous one, and for this reason, the term "double precision" is again somewhat misleading.

But if you delve deeper into the issue of floating-point numbers, you will see that the field that we call Fraction here is often called the mantissa. It is the mantissa that represents the key part in the formation of floating-point numbers.

There are many aspects involved here, but because many people may lose interest after seeing too many technical details, to make the process more enjoyable let us move on to a practical example. In code 01, in string 14, we used the value of 741 and converted it to a floating-point value. In this case, to a 32-bit value, that is, to a single-precision format. Therefore, we can use the orange scheme from Figure 06. I want you to try to focus on what will be shown so that you can understand this simple model first.

So, first we want to convert the value of 741 to binary format. To do this various methods can be used. However, the most understandable one for most people  is to divide by two. Let me note that if you do not know how to convert a number to a binary system do not worry, as this first value is quite simple. And it will be easy to understand how to do it. Image 07 below demonstrates how this is done.

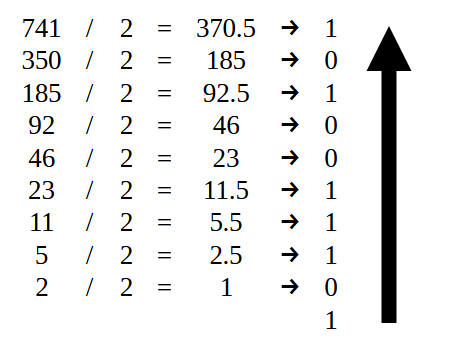
Figure 07

After all the divisions are completed, we end up with a sequence of zeros and ones. But in order for the value to be noted correctly, it must be noted in the order as shown by the arrow. As a result we get what is shown in the image below.

Image 08

All right, to get the same as what is shown in image 08 is the first part. Once this is done, we can proceed to the second step, which is to convert this binary value to a floating-point value. Now be careful, because this is the simplest case possible. However, it is necessary to understand it very well in order to be able to deal with more complex situations later.

We need to create our mantissa, that is, the fractional part. To do this, we need to move the point, which is in the rightmost position, to the left. So that we have only one bit left with a value equal to one. This transformation will result in what you see in the picture below.

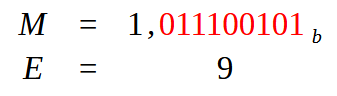
Image 09

Now let us look at the following: M is what is called the mantissa, that is, the fractional part of a floating—point number. E will be our exponent. But where did this value of nine come from? Well, it occurs because we have nine red values in the mantissa. But this value of 9 still needs to be worked on. And this is where the third phase of conversion begins. Depending on which approach we choose, we will process this value of 9 in one way or another, thereby generating different values. This is necessary to represent a floating-point number in hexadecimal format.

But before considering what to do with value 9, let us figure out how the fractional part of a floating-point number is formed.

Remember that we have 23 bits for a single precision value and 52 bits for a double precision value? Whereas, pecision consitutes 24 bits for single precision and 53 bits for double precision, doesn’t it? So, this very bit with value 1, which is highlighted in black on image 09, is that extra bit that appears. That is, it is NOT PRESENT, but is implied in Fraction field. Thus, Fraction field is formed as follows:

Figure 10

The number of green zeros in Image 10 depends on the number of bits in Fraction field. There will be as many zeros as necessary to fill in the rest of the field. So, now we have the fractional part of the floating point value. It remains to form a part of the exponent. Since the value is positive, Sign field will be zero. To form the exponent part, the type of precision used must be taken into account. If this is a single precision, we add E value shown in Figure 09 (which in this case is nine) to the bias value, which for this type is 127. As a result, we get the value of 136. This operation is shown in the figure below.

Figure 11

Now, finally, we can form a single-precision value to represent the number 741 in floating-point format. This value is shown just below.

Figure 12

Dividing the bits from Image 12 to build a hexadecimal representation, we get what is shown in Figure 13.

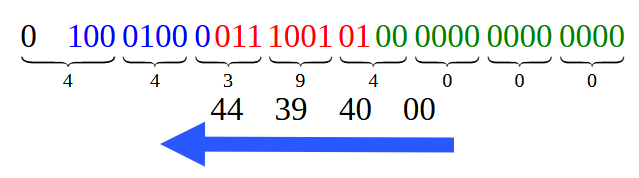
Figure 13

Note that each of the hexadecimal values shown in Figure 13 matches what we see in Image 01. However, you should remember to read them in the order as indicated by the arrow.  This is connected with one feature that we will consider in another, future article. Okay, that was the simplest case of all. But in this article we also considered another case, a little more complicated one, if I may say so. It is the case considered in code 02, where we essentially have a decimal point value. And what should we do in this situation?

Well, my dear reader, when a decimal point is used in a numeric value, things are a little different, but not much. The truth is that in this case, we should divide the binary conversion step into two parts: one —  for the part to the left of the decimal point, and the other —  for the part to the right of it. It seems complicated, right? But in reality everything is quite simple and logical, you just need to be attentive to what you are doing.

To begin with, the part that is TO the LEFT of the decimal point should be converted as shown in Figure 07. That is, we should only use the value 42, as shown below.

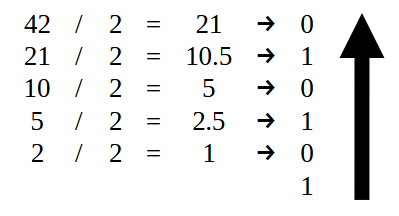
Figure 14

But the part to the RIGHT of the decimal point should be converted as shown in Figure 15. That is, we take 0.25 and convert the decimal part of the value specified in code 02 to binary format.

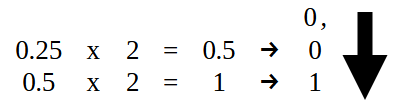
Figure 15

This results in the following: representation of number 42.25 in binary format, shown immediately below.

Figure 16

Pay very close attention to the fact that WE ALREADY HAVE A POINT in image 16. This will somewhat change what we will do in the next steps — in fact, this will be the stage shown in Figure 09, where we determined the value of the mantissa and exponent. Since we already have the decimal point indicated here in Figure 16, all we need to do is bias it so that only one bit remains with value 1 in the leftmost position. Exactly the same as in Figure 09. As a result we get the following which is shown in the image below.

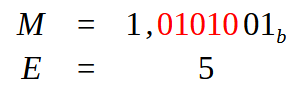
Figure 17

Note that in image 17 the values highlighted in red are exactly the ones to be biased in order for the point to take the correct position. Thus, the value for setting the exponent will be five. We also already have the mantissa value, which is used to form Fraction field. After calculating the value for single precision, we get what is shown below.

Figure 18

Please, note that the found hexadecimal value exactly matches the value shown in image 04. Of course, please, be reminded that it should be read in the direction of the arrow, in groups of two bytes. All right, but would we get the same result if we used double precision? That is, if string 4 in code 02 were uncommented for this directive to apply, we would use 64 bits instead of 32, thereby applying double precision in the system.

In this case, will we get the same data as in image 18? Well, we will get pretty much the same thing, my dear reader. In fact, the fractional part will remain the same. Of course, we will have to add more zeros to fill in all 52 bits required for the fractional part field in the double precision format. However, the exponent will be completely different, because instead of 127 (for single precision), we will use 1023. Thus, the only part that will be visually different in image 18 is the blue area indicating the exponent. To make this more clear, look at the following image, which shows how the value entry will look when using double precision.

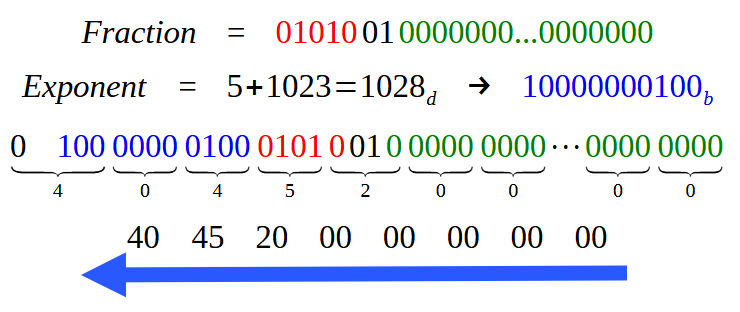
Figure 19

And to check if our estimate is correct, we run code 02 with the proposed change. The result will be as shown below.

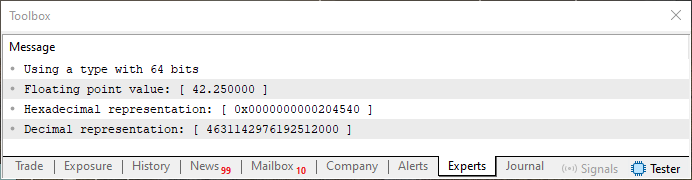
Figure 20

Final considerations

In this article, which is a brief introduction to the topic of floating-point values, we have considered how such a number is represented in memory, and how you can work with this type of values. I know that at this point, my dear reader, you may be a little puzzled by various aspects regarding floating-point values. And this is not surprising. I myself have spent a lot of time figuring out how this type of data is created, but especially how to perform calculations using this data. Although this is not my main goal here, who knows, maybe in the future I will be able to explain how to perform calculations using floating-point numbers. This is indeed a very fascinating topic to consider, especially through the lens of IEEE 754 standard.

Of course, there are other formats and ways to represent numbers containing a decimal point. However, since MQL5, like many other programming languages, uses exactly the format being discussed in this article, we recommend that you study this type of data thoughtfully. After all, such numbers often do not represent exactly the value that we think we are calculating. And I suggest you look at the links left below and learn how to round floating-point values, because there are clear rules for this, and it's not done for nothing.

However, it remains at your discretion. Based on what we have considered here, it is already quite possible to work with floating-point numbers. But additional aspects, such as rounding rules and a list of values that may or may not be represented, are necessary only for those who strive for high accuracy and correctness of values used in their applications. And this is not mandatory in the current article.

Links:

• 754
• Working with ONNX models in float16 and float8 formats