Atmosphere Clouds Model Optimization (ACMO): Theorie

Inhalt

1. Einführung
2. Implementierung des Algorithmus

Einführung

Die Suche nach den besten Lösungen für Optimierungsalgorithmen wird heutzutage zu einer immer wichtigeren Aufgabe. Einer der interessantesten Ansätze für dieses Problem ist der metaheuristische Algorithmus Atmosphere Clouds Model Optimization (ACMO), der trotz seiner mathematischen Komplexität einfach und verständlich erklärt werden kann. 

Stellen Sie sich einen riesigen virtuellen Himmel vor, in dem sich Wolken bilden und bewegen, genau wie in der realen Atmosphäre. Das Wetter ist hier nicht nur eine Reihe von Bedingungen, sondern ein lebendiges System, in dem Feuchtigkeit und Luftdruck jede Entscheidung beeinflussen. Inspiriert von Naturphänomenen nutzt der ACMO-Algorithmus die Prinzipien der Wolkenbildung, um den Lösungsraum zu erkunden, ähnlich wie sich Wolken am Himmel bilden, ausbreiten und wieder verschwinden, und versucht, optimale Pfade zu finden. Der Algorithmus wurde von Yan et al. vorgeschlagen und im Jahr 2013 veröffentlicht.

Hier werden wir jeden Schritt des ACMO-Algorithmus im Detail betrachten, beginnend mit der Vorbereitung des „Himmels“, in dem Wolken als potenzielle Lösungen geboren werden. Wir werden ihre Bewegungen durch den virtuellen Himmelsraum verfolgen und dabei beobachten, wie sie sich je nach Wetterbedingungen anpassen und verändern. Wenn Sie in diesen faszinierenden Prozess eintauchen, werden Sie sehen, wie Clouds, ähnlich wie Forschungsteams, danach streben, in einem Labyrinth von Möglichkeiten optimale Lösungen zu finden. Lassen Sie uns gemeinsam die Geheimnisse dieses Algorithmus lüften und Schritt für Schritt verstehen, wie er funktioniert.

Die Hauptidee des Algorithmus Atmosphere Clouds Model Optimization (ACMO) besteht darin, das Verhalten von Wolken in der Natur zu modellieren, um Optimierungsprobleme zu lösen. Der Algorithmus nutzt drei Schlüsselaspekte des Wolkenverhaltens aus:

• Entstehung. In Gebieten mit hoher Luftfeuchtigkeit bilden sich Wolken, die es dem Algorithmus ermöglichen, die Umgebung der aktuellen optimalen Lösungen zu erkunden.
• Bewegung. Die Wolken bewegen sich durch den Lösungsraum, was die Ausbreitung der Population fördert und ihre Vielfalt erhöht. Auf diese Weise wird vermieden, dass man in lokalen Optima stecken bleibt.
• Ausbreitung. Die Wolken sind über den gesamten Suchraum verteilt, sodass der Algorithmus ein breiteres Spektrum möglicher Lösungen abdecken kann und die Chancen, ein globales Optimum zu finden, steigen.

Implementierung des Algorithmus

Da das Konzept des ACMO-Algorithmus recht komplex ist, werden wir von einfach zu komplex übergehen. Lassen Sie uns die Grundidee des Algorithmus so einfach wie möglich beschreiben.

1. Vorbereiten des „Himmels“. Stellen Sie sich vor, wir erstellen einen virtuellen Himmel. Dieser Himmel ist in viele Regionen unterteilt. Jede Region hat ihre eigene Feuchtigkeit (Qualität der Lösungen) und ihren eigenen atmosphärischen Druck (gesammelte Sucherfahrung).

2. Geburt der Wolken. Wolken treten nur in den „feuchtesten“ Regionen auf. Jede Wolke besteht aus vielen Tröpfchen, und jedes Tröpfchen ist eine potenzielle Lösung für unser Problem.

3. Bewegung in der Wolke. Die Wolken stehen fast nie still. Sie bewegen sich von Regionen mit hohem Druck zu Regionen mit niedrigem Druck. Dies ist vergleichbar mit dem Wind, der in der realen Atmosphäre von einem Hochdruckgebiet zu einem Tiefdruckgebiet weht.

4. Ändern der Form von Wolken. Wenn sich Wolken bewegen, werden sie größer. Das Ausmaß, in dem sich die Wolken vergrößern, hängt von der Druckdifferenz zwischen den Regionen ab.

5. Verdunstung. Mit jedem Schritt verlieren die Wolken ein wenig von ihren Tropfen, und durch den Feuchtigkeitsverlust sinkt ihre Luftfeuchtigkeit. Wenn eine Wolke zu trocken wird, verschwindet sie vollständig.

6. Update des „Wetters“. Nach jeder Wolkenbewegung werden die Luftfeuchtigkeit und der Luftdruck in jeder Region neu berechnet. Wenn die Wolke eine gute Lösung gefunden hat, steigt die Luftfeuchtigkeit in dieser Region.

7. Wiederholung. Wiederholen der Schritte 2-6. Mit jeder Wiederholung erkunden die Wolken mehr und mehr Bereiche des virtuellen Himmels auf der Suche nach der besten Lösung.

8. Fertigstellung. Nach einer bestimmten Anzahl von Iterationen oder wenn eine ausreichend gute Lösung gefunden wurde, hält der Algorithmus an.

Dieser Algorithmus ist so, als ob wir viele Erkundungsgruppen (Wolken) auf die Suche nach einem Schatz (optimale Lösung) in einem riesigen Labyrinth (Suchraum) schicken würden. Jede Gruppe sucht auf ihre eigene Art und Weise, tauscht Informationen mit anderen aus, indem sie das „Wetter“ in den Regionen verändert, und findet schließlich gemeinsam den besten Weg.

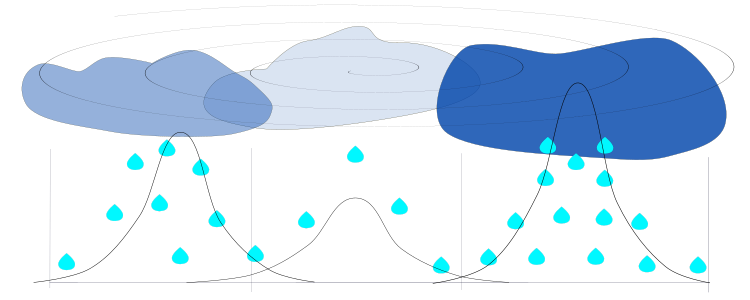
Abbildung 1. Wolken mit unterschiedlicher Dichte, Feuchtigkeit und Größe über Regionen. Der Niederschlag von Tropfen folgt einer Normalverteilung

Machen wir uns zunächst mit den externen Parametern von ACMO und ihrem Zweck anhand der nachstehenden Tabelle vertraut.

Parameter	Der Zweck des Parameters
popSize - Größe der Population	Größe der Tröpfchenpopulation, Population mit fester Größe und über die Wolken verteilte Tröpfchen.
cloudsNumber - Anzahl der Wolken	Anzahl der Wolken.
regionsNumber - Anzahl der Regionen	Jeder zu optimierende Parameter wird in die gleiche Anzahl von Regionen unterteilt.
dMin- Mindestanzahl von Tropfen	Die Mindestanzahl von Tropfen im Verhältnis zur durchschnittlichen Anzahl von Tropfen in den Wolken. Die Schwelle, unterhalb derer eine Wolke als trocken gilt.
λ - Schwellenwertfaktor	Schwellenwert der Feuchtigkeit einer Region, in der sich eine Wolke mit Regen(tröpfchen)erzeugung bilden kann.
γ - Trocknungsverhältnis	Trocknungsverhältnis, das die Menge an Feuchtigkeit in den Wolken bei jeder Iteration reduziert.
EnM0 - Anfangsentropie	Die anfängliche Entropie ist die Breite der Wolke, wenn sie erscheint.
HeM0 - anfängliche Hyperentropie	Hyperentropie - die Dichte einer Wolke, wenn sie erscheint. Der Parameter regelt die Form der Normalverteilung.

Als Nächstes wollen wir uns die Schritte des ACMO-Algorithmus ansehen.

1. Initialisierung:

• Die Suchraumaufteilung U in MD Regionen des Gebiets Ui.
• Initialisierung der Feuchtigkeitswerte HUi und des Luftdrucks PUi für jede Region.
• Einstellung der Algorithmusparameter: λ Schwellenwertfaktor, γ Trocknungsverhältnis, EnM0 Anfangsentropie, HeM0 Anfangshyperentropie und andere.

2. Wolkenerzeugung:

• Festlegung mehrerer Regionen S, in denen die Feuchtigkeit HUi einen dynamisch berechneten Schwellenwert Ht überschreitet.
• Für jede Region Ui aus S:
• Berechnung des Zentrums der Wolke CenterCk mit der Gleichung CenterCk = Center (Ui).
• Berechnung der Entropie EnCk und der Hypernetropie HeCk auf der Grundlage der Anfangsentropie EnM0, HeM0 und des Kontraktionsverhältnisses ζ.
• Erzeugung einer Wolke Ck mit dem Zentrum CenterCk, der Entropie EnCk und Hyperentropie HeCk.

3. Aktualisierung der Luftfeuchtigkeit und des Luftdrucks:

• Aktualisierung der Feuchtigkeitswerte HUi und des Luftdrucks PUi für jede Region Ui.

4. Phase der Wolkenbewegung:

• Für jede Wolke Ck:
• Bestimmung der Richtung der Wolkenbewegung auf der Grundlage des Unterschieds im atmosphärischen Druck zwischen der aktuellen Region und einer ausgewählten benachbarten Region.
• Verschiebung der Wolke Ck in Richtung eines niedrigeren Luftdrucks.

5. Phase der Wolkenausbreitung:

• Für jede Wolke Ck:
• Bestimme, welche Wolkentröpfchen sich aufgrund von Unterschieden im atmosphärischen Druck in andere Regionen ausbreiten.
• Ausbreitung von Wolkentröpfchen Ck in benachbarte Regionen mit niedrigerem Luftdruck.

6. Aktualisierung der Luftfeuchtigkeit und des Luftdrucks:

• Aktualisierung der Feuchtigkeitswerte HUi und des Luftdrucks PUi für jede Region Ui nach der Bewegung und Ausbreitung der Wolken.

7. Überprüfung der Abbruchbedingung:

• Erhöhen des Iterationszählers t.
• Wenn t < tmax, weiter zu 2 (Wolkenbildung).
• Ist t >= tmax, bricht der Algorithmus ab.

Wichtige Punkte:

• Ui Regionen bilden den Suchraum, jede Region ist durch HUi Luftfeuchtigkeit und PUi Luftdruck gekennzeichnet.
• Eine Wolke Ck bilden sich nur in Regionen mit ausreichender Luftfeuchtigkeit (HUi > Ht).
• Die Bewegung und Ausbreitung von Wolken erfolgt unter dem Einfluss des unterschiedlichen Luftdrucks in den verschiedenen Regionen.
• Die Werte für Luftfeuchtigkeit und Luftdruck werden nach jedem Zyklus der Wolkenbewegung und -ausbreitung aktualisiert.

Betrachten wir nun die wichtigsten Vorgänge bezüglich der Wolken im Detail.

1. Die Operation Cloudmove (C) ist für die Bewegung von Wolken zuständig.

1.1 Für jede Wolke Ck:

• Ein zufälliges Zielgebiet F wird aus dem Suchraum U ausgewählt.
• Die Druckdifferenz ΔP wird zwischen dem aktuellen Gebiet E, in dem sich die Wolke befindet, und dem Zielgebiet F berechnet.
• Wenn der Druck in F niedriger ist als in E (ΔP > 0), wird die Wolke Ck in ein Gebiet mit niedrigerem Druck verschoben.
• Die Geschwindigkeit der Wolkenbewegung Vk wird auf der Grundlage des Druckunterschieds und der Wolkenentropie berechnet.
• Das Zentrum der Wolke Ck wird um Vk verschoben.
• Die Feuchtigkeitsmenge in der Wolke Ck wird durch Verdunstung um γ * 100% verringert.
• Wenn die Anzahl der Tropfen nk kleiner als der Schwellenwert dN wird, wird die Wolke Ck aus der Vielzahl der Wolken C entfernt (tatsächlich wird die Wolke nicht entfernt, sondern in Regionen mit einer Luftfeuchtigkeit über dem Schwellenwert verschoben, wobei die Anfangswerte der Entropie und Hyperentropie festgelegt und für die aktuelle Iteration angepasst werden).

So bewegen sich die Wolken in Richtung der Gebiete mit niedrigerem Druck, während ihre Energie (Feuchtigkeitsmenge) allmählich abnimmt. Dieser Bewegungsmechanismus spiegelt das physikalische Verhalten von Wolken in der Natur wider.

2. Die Operation Cloudspread (C) ist für die Ausbreitung von Wolken zuständig.

2.1 Für jede Wolke Ck:

• Ermittele die aktuelle Region E, in der sich der Mittelpunkt der Wolke befindet.
• Ermittele die Region G, in die sich der Mittelpunkt der Wolke nach der Bewegungsphase bewegen wird.
• Berechne die Druckdifferenz ΔP = PE - PG zwischen der aktuellen und der neuen Region.
• Wenn sich die Regionen E und G unterscheiden, berechne den Streufaktor α = ΔP / ΔPmax.
• Wenn die Regionen E und G übereinstimmen, setz α = 0,3 (grundlegende Ausbreitungsgeschwindigkeit).
• Berechne die neue Wolkenentropie EnCk = EnCk × (1 + α), wobei α ein Verteilungsfaktor ist.
• Berechne die neue Hyperentropie der Wolke HeCk = HeCk × (1 + α), d. h. sie steigt proportional zum Ausbreitungsfaktor.
• Wenn die Entropie der Wolke Ck 5 × EnM0 übersteigt oder die darin enthaltene Feuchtigkeitsmenge unter dem Schwellenwert von dN liegt, wird die Wolke Ck aus der Menge C „entfernt“.

Die Hauptgedanken der Operationen 1 und 2:

• Je größer der Druckunterschied zwischen den Regionen ist, desto schneller bewegen sich die Wolken.
• Die Entropie wird erhöht, um den Suchraum zu erweitern.
  
• Die Hyperentropie der Wolke nimmt zu, um eine detailliertere Erkundung des Raums zu ermöglichen.
• Kriterien für die Wolkenverbreiterung: Die Entropie ist größer als 5 × EnM0 oder die Feuchtigkeitsmenge ist kleiner als dN.

In der Beschreibung des Algorithmus geben die Autoren keine Einschränkungen hinsichtlich der Anzahl der Regionen an, die eine Wolke abdecken kann. Der Algorithmus berücksichtigt nur zwei Regionen: die aktuelle Region E, in der sich das Zentrum der Wolke Ck befindet, und eine neue Region G (neues Zentrum nach der Bewegung). Allerdings werden die Wolken bei jeder Iteration größer und greifen auf benachbarte Regionen über, was zu einer erhöhten Luftfeuchtigkeit und einem höheren Luftdruck in den Gebieten führt, auf die die Tropfen fallen. So kann eine Wolke nacheinander von einer Region in eine andere wechseln, aber zu einem bestimmten Zeitpunkt arbeitet der Algorithmus nur mit zwei Regionen - der aktuellen und der neuen. Das bedeutet, dass die Wolkenbewegung und der Tröpfchenniederschlag in den Regionen getrennt betrachtet werden. Wolken und Tröpfchen sind nicht miteinander verbunden und stellen unterschiedliche Einheiten innerhalb des Algorithmus dar.

Der Algorithmus aktualisiert die Position der Wolke, berechnet eine neue Entropie und Hyperentropie und prüft, ob die Wolke die Kriterien für eine Verbreiterung übersteigt, legt aber keine ausdrücklichen Beschränkungen für die Anzahl der Regionen fest, die sie abdecken kann.

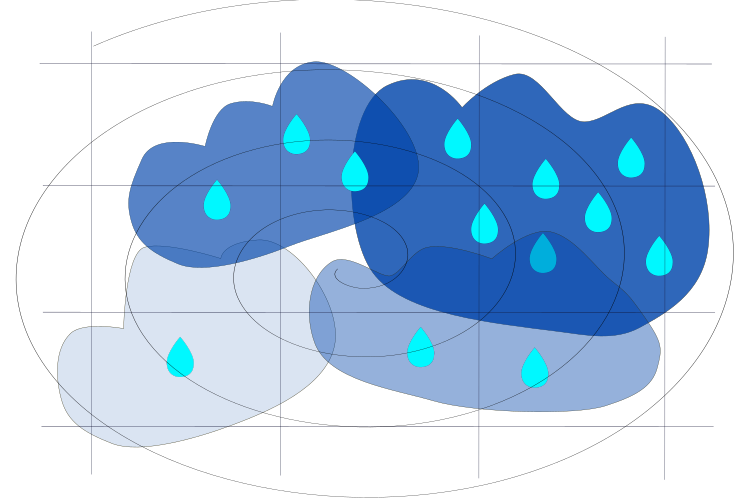
Bild 2. Bewegung der Wolken über Regionen mit niedrigerem Druck

Aus der Beschreibung des Algorithmus ergibt sich, dass die Region (und nicht die Wolke) eine bestimmte „Fitnessfunktion“ hat, nämlich die Luftfeuchtigkeit in der Region. Die Rolle der Wolke in diesem Algorithmus ist eher ein Indikator, der anzeigt, wie viele Tropfen in einer bestimmten Region fallen werden. Wichtige Punkte:

1. Die Region hat ihren eigenen Druck P, der die Geschwindigkeit der Wolkenausbreitung bestimmt.
2. Die Wolke Ck „besitzt“ die Tropfen nicht, sondern dient als Indikator dafür, wie viele Tropfen in der aktuellen Region E und der neuen Region G fallen werden.
3. Die Bewegung der Wolke von der Region E zur Region G wird durch den Druckgradienten ΔP = PE - PG bestimmt.
4. Die Tropfen gehören nicht zu einer bestimmten Wolke, sondern fallen in den Regionen, in denen sich die Wolken befinden.

Somit ist die Region, nicht die Wolke, die primäre Einheit, die die Dynamik des „Wetters“ in einem bestimmten System bestimmt. Dies unterscheidet diesen Algorithmus von Algorithmen mit mehreren Populationen.

Der Luftdruck ist ein wichtiges Merkmal jeder Region im Suchraum und wird verwendet, um die Richtung der Wolkenbewegung zu bestimmen, d. h. die Wolken bewegen sich von Hochdruckgebieten zu Tiefdruckgebieten. Der Druck in einer Region erhöht sich jedes Mal, wenn die Region bewertet wird (wenn der Zielfunktionswert für einen Punkt in dieser Region berechnet wird). Darin spiegelt sich der Gedanke wider, dass, je mehr wir ein bestimmtes Gebiet erforschen, der „Druck“ in diesem Gebiet zunimmt, was den Algorithmus veranlasst, andere, weniger erforschte Gebiete zu erkunden.

Nach dem Algorithmus der Autoren hängt die Veränderung der Wolkenform von der Differenz des Luftdrucks zwischen der aktuellen Region, in der sich die Wolke befindet, und der neuen Region, in die sich die Wolke bewegt, ab. Konkret geschieht dies wie folgt:

• Wenn der Druckunterschied ΔP = PE - PG groß ist, bedeutet dies, dass die Wolke aus einem Gebiet mit sehr unterschiedlichem Druck kommt und die Geschwindigkeit der Wolke höher ist.
• Wenn der Druckunterschied ΔP klein ist, bedeutet dies, dass sich die Wolke mit geringer Geschwindigkeit in ein Gebiet mit einem ähnlichen Druckwert bewegt.

Gemäß der Beschreibung des Algorithmus werden die Werte von Entropie und Hyperentropie bei der ersten Iteration wie folgt bestimmt:

1. Anfangsentropie EnM0 = Ij / A, wobei:

• A ist auf Stufe 6 eingestellt
• Ij ist die Länge der Region in der j-ten Dimension

2. Die Anfangsentropie HeM0 wird auf den Wert 0,5 gesetzt.

Die Entropie im Algorithmus bestimmt, wie weit sich die Wolke ausbreitet (Größe). In der ersten Iteration sollte die Wolke mindestens eine gesamte Suchregion abdecken.

Die Hyperentropie ist für die „Dicke“ der Wolke verantwortlich und regelt die Form der Normalverteilung, d. h. wie dicht die Tröpfchen in der Wolke angeordnet sind. Der anfängliche Wert von 0,5 wird experimentell gewählt, um ein Gleichgewicht zwischen einer zu dünnen und einer zu dichten Wolke herzustellen.

1. Die Entropie nimmt mit jeder Iteration zu. Dies bedeutet, dass sich die Wolken allmählich „ausdehnen“, um immer größere Suchbereiche abzudecken, und hilft dabei, das Feststecken in lokalen Optima zu vermeiden.
2. Die Hyperentropie hingegen erhöht die Dichte im Zentrum der Wolke. Dies führt dazu, dass die Wolke die Lösung der voraussichtlichen Region verfeinert.

Dieser Ansatz ermöglicht es dem Algorithmus, Lösungen zu verfeinern und gleichzeitig den Suchbereich zu erweitern und die Fähigkeit zu bewahren, aus lokalen Optima zu „entkommen“.

In einem mehrdimensionalen Raum wird die Definition eines Regionsindex für eine Wolke etwas komplizierter, aber das Prinzip bleibt dasselbe. So funktioniert es:

• Der Suchraum wird in Regionen über alle Dimensionen hinweg unterteilt. Wenn wir D Dimensionen haben und jede Dimension in M Intervalle unterteilt ist, haben wir insgesamt M × D Regionen.
• Der Regionsindex ist in diesem Fall nicht nur eine Zahl, sondern eine Reihe von Koordinaten, die die Position der Region entlang jeder Dimension angeben. Um den Regionalindex für eine Wolke zu bestimmen, prüft der Algorithmus, in welche Intervalle entlang jeder Dimension das Zentrum der Wolke fällt.

Wenn wir zum Beispiel einen dreidimensionalen Raum (D = 3) haben, der in 10 Intervalle für jede Dimension (M = 10) unterteilt ist, kann der Regionsindex wie (3, 7, 2) aussehen, was bedeutet, dass das dritte Intervall entlang der ersten Dimension, das siebte entlang der zweiten und das zweite entlang der dritten Dimension liegt.

Es ist notwendig, auf das Zentrum der Wolke zu achten, das nicht unbedingt der beste Tropfen in der Wolke ist. Hier sind einige wichtige Punkte:

• Das Zentrum der Wolke wird als ein bestimmter „Mittelpunkt“ der Region definiert, in der die Wolke erzeugt wird.
• Der beste Tropfen in der Wolke ist derjenige, der den besten Wert der Zielfunktion (den höchsten Fitnesswert) ergibt.
• Der Algorithmus enthält das Konzept des „Regionsfeuchtigkeitswertes“ (UiH), der den besten in einer bestimmten Region gefundenen Fitnesswert darstellt. Dieser Wert bezieht sich auf den besten Tropfen, nicht auf das Wolkenzentrum.
• Das Wolkenzentrum wird zur Bestimmung der Position der Wolke im Suchraum und zur Berechnung ihrer Bewegung verwendet, entspricht aber nicht unbedingt der besten Lösung.

Das Wolkenzentrum und der beste Tropfen sind also unterschiedliche Konzepte in diesem Algorithmus. Das Zentrum wird zur Navigation der Wolke im Suchraum verwendet, während das beste Tröpfchen die beste Lösung darstellt, die in der Region zum aktuellen Zeitpunkt gefunden wurde.

Dieser Ansatz ermöglicht es dem Algorithmus, den Suchraum effizient zu erkunden (unter Verwendung des Wolkenzentrums für die Bewegung) und gleichzeitig die besten in den Regionen gefundenen Lösungen zu verfolgen und zu speichern (die besten Tropfen, die in den Regionen gefallen sind).

Es gibt mehrere Fälle im ACMO-Algorithmus, in denen Wolken zerstört oder „aufgelöst“ werden. Schauen wir sie uns an:

1. Unzureichende Feuchtigkeit:

• Jede Wolke enthält eine bestimmte Menge an Feuchtigkeit.
• Wenn die Feuchtigkeitsmenge unter den Schwellenwert dN fällt, wird die Wolke als zu trocken angesehen und verschwindet.
• Das ist so ähnlich, wie sich kleine Wolken in der Natur auflösen.

2. Zu viel Entropie:

• Die Entropie einer Wolke zeigt, wie weit sie sich verbreitert hat.
• Wird die Entropie größer als das Fünffache der Anfangsentropie (5 × EnM0), gilt die Wolke als zu diffus und verschwindet.

Man kann sich das wie eine Wolke vorstellen, die sich so sehr gedehnt hat, dass sie sich einfach in Luft auflöst.

3. Natürliche Verdunstung:

• Nach jeder Bewegung der Wolke nimmt die Menge ihrer Feuchtigkeit um einen bestimmten Prozentsatz ab (γ * 100%).
• Wenn nach einer solchen Reduzierung die Feuchtigkeitsmenge kleiner als dN ist, verschwindet die Wolke.

Dies ist vergleichbar mit der allmählichen Verdunstung einer Wolke in der Natur.

4. Wenn Wolken sich vereinen:

• Obwohl dies auch nicht ausdrücklich im Algorithmus beschrieben ist, können in einigen ACMO-Varianten Wolken verschmelzen.
• Bei einer Verschmelzung scheint eine der Wolken (in der Regel die kleinere) zu verschwinden und Teil der größeren Wolke zu werden.

All diese Mechanismen helfen dem Algorithmus, den Suchraum von wenig aussichtsreichen Lösungen zu „bereinigen“ und sich auf die vielversprechendsten Bereiche zu konzentrieren. 

Man könnte sich fragen: Was würde passieren, wenn sich die Wolken in Tiefdruckgebiete verlagern und sich alle in denselben Regionen versammeln? Erstens sind Regionen mit niedrigem Druck nicht die schlechtesten Lösungen im Suchraum; es sind einfach Regionen, die schlecht erforscht sind. Selbst wenn alle Wolken in den Regionen mit dem niedrigsten Druck konzentriert sind, werden sie allmählich beginnen, den Druck in diesen Gebieten zu erhöhen. Irgendwann wird dies zur Entstehung neuer Regionen mit niedrigerem Druck führen, was die Wolken unweigerlich dazu zwingen wird, ihren derzeitigen Standort zu verlassen.

Die Wolken bleiben also nie lange an einem Ort und bewegen sich sowohl in Bereichen mit hochwertigen Lösungen als auch in weniger vielversprechenden Bereichen. Darüber hinaus ermöglichen die Mechanismen der Wolkenverdunstung und ihrer kontinuierlichen Ausdehnung, gefolgt von ihrer Zerstörung, die Bildung neuer Wolken, um die in guten Regionen zerstörten zu ersetzen. Damit wird ein neuer Zyklus der Verfeinerung vielversprechender Bereiche des Suchraums eingeleitet.

Bestimmung des Zentrums einer neuen Wolke Ck. Wenn der Feuchtigkeitswert in einer Region einen Schwellenwert überschreitet, kann sie eine neue Wolke erzeugen. Die Feuchtigkeitsschwelle Ht wird dynamisch nach folgender Gleichung berechnet:

Ht = Hmin + λ * (Hmax - Hmin), wobei:

• Hmin und Hmax - minimale und maximale Luftfeuchtigkeitswerte im gesamten Suchgebiet entsprechend
• λ - Schwellenwertfaktor gleich 0,7 auf der Grundlage experimenteller Tests

Berechnung von Entropie und Hyperentropie. Die Bedeutung der Entropie für neue Wolken EnM nimmt während der Suche ab und wird durch die Gleichung festgelegt:

EnMt = ζ * EnM0, wobei ζ ein anhand der Gleichung berechnetes Verdichtungsverhältnis ist:

ζ = 1 / (1 + e^(- (8 - 16 * (t / tmax))))

Die Hyperentropie der neu erzeugten Wolken nimmt mit jeder Iteration zu:

HeMt = ζ * HeM0, wobei ζ das Ausdehnungsverhältnis ist, das anhand der Gleichung berechnet wird:

ζ = 1 / (1 + e^(8 - 16 * (t / tmax))), wobei:

• EnM0j - Anfangsentropie gleich 0,2
  
• HeM0 - anfängliche Hyperentropie gleich 0,5
• t - aktuelle Iteration
• tmax - maximale Anzahl von Iterationen

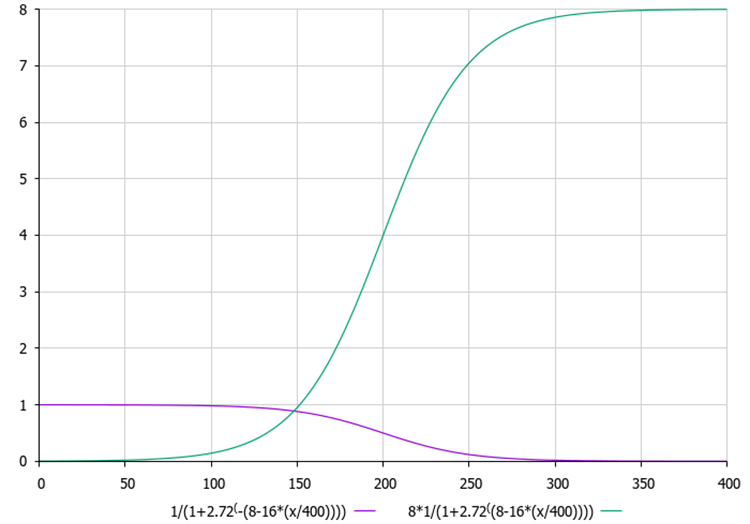
Abb. 3. Entropie- und Hyperentropiekurven für neue Wolken in Abhängigkeit von der aktuellen Epoche

Die Geschwindigkeit der Wolkenbewegung gehorcht dem folgenden Gesetz:

Vk = β * EnCk, wobei β durch die Gleichung ausgedrückt wird:

β = (PCk - PF) / (PMax - PMin), wobei:

• β - ein Faktor für den atmosphärischen Druck
• PMax und PMin - maximaler und minimaler atmosphärischer Druck im Suchraum
  
• PCk und PF - Druck in der augenblicklichen und der Zielregion
• EnCk - aktuelle Wolkenentropie
  

Nachdem wir nun die gesamte Theorie des ACMO-Modells für atmosphärische Wolkenbewegungen kennen, können wir mit der Implementierung des Algorithmus-Codes beginnen.

Wir beschreiben die Struktur S_ACMO_Region, die zur Darstellung einer Region mit meteorologischen Merkmalen verwendet wird. Die Struktur S_ACMO_Region enthält mehrere Felder, die jeweils Informationen über die Region speichern:

Die Felder der Struktur:

• humidity - Feuchtigkeitsgrad in der Region.
• pressure - Atmosphärischer Druck in der Region.
• pressure - Mittelpunkt der Region in Form eines Koordinatenvektors, der den zentralen Punkt angibt.
• x - Punkt mit dem höchsten Druck in der Region.

Init() - Initialisierungsmethode, die die Anfangswerte für die Strukturfelder festlegt.

• Die Luftfeuchtigkeit wird mit dem Wert „-DBL_MAX“ initialisiert, was eine extrem niedrige Luftfeuchtigkeit anzeigt.
• pressure - wird mit Null initialisiert, da der Druck noch nicht gemessen wurde.

Die Struktur S_ACMO_Region wird in einem meteorologischen Modell verwendet, in dem Informationen über verschiedene Regionen in Bezug auf ihre klimatischen Bedingungen gespeichert und verarbeitet werden müssen. Die Methode Init () stellt sicher, dass die Struktur vor der Verwendung ordnungsgemäß initialisiert wird. 

//——————————————————————————————————————————————————————————————————————————————
// Region structure
struct S_ACMO_Region
{
    double humidity; //humidity in the region
    double pressure; //pressure in the region
    double centre;   //the center of the region
    double x;        //point of highest pressure in the region

    void Init ()
    {
      humidity = -DBL_MAX;
      pressure = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Beschreibung der zwei Strukturen: S_ACMO_Area und S_ACMO_Cloud und ihre detailierte Besprechung:

 1. Die Struktur S_ACMO_Area stellt eine Region dar, die aus einer Reihe von Regionen besteht, die durch die Struktur S_ACMO_Region beschrieben werden und Informationen über mehrere Regionen in einem bestimmten Gebiet enthalten.

 2. Die Struktur S_ACMO_Cloud stellt die Wolke und ihre Merkmale dar. Die Felder der Struktur:

• center [] - der Array speichert die Koordinaten des Wolkenzentrums.
• entropy [] - der Array der Wolkenentropiewerte für jede Koordinate.
  
• entropyStart [] - der Array mit den Anfangsentropiewerten.
• hyperEntropie - der Wert der Hyperentropie.
  
• regionIndex [] - der Array mit den Indizes der Regionen, zu denen die Wolken gehören.
• droplets - die Anzahl der Tröpfchen in einer Wolke (ein herkömmlicher Begriff, der die Feuchtigkeit einer Wolke bezeichnet).

Die Methode Init (int coords) initialisiert Arrays in der Struktur und ändert ihre Größe je nach dem übergebenen Parameter coords.

Beide Strukturen werden im meteorologischen Modell zur Darstellung und Analyse von Regionen und Wolken verwendet. S_ACMO_Area wird verwendet, um Regionen zu gruppieren, während S_ACMO_Cloud dazu dient, die Eigenschaften von Wolken zu beschreiben.

//——————————————————————————————————————————————————————————————————————————————
struct S_ACMO_Area
{
    S_ACMO_Region regions [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Cloud structure
struct S_ACMO_Cloud
{
    double center       [];    // cloud center
    double entropy      [];    // entropy
    double entropyStart [];    // initial entropy
    double hyperEntropy;       // hyperEntropy
    int    regionIndex  [];    // index of regions
    double droplets;           // droplets

    void Init (int coords)
    {
      ArrayResize (center,       coords);
      ArrayResize (entropy,      coords);
      ArrayResize (entropyStart, coords);
      ArrayResize (regionIndex,  coords);
      droplets = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

Werfen wir einen Blick auf die Klasse C_AO_ACMO, die von einer anderen C_AO-Klasse geerbt wurde. Allgemeine Struktur der Klasse:

1. Die Klassenparameter, die die Rolle von externen Parametern des Algorithmus spielen:

• popSize - die Größe der Population.
• cloudsNumber - die Anzahl der Wolken.
• regionsNumber - die Anzahl der Regionen pro Dimension.
• dMin - die Mindestanzahl von Tropfen im Verhältnis zur durchschnittlichen Anzahl von Tropfen in den Wolken.
• EnM0 und HeM0 - die Anfangswerte der Entropie und Hyperentropie.
• λ - der Schwellenfaktor für die Bestimmung von Regengebieten.
• γ - die Abschwächungsrate.

2. Parameter-Array:

• params - das Array von Strukturen, wobei jedes Element den Namen und den Wert des Parameters enthält.

3.  Methoden:

• SetParams () - der Modellparameter aus dem Array „params“.
• Init () - initialisiert das Modell mit den angegebenen Suchgrenzen, dem Schritt und der Anzahl der Epochen.
• Moving () - die Methode ist für die Bewegung der Wolken zuständig.
• Revision () - die Methode, die eine Revision des Modellstatus durchführt.
• MoveClouds () - die Methode, die für die Bewegung der Wolken verantwortlich ist.
• GetRegionIndex () - die Methode zum Ermitteln des Regionsindexes für einen bestimmten Punkt.
• RainProcess() - die Methode, die für den Regen verantwortlich ist.
• DropletsDistribution () - die Methode zur Verteilung von Tröpfchen über Wolken.
• UpdateRegionProperties () - die Methode zum Aktualisieren der Regionseigenschaften.
• GenerateClouds () - die Methode zur Erzeugung von Wolken.
• CalculateHumidityThreshold () - die Methode zur Berechnung der Feuchtigkeitsschwelle.
• CalculateNewEntropy () - die Methode zur Berechnung der neuen Entropie für eine Wolke.

4. Mitglieder der Klasse:

   S_ACMO_Area areas [] - das Array der Gebiete enthält Informationen über verschiedene Regionen.

   S_ACMO_Cloud clouds [] - das Array der Wolken enthält Informationen über die Eigenschaften der Wolke.

   Private Variablen wie epochs, epochNow, dTotal, entropy [] und minGp werden verwendet, um den Zustand des Modells und der Berechnungen zu verfolgen.

Die Klasse C_AO_ACMO ist für die Simulation und Bewegung von Wolken in der Atmosphäre gedacht. Sie enthält verschiedene Parameter und Methoden, die es Ihnen ermöglichen, den Zustand der Wolken, ihre Bewegung und die Interaktion mit den Regionen zu verwalten.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACMO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACMO () { }
  C_AO_ACMO ()
  {
    ao_name = "ACMO";
    ao_desc = "Atmospheric Cloud Model Optimization";
    ao_link = "https://www.mql5.com/en/articles/15849";

    popSize       = 50;    //population size

    cloudsNumber  = 5;     // Number of clouds
    regionsNumber = 10;    // Number of regions per dimension  (M)
    dMin          = 0.2;   // Minimum number of drops relative to the average number of drops in the clouds (dN)
    EnM0          = 1.0;   // Initial value of entropy
    HeM0          = 0.5;   // Initial value of hyperentropy
    λ             = 0.7;   // Threshold factor (threshold of the rainiest regions)
    γ             = 0.2;   // Weaken rate

    ArrayResize (params, 8);

    params [0].name = "popSize";       params [0].val = popSize;

    params [1].name = "cloudsNumber";  params [1].val = cloudsNumber;
    params [2].name = "regionsNumber"; params [2].val = regionsNumber;
    params [3].name = "dMin";          params [3].val = dMin;
    params [4].name = "EnM0";          params [4].val = EnM0;
    params [5].name = "HeM0";          params [5].val = HeM0;
    params [6].name = "λ";             params [6].val = λ;
    params [7].name = "γ";             params [7].val = γ;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    cloudsNumber  = (int)params [1].val;
    regionsNumber = (int)params [2].val;
    dMin          = params      [3].val;
    EnM0          = params      [4].val;
    HeM0          = params      [5].val;
    λ             = params      [6].val;
    γ             = params      [7].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    cloudsNumber;  // Number of clouds
  int    regionsNumber; // Number of regions per dimension (M)
  double dMin;          // Minimum number of drops relative to the average number of drops in the clouds (dN)
  double EnM0;          // Initial value of entropy
  double HeM0;          // Initial value of hyperentropy
  double λ;             // Threshold factor
  double γ;             // Weaken rate


  S_ACMO_Area   areas  [];
  S_ACMO_Cloud  clouds [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  int    dTotal;         // Maximum total number of droplets (N)
  double entropy [];     // Entropy
  double minGp;          // Minimum global pressure


  void   MoveClouds                 (bool &rev);
  int    GetRegionIndex             (double point, int ind);
  void   RainProcess                (bool &rev);
  void   DropletsDistribution       (double &clouds [], int &droplets []);

  void   UpdateRegionProperties     ();

  void   GenerateClouds             ();
  double CalculateHumidityThreshold ();
  void   CalculateNewEntropy        (S_ACMO_Cloud &cl, int t);
};
//——————————————————————————————————————————————————————————————————————————————

Schauen wir uns nun die Methode Init der Klasse C_AO_ACMO an, die für die Initialisierung der Parameter des Wolkenmodells zuständig ist.

1. Die Methode akzeptiert drei Arrays (rangeMinP, rangeMaxP und rangeStepP), die die Grenzen und Schritte für die Modellparameter beschreiben. Der vierte Parameter ist epochsP. Er ist standardmäßig auf 0 gesetzt und gibt die Anzahl der Epochen an.

2. Aufruf der Methode StandardInit zur Durchführung der grundlegenden Initialisierung. War das nicht erfolgreich, gibt die Methode false zurück.

3. Initialisierung von Variablen: Die Methode setzt die Gesamtzahl der Epochen fest und setzt die aktuelle Epoche auf 0 zurück.

4. Initialisierung der Parameter:

• dTotal - entspricht der Größe der Grundgesamtheit.
• dMin - neu berechnet unter Berücksichtigung des Verhältnisses zwischen der Populationsgröße und der Anzahl der Wolken.

5. Array-Speicherzuweisung: Die Methode ändert die Größe der Arrays für Entropie und die Gebiete entsprechend der Anzahl der Koordinaten.

6. Initialisierung von Entropie und Regionen:

• Wird der Entropiewert für jede Koordinate c berechnet.
• Für jede Region r wird die Methode Init () aufgerufen, um die Region zu initialisieren.
• Der Mittelpunkt einer Region wird als Durchschnittswert zwischen dem Mindest- und dem Höchstwert, multipliziert mit der Anzahl der Regionen, berechnet.
• Dann durchläuft der Mittelpunkt die Methode SeInDiSp, die die Werte auf einen bestimmten Bereich normalisiert.
• Die Koordinate x wird für eine Region festgelegt (der höchste Feuchtigkeitswert, der sich standardmäßig in der Mitte der Region befindet).
  

7. Initialisierung der Wolke:

• Ändern der Größe des Wolken-Arrays entsprechend der Anzahl der Wolken.
• Die Methode Init wird für jede Wolke aufgerufen, um die Parameter zu initialisieren.

Die Methode Init führt die grundlegende Einrichtung und Initialisierung des Wolkenmodells durch und setzt die erforderlichen Parameter, Feldgrößen und Werte für die weitere Simulation. Sie ist so aufgebaut, dass sie zunächst die Standardinitialisierung der übergeordneten Klasse durchführt und dann spezifische Parameter in Bezug auf Koordinaten, Regionen und Wolken konfiguriert.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACMO::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  //----------------------------------------------------------------------------
  dTotal       = popSize;
  dMin         = dMin * (popSize / (double)cloudsNumber);

  ArrayResize (entropy, coords);
  ArrayResize (areas,   coords);

  for (int c = 0; c < coords; c++)
  {
    entropy [c] = (rangeMax [c] - rangeMin [c]) / regionsNumber;

    ArrayResize (areas [c].regions, regionsNumber);

    for (int r = 0; r < regionsNumber; r++)
    {
      areas [c].regions [r].Init ();
      areas [c].regions [r].centre = rangeMin [c] + entropy [c] * (r + 0.5);
      areas [c].regions [r].centre = u.SeInDiSp (areas [c].regions [r].centre, rangeMin [c], rangeMax [c], rangeStep [c]);
      areas [c].regions [r].x      = areas [c].regions [r].centre;
    }
  }

  ArrayResize (clouds, cloudsNumber);
  for (int i = 0; i < cloudsNumber; i++) clouds [i].Init (coords);

  minGp = DBL_MAX;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Zusammenfassung

In diesem Artikel sind wir in die Welt des ungewöhnlichen und faszinierenden ACMO-Algorithmus eingetaucht, der ein atmosphärisches meteorologisches Modell zur Lösung mehrdimensionaler Optimierungsprobleme darstellt. Dieser Algorithmus mag auf den ersten Blick wie ein Mehrpopulationsalgorithmus wirken, aber eine genauere Analyse offenbart seine Einzigartigkeit und Neuartigkeit.

Das Modell basiert auf drei Hauptkomponenten: Wolken, Regionen und Tröpfchen. Jede dieser Komponenten funktioniert unabhängig, aber ihr Zusammenspiel schafft ein harmonisches und effizientes System, in dem jeder Teil seine wichtige Rolle spielt. Wolken symbolisieren die Vielfalt der Lösungen, Regionen stellen Suchräume dar, und Tröpfchen sind Elemente, die Übergänge zwischen verschiedenen Lösungen schaffen. Diese Kombination macht den ACMO-Algorithmus nicht nur originell, sondern auch zu einem sehr leistungsfähigen Werkzeug im Bereich der Optimierung.

Im zweiten Teil des Artikels werden wir einen Schritt von der Theorie zur Praxis machen. Wir werden den Algorithmus mit verschiedenen Testfunktionen testen, um seine Leistung zu bewerten und seine Stärken zu ermitteln. Außerdem werden wir die Ergebnisse analysieren und vielleicht neue Horizonte für die Anwendung dieses innovativen Modells bei realen Problemen eröffnen.