Neuronale Netze im Handel: Transformer für die Punktwolke (Pointformer)
Einführung
Die Erkennung von Objekten in Punktwolken ist für viele reale Anwendungen wichtig. Im Vergleich zu Bildern bieten Punktwolken detaillierte geometrische Informationen und können die Struktur der Szene effektiv erfassen. Ihre unregelmäßige Beschaffenheit stellt jedoch eine große Herausforderung für das effiziente Lernen von Merkmalen dar.
Architekturen, die auf Transformer basieren, haben bemerkenswerte Erfolge bei der Verarbeitung natürlicher Sprache erzielt. Sie sind effektiv beim Lernen kontextabhängiger Repräsentationen und modellieren weitreichende Abhängigkeiten innerhalb von Eingabesequenzen. Der Transformer erfüllt zusammen mit seinem Selbstaufmerksamkeits-Mechanismus nicht nur die Anforderung der Permutationsinvarianz, sondern zeigt auch eine hohe Ausdruckskraft. Dennoch ist die direkte Anwendung von Transformeren auf Punktwolken rechnerisch unerschwinglich, da die Kosten quadratisch mit der Größe der Eingabe ansteigen.
Um dieses Problem zu lösen, haben die Autoren der Methode Pointformer, die in dem Artikel „3D Object Detection with Pointformer“ vorgestellt wurde, einen Ansatz vor, der die Stärken von Transformer-Modellen im Umgang mit mengenstrukturierten Daten nutzt. Pointformer verwendet eine U-Netz-Struktur, die aus mehrstufigen Pointformer-Blöcken besteht. Jeder Pointformer-Block besteht aus Transformer-basierten Modulen, die so konzipiert sind, dass sie sowohl sehr ausdrucksstark als auch für Objekterkennungsaufgaben geeignet sind.
In ihrer architektonischen Lösung verwenden die Autoren der Methode drei Transformer-Module:
- Der Local Transformer (LT) modelliert Interaktionen zwischen Punkten innerhalb einer lokalen Region. Er lernt kontextabhängige Merkmale auf Objektebene.
- Der Local-Global Transformer (LGT) erleichtert die Integration von lokalen und globalen Merkmalen mit höherer Auflösung.
- Der Global Transformer (GT) erfasst kontextabhängige Darstellungen auf der Ebene der Szene.
Das Ergebnis: Der Pointformer modelliert sowohl lokale als auch globale Abhängigkeiten und verbessert so die Leistung beim Lernen von Merkmalen in komplexen Szenen mit mehreren unübersichtlichen Objekten erheblich.
1. Der Algorithmus des Pointformers
Bei der Verarbeitung von Punktwolken ist es wichtig, ihre unregelmäßige, ungeordnete Beschaffenheit und unterschiedliche Größe zu berücksichtigen. Die Autoren von Pointformer haben Transformer-basierte Module entwickelt, die speziell für Punktmengenoperationen ausgelegt sind. Diese Module verbessern nicht nur die Aussagekraft der lokalen Merkmalsextraktion, sondern beziehen auch globale Kontextinformationen in die Punktdarstellungen ein.
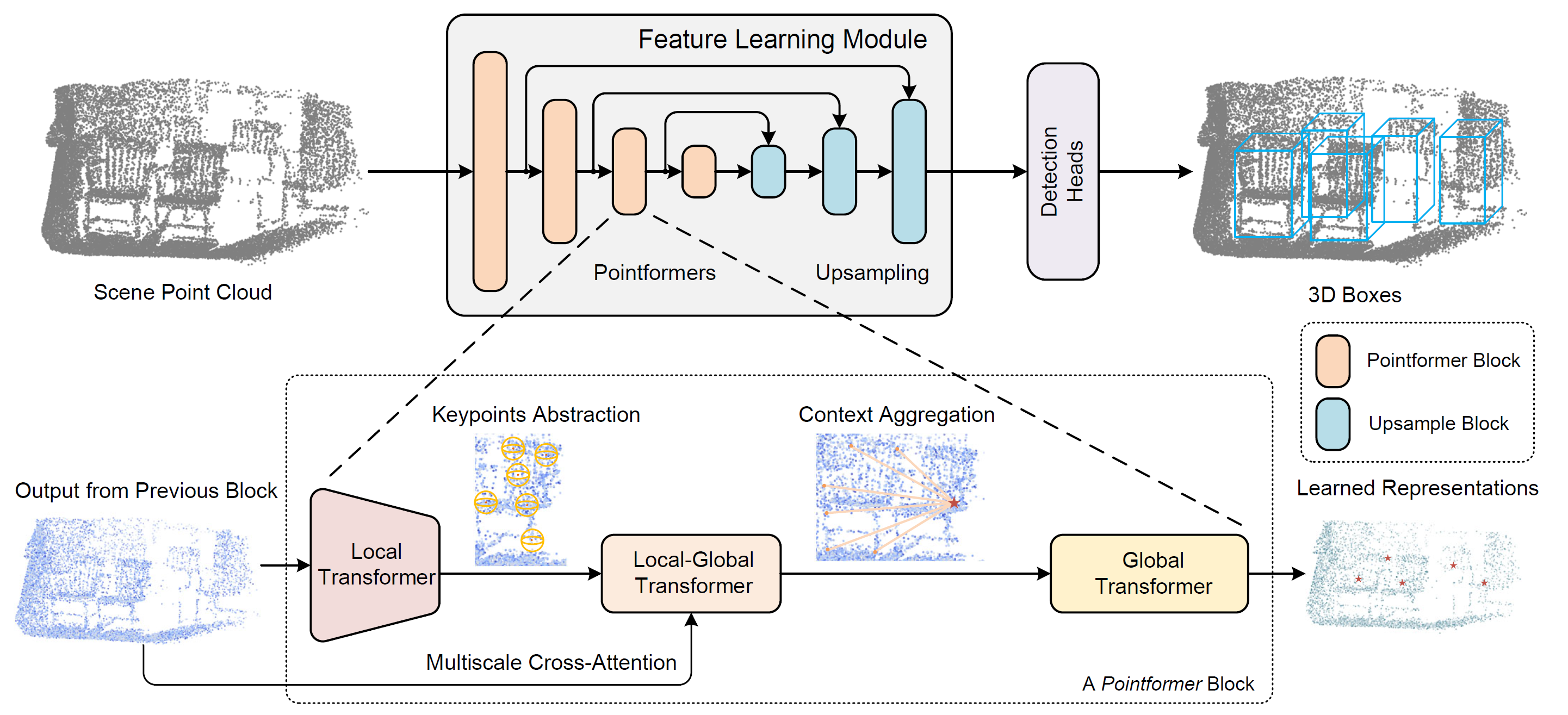
Der Pointformer-Block besteht aus drei Modulen: dem Local Transformer (LT), dem Local-Global Transformer (LGT) und dem Global Transformer (GT). Jeder Block beginnt mit der LT, die hochauflösende Eingaben von der vorherigen Schicht erhält und Merkmale für einen neuen, niedriger aufgelösten Punktesatz extrahiert. Anschließend wendet das LGT-Modul einen skalenübergreifenden Aufmerksamkeitsmechanismus an, um Merkmale aus beiden Auflösungen zu integrieren. Schließlich erfasst das GT-Modul kontextabhängige Darstellungen auf Szenenebene. Für das Upsampling verwenden die Autoren das Feature-Propagation-Modul von PointNet++.
Um eine hierarchische Darstellung der Punktwolkenszene zu erstellen, verwendet Pointformer eine High-Level-Methode, die Feature-Learning-Blöcke in verschiedenen Auflösungen erstellt. Zunächst wird Farthest Point Sampling (FPS) verwendet, um eine Teilmenge von Punkten auszuwählen, die als Zentren dienen. Für jeden Schwerpunkt wird eine lokale Nachbarschaft definiert, indem umliegende Punkte innerhalb eines bestimmten Radius ausgewählt werden. Diese lokalen Gruppen werden dann in Sequenzen organisiert und in eine Transformer-Schicht eingespeist. Ein gemeinsamer Transformer-Block wird auf alle lokalen Regionen angewendet. Je mehr Transformer-Schichten innerhalb eines Pointformer-Blocks gestapelt werden, desto aussagekräftiger wird das Modul, was zu verbesserten Merkmalsdarstellungen führt.
Die Methode berücksichtigt auch Merkmalskorrelationen zwischen benachbarten Punkten. Benachbarte Punkte können manchmal einen aufschlussreicheren Kontext liefern als der Schwerpunkt selbst. Da das Modell den Informationsaustausch zwischen allen Punkten innerhalb einer lokalen Region ermöglicht, werden alle Punkte gleich behandelt, was zu einer effektiveren Extraktion lokaler Merkmale führt.
Farthest Point Sampling (FPS) ist in Punktwolkensystemen weit verbreitet, da es in der Lage ist, nahezu gleichmäßige Stichprobenverteilungen zu erzeugen und dabei die Gesamtform der Eingabe zu erhalten. Dies gewährleistet eine breite Abdeckung der ursprünglichen Punktwolke mit einer begrenzten Anzahl von Zentroiden. FPS hat jedoch zwei große Nachteile:
- Es ist empfindlich gegenüber Ausreißern, was zu einer hohen Instabilität führen kann, insbesondere bei realen Punktwolken.
- FPS wählt Punkte aus, die eine strenge Teilmenge der ursprünglichen Punktwolke sind, was eine genaue Geometrie-Rekonstruktion behindern kann, insbesondere bei teilweiser Objektverdeckung oder spärlich abgetasteten Objekten.
Da die meisten Punkte auf den Oberflächen von Objekten liegen, ist der zweite Punkt besonders kritisch. Die stichprobenartige Erstellung von Vorschlägen kann zu einer natürlichen Diskrepanz zwischen der Qualität der Vorschläge und dem tatsächlichen Vorhandensein von Objekten führen.
Um diese Einschränkungen zu überwinden, haben die Autoren von Pointformer ein Modul zur Koordinatenverfeinerung eingeführt, das auf Self-Attention-Maps basiert. Dieses Modul extrahiert zunächst die Self-Attention-Maps aus der endgültigen Transformerebene für jeden Aufmerksamkeitskopf. Dann werden die Self-Attention-Maps gemittelt. Anschließend werden die verfeinerten Schwerpunktkoordinaten durch Anwendung einer aufmerksamkeitsgewichteten Mittelwertbildung über alle Punkte innerhalb der lokalen Region berechnet. Dieser Prozess verschiebt die Schwerpunktkoordinaten adaptiv näher an die tatsächlichen Zentren der Objekte.
Globale Informationen, die den Kontext der Szene und die Korrelation der Grenzen zwischen verschiedenen Objekten darstellen, sind für Erkennungsaufgaben ebenso wertvoll. Pointformer nutzt die Fähigkeit der Transformer-Module, weitreichende, nicht-lokale Abhängigkeiten zu modellieren. Das Modul Global Transformer ist so konzipiert, dass es Informationen über die gesamte Punktwolke überträgt. Alle Punkte werden in einer Gruppe gesammelt und dienen als Ausgangsdaten für das GT-Modul.
Die Verwendung eines Transformers auf Szenenebene ermöglicht die Erfassung kontextbezogener Darstellungen und erleichtert den Informationsaustausch zwischen verschiedenen Objekten. Diese globalen Darstellungen sind besonders vorteilhaft für die Erkennung von Objekten, die nur durch einige wenige Punkte repräsentiert werden.
Der Local-Global Transformer ist auch ein Schlüsselmodul für die Kombination lokaler und globaler Funktionen, die von den Modulen LT und GT extrahiert werden. LGT verwendet einen mehrskaligen Kreuzaufmerksamkeits-Mechanismus, um Beziehungen zwischen niedrig aufgelösten Zentren und hoch aufgelösten Punkten herzustellen. Formal gesehen handelt es sich um einen Transformer Kreuzaufmerksamkeits-Mechanismus. Die Ergebnisse von LT dienen als Abfragen (Queries), während die höher aufgelösten AusgabenGT als Schlüssel (Key) und Werte (Value) dienen.
Die Positionskodierung ist ein grundlegender Bestandteil der Transformer-Modelle, da sie eine Möglichkeit bietet, Positionsinformationen in die Eingabesequenz einzubauen. Bei der Anpassung der Transformer an Punktwolkendaten wird die Positionskodierung noch wichtiger, da die Punktkoordinaten selbst sehr informativ und entscheidend für die Erfassung lokaler geometrischer Strukturen sind.
Die Visualisierung der Methode Pointformer durch den Autor wird im Folgenden dargestellt.
2. Implementation in MQL5
Nachdem wir die theoretischen Aspekte der Pointformer-Methode erläutert haben, gehen wir nun zum praktischen Teil des Artikels über, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen.
Bei näherer Betrachtung der vorgeschlagenen Ansätze können wir einige Ähnlichkeiten mit der Methode PointNet++ erkennen. Beide Algorithmen verwenden den Mechanismus des „Farthest Point Sampling“ (Probenahme der entferntesten Punkte) zur Bildung von Zentroiden. Die Grundoperationen beider Methoden beruhen auf der Gruppierung von Punkten um Zentren. Deshalb habe ich mich für die Verwendung des Objekts CNeuronPointNet2OCL als übergeordnetes Objekt für die Konstruktion der neuen Klasse CNeuronPointFormer zu verwenden. Seine Struktur wird im Folgenden dargestellt.
class CNeuronPointFormer : public CNeuronPointNet2OCL { protected: CNeuronMLMHSparseAttention caLocalAttention[2]; CNeuronMLCrossAttentionMLKV caLocalGlobalAttention[2]; CNeuronMLMHAttentionMLKV caGlobalAttention[2]; CNeuronLearnabledPE caLocalPE[2]; CNeuronLearnabledPE caGlobalPE[2]; CNeuronBaseOCL cConcatenate; CNeuronConvOCL cScale; //--- CBufferFloat *cbTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override ; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronPointFormer(void) {}; ~CNeuronPointFormer(void) { delete cbTemp; } //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronPointFormer; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
In CNeuronPointNet2OCL haben wir 2 Skalenebenen verwendet, um lokale Merkmale zu extrahieren. In der neuen Klasse behalten wir ein ähnliches Maß an Skalierung bei, heben aber die Qualität der Merkmalsextraktion durch den Einsatz der vorgeschlagenen Aufmerksamkeitsmodule auf ein neues Niveau. Diese Verbesserung spiegelt sich in den internen Arrays der neuronalen Schichten wider, deren Zweck bei der Implementierung der Methoden in unserer neuen Klasse CNeuronPointFormer deutlich werden wird.
Unter den internen Komponenten gibt es nur einen dynamisch zugewiesenen Puffer, den wir im Destruktor der Klasse ordnungsgemäß freigeben werden. Der Klassenkonstruktor bleibt leer. Die Initialisierung aller internen Objekte wird in der Methode Init durchgeführt, deren Parameter von der übergeordneten Klasse kopiert werden.
bool CNeuronPointFormer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, uint output, bool use_tnets, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronPointNet2OCL::Init(numOutputs, myIndex, open_cl, window, units_count, output, use_tnets, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir zunächst die entsprechende Methode der übergeordneten Klasse auf, die die empfangenen Parameter kontrolliert und die geerbten Objekte initialisiert.
In der übergeordneten Klasse erstellen wir zwei interne Ebenen der lokalen Probenteilung. Jede dieser Schichten gibt einen 64-dimensionalen Merkmalsvektor für jeden Punkt in der Eingabepunktwolke aus.
Nach jeder lokalen Probenteilungsschicht werden wir Aufmerksamkeitsmodule einfügen, wie von den Autoren der Pointformer-Methode vorgeschlagen. Die Architektur der Aufmerksamkeitsmodule für beide Schichten wird identisch sein, sodass wir die Objekte in einer Schleife initialisieren werden.
for(int i = 0; i < 2; i++) { if(!caLocalAttention[i].Init(0, i*5, OpenCL, 64, 16, 4, units_count, 2, optimization, iBatch)) return false;
Zunächst initialisieren wir das lokale Aufmerksamkeitsmodul, das mit der Methode CNeuronMLMHSparseAttention Block implementiert ist.
Es ist zu beachten, dass unser Ansatz leicht vom ursprünglichen Pointformer-Algorithmus abweicht. Wir glauben jedoch, dass die Kernlogik erhalten bleibt. Bei der Pointformer-Methode reichert das lokale Aufmerksamkeitsmodul jeden Punkt in einer lokalen Region mit gemeinsamen Kontextmerkmalen an und lenkt so die Aufmerksamkeit auf das Objekt als Ganzes. Es liegt auf der Hand, dass Punkte, die zu demselben Objekt gehören, starke Abhängigkeiten aufweisen. Durch den Einsatz der spärlichen Aufmerksamkeit sind wir nicht auf eine feste lokale Region beschränkt, sondern können stattdessen Punkte mit hoher relationaler Bedeutung hervorheben. Dies ist vergleichbar mit der Identifizierung von Unterstützungs- und Widerstandsniveaus in der technischen Analyse, wo der Preis wiederholt mit bestimmten Schwellenwerten über verschiedene historische Segmente hinweg interagiert.
Als Nächstes wird das lokal-globale Aufmerksamkeitsmodul initialisiert, das den feinkörnigen Kontext aus den Originaldaten in die Merkmale der lokalen Objekte integriert.
if(!caLocalGlobalAttention[i].Init(0, i*5+1, OpenCL, 64, 16, 4, 64, 2, units_count, units_count, 2, 2, optimization, iBatch)) return false;
Der globale Aufmerksamkeitsblock dient dazu, kontextabhängige Repräsentationen auf der Ebene der Szene zu identifizieren.
if(!caGlobalAttention[i].Init(0, i*5+2, OpenCL, 64, 16, 4, 2, units_count, 2, 2, optimization, iBatch)) return false;
Und natürlich werden wir interne Schichten von trainierbarer Positionskodierung hinzufügen. Hier verwenden wir eine separate Positionskodierung für die lokale und die globale Darstellung.
if(!caLocalPE[i].Init(0, i*5+3, OpenCL, 64*units_count, optimization, iBatch)) return false; if(!caGlobalPE[i].Init(0, i*5+4, OpenCL, 64*units_count, optimization, iBatch)) return false; }
Es ist wichtig zu erwähnen, dass wir den von den Pointformer-Autoren vorgeschlagenen Block zur Verfeinerung der Schwerpunktkoordinaten nicht implementieren. Zunächst haben wir in unserer Implementierung von PointNet++ jeden Punkt in der Wolke als Schwerpunkt seiner lokalen Region bezeichnet. Eine Änderung der Punktkoordinaten könnte daher die gesamte Szene verzerren. Zweitens wird ein Teil der Verfeinerungsfunktion inhärent von den trainierbaren Positionskodierungsschichten übernommen.
Eine kurze Anmerkung zur Skalierung der Merkmalsextraktion. Die initialisierten Module selbst weisen nicht ausdrücklich auf unterschiedliche Skalen für die Merkmalsextraktion hin. Es gibt jedoch zwei Punkte. In der übergeordneten Klasse haben wir unterschiedliche Radien für die lokale Probenteilung verwendet. Hier werden wir verschiedene Stufen der Sparsamkeit in den lokalen Aufmerksamkeitsmodulen einführen.
caLocalAttention[0].Sparse(0.1f); caLocalAttention[1].Sparse(0.3f);
Wir fügen die Ergebnisse von zwei globalen Aufmerksamkeitsstufen zu einem einzigen Tensor zusammen.
if(!cConcatenate.Init(0, 10, OpenCL, 128 * units_count, optimization, iBatch)) return false;
Anschließend wird die Dimensionalität auf das Niveau der Originaldaten des globalen Punktwolken-Deskriptor-Extraktionsblocks reduziert, der in der übergeordneten Klassenmethode initialisiert wurde.
if(!cScale.Init(0, 11, OpenCL, 128, 128, 64, units_count, 1, optimization, iBatch)) return false;
Am Ende der Initialisierungsmethode fügen wir die Erstellung eines Puffers für die Speicherung von Zwischendaten hinzu.
if(!!cbTemp) delete cbTemp; cbTemp = new CBufferFloat(); if(!cbTemp || !cbTemp.BufferInit(caGlobalAttention[0].Neurons(), 0) || !cbTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Danach geben wir das logische Ergebnis der Operationen an das aufrufende Programm zurück und schließen die Methode ab.
Der nächste Entwicklungsschritt besteht in der Implementierung des Feed-Forward-Pass-Algorithmus innerhalb der Methode feedForward. Anders als bei der Initialisierungsmethode können wir uns hier nicht vollständig auf die entsprechende Methode der Elternklasse verlassen. Bei dieser neuen Methode müssen wir Operationen integrieren, die sowohl geerbte als auch neu eingeführte Komponenten betreffen.
Wie zuvor erhält die Vorwärtsdurchgangsmethode einen Zeiger auf das Eingabedatenobjekt als einen ihrer Parameter. Im Methodenrumpf speichern wir diesen Zeiger sofort in einer lokalen Variablen.
bool CNeuronPointFormer::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- LocalNet CNeuronBaseOCL *inputs = NeuronOCL;
Normalerweise vermeiden wir es, eingehende Zeiger in lokalen Variablen zu speichern, sofern dies nicht notwendig ist. In diesem Fall implementieren wir jedoch einen Algorithmus, der eine sequentielle Verarbeitung durch zwei verschachtelte Merkmalsextraktionsblöcke beinhaltet, die auf unterschiedlichen Skalen arbeiten. In diesem Zusammenhang vereinfacht die Arbeit mit einer lokalen Variablen die Logik, da sie es uns ermöglicht, den Zeiger während der Iteration verschiedenen Objekten neu zuzuweisen.
Als Nächstes erstellen wir die oben erwähnte Schleife.
for(int i = 0; i < 2; i++) { if(!cTNetG || i > 0) { if(!caLocalPointNet[i].FeedForward(inputs)) return false; }
Innerhalb der Schleife beginnen wir mit lokalen Operationen für eine Probenteilung, wobei wir die Objekte verwenden, die in der übergeordneten Klasse deklariert und initialisiert wurden.
Es ist wichtig, daran zu erinnern, dass der Algorithmus der Elternklasse eine Option zur Projektion der Eingabedaten in einen kanonischen Raum enthält. Dieser Vorgang wird nur vor der ersten Schicht der lokalen Probenteilung durchgeführt. Daher prüfen wir zu Beginn der Schleife, ob diese Projektion erforderlich ist. Ist dies nicht der Fall, fahren wir direkt mit dem Schritt der lokalen Probenteilung fort.
Wenn eine Projektion erforderlich ist, wird zunächst die Projektionsmatrix erstellt.
else { if(!cTurnedG) return false; if(!cTNetG.FeedForward(inputs)) return false;
Dann führen wir die Projektion der Originaldaten durch.
int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), NeuronOCL.Neurons() / window, window, window)) return false;
Erst danach führen wir ein Probenteilung der lokalen Daten durch.
if(!caLocalPointNet[i].FeedForward(cTurnedG.AsObject())) return false; }
Das Ergebnis der Schicht der lokalen Probenteilung wird direkt an das lokale Aufmerksamkeitsmodul weitergeleitet.
//--- Local Attention if(!caLocalAttention[i].FeedForward(caLocalPointNet[i].AsObject())) return false;
Es ist wichtig zu beachten, dass wir die Daten ohne Positionskodierung in das lokale Aufmerksamkeitsmodul einspeisen. Ich möchte Sie daran erinnern, dass der Mechanismus der Selbstaufmerksamkeit von Natur aus unabhängig von der Reihenfolge der Eingabeelemente ist. Daher identifizieren wir innerhalb des lokalen Aufmerksamkeitsblocks Elemente mit starkem gegenseitigem Einfluss, unabhängig von ihren räumlichen Koordinaten.
Auf den ersten Blick mag die Formulierung „lokale Aufmerksamkeit ohne Koordinatenabhängigkeit“ kontraintuitiv klingen. Schließlich scheint die lokale Aufmerksamkeit eine gewisse räumliche oder örtliche Einschränkung zu implizieren. Aber lassen Sie uns die Sache aus einer anderen Perspektive betrachten. Betrachten Sie ein Preischart. Wir können die Informationen in zwei Kategorien unterteilen: Koordinaten und Merkmale. In dieser Analogie dient die Zeit als Koordinate, während das Preisniveau das Merkmal darstellt. Wenn wir die Koordinaten (Zeit) entfernen, bleibt eine Punktwolke im Merkmalsraum übrig. Die Regionen, in denen ein Preisniveau häufiger auftritt, weisen naturgemäß eine höhere Punktedichte auf. Diese Punkte können zeitlich weit auseinander liegen. Häufig entsprechen diese Bereiche jedoch Unterstützungs- und Widerstandsniveaus. In diesem Sinne arbeitet unser lokales Aufmerksamkeitsmodul in einem lokalen Merkmalsraum.
Nach diesem Schritt wenden wir die Positionskodierung sowohl auf den Ausgang des lokalen Aufmerksamkeitsmoduls als auch auf den Ausgang der lokalen Probenteilungsschicht an.
//--- Position Encoder if(!caLocalPE[i].FeedForward(caLocalAttention[i].AsObject())) return false; if(!caGlobalPE[i].FeedForward(caLocalPointNet[i].AsObject())) return false;
Im nächsten Schritt reichern wir im Modul der lokal-globalen Aufmerksamkeit die lokalen Aufmerksamkeitsdaten mit Informationen aus dem globalen Kontext an, wobei wir die Koordinaten der Objekte berücksichtigen.
//--- Local to Global Attention if(!caLocalGlobalAttention[i].FeedForward(caLocalPE[i].AsObject(), caGlobalPE[i].getOutput())) return false;
Und die Operationen unserer Schleife werden durch das globale Aufmerksamkeitsmodul vervollständigt, in dem die Informationen der Objekte mit dem allgemeinen Kontext der Szene angereichert werden.
//--- Global Attention if(!caGlobalAttention[i].FeedForward(caLocalGlobalAttention[i].AsObject())) return false; inputs = caGlobalAttention[i].AsObject(); }
Bevor wir zur nächsten Iteration der Schleife übergehen, stellen wir sicher, dass wir den Zeiger auf das Quelldatenobjekt in der lokalen Variablen ändern.
Nach erfolgreichem Abschluss aller Iterationen unserer Schleife zur sequentiellen Aufzählung der inneren Schichten fügen wir die Ergebnisse aller globalen Aufmerksamkeitsmodule zu einem einzigen Tensor zusammen. Auf diese Weise können wir die Merkmale von Objekten in verschiedenen Maßstäben weiter berücksichtigen.
if(!Concat(caGlobalAttention[0].getOutput(), caGlobalAttention[1].getOutput(), cConcatenate.getOutput(), 64, 64, cConcatenate.Neurons() / 128)) return false;
Verringern wir die Größe des verketteten Tensors ein wenig mit Hilfe einer Skalierungsschicht.
if(!cScale.FeedForward(cConcatenate.AsObject())) return false;
Dann übergeben wir die empfangenen Daten an die Methode feedForward der Klasse CNeuronPointNetOCL, von der unsere übergeordneten Klasse abgeleitet ist. Sie implementiert einen Mechanismus zur Erzeugung eines globalen Punktwolken-Deskriptors.
if(!CNeuronPointNetOCL::feedForward(cScale.AsObject())) return false; //--- return true; }
Vergessen wir nicht, den Prozess bei jedem Schritt zu kontrollieren. Wenn alle Operationen innerhalb der Methode erfolgreich abgeschlossen sind, geben wir einen booleschen Wert zurück, der dieses Ergebnis an die aufrufende Funktion angibt.
Wir gehen nun zur Konstruktion der Backpropagation-Algorithmen über. Wie Sie wissen, geht es dabei um die Umsetzung zweier wichtiger Methoden:
- calcInputGradients - ist zuständig für die Verteilung der Fehlergradienten auf alle relevanten Komponenten auf der Grundlage ihres Beitrags zum Endergebnis;
- updateInputWeights - ist zuständig für die Aktualisierung der trainierbaren Parameter des Modells.
Um die zweite Methode zu konstruieren, können wir einfach die Struktur der zuvor beschriebenen Methode feedForward wiederverwenden. Wir behalten nur die hierarchische Reihenfolge der Methodenaufrufe für die Komponenten bei, die trainierbare Parameter enthalten. Dann ersetzen wir jeden Aufruf von feedForward durch die entsprechende Methode zur Aktualisierung der Parameter. Die sich daraus ergebende Umsetzung finden Sie in der Anlage zur Überprüfung.
Der Algorithmus für die Methode calcInputGradients erfordert eine genauere Betrachtung. Wie zuvor entspricht die Struktur dieser Methode der von feedForward, jedoch in umgekehrter Richtung. Es gibt jedoch einige Nuancen, die mit dem parallelen Charakter des Informationsflusses in diesem Modell zusammenhängen.
Die Methode erhält als Parameter einen Zeiger auf das Objekt der vorherigen Schicht, das die propagierten Fehlergradienten erhält. Diese Gradienten müssen im Verhältnis zum Einfluss der einzelnen Datenelemente auf das Endergebnis des Modells verteilt werden.
bool CNeuronPointFormer::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Im Hauptteil der Methode wird sofort die Relevanz des empfangenen Zeigers geprüft. Denn wenn sie ungültig ist, hat es keinen Sinn, weitere Operationen durchzuführen.
Dabei ist zu beachten, dass der Fehlergradient auf der Ebene des Schichtausgangs zum Zeitpunkt des Aufrufs dieser Methode bereits im entsprechenden Datenpuffer enthalten ist. Wir übertragen sie also auf die innere Skalierungsschicht, indem wir die entsprechende Methode in der Vorgängerklasse aufrufen.
if(!CNeuronPointNetOCL::calcInputGradients(cScale.AsObject())) return false;
Als Nächstes wird der Fehlergradient auf die verkettete Datenschicht übertragen.
if(!cConcatenate.calcHiddenGradients(cScale.AsObject())) return false;
Dann verteilen wir sie auf die entsprechenden Module der globalen Aufmerksamkeit.
if(!DeConcat(caGlobalAttention[0].getGradient(), caGlobalAttention[1].getGradient(), cConcatenate.getGradient(), 64, 64, cConcatenate.Neurons() / 128)) return false;
Hier müssen wir den Fehlergradienten konsequent durch die Module aller internen Schichten führen. Zu diesem Zweck erstellen wir eine umgekehrte Iterationsschleife.
CNeuronBaseOCL *inputs = caGlobalAttention[0].AsObject(); for(int i = 1; i >= 0; i--) { //--- Global Attention if(!caLocalGlobalAttention[i].calcHiddenGradients(caGlobalAttention[i].AsObject())) return false;
In dieser Schleife wird zunächst der Fehlergradient auf der Ebene des lokal-globalen Aufmerksamkeitsmoduls definiert. Dann verteilen wir sie auf die Schichten der trainierbaren Positionskodierung.
if(!caLocalPE[i].calcHiddenGradients(caLocalGlobalAttention[i].AsObject(), caGlobalPE[i].getOutput(), caGlobalPE[i].getGradient(), (ENUM_ACTIVATION)caGlobalPE[i].Activation())) return false;
Anschließend übertragen wir den Fehlergradienten aus den entsprechenden Schichten der Positionskodierung in das lokale Aufmerksamkeitsmodul und die lokale Probenteilungsschicht.
if(!caLocalAttention[i].calcHiddenGradients(caLocalPE[i].AsObject())) return false; if(!caLocalPointNet[i].calcHiddenGradients(caGlobalPE[i].AsObject())) return false;
Ferner ist anzumerken, dass das lokale Aufmerksamkeitsmodul auch die Ergebnisse der lokalen Probenteilungsschicht als Eingangsdaten verwendet. Daher muss es seinen Teil des Fehlergradienten an das gegebene Objekt weitergeben. Der entsprechende Datenpuffer enthält jedoch bereits den Fehlergradienten aus der Lagekodierungsschicht, der nicht verloren gehen sollte. Daher müssen wir, bevor wir den Fehlergradienten vom lokalen Aufmerksamkeitsmodul weitergeben, die vorhandenen Informationen in einem temporären Speicherpuffer speichern.
An dieser Stelle ist es wichtig zu erwähnen, dass wir absichtlich einen dynamischen Zeiger auf das Datenspeicherpufferobjekt erstellt haben. Außerdem haben wir seine Größe dem Fehlergradientenpuffer der lokalen Probenteilungsschicht angepasst. So können wir einen einfachen Austausch von Zeigern auf Objekte vornehmen, anstatt Daten zu kopieren.
CBufferFloat *temp = caLocalPointNet[i].getGradient();
caLocalPointNet[i].SetGradient(cbTemp, false);
cbTemp = temp;
Jetzt können wir den Fehlergradienten sicher vom lokalen Aufmerksamkeitsmodul übertragen, ohne befürchten zu müssen, dass zuvor gespeicherte Daten verloren gehen.
if(!caLocalPointNet[i].calcHiddenGradients(caLocalAttention[i].AsObject())) return false; if(!SumAndNormilize(caLocalPointNet[i].getGradient(), cbTemp, caLocalPointNet[i].getGradient(), 64, false, 0, 0, 0, 1)) return false;
Dann summieren wir den Fehlergradienten aus den beiden Datensträngen.
Der nächste Schritt besteht darin, den Fehlergradienten auf die Ebene der Quelldaten zu übertragen. Aber auch hier gibt es eine Nuance. Je nach Iteration der Schleife wird der Fehlergradient an die globale Aufmerksamkeitsmodulschicht der vorherigen inneren Schicht oder an das in den Methodenparametern enthaltene Quelldatenobjekt weitergegeben. Im letzteren Fall ist der Algorithmus ähnlich wie die Methode der Elternklasse. Im ersten Fall sollten wir uns jedoch daran erinnern, dass wir den Fehlergradienten bereits bei der Dekonkatenierung der Daten aus dem Modul zur Erstellung des globalen Deskriptors der analysierten Datenwolke gespeichert haben. In diesem Fall ersetzen wir auch die Zeiger auf die Datenpuffer. Aus diesem Grund haben sie die gleiche Größe.
if(i > 0) { temp = inputs.getGradient(); inputs.SetGradient(cbTemp, false); cbTemp = temp; }
Als Nächstes wird geprüft, ob der Fehlergradient auf der Projektion des kanonischen Raums angepasst werden muss. Besteht kein Bedarf, wird der Farbverlauf sofort an das entsprechende Objekt übergeben.
if(!cTNetG || i > 0) { if(!inputs.calcHiddenGradients(caLocalPointNet[i].AsObject())) return false; }
Wurde die Projektion in den kanonischen Raum jedoch während des Vorwärtsdurchgangs durchgeführt, so wird der Fehlergradient zunächst an die Ebene des Projektionsschichtmoduls weitergegeben.
else { if(!cTurnedG) return false; if(!cTurnedG.calcHiddenGradients(caLocalPointNet[i].AsObject())) return false;
Dann verteilen wir den Fehlergradienten auf die Originaldaten und die Projektionsmatrix.
int window = (int)MathSqrt(cTNetG.Neurons()); if(IsStopped() || !MatMulGrad(inputs.getOutput(), inputs.getGradient(), cTNetG.getOutput(), cTNetG.getGradient(), cTurnedG.getGradient(), inputs.Neurons() / window, window, window)) return false;
Wir passen die Steigung der Projektionsmatrix an den Abweichungsfehler von der orthogonalen Matrix an.
if(!OrthoganalLoss(cTNetG, true)) return false;
Hier organisieren wir auch die Operationen, um die Datenpuffer zu tauschen, um Fehlergradienten von 2 Daten-Threads zu erhalten.
CBufferFloat *temp = inputs.getGradient(); inputs.SetGradient(cTurnedG.getGradient(), false); cTurnedG.SetGradient(temp, false);
Wir propagieren den Fehlergradienten vom Modul zur Erzeugung der Projektionsmatrix in den kanonischen Raum auf die Ebene der Originaldaten.
if(!inputs.calcHiddenGradients(cTNetG.AsObject())) return false;
Dann summieren wir den Fehlergradienten auf der Ebene der Ausgangsdaten aus 2 Datensträngen.
if(!SumAndNormilize(inputs.getGradient(), cTurnedG.getGradient(), inputs.getGradient(), 1, false, 0, 0, 0, 1)) return false; }
Als Nächstes ermitteln wir erneut die Notwendigkeit, den Fehlergradienten aus anderen Informationssträngen zu summieren, und ersetzen den Zeiger in der lokalen Variablen durch das Quelldatenobjekt. Dann geht es mit der nächsten Iteration der Schleife weiter.
if(i > 0) { if(!SumAndNormilize(inputs.getGradient(), cbTemp, inputs.getGradient(), 64, false, 0, 0, 0, 1)) return false; inputs = caGlobalAttention[i - 1].AsObject(); } else inputs = NeuronOCL; } //--- return true; }
Nach Abschluss aller Iterationen geben wir einen booleschen Wert an die aufrufende Funktion zurück, der den Erfolg der Gradientenverteilungsoperationen angibt, und beenden die Ausführung der Methode.
Damit vervollständigen wir den Überblick über die algorithmische Implementierung der Methoden in unserer neu entwickelten Klasse CNeuronPointFormer, die die von den Autoren der Methode Pointformer vorgeschlagenen Ansätze integriert. Der vollständige Code für diese Klasse und alle zugehörigen Methoden ist im Anhang verfügbar.
Wir gehen nun dazu über, die Modellarchitektur zu beschreiben, in die die neue Klasse integriert ist. Dieses Mal ist die Integration recht einfach. Wie zuvor wird die neue Klasse in das Encoder-Modell integriert, das Informationen über den Umweltzustand verarbeitet. Wir verwenden die gleiche Basisarchitektur wie im vorherigen Artikel. Die Modellarchitektur bleibt praktisch unverändert. Wir ersetzen nur den von der übergeordneten Klasse geerbten Ebenentyp durch unseren neu entwickelten, während wir alle anderen Parameter beibehalten. Eine solche Modifikation erfordert weder Änderungen an den Architekturen der Modelle von Akteur oder Kritiker, noch an den Trainingsalgorithmen oder den Interaktionsmechanismen mit der Umwelt. Diese Komponenten wurden ohne Änderungen wiederverwendet. Daher werden wir in diesem Artikel nicht näher auf sie eingehen. Die vollständige Architektur aller Modelle sowie der vollständige Quellcode aller Programme, die bei der Erstellung dieses Artikels verwendet wurden, sind im Anhang zu finden.
3. Tests
Wir haben erhebliche Anstrengungen unternommen, um unsere Interpretation der von den Autoren von Pointformer vorgeschlagenen Techniken mit MQL5 umzusetzen.
Es ist wichtig zu beachten, dass die in diesem Artikel vorgestellte Implementierung einige Unterschiede zum ursprünglichen Pointformer-Algorithmus aufweist. Daher können die von uns erzielten Ergebnisse bis zu einem gewissen Grad von den in der Originalstudie berichteten Ergebnissen abweichen.
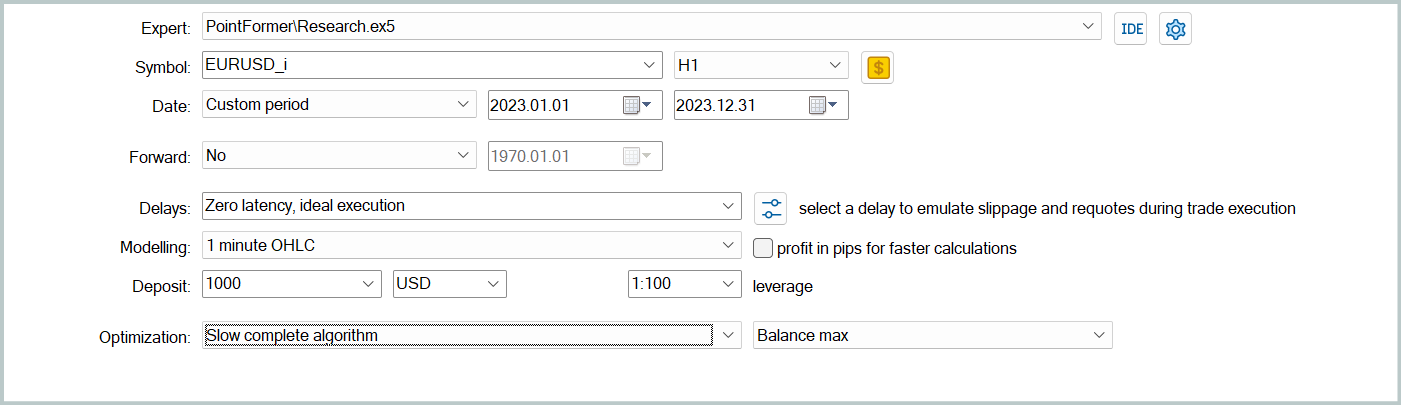
Nun ist es an der Zeit, die Ergebnisse unserer Umsetzung zu untersuchen. Wie in früheren Arbeiten haben wir die Modelle anhand realer historischer Daten von EURUSD für das Jahr 2023 mit dem Zeitrahmen H1 trainiert. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
Zunächst führten wir ein iteratives Offline-Training der Modelle durch, indem wir den Expert Advisor „...\PointFormer\Study.mq5“ im Echtzeitmodus ausführten. Dieser EA führt keine Handelsoperationen durch. Seine Logik ist ausschließlich auf das Training der Modelle ausgerichtet.
Die ersten Trainingsiterationen werden mit Daten durchgeführt, die während des Modelltrainings aus früheren Studien gesammelt wurden. Die Struktur und die Parameter der Trainingsdaten blieben unverändert.
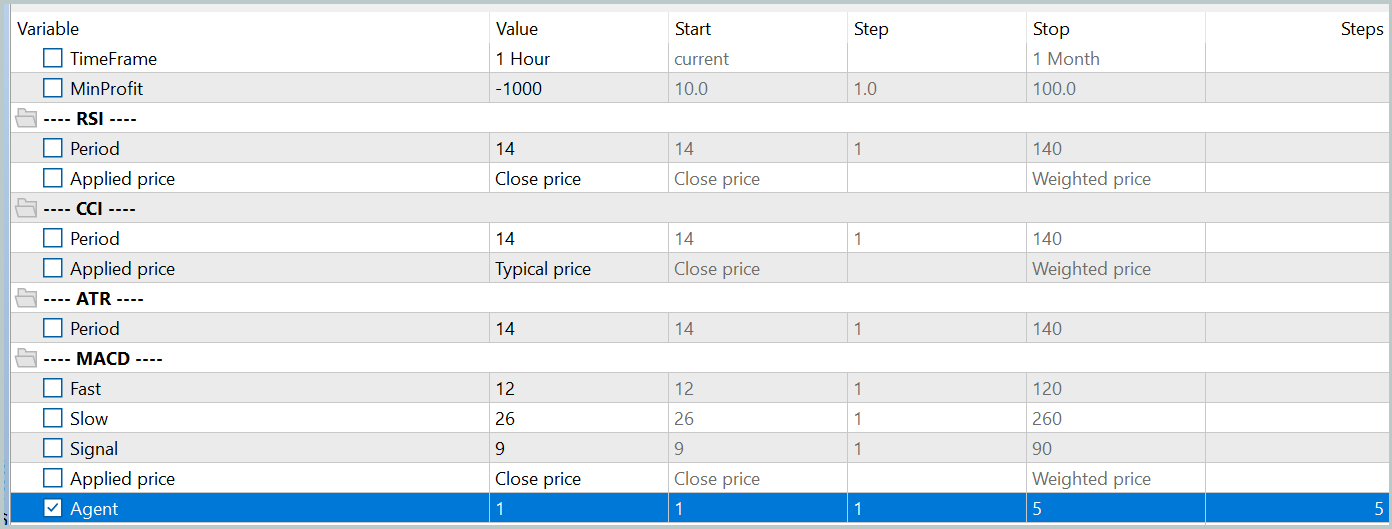
Anschließend aktualisieren wir den Trainingsdatensatz, um die aktuelle Handlungspolitik des Akteurs besser widerzuspiegeln. Dies ermöglicht eine genauere Bewertung seines Verhaltens während des Trainings und eine bessere Anpassung der Optimierungsrichtung der Strategie. Dazu starten wir im Strategy Tester einen langsamen Optimierungsmodus, indem wir die Umgebungsinteraktion Expert Advisor „...\PointFormer\Research.mq5“ verwenden.
Danach wiederholen wir den Prozess der Modellbildung.
Das Training der Modelle und die Aktualisierung des Trainingsdatensatzes werden iterativ über mehrere Zyklen durchgeführt. Ein guter Hinweis darauf, dass das Training abgeschlossen werden kann, ist das Erreichen akzeptabler Ergebnisse in allen Durchgängen der letzten Iteration der Datensatzaktualisierung.
Es sei darauf hingewiesen, dass geringfügige Abweichungen bei den Ergebnissen einzelner Durchgänge zulässig sind. Dies ist auf die Verwendung einer stochastischen Strategie durch den Akteur zurückzuführen, die natürlich eine gewisse Zufälligkeit in den Handlungen innerhalb des erlernten Verhaltensbereichs beinhaltet. Wenn die Modelle weiter trainieren, nimmt dieses stochastische Verhalten in der Regel ab. Eine gewisse Variabilität bei den Maßnahmen bleibt jedoch akzeptabel, wenn sie die Gesamtrentabilität der Politik nicht wesentlich beeinträchtigt.
Nach mehreren Iterationen des Modelltrainings und der Aktualisierung der Datensätze ist es uns gelungen, eine Strategie zu entwickeln, die sowohl in den Trainings- als auch in den Testdatensätzen Gewinne erzielt.
Wir bewerteten die Leistung des trainierten Modells mit dem MetaTrader 5 Strategy Tester, indem wir Tests mit historischen Daten vom Januar 2024 durchführten, während alle anderen Parameter unverändert blieben. Die Testergebnisse werden im Folgenden vorgestellt.
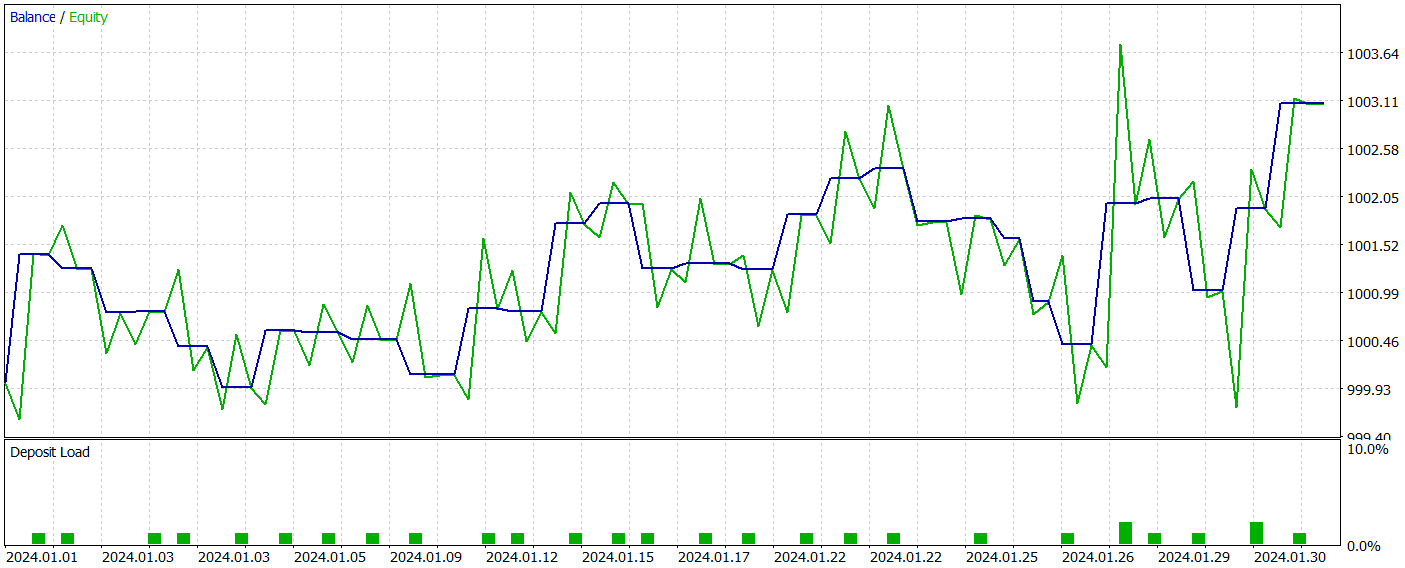
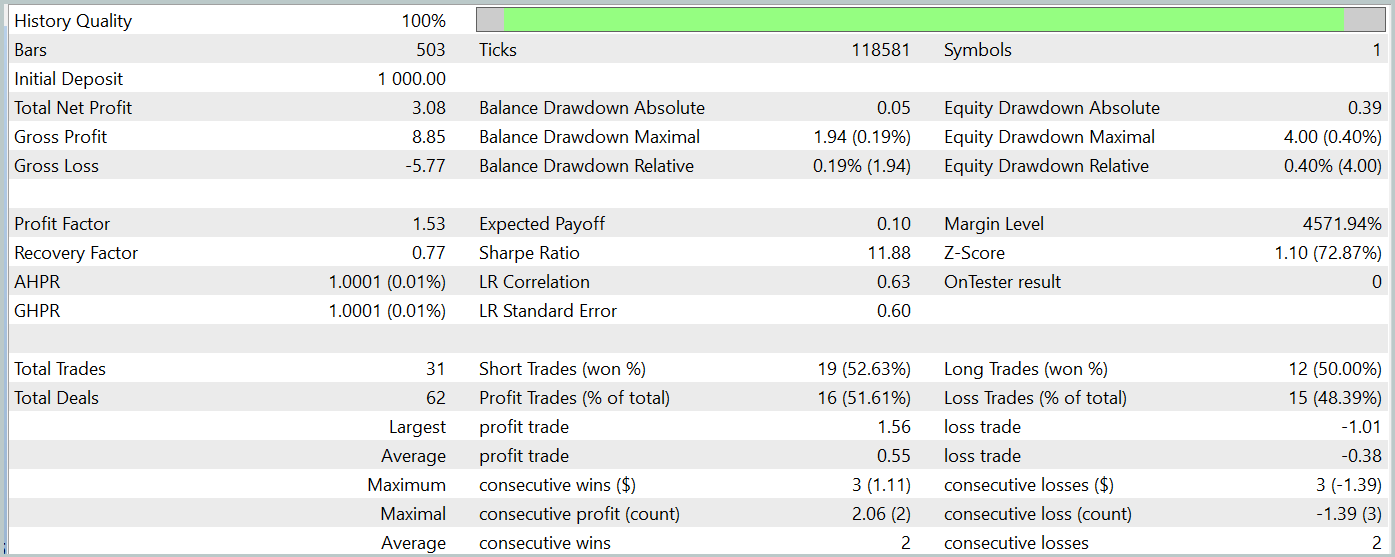
Während des Testzeitraums führte das trainierte Modell insgesamt 31 Handelsoperationen durch, von denen die Hälfte mit Gewinn abgeschlossen wurde. Ein um fast 50 % höherer Wert bei den maximal und durchschnittlich gewinnbringenden Geschäften im Vergleich zu den Verlusten führte zu einem Gewinnfaktor von 1,53. Trotz des beobachteten Aufwärtstrends der Aktienkurve können wir aufgrund der begrenzten Anzahl von Handelsgeschäften keine endgültigen Schlussfolgerungen über die Wirksamkeit des Modells über einen längeren Zeitraum ziehen.
Schlussfolgerung
In diesem Artikel haben wir die Methode Pointformer untersucht, die eine neue Architektur für die Arbeit mit Punktwolkendaten einführt. Der vorgeschlagene Algorithmus kombiniert lokale und globale Transformeren und ermöglicht die effektive Extraktion lokaler und globaler räumlicher Muster aus mehrdimensionalen Daten. Pointformer nutzt Aufmerksamkeitsmechanismen, um Informationen in Bezug auf den räumlichen Kontext zu verarbeiten, und unterstützt das Lernen unter Berücksichtigung der relativen Bedeutung der einzelnen Punkte.
Im praktischen Teil des Artikels haben wir unsere Vision der vorgeschlagenen Ansätze in der Sprache MQL5 umgesetzt. Wir haben das Modell auf der Grundlage der beschriebenen Algorithmen trainiert und getestet. Und die Ergebnisse zeigen das Potenzial der Methode für die Analyse komplexer Datenstrukturen.
Dennoch muss anerkannt werden, dass weitere Forschungs- und Optimierungsarbeiten erforderlich sind, um ein umfassenderes Verständnis der Fähigkeiten von Pointformer im Zusammenhang mit der Finanzdatenanalyse zu erlangen.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15820
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Anwendung der lokalisierten Merkmalsauswahl in Python und MQL5
Anwendung der lokalisierten Merkmalsauswahl in Python und MQL5
 Entwicklung eines Replay-Systems (Teil 64): Abspielen des Dienstes (V)
Entwicklung eines Replay-Systems (Teil 64): Abspielen des Dienstes (V)
 Entwicklung eines Replay-Systems (Teil 65): Abspielen des Dienstes (VI)
Entwicklung eines Replay-Systems (Teil 65): Abspielen des Dienstes (VI)
 Optimierung mit der bakteriellen Chemotaxis (BCO)
Optimierung mit der bakteriellen Chemotaxis (BCO)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
auf historischen Daten vom Januar 2024.
Warum erst im Januar, ist es nicht schon September? Oder ist damit gemeint, dass man jeden Monat neu trainieren muss?
Warum erst im Januar, es ist doch schon September? Oder heißt es, dass man jeden Monat umschulen muss?
Man kann ein Modell nicht auf der Grundlage von Daten aus einem Jahr trainieren und eine stabile Leistung über denselben oder einen längeren Zeitraum erwarten. Um eine stabile Modellleistung für 6-12 Monate zu erhalten, braucht man einen viel längeren Verlauf zum Trainieren. Folglich wird das Trainieren des Modells mehr Zeit und Kosten in Anspruch nehmen.