
群体优化算法:混合蛙跳算法(SFL)
目录
1. 概述
混合蛙跳(SFL)算法是由M.Eusuff 和其他一些作者在2003年提出的。该算法结合了模因算法和粒子群算法的原理,其设计灵感来自一群青蛙在觅食过程中的行为。
SFL算法最初是作为一种求解组合优化问题的元启发式方法而开发的。它是基于数学函数和启发式搜索的使用。
SFL算法由几个相互作用的虚拟青蛙种群组成,称为模因复合体。虚拟青蛙是模因的宿主或载体,模因代表了文化进化的一个单元。每个模因复合体都使用类似于粒子群优化的方法进行独立的局部搜索,但重点是局部搜索。
为了支持全局探索,虚拟青蛙被周期性地混洗,并使用类似于混洗复杂进化(Shuffled Complex Evolution,SCE)算法的方法重组为新的模因。此外,随机虚拟青蛙在种群中被生成和替换,以允许随机生成改进的信息。
混合蛙跳是解决复杂优化问题的一种有效方法,它可以在各种应用领域实现最佳解决方案。在本文中,我们将介绍该算法的基本原理和应用,以及它的优点和局限性。
2. 算法
模因学(Memetics)是一种基于模因概念的进化信息传递模型的方法。模因(Memes)是基因的类似物,通过模仿、学习和其他方式在人与人之间传播文化信息。模因的概念和模因学的基础是由C.R. Dawkins 在1976年提出的。模因可以垂直传播——来自前辈、父母、教育者、书籍、文化文物等。模因在人与人之间、文化与文化之间的横向传播也是可能的。尽管模因是纯粹的信息,但它们的功能会导致人类行为的重大变化。
模因算法(M-算法,M-algorithms)是基于模因概念和新达尔文主义进化原理的混合种群元启发式搜索引擎优化算法。在M-算法的上下文中,模因是局部优化算法的实现,该算法在每次迭代或一定次数的迭代后细化当前解。M-算法可以被视为一种基于群体的全局搜索算法和一种或多种经典的或基于群体的局部优化算法的混合。最初,M-算法被提出作为提高遗传算法效率的选项之一。
M-算法的效率很大程度上取决于其自由参数的值。大量研究表明,所用模因的选择对这些算法的效率有很大影响。因此,这个问题在专门研究M-算法的工作中占据了中心位置之一。
模因代表了革命性的思想之一,暗示了基因进化与人类文化进化之间的相似性。Dawkins 认为,模因是文化交流的一个单位,相当于文化中的基因。模因可以是一个手势、一个单词或一个想法。任何可以通过模仿学习在人与人之间传递的文化信息单位都是模因。
模因算法与遗传算法不同,它模仿文化进化的过程。莫斯卡托的方法使用了模因进化的类比。模因算法包括以下几个阶段:局部搜索、合作、竞争和搜索终止准则。模因类是一类广泛的算法,由一个共同的想法统一起来:将个体的个体学习纳入遗传算法,并使用关于可能解的空间结构的信息。平衡总体和局部搜索的问题可以被视为在搜索空间的广泛和密集探索之间保持平衡的一般问题。
模因算法大致包括以下组件:
1. 局部搜索,为了实现它,我们可以使用模拟退火和提升算法。
2. 合作,个体之间的信息交换可以通过类似于在遗传算法中使用两点交叉算子的程序来进行。
3. 竞争,选择与遗传算法中的选择相似,通常包括选择种群中最适者,并将不太适合的个体排除在外。
4. 搜索结束条件,在模因算法中,除了计算迭代次数和评估结果的改进外,这可能包括估计个体的多样性。
模因算法是一类广泛的算法,由个体的个体学习和使用关于可能解的空间结构的信息的共同思想结合在一起。
模因和基因一样,都是复制因子,即能够自我繁殖的物体。对于模因来说,生存和繁殖取决于传播模因的宿主的存在。模因可以改变,形成新的模因,并参与资源的争夺——人们的思想。
模因通常被组合成复合物或模因复合体,以加强对载体的争夺。模因复合体类似于构成生物遗传密码的基因的共生集合。模因复合体的一个例子是宗教。模因复合体对塑造个人和社会行为有着深远的影响。
让我们直接转到混合蛙跳算法。该算法的主要思想是将具有全局领头者G的整个青蛙种群划分为模因。每个模因(组)都有一个领头者L(图1)。

图1. 有全局领头者(G)的青蛙种群,划分为具有局部领头者(L)的模因
在每一个模因中,青蛙都倾向于向局部领头者的方向移动。如果其中一只青蛙的位置有所提高,则会更新领头者。模因在搜索空间中不分离,并且可能有重叠。因此,一只位于一个模因范围内的青蛙很可能属于另一个。这创造了一个动态的环境,青蛙可以根据它们在搜索空间中的位置变化,在空间上从一个模因移动到另一个。
我们考虑一个全局条件优化问题,其中适应度函数服从最大化。SFL算法包括以下基本步骤。
1.0 算法初始化
1.1 创建具有随机坐标的初始青蛙种群。
1.2 确定每只青蛙的适合度。
1.3 模因复合体(亚群)的创建,青蛙在模因复合体中的分布。
2.0 搜索最佳解决方案的循环
2.1 对于每个模因复合体:
2.1.1 确定最佳青蛙。
2.1.2 将剩余的青蛙移向模因复合体中最好的青蛙。
2.2 如果移动青蛙并不能改善其适应度:
2.2.1 把它移向全局更好的青蛙。
2.2.2 如果还是不能提高适应度,就将青蛙移动到场地上的一个随机位置。
3.0 测量青蛙的适应度
3.1 测量种群中每只青蛙的适应度。
3.2 更新每个模因复合体和整个种群中最好的青蛙的信息。
4.0 确定全局最佳青蛙并更新模因
4.1 为整个种群确定全局最佳青蛙。
4.2 如果这是最后一个循环:
4.2.1 重置模因复合体循环计数器。
4.2.2 为青蛙生成随机索引。
4.2.3 使用新索引将青蛙复制到模因复合体中。
4.2.4 确定每个模因复合体中的最佳青蛙。
4.2.5 重置蛙类的适应度和步幅。
4.3 如果这不是最后一个循环:
4.3.1 将种群中青蛙的适应度和坐标复制到相应的模因复合体蛙中。
4.3.2 确定每个模因复合体中的最佳青蛙。
4.3.3 根据每只青蛙的适应度,确定下一次跳跃的方向。
因此,SFL算法的基础是每个模因复合体内的局部搜索和通过交换关于最佳模因复合体代理的位置的信息进行的全局搜索的组合。
该算法是对SFL算法的修改,在该算法中,在局部搜索阶段,代理并不完全朝着相应模因复合体的最佳代理的方向移动,而是朝着一些随机扰动的方向移动。该算法与许多群体算法(包括人工免疫系统算法)的顺序和并行杂交都是已知的。
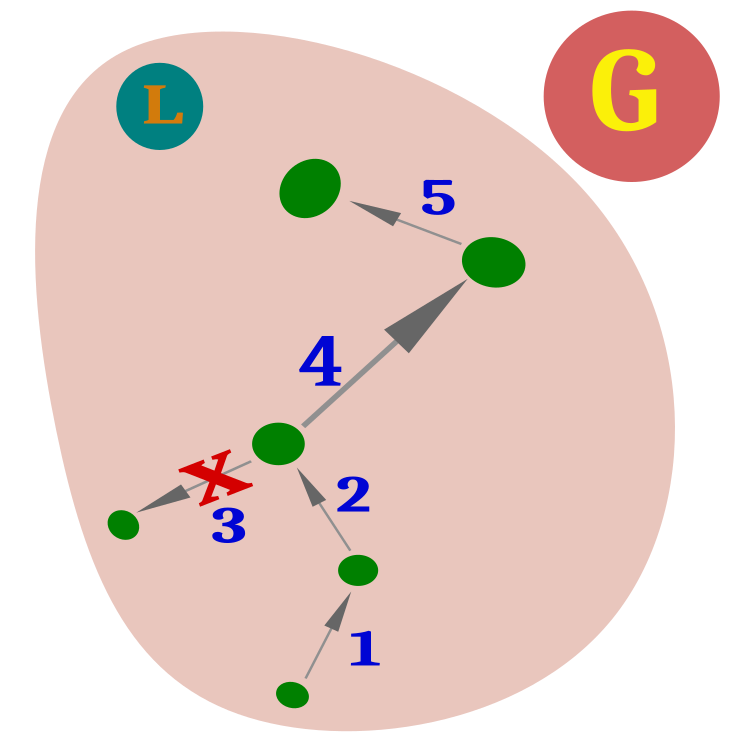
图 2青蛙跳跃。如果上一步没有成功,那么下一步将从同一个地方跳
SFL优化算法的逻辑单元是青蛙。它可以用 S_Frog 结构来描述,该结构表示搜索空间中的代理。
S_Frog 结构包含以下字段:
- c - 青蛙当前位置的坐标数组。
- cPrev - 青蛙先前位置的坐标数组。
- f - 青蛙当前位置的适应度函数。
- fPrev - 青蛙先前位置的适应度函数。
- frogStep - 青蛙所在步骤的编号。
//—————————————————————————————————————————————————————————————————————————————— struct S_Frog { void Init (int coords) { ArrayResize (c, coords); ArrayResize (cPrev, coords); f = -DBL_MAX; fPrev = -DBL_MAX; frogStep = 0; } double c []; //coordinates double cPrev []; //previous coordinates double f; //fitness double fPrev; //previous fitness int frogStep; //frog step }; //——————————————————————————————————————————————————————————————————————————————
S_Memeplex结构描述了算法中的模因复合体。它包含以下字段:
- frogs - 组成模因复合体的青蛙数组。
- fBest - 模因复合体中所有青蛙的适应度函数的最佳值。
- cBest - 与模因复合体中的适应度函数的最佳值相对应的坐标数组。
//—————————————————————————————————————————————————————————————————————————————— struct S_Memeplex { S_Frog frogs []; double fBest; //best fitness double cBest []; //best coordinates }; //——————————————————————————————————————————————————————————————————————————————
C_AO_SFL类提供了初始化算法、移动蛙类和修改种群的方法。它还包含用于转换值和生成随机数的辅助方法。
让我们编写包含以下字段的SFL算法类:
- cB - 存储最佳坐标的数组;
- fB - 存储最佳坐标的适应度函数值的变量;
- frogs - 存储种群中所有青蛙的数组;
- mems - 存储模因(青蛙组)的数组;
- rangeMax - 存储每个搜索坐标的最大值的数组;
- rangeMin - 存储每个搜索坐标的最小值的数组;
- rangeStep - 存储每个坐标的搜索步骤。
公有类方法:
- Init - 用于初始化算法参数的方法,接受以下参数:
- coordinatesNumberP - 搜索坐标的数量;
- populationSizeP - 种群规模(青蛙数量);
- numbMemsP - 模因的数量(青蛙群);
- numbCyclesP - 模因复合体中的循环数;
- frogStepsToLocalMaxP - 蛙步数达到局部最大值;
- movConstantP - 青蛙的位移常数(搜索步长)。
Moving - 实现青蛙在搜索空间中移动的方法。
Revision - 实现对青蛙种群的修改并更新最佳坐标的方法。
SeInDiSp - 通过给定步骤将值从一个范围转换为另一个范围的辅助方法。
RNDfromCI - 在给定间隔内生成随机数的辅助方法。
私有类字段的描述:
- coordinatesNumber - 搜索坐标的数量;
- frogsNumber - 种群中青蛙的数量;
- numbMems - 模因的数量(青蛙群);
- numbCycles - 模因复合体中的循环数;
- frogStepsToLocalMax - 蛙步数达到局部最大值;
- movConstant - 蛙类的位移常数(搜索步长);
- memsFrogs - 每个模因复合体中的青蛙数量;
- numbCyclesCNT - 循环计数器;
- vect - 存储向量的数组;
- indexes - 存储索引的数组;
- revision - 指示需要进行总体修订的标志。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_SFL { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Frog frogs []; //all frogs public: S_Memeplex mems []; //memeplexes public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordinatesNumberP, //coordinates number const int populationSizeP, //population size const int numbMemsP, //number of memeplexes const int numbCyclesP, //number of cycles in the memeplex const int frogStepsToLocalMaxP, //frog steps to the local maximum const double movConstantP); //movement step (0.0 .. 1.0) public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coordinatesNumber; //coordinates number private: int frogsNumber; //frogs number private: int numbMems; //number of memeplexes private: int numbCycles; //number of cycles in the memeplex private: int frogStepsToLocalMax; //frog steps to the local maximum private: double movConstant; //movement step (0.0 .. 1.0) private: int memsFrogs; //number of frogs in the memplex private: int numbCyclesCNT; //cycle counter private: double vect []; //vector private: int indexes []; //indexes private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
要初始化算法,我们将使用Init初始化方法,该方法有几个参数:
- coordinatesNumberP - 坐标数量
- populationSizeP - 种群规模
- numbMemsP - 模因复合体数量
- numbCyclesP - 模因复合体中的循环数
- frogStepsToLocalMaxP - 局部最大蛙步数
- movConstantP - 移动步长(从0.0到1.0)
首先,该方法重置随机数生成器,并设置fB(-DBL_MAX)和revision(false)变量的初始值
接下来,该方法创建具有所需大小的rangeMax、rangeMin、rangeStep、vect、indexes、cB、frogs和mems数组。该方法使用传递坐标数的Init方法初始化frogs数组中的每个青蛙和mems数组中每个模因复合体中的每个青蛙。
然后,该方法在-DBL_MAX中设置每个模因复合体的fBest变量的初始值,并为每个具有所需大小的模因复合体创建cBest数组。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SFL::Init (const int coordinatesNumberP, //coordinates number const int populationSizeP, //population size const int numbMemsP, //number of memeplexes const int numbCyclesP, //number of cycles in the memeplex const int frogStepsToLocalMaxP, //frog steps to the local maximum const double movConstantP) //movement step (0.0 .. 1.0) { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coordinatesNumber = coordinatesNumberP; frogsNumber = populationSizeP; numbMems = numbMemsP; numbCycles = numbCyclesP; frogStepsToLocalMax = frogStepsToLocalMaxP; movConstant = movConstantP; memsFrogs = frogsNumber / numbMems; numbCyclesCNT = 0; ArrayResize (rangeMax, coordinatesNumber); ArrayResize (rangeMin, coordinatesNumber); ArrayResize (rangeStep, coordinatesNumber); ArrayResize (vect, coordinatesNumber); ArrayResize (indexes, frogsNumber); ArrayResize (cB, coordinatesNumber); ArrayResize (frogs, frogsNumber); for (int i = 0; i < frogsNumber; i++) { frogs [i].Init (coordinatesNumber); } ArrayResize (mems, numbMems); for (int i = 0; i < numbMems; i++) { ArrayResize (mems [i].frogs, memsFrogs); for (int frgs = 0; frgs < memsFrogs; frgs++) { mems [i].frogs [frgs].Init (coordinatesNumber); } mems [i].fBest = -DBL_MAX; ArrayResize (mems [i].cBest, coordinatesNumber); } } //——————————————————————————————————————————————————————————————————————————————
Moving方法用于在搜索空间中移动青蛙。这个方法相当大,所以我们将分部分进行分析。
在代码的开头,我们检查revision变量的值,如果为“false”,则执行以下代码块:
- 设置fB变量初始值,该值表示函数的最佳估计值。在这种情况下,将为其指定-DBL_MAX值(负无穷大)。
- 启动循环,在其中会初始化每个青蛙。对于每只青蛙:
- 为每个c坐标启动循环。
- 使用RNDfromCI函数为c坐标生成一个随机值,该函数返回给定范围内的随机数。
- c坐标值使用SeInDiSp函数转换为范围,该函数允许您在某个范围内按特定步长移动值。
- 青蛙的f函数值设置为-DBL_MAX。
- 将青蛙的前一个fPrev函数值设置为-DBL_MAX。
- frogStep设置为0。
- 为每个c坐标启动循环。
- 计算vect[c],这是movConstant范围的最大值和最小值之差的乘积。
- revision变量设置为“true”,表示初始化已完成。
- numbCyclesCNT变量设置为0。
因此,此代码初始化青蛙,设置函数和其他参数的初始值,还计算每个c坐标的vect[c]值。
if (!revision) { fB = -DBL_MAX; for (int frgs = 0; frgs < frogsNumber; frgs++) { for (int c = 0; c < coordinatesNumber; c++) { frogs [frgs].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); frogs [frgs].c [c] = SeInDiSp (frogs [frgs].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); frogs [frgs].f = -DBL_MAX; frogs [frgs].fPrev = -DBL_MAX; frogs [frgs].frogStep = 0; } } for (int c = 0; c < coordinatesNumber; c++) { vect [c] = (rangeMax [c] - rangeMin [c]) * movConstant; } revision = true; numbCyclesCNT = 0; }
如果revision标志为“true”,则表示算法已进入移动青蛙的阶段。我们已经熟悉了方法变量,所以我们不再详细讨论它们。这部分代码根据每只青蛙的单个步骤实现蛙跳。在第一步中,青蛙向局部领头蛙跳跃,如果青蛙的位置有所改善,则计算尝试次数,否则增加步数。换言之,根据算法的外部参数,分配固定次数的尝试以向局部领头蛙跳跃。
对于领头蛙,使用了不同的运动原理,与模因复合体中的所有其他原理不同。领头蛙只是在其位置附近的一个小范围内随机跳跃。
与领头蛙不同,所有其他青蛙都会根据以下等式向领头羊跳跃:
该算式表明,青蛙的新坐标将通过向领头蛙移动它们之间的距离来获得,归一化为所有坐标的欧几里得距离,同时引入rnd随机分量。coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance);
else { int cnt = 0; double eDistance = 0.0; //euclidean distance double coordDiff = 0.0; //the difference in coordinates for (int m = 0; m < numbMems; m++) { for (int frgs = 0; frgs < memsFrogs; frgs++) { //2.1 move the frogs towards the best one in the memeplex----------------- if (mems [m].frogs [frgs].frogStep < frogStepsToLocalMax) { if (mems [m].frogs [frgs].fPrev != -DBL_MAX && mems [m].fBest != -DBL_MAX) { if (mems [m].frogs [frgs].fPrev == mems [m].fBest) { for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd; coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * 0.2; mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } else { eDistance = 0.0; coordDiff = 0.0; //calculate Euclidean distance---------------------------------- for (int c = 0; c < coordinatesNumber; c++) { coordDiff = mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]; coordDiff *= coordDiff; eDistance += coordDiff; } eDistance = sqrt (eDistance); for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((mems [m].cBest [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance); mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } } else { for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); rnd = rnd < 0.0 ? -rnd * rnd : rnd * rnd; coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c]; mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } } else { //2.2 move towards global if the move is worse than the previous one----- if (mems [m].frogs [frgs].frogStep /*==*/ >= frogStepsToLocalMax) { eDistance = 0.0; coordDiff = 0.0; //calculate Euclidean distance------------------------------------ for (int c = 0; c < coordinatesNumber; c++) { coordDiff = cB [c] - mems [m].frogs [frgs].cPrev [c]; coordDiff *= coordDiff; eDistance += coordDiff; } eDistance = sqrt (eDistance); for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); coord = mems [m].frogs [frgs].cPrev [c] + rnd * vect [c] * ((cB [c] - mems [m].frogs [frgs].cPrev [c]) / eDistance); mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } //2.3 move randomly across the field -------------------------------- else { for (int c = 0; c < coordinatesNumber; c++) { rnd = RNDfromCI (-1.0, 1.0); coord = RNDfromCI (rangeMin [c], rangeMax [c]); mems [m].frogs [frgs].c [c] = SeInDiSp (coord, rangeMin [c], rangeMax [c], rangeStep [c]); } } } frogs [cnt] = mems [m].frogs [frgs]; cnt++; } } //-------------------------------------------------------------------------- numbCyclesCNT++; }
Revision方法设计用于在算法的每次迭代中确定全局领头蛙,并确定局部领头蛙。如果分配给青蛙在每个模因复合体中移动的循环数用完,那么我们执行一次混洗——我们将青蛙随机重新分配给模因复合体,从而在模因复合体之间交换信息。这种方法还考虑了相应的跳跃步骤——青蛙在下一次迭代时的移动方向(朝向局部或全局领头蛙,或在搜索空间中的随机方向)。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_SFL::Revision () { //4.1 determine the globally best one by population------------------------------- for (int i = 0; i < frogsNumber; i++) { if (frogs [i].f > fB) { fB = frogs [i].f; ArrayCopy (cB, frogs [i].c, 0, 0, WHOLE_ARRAY); } } int cnt = 0; //if the last loop========================================================= if (numbCyclesCNT >= numbCycles) { //4.2.0 reset the memeplex cycle counter----------------------------------- numbCyclesCNT = 0; //4.2.1 generate random indices-------------------------------------- for (int i = 0; i < frogsNumber; i++) indexes [i] = i; Shuffle (indexes, frogsNumber); //4.2.2 copy to memeplexes accidentally------------------------------------ for (int m = 0; m < numbMems; m++) { mems [m].fBest = -DBL_MAX; for (int frgs = 0; frgs < memsFrogs; frgs++) { mems [m].frogs [frgs] = frogs [indexes [cnt]]; cnt++; //4.2.3 determine the best one in each memeplex--------------------------- if (mems [m].frogs [frgs].f > mems [m].fBest) { mems [m].fBest = mems [m].frogs [frgs].f; ArrayCopy (mems [m].cBest, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY); } //4.2.4 reset frogs' fitness and step------------------------ mems [m].frogs [frgs].f = -DBL_MAX; mems [m].frogs [frgs].fPrev = -DBL_MAX; mems [m].frogs [frgs].frogStep = 0; } } } //if NOT the last cycle====================================================== else { for (int m = 0; m < numbMems; m++) { for (int frgs = 0; frgs < memsFrogs; frgs++) { mems [m].frogs [frgs].frogStep++; //4.3.1 copy the fitness and coordinates of frogs from the population to the //corresponding frog memeplexes mems [m].frogs [frgs].f = frogs [cnt].f; ArrayCopy (mems [m].frogs [frgs].c, frogs [cnt].c, 0, 0, WHOLE_ARRAY); //4.3.2 determine the best one in each memeplex--------------------------- if (frogs [cnt].f > mems [m].fBest) { mems [m].fBest = frogs [cnt].f; ArrayCopy (mems [m].cBest, frogs [cnt].c, 0, 0, WHOLE_ARRAY); } //4.3.3 determine the direction of the next jump------------------------ if (mems [m].frogs [frgs].frogStep <= frogStepsToLocalMax) { if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev) { mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f; ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY); mems [m].frogs [frgs].frogStep = 0; } } else { if (mems [m].frogs [frgs].frogStep >= frogStepsToLocalMax + 1) { if (mems [m].frogs [frgs].f > mems [m].frogs [frgs].fPrev) { mems [m].frogs [frgs].fPrev = mems [m].frogs [frgs].f; ArrayCopy (mems [m].frogs [frgs].cPrev, mems [m].frogs [frgs].c, 0, 0, WHOLE_ARRAY); mems [m].frogs [frgs].frogStep = 0; } } else { mems [m].frogs [frgs].f = -DBL_MAX; mems [m].frogs [frgs].fPrev = -DBL_MAX; mems [m].frogs [frgs].frogStep = 0; } } cnt++; } } } } //——————————————————————————————————————————————————————————————————————————————
在SFL优化算法中,我们需要在模因之间随机混合青蛙。随机混洗问题之所以有趣,是因为它的算法解决方案并不平凡,但 Ronald Fisher 和 Frank Yates 提供了一种有效而快速的算法。以前,我们没有使用类似的概念,因为没有必要。它被广泛应用于计算机科学,特别是在遗传算法、密码学和统计学领域。
Fisher Yates算法的主要优点:
1. 易于实现:Fisher Yates算法易于在任何编程语言中实现。它不需要复杂的数学计算或特殊的库。
2. 效率:Fisher-Yates算法在线性时间内运行。换句话说,执行时间取决于需要重新排列的元素的数量。这使得它对于大型数据集非常有效。
3. 随机性:Fisher-Yates算法确保了高度随机的排列。这对于许多应用程序(如随机测试、加密和模拟)都很重要。
4. 输入独立性:Fisher-Yates算法可以应用于任何数据集,而无需知道其结构或属性。这使它成为许多任务的通用工具。
5. 伪随机性:Fisher-Yates 算法生成伪随机排列,可用于许多需要随机性(但不一定是真随机性)的应用中。
总体而言,Fisher-Yates算法简单、高效且通用。对于涉及随机性和数据替换的许多问题,它是一个有用的工具。
//—————————————————————————————————————————————————————————————————————————————— void Shuffle (int & arr [], int size) { int index, temp; for (int i = size - 1; i > 0; i--) { index = MathRand () % (i + 1); temp = arr [i]; arr [i] = arr [index]; arr [index] = temp; } } //——————————————————————————————————————————————————————————————————————————————
3. 测试结果
SFL 试验结果:
C_AO_SFL:50;25;15;5;0.7
=============================
5 Rastrigin's; Func runs 10000 result: 66.52578871476199
Score: 0.82429
25 Rastrigin's; Func runs 10000 result: 52.38937199890908
Score: 0.64913
500 Rastrigin's; Func runs 10000 result: 44.5591163558836
Score: 0.55211
=============================
5 Forest's; Func runs 10000 result: 0.5762718670482314
Score: 0.32597
25 Forest's; Func runs 10000 result: 0.16329693292687839
Score: 0.09237
500 Forest's; Func runs 10000 result: 0.04968320483668511
Score: 0.02810
=============================
5 Megacity's; Func runs 10000 result: 3.1599999999999997
Score: 0.26333
25 Megacity's; Func runs 10000 result: 1.016
Score: 0.08467
500 Megacity's; Func runs 10000 result: 0.3004
Score: 0.02503
=============================
All score: 2.84501
当观察SFL算法的动画时,没有检测到单个模因的聚类或分组,尽管预期会相反。优化代理(点)在整个场中无序分布,粒子的运动没有模式。该算法的低收敛质量是显而易见的,表现为陷入局部极值,局部极值可以由收敛图上的长光滑部分决定。然而,随着优化参数数量的增加,“步进”会减少。
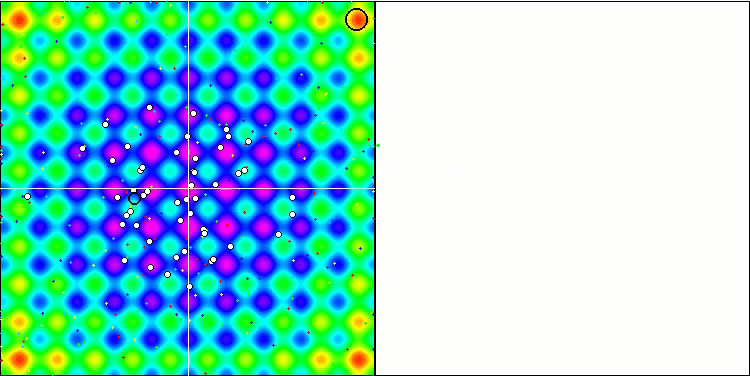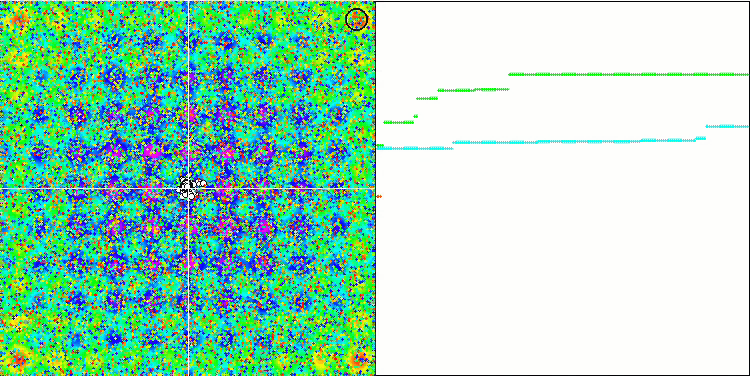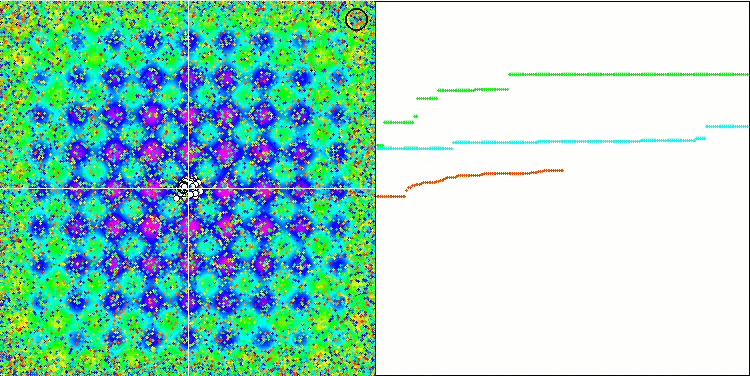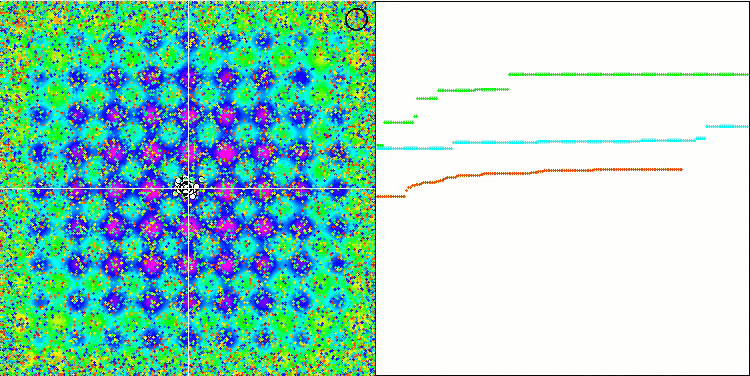
Rastrigin测试函数上的SFL。
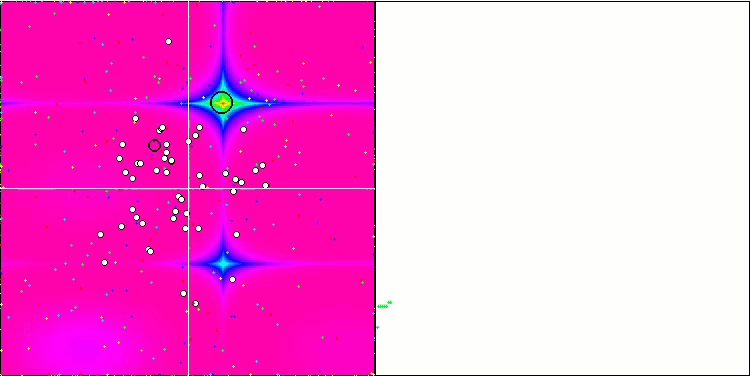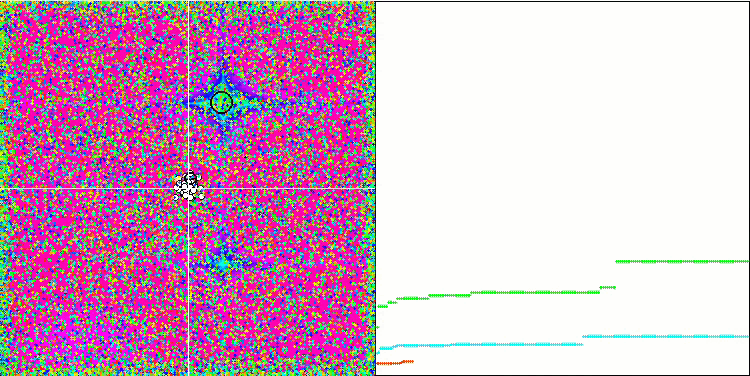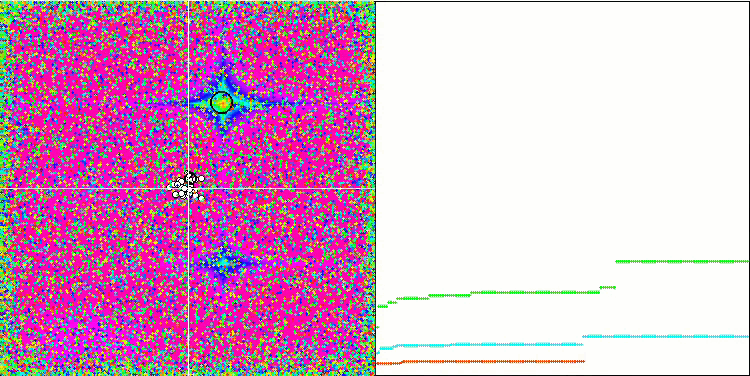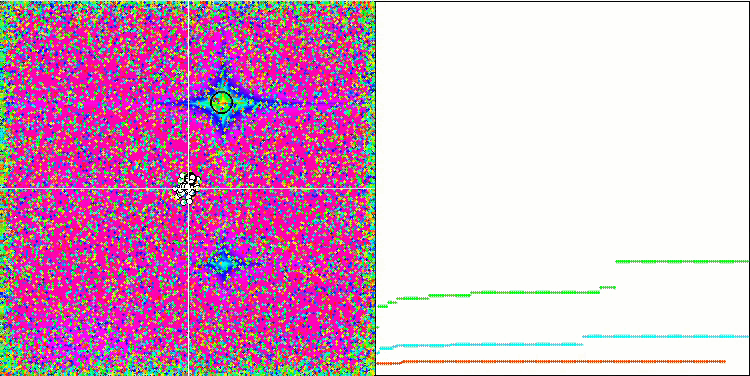
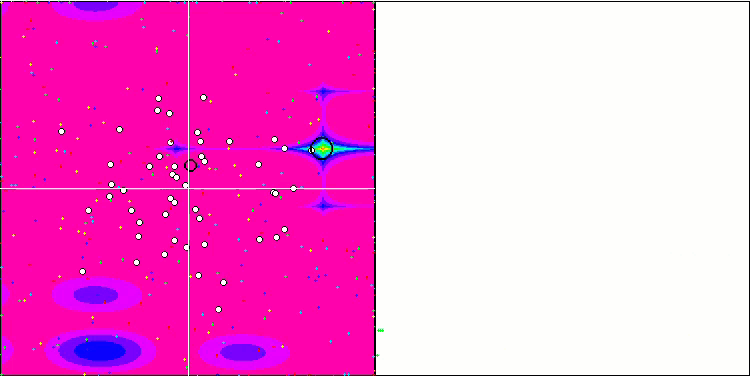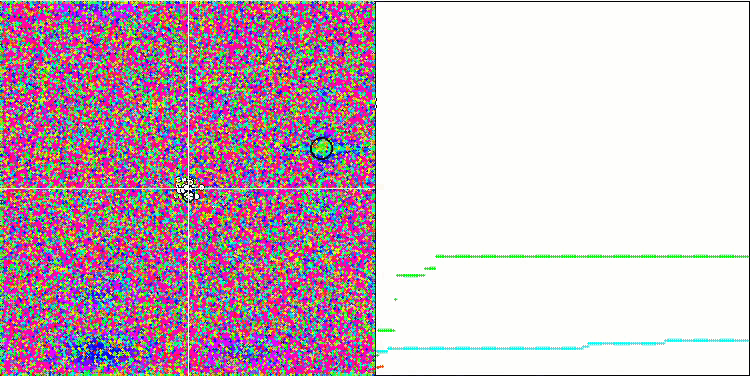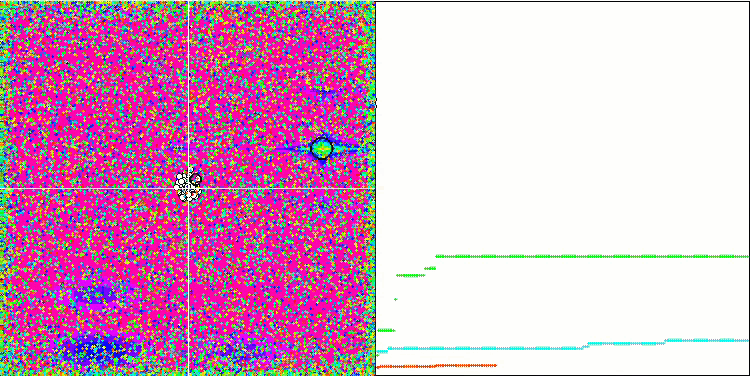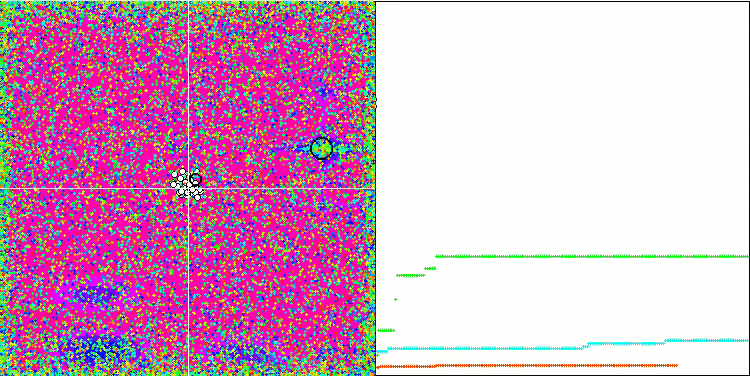
Forest测试函数上的SFL。
Megacity 测试函数上的SFL。
现在是下结论的时候了。根据结果表,SFL算法在优化方面显示出低于平均水平的结果。尽管SFL在光滑Rastrigin函数上有一些优势,但仅推荐它作为光滑函数的首选算法是不够的。在 Forest 和 Megacity 弯曲函数上,与光滑函数相比,SFL表现出更差的结果。这可以解释为,在优化函数的平坦部分,跳跃的青蛙不会提高它们的位置,并不断返回到原来的位置,而无法在地形上“捕捉”。
| AO | 描述 | Rastrigin | Rastrigin 最终 | Forest | Forest 最终 | Megacity (discrete) | Megacity 最终 | 最终结果 | ||||||
| 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params (500 F) | ||||||
| SSG | 树苗播种和生长(saplings sowing and growing) | 1.00000 | 1.00000 | 0.55665 | 2.55665 | 0.72740 | 0.94522 | 1.00000 | 2.67262 | 0.76364 | 0.85977 | 1.00000 | 2.62340 | 100.000 |
| HS | 和声搜索(harmony search) | 0.99676 | 0.95282 | 0.48178 | 2.43136 | 1.00000 | 0.98931 | 0.44806 | 2.43736 | 1.00000 | 1.00000 | 0.41537 | 2.41537 | 92.329 |
| ACOm | 蚁群优化M(ant colony optimization M) | 0.34611 | 0.17985 | 0.17044 | 0.69640 | 0.86888 | 1.00000 | 0.77362 | 2.64249 | 1.00000 | 0.88930 | 0.05606 | 1.94536 | 65.347 |
| IWO | 入侵性杂草优化(invasive weed optimization) | 0.95828 | 0.67083 | 0.29807 | 1.92719 | 0.70773 | 0.46349 | 0.31773 | 1.48896 | 0.80000 | 0.42067 | 0.33289 | 1.55356 | 61.104 |
| COAm | 布谷鸟优化算法M(COAm) | 0.92400 | 0.46794 | 0.26004 | 1.65199 | 0.58378 | 0.34034 | 0.16526 | 1.08939 | 0.72727 | 0.33025 | 0.17083 | 1.22835 | 47.612 |
| FAm | 萤火虫算法M(firefly algorithm M) | 0.59825 | 0.33980 | 0.17135 | 1.10941 | 0.51073 | 0.42299 | 0.49790 | 1.43161 | 0.34545 | 0.28044 | 0.35258 | 0.97847 | 41.537 |
| ABC | 人工蜂群(artificial bee colony) | 0.78170 | 0.32715 | 0.20822 | 1.31707 | 0.53837 | 0.21455 | 0.13344 | 0.88636 | 0.56364 | 0.26569 | 0.13926 | 0.96858 | 36.849 |
| GSA | 重力搜索算法(gravitational search algorithm) | 0.70167 | 0.45217 | 0.00000 | 1.15384 | 0.31660 | 0.36416 | 0.33204 | 1.01280 | 0.59395 | 0.35054 | 0.00000 | 0.94448 | 36.028 |
| BA | 蝙蝠算法(bat algorithm) | 0.40526 | 0.63761 | 0.84451 | 1.88738 | 0.20841 | 0.17477 | 0.25989 | 0.64308 | 0.29698 | 0.09963 | 0.17371 | 0.57032 | 35.888 |
| BFO | 细菌觅食优化(bacterial foraging optimization) | 0.67203 | 0.30963 | 0.11813 | 1.09979 | 0.39702 | 0.26623 | 0.20652 | 0.86976 | 0.52122 | 0.33211 | 0.18932 | 1.04264 | 34.693 |
| EM | 类电磁算法(electroMagnetism-like algorithm) | 0.12235 | 0.46278 | 1.00000 | 1.58513 | 0.00000 | 0.03498 | 0.34880 | 0.38377 | 0.00000 | 0.00000 | 0.10924 | 0.10924 | 22.091 |
| SFL | 混合蛙跳(shuffled frog-leaping) | 0.40072 | 0.23739 | 0.26548 | 0.90360 | 0.20153 | 0.04147 | 0.02652 | 0.26952 | 0.27273 | 0.05535 | 0.06639 | 0.39446 | 15.203 |
| MA | 猴子算法(monkey algorithm) | 0.33192 | 0.33451 | 0.14644 | 0.81287 | 0.10012 | 0.07891 | 0.08932 | 0.26836 | 0.21818 | 0.04243 | 0.10720 | 0.36781 | 13.603 |
| FSS | 鱼群搜索(fish school search) | 0.46812 | 0.25337 | 0.11302 | 0.83451 | 0.12840 | 0.05013 | 0.06516 | 0.24369 | 0.16971 | 0.04796 | 0.08283 | 0.30050 | 12.655 |
| PSO | 粒子群优化(particle swarm optimisation) | 0.20449 | 0.08200 | 0.07160 | 0.35809 | 0.18895 | 0.10486 | 0.21738 | 0.51119 | 0.23636 | 0.05903 | 0.01957 | 0.31496 | 10.031 |
| RND | 随机(random) | 0.16826 | 0.09743 | 0.08019 | 0.34589 | 0.13496 | 0.04810 | 0.04715 | 0.23021 | 0.16971 | 0.03875 | 0.04922 | 0.25767 | 5.302 |
| GWO | 灰狼优化器(grey wolf optimizer) | 0.00000 | 0.00000 | 0.02256 | 0.02256 | 0.06570 | 0.00000 | 0.00000 | 0.06570 | 0.32727 | 0.07378 | 0.02557 | 0.42663 | 1.000 |
总结
SFL更像是其他优化算法的“上层建筑”,可以用作在模因复合体中移动代理的逻辑。SFL最初是作为一种提高现有算法优化质量的技术而发明的。作为一种独立的优化算法,SFL在前面讨论的总体算法中表现出低于平均水平的结果。SFL在将逻辑步骤组合到算法中以增强探索和开发方面具有巨大的实验潜力。SFL具有高度的灵活性和适应性,适用于特定优化问题中的特定用途。
算法测试结果的直方图如下所示(从0到100,越多越好,在档案中有一个脚本,用于使用这篇文章中描述的方法计算评级表)。
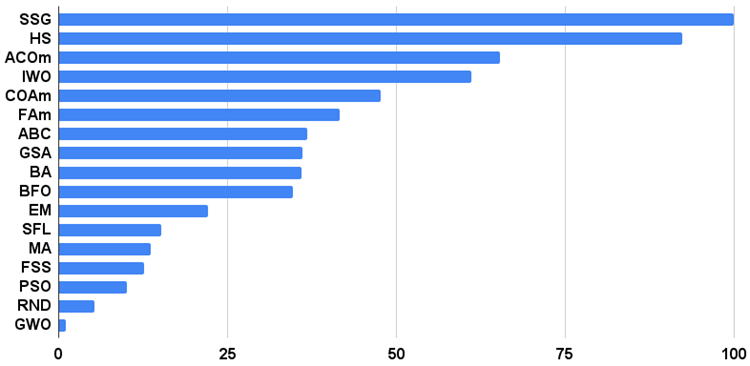
图3. 测试算法最终结果的直方图
混合蛙跳(SFL)算法的优点和缺点:
1. 外部参数的数量少。
2. 算法架构的独创性,在模因中使用其他优化算法的能力。
缺点:
1. 计算复杂度高。
2. 平滑和离散函数的结果较差。
3. 在过于水平的“平板”上功能会卡住
每一篇文章都有一个归档,其中包含以前所有文章的算法代码的最新版本。本文以作者积累的经验为基础,代表作者的个人观点。结论和判断是基于实验得出的。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/13366
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 神经网络变得简单(第 59 部分):控制二分法(DoC)
神经网络变得简单(第 59 部分):控制二分法(DoC)
 为 Metatrader 5 开发MQTT客户端:TDD方法——第4部分
为 Metatrader 5 开发MQTT客户端:TDD方法——第4部分
我只是画了个草图,因为如果我要制作一些装置,就应该没有潜在的问题--我被使用字符串搜索的循环 "迷住了"(!)--在大型程序中,它的效率可能超级低。
ini 文件不仅包含字符串参数,还包含其他类型的参数(尽管它们用文本表示)。
在工厂中使用单例就可以了。函数对象中的单例--在本例中只是为了示例的可操作性--可以实现多重性。
我在初始化阶段使用字符串解析。我认为这只需要不到一毫秒的时间。老实说,我没有感觉到任何潜在的问题。
感谢作者的出色工作和无偿使用的机会!
我正在研究一下代码。并用这样一个恐怖的东西取代了这个美丽的东西。
增益是多少?真的太可怕了。抱歉,如果有的话))
按理说,根据请求创建函数应该在类本身中进行(而不是在类名和枚举元素的匹配片段上进行字符串舞蹈和 "绑定")。这里有作者的一个变体。这里还有另一种说法--类似于这样:
Functions.mqh 文件:
在这样的脚本中使用:
对不起,我当然错了,就在那行代码中:
static FunctionInstance *pointers[] = {C_Function::fabric<C_Skin>(), C_Function::fabric<C_Forest>(), C_Function::fabric<C_Megacity>(), C_Function::fabric<C_Rastrigin>(), C_Function::fabric<C_Universe>()};不会为每种类型创建一个对象?
......那么,如何在整个程序期间只使用一种类型?
有什么收获?我的意思是,这真的很糟糕。我向你道歉。)
这个问题很难回答我也不知道。
对不起,我当然错了,就在那行代码里:
不是每种类型都会创建一个对象吗?
......那怎么会在整个程序期间只使用一种类型呢?
这一行是创建工厂的地方。它们确实是为所有类保留的(在开始时)。工厂通过明确调用 create 来创建工作对象。