种群优化算法：猴子算法（MA）

内容：

1. 概述
2. 算法
3. 测试结果

1. 概述

猴子算法（MA）是一种元启发式搜索算法。 本文将讲述该算法的主要组成部分，并提出上涨（向上走势）、局部跳跃和全局跳跃的解决方案。 该算法由 R. Zhao 和 W.Tang 于 2007 年提出。 该算法模拟猴子在山上移动和跳跃寻找食物时的行为。 据推测，猴子遵循这样一个事实，即山越高，山顶上的食物就越多。

猴子探索的区域是适应度函数地域，因此最高的山对应于问题的解（我们考虑全局最大化问题）。 从当前位置开始，每只猴子都会向上移动，直至抵达山顶。 攀爬过程旨在逐步提高目标函数的值。 然后，猴子向随机方向进行一系列局部跳跃，希望找到更高的山峰，并重复向上的运动。 在进行了一定次数的攀爬和局部跳跃后，猴子认为它已经充分探索了初始位置附近的地域。

为了探索搜索新的空间区域，猴子进行了一次长距离跳跃。 上述步数在算法参数中重复指定次数。 该问题的解则声明为给定猴子种群发现的最高顶点。 然而，MA 算法在攀登过程中花费了大量的计算时间用于寻找局部最优解。 全局跳跃过程可以加快算法的收敛速度。 这个过程的目的是迫使猴子寻找新的搜索机会，以免陷于本地搜索。 该算法具有结构简单、可靠性较高、能很好地搜索局部最优解等优点。

MA 算法是一种新型的进化算法，可以解决许多具有非线性、不可微分性、和高维性的复杂优化问题。 与其它算法的不同之处在于，MA 算法花费的时间主要集中于攀爬过程中寻找局部最优解。 在下一章节中，我将讲述算法的主要组件、表示的解、初始化、攀登、观察和跳跃。

2. 算法

为了便于理解猴子算法，从伪代码开始是合理的。

MA 算法的伪代码：

1. 将猴子随机分布在搜索空间当中。
2. 测量猴子位置的高度。
3. 执行固定次数的局部跳转。
4. 如果在步骤 3 中得到的新顶点更高，则y以后应从该位置进行局部跳转。
5. 如果局部跳转次数限制已用尽，且未找到新顶点，则进行全局跳转。
6. 在步骤 5 之后，重复步骤 3
7. 从步骤 2 开始重复，直到满足停止准则。

我们来更详细地分析伪代码的每个关键点。

1. 在优化伊始，猴子对于搜索空间是未知的。 动物被随机定位在未知的地形中，因为食物出现的位置在任何地方都有同样可能。

2. 测量猴子所在高度的过程是由适应度函数履行任务。

3. 进行局部跳转时，算法参数中指定的数字有限制。 这意味着猴子正试图通过在觅食区域进行小范围局部跳跃来改善其当前位置。 如果新找到的食物来源更好，则转到步骤 4。

4. 找到新的食物来源，重置局部跳跃计数。 现在，将从该位置寻找新的食物来源。

5. 如果局部跳跃不能导致发现更好的食物来源，猴子得出结论，当前区域已充分探索，是时候寻找更远的新地方了。 在此刻，出现进一步跳跃的方向问题？ 该算法的思路是取所有猴子的坐标中心，从而提供一些交流 — 猴群中每只猴子之间的交流：猴子可以大声尖叫，并且具有良好的空间听力，能够判定彼此间的确切位置。 同时，知道彼此的位置（伙伴们不会在没有食物的地方呼唤），故可大致计算出食物的最佳新位置，因此，有必要朝这个方向跳跃。

在原始算法中，猴子沿着一条穿过所有猴子坐标中心和动物当前位置的线进行全局跳跃。 跳转的方向可以是朝向坐标中心，也可以是与中心相反的方向。 从中心朝反方向的跳跃，与为所有猴子寻找具有近似坐标的食物的逻辑相矛盾，这已被我使用该算法的实验所证实 — 事实上，它有 50% 的概率，这是与全局最优值的距离。

实践表明，跳出坐标中心之外，比不跳或朝反方向跳跃更有利可图。 不会发生所有猴子集中在某一点的情况，尽管乍一看这种逻辑不可避免。 事实上，猴子已经用尽了局部跳跃的极限，跳得比中心更远，从而扭转了种群中所有猴子的位置。 如果我们在脑海中想象高等类人猿服从这个算法，我们会看到动物团伙不时跳过群体的几何中心，而团伙本身则朝着食物更丰富的来源移动。 这种“团伙移动”的效果在算法的动画上可以清晰地看到（原来的算法没有这个效果，且结果更差）。

6. 进行全局跳跃后，猴子开始把食物来源的位置指定到新的地方。 该过程一直持续到满足停止准则。

该算法的整个思路可以很容易地适应单个示意图。 猴子的运动用图例 1 中带有数字的圆圈表示。 每个数字都是猴子的新位置。 黄色小圆圈表示失败的局部跳转尝试。 数字 6 表示局部跳跃极限已用尽，且未找到新的最佳食物来源位置。 没有数字的圆圈代表其余团伙的位置。 团伙的几何中心由一个带有坐标（x，y）的小圆圈表示。

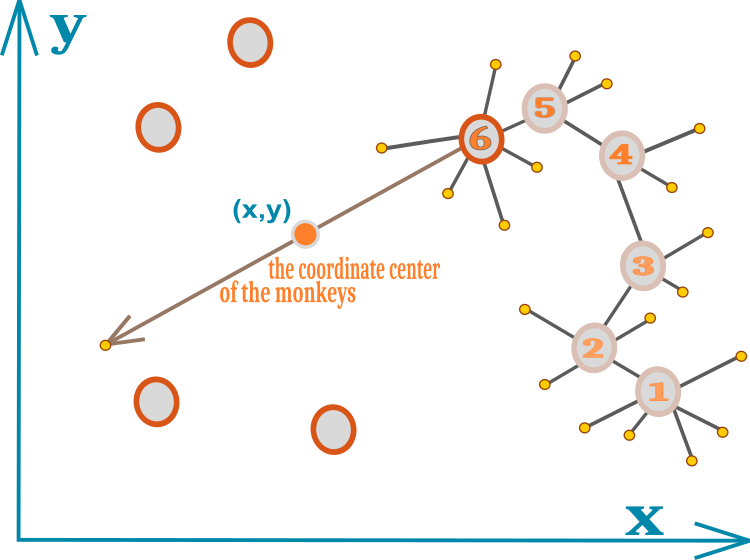
图例 1. 猴子按团伙移动的示意图

我们来看一下 MA 的代码。

用 S_Monkey 结构描述猴子团伙很方便。 该结构包含具有当前坐标的 c [] 数组、具有最佳食物坐标的 cB [] 数组（正是从具有这些坐标的位置发生局部跳跃）、h 和 hB — 分别是当前位置的高度值，和最高点的值。 lCNT — 局部跳转计数器，用于限制尝试改善位置的次数。

//——————————————————————————————————————————————————————————————————————————————
struct S_Monkey
{
  double c  []; //coordinates
  double cB []; //best coordinates
  double h;     //height of the mountain
  double hB;    //best height of the mountain
  int    lCNT;  //local search counter
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_MA 猴子算法类与前面讨论的算法没有什么不同。 猴子团伙在类中表示为 m[] 结构数组。 类中声明的方法和成员代码量都很小。 这是由于算法简洁，因此与许多其它优化算法不同，此处无需排序。 我们将需要数组来设置优化参数的最大值、最小值和步长，以及常量变量以便能将算法的外部参数传递给它们。 我们继续讲述包含 MA 主逻辑的方法。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MA
{
  //----------------------------------------------------------------------------
  public: S_Monkey m       []; //monkeys
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double hB;           //best height of the mountain

  public: void Init (const int    coordNumberP,     //coordinates number
                     const int    monkeysNumberP,   //monkeys number
                     const double bCoefficientP,    //local search coefficient
                     const double vCoefficientP,    //jump coefficient
                     const int    jumpsNumberP);    //jumps number

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordNumber;       //coordinates number
  private: int    monkeysNumber;     //monkeys number

  private: double b [];              //local search coefficient
  private: double v [];              //jump coefficient
  private: double bCoefficient;      //local search coefficient
  private: double vCoefficient;      //jump coefficient
  private: double jumpsNumber;       //jumps number
  private: double cc [];             //coordinate center

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

公开 Init() 方法初始化算法。 在此，我们设置数组的大小。 我们用尽可能小的“双精度”值初始化猴子找到的最佳领土的品质，我们将对 MA 结构数组的相应变量执行相同的操作。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Init (const int    coordNumberP,    //coordinates number
                    const int    monkeysNumberP,  //monkeys number
                    const double bCoefficientP,   //local search coefficient
                    const double vCoefficientP,   //jump coefficient
                    const int    jumpsNumberP)    //jumps number
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  coordNumber   = coordNumberP;
  monkeysNumber = monkeysNumberP;
  bCoefficient  = bCoefficientP;
  vCoefficient  = vCoefficientP;
  jumpsNumber   = jumpsNumberP;

  ArrayResize (rangeMax,  coordNumber);
  ArrayResize (rangeMin,  coordNumber);
  ArrayResize (rangeStep, coordNumber);
  ArrayResize (b,         coordNumber);
  ArrayResize (v,         coordNumber);
  ArrayResize (cc,        coordNumber);

  ArrayResize (m, monkeysNumber);

  for (int i = 0; i < monkeysNumber; i++)
  {
    ArrayResize (m [i].c,  coordNumber);
    ArrayResize (m [i].cB, coordNumber);
    m [i].h    = -DBL_MAX;
    m [i].hB   = -DBL_MAX;
    m [i].lCNT = 0;
  }

  ArrayResize (cB, coordNumber);
}
//——————————————————————————————————————————————————————————————————————————————

第一个公开方法 Moving()，需要在每次迭代时执行，实现猴子跳跃逻辑。 在第一次迭代中，若 “revision” 标志为 “false” 时，则有必要采用所研究空间坐标范围内的随机值初始化代理者，这相当于猴子在团伙栖息地内的随机位置。 为了减少重复的乘法运算，例如计算全局和局部跳转的系数，我们将相应坐标的值（每个坐标可以有自己的维度）存储在 v [] 和 b [] 数组当中。 我们将每只猴子的局部跳跃计数器重置为零。 

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    for (int c = 0; c < coordNumber; c++)
    {
      m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      m [monk].c [c] = SeInDiSp  (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      m [monk].h     = -DBL_MAX;
      m [monk].hB    = -DBL_MAX;
      m [monk].lCNT  = 0;
    }
  }

  for (int c = 0; c < coordNumber; c++)
  {
    v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient;
    b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient;
  }

  revision = true;
}

为了计算所有猴子的坐标中心，需用到 cc [] 数组，其维度对应于坐标数量。 此处的思路是将猴子的坐标相加，然后将结果总和除以团伙规模。 因此，坐标的中心既是坐标的算术平均值。

//calculate the coordinate center of the monkeys----------------------------
for (int c = 0; c < coordNumber; c++)
{
  cc [c] = 0.0;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    cc [c] += m [monk].cB [c];
  }

  cc [c] /= monkeysNumber;
}

根据伪代码，如果没有达到局部跳跃的极限，猴子就以相等的概率从它当前位置向各个方向跳跃。 局部跳跃圆圈的半径由局部跳跃系数调节，该系数根据 b[] 数组坐标的维数重新计算。

//local jump--------------------------------------------------------------
if (m [monk].lCNT < jumpsNumber) //local jump
{
  for (int c = 0; c < coordNumber; c++)
  {
    m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]);      
    m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

我们继续讨论 MA 算法逻辑中非常重要的部分 — 算法的性能在很大程度上取决于全局跳转的实现。 不同的作者从不同的角度应对这个问题，提供了各种各样的解。 根据研究，局部跳跃对算法的收敛性影响不大。 全局跳跃决定了算法从局部极值“跳跃”的能力。 我对全局跳跃的实验揭示出针对这种特定算法这是仅有的可行方法，能改善结果。

上面，我们讨论了朝坐标中心跳跃的可取性，如果终点在中心后面，而不是在中心和当前坐标之间，那就更好了。 这种方式应用了我们在关于杜鹃鸟优化算法（COA）一文中详述的 利维（Levy）飞行方程。

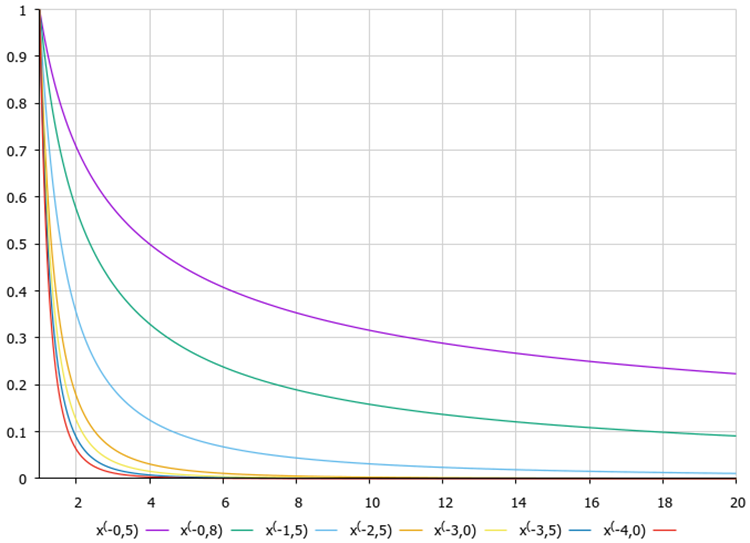
图例 2. 利维（Levy）飞行函数的图形取决于方程度数

猴子坐标使用以下公式计算：

m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);

其中:

cc [c] — 坐标中心的坐标，

v [c] — 重新计算搜索空间维度的跳跃半径系数，

r2 — 1 到 20 范围内的数字。

通过在此操作中应用利维（Levy）飞行，我们达成了猴子命中坐标中心附近的概率更高，以及远离中心附近的概率较低。 以这种方式，我们在研究和开发搜索之间提供平衡，同时发现新的食物来源。 如果收到的坐标超出允许范围的下限，那么传递的坐标对应范围上限的距离。 超过上限时也会这样做。 在坐标计算结束时，检查得到的数值是否符合边界和研究步骤。

//global jump-------------------------------------------------------------
for (int c = 0; c < coordNumber; c++)
{
  r1 = RNDfromCI (0.0, 1.0);
  r1 = r1 > 0.5 ? 1.0 : -1.0;
  r2 = RNDfromCI (1.0, 20.0);

  m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
          
  if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]);
  if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]);
          
  m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
}

进行局部/全局跳转后，跳转计数器加 1。

m [monk].lCNT++;

Revision() 是计算适应度函数后，每次迭代调用的第二个公开方法。 如果找到更好的全局解，该方法将更新全局解。 在局部和全局跳转后，处理结果的逻辑彼此不同。 在局部跳转的情况下，有必要检查当前位置是否有改善，并更新它（在下一次迭代中，跳跃是从这个新位置开始的），而在全局跳转的情况下，无需检查改善 — 无论如何都会从这个位置开始新的跳转。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Revision ()
{
  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    if (m [monk].h > hB)
    {
      hB = m [monk].h;
      ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY);
    }

    if (m [monk].lCNT <= jumpsNumber) //local jump
    {
      if (m [monk].h > m [monk].hB)
      {
        m [monk].hB = m [monk].h;
        ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
        m [monk].lCNT = 0;
      }
    }
    else //global jump
    {
      m [monk].hB = m [monk].h;
      ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
      m [monk].lCNT = 0;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

我们可以注意到该算法的方法与一组群体智能算法的相似性，例如粒子群（PSO）和其它具有类似搜索策略逻辑的算法。

3. 测试结果

MA 算法测试台结果：

2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:36:26.877    Test_AO_MA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 64.89788419898215
2023.02.22 19:36:26.878    Test_AO_MA (EURUSD,M1)    Score: 0.80412
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 55.57339368461394
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    Score: 0.68859
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 41.41612351844293
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    Score: 0.51317
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.4307085210424681
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    Score: 0.24363
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.19875891413613866
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    Score: 0.11243
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.06286212143582881
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    Score: 0.03556
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    =============================
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 2.8
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    Score: 0.23333
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 0.96
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    Score: 0.08000
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.34120000000000006
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    Score: 0.02843

注意算法在测试函数上的可视化，应该关注的是，在行为中没有形态，这与 RND 算法非常相似。 局部极端中有一些低密度的代理者，表明试图通过算法来细化解，但没有明显的堵塞。

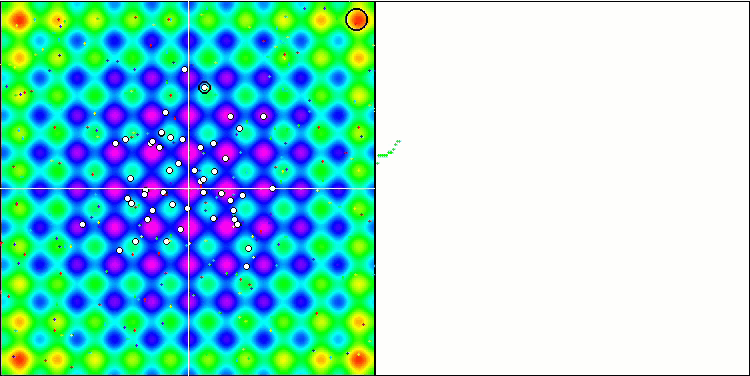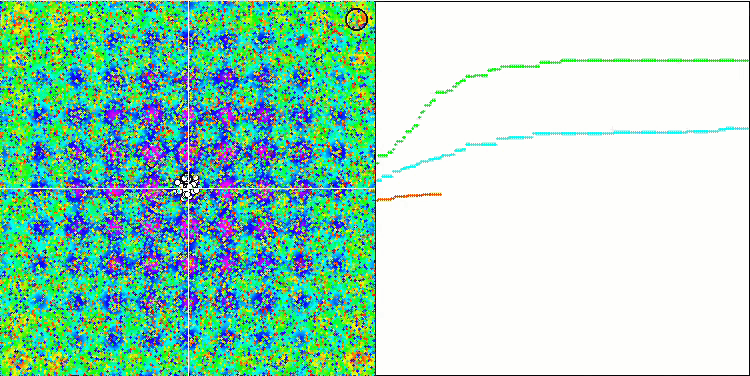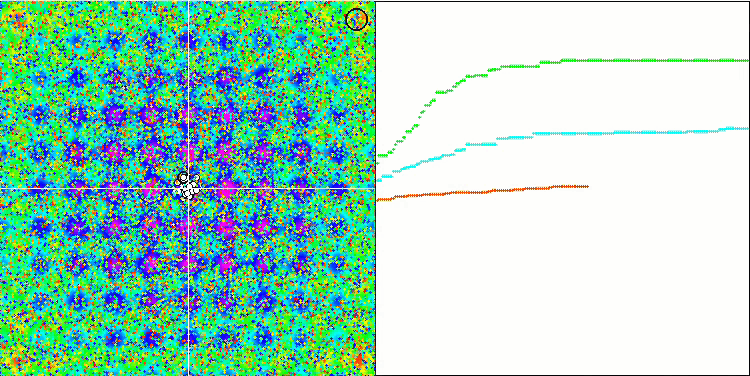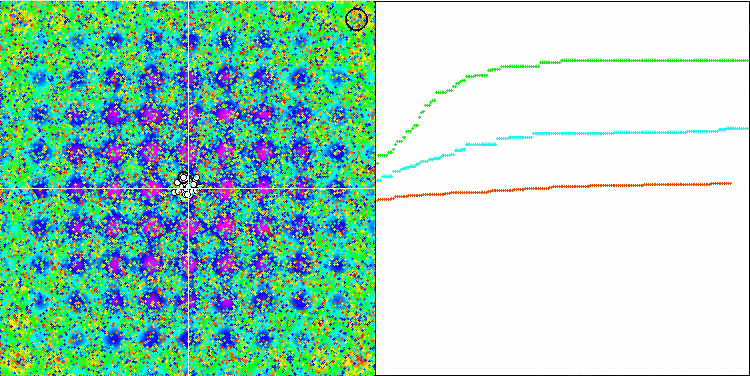
  Rastrigin 测试函数上的 MA

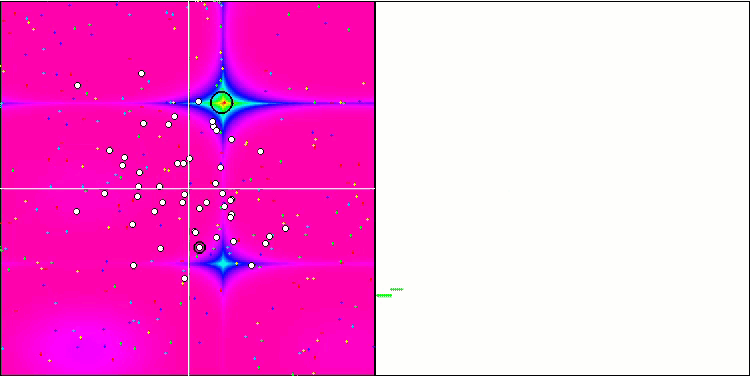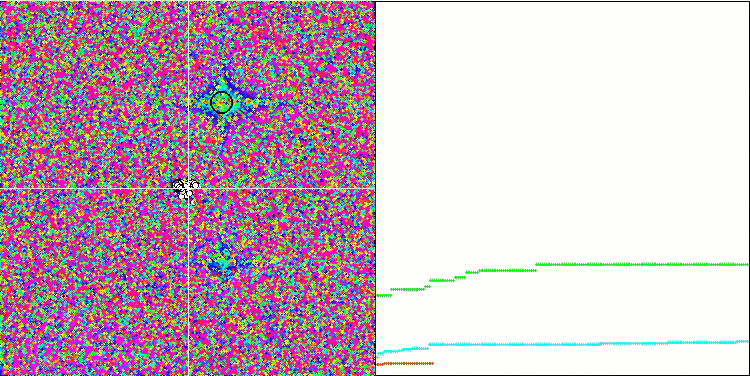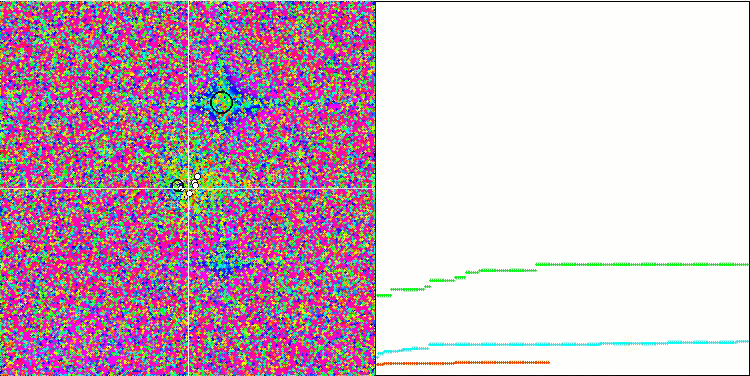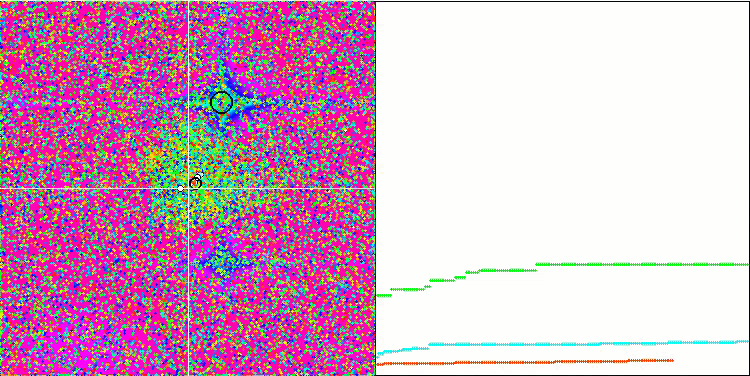
  基于 Forest 测试函数的 MA。

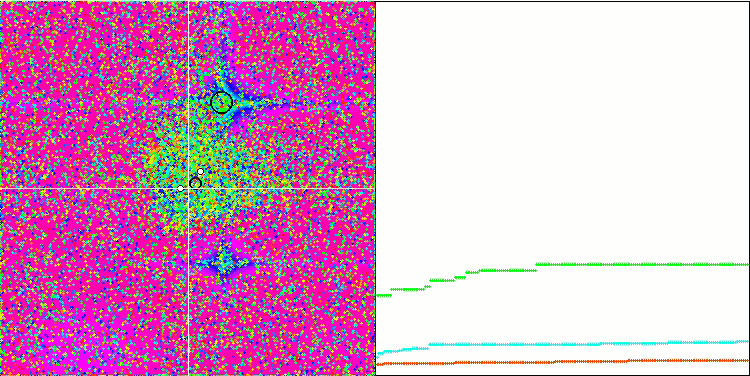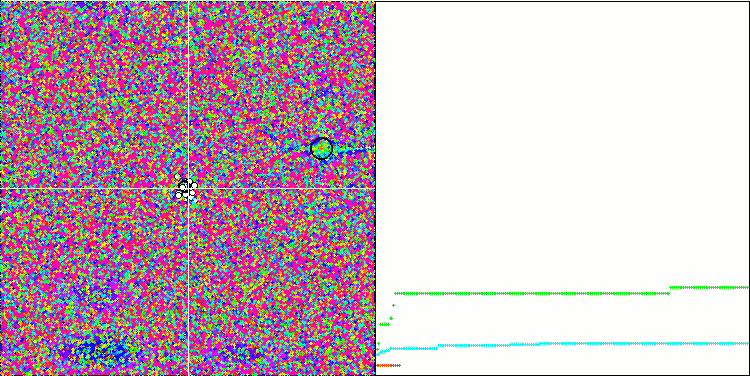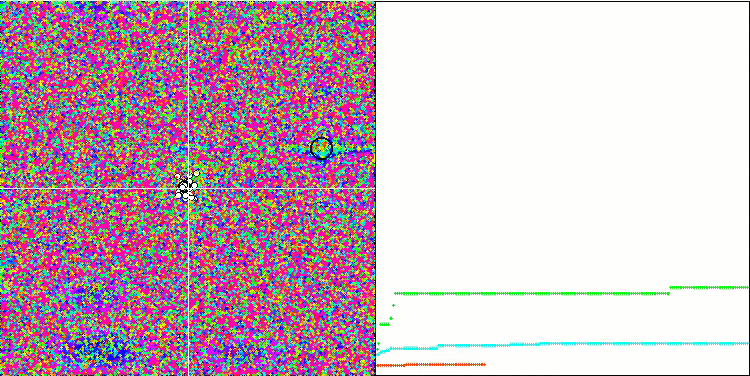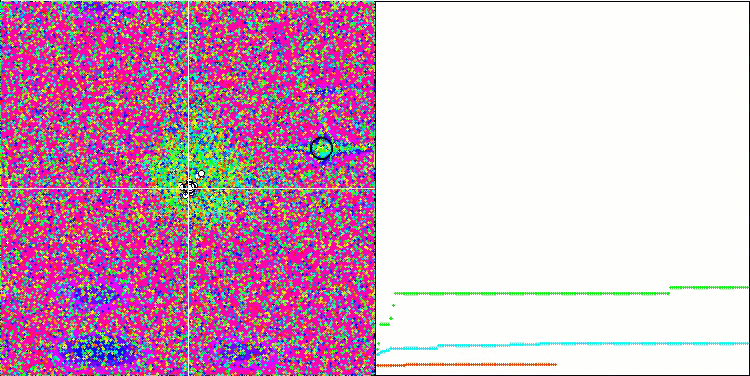
  基于 Megacity 测试函数上的 MA

我们继续分析测试结果。 基于评分结果，MA 算法在 GSA 和 FSS 之间排名垫底。 由于测试算法基于比较分析原则，其中结果的的分是最佳和最差之间的相对值，因此在一个测试中结果突出，而在其它测试中结果不佳的算法的出现，有时会导致其它测试参与者的参数发生变化。

但是 MA 算法的结果并没有导致表中其它测试参与者任何结果的重新计算。 MA 算法没有一个最差的测试结果，尽管有些算法的相对结果为零，以及较高评级（例如，GSA）。 因此，尽管该算法的行为相当适中，搜索能力表达得不够好，但算法显示出稳定的结果，这对于优化算法来说是一个积极的品质。

算法	说明	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果
		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)
HS	和弦搜索	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.000
ACOm	蚁群优化 M	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	入侵杂草优化	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	杜鹃优化算法 M	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	萤火虫算法 M	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	蝙蝠算法	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	人工蜂群	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	细菌觅食优化	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	引力搜索算法	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
MA	猴子算法	0.33300	0.35107	0.17340	0.85747	0.03684	0.07891	0.11546	0.23121	0.05838	0.00383	0.25809	0.32030	14.848
FSS	鱼群搜索	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	粒子群优化	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	随机	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	灰狼优化器	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

总结

经典的 MA 算法基本上包括使用攀爬过程来寻找局部最优解。 攀爬步长对局部解近似的准确性起着决定性的作用。 局部跳跃的攀爬步长越小，求解的精度就越高，但需要更多的迭代才能找到全局最优值。 为了通过减少迭代次数来降低计算时间，许多研究人员建议在优化的初始阶段使用其它优化方法，例如 ABC，COA，IWO，并采用 MA 算法来细化全局解。 我不赞成这种方式。 我相信，立即使用所讲述的算法替代 MA 算法更方便，尽管 MA 算法具有发展潜力，令其成为深入实验和研究的良好对象。 

猴子算法是一种基于种群的算法，其根源在于自然界。 与许多其它元启发式算法一样，该算法是进化的，能够解决许多优化问题，包括非线性、不可微分性和搜索空间的高维性、以及高收敛率。 猴子算法的另一个优点是该算法由少量参数控制，令其相当容易实现。 尽管结果具有稳定性，但因其低收敛率，故不推荐猴子算法来解决计算复杂度高的问题，因为它需要大量的迭代。 还有许多其它算法在更短的时间内（迭代次数）能做到同样的工作。

尽管我进行了多次实验，但该算法的经典版本无法超过评级表底端的第三个，陷入局部极端，并且在离散函数上工作得非常糟糕。 我没有特别想写一篇关于它的文章，所以我尝试改进它。 其中一项尝试显示收敛指标的一些改进，并通过在全局跳跃中使用概率偏差，并修改全局跳跃本身的原理来提高结果的稳定性。 许多 MA 算法研究人员指出需要对算法进行现代化改造，因此对猴子算法进行了许多修改。 我无意针对 MA 算法研究各种修改，因为算法本身并不出色，不过是粒子群（PSO）的变体。 实验的结果是本文给出的算法的最终版本，没有额外的 “m”（修订）标记。

算法测试结果的直方图如下。

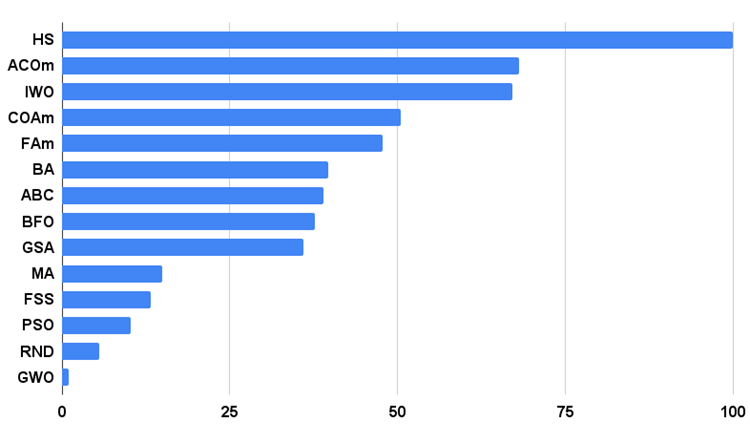
图例 3. 算法测试结果的直方图

MA 算法的优点和缺点:

优点:
1. 易于实现。
2. 尽管收敛率低，但具有良好的可扩展性。
3. 离散函数性能好。
4. 外部参数少。

缺点：
1. 收敛率低。
2. 搜索需要大量迭代。
3. 综合效率低。

每篇文章都提供一个存档，其中包含所有以前文章的算法代码的当前更新版本。 本文基于作者积累的经验，仅代表他的个人观点。 结论和判断基于实验。