
种群优化算法:鱼群搜索(FSS)
内容
1. 概述2. 算法描述
3. 测试结果
1. 概述
鱼群是聚集在一个地方的任何一堆鱼的总称。 鱼类聚集可以是结构化的,也可以是非结构化的。 非结构化聚集可能是一组混合物种和大小,它们随机聚集在某些局部资源(如食物或筑巢地点)附近。
此外,聚集相遇到一起,并如同社会般互动,那么可以说它们就是团体。 它们中的大多数处于其生命周期的同一阶段,彼此积极接触,并且随时可以表现出对群体成员有用的生物活性和有组织的活动。
与个体相对比,在更好地保护免受捕食者侵害和增加获取食物的竞争方面,群体生活的优势是在这两者之间达成了折衷。
鱼类在自然界中以若干种途径形成群体。 按常规,更喜欢由本物种的个体组成的较大团体。 群落中任何在外貌上出格,或有某种形体差别的成员,都会成为捕食者的主要目标。 这一事实解释了为什么鱼类更喜欢雷同个体的群体。 如此方式就实现了整个团体的同质化。
当鱼类以相同的速度和方向同步游泳时,团体的组织非常严格。 发生这种情况是由于鱼类都是相同的物种,按年龄和大小,彼此之间保持一定距离。 鱼类团体能够执行复杂的动作,就好像它们具有群体智慧和共同的头脑一样。 团体形成的微妙之处远未被完全理解,尤其是运动和喂养方式的各个方面。
已经提出了许多假设来解释群居行为,包括更好的定向、同步狩猎、迷惑捕食者、和降低被捕猎的风险。 鱼群里的鱼类似乎能分享信息,从而在近距离控制彼此的行为。 每条鱼的摄食行为会迅速刺激其它鱼积极寻找食物。 团聚的鱼群在细长的方阵中游弋,经常快速上升和下降,并绕轴线旋转,同时它们改变鱼群的形状,避免相互碰撞。 这种机动需要一个非常快速的响应系统。 团体生活方式意味着鱼类拥有感官系统,可以立即对它们感应到与邻居相对位置的微小变化,并做出反应。
为了创建更完整的图片,以这种行为进行数学建模。 最常见的数学模型假设团体中的个体生物遵循三个基本规则:
- 移动方向与邻居相同
- 始终与邻居保持近距离
- 避免与邻居发生碰撞
团聚的鱼群如何选择游弋方向的问题仍未解决。 在迁移过程中,似乎大多数成员都知道该去哪里。如果一个团体里的所有成员都同样意识到食物的可用性,那么小型组群中仍然有一些领导者比其它邻居更大胆。 这种团体行为促使众多研究人员不仅创建出一个数学模型,而且还创建了一个解决各种优化问题的算法模型。
2. 算法说明
鱼群搜索(FSS)是群体智能算法的一个子家族,属于元启发式算法类。 它由 Bastos Filho 和 Lima Neto 于 2008 年提出,并于 2009 年首次发表。 在 FSS 中,简单的代理者被称为鱼,每条鱼都有一个权重,代表其在搜索过程中取得“成功”。 权重的数值和变化会影响个体和团体运动。 内置的配食和协调的行动机制迫使团体朝着正梯度的方向前进,以增加权重,并找到局部和全局的最佳地点。 FSS 是为多模态搜索空间中的连续优化问题而开发的。 这也促使其他研究人员提出了解决其他问题的选择,例如二元问题的优化和多目标优化。
在 FSS 算法中,可以简化为想象鱼类在有条件的水族箱中游泳,水族箱的外壁是所研究函数定义域的边界。 鱼的权重是衡量成功寻找食物(解)的指标。 此外,它还扮演着鱼的记忆作用。 权重的存在是算法的主要思想,也是与一群粒子的区别。 FSS 算法的这一特性消除了查找和修复全局最佳解的需要,就像一群粒子一样。
FSS 算法的算子分为两组:
- 投喂算子(feeding operator)正式确定区域勘探的成功
- 游泳算子(swimming operators)为单个鱼和整个团体实现迁移算法
投喂算子计算鱼的权重。 基本思想是让鱼群朝正梯度“游弋”,以便“进食”并“增重”。 总的来说,权重较大的鱼对整个搜索过程的影响更大,这会导致鱼群质量的中心在迭代中向搜索空间中更好的位置移动。 给定迭代中的权重增量与适应度函数值的归一化差值成正比:
fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness);
其中:
- weight - 鱼的权重
- delta_fitness - 适应度函数值之间的差值
- max_delta_fitness - 所有鱼之间适应度函数差值的最大值
浮动算子(Floating operators)根据运动类型分为三种类型:
- 个体;
- 本能集体;
- 集体意志;
个体游弋可以解释为鱼在当前位置附近进行局部搜索。 个体的运动矢量是随机定向的,并且具有不同的值。
fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r;
其中:
- new_position - 相应坐标处的新位置
- current_position - 相应坐标上的当前位置
- step_ind - 个体移动步骤的计算为
initial_step_ind * (rangeMax [d] - rangeMin [d]);
其中:
- initial_step_ind - 个体运动的算法参数
- rangeMax and rangeMin - 优化的参数值范围
- r - 随机数值 [-1.0;1.0]
示意性地,个体游弋如图例 1 所示。
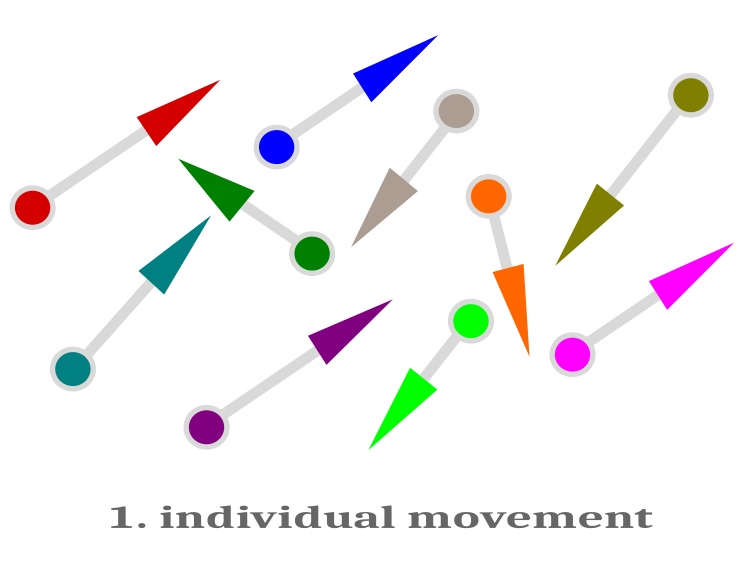
图例 1. 个体游弋 每条鱼的运动向量是随机方向的,并且具有不同的标量值
个体游弋后,测量适应度函数。 如果鱼的最终位置没有改善,那么我们认为这条特殊的鱼没有任何运动,它仍然停在原地。 只有那些改善了适应度函数的鱼才会移动到新的位置。
个体游弋完成后,执行本能集体运动算子。 我们先看一下图例 2。
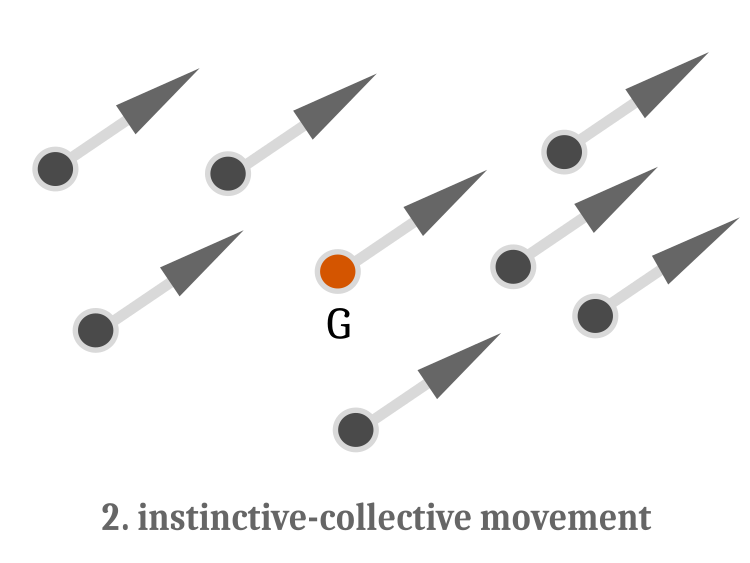
图例 2. 本能集体游弋:其运动特征适配于所有相对于质心G 的方向和幅度相同的鱼类。
本能集体运动是为了调整鱼群团的一般位置,同时考虑到上一次迭代中每条鱼的适应度函数的变化。 新坐标的计算方法如下:
fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d];
其中:
- new_position - 鱼在相应坐标处的新位置
- current_position - 相应坐标上的当前位置
- collective_instinct - 沿相应坐标的移动量,计算公式为:
collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness;
其中:
- delta_position - 在个体游弋阶段获得的当前坐标与先前位置之间的差值
- delta_fitness - 个体游弋时当前位置和前一个位置的适应度函数变化
本能集体游弋正式将一群鱼群团同步移动到新地方,从而建立寻找食物的新地点,而个体运动可以改善局部的情况。
现在,我们来研究集体意志游弋。 它分为两种类型:
- 从质心 — 如果与之前的位置相比,团体的整体位置没有改善,而鱼群向两侧扩散,象征着进一步寻找食物(图例 3)
- 如果发生改善,则移动到质心。 然后鱼群移动到质心,挤压成环,象征着对猎物的攻击。 从算法上讲,这意味着完善优化问题的解(图例 4)。

图例 3. 集体意志游弋。 方向矢量从质心 G 开始定向
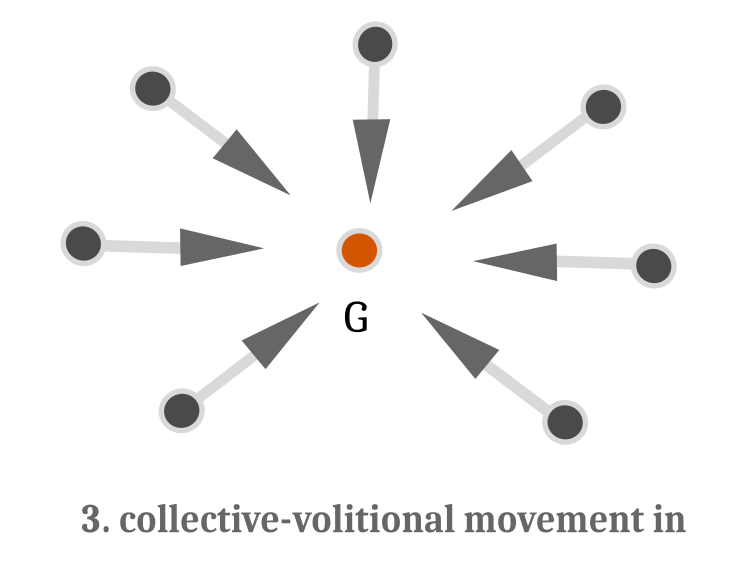
图例 4. 集体意志游弋。 方向矢量指向质心 G
引入了质心的概念,用于计算集体意志游弋。 从这里开始,集体意志游弋方程将如下所示:
fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator);
其中:
- pos 是相同的 current_position
- search_operator - 如果之前的移动导致位置改善,则为 1,如果没有,则为 -1
- step_vol [d] - 集体运动步长,计算公式为:
step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]);
其中:
- initial_step_vol - 集体运动的算法参数
- barycenter [d] - 质心,计算方式为鱼的权重之和乘以坐标:
barycenter [d] += fishes [f].weight * fishes [f].current_position [d];
并除以鱼群团的总权重:
barycenter [d] /= current_total_weight;
该算法的伪代码如下所示:
1) 用随机数初始化鱼的位置
2) 个体运动
3) 适应度函数计算
4) 重新定义每条鱼的权重
5) 本能集体运动
6) 集体意志运动
7) 重新计算总权重
8) 适应度函数计算
9) 从步骤 2)重复,直到满足停止准则
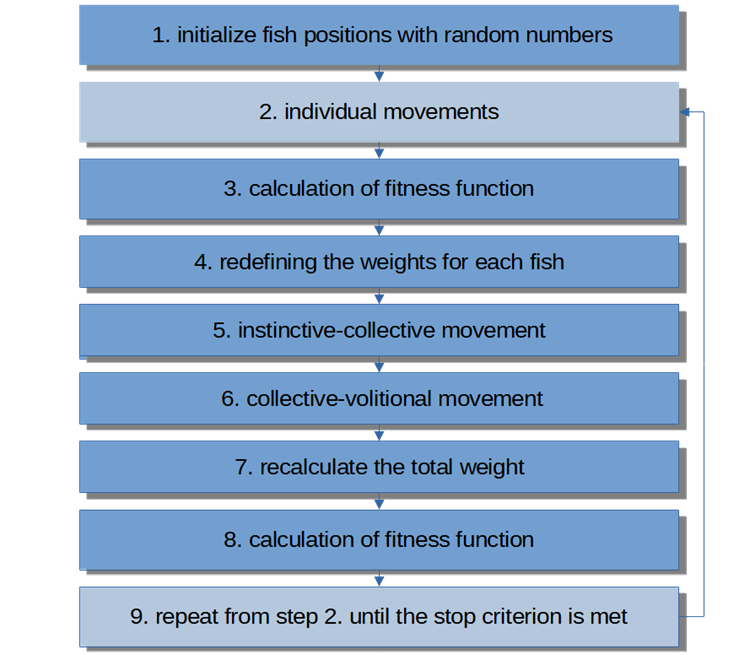
图例 5. FSS 算法框图
我们开始讲述代码。
正如您可能猜到的那样,该算法最简单的逻辑单元是描述鱼的结构。 由于我们需要若干次初始化鱼群,因此建议“清零”此结构,因为它相对较大,尤其对于 Init() 方法,这将迫使我们稍微优化代码。 该结构包括当前位置、新位置的坐标数组、以及自上次移动以来的坐标差值。 默认等于 1000 个标准单位的权重可能拥有任何数值。 鱼群的特征还在于当前、前一个适应度函数的数值,以及它们之间的差值。 在 Init() 方法中,适应度函数采用可能的最小“双精度”值进行初始化。 因此,适应度差值为零,因为鱼还没有移动。
//—————————————————————————————————————————————————————————————————————————————— struct S_Fish { void Init (int dimensions) { ArrayResize (current_position, dimensions); ArrayResize (new_position, dimensions); ArrayResize (delta_position, dimensions); weight = 1000.0; fitness = -DBL_MAX; delta_fitness = 0.0; } double current_position []; double new_position []; double delta_position []; double weight; double fitness; double new_fitness; double delta_fitness; }; //——————————————————————————————————————————————————————————————————————————————
我们来声明 C_AO_FSS 类 — 在数学上表示自然群落模型的一个鱼群。 此处没有什么不寻常的。 与用户程序交互还需要两个公开方法 — 考虑到鱼的坐标,和团体中的交互,以及数组所需的优化函数的数值范围。
在 Init() 初始化类的公开方法中,需要将变量重置为其原始值,并为数组分配内存。 特别注意初始化和 swimmingRegime 变量。 根据我们看到的伪代码,适应度函数的计算执行两次:第一次 — 在个体运动之后;第二次 — 在两种类型的集体运动之后。 这与我们采用的算法-应用程序链接预案相矛盾,其内指出每次迭代都有一个顺序:first_method -> calculation_fitness_functions -> second_method。 应用这两个变量是为了解决此问题,并更改规范算法中的操作顺序。 init 变量在算法开始时应为 “false”。 这是一个标志,指示必须初始化鱼群,计算适应度函数,并再次进行运动,因为算法的整个逻辑采用坐标的当前值和先前值,与适应度函数之间的差值。 缺了这些,我们就无法获得数值差。 第二个重要的标志是 swimmingRegime。 它允许我们重新定义描述鱼群运动的调用方法的顺序,令其与我们的结构相匹配。 数值 1 对应于“个体”游弋的调用,否则我们调用上面研究的群体运动顺序。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::Init (const int dimensionsP, const int fishSchSizeP, const double initial_step_indP, const double initial_step_volP) { MathSrand (GetTickCount ()); init = false; swimmingRegime = 1; dimensions = dimensionsP; ArrayResize (rangeMax, dimensions); ArrayResize (rangeMin, dimensions); ArrayResize (rangeStep, dimensions); num_of_individuos = fishSchSizeP; ArrayResize (fishes, num_of_individuos); for (int i = 0; i < num_of_individuos; i++) { fishes [i].Init (dimensions); } global_best = -DBL_MAX; ArrayResize (global_best_position, dimensions); total_weight = num_of_individuos; initial_step_ind = initial_step_indP; ArrayResize (step_ind, dimensions); initial_step_vol = initial_step_volP; ArrayResize (step_vol, dimensions); ArrayResize (collective_instinct, dimensions); ArrayResize (barycenter, dimensions); } //——————————————————————————————————————————————————————————————————————————————
每次迭代中调用的第一个公开方法 Swimming () 判定对个体和组鱼群运动的调用顺序。 如果是第一次调用该方法,则通过两个算法参数 initial_step_ind 和 initial_step_vol,将个体和团体移动步骤初始化为沿相应坐标可能范围的一部分。 一些作者建议将值分别设置为 0.01 和 0.001。 然而,我取用这些数值并未得到好的结果。 所以我取用 0.1 和 0.8。 此外,在算法的第一次运行时,鱼群位置坐标的当前值在优化参数范围内采拥随机数进行初始化。 在后续方法调用期间,将根据 swimmingRegime 标志调用相应的运动类型。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::Swimming (int i) { //---------------------------------------------------------------------------- if (!init) { global_best = -DBL_MAX; swimmingRegime = 1; for (int d = 0; d < dimensions; d++) { step_ind [d] = initial_step_ind * (rangeMax [d] - rangeMin [d]); step_vol [d] = initial_step_vol * (rangeMax [d] - rangeMin [d]); } for (int f = 0; f < num_of_individuos; f++) { fishes [f].Init (dimensions); for (int d = 0; d < dimensions; d++) { fishes [f].new_position [d] = RNDfromCI (rangeMin [d], rangeMax [d]); fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } } //---------------------------------------------------------------------------- else { switch (swimmingRegime) { case 1: apply_individual_movement (); //individual movement break; default: apply_instintive_collective_movement (); //instinctively-collective movement apply_collective_volitive_movement (); //collective-volitional movement update_total_weight (); //recalculate the total weight break; } } } //——————————————————————————————————————————————————————————————————————————————
每次迭代时调用的第二个公开方法 Regrouping() 主要判定对游弋方法的调用顺序 — 个体、本能集体、集体意志。 确保调用顺序的方法的附加功能由 swimmingRegime 标志提供,该标志取值为 1 和 2。 在经典版本中,这对于我采用的结构重新定义调用鱼群运动方法的顺序是必要的:first_open_method -> _fitness_function_calculation -> second_open_method。 根据 Init 标志,如果算法处于第一次迭代,我们将存储坐标的当前位置和适应度函数的值,以便进一步计算它们的差值,因为假设该方法是在计算适应度函数之后调用的。 如果 Init 标志指示算法处于第二次及后续迭代中,则在个体移动之后,有必要获得适应度函数的当前值和先前值之间的差值,以及当前和先前位置坐标之间的差值。 只有位置改善的条件下才计算差值,否则我们认为没有变动。 故此,我们将鱼群的权重值重置为初始状态,运动和适应度函数的差值等于零。 如果达到最佳解,我们会立即通过调用 updates_optimal_solution() 方法更新最佳解,并调用 apply_feeding() 方法应用到鱼群投喂。 如果 swimmingRegime 标志不等于 1,则应用集体本能和集体意志运动。 执行后,将 swimmingRegime 设置为 1。 接下来将是个体运动。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::Regrouping () { //---------------------------------------------------------------------------- if (swimmingRegime == 1 { if (!init) { for (int f = 0; f < num_of_individuos; f++) { ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY); ArrayInitialize (fishes [f].delta_position, 0.0); fishes [f].fitness = fishes [f].new_fitness; fishes [f].delta_fitness = 0.0; } init = true; return; } for (int f = 0; f < num_of_individuos; f++) { //remember the best position for the fish if (fishes [f].new_fitness > fishes [f].fitness) { fishes [f].delta_fitness = fishes [f].new_fitness - fishes [f].fitness; //fabs fishes [f].fitness = fishes [f].new_fitness; for (int d = 0; d < dimensions; d++) { fishes [f].delta_position [d] = fishes [f].new_position [d] - fishes [f].current_position [d]; } ArrayCopy (fishes [f].current_position, fishes [f].new_position, 0, 0, WHOLE_ARRAY); } else { ArrayInitialize (fishes [f].delta_position, 0.0); fishes [f].delta_fitness = 0.0; } } swimmingRegime = 2; updates_optimal_solution (); apply_feeding (); return; } //---------------------------------------------------------------------------- swimmingRegime = 1; updates_optimal_solution (); } //——————————————————————————————————————————————————————————————————————————————
以下简单的私密方法则当它们如果达到,更新算法的最佳结果。 为此,我们只需将每条鱼的适应度函数值与全局值进行比较。 如果它们更佳,那就保存它们。
//—————————————————————————————————————————————————————————————————————————————— // update the best overall solution void C_AO_FSS::updates_optimal_solution () { for (int f = 0; f < num_of_individuos; f++) { if (fishes [f].fitness > global_best) { global_best = fishes [f].fitness; ArrayCopy (global_best_position, fishes [f].current_position, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
我们已经研究了以上提供的个体游弋私密方法的等式。 那么,此处的一切都很简单:我们将一个个体的步长乘以 -1.0 到 1.0 范围内的随机数就得到每条鱼的当前坐标,其给出了正方向和负方向的增量。 如果优化的参数值超出范围,则为坐标设置边界值。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::apply_individual_movement () { // move the fish to new places----------------------------------------------- double r = 0.0; for (int f = 0; f < num_of_individuos; f++) { for (int d = 0; d < dimensions; d++) { r = RNDfromCI (-1.0, 1.0); fishes [f].new_position [d] = fishes [f].current_position [d] + step_ind [d] * r; fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } } //——————————————————————————————————————————————————————————————————————————————
喂养方法不应引起理解困难。 事实上,鱼群的权重被确定为鱼本身的适应函数差值与整个鱼群之间最大差值的商。 不过,所有鱼群之间的最大差值可能会等于零。 该算法经典版本的描述说到,鱼的权重必须始终为正。 一般来讲,通常只考虑适应度函数取正值的情况,但我发现这个需求没有实际意义。 我准许鱼的权重可以取负值,因此,如果所有鱼中适应度函数的最大差值(这是我们必须将每条鱼的体量归一化所取的值)为零,那么鱼的权重等于 1。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::apply_feeding () { double max_delta_fitness = -DBL_MAX; //find the maximum weight among fish for (int f = 0; f < num_of_individuos; f++) { if (fishes [f].delta_fitness > max_delta_fitness) max_delta_fitness = fishes [f].delta_fitness; } //feed the fish for (int f = 0; f < num_of_individuos; f++) { if (max_delta_fitness != 0.0) { fishes [f].weight = fishes [f].weight + (fishes [f].delta_fitness / max_delta_fitness); } else fishes [f].weight = 1; } } //——————————————————————————————————————————————————————————————————————————————
本能集体运动的私密方法包括通过增加集体本能值来改变每条鱼的坐标,而集体本能值又只不过是当前和先前迭代中位置差值与先前运动中实现的适应函数差值的乘积。 在此,若超出优化参数的边界时,我们为其分配边界值。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::apply_instintive_collective_movement () { double sum_delta_fitness = 0.0; for (int f = 0; f < num_of_individuos; f++) { sum_delta_fitness += fishes [f].delta_fitness; } for (int f = 0; f < num_of_individuos; f++) { for (int d = 0; d < dimensions; d++) { collective_instinct [d] = fishes [f].delta_position [d] * fishes [f].delta_fitness; if (sum_delta_fitness != 0.0) { collective_instinct [d] /= sum_delta_fitness; } fishes [f].new_position [d] = fishes [f].current_position [d] + collective_instinct [d]; fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } } //——————————————————————————————————————————————————————————————————————————————
集体意志游弋的私密方法,其中计算鱼群的质心,以及当前的总权重。 如果鱼群的总权重增加,那么鱼取开始向质心移动,否则 — 远离质心。 早前详细讨论了这个等式。 鱼群的总权重由下面讨论的特殊方法更新。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::apply_collective_volitive_movement () { //---------------------------------------------------------------------------- double current_total_weight = 0.0; for (int f = 0; f < num_of_individuos; f++) { current_total_weight += fishes [f].weight; } ArrayInitialize (barycenter, 0.0); for (int f = 0; f < num_of_individuos; f++) { for (int d = 0; d < dimensions; d++) { barycenter [d] += fishes [f].weight * fishes [f].current_position [d]; } } for (int d = 0; d < dimensions; d++) { barycenter [d] /= current_total_weight; } //---------------------------------------------------------------------------- double search_operator = current_total_weight > total_weight ? 1.0 : -1.0; double r = 0.0; double pos = 0.0; for (int f = 0; f < num_of_individuos; f++) { for (int d = 0; d < dimensions; d++) { r = RNDfromCI (0.0, 1.0); pos = fishes [f].current_position [d]; fishes [f].new_position [d] = pos + (((pos - barycenter [d]) * step_vol [d] * r) * search_operator); fishes [f].new_position [d] = SeInDiSp (fishes [f].new_position [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } } //——————————————————————————————————————————————————————————————————————————————
实际上,这是更新鱼群总权重的方法。 这里的一切都很简单。 我们把每条鱼的权重汇总起来。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_FSS::update_total_weight () { total_weight = 0.0; for (int f = 0; f < num_of_individuos; f++) { total_weight += fishes [f].weight; } } //——————————————————————————————————————————————————————————————————————————————
3. 测试结果
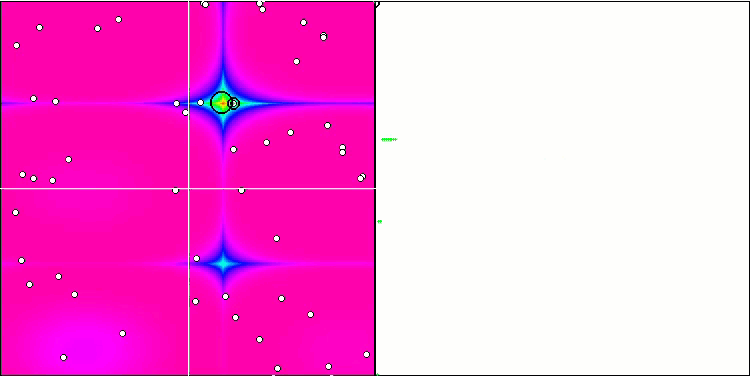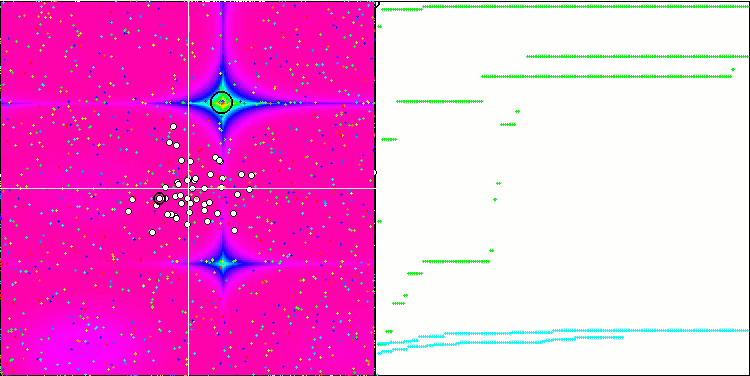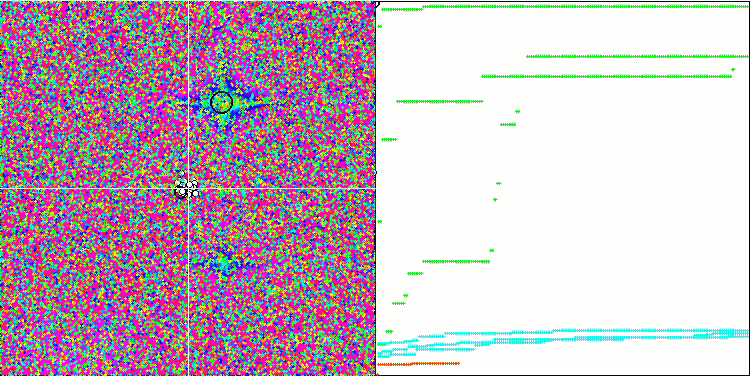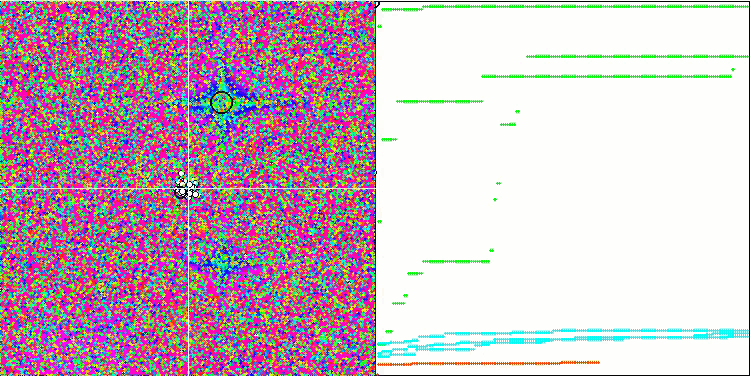
我们进入最后一个也是最有趣的部分 — 结果。 该算法包含有趣的技巧,诸如无需考虑全局最优,引入质心和本能意志运动的概念,暗示收敛或从团体质心散射,取决于整体位置是否得到改善。 所有这些都为算法在所研究函数上的原始行为带来了希望。
一般来说,空间搜索区域的行为具有独创性,即鱼类分散到空间的不同部分,类似于蜜蜂算法中观察到的情况,尽管详细研究方程和 FSS 的工作原理并不意味着将团体分散到单独的群中。 通常来说,该算法表现不佳,在整体结果方面仅略胜 PSO 算法。
如果我们考虑个别测试,FSS 仍然设法在其中的一些测试中表现出色。 特别是在平滑 Skin 函数上,FSS 算法比狼群算法更好,显示出良好(但并非最佳)得结果,这很容易解释。 该算法使用处于研究得函数表面的梯度,参考每个坐标的增量,以及每次迭代时适应度函数的变化。 由于 Skin 函数是平滑的,因此该算法可以很好地“贴合”表面变化。
至于 Forest 函数,算法显示的结果低于平均值。 测试函数的平滑变化在一定程度上有助于算法得空间导航,但它无法找到全局最大值。 在参考 Megacity 时,FSS 的缺点变得更加明显。 当所研究的函数在单一代理者的当前位置附近没有变化时,算法确实“不喜欢”它,并且该算法无法进行长距离跳跃,以便识别潜在得更好的新地方。 故此,它会卡在任何附近没有增量的局部极值中。
尽管 Megacity 测试对于任何优化算法来说都非常困难,并且表格中的其它参与者,相比较而言总体上并不比 FSS 领先多少,但仍然有必要认识到该算法在离散问题上的能力较弱。 在一些测试中,随机搜索显示出最佳结果。 正如我们在动画中看到的,在算法操作中看不到“聚类”。 您也许还记得上一篇文章中描述的优化算法“晶化”。
FSS 算法结果:
2022.12.08 13:14:06.033 Test_AO_FSS (EURUSD,M1) =============================
2022.12.08 13:14:08.388 Test_AO_FSS (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.892861444841324
2022.12.08 13:14:08.388 Test_AO_FSS (EURUSD,M1) Score: 0.99391
2022.12.08 13:14:12.557 Test_AO_FSS (EURUSD,M1) 20 Skin's; Func runs 10000 result: 3.11410005347766
2022.12.08 13:14:12.557 Test_AO_FSS (EURUSD,M1) Score: 0.56920
2022.12.08 13:14:47.176 Test_AO_FSS (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.20519552002827
2022.12.08 13:14:47.176 Test_AO_FSS (EURUSD,M1) Score: 0.11341
2022.12.08 13:14:47.176 Test_AO_FSS (EURUSD,M1) =============================
2022.12.08 13:14:49.498 Test_AO_FSS (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.5057381856551146
2022.12.08 13:14:49.498 Test_AO_FSS (EURUSD,M1) Score: 0.85172
2022.12.08 13:14:53.825 Test_AO_FSS (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.21468156279781656
2022.12.08 13:14:53.825 Test_AO_FSS (EURUSD,M1) Score: 0.12143
2022.12.08 13:15:31.235 Test_AO_FSS (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.056970068652984526
2022.12.08 13:15:31.235 Test_AO_FSS (EURUSD,M1) Score: 0.03223
2022.12.08 13:15:31.235 Test_AO_FSS (EURUSD,M1) =============================
2022.12.08 13:15:34.066 Test_AO_FSS (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 11.0
2022.12.08 13:15:34.066 Test_AO_FSS (EURUSD,M1) Score: 0.91667
2022.12.08 13:15:38.467 Test_AO_FSS (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 1.03
2022.12.08 13:15:38.467 Test_AO_FSS (EURUSD,M1) Score: 0.08583
2022.12.08 13:16:16.589 Test_AO_FSS (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.31
2022.12.08 13:16:16.589 Test_AO_FSS (EURUSD,M1) Score: 0.02583
2022.12.08 13:16:16.589 Test_AO_FSS (EURUSD,M1) =============================
2022.12.08 13:16:16.589 Test_AO_FSS (EURUSD,M1) All score for C_AO_FSS: 0.4122477188979048
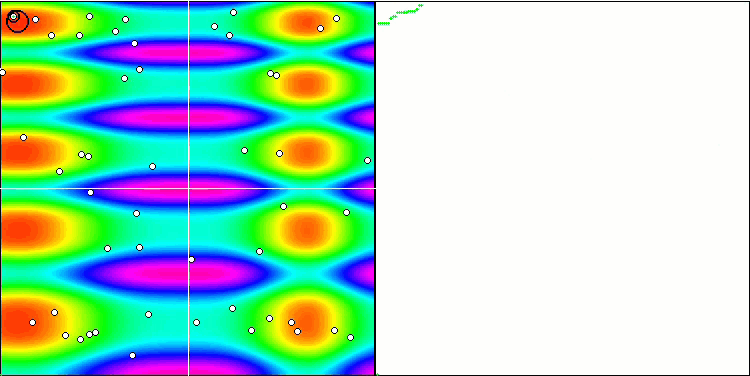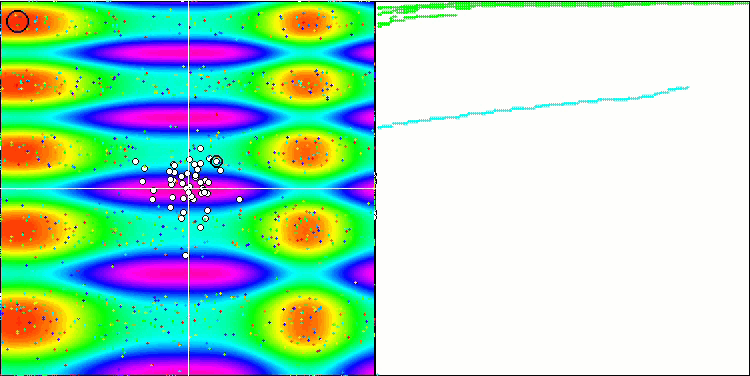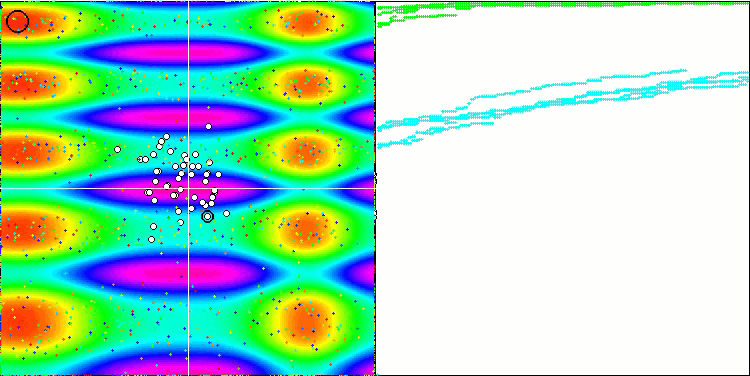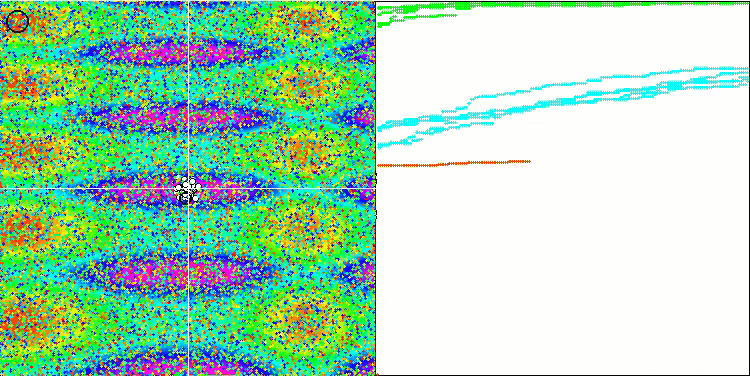
基于 Skin 测试函数的 FSS。
基于 Forest 测试函数的 FSS。
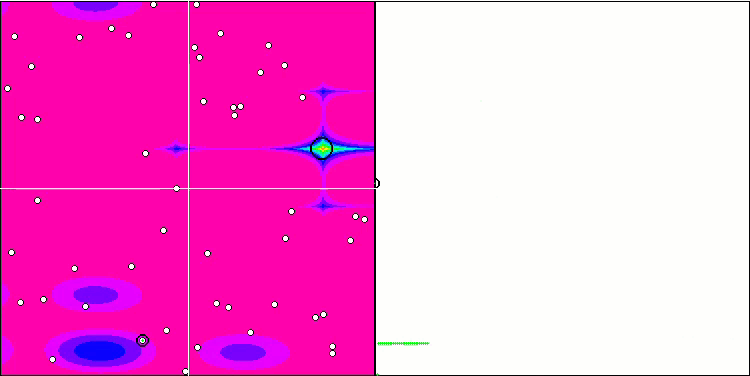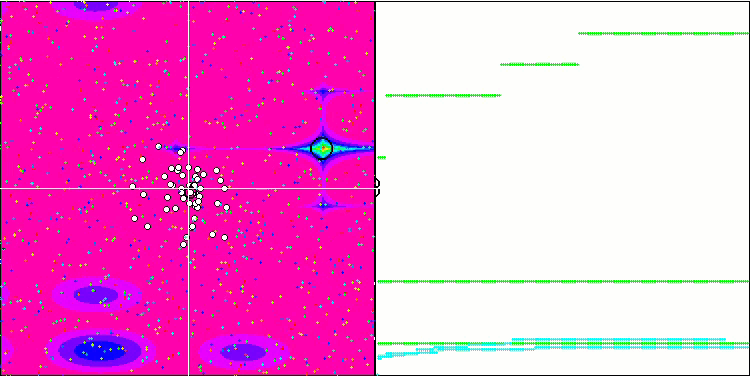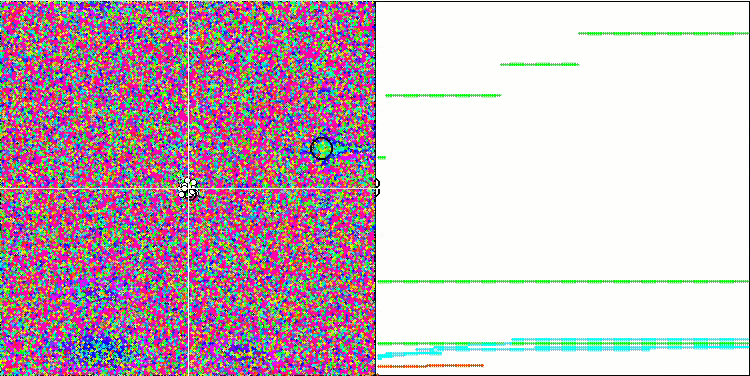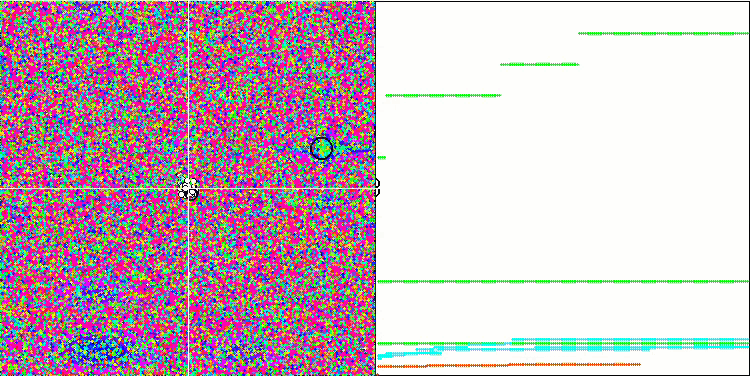
基于 Megacity 测试函数的 FSS。
此为最终的表格。 它具有额外的列,以便更方便地单独评估每个测试函数的算法,这令我们能够更公平地争论每种算法对某些任务的适用性。
| 算法 | 说明 | Skin | Skin 最终 | Forest | Forest 最终 | Megacity (离散) | Megacity 最终 | 最终结果 | ||||||
| 2 参数 (1 F) | 40 参数 (20 F) | 1000 参数 (500 F) | 2 参数 (1 F) | 40 参数 (20 F) | 1000 参数 (500 F) | 2 参数 (1 F) | 40 参数 (20 F) | 1000 参数 (500 F) | ||||||
| 杜鹃优化算法 | 1.00000 | 0.85911 | 0.14316 | 0.66742 | 0.99283 | 0.28787 | 0.04551 | 0.44207 | 1.00000 | 0.24917 | 0.03537 | 0.42818 | 0.51255778 | |
| 蚁群优化 | 0.98229 | 0.79108 | 0.12602 | 0.63313 | 1.00000 | 0.62077 | 0.11521 | 0.57866 | 0.38333 | 0.44000 | 0.02377 | 0.28237 | 0.49805222 | |
| 人工蜂群 M | 1.00000 | 0.63922 | 0.08076 | 0.57333 | 0.99908 | 0.20112 | 0.03785 | 0.41268 | 1.00000 | 0.16333 | 0.02823 | 0.39719 | 0.46106556 | |
| 人工蜂群 | 0.99339 | 0.73381 | 0.11118 | 0.61279 | 0.99934 | 0.21437 | 0.04215 | 0.41862 | 0.85000 | 0.16833 | 0.03130 | 0.34988 | 0.46043000 | |
| 灰狼优化器 | 0.99900 | 0.48033 | 0.18924 | 0.55619 | 0.83844 | 0.08755 | 0.02555 | 0.31718 | 1.00000 | 0.10000 | 0.02187 | 0.37396 | 0.41577556 | |
| 鱼群搜索 | 0.99391 | 0.5692 | 0.11341 | 0.55884 | 0.85172 | 0.12143 | 0.03223 | 0.33513 | 0.91667 | 0.08583 | 0.02583 | 0.34278 | 0.41224778 | |
| 粒子群优化 | 0.99627 | 0.38080 | 0.05089 | 0.47599 | 0.93772 | 0.14540 | 0.04856 | 0.37723 | 1.00000 | 0.09333 | 0.02233 | 0.37189 | 0.40836667 | |
| 随机 | 0.99932 | 0.44276 | 0.06827 | 0.50345 | 0.83126 | 0.11524 | 0.03048 | 0.32566 | 0.83333 | 0.09000 | 0.02403 | 0.31579 | 0.38163222 | |
随机启发式方法不能保证精确解,但作为常规,它们允许在可接受的时间内找到足够接近实际的解。 然而,实践表明,一些算法能够表现出优异的收敛能力,尽管 FSS 并不属于此类。 一般来说,鱼群搜索算法是基于一群粒子算法的特例。 故此,它既继承了优点,也继承了缺点。 独特的算法功能包括将鱼群(团)分成单独的群组,这在粒子群中没有观察到。 该算法可以相对较好地处理平滑函数,尽管不确定 FSS 能否很好地处理拥有多个变量的函数。
1. 该算法可以很好地处理平滑函数。
2. 鱼群被分成不同群组的能力,这令该算法能够进一步探索其它潜在的更好局部极值。
缺点:
1. 单个测试中结果的较大分散表明算法不稳定。
2. 离散函数和带中断的函数收敛性非常弱。 这几乎不适用于离散函数。
3. 可扩展性较弱。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/11841
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
你好,能否展示一下这种优化算法的应用?
这真的很有趣,我想应用并做一些基准测试。
谢谢你好,能否展示一下这种优化算法的应用?
这真的很有趣,我想应用并做一些基准测试。
谢谢
嗨,抱歉,我不太理解您的问题
你好,Andrey,我想知道如何在 EA 中应用这种算法。
谢谢
你好,Andrey,我想知道如何在 EA 中应用这种算法。
谢谢
我无法一言以蔽之地描述这个示例,我可能需要单独写一篇文章来介绍。不过,您可以在网站上搜索有关智能交易系统自动优化示例的文章,并应用我文章中的一种算法。