MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
种群优化算法：人工蜂群（ABC）

种群优化算法：人工蜂群（ABC）

MetaTrader 5 — 示例 | 4 四月 2023, 11:15
1 433 0
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法说明
  3. 修改版
  4. 测试结果


1. 概述

群居昆虫是高度进化的生物，可以执行许多单体昆虫无法完成的复杂任务。 沟通、筑造复杂的巢穴、环境控制、保护、和分工只是蜜蜂已进化到在社会性群居地茁壮成长的少数行为。 蜂群属于群体生物，在寻找最佳解决方案方面表现出非凡的能力。 在自然界中，它们在蜂巢附近寻找花簇来采集花蜜和花粉。 有时搜索半径可以增加到几公里。 返回的蜜蜂则是通过即兴舞蹈报告它们的发现。

乍一看，这似乎是不可能的，但它们能够通过有节奏的运动相互传递有关地理位置的信息。 取决于它们同胞间的舞蹈强度，蜂群得到有关指定地点的花朵数量和估算花蜜量的结论。 潜在的食物越丰富，舞蹈动作就越激烈。 这种不寻常的现象是在 20 世纪中叶由昆虫研究员卡尔·冯·弗里施（Karl von Frisch）发现的。

多年来，蜜蜂觅食方法仅在生物学家之间研究。 然而，在开发新的优化算法时，应用群体行为的兴趣正在增长。 在 2005 年，Dervis Karaboga 教授对研究结果产生了兴趣。 他发表了一篇科学论文，是第一个描述群体智能模型的人，主要受到蜂群舞蹈的启发。 该模型被称为人工蜂群。


2. 算法说明

人工蜂群有许多不同的实现，区别在于蜂巢中管理蜂群的原则、以及区域探索规则上有所不同。 在本文中，我将讨论我对经典算法版本的解释。

该算法的思路是基于蜂群在寻找尽可能多的获取花蜜的地方时的行为。 首先，所有的蜜蜂都朝随机的方向飞出蜂巢，充当侦察员，试图寻找有花蜜的区域。 之后，蜜蜂返回蜂巢，并以特殊的方式告诉其它个体在哪里找到了花蜜、以及发现了多少花蜜。

工蜂被发配到发现的区域。 在这个地区发现的花蜜越多，向那个方向飞的蜜蜂就越多。 侦察兵再次飞去寻找其它区域，但均在已发现区域的附近。 因此，所有的蜜蜂被分为两种：采集花蜜的工蜂，和探索新区域的侦察蜂。 花蜜采集区域具有的量值，与其花蜜量相对应。 沿穿过区域中心的线，较低等级的区域由相对于较高等级的区域进行置换。

由图示，工蜂按区域分布可以在图例 1 中可视化。

ABCarea

图例 1. 取决于区域排名，前往该区域的蜜蜂数量

区域 1 的等级较高，它包含的花蜜最多，因此更多的蜜蜂倾向于飞往那里。 通过蜜蜂的数量，我们可以直观地判定区域 4 的等级（值）最低。 蜜蜂以特殊舞蹈的形式报告有关每个区域价值的信息。 每个蜂巢都有自己的舞姿，其中对该地区花蜜的方向和数量进行编程。

假设全局位置的极值是花蜜最多的区域，并且只有一个这样的区域。 其它地方也有花蜜，尽管数量较少。 蜜蜂生活在多维空间中，其中每个坐标代表函数的一个参数，且其需要优化。 如果我们正在寻找全局最大值，则发现的花蜜量就是此刻目标函数的值。 如果我们正在寻找全局最小值，那么将目标函数乘以 -1 就足够了。

由于花蜜采集区域具有确定的价值，因此只有等级最高的区域才有权移到（中心移位）花蜜浓度最高的地点。 较低等级的区域则移至最高浓度的中心，并检查与其它较高等级区域的交叉点。 以这样的方式，不允许蜜蜂集中在一些狭窄的小区域内，并且由工蜂提供的搜索空间服务应尽可能地高效，从而防止食物来源的枯竭。 在优化方面，这消除或最大限度地减少了陷入局部极值的情况。 在区域分散，并沿着等级链相互移动到其最优位置后，蜜蜂侦察兵将深入侦察它们的邻域。

许多养蜂人建议将侦察蜂遣派到搜索空间的随机区域，但我的经验表明，这种“侦察”的实际价值接近于零，并且只对一、两个维度有用。 换言之，如果我们谈论的是多维空间，那么自由度就会呈几何级数增加，并且很难偶然发现更有价值的花蜜来源。 蜂巢的资源只会被浪费。 将侦察兵派往已知搜索区域的邻域更有用，这样坐标就不会分散，而是专门集中在可能的花蜜来源区域。

如果这些区域彼此相交，则必须偏转中心，令这些区域仅接触边界。 如图例 2 所示。

ABCcrossArea

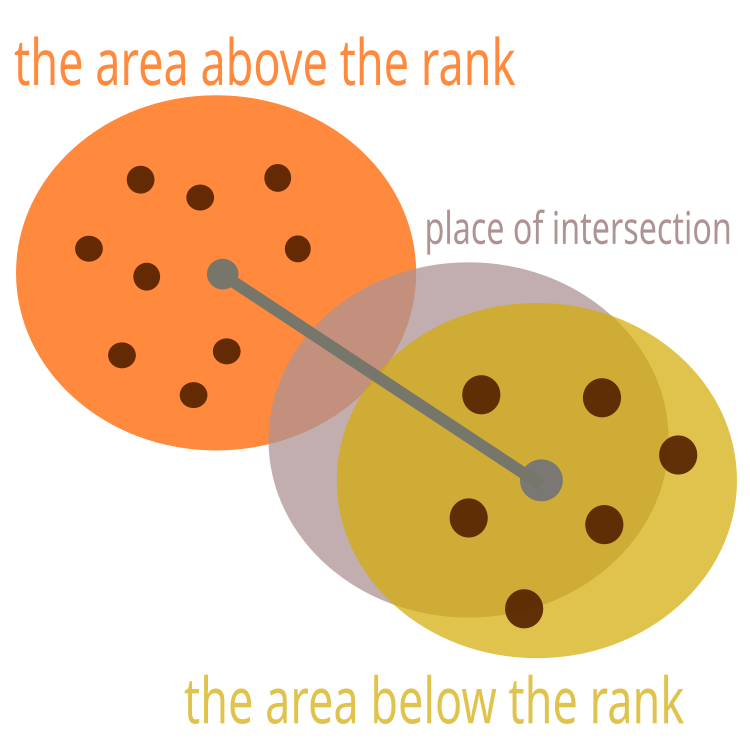
图例 2. 等级较低的区域应偏转

区域的排位并非严格设定的，而是动态形成的。 侦察蜂的发现会被分配到它们飞过区域的附近地区。 如果发现更有价值的食物来源，该区域的中心将转移到那里。 它甚至可能成为新的最佳花蜜采集中心。 其余区域现在将相对于它偏转。 换言之，它们沿排位链并相对于它偏移。

传递信息的方法，称为蜂之舞，是整个蜂巢战略的基本要素。 蜂巢的可用资源理应合理地分配到采集区域，那么遣派的蜜蜂数量应与区域的价值成正比。 这意味着相同数量的蜜蜂将被遣派到同等价值的区域。

我们继续讨论算法本身。 下面列出了执行步骤：

  1. 所有蜜蜂都作为侦察员沿着搜索空间随机飞行。
  2. 测量来自每只蜜蜂采集的花蜜量。
  3. 分拣蜜蜂。
  4. 根据从蜜蜂获得的花蜜量信息分配区域。
  5. 将工蜂遣派到该区域。 该区域的花蜜越多，遣派的蜜蜂就越多。
  6. 在随机选择的区域附近派遣侦察蜂。
  7. 测量来自每只蜜蜂那里采集到的花蜜量。
  8. 按花蜜量对区域进行排名。
  9. 重复上述步骤 直到满足停止准则。

为了便于直观感知，我们制作了算法的框图，如图例 3。


ABCsceme

图例 3. 算法框图

我们更详细地讲述蜂群算法代码。

一只蜜蜂是算法的基本逻辑单元。 它可以通过结构来讲述。 您可能还记得，蜜蜂的位置是由坐标、与采集的花蜜区域的隶属关系、以及花蜜的数量来设置的。 那么，蜂巢的蜜蜂可由一个数组表示。 每个都可以据其索引来访问。

//——————————————————————————————————————————————————————————————————————————————
struct S_Bee
{
  double c []; //coordinates
  int    aInd; //area index
  double n;    //nectar
};
//——————————————————————————————————————————————————————————————————————————————

第二个更大的逻辑单元是花蜜采集区域。 它由花蜜最集中的中心点，以及决定该区域价值的花蜜量来定义。 在最高等级的区域（列表中的第一个），中心坐标和花蜜的最高浓度重合。 而对于列表中排名第二和更低的区域，它们可能不一致，因为它们被转移了。 该区域的初始化以重置花蜜量指标，并将坐标分配给优化函数的相应编号的参数。 

//——————————————————————————————————————————————————————————————————————————————
struct S_Area
{
  void Init (int coordinatesNumber)
  {
    n = -DBL_MAX;

    ArrayResize (cC, coordinatesNumber);
    ArrayResize (cB, coordinatesNumber);
  }

  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

我们将蜜蜂的舞蹈描述为一个结构，其数组将与区域的数量相对应。

//——————————————————————————————————————————————————————————————————————————————
struct S_BeeDance
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

我将蜂巢描述为一个类,设置搜索区域、蜜蜂、最佳坐标、以及在所有迭代中发现的最大花蜜量。 此外，针对蜜蜂和区域进行分类，以及移动蜜蜂和彼此相对区域的所有必要方法均在此处定义。 在此，我们可以看到以前算法中已经熟悉的函数声明：生成随机均匀分布的数字，缩放到一个范围，然后从范围内选择一个数字并带有步长。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABC //Bees Hive
{
  //============================================================================
  public: S_Area areas     []; //nectar collection areas
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Bee  bees      []; //all the bees of the hive
  public: double cB        []; //best coordinates
  public: double nB;           //nectar of the best coordinates

  public: void InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP); //scout area radius

  public: void TasksForBees ();
  public: void CollectingNectar ();

  //============================================================================
  private: void   BeeFlight      (double &cC [] , S_Bee &bee);
  private: void   ScoutBeeFlight (double &cC [] , S_Bee &bee);
  private: void   MarkUpAreas    ();
  private: void   SortingBees    ();
  private: void   SortingAreas   ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: int    coordinates;      //coordinates number
  private: int    beesNumber;       //the number of all bees
  private: int    workerBeesNumber; //worker bees number
  private: int    areasNumber;      //areas number
  private: S_Bee  beesT       [];   //temporary, for sorting
  private: S_Area areasT      [];   //temporary, for sorting
  private: int    indA        [];   //array for indexes when sorting
  private: double valA        [];   //array for nectar values when sorting
  private: int    indB        [];   //array for indexes when sorting
  private: double valB        [];   //array for nectar values when sorting
  private: double areasRadius [];   //radius for each coordinate
  private: double scoutRadius [];   //scout radius for each coordinate

  private: double collectionRadius;   //collection radius
  private: double scoutAreaRadius;    //scout area radius
  private: double hypersphereRadius;  //hypersphere radius
  private: double distHyperspCenters; //distance hyperspheres centers
  private: double scoutHyperspRadius; //scout hypersphere radius
  private: bool   scouting;           //scouting flag

  private: S_BeeDance beeDance [];    //bee dance
};
//——————————————————————————————————————————————————————————————————————————————

每次新优化都必须从类初始化开始。 整个蜂巢和蜜蜂单体，以及区域的花蜜量值均被重置。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::InitHive (const int    coordinatesP,      //number of opt. parameters
                         const int    beesNumberP,       //bees number
                         const int    workerBeesNumberP, //worker bees number
                         const int    areasNumberP,      //areas number
                         const double collectionRadiusP, //collection radius
                         const double scoutAreaRadiusP)  //scout area radius
{
  MathSrand (GetTickCount ());
  scouting = false;
  nB       = -DBL_MAX;

  coordinates      = coordinatesP;
  beesNumber       = beesNumberP;
  workerBeesNumber = workerBeesNumberP;
  areasNumber      = areasNumberP < 3 ? 3 : areasNumberP;

  collectionRadius = collectionRadiusP; //collection radius
  scoutAreaRadius  = scoutAreaRadiusP;  //scout area radius

  ArrayResize (areas,  areasNumber);
  ArrayResize (areasT, areasNumber);
  for (int i = 0; i < areasNumber; i++)
  {
    areas  [i].Init (coordinates);
    areasT [i].Init (coordinates);
  }

  ArrayResize (beeDance, areasNumber);

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (indA, areasNumber);
  ArrayResize (valA, areasNumber);

  ArrayResize (areasRadius, coordinates);
  ArrayResize (scoutRadius, coordinates);
  for (int i = 0; i < coordinates; i++)
  {
    areasRadius [i] = (rangeMax [i] - rangeMin [i]) * collectionRadius;
    scoutRadius [i] = (rangeMax [i] - rangeMin [i]) * scoutAreaRadius;
  }

  double sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += areasRadius [i] * areasRadius [i];
  hypersphereRadius  = MathSqrt (sqr) * collectionRadius;

  distHyperspCenters = hypersphereRadius * 2.0;

  sqr = 0.0;
  for (int i = 0; i < coordinates; i++) sqr += scoutRadius [i] * scoutRadius [i];
  scoutHyperspRadius = MathSqrt (sqr) * scoutAreaRadius;

  ArrayResize (indB, beesNumber);
  ArrayResize (valB, beesNumber);

  ArrayResize (bees,  beesNumber);
  ArrayResize (beesT, beesNumber);
  for (int i = 0; i < beesNumber; i++)
  {
    ArrayResize (bees  [i].c, coordinates);
    ArrayResize (beesT [i].c, coordinates);
    bees  [i].n = -DBL_MAX;
    beesT [i].n = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

最简单也是开放的类方法就是给蜜蜂分派任务。 这里的一切都很简单。 如果有尚未探索区域，则重置整个蜂巢的花蜜值，并启动区域标记。 我们在每个世代上调用该方法，直到获得适应度函数的值。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::TasksForBees ()
{
  if (!scouting)
  {
    nB = -DBL_MAX;
  }
  MarkUpAreas ();
}
//——————————————————————————————————————————————————————————————————————————————

第二个公开方法在每个世代调用。 在获取适应度函数的值后执行启动。 在这种情况下，如果尚未进行探索，我们按花蜜值对蜜蜂进行排序，并将列表中第一批蜜蜂的坐标和花蜜数量复制到相应的区域中。 如果地点勘探已经进行，那么我们复制采集花蜜区域的坐标和花蜜数量，前提是结果有所改善。 此外，更新整个蜂巢的最佳结果。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::CollectingNectar ()
{
  if (!scouting)
  {
    SortingBees ();

    for (int a = 0; a <areasNumber; a++)
    {
      ArrayCopy (areas [a].cB, bees [a].c, 0, 0, WHOLE_ARRAY);
      areas [a].n = bees [a].n;
    }

    scouting = true;
  }
  else
  {
    //transfer the nectar to the hive---------------------------------------------
    for (int b = 0; b < beesNumber; b++)
    {
      if (bees [b].n > areas [bees [b].aInd].n)
      {
        ArrayCopy (areas [bees [b].aInd].cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        areas [bees [b].aInd].n = bees [b].n;
      }

      if (bees [b].n > nB)
      {
        ArrayCopy (cB, bees [b].c, 0, 0, WHOLE_ARRAY);
        nB = bees [b].n;
      }
    }

    SortingAreas ();
  }
}
//——————————————————————————————————————————————————————————————————————————————

MarkUpAreas () 方法值得详细研究。 我们将代码分解成多个部分。

在探索区域之前，没有关于寻找花朵采集花蜜的任何信息，我们将派遣所有蜜蜂进行初步探索。 在这个阶段，所有的蜜蜂都扮演着侦察员的角色。 由于没有关于花蜜的信息，我们向随机方向派遣侦察员，生成的随机数均匀分布在坐标范围内。

//if the areas is not scouting - send all the bees to scouting----------------
if (!scouting)
{
  for (int b = 0; b < beesNumber; b++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      bees [b].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      bees [b].c [c] = SeInDiSp  (bees [b].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

探索区域后，有必要将花蜜浓度最大的坐标复制到该区域的中心。 换言之，有必要将该区域移到更好的位置。 执行此操作后，我们需要确保该区域不与较高排位的区域相交。 我们可以通过测量区域中心之间的距离来检测区域的交点。 如果中心之间的距离小于两个半径（算法参数之一），则区域相交。 如果检测到相交，则将该区域转移到两个半径距离的地点，而最佳结果的坐标（最大花蜜浓度的坐标）保留在相同位置。 因此，这些区域持续变动。 最好的区域迫使其余区域转移。 其余区域，在偏转的同时，可以到达更丰富的食物来源，在排序后成为最好的，这在下一个方法中发生。

for (int s = 0; s < areasNumber; s++)
{
  //move the center of the area to the best point in with more nectar-------
  ArrayCopy (areas [s].cC, areas [s].cB, 0, 0, WHOLE_ARRAY);

  //ordinary area-----------------------------------------------------------
  if (s != 0)
  {
    //check if there is no intersection of a region with a region of higher rank
    //measure the distance from the centers of the regions
    double centersDistance = 0.0;

    for (int c = 0; c < coordinates; c++) centersDistance += pow (areas [s].cC [c] - areas [s - 1].cC [c], 2.0);
    centersDistance = MathSqrt (centersDistance);

    //the areas intersect, then need to move the current area
    if (centersDistance < distHyperspCenters)
    {
      double incrementFactor = (distHyperspCenters - centersDistance) / centersDistance;
      double coordDistance   = 0.0;

      for (int c = 0; c < coordinates; c++)
      {
        coordDistance = areas [s].cC [c] - areas [s - 1].cC [c];
        areas [s].cC [c] = areas [s].cC [c] + (coordDistance * incrementFactor);

        areas [s].cC [c] = SeInDiSp (areas [s].cC [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}

这就是蜜蜂跳舞的地方。 依据有关区域的方向和花蜜数量的信息，并应用随机分量，我们标记随机数的分布区域，如此令蜜蜂在下一次迭代中选择区域的概率与该区域的花蜜量成正比。 简而言之，在数字线上，我们绘制了段，其长度对应于面积最差的每个区域的花蜜值之间的差值。

//send bees to the marked areas-----------------------------------------------
double r = 0.0;

beeDance [0].start = bees [0].n;
beeDance [0].end   = beeDance [0].start + (bees [0].n - bees [areasNumber - 1].n);

for (int a = 1; a < areasNumber; a++)
{
  if (a != areasNumber - 1)
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a].n - bees [areasNumber - 1].n);
  }
  else
  {
    beeDance [a].start = beeDance [a - 1].end;
    beeDance [a].end   = beeDance [a    ].start + (bees [a - 1].n - bees [a].n) * 0.1;
  }
}

在方法代码的这一部分中，依据工蜂舞蹈传递的概率随机选择区域。 为此，我们在数字线上用舞蹈标记来生成一个随机数。 对于侦察峰来说，跳舞并不重要，因为它们以相同的概率在任何区域附近飞行，从而扩展了蜜蜂策略的搜索能力。 由此自然而然，每个蜂巢参与者在扮演角色时都有一定的价值。

for (int b = 0; b < beesNumber; b++)
{
  if (b < workerBeesNumber)
  {
    r = RNDfromCI(beeDance [0].start, beeDance [areasNumber - 1].end);
        
    for (int a = 0; a < areasNumber; a++)
    {
      if (beeDance [a].start <= r && r < beeDance [a].end)
      {
        bees [b].aInd = a;
        break;
      }
    }

    BeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
  else
  {
    //choose the area to send the bees there
    r = RNDfromCI (0.0, areasNumber - 1);

    bees [b].aInd = (int)r; //area index

    ScoutBeeFlight (areas [bees [b].aInd].cC, bees [b]);
  }
}

这个私密方法实现了蜜蜂的飞行。 这里的一切都很简单，尽管乍一看它看起来难以理解和复杂。 蜜蜂飞到离中心有立方概率偏移的区域。 因此，从区域中心到其边界的概率降低。 请记住，这是该区域的中心，而不是之前找到的最佳位置。 即使在这个简单的动作中，也可以追踪蜜蜂的策略，确保不断寻找新的食物来源。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::BeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (0.0, 1.0);
    r  = r * r * r;
    r = Scale (r, 0.0, 1.0, 0.0, areasRadius [c], false);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

与前面的方法不同，这里描述了侦察蜂的飞行。 蜜蜂飞出了算法设置中指定的半径范围内的区域。 尽管设置相同，但在初始化类时会预先计算半径，因为坐标范围可能不同，因此半径应该与其相应。 为了派遣侦察蜂的飞行方向，我们需要在从区域半径到区域半径和探索半径之和的范围内生成一个随机数，然后简单地将结果值添加到区域的中心。 以如此简单的方式，侦察蜂将偶然出现在该区域附近，而坐标不会分散在整个搜索空间中。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABC::ScoutBeeFlight (double &cC [] , S_Bee &bee)
{
  double r = 0.0;

  for (int c = 0; c < coordinates; c++)
  {
    r  = RNDfromCI (areasRadius [c], areasRadius [c] + scoutRadius [c]);
    r *= RNDfromCI (0.0, 1.0) > 0.5 ? 1.0 : -1.0;

    bee.c [c] = SeInDiSp  (cC [c] + r, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

算法中有两种具体方法 — 蜜蜂排序和区域排序。 解释它们并无太大意义，这只是一个简单的泡沫排序。 我几乎在所有优化算法（需要完全排序）中都用到它，因为这种方法很简单，并且很容易针对特定任务进行修改，同时提供了所有排序方法中最佳速度之一。

//——————————————————————————————————————————————————————————————————————————————
//Sorting of bees
void C_AO_ABC::SortingBees ()
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Sorting of areas
void C_AO_ABC::SortingAreas ()
//——————————————————————————————————————————————————————————————————————————————

是时候收集所有已研究的代码，并编译它了。 运行测试台后，我们可以看到以下动画，其中展示了蜜蜂算法的行为。 蜜蜂在不同的区域均可清楚地观察到。 我们可以看到这些区域是如何相互取代的。 准确性和特殊“群”的数量取决于算法设置。

Skin

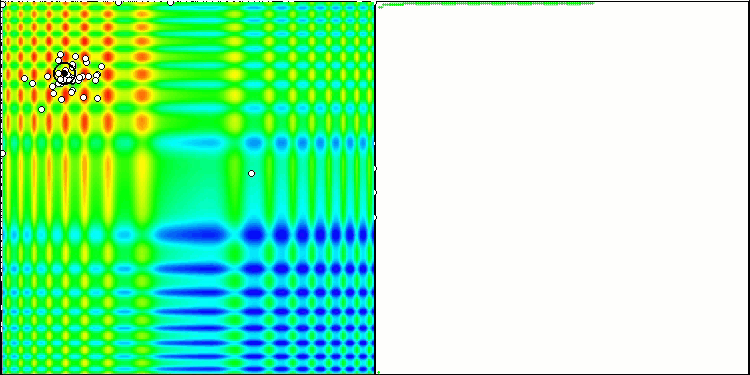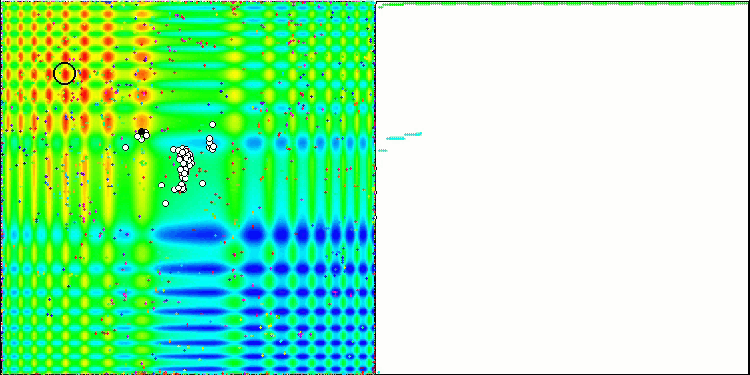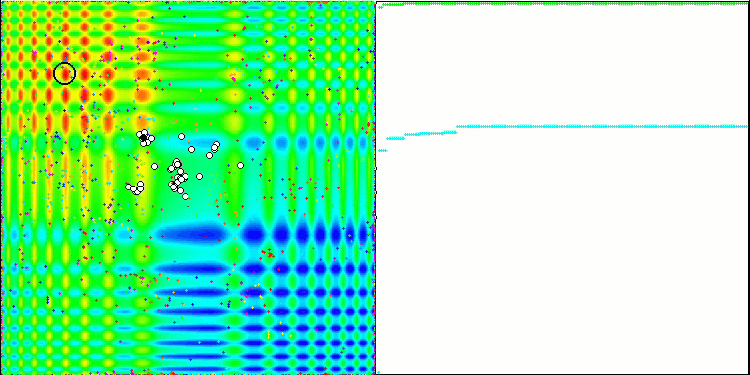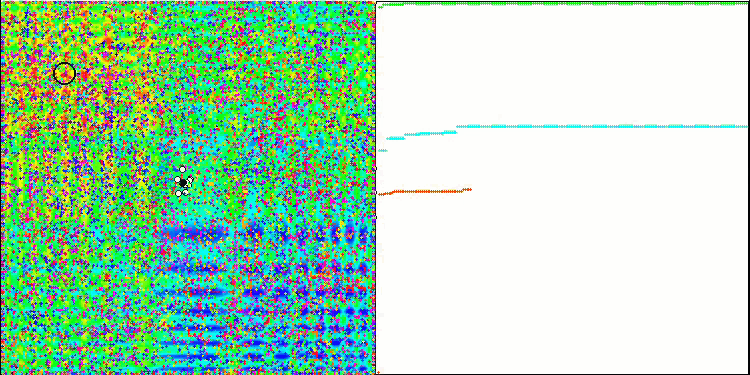
Skin 测试函数上的 ABC

Forest

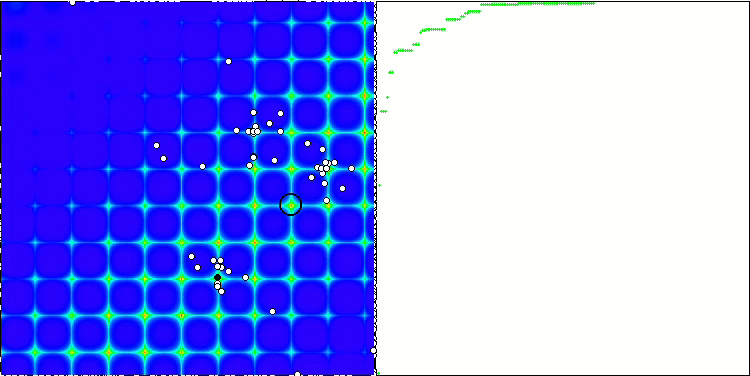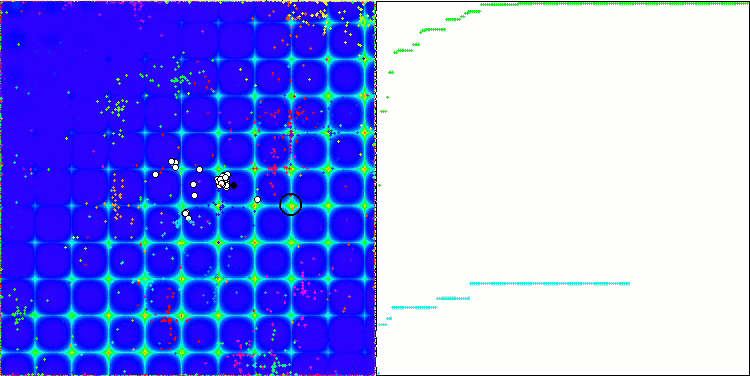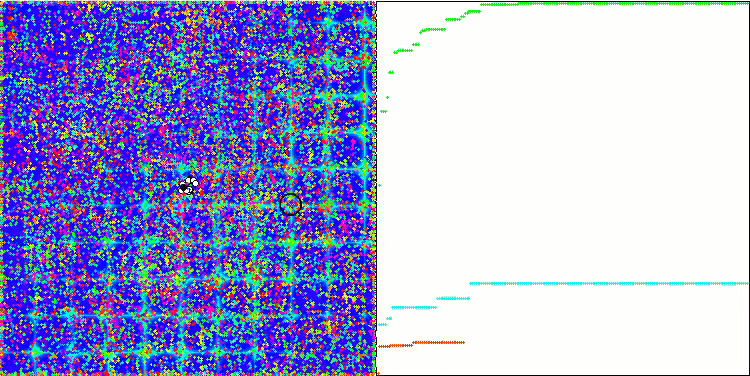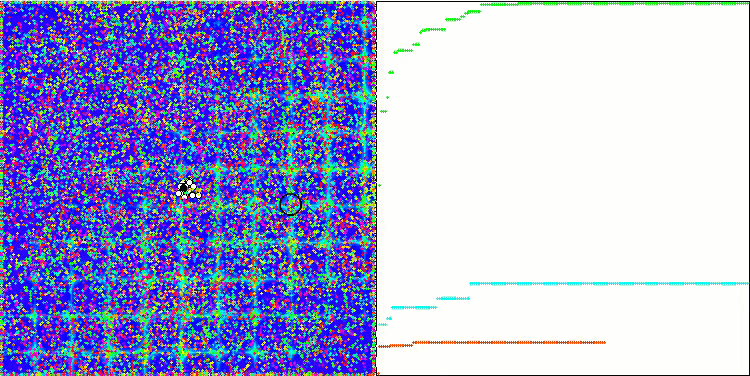
Forest 测试函数上的 ABC

Megacity

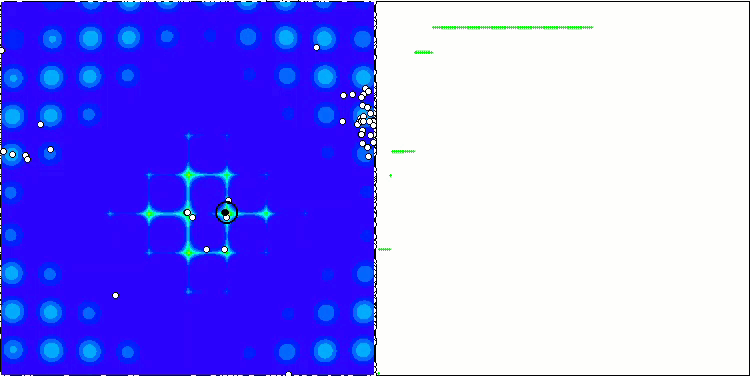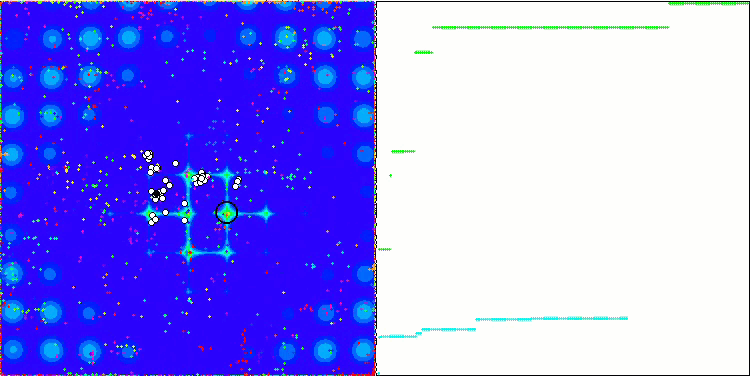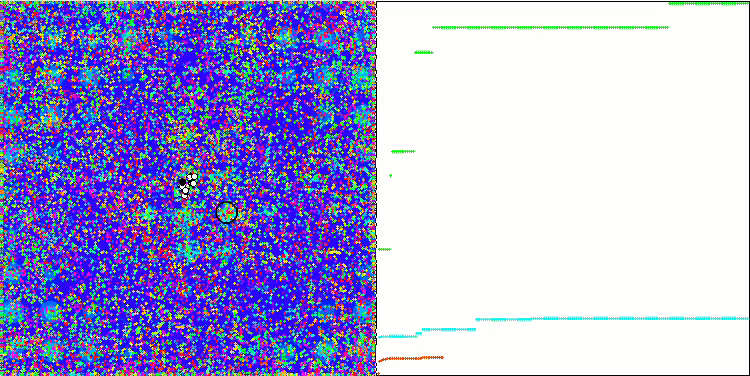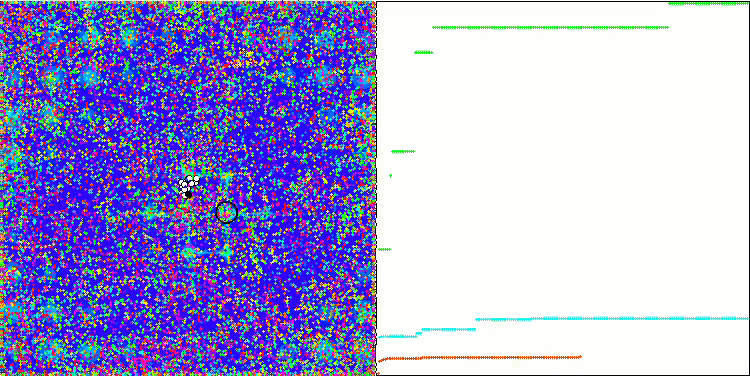
Megacity 测试函数上的 ABC

以下是测试函数的算法结果：

2022.11.21 13:14:06.669    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    1 Skin's; Func runs 1000 result: 14.018634225602678; Func runs 10000 result: 14.06060189007221
2022.11.21 13:14:28.483    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.99772; Score2: 1.00000
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    20 Skin's; Func runs 1000 result: 7.459929501115262; Func runs 10000 result: 8.320771456653533
2022.11.21 13:14:50.310    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.64085; Score2: 0.68769
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.69267387794685; Func runs 10000 result: 4.838631770950824
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.49029; Score2: 0.49823
2022.11.21 13:15:30.049    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.063567301715784; Func runs 10000 result: 15.912087696850861
2022.11.21 13:15:51.880    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.94435; Score2: 0.99755
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.0207584941876133; Func runs 10000 result: 4.1918977577943295
2022.11.21 13:16:13.721    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.18937; Score2: 0.26279
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.2004991531402736; Func runs 10000 result: 1.288357831462411
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.07526; Score2: 0.08077
2022.11.21 13:17:01.467    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 10.4; Func runs 10000 result: 15.0
2022.11.21 13:17:23.227    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.69333; Score2: 1.00000
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.5499999999999998; Func runs 10000 result: 2.31
2022.11.21 13:17:44.936    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.10333; Score2: 0.15400
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    500 Megacity's; Func runs 1000 result: 0.6180000000000001; Func runs 10000 result: 0.6568
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    Score1: 0.04120; Score2: 0.04379
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    =============================
2022.11.21 13:18:29.588    Test_AO_ABC1 (EURUSD,M1)    All score for C_AO_ABC: 0.49447371765340953

该算法对于这两个双变量测试函数均完全收敛，是极好的收敛性指标。 评价其余结果为时尚早。 最好将结果放在表格中，并与其它优化算法进行比较，再得出结论。


3. 修改版

在开发和设计任何优化算法时，总是会出现这样的问题：“算法是否按预期工作，或者代码中的某处是否存在错误？” 随机搜索过程本质上是随机的，因此不清楚优化结果是由算法获得的，还是因某处存在错误，且结果真的是非随机的？ 在开发蜂群算法时，我遇到了类似的现象。 在测试集中的五个测试中的首次测试中，算法显然在它开始搜索的地方卡住了，根本没有试图收敛。 从逻辑角度来看，这个错误以一种完全令人难以置信的方式解决了。 我所做的全部就是在第一个世代上额外第二次初始化 hive 类，尽管该类在世代开始之前已经预先初始化过了（Test_AO_ABC.mq5 代码的 142 行）。 如果有人设法解开这个谜团，那么我很高兴在评论中听到解决方案。

部分由于上述原因，另外部分原因则是首轮测试的结果并不完全令人满意（尽管后来很明显我需要尝试算法设置），我迸发出了改变蜜蜂搜索策略的想法。 在原始版本中，蜜蜂的飞行与面积值成比例。 在新算法中，每个区域应该有固定数量的蜜蜂。 换句话说，无论区域等级如何，它们中的每一个总是有相同数量的蜜蜂。 因此，该区域在逻辑上被转化为“蜂群”的概念。

现在，以如下结构，替代区域结构：

//——————————————————————————————————————————————————————————————————————————————
struct S_BeesSwarm
{
  void Init (int coordinatesNumber, int beesNumber)
  {
    ArrayResize (bees, beesNumber);

    for (int i = 0; i < beesNumber; i++)
    {
      ArrayResize (bees [i].c, coordinatesNumber);
      bees [i].n = -DBL_MAX;
    }

    n = -DBL_MAX;

    ArrayResize     (cC, coordinatesNumber);
    ArrayInitialize (cC, -DBL_MAX);
  }

  S_Bee  bees []; //bees
  double cC   []; //center coordinates
  double cB   []; //best coordinates
  double n;       //nectarAmount
};
//——————————————————————————————————————————————————————————————————————————————

这个结构也有一个初始化函数，但另外还有 bees[] 数组。

通常，代码的其余部分与经典版本非常相似，您不必过多地关注它。 代码附于文后的存档之中。 值得特别注意是算法逻辑的差别。 在分步形式中，它看起来像这样：

  1. 为第一个蜂群创建一个中心，并将蜜蜂放置在中心周围。
  2. 为后续蜂群创建一个中心，并检查从中心到先前蜂群的距离是否大于或等于 R*2（两倍半径），并将蜜蜂放置在中心附近。
  3. 派遣侦察蜂，令每只蜜蜂比其它蜂群的距离大于或等于 R（半径）。
  4. 获取所有蜜蜂的适应度函数的值。
  5. 对蜂群进行排序。
  6. 将蜜蜂放在每个蜂群的中心周围。
  7. 从第 4 步开始重复，直到满足停止准则。

您可能已经注意到，搜索策略存在根本差异。 而在经典版本中，每个区域可以有不同数量的蜜蜂，而这里的蜂群总是相同的大小。 这样做是为了确保即使食物来源干涸，也能继续探索区域，从而对超空间中的表面进行更彻底的探索。 测试证实了这种方式的合法性。 结果得以改善。 侦察蜂不会在区域附近飞行，而是落入自由空间区域，甚至，遵循区域规则，就像经典版本一样。 在蜜蜂的经典版本中，侦察峰的行为并不像描述的那样，因为它们完全随机地分散，且不关心它们是否进入先前已探索的区域，从而失去了最基本的探索。 数组中的最后一个群是侦察群。 对于这个蜂群，“不要进入别人的空间”的规则也适用，但不是整个蜂群，而是侦察蜂个体。

以下是修改版本的结果：

2022.11.21 21:53:19.695    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    1 Skin's; Func runs 1000 result: 14.009060385607679; Func runs 10000 result: 14.060603974847265
2022.11.21 21:53:25.104    Test_AO_ABCm (EURUSD,M1)    Score1: 0.99720; Score2: 1.00000
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    20 Skin's; Func runs 1000 result: 7.826824877236677; Func runs 10000 result: 8.735832346695558
2022.11.21 21:53:30.452    Test_AO_ABCm (EURUSD,M1)    Score1: 0.66082; Score2: 0.71028
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.645933304640949; Func runs 10000 result: 4.844246724239038
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    Score1: 0.48774; Score2: 0.49853
2022.11.21 21:53:40.060    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.44507700105064; Func runs 10000 result: 15.662273922787355
2022.11.21 21:53:45.363    Test_AO_ABCm (EURUSD,M1)    Score1: 0.96827; Score2: 0.98188
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.6397442648278924; Func runs 10000 result: 4.759146560755886
2022.11.21 21:53:50.697    Test_AO_ABCm (EURUSD,M1)    Score1: 0.22818; Score2: 0.29836
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.2349621811342104; Func runs 10000 result: 1.4191098624570897
2022.11.21 21:54:01.111    Test_AO_ABCm (EURUSD,M1)    Score1: 0.07742; Score2: 0.08897
2022.11.21 21:54:01.112    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 12.0; Func runs 10000 result: 15.0
2022.11.21 21:54:06.434    Test_AO_ABCm (EURUSD,M1)    Score1: 0.80000; Score2: 1.00000
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.7; Func runs 10000 result: 2.35
2022.11.21 21:54:11.768    Test_AO_ABCm (EURUSD,M1)    Score1: 0.11333; Score2: 0.15667
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    500 Megacity's; Func runs 1000 result: 0.572; Func runs 10000 result: 0.67
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    Score1: 0.03813; Score2: 0.04467
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    =============================
2022.11.21 21:54:22.235    Test_AO_ABCm (EURUSD,M1)    All score for C_AO_ABCm: 0.508357869056105

我们可以看出，修改后的算法在两个变量的两个函数上重复了成功，显示 100% 收敛。 总体来说，结果有所改善，最终得分变得更高：0.50836。 不幸的是，这并没有显着改善结果。 具有大量变量的函数的收敛问题与经典算法版本的实现相当。

顺便说一下，在修改后的版本中不再需要重新初始化配置单元的错误。


4. 测试结果

AO

运行次数

Skin

Forest

Megacity (离散)

最终结果

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

ACOm

1000

0.99502

0.69826

0.50498

0.99087

0.22374

0.08408

0.78667

0.11667

0.04224

0.54688

10,000

0.99599

0.86403

0.58800

0.99302

0.65571

0.17442

0.78667

0.26133

0.08208

RND

1000

0.98744

0.61852

0.49408

0.89582

0.19645

0.14042

0.77333

0.19000

0.14283

0.51254

10,000

0.99977

0.69448

0.50188

0.98181

0.24433

0.14042

0.88000

0.20133

0.14283

ABCm

1000

0.99720

0.66082

0.48774

0.96827

0.22818

0.07742

0.80000

0.11333

0.03813

0.50836

10,000

1.00000

0.71028

0.49853

0.98188

0.29836

0.08897

1.00000

0.15667

0.04467

ABC

1000

0.99772

0.64085

0.49029

0.94435

0.18937

0.07526

0.69333

0.10333

0.04120

0.49447

10,000

1.00000

0.68769

0.49823

0.99755

0.26279

0.08077

1.00000

0.15400

0.04379

PSO

1000

0.98436

0.72243

0.65483

0.71122

0.15603

0.08727

0.53333

0.08000

0.04085

0.47695

10,000

0.99836

0.72329

0.65483

0.97615

0.19640

0.09219

0.82667

0.10600

0.04085


我们汇总一下。 令人惊讶的是，蜂群算法在两个测试函数（平滑 Skin 和离散 Megacity）的所有五次测试中都显示出 100% 的收敛性，从而展示了惊人的收敛速度和品质。 然而，这仅适用于具有两个变量的函数。 在可伸缩性方面，该算法不如评级表的其它成员。 具有多个变量的函数绝对不是蜂群的强项。 这既可以在测试台的动画中看到，也可以在表中提供的结果中看到。

ABC 算法要求用户在若干个参数设置上做些手脚，如群体规模，侦察峰数量、和面积半径。 如果未针对特定应用程序正确选择这些设置，则算法可能会过早收敛，或根本不收敛。 此外，ABC 还存在缺点，譬如复杂函数收敛慢、局部解捕获、搜索属性平庸。

优点:
1. 相对快速。
2. 具有惊人的收敛性，适用于变量很少的平滑和离散函数。

缺点:
1. 算法参数对结果的影响强烈。
2. 非通用性。
3. 局部极端卡陷。
4. 可扩展性平均。


本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/11736

附加的文件 |
下载ZIP
94_The_world_of_AO_qABCn.zip (44.93 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
神经网络变得轻松（第三十四部分）：全部参数化的分位数函数 神经网络变得轻松（第三十四部分）：全部参数化的分位数函数
我们继续研究分布式 Q-学习算法。 在之前的文章中，我们研究了分布式和分位数 Q-学习算法。 在第一种算法当中，我们训练了给定数值范围的概率。 在第二种算法中，我们用给定的概率训练了范围。 在这两个发行版中，我们采用了一个先验分布知识，并训练了另一个。 在本文中，我们将研究一种算法，其允许模型针对两种分布进行训练。
非线性指标 非线性指标
在本文中，我将尝试研究一些构建非线性指标的方法，并探索其在交易中的用处。 MetaTrader 交易平台中有相当多的指标采用非线性方式。
种群优化算法：灰狼优化器（GWO） 种群优化算法：灰狼优化器（GWO）
我们来研究一种最新的现代优化算法 — 灰狼优化。 测试函数的原始行为令该算法成为以前研究过的算法中最有趣的算法之一。 这是训练神经网络的顶级算法之一，具有许多变量的平滑函数。
构建自动运行的 EA（第 07 部分）：账户类型（II） 构建自动运行的 EA（第 07 部分）：账户类型（II）
今天，我们将看到如何创建一个在自动模式下简单安全地工作的智能系统。 交易者应当始终明白自动 EA 正在做什么，以便若它“偏离轨道”，交易者可以尽早将其从图表中删除，并控制事态。