
群体优化算法:带电系统搜索(CSS)算法
目录
1.概述
在物理学中,电荷周围的空间具有一种称为电场的特性。这种场对其他带电物体产生一种力。点电荷周围的电场由库仑定律决定。库仑证实,任何两个带电小球之间的电场力与粒子间沿连接线的距离的平方成反比,与两个粒子的电荷乘积成正比。此外,还可以利用高斯定律,即电场大小与粒子间的距离成正比,来求得带电球体内部某个点的电场大小。利用这些原理,CSS 定义了一组可能的解决方案,称为带电粒子。每个粒子都被视为一个带电的球体(与电磁算法不同,电磁算法中的粒子是一个一维点),可以对其他介质(带电粒子)产生电效应。
另一方面,牛顿第二定律解释说,物体的加速度与作用在该物体上的净力成正比。因此,作用在粒子上的电场力会导致粒子加速。根据牛顿力学,如果粒子在空间中的位置、速度和加速度在前一时刻是已知的,那么被视为无限小质量点的粒子在任何时候的位置都是完全已知的。CSS 利用牛顿力学的运动规律来确定粒子的位置。理论上,这些定律的应用应该在算法的探索和开发之间提供良好的平衡。
带电系统搜索(CSS)由 A. Kaveh 和 S. Talatahari 于 2010 年首次提出。
优化是解决数学建模和机器学习问题的重要组成部分。元启发式算法是一类有效且流行的优化方法。元启发式可以理解为一种算法,它随机搜索接近最优的问题的可能解决方案,直到满足特定条件或达到给定的迭代次数。
在科学文献中,元启发式被认为是将基本的启发式方法结合到更高级别的算法方案中,从而更有效地探索搜索空间和决策。这通常比开发新的专门启发式方法所需的工作量要少。我们面临的挑战是如何调整通用的元启发式方案,以解决困难的优化问题。此外,元启发式的有效实现可以确保在可接受的时间内找到接近最优的解决方案。通过各种不同的方法来理解元启发式方法,我们就有可能提出一些基本特性来描述元启发式方法。近年来,元启发式方法的使用越来越多,人们一直在努力提高算法的能力,缩短优化时间。
2.算法
CSS算法以球体的形式操作带电粒子。球体的最小尺寸由外部参数决定(它是沿着搜索空间的所有坐标的最大可能欧几里得距离的一部分),当粒子以小于球体半径的距离接近时,排斥力作用在粒子上。同时,粒子之间的作用力方向也会受到它们之间电荷差异的影响。该算法会考虑上一次迭代时的坐标值,从而模拟粒子速度。加速度(粒子运动的一个组成部分)受电荷及其相互距离的影响。
综上所述,让我们写下该算法的伪代码步骤:
1.用搜索空间中的初始随机位置初始化粒子,同时为上一次迭代设置空间中的随机位置(我们假设有上一次迭代)。
2.计算适应度函数值。
3.利用公式计算粒子的下一个位置。
4.在所有粒子中确定适应度函数的最佳值和最差值。
5.重复步骤 2,直到满足停止条件。
让我们来看看粒子相互运动的计算公式。带电粒子的主要特征是其电荷:
q = (φp - φw) / (φb - φw)
其中:- q - 当前粒子电荷
- φp - 粒子适应度函数值
- φb - 所有粒子中的最佳适应度函数值
- φw - 所有粒子中最差的适应度函数值
要确定粒子间的距离,我们将使用公式:
r(i,j) = (|Xi - Xj|) / (|(Xi - Xj) * 0.5 - Xb|)
其中:
- || - 欧氏距离
- r(i,j)--粒子 i 和 j 之间的距离
- Xi和Xj--i和j粒子的相应坐标
- Xb - 在所有迭代中找到的最佳位置的相应坐标。
显然,在这里,作者的想法是考虑粒子相对于最佳全局坐标的位置。这可能是个好主意,但我的实验表明,这种算法的最佳解决方案是只计算等式中的分子。
与电磁EM算法一样,相互作用力可以是吸引的,也可以是排斥的。让我们来表示变量 c 的方向符号。使用以下条件表达式来考虑力的方向:
如果 φi < φj,则 c =-1,否则 c = 1
其中:
- c - 相互作用力方向的符号
- φi 和 φj - i 和 j 粒子的适应度函数值
力方向的符号可以这样解释,即适应度函数值较小的粒子排斥,而值较大的粒子吸引。
由于我们一致认为,与EM算法不同,粒子是一个半径大于0的球体(算法的外部参数),因此粒子上的力与相应的坐标共线(在我们的算法中,粒子上的总力是一组矢量),可以表示为方程:
F = qi * Q * c * (Xj - Xi)
其中:
- F - 影响粒子的作用力
- qi - 计算作用力的粒子
- Q - 考虑到两个粒子的相对位置的分量,取决于它们的球体相互穿透,Q 的方程:
Q = ((qj * r(i,j) * b1) / a^3) + (qj * b2) / r(i,j)^2
其中:
- qj - 影响所考虑粒子的电荷量
- b1 和 b2 表示“启用/禁用”相应的表达式项。对于r>=颗粒半径,b1=0 并且 b2=1。否则,b1 = 1,b2 = 0。
最后,我们可以利用公式计算出粒子运动的新坐标:
Xn = X + λ1 * U * V + λ2 * U * coordinatesNumber * (F / qi)
其中:
- Xn - 新坐标
- λ1 - 权重系数(外部参数),决定第二项 - 速度的影响程度
- λ2 - 权重系数(外部参数),决定第三项 - 加速度的影响程度
- U - 范围 [0;1] 内的随机数
- V - 当前迭代与上一次迭代的坐标之间的差
- coordinatesNumber - 坐标数。这个 "比率 "并不包括在最初的等式中。我引入它的原因是,随着搜索空间维度的增加,λ2 比率也必须增加(因此,引入它是为了避免 "冻结 "粒子的效果)。
λ1 和 λ2 的相对值决定了多样化和搜索集约化之间的平衡。增加 λ1 参数值会增强粒子先前位置的影响,从而提高算法的研究特性。较大的 λ2 值会导致吸引力的强烈影响,并可能导致算法的过早收敛。相反,小数值会减慢算法的收敛速度,从而为搜索区域提供更广阔的探索空间。
让我们开始分析 CSS 算法代码。该算法的搜索代理是一个粒子,可以方便地表示为 S_Particle 结构。
粒子结构包括以下字段:
- -c:粒子坐标数组。该数组包含粒子在空间中的当前坐标。
- -cPrev:前一个粒子坐标数组。该数组包含粒子在空间中的前一个坐标。
- -cNew:新粒子坐标数组。该数组包含将用于下一次算法迭代的新粒子坐标。
- -q:粒子电荷。该值代表分配给该粒子的电荷。电荷只能取 0 以外的正值。
- -f:粒子适应度函数值。
由于粒子及其电荷结构中新坐标数组的存在,尽管这些量可以以变量的形式保留,供所有粒子通用(乍一看,这似乎是合乎逻辑的),但由于其特点,简化算法成为可能。
//—————————————————————————————————————————————————————————————————————————————— struct S_Particle { double c []; //coordinates double cPrev []; //coordinates double cNew []; //coordinates double q; //particle charge double f; //fitness }; //——————————————————————————————————————————————————————————————————————————————
声明 C_AO_CSS 类,其中包括:
- - p:粒子数组
- - rangeMax:数组,包含每个坐标的最大搜索范围值
- - rangeMin:数组,包含每个坐标的最小搜索范围值
- - rangeStep:数组,包含每个坐标的搜索步长
- - cB:数组,包含找到的最佳坐标
- - fB:最佳坐标的适应度函数值
- - fW:最差坐标的适应度函数值
类方法:
- - Init:初始化算法参数(坐标数、粒子数、半径大小、速度和加速度比)
- - Moving:执行粒子移动
- - Revision:对最佳坐标进行更新
类的私有属性:
- - coordinatesNumber:坐标数
- - particlesNumber:粒子数
- - radius:半径大小
- - speedCo: 速度比
- - accelCo:加速度比
- - F:力矢量
- - revision:表示需要修订的标志
类的私有方法:
- - SeInDiSp: 以给定步长计算给定范围内的新坐标值
- - RNDfromCI:在给定区间内生成随机数
//—————————————————————————————————————————————————————————————————————————————— class C_AO_CSS { //---------------------------------------------------------------------------- public: S_Particle p []; //particles public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: double fW; //FF of the worst coordinates public: void Init (const int coordinatesNumberP, //coordinates number const int particlesNumberP, //particles number const double radiusSizeP, //radius size const double speedCoP, //speed coefficient const double accelCoP); //acceleration coefficient public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coordinatesNumber; //coordinates number private: int particlesNumber; //particles number private: double radius; //radius size private: double speedCo; //speed coefficient private: double accelCo; //acceleration coefficient private: double F []; //force vector private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
C_AO_CSS 方法初始化类对象的参数。它的参数包括坐标数、粒子数、半径大小、速度和加速度比。
在该方法中,会重置随机数发生器,以及设置 fB 和 revison 变量的初始值。然后将参数值赋值给相应的对象变量。
接下来,rangeMax、rangeMin、rangeStep、F、p 和 cB 数组的大小会随着坐标和粒子数量的变化而变化。
然后循环调整每个粒子的数组大小,并为每个粒子设置变量 f 的初始值。
方法结束时,cB 数组的大小会随着坐标数的变化而变化。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSS::Init (const int coordinatesNumberP, //coordinates number const int particlesNumberP, //particles number const double radiusSizeP, //radius size const double speedCoP, //speed coefficient const double accelCoP) //acceleration coefficient { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coordinatesNumber = coordinatesNumberP; particlesNumber = particlesNumberP; radius = radiusSizeP; speedCo = speedCoP; accelCo = accelCoP; ArrayResize (rangeMax, coordinatesNumber); ArrayResize (rangeMin, coordinatesNumber); ArrayResize (rangeStep, coordinatesNumber); ArrayResize (F, coordinatesNumber); ArrayResize (p, particlesNumber); for (int i = 0; i < particlesNumber; i++) { ArrayResize (p [i].c, coordinatesNumber); ArrayResize (p [i].cPrev, coordinatesNumber); ArrayResize (p [i].cNew, coordinatesNumber); p [i].f = -DBL_MAX; } ArrayResize (cB, coordinatesNumber); } //——————————————————————————————————————————————————————————————————————————————
移动粒子(搜索代理)的主要逻辑在 Moving() 方法中实现。
在第一次迭代时,用范围从 rangeMin 到 rangeMax 的随机数初始化粒子坐标的初始值,并取粒子适应度值等于 `-DBL_MAX`。
RadiusSize_P 算法的外部参数是以所有坐标的最大可能欧氏距离为单位确定粒子大小的,即每个坐标的最大允许值和最小允许值之间的平方差之和的根。
在代码末尾,"revision "变量被设置为 "true"。
//---------------------------------------------------------------------------- if (!revision) { fB = -DBL_MAX; for (int obj = 0; obj < particlesNumber; obj++) { for (int c = 0; c < coordinatesNumber; c++) { p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); p [obj].cPrev [c] = RNDfromCI (rangeMin [c], rangeMax [c]); p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); p [obj].cPrev [c] = SeInDiSp (p [obj].cPrev [c], rangeMin [c], rangeMax [c], rangeStep [c]); p [obj].f = -DBL_MAX; } } double r = 0.0; double t = 0.0; for (int c = 0; c < coordinatesNumber; c++) { t = rangeMax [c] - rangeMin [c]; r += t * t; } radius *= sqrt (r); revision = true; }
Moving() 方法代码的剩余部分在第二次迭代和后续迭代中执行,负责在搜索空间中移动粒子。
首先计算适应度函数 fB 值和 fW 值之间的差值(所有迭代中找到的最佳坐标和当前迭代中粒子的最差坐标),并将其存储在 "difference" 变量中。如果 "difference" 为 0.0,则赋值为 1.0。
然后是循环,在循环中为每个粒子计算一个新值。对于每个粒子 i,都会计算出新的电荷 q 值。
接下来,对变量 summ1、summ2、q、e、c、b1、b2、X、Q、U、V、t1 和 t2 进行声明和初始化,以便在上述公式中使用。
在循环中,对于每个粒子,我们都要计算出作用在粒子群中所有其他粒子上的总力 F。对每 i 个粒子进行循环,计算 summ1 和 summ2 的总和。然后计算 i 和 j 粒子之间的 r 距离。如果 r 为 0.0,则其值为 0.01,以避免除以 0。然后根据 r 和 "radius "的值计算出 b1 和 b2 的值。然后,根据两个粒子的适应度值计算出力的方向 c 值。接下来,我们计算 Q 值。然后计算每个 k 坐标的力值 F[k]。
有了作用在粒子上的力的矢量值,我们就可以计算出粒子运动的新坐标值。然后进行一个循环,更新粒子 i 先前的坐标值和当前的坐标值。
代码中用注释元素的方式保留了部分原始公式,以显示 CSS 作者是如何完成的。
double difference = fB - fW; if (difference == 0.0) difference = 1.0; for (int i = 0; i < particlesNumber; i++) { p [i].q = ((p [i].f - fW) / difference) + 0.1; } double summ1 = 0.0; double summ2 = 0.0; double q = 0.1; double e = 0.001; double c = 0.0; double b1 = 0.0; double b2 = 0.0; double X = 0.0; double Q = 0.0; double U = 0.0; double V = 0.0; double t1 = 0.0; double t2 = 0.0; for (int i = 0; i < particlesNumber && !IsStopped (); i++) { ArrayInitialize (F, 0.0); for (int j = 0; j < particlesNumber && !IsStopped (); j++) { if (i == j) continue; summ1 = 0.0; summ2 = 0.0; for (int k = 0; k < coordinatesNumber && !IsStopped (); k++) { t1 = p [i].c [k] - p [j].c [k]; summ1 += t1 * t1; //t2 = t1 * 0.5 - cB [k]; //summ2 += t2 * t2; } //r = sqrt (summ1) / (sqrt (summ2) + e); r = sqrt (summ1); if (r == 0.0) r = 0.01; if (r >= radius) { b1 = 0.0; b2 = 1.0; } else { b1 = 1.0; b2 = 0.0; } c = p [i].f < p [j].f ? -1.0 : 1.0; q = p [j].q; Q = ((q * r * b1 / (radius * radius * radius)) + (q * b2 / (r * r))) * c; for (int k = 0; k < coordinatesNumber && !IsStopped (); k++) { F [k] += /*p [i].q */ Q * (p [j].c [k] - p [i].c [k]); } } for (int k = 0; k < coordinatesNumber && !IsStopped (); k++) { V = p [i].c [k] - p [i].cPrev [k]; U = RNDfromCI (0.0, 1.0); X = p [i].c [k] + speedCo * U * V + accelCo * U * coordinatesNumber * (F [k] / p [i].q); p [i].cNew [k] = SeInDiSp (X, rangeMin [k], rangeMax [k], rangeStep [k]); } } for (int i = 0; i < particlesNumber && !IsStopped (); i++) { for (int k = 0; k < coordinatesNumber && !IsStopped (); k++) { p [i].cPrev [k] = p [i].c [k]; p [i].c [k] = p [i].cNew [k]; } }
最后是 Revision() 方法。
在该方法开始时,变量 fW 被赋予 double 类型的最大值(DBL_MAX),这样我们就能以适应度函数的最小值确定最差的粒子。
然后在所有系统粒子中进行循环。每个粒子都会执行以下操作:
- 如果当前粒子的 f 值大于 fB(所有粒子的最佳适应度函数),则用当前粒子的 f 值更新 fB 值,并从当前粒子的位置复制 cB 数组(最佳位置)。
- 如果当前粒子的 f 值小于 fW 值(所有粒子的适应度函数最小值),则用当前粒子的 f 值更新 fW 值。
因此,这段代码会在所有粒子中找出最佳和最差的适应度函数,并更新相应的值。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSS::Revision () { fW = DBL_MAX; for (int i = 0; i < particlesNumber; i++) { if (p [i].f > fB) { fB = p [i].f; ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY); } if (p [i].f < fW) { fW = p [i].f; } } } //——————————————————————————————————————————————————————————————————————————————
3.测试结果
测试平台上带电系统搜索算法的打印输出:
C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Rastrigin's; Func runs 10000 result:70.43726076935499
Score:0.87276
25 Rastrigin's; Func runs 10000 result:68.88569793414477
Score:0.85353
500 Rastrigin's; Func runs 10000 result:66.01225385184436
Score:0.81793
=============================
5 Forest's; Func runs 10000 result:0.4891262437640296
Score:0.27667
25 Forest's; Func runs 10000 result:0.1494549763925046
Score:0.08454
500 Forest's; Func runs 10000 result:0.07829232143185726
Score:0.04429
=============================
5 Megacity's; Func runs 10000 result:2.04
Score:0.17000
25 Megacity's; Func runs 10000 result:0.744
Score:0.06200
500 Megacity's; Func runs 10000 result:0.26880000000000004
Score:0.02240
=============================
All score:3.20412
算法运算结果的打印结果显示总体结果较低。需要注意的是,对于 10、50 和 1000 个变量的 Rastrigin 函数,适应度函数值的结果差别不大。下面,我们将尝试弄清楚这意味着什么。
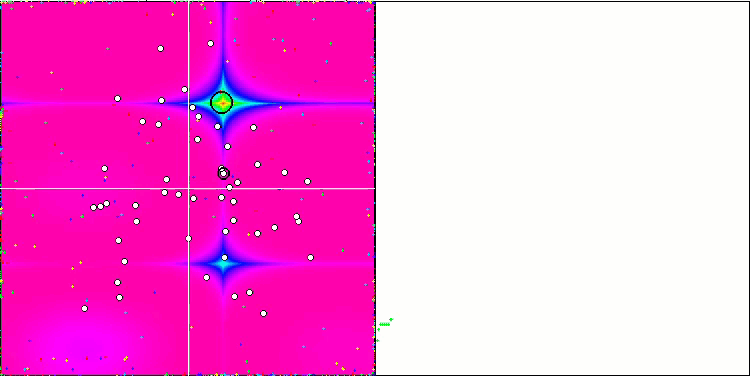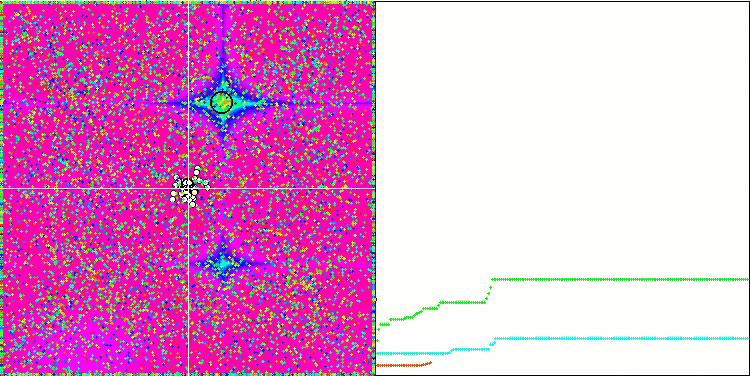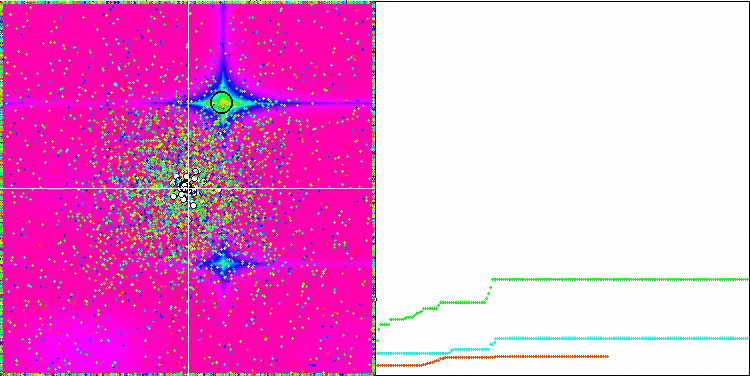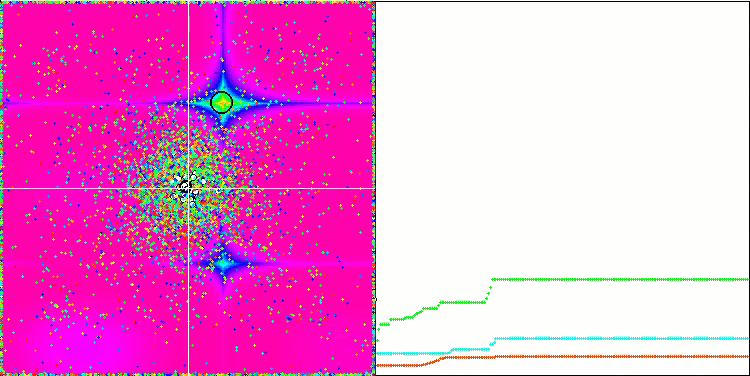
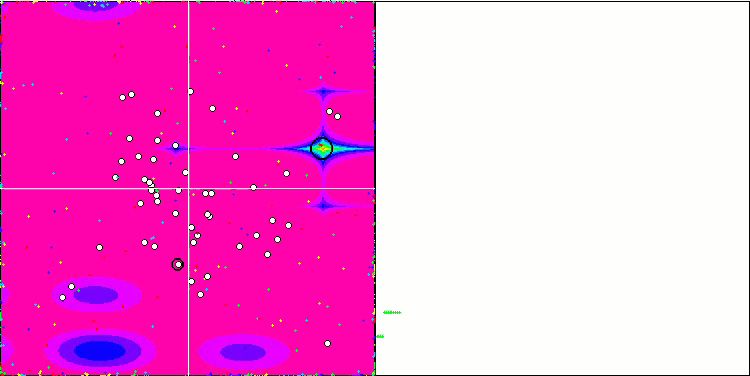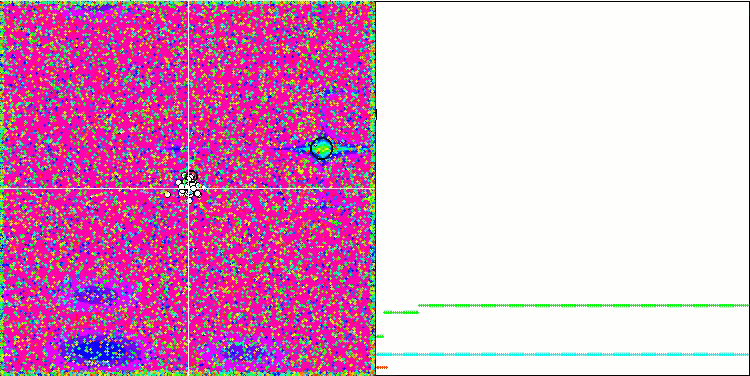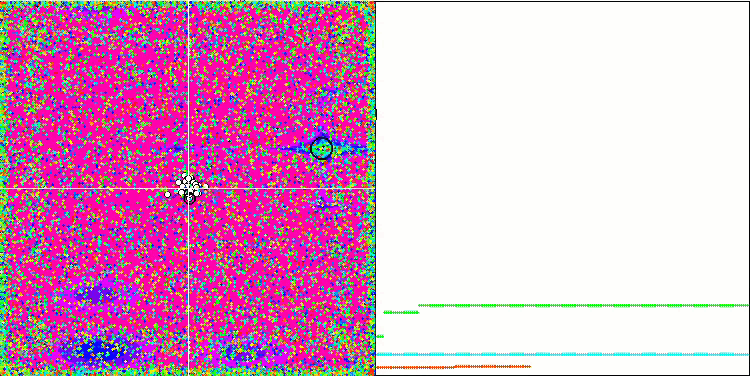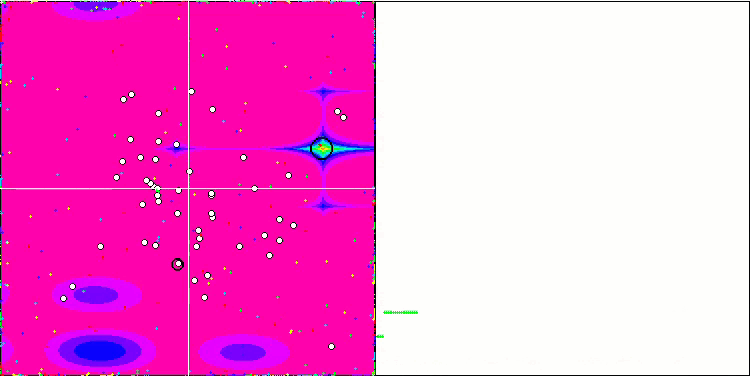
对 Rastrigin 测试函数的可视化显示,粒子群沿着重要的局部极值出现了明显的分化,这意味着对局部区域进行了很好的研究,但在 Forest 和 Megacity 函数中却没有观察到类似的行为,粒子群的表现就像一团没有形状的云。收敛图中较长的水平部分表明,该算法有陷入局部极值的倾向,不过,该算法在平滑 Rastrigin 函数上的出色可扩展性在一定程度上弥补了这一重大缺陷。
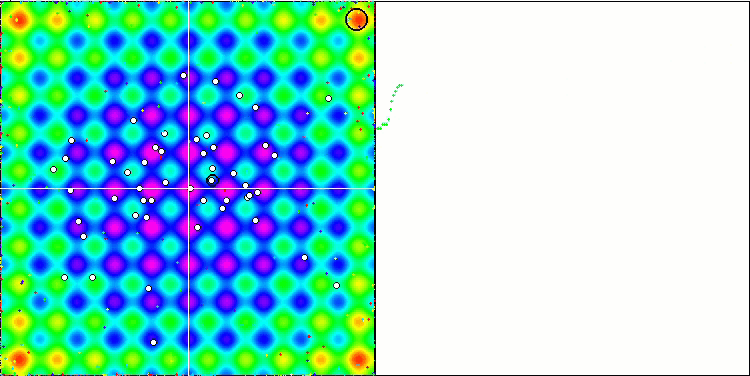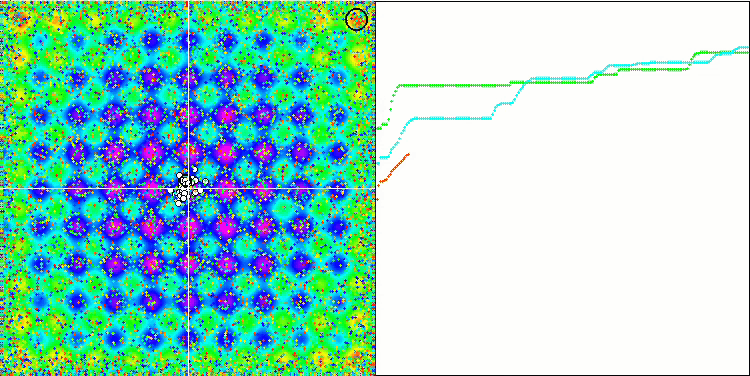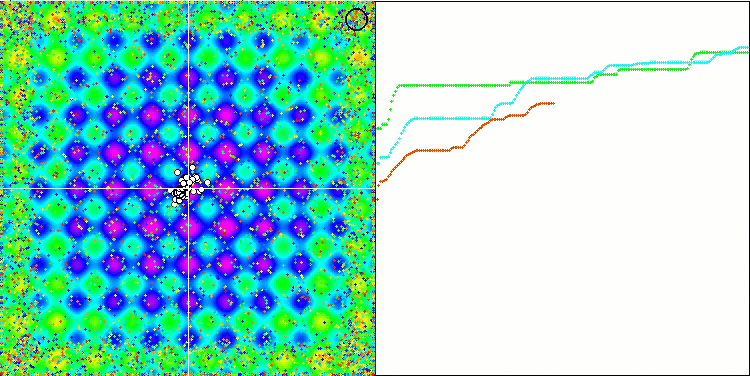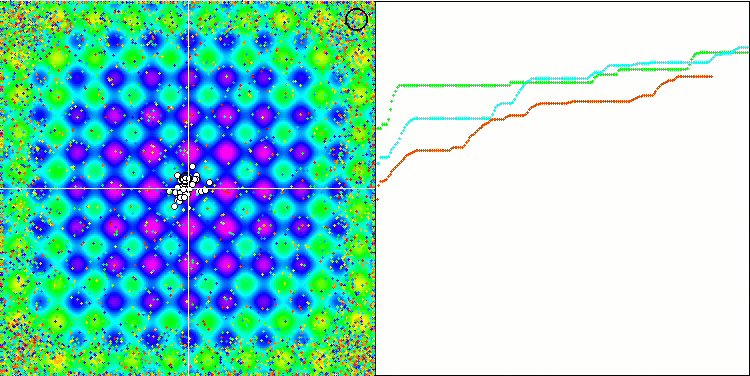
关于Rastrigin 测试函数的 CSS。
Forest测试函数 上的 CSS。
Megacity测试函数上 的 CSS。
对 CSS 算法的测试为优化平滑函数找到了新的领先者。之前的 Rastrigin 函数领先者也是一种受无生命自然启发的算法--电磁搜索(EM)。这次的新纪录比之前的纪录高出近 10%。遗憾的是,该算法在具有尖锐全局极值的 Forest 函数和离散 Megacity 函数上表现出最差的结果。由于 Rastrigin 算法在 1000 个变量上取得了令人印象深刻的结果,该算法在 20 个总参数中排名第 13 位。在测试规定的 10,000 次 CSS 算法运行过程中,CSS 无法接近全局极值的 90%(见上图测试平台的打印结果)。
| # | AO | 描述 | Rastrigin | Rastrigin 最终 | Forest | Forest 最终 | Megacity (discrete) | Megacity 最终 | 最终结果 | ||||||
| 10 p(5 F) | 50 p(25 F) | 1000 p(500 F) | 10 p(5 F) | 50 p(25 F) | 1000 p(500 F) | 10 p(5 F) | 50 p(25 F) | 1000 p(500 F) | |||||||
| 1 | SDS | 随机扩散搜索(stochastic diffusion search) | 0.99737 | 1.00000 | 0.58904 | 2.58641 | 0.96893 | 1.00000 | 0.95092 | 2.91985 | 1.00000 | 1.00000 | 0.72149 | 2.72149 | 100000 |
| 2 | SSG | 树苗播种和生长(saplings sowing and growing) | 1.00000 | 0.95313 | 0.51630 | 2.46944 | 0.72740 | 0.69680 | 1.00000 | 2.42421 | 0.69612 | 0.65918 | 1.00000 | 2.35531 | 87.506 |
| 3 | HS | 和声搜索(harmony search) | 0.99676 | 0.90817 | 0.44686 | 2.35179 | 1.00000 | 0.72930 | 0.44806 | 2.17736 | 0.91159 | 0.76578 | 0.41537 | 2.09274 | 79.501 |
| 4 | ACOm | 蚁群优化M(ant colony optimization M) | 0.34611 | 0.17142 | 0.15808 | 0.67562 | 0.86888 | 0.73719 | 0.77362 | 2.37968 | 0.91159 | 0.68163 | 0.05606 | 1.64929 | 55.026 |
| 5 | IWO | 入侵性杂草优化(invasive weed optimization) | 0.95828 | 0.63939 | 0.27647 | 1.87415 | 0.70773 | 0.34168 | 0.31773 | 1.36714 | 0.72927 | 0.32539 | 0.33289 | 1.38756 | 54.060 |
| 6 | MEC | 思维进化计算(mind evolutionary computation) | 0.99270 | 0.48648 | 0.21148 | 1.69066 | 0.60762 | 0.29973 | 0.25459 | 1.16194 | 0.85083 | 0.31978 | 0.26170 | 1.43231 | 49.669 |
| 7 | COAm | 布谷鸟优化算法 M(cuckoo optimization algorithm M) | 0.92400 | 0.44601 | 0.24120 | 1.61121 | 0.58378 | 0.25090 | 0.16526 | 0.99994 | 0.66298 | 0.25666 | 0.17083 | 1.09047 | 42.223 |
| 8 | FAm | 萤火虫算法 M(firefly algorithm M) | 0.59825 | 0.32387 | 0.15893 | 1.08106 | 0.51073 | 0.31182 | 0.49790 | 1.32045 | 0.31491 | 0.21880 | 0.35258 | 0.88629 | 36.941 |
| 9 | ABC | 人工蜂群(artificial bee colony) | 0.78170 | 0.31182 | 0.19313 | 1.28664 | 0.53837 | 0.15816 | 0.13344 | 0.82998 | 0.51381 | 0.20758 | 0.13926 | 0.86064 | 32.977 |
| 10 | BA | 蝙蝠算法(bat algorithm) | 0.40526 | 0.60773 | 0.78330 | 1.79629 | 0.20841 | 0.12884 | 0.25989 | 0.59714 | 0.27073 | 0.08135 | 0.17371 | 0.52579 | 32.236 |
| 11 | GSA | 重力搜索算法(gravitational search algorithm) | 0.70167 | 0.43098 | 0.00000 | 1.13265 | 0.31660 | 0.26845 | 0.33204 | 0.91710 | 0.54144 | 0.27208 | 0.00000 | 0.81352 | 31.522 |
| 12 | BFO | 细菌觅食优化(bacterial foraging optimization) | 0.67203 | 0.29511 | 0.10957 | 1.07671 | 0.39702 | 0.19626 | 0.20652 | 0.79980 | 0.47514 | 0.25807 | 0.18932 | 0.92253 | 30.702 |
| 13 | CSS | 带电系统搜索(charged system search) | 0.56605 | 0.70573 | 1.00000 | 2.27178 | 0.14081 | 0.01980 | 0.16282 | 0.32343 | 0.09393 | 0.00000 | 0.03481 | 0.12874 | 29.743 |
| 14 | EM | 类电磁算法(electroMagnetism-like algorithm) | 0.12235 | 0.44109 | 0.92752 | 1.49096 | 0.00000 | 0.02578 | 0.34880 | 0.37458 | 0.00000 | 0.00562 | 0.10924 | 0.11486 | 20.252 |
| 15 | SFL | 混合蛙跳(shuffled frog-leaping) | 0.40072 | 0.22627 | 0.24624 | 0.87323 | 0.20153 | 0.03057 | 0.02652 | 0.25862 | 0.24862 | 0.04769 | 0.06639 | 0.36270 | 14.050 |
| 16 | MA | 猴子算法(monkey algorithm) | 0.33192 | 0.31883 | 0.13582 | 0.78658 | 0.10012 | 0.05817 | 0.08932 | 0.24762 | 0.19889 | 0.03787 | 0.10720 | 0.34396 | 12.564 |
| 17 | FSS | 鱼群搜索(fish school search) | 0.46812 | 0.24149 | 0.10483 | 0.81445 | 0.12840 | 0.03696 | 0.06516 | 0.23052 | 0.15471 | 0.04208 | 0.08283 | 0.27961 | 11.880 |
| 18 | PSO | 粒子群优化(particle swarm optimisation) | 0.20449 | 0.07816 | 0.06641 | 0.34906 | 0.18895 | 0.07730 | 0.21738 | 0.48363 | 0.21547 | 0.05049 | 0.01957 | 0.28553 | 9.246 |
| 19 | RND | 随机(random) | 0.16826 | 0.09287 | 0.07438 | 0.33551 | 0.13496 | 0.03546 | 0.04715 | 0.21757 | 0.15471 | 0.03507 | 0.04922 | 0.23900 | 5.083 |
| 20 | GWO | 灰狼优化器(grey wolf optimizer) | 0.00000 | 0.00000 | 0.02093 | 0.02093 | 0.06570 | 0.00000 | 0.00000 | 0.06570 | 0.29834 | 0.06170 | 0.02557 | 0.38561 | 1.000 |
总结
我不得不进行大量的实验和代码编辑,以迫使粒子在场中移动,而不会“粘在一起”和“冻结”。算法作者没有考虑到优化参数的数量对优化质量的影响(随着问题维度的增加,收敛性会不成比例地迅速恶化)。在等式中加入更多坐标可以增强加速度的效果,提高 CSS 的性能(如果不做这些改动,算法显示的结果很差)。粒子运动的固有规律对于研究目的的任何变化都过于反复无常,因此使提高这种有趣的优化算法性能的尝试变得复杂。
该算法是优化平滑函数的有效方法。它使用了由库仑力相互连接的带电粒子云。当使用这种有趣的算法时,应该考虑到它对离散搜索空间域问题的低适用性。不过,在以往探讨过的多变量平滑函数优化算法中,这是最好的优化算法。CSS 可用于具有大量变量的所有优化领域。它既不需要梯度信息,也不需要搜索空间的连续性。
为了更直观地表示各个算法的优点和缺点,可以使用图1中的色标来表示上表。根据具体的优化问题,表的颜色等级可以更清楚地表示使用每个单独算法的可能性。目前,我还无法找到一个完美通用的算法来解决任何问题(也许我能在后续的研究中找到一个)。
例如,如果我们考虑评级中的第一个算法(SDS),那么它在单个测试问题上不是最好的(表中给出了具有多个变量的光滑函数的平均值)。至于 ACOm 算法,其单独的结果远低于表中的平均值(它对平滑函数的求解出奇地差),但它对 Forest 和离散 Megacity 的处理非常好(它最初是为解决离散问题而设计的,如旅行推销员问题),尽管可扩展性还有很多不足之处。
最后介绍的算法(CSS)在有 1000 个变量的 Rastrigin 函数上运行良好(对于训练有许多参数的神经网络来说,这可能是一个很好的选择),在所有之前探讨过的优化算法中显示出最好的结果,尽管从总结果来看,它在表中看起来并不是最好的。因此,根据问题的具体情况正确选择算法非常重要。
使用各种搜索策略对优化算法进行大规模测试后,发现了一个意想不到的事实 - 使用搜索策略可能比使用简单的随机搜索选择最佳结果更糟糕 - RND 从最底层算起位居第二名,而不是最后一名;GWO 结果比随机搜索更糟糕,但有 10 个参数的离散 Megacity 除外。
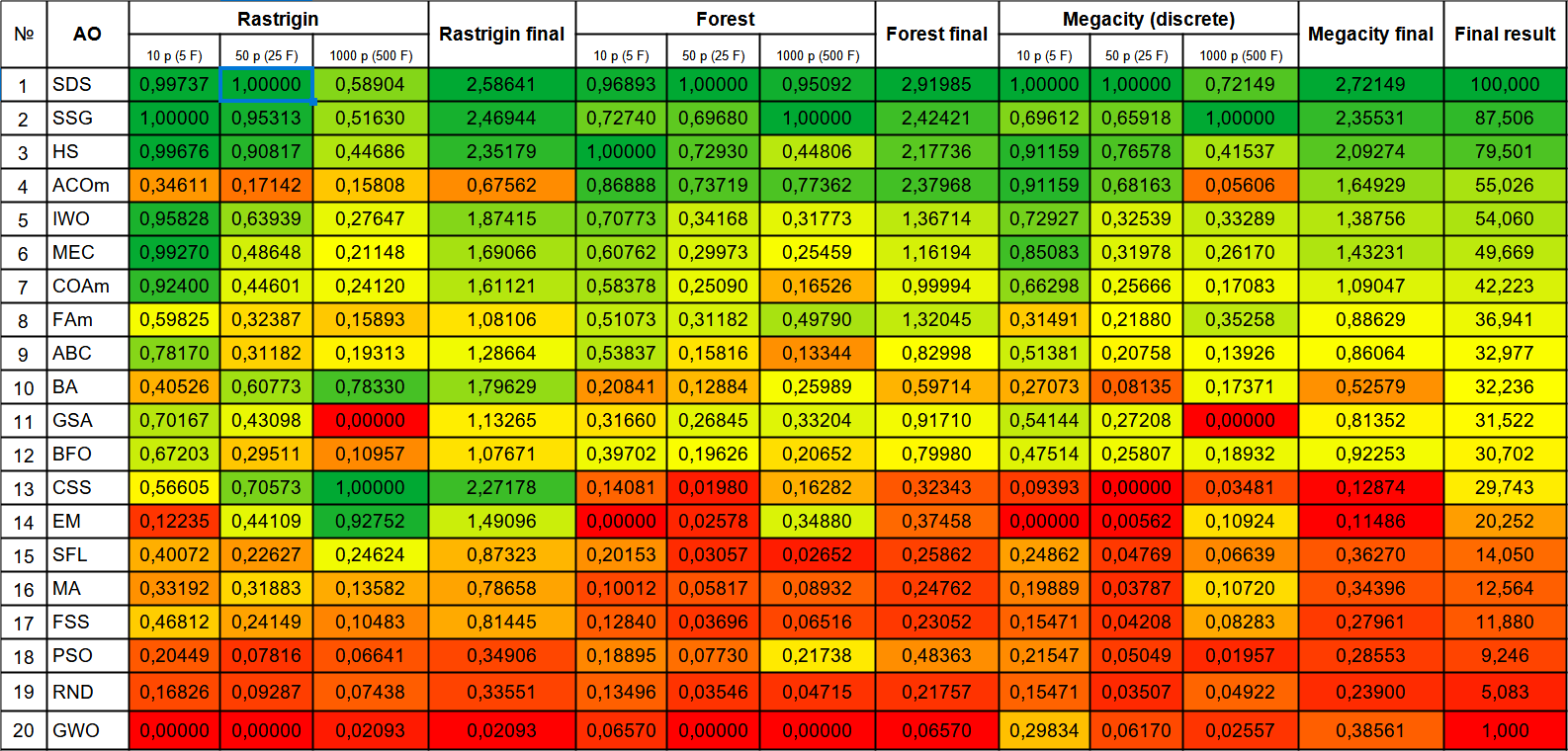
图 1.根据相关测试对算法进行颜色分级
算法测试结果直方图如下(从 0 到 100,越多越好,存档中有一个使用本文所述方法计算评级表的脚本):
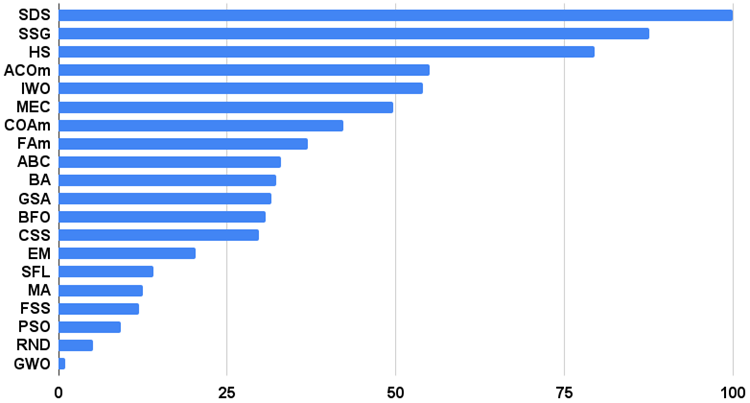
图 2.测试算法最终结果直方图
带电系统搜索(CSS)算法的优点和缺点:
优点:
1.平滑函数的高可扩展性。
2.外部参数数量少。
缺点:
1.离散函数的结果差。
2.收敛性低。
3.容易陷入局部极值。
每篇文章都附有一个存档,其中包含前几篇文章所述算法代码的最新版本。文章作者不对规范算法描述的绝对准确性负责。为提高搜索能力,已对其中多项功能进行了修改。文章中提出的结论和判断都是基于实验结果。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/13662
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 神经网络变得简单(第 63 部分):决策转换器无监督预训练(PDT)
神经网络变得简单(第 63 部分):决策转换器无监督预训练(PDT)
 开发具有 RestAPI 集成的 MQL5 强化学习代理(第 1 部分):如何在 MQL5 中使用 RestAPI
开发具有 RestAPI 集成的 MQL5 强化学习代理(第 1 部分):如何在 MQL5 中使用 RestAPI
 神经网络变得简单(第 62 部分):在层次化模型中运用决策转换器
神经网络变得简单(第 62 部分):在层次化模型中运用决策转换器
有人真的用这些算法赚钱的吗?