种群优化算法：类电磁算法（EM - ElectroMagnetism）

内容：

1. 概述
2. 算法
3. 测试结果

1. 概述

在过去的几十年间，世界各地的研究人员提出了许多元启发式搜索方法来解决复杂的全局优化问题，以及改进它们的方法。

类电磁（ЕМ）算法是一种相对较新的元启发式搜索算法，基于物理空间中电磁粒子行为的模拟，由 I. Birbil 和 S.С. Fang 于 2003 年首次引入。 它被描述为一种群体的进化算法，具有随机噪声和基于电磁的带电粒子之间相互作用。

该算法的灵感来自电磁学理论中电荷的吸引和排斥机制，用于在连续域中不受限制地求解非线性优化问题。 由于其能够解决复杂的全局优化问题，EM 在许多领域被广泛用作优化工具。

关于电磁学和电荷的有趣事实：

• 有两种类型的电荷：正电荷和负电荷。 所有电荷即可为正值亦或为负值。
• 电磁场可以无线电波的形式传输信息。 我们每天在收听广播或看电视时即利用的此功能。
• 我们有地球磁场，它可以保护我们免受太阳风和宇宙射线的伤害。
• 有各种各样的材料可以被磁化，这令制造电磁铁成为可能。 电磁铁可用于各种应用，例如发电机。
• 有很多应用都基于电磁学。 例如，计算机、移动电话和其它设备均用到电磁技术。
• 所有发光物体（例如灯泡和车灯）都会发出电磁辐射。
• 电磁学在医学中也扮演着重要角色。 MRI 和 CT 等医疗设备均利用电磁场创建人体内部图像。
• 一些动物，如鲨鱼和电鳗，可以利用电磁在水中导航。
• 电磁力是自然界的四种基本力之一，另外还有万有引力、弱力和强力。

2. 算法

EM 以电磁学理论为指导，模拟电荷的吸引-排斥机制，利用有限变量实现全局最优解。 在算法中，所有解都被视为搜索空间中的带电粒子，每个粒子的电荷与目标函数的值相关联。 具有较佳目标输出的粒子将施加吸引力，而具有较差目标值的粒子将向其它粒子施加排斥力。 目标函数的值越好，粒子之间的吸引力或排斥力就越高。

该算法的原理是在初始阶段形成一组随机解，每个解由对应于电磁粒子上的电荷的坐标向量表示。 进而，在算法的每次迭代中，在电磁力的作用下模拟这些电荷在空间中的运动。 在运动时，每个电荷与其它电荷相互作用，导致运动方向和速度的变化。 结果，目标函数的最优值的解逐渐收敛。

EM 算法的主要组成部分是：

1. 形成初始解（电荷）群，其中每个电荷由坐标向量表示，并对应于优化问题的某个解。
2. 计算电荷之间相互作用的电磁力。 计算于算法的每次迭代中执行，并取决于电荷（解）之间的距离。
3. 电荷在电磁相互作用力影响下在空间中的运动。
4. 目标函数在每次迭代时更新公式解的群（例如，目标函数可以是机器学习问题中的损失函数）。
5. 判定算法停止的条件，例如，达到目标函数的某个值。

粒子相互作用，根据电荷和它们之间的距离吸引或排斥。 该算法在若干次迭代中执行，每次迭代都会更新粒子的坐标和电荷，并计算适应度函数的新值。

EM 优化算法的逻辑单元是一个粒子。 它可以通过 S_Particle 结构来描述，它是搜索空间中的代理者。 每个粒子都有 c[] 坐标，它决定了其在搜索空间中的位置，以及 C 电荷，它影响与其它粒子的相互作用。 对于每个粒子，计算适应度函数 f 的值，该值评估对应于给定坐标的解的质量。 此外，对于每个粒子，计算到其它粒子的距离 R 和力矢量 F，其可判定粒子在搜索空间中的运动方向。

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c  [];   //coordinates
  double C;       //charge
  double f;       //fitness
  double R  [];   //euclidean distance to other particles
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_EM 类是电磁优化算法的实现。 它基于给出的一组实数上查找函数的最佳值。 该算法基于模拟物理系统中磁性和电粒子之间的相互作用过程。

该类包含以下字段：

• S_Particle p[] - 表示优化问题潜在解的粒子数组。
• double rangeMax[] — 每个坐标的最大搜索范围值数组。
• double rangeMin[] — 每个坐标的最小搜索范围值数组。
• double rangeStep[] - 每个坐标的搜索步骤数组。
• double cB[] — 最佳解的坐标数组。
• double fB - 最佳函数解的值。

该类包含以下方法：

• void Init() 初始化算法，设置坐标数、粒子数、环境常数和移动步长。
• void Moving(int iter) 根据磁场和电场相互作用的规则迭代运动粒子的算法。
• void Revision() 对粒子进行修订，检查它们是否超出搜索范围，并在必要时调整它们的位置。

该类还包含私有字段：

• int coordinatesNumber —坐标数。
• int particlesNumber — 粒子数。
• double envConstant — 环境常数。
• double movConstant — 移动步长。
• double exponent — 距离指数。
• double vect[] — 向量数组。
• bool revision — 指示粒子需要修订的标志。

该类包含私密方法：

• double SeInDiSp(double In, double InMin, double InMax, double Step) 在均匀网格上分配点。
• double RNDfromCI(double min, double max) 在给定范围内生成一个随机数。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_EM
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double envConstantP,       //environmental constant
                     const double movConstantP,       //movement step
                     const double exponentP);         //exponent

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double envConstant;       //environmental constant
  private: double movConstant;       //movement step
  private: double exponent;          //exponent
  private: double vect    [];        //vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

“电磁算法”优化算法初始化方法从重置随机数生成器和设置某些变量的初始值开始。 然后，该方法将几个参数作为输入：坐标数、粒子数、环境值和移动步长。 接下来，该方法创建多个所需大小的数组，并用初始值填充它们。

数组存储每个坐标范围的最大值和最小值、更改坐标的步骤、矢量和每个粒子的当前位置。 然后，该方法创建一个粒子数组，并为每个粒子创建数组来存储其坐标、与其它粒子的距离矩阵、作用力矢量和函数的当前最佳值。 最后，该方法创建一个数组来存储所有粒子的最佳坐标。 因此，该方法初始化“电磁算法”优化算法工作所需的所有变量和数组。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Init (const int    coordinatesNumberP, //coordinates number
                    const int    particlesNumberP,   //particles number
                    const double envConstantP,       //environmental constant
                    const double movConstantP,       //movement step
                    const double exponentP)          //exponent
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  envConstant       = envConstantP;
  movConstant       = movConstantP;
  exponent          = exponentP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,  coordinatesNumber);
    ArrayResize (p [i].R,  particlesNumber);
    ArrayResize (p [i].F,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Moving() 方法是每次迭代时必须执行的第一个方法。 它负责在解的搜索空间中粒子的运动。 首先，该方法检查粒子是否已初始化。 如果还没有，则每个粒子接收给定限制内的随机坐标，并将其当前估计值和电荷重置为零。 另外还计算搜索空间每个维度中最大值和最小值之间的差异向量 vect []。

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].C     = 0.0;
      p [obj].f     = -DBL_MAX;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = rangeMax [c] - rangeMin [c];
  }

  revision = true;
}

如果已经进行了初始化，则该方法基于“每个粒子距全局最大值的偏差”与“所有粒子距全局最大值的偏差之和”的归一化数值来计算每个粒子的电荷。 计算差值的总和如下：

//calculate the sum of the differences of the fitness of the particles with the global value
for (int obj = 0; obj < particlesNumber; obj++)
{
  sumDiff += fB - p [obj].f;
}

粒子电荷按以下等式计算：

p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));

如您所见，等式中的电荷值为正。 稍后将在算法中研究电荷的符号。 如果与全局最大值的偏差之和为零，则假定粒子的电荷为零。 计算出的粒子电荷将判定在作用力计算步骤中粒子与其它相关粒子的作用力的幅度。 计算粒子电荷的代码如下所示：

//calculating the charge of particles=======================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  if (sumDiff == 0.0)
  {
    p [obj].C = 0.0;
  }
  else
  {
    p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
  }
}

在我们开始计算粒子之间的距离之前，有必要重置从粒子到其它粒子的距离数组，并重置粒子作用力矢量：

//calculation of Euclidean distances between all particles==================
for (int obj = 0; obj < particlesNumber; obj++)
{
  ArrayInitialize (p [obj].R, 0.0);
  ArrayInitialize (p [obj].F, 0.0);
}

然后计算所有粒子对之间的距离，以及在它们之间的作用力。 它使用基于库仑（Coulomb）定律的公式，该公式描述了带电粒子之间的相互作用。 在每个粒子上的作用力计算，是其它粒子在其上的所有作用力的矢量和。

根据电磁理论，一个粒子对另一个粒子的作用力与两个粒子之间的距离成反比，与它们的电荷乘积成正比。 具有较低目标值的粒子对具有相对较高目标值的粒子施加排斥力。 类似地，它将更强粒子推离目标值较差的区域。 另一方面，具有较高目标值的粒子对具有相对较低值的粒子施加吸引力。

考虑到所有其它粒子产生的所有相关力，计算粒子的作用力矢量总合。 这个合力矢量决定了粒子在运动阶段移动的方向。 该算法的作者建议将粒子的作用力矢量基于所有粒子之间的作用力矢量归一化。 我的实验表明，若不进行归一化，结果会更好，代码呈现的是没有归一化的情况。

取决于哪个粒子具有更大的目标函数值，我们设置作用力的方向（模仿电荷符号）。

for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int obj2 = 0; obj2 < particlesNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (p [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = p [obj].c [c] - p [obj2].c [c];
          p [obj].R [obj2] += diffDist * diffDist;
        }

        p [obj].R [obj2] = sqrt (p [obj].R [obj2]);
        p [obj2].R [obj] = p [obj].R [obj2];

        //calculation of the force------------------------------------------
        Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent));

        for (int c = 0; c < coordinatesNumber; c++)
        {
          if (p [obj].f > p [obj2].f)
          {
            p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;

          }
          else
          {
            p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
          }
        }
      }
    }
  }
}

最后，根据每个粒子的当前位置和作用在其上的作用力，计算每个粒子的新坐标。 粒子没有质量，这意味着没有加速度。 与 GSA 引力搜索算法相反，粒子会立即移动到新的位置。 移动坐标受搜索范围和变更步长的限制。

注释掉的代码返回范围另一侧的粒子，与相应坐标保持一定距离，以防粒子超出范围。

//calculation of particle motions===========================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (0.0, 1.0);
    p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant;

    //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]);
    //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]);

    p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Revision() 方法（EM 优化算法中必须在每次迭代中执行的第二个方法）负责检查粒子在当前迭代中的最佳位置。 在该方法内部，它遍历所有粒子，并将其适应度函数的值与当前的最佳 fB 值进行比较。 如果当前粒子的适应度函数的值大于 fB，则更新 fB，并将粒子的位置复制到 cB 数组之中。

因此，Revision() 方法允许在算法的每次迭代中跟踪粒子的最佳位置，并将其存储在 cB 数组当中。 这有助于优化寻找最佳解的过程，并提高算法的效率。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Revision ()
{
  for (int s = 0; s < particlesNumber; s++)
  {
    if (p [s].f > fB)
    {
      fB = p [s].f;
      ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

“电磁算法”优化算法中的 SeInDiSp() 方法将 In 变量的值限制在给定范围内 [InMin, InMax]。 如果 In 小于或等于 InMin，则该方法返回 InMin。 如果 In 大于或等于 InMax，则该方法返回 InMax。 如果步长为零，则该方法返回原始 In 值。 否则，该方法按照以下公式计算一个新的 In 值：InMin + Step * (In - InMin) / Step，其中 MathRound() 是将数字舍入到最接近整数的方法。

因此，SeInDiSp() 方法允许在指定的限制和指定的步长内控制 In 变量值的变化，这有助于更高效、更快速地优化函数。

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

EM 算法试验台结果：

2023.03.26 18:27:39.259    C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259    =============================
2023.03.26 18:27:43.215    5 Rastrigin's; Func runs 10000 result: 59.939529106561224
2023.03.26 18:27:43.215    Score: 0.74268
2023.03.26 18:27:52.960    25 Rastrigin's; Func runs 10000 result: 59.780143424645416
2023.03.26 18:27:52.960    Score: 0.74071
2023.03.26 18:29:22.856    500 Rastrigin's; Func runs 10000 result: 63.94951378068386
2023.03.26 18:29:22.856    Score: 0.79237
2023.03.26 18:29:22.856    =============================
2023.03.26 18:29:28.901    5 Forest's; Func runs 10000 result: 0.28698617113254693
2023.03.26 18:29:28.901    Score: 0.16233
2023.03.26 18:29:38.103    25 Forest's; Func runs 10000 result: 0.1571444033424823
2023.03.26 18:29:38.103    Score: 0.08889
2023.03.26 18:30:53.341    500 Forest's; Func runs 10000 result: 0.11734383105881332
2023.03.26 18:30:53.341    Score: 0.06638
2023.03.26 18:30:53.341    =============================
2023.03.26 18:30:58.108    5 Megacity's; Func runs 10000 result: 1.3599999999999999
2023.03.26 18:30:58.108    Score: 0.11333
2023.03.26 18:31:08.897    25 Megacity's; Func runs 10000 result: 0.776
2023.03.26 18:31:08.897    Score: 0.06467
2023.03.26 18:32:23.199    500 Megacity's; Func runs 10000 result: 0.34320000000000006
2023.03.26 18:32:23.199    Score: 0.02860
2023.03.26 18:32:23.199    =============================
2023.03.26 18:32:23.199    All score: 2.79996

关注 EM 算法在测试函数上的动画，我们可以想象搜索空间领域的某种“电磁化”。 粒子按照测试函数表面的特征形成高电荷分组。 不幸的是，收敛的质量明显较低，但不可否认的是，图像很漂亮。

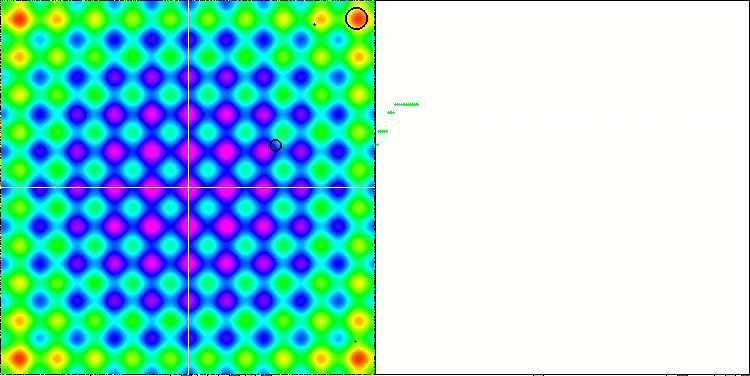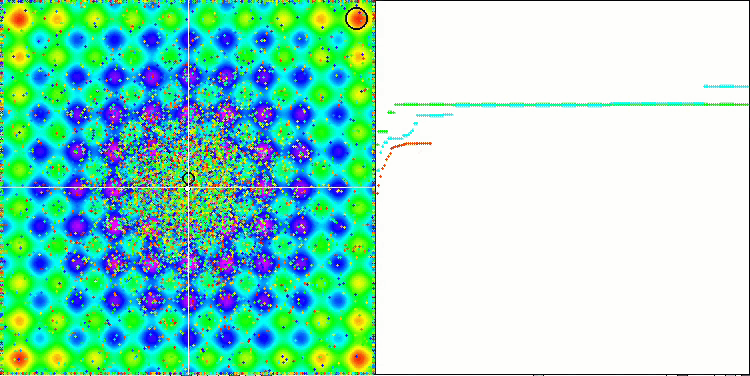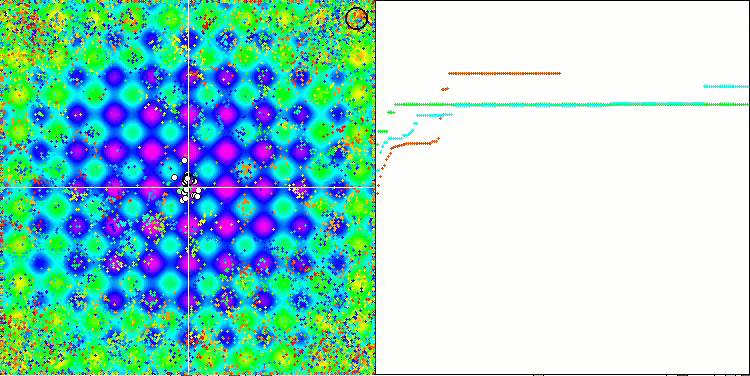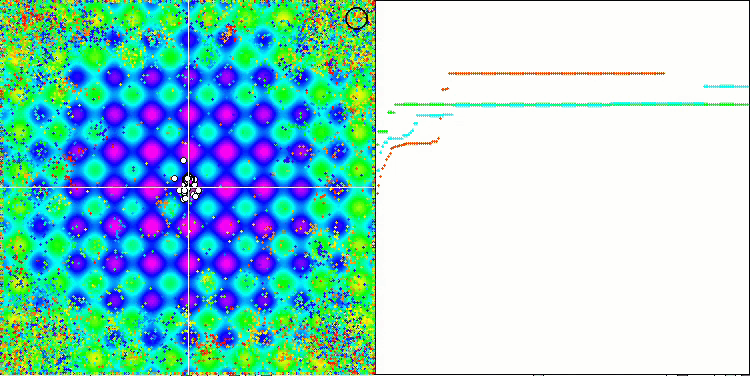
  Rastrigin 测试函数上的 EM

  基于 Forest 测试函数的 EM。

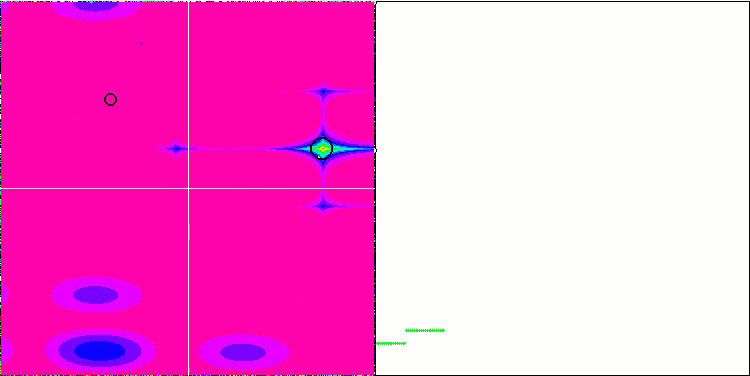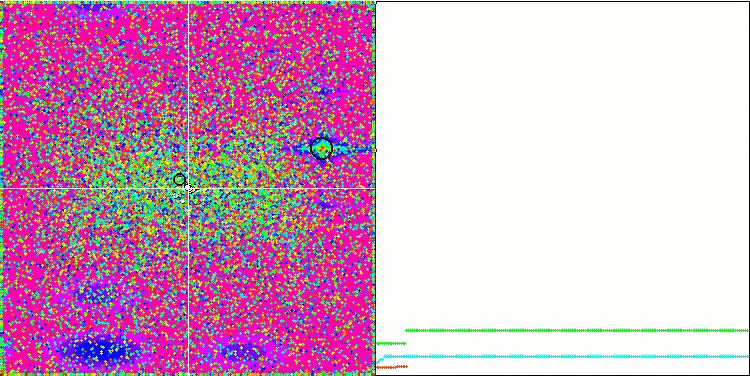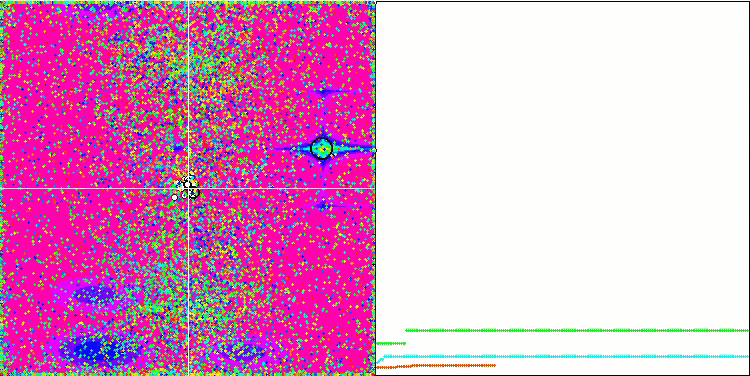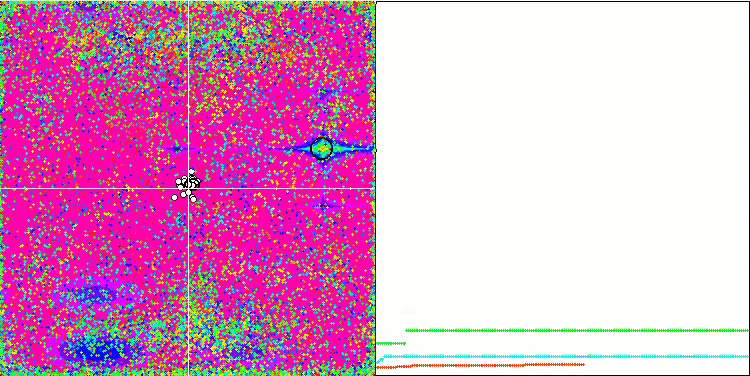
  基于 Megacity 测试函数上的 EM。

我们继续讨论 EM 优化算法的测试结果。 EM 的表现低于平均水平，最终得分为 22 分。 该算法在几乎所有测试中都展现出较差的结果。 例外是具有 1000 个参数的 Rastrigin 函数测试，其中 EM 被证明比 SSG 和 BA 等强大的算法更好。 甚而，函数在 1000 个参数下的绝对值竟然高于具有 10 个和 50 个参数的测试！

这是搜索结果首次随着优化参数数量的增加而提升。 最有可能的是，这种现象与 EM 搜索策略本身的特殊性有关。 有必要注意 EM 存在的梯度敏感性，和所研究函数定义的整个区域的可微性。

算法	说明	Rastrigin			Rastrigin 最终	Forest			Forest 最终	Megacity (离散)			Megacity 最终	最终结果
		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)		10 参数 (5 F)	50 参数 (25 F)	1000 参数 (500 F)
SSG	树苗播种和生长	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100.000
HS	和弦搜索	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
ACOm	蚁群优化 M	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
IWO	入侵杂草优化	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
COAm	杜鹃优化算法 M	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
FAm	萤火虫算法 M	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
ABC	人工蜂群	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
GSA	引力搜索算法	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
BA	蝙蝠算法	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
BFO	细菌觅食优化	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
EM	类电磁算法	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
MA	猴子算法	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
FSS	鱼群搜索	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
PSO	粒子群优化	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
RND	随机	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
GWO	灰狼优化器	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

总结

1. EM 算法是一种高效的优化方法，能够解决各种优化问题，特别是那些与处理大量数据和平滑函数的高维相关的问题。
2. 该算法基于模拟物理空间中电磁粒子的行为，这令它在处理复杂的多维函数时能够实现结果的高精度。
3. EM 算法不需要梯度计算，这令它更通用，更容易应用于各种问题，但它对正在优化的函数中梯度的存在很敏感。
4. 该算法可以根据具体的优化问题进行修改和定制，这令其成为优化各种函数的灵活工具。
5. EM 算法有各种改编版本，可以在基础版本上进行改进，并适应特定的优化问题。
6. EM 算法可用于机器学习、人工智能、金融市场优化、等各个领域。

电磁算法的主要优点是能够求解多维空间和大维的优化问题，同时保持结果的高精度。

因此，EM 算法是优化各种函数的有效工具，可用于广泛的优化问题，特别是在处理大量数据和/或高维时。

此评级可用于选择最合适的算法来解决特定的优化问题。 但是，算法的效率取决于众多因素，例如问题的大小、函数的类型、变量的数量、等等。 因此，算法的选择应基于对特定问题的彻底分析。

图例 1 展示算法的测试结果

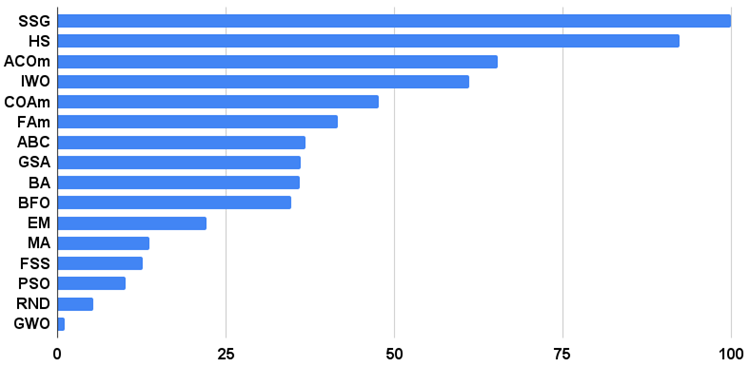
图例 1. 算法测试结果的直方图

电磁算法（EM）的优缺点：

优点:
1. 易于实现。
2. 平滑函数令人印象深刻的可扩展性。
3. 外部参数少。

缺点:
1. 计算复杂度高。
2. 离散函数结果不佳。
3. 在具有平坦水平“平台”的函数上会卡住。

每篇文章都提供一个存档，其中包含所有以前文章的算法代码的当前更新版本。 本文基于作者积累的经验，仅代表他的个人观点。 结论和判断基于实验。