群体优化算法：粒子群（PSO）

      它们形成不同的群，漂浮在阳光下

                                        或跟随雷云。 它们有可能从大气排放中汲取能量。

但在危机时刻，或者更广泛地说，威胁到它们生存的突然变化，它们就团结起来.

斯坦尼斯瓦夫·莱姆（Stanisław Lem）《无敌》（"The Invincible"）

内容

1. 概述
2. 算法原理
3. 经典实现
4. 修订版
5. 测试结果
   

1. 概述

大概有不少人读过斯坦尼斯瓦夫·莱姆（Stanisław Lem）的精彩科幻畅销书《无敌》（"The Invincible"）。 令人惊讶的是，对“群体”智能的最早描述之一正是随着这部科幻小说的发行而诞生的。 这个故事是有关未集中控制的幸存机器人。 值得注意的是，最简单且数量庞大的标本幸存下来，而非那些最复杂、最聪明、和最强大的标本。

在数千年的宏观演化过程中，这些机器已经学会了有效地应对他们的竞争对手，在智力和能源利用方面都遥遥领先。 他们不仅要与其他机器人作战，还要与星球上的生命世界作战。 这部作品中的幻想元素能够可靠地与进化和自然本身进行比较。

自远古时代以来，人们就对群体动物的行为（所谓的群体行为）感兴趣 — 迁徙到温暖国度的鸟群如何运作；蜂群如何生产食物；蚁群如何在创造复杂结构的同时生存；鱼群如何在行动整齐划一，且为什么它们的行为如此同步。 社会中的独立组织展现出协调良好的整体有机体的某些模式，这些都激发了算法优化领域的新思路。

群体智能描述的是模拟自组织系统的集体行为。 此类算法的数量相当多。 在 J.Kennedy 和 R.Eberhart 于 1995 年编写的规范版本中，该方法的基础模型是通过简化雷诺兹（Reynolds）模型获得的。 这种简化的成果，种群中不同的个体开始作为单独物体出现，这些物体没有大小，但具有一定的速度。

由于这极端类似物质粒子，产出的的简单物体被称为粒子，它们的种群被称为群体。 在每个时刻（每次迭代），粒子在空间中都具有一定位置和速度矢量。 针对粒子的每个位置，计算出目标函数的相应值，并在此基础上，根据一定的规则，粒子在搜索空间中改变其位置和速度。 在判定粒子的下一个位置时，也会考虑来自所有其它相邻粒子当中的最佳位置信息，对应于适应度函数的任务。

群算法示例：

• 粒子群法
• 蚂蚁算法
  
• 蜜蜂算法
  
• 人工免疫系统
  
• 灰狼算法
  
• 蝙蝠算法
  
• 引力搜索算法
  
• 利他主义算法
  
• 以及许多其它

从模拟集体行为到集体优化的过渡基于以下生物学思想：群居的生物体团结一致，能改善其生活条件。 平均而言，群居中的每个生物体，在与捕食者的斗争中都有更好的生存机会，与独立生物体相比，群居可以更有效地搜索、加工和储存食物，等等。 换言之，任何群居生物在其生存的整个时间段里，都会以不同程度的效率解决各种优化问题，例如，最大化食物量，同时最小化来自捕食者的损失。 考虑到这些，形成了构造各种数学优化方法的基础。

粒子群自始创以来，就是最著名和最流行的优化算法之一。 其各种实现的众多作者声称该算法在优化具有许多参数的复杂函数方面非常有效，甚至也适用于训练神经网络。

在本文中，我将尝试找出该算法是否真的适合解决复杂问题。 在算法的经典版本，及其许多修订版中，存在重大限制，关联的事实就是优化函数必须是平滑和连续的，这意味着它完全不适合离散函数。 然而，根据该系列文章，所有正在考虑的算法都将以这种方式进行修改（如果有任何限制），从而消除缺陷，令算法至少能纯技术性地工作。 换言之，所有算法都必须无无差别对待函数的平滑性（例如在交易者的问题中），并且在参数步骤上没有限制。

2. 算法原理

虽然上一篇文章介绍了优化世界，但它没有涵盖主程序（EA、脚本、指标）与优化算法核心的相交原理。 注意这一点很重要，因为无论如何，细心的读者都会有一个问题：为什么算法和示例程序要以这种方式编写。 优化算法的现有版本，均以这般方式构造，算法引用适应度函数作为外部对象，而算法是主要的可执行程序。

下面的图例 1 显示出算法将优化的参数传递给适应度函数，并获取适应度值（评估准则）的图表。 该系统不便于构建程序来解决用户、包括交易者的问题。 为何不方便呢？ 例如，我们不能调用测试器依据整个历史记录运行。

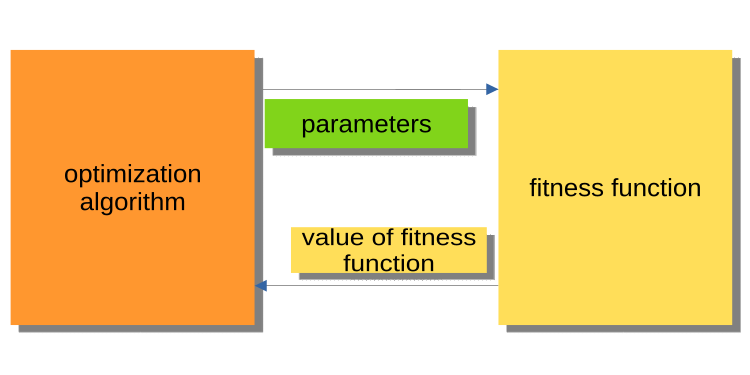
图例 1. PSO 与适应度函数的相交

图例 2 中显示出的结构则要方便得多。 这里的优化算法不是一个独立的程序，而是一个单独的模块、或“黑匣子”。 该模块为每个优化参数提供“最小”、“最大”、和“步长”参数。 MQL 程序根据请求接收优化的参数，并返回适应度值，换眼言之，适应度函数值。 这种结构允许构建一系列非常灵活的解决方案，从在智能交易系统中使用自动优化，到编写自定义优化管理器。

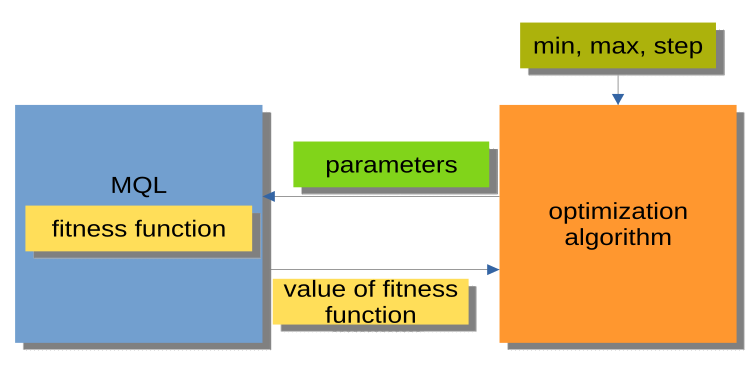
图例 2. PSO 与 MQL程序的相交

还值得一提的是，调用优化算法方法（图例 2 中的 MQL 模块）的组织可用一个针对所有优化算法 （AO） 都通用的相同设计流图来表示：

Initialization_АО_0

迭代周期（世代）
{
1) Method_АО_1
2) 获取优化参数的每个变体的适应度值
3) Method_АО_2
}

因此，我们看到只用到了三种公开方法：Initialization_АО_0，Method_АО_1 和 Method_АО_2。 这足以在任何复杂程度的用户项目中组织优化过程。

PSO 工作流本身如图例 3 所示，包括以下逻辑步骤：

1. 随机粒子生成（第一次迭代）
2. 获取每个粒子的适应度值
3. 获取所有粒子的一般适应度值
4. 粒子速度调节
5. 断点或转到步骤 2
   
6. 程序完成。

图例 3. PSO 工作流

我们来更详细地研究粒子群算法。

群体智能系统由许多粒子相互之间，以及与环境相互作用组成。 每个粒子都遵循简单的规则，尽管没有中央行为控制系统来告诉每个粒子该做什么。 它们之间的局部和随机相交作用导致出现不受个体控制的智能群体行为。
如果我们用羊群来类比，那么我们可以说所有粒子都必须执行简单的任务：

• 避免与其它粒子相交;
• 根据周围粒子的速度调整速度;
• 尽量在自己与环境之间保持相当小的距离。

PSO 算法从种群初始化开始。 第二步是计算每个粒子的适应度值，然后更新单个和全局最佳分数，然后更新粒子的速度和位置。 当使用 PSO 时，数值优化问题的可能解由粒子的位置表示。 此外，每个粒子都有一个当前速率，反映其至新位置的绝对大小和方向，据推测更好的解/位置。

粒子还存储其适应度值、当前位置、已知最佳位置（含有已知最适应度的以前位置）、和已知最佳位置的适应度。 重复步骤 2 到 4，直到满足完成条件。 在第一次迭代中，所有粒子都被打散，以便找到最佳解（探索）。 每个颗粒都进行评估。 找到了邻域拓扑的最佳解，并更新群体中每个成员的个体和全局最佳粒子。 收敛是将所有粒子吸引到具有最佳解的粒子周围来达成的。 

尽管 PSO 算法的核心非常简单，但我们需要理解它，以便能够修改本文中的代码，来满足我们的需求。 PSO 是一个迭代过程。 在主处理循环的每次迭代中，首先更新每个粒子的当前速度。 粒子的当前速度，其局部信息和群的全局信息，需要通盘考虑。 然后取该粒子的新速度值更新每个粒子的位置。

在数学上，这两个粒子坐标更新方程如下所示：

v(t+1) = w * v(t) + c1 * rp * (p(t) –  x(t)) + (c2 * rg * (g(t) –  x(t))

x(t+1) = x(t) + v(t+1)

位置更新过程实际上比建议的方程简单得多。 第一个方程用于更新粒子的速度。

v(t+1) 项表示时间 t+1 处的速度。 新的速度取决于三项。

• 第一个: w * v(t)。 w 因子称为惯性的重量分数，只是一个常数；v(t) 是时间 t 处的当前速度。
  
  
• 第二项: c1 * rp * (p(t) – x(t))。 c1 因子是一个常数，称为认知（或个人或局部）权重分数。 rp 乘数是 [0, 1] 范围内的随机变量。 p(t) 向量是迄今为止找到的粒子的最佳位置，x(t) 向量是粒子的当前位置。
  
  
• 第三项: 速度更新 c2 * rg * (g(t) – x(t)。 c2 因子是一个常数，称为社会（或全局）权重分数。 rg 乘数是 [0, 1] 范围内的随机变量。 g(t) 矢量的值是迄今为止在群体中发现的任何粒子的已知最佳位置。 一旦确定了新速度 v(t+1)，它就被用来计算粒子的新位置 x(t+1)。

3. 经典实现

描述空间中一组坐标（优化参数）的逻辑单元是粒子，可用结构来表示，其中 c[] 是粒子的坐标，cB[] 是粒子所有迭代的最佳坐标，v[] 是粒子每个坐标的速度，ff - 粒子的当前适应度值，ffB - 粒子在所有迭代中的最佳适应度值。 在粒子结构的构造函数中，我们可用 “double” 数据类型初始化 ff 和 ffB 的值，它们表示最小可能值，因为该算法旨在找到函数的最大值（要找到最小值，在最大适应度结果值前面添加一个 “-” 符号就足够了）。

//——————————————————————————————————————————————————————————————————————————————
struct S_Particles
{
  public:
    double c  []; //coordinates
    double cB []; //best coordinates
    double v  []; //velocity

    double ff;    //the value of the fitness function
    double ffB;   //best value fitness function

    S_Particles ()
    {
      ff  = -DBL_MAX;
      ffB = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

我们的 PSO 算法类实现只有三个公开方法 InitPS()、Preparation() 和 Dwelling()（Initialization_АО_0，Method_АО_1 和 Method_АО_2）。 在私密方法之外，GenerateRNDparticles () 和 ParticleMovement () 对于 PSO 来说是唯一的，而其余的已经在上一篇文章中讨论过了。 p [] 结构数组是一群粒子。 除了事实上每个粒子都有适应度值、自己的坐标、和最佳坐标之外，群体作为一个整体还具有最佳坐标 cB，和最佳适应度值 ffB。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_PSO
{
  public:
  //----------------------------------------------------------------------------
  S_Particles p    []; //particles
  double rangeMax  []; //maximum search range
  double rangeMin  []; //manimum search range
  double rangeStep []; //step search
  double cB        []; //best coordinates
  double ffB;          //FF of the best coordinates

  void InitPS (const int    params,       //number of opt. parameters
               const int    size,         //swarm size
               const double inertiaP,     //inertia
               const double selfBoostP,   //boost
               const double groupBoostP); //group boost

  void Preparation ();
  void Dwelling ();

  private:
  //----------------------------------------------------------------------------
  int swarmSize; //swarm size
  int parameters;//number of optimized parameters

  double inertia;
  double selfBoost;
  double groupBoost;
  bool   dwelling;

  void   GenerateRNDparticles ();
  void   ParticleMovement     ();
  double SeInDiSp             (double in, double inMin, double inMax, double step);
  double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

InitPS() 方法是在优化开始之前初始化算法（Initialization_АО_0）。 方法参数值分配给方法中的私密成员，并把大小分配到群体，和群体中每个粒子的内部参数。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::InitPS (const int    paramsP,
                       const int    sizeP,
                       const double inertiaP,
                       const double selfBoostP,
                       const double groupBoostP)
{
  ffB = -DBL_MAX;

  parameters = paramsP;
  swarmSize  = sizeP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);

  dwelling = false;

  inertia    = inertiaP;
  selfBoost  = selfBoostP;
  groupBoost = groupBoostP;

  ArrayResize (p, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (p [i].c,  parameters);
    ArrayResize (p [i].cB, parameters);
    ArrayResize (p [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

Preparation () 方法在每次迭代（世代）时首先调用（Method_АО_1）。 该方法很简单，但非常重要。 根据该方法是在第一个世代还是在后续世代（由 dwelling 标志确定）上调用，将重置群体适应度值，并创建随机群，或者粒子将移动到新坐标。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::Preparation ()
{
  if (!dwelling)
  {
    ffB = -DBL_MAX;
    GenerateRNDparticles ();
    dwelling = true;
  }
  else ParticleMovement ();
}
//——————————————————————————————————————————————————————————————————————————————

在 GenerateRNDparticles () 方法中随机生成群体种群。 粒子在为每个它们指定的范围内具有随机坐标，并且每个坐标拥有随机速度。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::GenerateRNDparticles ()
{
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      p [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      p [s].c  [k] = SeInDiSp (p [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      p [s].cB [k] = p [s].c [k];
      p [s].v  [k] = RNDfromCI (0.0, (rangeMax [k] - rangeMin [k]) * 0.5);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

ParticleMovement() 方法触发将粒子移动到新位置的算法。 为达此目的，有必要根据上述公式计算每个坐标的速度。 我不知道为什么使用术语“速率（velocity）”，因为它基本上是一个位移值，或者换句话说，粒子此刻的位置和它应该移动的位置之间的差异。 计算出每个坐标的差值后，我们只需把当前值相加即可。 之后，检查在给定步骤中超出优化参数的最小/最大边界（对于粒子，这些是坐标）是否不可接受。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::ParticleMovement ()
{
  double rp;       //random component of particle movement
  double rg;
  double velocity;
  double posit;
  double positBest;
  double groupBest;

  for (int i = 0; i < swarmSize; i++)
  {
    for (int k = 0; k < parameters; k++)
    {
      rp = RNDfromCI (0.0, 1.0);
      rg = RNDfromCI (0.0, 1.0);
      
      velocity  = p [i].v  [k];
      posit     = p [i].c  [k];
      positBest = p [i].cB [k];
      groupBest = cB [k];

      p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit);
      p [i].c [k] = posit + p [i].v [k];

      p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Dwelling () 方法是优化（Method_АО_2） 算法的第三个公开方法。 该方法的目的是更新每个粒子相对于其先前性能的最佳坐标和适应度值，并在必要时更新群体的适应度，和群的最佳坐标。 在迭代循环中获取适应度值后，调用该方法。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSO::Dwelling ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    //remember the best position for the particle
    if (p [i].ff > p [i].ffB)
    {
      p [i].ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k];
    }

    if (p [i].ff > ffB)
    {
      ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

该函数在指定范围内依据给定步长离散化 “双精度” 数字。

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_PSO::SeInDiSp (double in, double inMin, double inMax, double step)
{
  if (in <= inMin) return (inMin);
  if (in >= inMax) return (inMax);
  if (step == 0.0) return (in);
  else return (inMin + step * (double)MathRound ((in - inMin) / step));
}
//——————————————————————————————————————————————————————————————————————————————

该函数获取指定范围内的随机 “双精度” 数字。

//——————————————————————————————————————————————————————————————————————————————
// Random number generator in the custom interval
double C_AO_PSO::RNDfromCI (double min, double max)
{
  if (min == max) return (min);
  double Min, Max;
  if (min > max)
  {
    Min = max;
    Max = min;
  }
  else
  {
    Min = min;
    Max = max;
  }
  return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0)));
}
//——————————————————————————————————————————————————————————————————————————————

理论结束了。 我们开始实践。

由于我采用了与图例 2 中描述的本系列的第一篇文章（我将在未来继续这样做）相同的结构来构建算法，因此我们将算法连接到测试台并不困难。

当在测试台运行时，我们将看到类似于下面显示的动画。 在这种情况下，我们可以清楚地看到一群粒子的行为。 群体行为真的很像自然界中的群体。 在函数的热图上，它以密集云的形式移动。

您可能还记得，黑色圆圈表示函数的全局最优值（最大值），而黑点表示在当前迭代时获得的搜索算法的最佳平均坐标。 我解释一下平均值的来源。 热图在坐标上是二维的，正在优化的函数可以包含数百个变量（测量值）。 故此，结果按坐标取平均值。

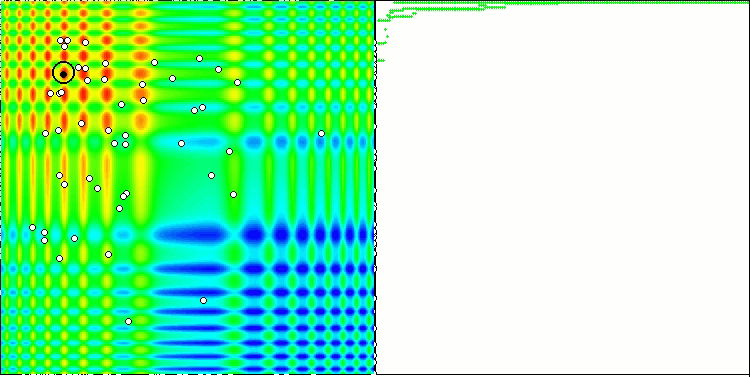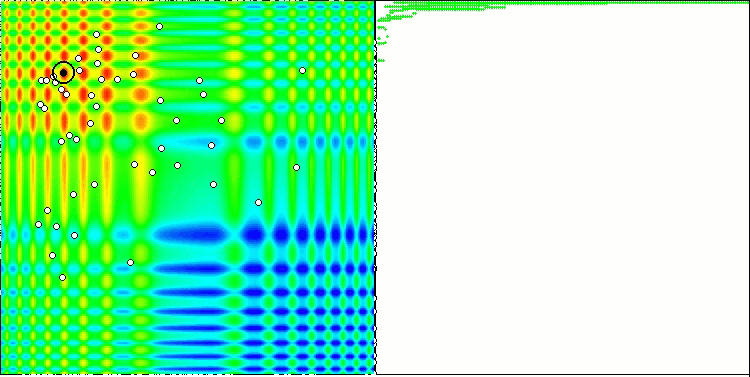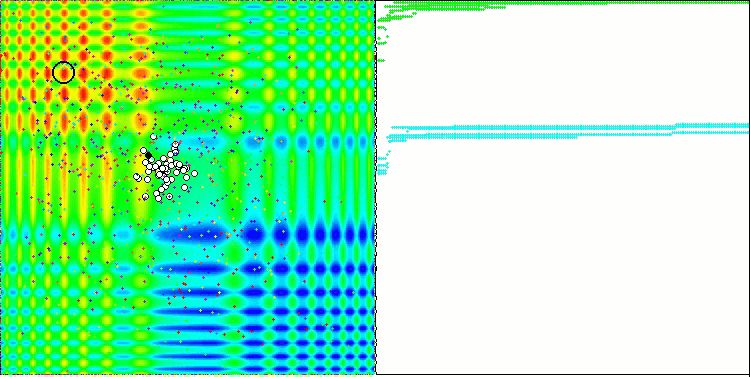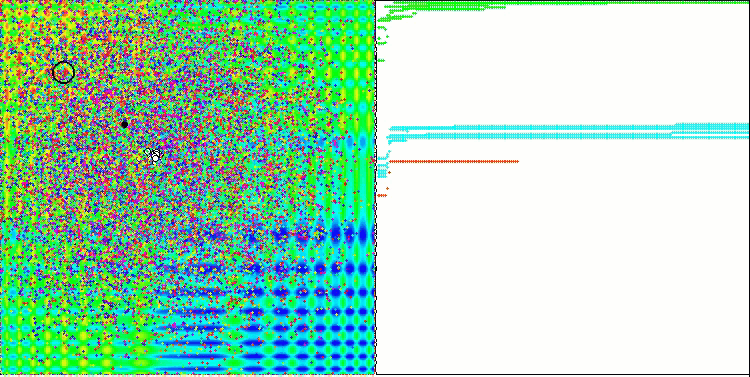
  基于 Skin 测试函数的 PSO

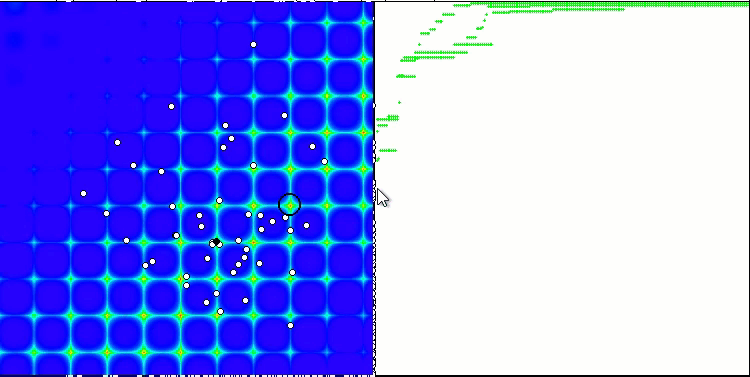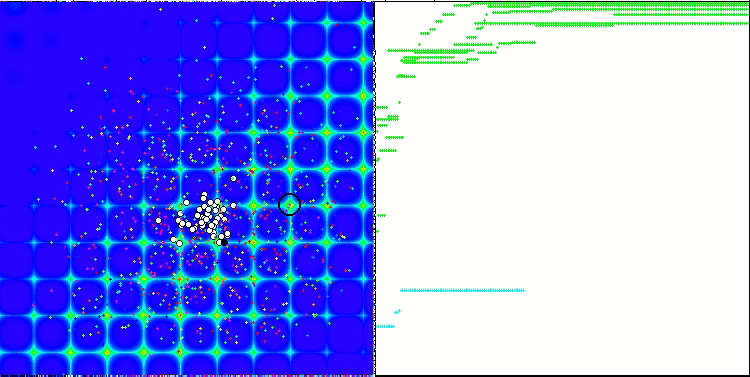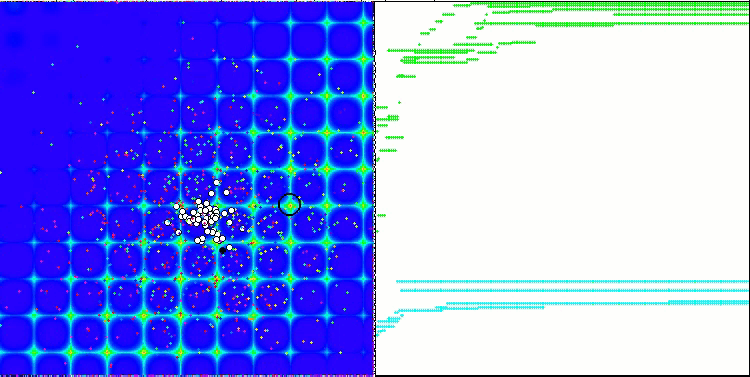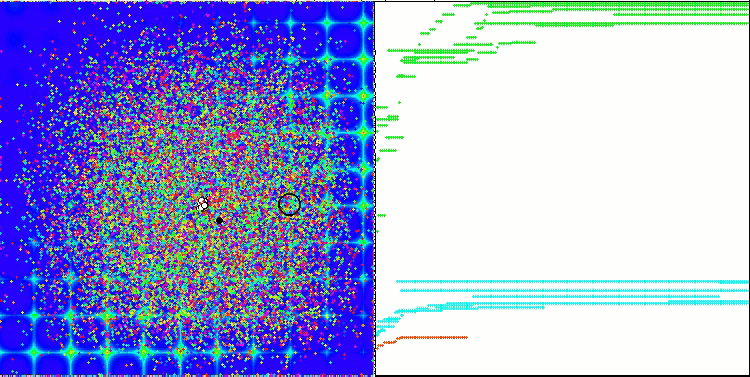
  基于 Forest 测试函数的 PSO。

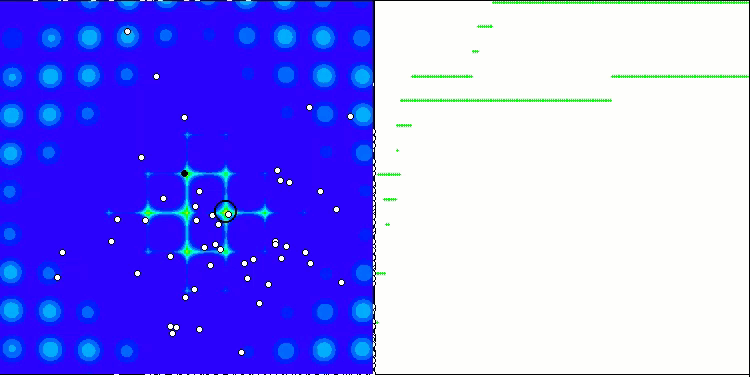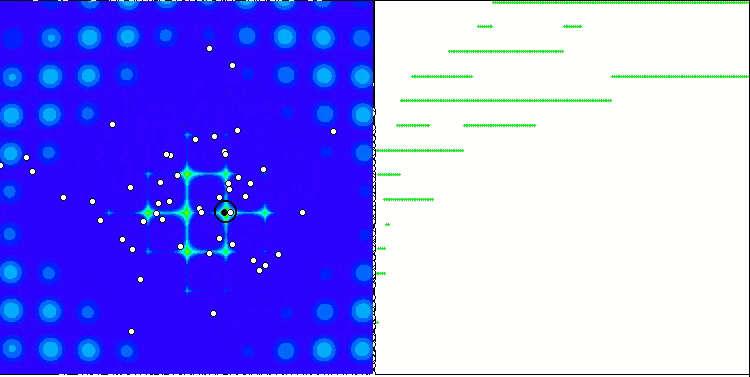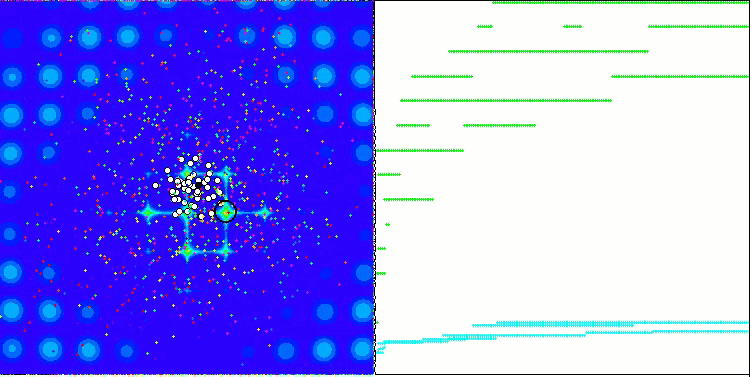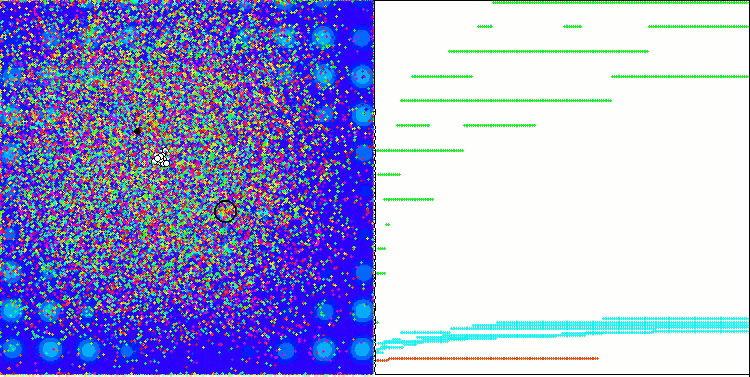
  基于 Megacity 测试函数的 PSO。

正如您在动画中看到的，测试表明 PSO 可以很好地应对平滑的第一个函数，但仅在优化两个变量的时候。 随着搜索空间维度的增加，算法的效率急剧下降。 这在第二个和第三个离散函数上尤其明显。 结果明显比上一篇文章中描述的随机算法更差。 我们将回到结果，并在形成结果比较表格时详细讨论它们。

看着著名的 PSO 算法如何惨败于随机算法，人们可能想给该算法第二次机会。 在下一节中，我将尝试修改 PSO 算法。

4. 修订版

在我看来，PSO 的弱点是：

1) 每个坐标必然会变化的概率几乎等于 1。 这意味着群体中的每个粒子在每次迭代中充其量只是在全局区域的局部极值的某个地方振荡，而在最坏的情况下，它永远不会准确地达到全局极值的点。 这意味着算法的一个特征 — 在局部极值处卡顿，即收敛性差。

2) 该算法不能很好地处理离散函数，部分是源于第一个缺陷。 粒子坐标跳到正在优化的函数表面的最近“区域”，故无法详细研究任何局部极值的邻域。

3) 算法探索新领域的能力较弱。 群体集中在一个地方的某处，而不会试图逃离局部的“洞”。 一些作者提到尝试创建多群体修改实现，但优化复杂多变量函数的问题仍然悬而未决，由于相互距离的原理尚不清楚，因为不仅必须满足联动的原理，而且还必须满足相互排斥的可能性。 否则，这样的实现就没有意义了，因为单个群体终将简单地汇聚在一个区域或点上。 与此同时，简单的一个、或双变量函数的优化是通过收敛性极佳的最简单的方法进行的。

那么，我们可以做些什么来改进算法呢？

很明显（尽管不一定是真的），我们需要将来自其它粒子的最好单个坐标传递给粒子。 “供体”粒子的整体坐标越好，通过坐标的概率就越大。 选择粒子的概率偏移如图例 4 所示。 我们生成一个从 0 到 1 的随机数，用抛物线函数转换结果数字，然后将其缩放到群体中粒子序列号的范围，从 0 到 SwarmSize-1。 为此，我们需要为 PSOm（修改后的算法）引入一个附加参数 — 复制坐标的概率，我们还需要对群体进行排序，以便粒子越好，越接近索引 0。

图例 4. 偏移粒子选择概率

我们稍微改变一下 ParticleMovement () 方法。 生成一个随机数 [0;1]。 如果揭晓数字大于 'copy' 参数，那么我们将对上面详述的粒子执行常规操作，否则我们将复制另一个粒子的坐标，并根据图例 4 中图形所示的规则选择索引。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSOm::ParticleMovement ()
{
  double rp;       //random component of particle movement
  double rg;
  double velocity;
  double posit;
  double positBest;
  double groupBest;

  for (int i = 0; i < swarmSize; i++)
  {
    for (int k = 0; k < parameters; k++)
    {
      rp = RNDfromCI (0.0, 1.0);
      rg = RNDfromCI (0.0, 1.0);

      double rC = RNDfromCI (0.0, 1.0);

      if (rC > copy)
      {
        velocity  = p [i].v  [k];
        posit     = p [i].c  [k];
        positBest = p [i].cB [k];
        groupBest = cB [k];

        p [i].v [k] = inertia * velocity + selfBoost * rp * (positBest - posit) + groupBoost * rg * (groupBest - posit);
        p [i].c [k] = posit + p [i].v [k];

        p [i].c [k] = SeInDiSp (p [i].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      }
      else p [i].c [k] = p [GetPartcileAdress ()].cB [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Dwelling () 方法也应更改。 添加调用 SortParticles () 排序函数。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_PSOm::Dwelling ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    //remember the best position for the particle
    if (p [i].ff > p [i].ffB)
    {
      p [i].ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) p [i].cB [k] = p [i].c [k];
    }

    if (p [i].ff > ffB)
    {
      ffB = p [i].ff;
      for (int k = 0; k < parameters; k++) cB [k] = p [i].c [k];
    }
  }

  SortParticles ();
}
//——————————————————————————————————————————————————————————————————————————————

GetParticleAdress () 函数提供粒子定位的选择，其概率向最佳粒子偏移。

//——————————————————————————————————————————————————————————————————————————————
//shift of probability in the smaller party (to an index 0)
int C_AO_PSOm::GetParticleAdress ()
{
  double x = RNDfromCI (-1.0, 0.0);
  x = x * x;
  x = Scale (x, 0.0, 1.0, 0, swarmSize - 1);
  x = SeInDiSp (x, 0, swarmSize - 1, 1);
  return ((int)x);
}
//——————————————————————————————————————————————————————————————————————————————

SortParticles () 函数是传统的气泡排序。

//——————————————————————————————————————————————————————————————————————————————
//Sorting of particles
void C_AO_PSOm::SortParticles ()
{
  //----------------------------------------------------------------------------
  int   cnt = 1;
  int   t0 = 0;
  double t1 = 0.0;
  //----------------------------------------------------------------------------

  // We will put indexes in the temporary array
  for (int i = 0; i < swarmSize; i++)
  {
    ind [i] = i;
    val [i] = p [i].ffB; //ffPop [i];
  }

  while (cnt > 0)
  {

    cnt = 0;
    for (int i = 0; i < swarmSize - 1; i++)
    {
      if (val [i] < val [i + 1])
      {
        t0 = ind [i + 1];
        t1 = val [i + 1];
        ind [i + 1] = ind [i];
        val [i + 1] = val [i];
        ind [i] = t0;
        val [i] = t1;

        cnt++;
      }
    }
  }

  // On the received indexes create the sorted temporary population
  for (int u = 0; u < swarmSize; u++) pT [u] = p [ind [u]];

  // Copy the sorted array back
  for (int u = 0; u < swarmSize; u++) p [u] = pT [u];
}
//——————————————————————————————————————————————————————————————————————————————

该函数将数字从一个数字范围缩放到另一个数字范围。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_PSOm::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return (OutMIN);
    if (In > InMAX) return (OutMAX);
    return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
  }
}
//——————————————————————————————————————————————————————————————————————————————

5. 测试结果

最后，我们来总结一下目前的研究结果。 不幸的是，无论我多么希望获得优良的结果，PSO 算法都没有证明自己的合理性。 研究表明，对于具有断点和大量参数的离散函数，其收敛性较弱。 修改算法的尝试没有成功，结果比经典实现更糟糕。

将 copy 参数增加到接近 0.8 的值，仍然能够显示即时收敛，但仅限于测试中的第一个平滑函数，并且只能有两个参数。 至于其它测试，此参数只会令结果恶化。 PSO 的经典实现仅在拥有 1000 个参数的 Skin 函数上展现出一些有趣的东西。 其它测试结果则是平庸之极。

最终测试结果分别为，经典算法 0.47695，以及修改后的算法 0.45144。 结果如下表所示。 测试台允许我们在设置中选择测试运行次数（默认值为 5），因此如果计算能力允许，读者可以将此参数设置得更高，来获得统计上更准确的结果。

算法	运行次数	Skin			Forest			Megacity (离散)			最终结果
		2 参数 (1 F)	40 参数 (20 F)	1000 参数 (500 F)	2 参数 (1 F)	40 参数 (20 F)	1000 参数 (500 F)	2 参数 (1 F)	40 参数 (20 F)	1000 参数 (500 F)
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
	10,000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283
PSO	1000	0.98436	0.72243	0.65483	0.71122	0.15603	0.08727	0.53333	0.08000	0.04085	0.47695
	10,000	0.99836	0.72329	0.65483	0.97615	0.19640	0.09219	0.82667	0.10600	0.04085
PSOm	1000	0.96678	0.64727	0.57654	0.80616	0.13388	0.06800	0.53333	0.08067	0.04211	0.45144
	10,000	0.99505	0.64986	0.57654	0.90401	0.18194	0.07104	0.74667	0.10400	0.04211

综上所述，PSO 除了在精炼搜索区域收敛缓慢（局部搜索能力差）之外，还倾向于在平均最优点上导致快速和过早收敛。 简单地说，该算法非常弱，不适合优化复杂的离散函数，尤其是多参数函数。

一般有几种方式可用来改善 PSO。 群体规模是重要因素之一。 更高大的群体规模可以提升更快、更准确的收敛的可能性。 然而，在实际问题中，适应度函数的运行次数往往存在阈值，增加群体规模只会成比例地减少世代次数，从而降低群体进化的可能性。

第二种方法是在探索和发展之间取得平衡。 在迭代开始时，高强度的探索将为找到接近全局最优解提供很高的机会。 同时，在迭代结束时，高强度的探索能令粒子有机会在有希望的领域找到最准确的解。 群体调用其它方法阶段之前进行预优化，是另一种可提高 PSO 底层性能的技术，如今十分常用。 为每个子群组分配不同的任务或目标，也可以提高 PSO 在多任务问题中的有效性。 

提高 PSO 性能的另一种方法是建立速率方程的组成分量（动态速度控制）。 这种方式可以将粒子发送到不同的方向，并导致更快地收敛到全局最优值，但这只是一个假设。

优点:

1. 该算法非常简单，且对计算资源要求不高，代码运行速度非常快捷，因为经典实现甚至无需对数组进行排序。
2. 该算法针对平滑函数做得很好。 到目前为止，PSO 在优化具有多个参数的平滑函数方面，名列前茅。
   

缺点:

1. 优化函数研究的质量低。 该算法不能用于解决需要若干唯一解集合的问题。
2. 低速和收敛精度。
3. 不适合离散函数的优化。
   
4. 几乎完全不可扩展。