种群优化算法：二进制遗传算法（BGA）。第 II 部分

内容

1. 概述
2. 算法
3. 测试结果

1. 概述

在上一篇文章中，我们领略了所有重要的基本概念和方法，这些不仅在遗传算法里用到，而且在任何群体优化算法里都会以某种方式用到。现在，基于这些知识，我们可以详研当前“第二卷书籍”的主要主题 — 二进制遗传算法（BGA）。从一般信息开始，我们转到这个非凡的搜索策略的代码，最后是测试结果。

遗传算法（GA） 是指进化算法，包括各种方式，诸如遗传算法、遗传编程、进化策略、等等。它们基于进化和遗传的思路，其解元表示为种群，并应用遗传算子（例如交叠和突变）来创建新一代解元。

遗传算法使用自然选择和遗传学原理来解决优化问题。本文中讨论的二进制遗传算法（BGA）是遗传算法所有类型中的第一种。因此，BGA 属于进化算法一类，是遗传算法的特定变体，利用了数据的二进制表示。

创建遗传算法的工作始于 20 世纪中叶。创始人之一是 John Holland，他于 1975 年出版了他的书籍《自然和人工系统中的适应》，其中他引入遗传算法作为解决优化问题的整体方式方向。

遗传二进制算法的开发受到若干个因素和思路的启发。主要的：

• 自然选择和进化原理：BGA 基于查尔斯·达尔文（Charles Darwin）提出的自然选择和进化原理。该思想是，一个种群中存在多种解元，更能适应环境的那些解元更有可能生存，并将其特征传递给下一代。
• 基因和遗传学：BGA 还使用基因学概念，例如基因、染色体、和遗传。BGA 中的解元表示为二进制字符串，其中单独的比特位组代表特定基因，而基因又代表被优化的参数。基因算子，诸如交叠和突变，以二进制字符串形式应用于，以便创建新一代解元。

总体上，BGA 的发展是进化算法、基因学、和优化领域思想结合的产物。创建它是为了利用自然选择和基因学原理解决优化问题，它的发展一直持续到今天，已经创建了大量的 GA 选项，以及广泛运用遗传算法中的想法和方法作为混血算法的一部分，包括非常复杂的那些。

二进制遗传算法（BGA）使用数据的二进制表示。这意味着每个单独的（解元） 都表示为一连串比特位（0 和 1）。遗传算子（例如交叠和突变）应用于比特位字符串，以便创建新一代解元。

有趣的事实：遗传算法，包括 BGA 在内，都可用于创建和改进人工智能。例如，它们可用于发展神经网络，从而允许创建更高效的机器学习模型。

通俗来讲，遗传算法，特别是 BGA 是解决复杂优化问题的强大工具，而传统方法由于缺乏解析手段而不够有效。MetaTrader 5 使用二进制 GA，以至于研究这种非凡算法的操作原理更加令人兴奋。

2. 算法

二进制遗传算法包括以下步骤：

1. 种群初始化 — 创建由具有随机二进制值的染色体组成的初始种群。
2. 适应度评估 — 估算子种群中每个独体（染色体）的适应度。
3. 选择 — 使用轮盘方法选择亲本，以便创建后代。
4. 交叠 — 将亲本染色体分成多个部分，并用亲本两方的片段创建新的子染色体。
5. 颠倒 — 在随机选择的点分裂子独体的染色体，并交换所得部分。
   
6. 突变 — 以给定的突变概率随机更改后代基因中的比特位。
7. 后代适应度评估 — 估算每个新后代的适应度。
8. 形成新的种群 — 将后代种群放在总种群的末尾，并按适应度值排序。
9. 停止准则 — 从步骤 3 开始重复该过程，直到达到停止准则。

我们将使用优化参数的 “max” 和 “min” 之间的距离来确保 BGA 仅配以正数值，简化二进制字符串的操作，并提高计算速度。我们将以这种方式获得的正距离值以二进制格雷码的形式表示，并将它们按顺序放置在一个共同的染色体符号数组中，如图例 1 所示。当执行交叠方法时，染色体断点位于染色体上的随机位置，而不一定位于基因连接点。断点也可以位于基因空间内。

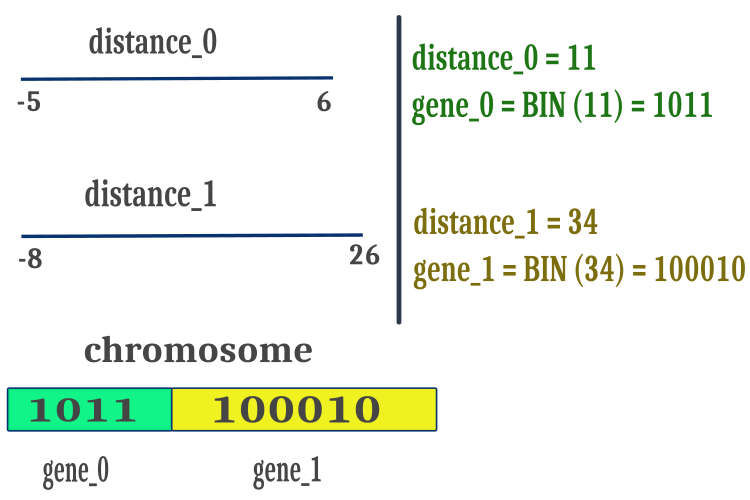
图例 1. 将独体的特征（优化参数）置于染色体之中

遗传算法有大量的外部参数，故此更仔细地考虑它们是合理的。默认设置几乎与许多科学出版物作者的建议完全一致。我已经测试并选择了它们，以便在大多数类型的任务中提供最高效率。然而，在拥有 10 个甚至 50 个优化参数的单独函数上，测试中任何方向上偏离这些参数都可能导致达成 100% 收敛，但同时会显著降低在其它任务上的效率。因此，对于大多数实际情况，默认设置是最优选择。

• Population_P（种群大小 = 50）— 种群的每代之中子独体数量。测试中涵盖的大多数算法都用到了这个种群大小，并在解元多样性和收敛速度之间提供了平衡。
  

• ParentPopulation_P（亲本种群数量 = 50）— 被选中用于繁殖和创造下一代的亲本数量。减小该参数值可以提高平滑函数的收敛性（提高准确性），增加该值可以提高离散函数的收敛性（增加遗传素材的多样性）。
  

• CrossoverProbab_P（crossover probability = 1.0）— 在两个选定的亲本之间执行交叠操作的概率。交叠的高概率会增加算法的组合能力。减小该值会增加收敛速度，但会增加卡顿的概率。
  

• CrossoverPoints_P（交叠点数 = 3）— 两个亲本染色体之间发生交叠点的数量。增加点的数量会导致参数之间更密集的混合，且在限制中，减少为算法的随机行为。
  

• MutationProbab_P（突变概率 = 0.001）— 染色体基因型中每个比特位发生突变的概率。突变允许对遗传物质进行随机更改，并为种群添加新的解元。低概率会增加算法的收敛速度，但会降低多样性，而过高的概率会导致有用信息的丢失。

• InversionProbab_P（颠倒概率 = 0.7）— 在染色体上执行颠倒操作的概率。颠倒概率高会增加遗传物质的多样性，但概率过高会导致算法的随机行为。

• DoubleDigitsInChromo_P（基因中的小数位数）— 染色体中以二进制形式表示的实数（优化参数）的小数位数。增加该值会导致计算复杂性增加，及优化时间增加（如果不直接使用二进制形式解决问题，设置超过 16 是没有意义的 — 当转换为双精度时，输出比特位将丢失）。

我们转到代码回顾。

初始化个体时，必须确定正在优化的参数的二进制表示中的比特位数量。假设我们需要考虑 5 个小数位，这对应于一定的格雷代码长度。不过，该代码中编码也许会超过所需数量。因此，我们需要判定可以用二进制格式编码的最大实数。将来，我们可以将编码的数字缩放到优化输出参数的所需范围。对于实数的小数部分，我们使用给定数量的位数（在参数中指定），而对于整数部分 — 按二进制形式的所需容量。

例如，如果 digitsInGrayCode 函数的输入参数为 3，则函数将返回使用 3 位格雷码的 ulong 类型的最大值，即 7（二进制为 111）。

为了检测给定数量比特位所能编码的最大可能实数的小数和整数部分，我们将调用 GetMaxDecimalFromGray 函数。

//——————————————————————————————————————————————————————————————————————————————
//Calculation of the maximum possible ulong number using the Gray code for a given number of bits
ulong GetMaxDecimalFromGray (int digitsInGrayCode)
{
  ulong maxValue = 1;

  for (int i = 1; i < digitsInGrayCode; i++)
  {
    maxValue <<= 1;
    maxValue |= 1;
  }

  return maxValue;
}
//——————————————————————————————————————————————————————————————————————————————

为了表示染色体中的每个基因（基因在染色体上的位置），我们将用到 S_BinaryGene 结构，其中包含以二进制格式操控基因的字段和方法：

• “gene” — 表示基因的字符数组。
• “integPart” — 基因整数部分的字符数组。
• “fractPart” — 基因分数部分的字符数组。
• “integGrayDigits” — 基因整数部分的格雷位数。
• “fractGrayDigits” — 基因小数部分的格雷位数。
• “length” — 基因总长度。
• “minDoubleRange” — 实数范围的最小值。
• “maxDoubleRange” — 实数范围的最大值。
• “maxDoubleNumber” — 基因可表示的最大实数。
• “doubleFract” — 基因的小数部分转换为实数的值。

结构方法：

• “Init” — 初始化结构字段。接受实数范围的最小值和最大值，以及基因小数部分的位数。在该方法中，按格雷码计算基因编码部分的最大实数值。
  

• “ToDouble” — 将基因转换为实数。接受格雷码字符的 “chromo”（染色体） 数组，和 “indChr” 基因起始索引。该方法读取染色体的一个区域，将读取的基因转换为十进制值，然后将其缩放到指定的实数范围。

• “Scale” — 将 “In” 输入值从 “InMIN” 和 “InMAX” 范围缩放到 “OutMIN” 和 “OutMAX” 输出范围。这是 “ToDouble” 中用到的辅助方法。

//——————————————————————————————————————————————————————————————————————————————
struct S_BinaryGene
{
  char   gene      [];
  char   integPart [];
  char   fractPart [];

  uint   integGrayDigits;
  uint   fractGrayDigits;
  uint   length;

  double minDoubleRange;
  double maxDoubleRange;
  double maxDoubleNumber;
  double doubleFract;

  //----------------------------------------------------------------------------
  void Init (double min, double max, int doubleDigitsInChromo)
  {
    doubleFract = pow (0.1, doubleDigitsInChromo);
    
    minDoubleRange = min;
    maxDoubleRange = max - min;

    ulong decInfr = 0;

    for (int i = 0; i < doubleDigitsInChromo; i++)
    {
      decInfr += 9 * (ulong)pow (10, i);
    }
    
    //----------------------------------------
    DecimalToGray (decInfr, fractPart);
    
    ulong maxDecInFr = GetMaxDecimalFromGray (ArraySize (fractPart));
    double maxDoubFr = maxDecInFr * doubleFract;
    
    
    //----------------------------------------
    DecimalToGray ((ulong)maxDoubleRange, integPart);
    
    ulong  maxDecInInteg = GetMaxDecimalFromGray (ArraySize (integPart));
    double maxDoubInteg  = (double)maxDecInInteg + maxDoubFr;

    maxDoubleNumber = maxDoubInteg;

    ArrayResize (gene, 0, 1000);
    integGrayDigits = ArraySize (integPart);
    fractGrayDigits = ArraySize (fractPart);
    length          = integGrayDigits + fractGrayDigits;

    ArrayCopy (gene, integPart, 0,                0, WHOLE_ARRAY);
    ArrayCopy (gene, fractPart, ArraySize (gene), 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double ToDouble (const char &chromo [], const int indChr)
  {
    double d;
    if(integGrayDigits > 0)d = (double)GrayToDecimal(chromo, indChr, indChr + integGrayDigits - 1);
    else                   d = 0.0;

    d +=(double)GrayToDecimal(chromo, indChr + integGrayDigits, indChr + integGrayDigits + fractGrayDigits - 1) * doubleFract;

    return minDoubleRange + Scale(d, 0.0, maxDoubleNumber, 0.0, maxDoubleRange);
  }

  //----------------------------------------------------------------------------
  double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
  {
    if (OutMIN == OutMAX) return (OutMIN);
    if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
    else
    {
      if (In < InMIN) return OutMIN;
      if (In > InMAX) return OutMAX;

      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

为了描述个体，我们需要 S_Agent 结构，它代表个体、以及除染色体外，还包含以下数据：

• “c” — 个体坐标值的数组，为实数。 
• “f” — 个体适应度值。
• “genes” — “S_BinaryGene” 结构数组，描述每个基因在染色体中的位置，以及将二进制码转换为实数的规则。
• “chromosome” — 个体染色体特征的数组。
• “calculated” — 布尔值，指示是否已计算个体的数值（该字段存在，但在代码中未用）。

结构方法：

• “Init” — 初始化结构字段。接受 “coords” 坐标的数量，“min” 和 “max” 数组的数量，每个优化参数的最小值和最大值，以及 doubleDigitsInChromo — 基因小数部分中实数的位数。该方法为每个坐标创建和初始化基因，并设置初始适应度值，和 “calculated” 标志。

• “ExtractGenes” — 从染色体中提取基因值，并存储在 “c” 数组之中，调用 “S_BinaryGene” 结构中的 “ToDouble” 方法将基因从染色体转换为实数。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (const int coords, const double &min [], const double &max [], int doubleDigitsInChromo)
  {
    ArrayResize(c, coords);
    f = -DBL_MAX;

    ArrayResize(genes, coords);
    ArrayResize(chromosome, 0, 1000);

    for(int i = 0; i < coords; i++)
    {
      genes [i].Init(min [i], max [i], doubleDigitsInChromo);
      ArrayCopy(chromosome, genes [i].gene, ArraySize(chromosome), 0, WHOLE_ARRAY);
    }

    calculated = false;
  }

  void ExtractGenes ()
  {
    uint pos = 0;

    for (int i = 0; i < ArraySize (genes); i++)
    {
      c [i] = genes [i].ToDouble (chromosome, pos);
      pos  += genes [i].length;

    }
  }

  double c []; //coordinates
  double f;    //fitness

  S_BinaryGene genes [];
  char chromosome    [];
  bool calculated;
};
//——————————————————————————————————————————————————————————————————————————————

以下代码表述 S_Roulette 结构的定义，它表示轮盘片段。

结构字段：

• “start” — 轮盘片段起始点值。
• “end” — 轮盘片段终点。

//——————————————————————————————————————————————————————————————————————————————
struct S_Roulette
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

声明实现遗传算法的 C_AO_BGA 类：

• “cB” — 最佳坐标值的数组。
• “fB” — 最佳坐标的适应度值。
• “a” — 表示个体的 S_Agent 结构数组。
• “rangeMax” — 最大搜索范围值的数组。
• "rangeMin" — 最小搜索范围值的数组。
• “rangeStep” — 表示搜索步骤的值数组。

类方法：

• “Init” — 初始化类字段。它接受以下参数：“coordsP” 坐标数、“popSizeP” 种群大小、“parentPopSizeP” 亲本种群大小、“crossoverProbabP” 交叠概率、“crossoverPointsP” 交叠点数、“mutationProbabP” 突变概率、“inversionProbabP” 颠倒概率、“doubleDigitsInChromoP” 基因中的小数位数。该方法初始化遗传算法操作所需的内部变量和数组。

• “Moving” — 遗传算法的主要方法，基于种群执行操作，例如交叠、突变、颠倒、和适应度评估。

• “Revision” — 该方法执行种群修订，针对个体进行排序，并选择最佳。

该类的私密字段和方法用于内部实现遗传算法，包括轮盘操作、值缩放、排序、等操作。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BGA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP);//number of decimal places in the gene

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;               //coordinates number
  private: int    popSize;              //population size
  private: int    parentPopSize;        //parent population size
  private: double crossoverProbab;      //crossover probability
  private: int    crossoverPoints;      //crossover points
  private: double mutationProbab;       //mutation probability
  private: double inversionProbab;      //inversion probability
  private: int    doubleDigitsInChromo; //number of decimal places in the gene
  private: bool   revision;

  private: S_Agent    parents    [];  //parents
  private: int        ind        [];  //temporary array for sorting the population
  private: double     val        [];  //temporary array for sorting the population
  private: S_Agent    pTemp      [];  //temporary array for sorting the population
  private: char       tempChrome [];  //temporary chromosome for inversion surgery
  private: uint       lengthChrome;   //length of the chromosome (the length of the string of characters according to the Gray code)
  private: int        pCount;         //indices of chromosome break points
  private: uint       poRND      [];  //temporal indices of chromosome break points
  private: uint       points     [];  //final indices of chromosome break points
  private: S_Roulette roulette   [];  //roulette

  private: void   PreCalcRoulette ();
  private: int    SpinRoulette    ();
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: void   Sorting   (S_Agent &p [], int size);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);
};
//——————————————————————————————————————————————————————————————————————————————

下面的代码表示 C_AO_BGA 类的 Init 方法的实现。该方法初始化遗传算法工作所需的类字段和数组。

方法输入：

• “coordsP” — 坐标数量。
• “popSizeP” — 种群大小。
• “parentPopSizeP” — 亲本种群大小。
• “crossoverProbabP” — 交叠概率。
• “crossoverPointsP” — 交叠点的数量。
• “mutationProbabP” — 突变概率。
• “inversionProbabP” — 颠倒概率。
• “doubleDigitsInChromoP” — 基因中的小数位数。

Init 方法在执行遗传算法之前初始化类字段和数组。它设置类字段的值，检查和调整某些参数的值，并通过为数组分配内存来调整数组的大小。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Init (const int    coordsP,               //coordinates number
                     const int    popSizeP,              //population size
                     const int    parentPopSizeP,        //parent population size
                     const double crossoverProbabP,      //crossover probability
                     const int    crossoverPointsP,      //crossover points
                     const double mutationProbabP,       //mutation probability
                     const double inversionProbabP,      //inversion probability
                     const int    doubleDigitsInChromoP) //number of decimal places in the gene
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords               = coordsP;
  popSize              = popSizeP;
  parentPopSize        = parentPopSizeP;
  crossoverProbab      = crossoverProbabP;
  crossoverPoints      = crossoverPointsP;
  pCount               = crossoverPointsP;
  mutationProbab       = mutationProbabP;
  inversionProbab      = inversionProbabP;
  doubleDigitsInChromo = doubleDigitsInChromoP;

  if (crossoverPoints < 1) crossoverPoints = 1;
  if (pCount < 1) pCount = 1;

  ArrayResize (poRND,  pCount);
  ArrayResize (points, pCount + 2);

  ArrayResize (ind,   parentPopSize + popSize);
  ArrayResize (val,   parentPopSize + popSize);
  ArrayResize (pTemp, parentPopSize + popSize);
  ArrayResize (a,     popSize);

  ArrayResize (parents,  parentPopSize + popSize);
  ArrayResize (roulette, parentPopSize);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

操控个体遗传物质的所有基本操作都调用 C_AO_BGA 类的 Moving 方法执行。Moving 方法执行遗传算法步骤，包括选择亲本、交叠、颠倒、和染色体突变、以及对个体的基因和坐标进行操作。

该方法在逻辑上分为若干个部分：

1. "if (!revision)" — 如果 “revision” 等于 “false”，则初始化种群独体：

• 调用 Init 方法，遵照给定参数初始化独体。
• 以 0 或 1 随机值填充每个基因来生成随机染色体。
• 调用 ExtractGenes 方法从染色体中提取基因。
• 调用 SeInDiSp 函数将 “c” 独体的坐标减少到一个范围。
• 每个独体的 “f” 适应度值设置为 “-DBL_MAX”。
• "lengthChrome = ArraySize (a [0].chromosome)" — 独体染色体的长度（所有独体的长度相同）。
• "ArrayResize (tempChrome, lengthChrome)" — 将 “tempChrome” 临时数组的大小替换为 “lengthChrome”。

2. 对于种群中的每个独体：

• 亲本选择轮盘的初步计算是调用 PreCalcRoulette 方法执行的。
• 亲本则是调用 SpinRoulette 方法选择的。
• 所选亲本独体的染色体被复制到当前独体的染色体之中。
• 交叠操作按 crossoverProbab 概率执行。
• 第二个亲本被选中。
• 判定染色体断点。
• 亲本独体的染色体是交叠的。
• 颠倒运算按 inversionProbab 概率执行。
• 判定随机染色体断点。
• 染色体的某些部分会改变位置。
• 对具有 mutationProbab 概率的每个染色体基因执行突变操作。
• 调用 ExtractGenes 方法从染色体中提取基因。
• 调用 SeInDiSp 函数将 “c” 独体的坐标减少到一个范围。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      a [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);

      int r = 0;

      for (int len = 0; len < ArraySize (a [i].chromosome); len++)
      {
        r  = MathRand (); //[0,32767]

        if (r > 16384) a [i].chromosome [len] = 1;
        else           a [i].chromosome [len] = 0;
      }

      a [i].ExtractGenes ();

      for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a [i].f = -DBL_MAX;
      a [i].calculated = true;
    }

    lengthChrome = ArraySize (a [0].chromosome);
    ArrayResize (tempChrome, lengthChrome);

    for (int i = 0; i < parentPopSize + popSize; i++)
    {
      parents [i].Init (coords, rangeMin, rangeMax, doubleDigitsInChromo);
      parents [i].f = -DBL_MAX;
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    pos       = 0;
  double r         = 0;
  uint   p1        = 0;
  uint   p2        = 0;
  uint   p3        = 0;
  uint   temp      = 0;

  for (int i = 0; i < popSize; i++)
  {
    PreCalcRoulette ();

    //selection, select and copy the parent to the child------------------------
    pos = SpinRoulette ();

    ArrayCopy (a [i].chromosome, parents [pos].chromosome, 0, 0, WHOLE_ARRAY);

    //crossover-----------------------------------------------------------------
    r = RNDfromCI (0.0, 1.0);

    if (r < crossoverProbab)
    {
      //choose a second parent to breed with------------------------------------
      pos = SpinRoulette ();

      //determination of chromosome break points--------------------------------
      for (int p = 0; p < pCount; p++)
      {
        poRND [p] = (int)RNDfromCI (0.0, lengthChrome);
        if (poRND [p] >= lengthChrome) poRND [p] = lengthChrome - 1;
      }
      ArraySort (poRND);
      ArrayCopy (points, poRND, 1, 0, WHOLE_ARRAY);
      points [0] = 0;
      points [pCount + 1] = lengthChrome - 1;

      r = RNDfromCI (0.0, 1.0);

      int startPoint = r > 0.5 ? 0 : 1;

      for (int p = startPoint; p < pCount + 2; p += 2)
      {
        if (p < pCount + 1)
        {
          for (uint len = points [p]; len < points [p + 1]; len++) a [i].chromosome [len] = parents [pos].chromosome [len];
        }
      }
    }

    //perform an inversion------------------------------------------------------
    //(break the chromosome, swap the received parts, connect them together)
    r = RNDfromCI (0.0, 1.0);

    if (r < inversionProbab)
    {
      p1 = (int)RNDfromCI (0.0, lengthChrome);
      if (p1 >= lengthChrome) p1 = lengthChrome - 1;

      //copying the second part to the beginning of the temporary array
      for (uint len = p1; len < lengthChrome; len++) tempChrome [len - p1] = a [i].chromosome [len];

      //copying the first part to the end of the temporary array
      for (uint len = 0; len < p1; len++)       tempChrome [lengthChrome - p1 + len] = a [i].chromosome [len];

      //copying a temporary array back
      for (uint len = 0; len < lengthChrome; len++)   a [i].chromosome [len] = tempChrome [len];
    }

    //perform mutation---------------------------------------------------------
    for (uint len = 0; len < lengthChrome; len++)
    {
      r = RNDfromCI (0.0, 1.0);
      if (r < mutationProbab) a [i].chromosome [len] = a [i].chromosome [len] == 1 ? 0 : 1;
    }

    a [i].ExtractGenes ();

    for (int c = 0; c < coords; c++) a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

    a [i].calculated = true;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revision 方法执行种群修订，按适应度函数的值对独体进行排序，并更新最佳解元的 “fB” 适应度、及其 “cB” 坐标。在针对种群进行排序之前，会将子种群复制到总种群的末尾。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = a [i - parentPopSize];
  }

  Sorting (parents, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

初步轮盘布局代码表示 PreCalcRoulette 方法。该方法基于独体的适应度函数，初步计算独体轮盘选择的范围值。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BGA::PreCalcRoulette ()
{
  roulette [0].start = parents [0].f;
  roulette [0].end   = roulette [0].start + (parents [0].f - parents [parentPopSize - 1].f);

  for (int s = 1; s < parentPopSize; s++)
  {
    if (s != parentPopSize - 1)
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s].f - parents [parentPopSize - 1].f);
    }
    else
    {
      roulette [s].start = roulette [s - 1].end;
      roulette [s].end   = roulette [s].start + (parents [s - 1].f - parents [s].f) * 0.1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

SpinRoulette 方法确保选择亲本独体的位置。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BGA::SpinRoulette ()
{
  double r = RNDfromCI (roulette [0].start, roulette [parentPopSize - 1].end);

  for (int s = 0; s < parentPopSize; s++)
  {
    if (roulette [s].start <= r && r < roulette [s].end) return s;
  }

  return 0;
}
//——————————————————————————————————————————————————————————————————————————————

3. 测试结果

BGA 测试台结果：

C_AO_BGA:50:50:1.0:3:0.001:0.7:3
=============================
5 Hilly's; Func runs: 10000; result: 0.9999191151339382
25 Hilly's; Func runs: 10000; result: 0.994841435673127
500 Hilly's; Func runs: 10000; result: 0.5048331764136147
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.9997457419655973
500 Forest's; Func runs: 10000; result: 0.32054251149158375
=============================
5 Megacity's; Func runs: 10000; result: 0.9066666666666668
25 Megacity's; Func runs: 10000; result: 0.9640000000000001
500 Megacity's; Func runs: 10000; result: 0.23034999999999997
=============================
All score: 6.92090 (76.90%)

BGA 优化的可视化清晰地演示了算法的高度收敛性。有趣的是，在优化过程期间，种群的一部分仍远离全局极值，这表明探索了搜索空间的新未知区域，保持了种群中解元的多样性。不过，该算法在调用 Megacity 离散函数时面临一定的困难，对于大多数算法来说其都有问题。尽管在操控这个复杂函数时结果存在一些差异，但 BGA 的性能明显优于其它算法。

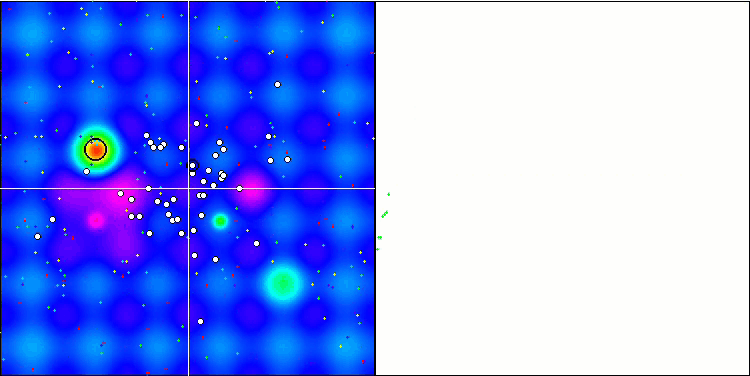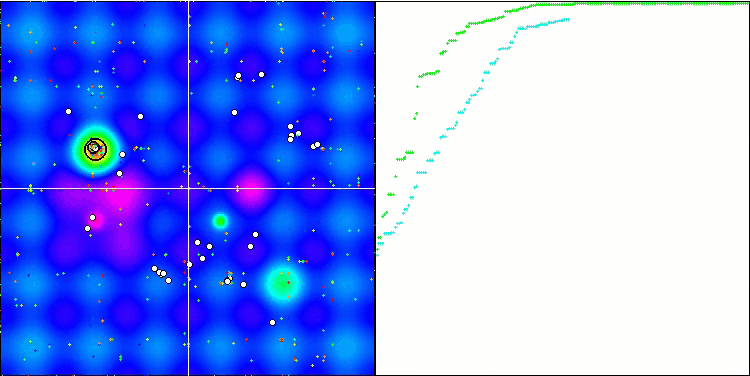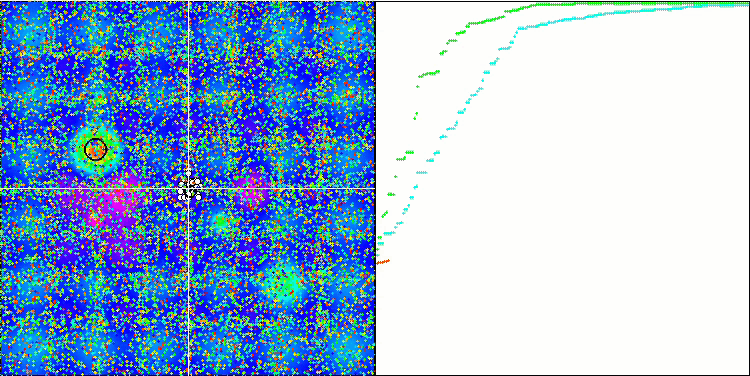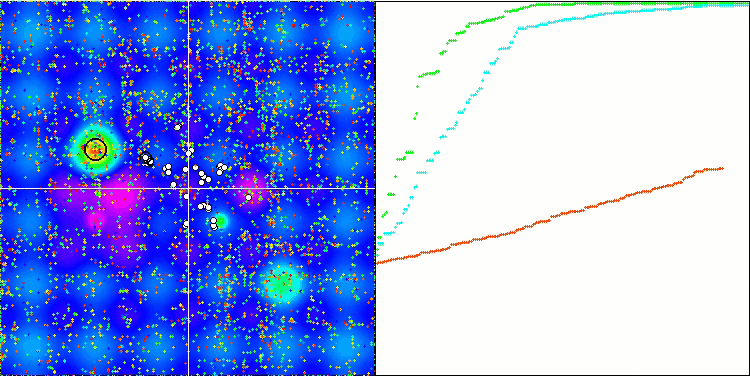
BGA 依据 Hilly 测试函数

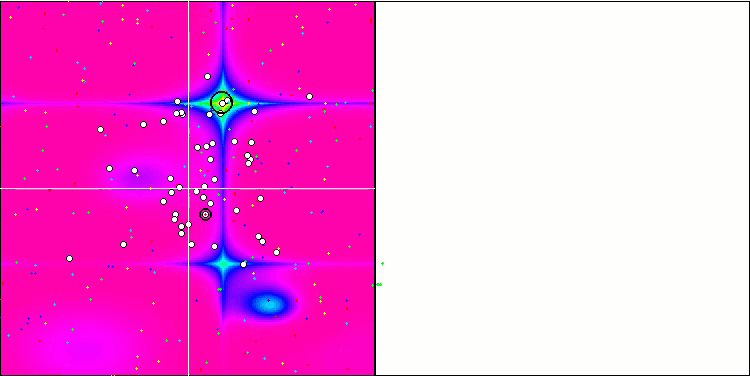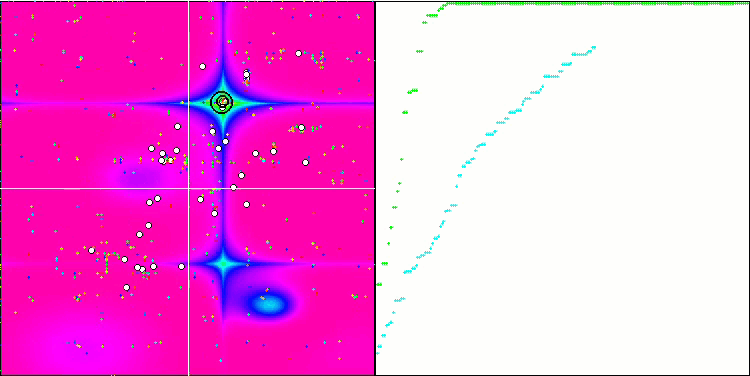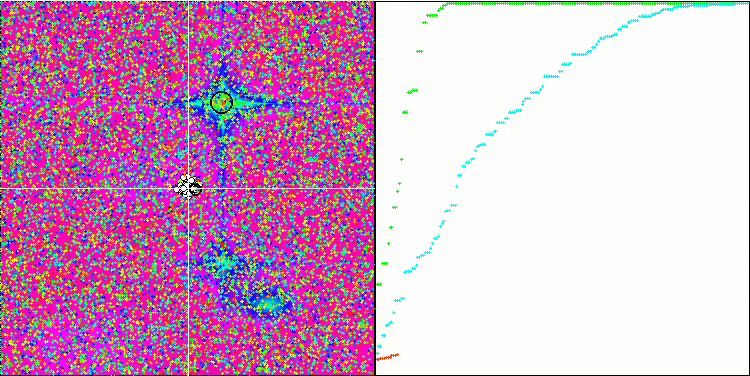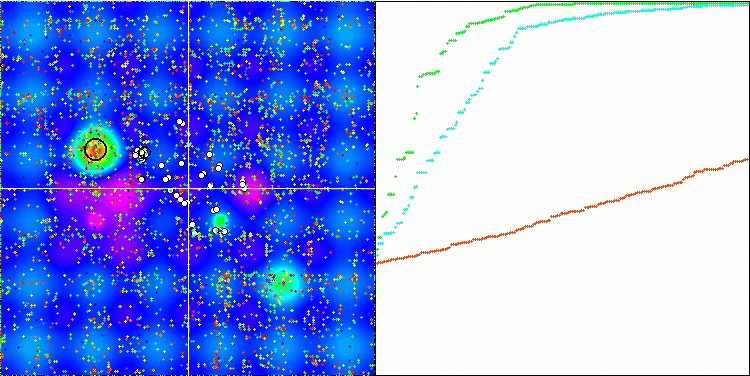
BGA 依据 Forest 测试函数

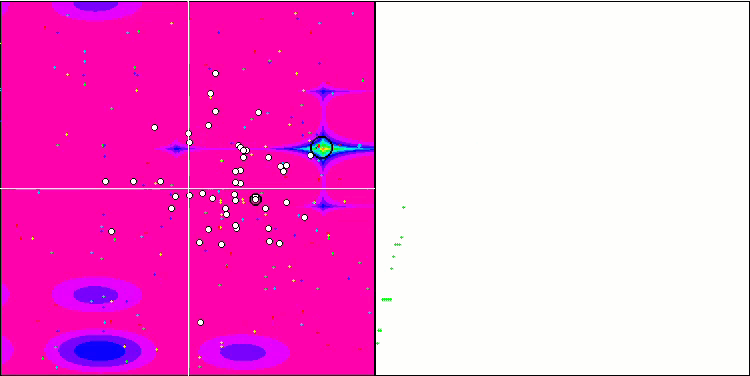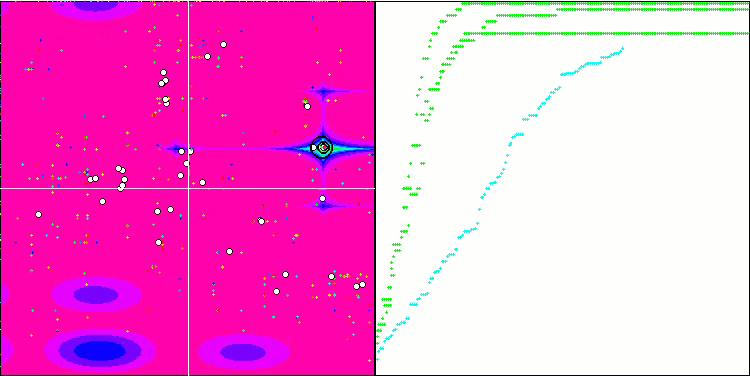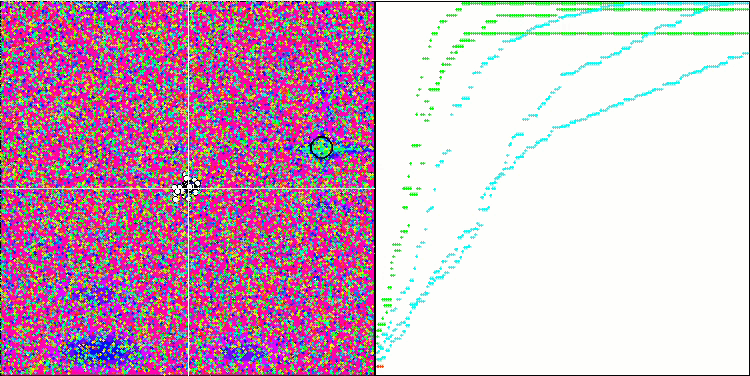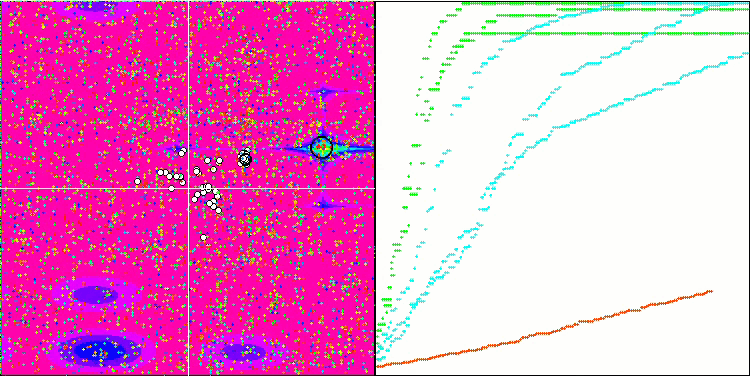
BGA 依据 Megacity 测试函数

BGA 在榜单中名列前茅，在所有三个测试函数的大多数测试中表现最佳。BGA 在 Megacity 离散函数上演示出特别令人印象深刻的结果，优于其它算法。

# AO 说明 Hilly Hilly 最终 Forest Forest 最终 Megacity (离散) Megacity 最终 最终结果 最大 % 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 1 BGA 二进制遗传算法 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90 2 (P+O)ES (P+O) 进化策略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18 3 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44 4 SIA 模拟各向同性退火 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76 5 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06 6 HS 谐声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79 7 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95 8 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22 9 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31 10 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93 11 MEC 心智进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55 12 IWO 入侵性杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81 13 Micro-AIS 微人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54 14 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21 15 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44 16 NMm Nelder-Mead 方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92 17 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87 18 GSA 重力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34 19 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72 20 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06 21 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93 22 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43 23 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06 24 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77 25 MA 猴子算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40 26 SFL 蛙跳 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38 27 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84 28 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37 29 GWO 灰狼优化器 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32 30 CSS 收费系统搜索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46 31 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85

总结

在本文中，我们实证了 BGA 的经典版本，这是常用 GA 遗传算法的一个特例，所有结论都与它特性相关。尽管用二进制表示解元的想法由来已久，但使用二进制码的方式至今仍然适用。它通过在一条染色体中编码信息，将优化问题的独立空间维度组合成一个整体，而这用传统的实值特征编码很难实现，令该算法从其它优化算法中脱颖而出。

尽管 BGA 策略的数学和逻辑对我来说完全清楚，但我仍然对染色体发生的事情着迷。它可以比作一个神奇的万花筒。当我们旋转万花筒时，不同的形状和颜色组合成独特的图案，创造出一幅壮观的画面。与其类似，BGA 中的交叠算子将染色体随机切成若干个部分，包括内部参数区域。然后将这些碎片放在一起，就像摇晃万花筒的碎片一样。这令我们能够结合不同解元的最佳特征，并创建一个新的、更优化的组合。就像万花筒一样，BGA 交叠的结果可能令人惊讶和出乎意料，将简单的染色体变成真正的最佳解元“钻石”。

我有信心，在这两卷文章里有关遗传算法中所用方法和工具的信息，将帮助您扩展知识，并在工作和研究中达到新的高度。进化的力量不断体现在自然、技术、和人类脑海中，而 BGA 是众多令人惊叹的算法之一，它将帮助我们达到新的高度和成就。

BGA 可以有效地解决各种问题，无论是光滑表面、离散问题，还是大规模问题，包括随机方法，在分析解元有限的情况下开辟了新的可能性。

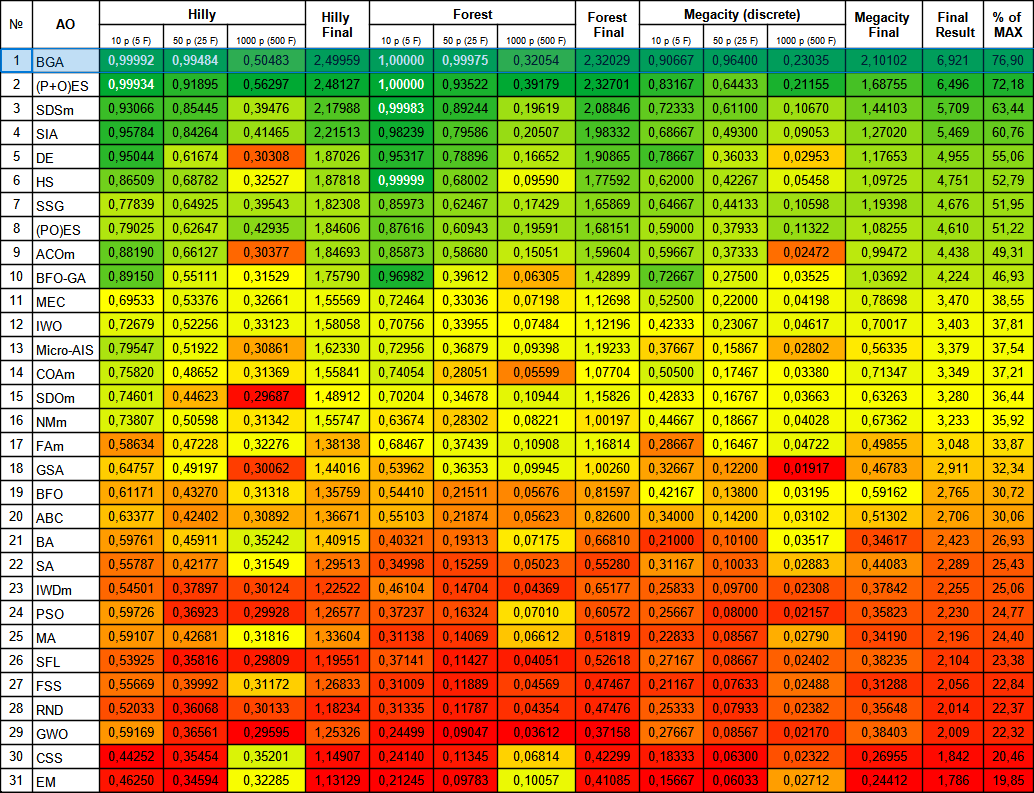
图例 2. 算法颜色渐变是根据相关测试，而大于或等于 0.99 的结果，会以白色高亮显示

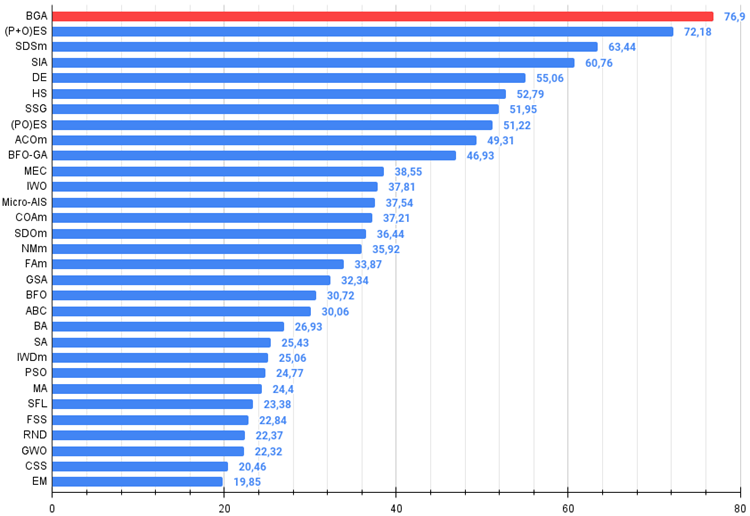
图例 3. 算法测试结果的直方图（标尺从 0 到 100，越多越好，

其中 100 是理论上的最大可能结果（存档提供了一个计算排位表格的脚本）。

二进制遗传算法（BGA）的优缺点专适于所提出的实现：

优势：

1. 高效解决各种问题。
2. 抗粘连性。
3. 在平滑和复杂的离散函数上都有可喜的结果。
4. 高收敛性。

缺点：

1. 大量的外部参数。
   
2. 相当复杂的实现。
   
3. 计算复杂度高。
   

本文附有一个存档，其中包含前几篇文章中讲述的算法代码的当前更新版本。文章作者不对规范算法讲述的绝对准确性负责。它们当中进行了多处修改，从而提升搜索能力。文章中表述的结论和论断是基于实验的结果。