MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
种群优化算法：Boids（虚拟生物）算法

种群优化算法：Boids（虚拟生物）算法

MetaTrader 5 — 示例 | 22 十月 2024, 11:08
452 0
Andrey Dik
Andrey Dik

内容

概述
算法描述
测试结果


1. 概述

观察自然界中动物的集群行为，我们不由自主地赞叹它们协调一致和高效互动的能力。它们仿佛受到一种无形力量的控制，能够像单个生物体一样同步调整自己的位置，克服障碍，找出最优路径。这种基于简单交互规则却表现出了非常优秀的运动和谐性，促成了许多元启发优化算法的生成。

通过研究鸟类集群的复杂迁徙路线，科学家们发现它们遵循的原则与种群智能算法相似。因此，鱼群就像活细胞一样，形成脉动的结构，让人联想到基于元胞自动机的优化方法。足类哺乳动物的集群行为、它们对危险的协调反应，以及一群椋鸟的同步飞行，都展现了动物们协调行为的惊人能力。

这些自然界中优秀的例子启发人们开发强大的优化工具，这些工具能够解决从规划行动路线到设计高效控制系统等复杂问题。

Boids算法（由“bird”（鸟）和“-oid”（类似物）组合而成）是克雷格·雷诺兹（Craig Reynolds）于1986年创建的一种计算机算法，它模拟动物群体，特别是鸟类的行为。该算法旨在模仿动物群体的自然行为，其中每个个体都根据简单的规则移动，这些规则最终导致了群体行为的出现。它基于以下三条规则：

1. 分离。每个物体（或“boid”）都试图尽量减少与附近物体碰撞的可能性。
2. 对齐。每个物体都努力确保其运动方向与附近物体的平均运动方向相一致。
3. 凝聚力。 每个物体都努力使其位置接近于附近物体的平均位置。

这三条简单的规则使我们能够模拟鸟群或昆虫群体的复杂行为。Boids算法在计算机图形学中得到了广泛地应用，用于创建鸟群、昆虫群或鱼群的动画。

原始的Boids算法有几个目标和应用：

1. 创建逼真的动画。Boids算法能够创建逼真的动物群体动画，这已成为计算机图形学和动画发展的重要方向之一。
2. 行为模式。 Boids允许根据个体的简单规则模拟复杂的集体行为。这一技术在动物行为研究、机器人技术、交通管理等多个领域都得到了应用。

Boids算法促成了其他算法的发展，如粒子群优化（PSO）算法和种群行为建模算法。

Boids算法仍然是模拟集体行为的一种流行工具，并且仍然在科学技术领域的各个分支中作为研究和开发的主题。

在下面的动画中，我们可以看到这些相同的Boids的行为，它们可以聚集成紧凑的群体，分散飞行，还可以与邻居的速度保持同步。在录制动画时，算法的设置是实时更改的，这使得我们能够看到相应的设置对Boids行为的影响。

Boids

初始化Boids算法

config

按下F3键可以调出Boids算法的设置窗口。我们可以将“#reset”参数赋值为“1”来重启该算法。


2. 算法

使用Craig Reynolds开发的Boids算法最初是为了模拟动物的集群行为，例如鸟群、昆虫群等。然而，由其具有灵活性和适应性，该算法已在包括优化和搜索在内的多个领域得到了应用。在优化和搜索的背景下，Boids算法可用于解决与一组智能体的协调行为相关的问题。例如，它可以用于模拟探索未知领域的群体行为。

值得注意的是，Boids算法本身并不是传统意义上的搜索算法。它并不是为了在给定的可能解空间中寻找最优解而设计的，就像梯度下降算法或遗传算法所做的那样。相反，Boids算法基于一组简单规则来模拟一组智能体的行为，这使得它能够在群体层面上模拟复杂且协调的行为。

Boids算法适用于函数的极值分布式搜索。在这种情况下，每个“boid”都代表一个搜索智能体，它在可能的解的空间中移动。每个智能体不仅仅跟随其他“boid”，而是可以使用其当前位置处的函数值来调整其运动或考虑种群中其他boid的适应度。

在使用Craig Reynolds模拟群体行为的Boids算法中，诞生了种群智能的概念。种群智能描述了一个去中心化自组织系统的集体行为，其中包含粒子群优化（Particle Swarm Optimization, PSO）算法。

群体智能系统通常由多个代理（boids）组成，这些代理在局部范围内相互作用，并且与环境进行交互。这些行为想法通常来源于自然界，尤其是生物系统。每个boid都在遵循非常简单的规则。尽管没有中央行为控制系统指示每个boid应该做什么，但局部且带有一定随机性的交互，引发了超出单个boid控制范围的智能群体行为。

Boids算法有很多外部参数，每个参数都对boids的运动特性产生了显著地影响。让我们来看看这些参数：

  1. cohesionWeight - 凝聚权重决定了群体成员之间的吸引力。
  2. cohesionDist - 凝聚距离决定了群体成员之间的距离，在这个距离的范围内，他们开始相互吸引。
  3. separationWeight -分离权重决定了群体成员相互排斥的程度。
  4. separationDist - 分离距离决定了群体成员之间的距离，在该距离处，它们开始相互排斥。
  5. alignmentWeight - 对齐权重决定了群体成员将如何朝着彼此的运动方向对齐。
  6. alignmentDist - 对齐距离决定了群体成员之间的距离，在该距离处，它们开始朝着彼此的运动方向上对齐。
  7. minSpeed - boids最小移动速度。
  8. maxSpeed - boids最大移动速度。

进行一系列实验来调整这些参数以获得所需的群体行为是非常重要的。你可以从建议的参数值开始，并逐步调整取值，以观察它们如何影响群体行为。请注意，从绝对意义上来讲，Boids算法并没有“正确”或“最佳”的参数值。这完全取决于具体的任务和场景。

接下来，让我们开始编写Boids算法的代码。为了描述每个智能体，我们定义了S_Boids_Agent结构。让我们来看看当前的进展：


1. 该结构包含以下字段：

  • x[] -用于存储当前智能体坐标的数组。
  • dx[] - 当前智能体速度的数组
  • m -智能体集群。

2. Init -使用 S_Boids_Agent初始化结构字段。设置“coords”为整数性参数，使用ArrayResize函数调整“x”和“dx”数组的大小。

此代码表示Boids算法中智能体的基本数据结构，并在创建新智能体时初始化其字段。这使得每个智能体都有自己的坐标和速度，这是Boids算法的一个关键方面。其中“m”字段是我主动添加的，旨在考虑移动boids的适应度函数曲面时，将集群纳入考量。

//——————————————————————————————————————————————————————————————————————————————
struct S_Boids_Agent
{
    double x  [];
    double dx [];
    double m;

    void Init (int coords)
    {
      ArrayResize (x,  coords);
      ArrayResize (dx, coords);
    }
};
//——————————————————————————————————————————————————————————————————————————————

让我们定义Boids算法中的C_AO_Boids类，该类是C_AO种群算法基类的继承者，并包含以下字段和方法：

1. 公共字段:

  • ao_name - 优化算法名称。
  • ao_desc - 优化算法描述。
  • popSize - 种群大小
  • params - 算法参数数组。
  • cohesionWeight - 凝聚权重。
  • cohesionDist - 凝聚距离。
  • separationWeight - 分离权重。
  • separationDist - 分离距离。
  • alignmentWeight - 对齐权重。
  • alignmentDist - 对齐距离。
  • maxSpeed - 最大速度。
  • minSpeed - 最小速度。
  • agent - 智能体载体。

2. 可用的选项有：

  • C_AO_Boids -用于初始化类字段的类构造函数。
  • SetParams - 算法参数设置方法。
  • Init - 算法初始化方法。该方法需要最小和最大搜索范围、搜索步长和迭代次数。
  • Moving - 智能体移动方法。
  • Revision - 智能体修改方法。

3. 私有字段：

  • distanceMax - 搜索空间中最大可能的欧几里得距离。
  • speedMax - 最大速度。
//——————————————————————————————————————————————————————————————————————————————
class C_AO_Boids : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_Boids () { }
  C_AO_Boids ()
  {
    ao_name = "Boids";
    ao_desc = "Boids Algorithm";
    ao_link = "https://www.mql5.com/en/articles/14576";

    popSize          = 50;   //population size

    cohesionWeight   = 0.6;
    cohesionDist     = 0.001;

    separationWeight = 0.005;
    separationDist   = 0.03;

    alignmentWeight  = 0.1;
    alignmentDist    = 0.1;

    maxSpeed         = 0.001;
    minSpeed         = 0.0001;

    ArrayResize (params, 9);

    params [0].name = "popSize";          params [0].val = popSize;

    params [1].name = "cohesionWeight";   params [1].val = cohesionWeight;
    params [2].name = "cohesionDist";     params [2].val = cohesionDist;


    params [3].name = "separationWeight"; params [3].val = separationWeight;
    params [4].name = "separationDist";   params [4].val = separationDist;

    params [5].name = "alignmentWeight";  params [5].val = alignmentWeight;
    params [6].name = "alignmentDist";    params [6].val = alignmentDist;

    params [7].name = "maxSpeed";         params [7].val = maxSpeed;
    params [8].name = "minSpeed";         params [8].val = minSpeed;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double cohesionWeight;   //cohesion weight
  double cohesionDist;     //cohesion distance

  double separationWeight; //separation weight
  double separationDist;   //separation distance

  double alignmentWeight;  //alignment weight
  double alignmentDist;    //alignment distance

  double minSpeed;         //minimum velocity
  double maxSpeed;         //maximum velocity

  S_Boids_Agent agent [];

  private: //-------------------------------------------------------------------
  double distanceMax;
  double speedMax [];

  void   CalculateMass    ();
  void   Cohesion         (S_Boids_Agent &boid, int pos);
  void   Separation       (S_Boids_Agent &boid, int pos);
  void   Alignment        (S_Boids_Agent &boid, int pos);
  void   LimitSpeed       (S_Boids_Agent &boid);
  void   KeepWithinBounds (S_Boids_Agent &boid);
  double Distance         (S_Boids_Agent &boid1, S_Boids_Agent &boid2);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids 类的初始化方法：基于传入的参数初始化类变量。该方法使用 StandardInit 方法执行标准初始化，需要输入最小搜索范围、最大搜索范围以及搜索步长作为参数。

如果标准初始化操作成功，那么该方法会根据“种群大小”（popSize）来调整“智能体”（agent）数组或集合的大小。对于“智能体”（agent）数组或集合中的每个元素，都会调用 Init 方法，并传入一个名为 coords 的参数。

接下来，该方法会计算最大距离和最大速度这两个参数，这两个参数在 Boids 算法中用于确定智能体（agents）的移动。

接下来，该方法会为 Boids 算法的各种参数设置全局变量，这些参数包括凝聚权重（cohesion weight）、凝聚距离（cohesion distance）、分离权重（separation weight）、分离距离（separation distance）、对齐权重（alignment weight）、对齐距离（alignment distance）、最大速度（maximum speed）以及最小速度（minimum speed）。

如果初始化成功，该方法返回“true”，否则返回“false”。

该方法使用给定的参数完成Boids优化算法的初始化设置，以确保执行优化。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_Boids::Init (const double &rangeMinP  [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += pow (speedMax [c], 2);
  }

  distanceMax = sqrt (distanceMax);

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);


  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类的Moving方法被用于在优化过程中移动智能体。该方法执行以下操作：

  1. 检查全局变量“reset”的值。如果其为1.0，则“revision”标识设置为“false”。当全局“reset”变量的值设置为0.0时，退出该方法。
  2. 从全局变量中提取算法参数的值。
  3. 如果 "revision"标识的值为 "false"，则使用指定范围内的随机值初始化智能体的坐标和速度。当 "revision" 标识的值设置为 "true" 时，退出该方法。
  4. 如果"revision"标识的值不是"false"，则对每个智能体执行以下操作：
    • 调用CalculateMass、Cohesion、Separation、Alignment、LimitSpeed和KeepWithinBounds方法来更新智能体速度。
    • 智能体坐标会根据其速度进行更新。
    • 智能体坐标被复制到“a”数组的相应元素中。
/——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    CalculateMass    ();
    Cohesion         (agent [i], i);
    Separation       (agent [i], i);
    Alignment        (agent [i], i);
    LimitSpeed       (agent [i]);
    KeepWithinBounds (agent [i]);

    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类的CalculateMass方法用于计算Boids算法中每个智能体的“集群”。使用此方法的情况：

  1. 初始化变量“maxMass”和“minMass”，用于存储所有智能体中适应度函数的最大值和最小值。
  2. 对于种群中的每个智能体，都需要检查其适应度函数“a[i].f”是否大于当前的“maxMass”的最大值或者小于当前“minMass”的最小值。如果满足上述条件，则更新相应的最大值和最小值。
  3. 测试完所有智能体后，每个智能体的“mass”（集群）会根据其适应度函数相对于最小值和最大值的比例来计算得出。

这种方法为Boids算法中的每个智能体计算了“mass”（集群），这正是原算法逻辑中所缺失的。它令我们考虑到boids移动所依赖的地形“表面”。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.0, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类中的Cohesion方法用于实现Boids算法中的“凝聚”行为。这种行为使智能体向其邻居的“质心”移动。该方法执行以下任务：

  1. 初始化“centerX”数组以存储质心的坐标，同时使用“numNeighbors”变量统计邻居的数量。
  2. 对于种群中的每个智能体，都会检查它是否不是自身（因为智能体不应将自己视为邻居）并且是否在一定的距离范围内。如果两个条件都满足，则将该智能体的坐标添加到“centerX”中，并将“numNeighbors”参数值增加1。
  3. 如果至少找到一个邻居，则将“centerX”坐标除以邻居的数量，以此获得邻居质心的坐标。然后，根据“cohesionWeight”（凝聚权重）调整智能体“boid.dx”的速度，使其朝向质心移动。

该方法实现了Boids算法中的“凝聚”行为，有助于智能体作为群体一起移动。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Cohesion (S_Boids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize     (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int    numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c];
        }

        numNeighbors++;
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    centerX [c] /= numNeighbors;
    boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

在Boids算法中，使用C_AO_Boids类中的Separation方法实现智能体的“分离”（Separation）行为。“分离”（Separation）行为是避免智能体之间因靠得太近而造成相互碰撞。使用此方法的情况：

  1. 初始化“moveX”数组存储智能体坐标的变化。
  2. 对于种群中的每个智能体，都会检查它是否不是自身（因为智能体不应将自己视为邻居）以及它是否位于一定的距离范围内（定义为“distanceMax * separationDist”）。如果这两个条件都满足，则将当前智能体与其邻居的坐标之差添加到“moveX”参数中。
  3. 检查完所有邻居后，通过“separationWeight”（分离权重）参数来调整“boid.dx”智能体的速度，使其与“moveX”方向相反。

此方法实现了Boids算法中的“分离”行为，有助于避免智能体之间相互碰撞。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Separation (S_Boids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize     (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类的“Alignment”方法用于实现Boids算法中的“对齐”行为。这样操作使得智能体与其邻居朝同一方向移动。该方法如下：

  1. 初始化数组“avgDX”存储邻居的平均速度，初始化变量“numNeighbors”统计邻居的数量。
  2. 对于种群中的每个智能体，都会检查它是不是自身（因为智能体不应将自己视为邻居）以及它是否位于一定的距离范围内（定义为“distanceMax * alignmentDist”）。如果这两个条件都满足，则将邻居的速度添加到“avgDX”中，并将“numNeighbors”参数增加1。
  3. 如果至少找到一位邻居，则将“avgDX”中的速度除以邻居的数量以获得平均速度。然后，根据“alignmentWeight”（对齐权重）调整“boid.dx”智能体的速度，使其趋向于平均速度。

该方法实现了Boids算法中的“对齐”行为，有助于智能体朝着相同方向一起移动。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Alignment (S_Boids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize     (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

    for (int c = 0; c < coords; c++)
    {
      avgDX   [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类的LimitSpeed方法用于限制Boids算法中智能体的速度。这样操作能够阻止了智能体速度的无限增加，以便符合自然界中真实动物的情况。该方法执行以下操作：

  1. 初始化变量“speed”用于存储智能体的当前速度，初始化变量“d”用于临时存储数据。
  2. 智能体的当前速度是根据其每个坐标的速度计算得出的。
  3. 对于智能体的每个坐标，执行以下操作：
    • 参数“d”用于计算为最大和最小范围值之间的差，再乘以最小速度因子。 
    • 根据“speedMax”（最大可能速度）和“maxSpeed”（最大速度因子）调整“boid.dx”智能体的速度。
    • 如果智能体速度的绝对值小于“d”，则将智能体速度设置为等于“d”（保留符号）。

该方法实现了Boids算法中的“速度限制”行为，有助于控制智能体的移动速度，并阻止boids静止下来。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::LimitSpeed (S_Boids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = sqrt (speed);

  double d = 0;

  for (int c = 0; c < coords; c++)
  {
    d = (rangeMax [c] - rangeMin [c]) * minSpeed;

    boid.dx [c] = (boid.dx [c] / speed) * speedMax [c] * maxSpeed;

    if (fabs (boid.dx [c]) < d)
    {
      if (boid.dx [c] < 0.0) boid.dx [c] = -d;
      else                   boid.dx [c] =  d;
    }

  }
}
//——————————————————————————————————————————————————————————————————————————————

在Boids算法中，使用C_AO_Boids类的KeepWithinBounds方法将智能体的移动限制在指定的边界内。这样操作能够防止智能体超出指定的边界。

  1. 对于智能体的每个坐标，都需要检查它是否位于指定的边界之外（定义为“rangeMin”和“rangeMax”）。
  2. 如果智能体的坐标小于“rangeMin”，则将其设置为“rangeMax ”，这样做的目的是将智能体移动到边界的另一侧。
  3. 如果智能体的坐标大于“rangeMax”，则将其设置为“rangeMin"，这样做的目的是将智能体“移动”到边界的另一侧。

该方法实现了Boids算法中的“边界约束”，将智能体位置框定在给定的边界内。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::KeepWithinBounds (S_Boids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    double margin     = 0; //(rangeMax [c] - rangeMin [c])* 0.00001;
    double turnFactor = (rangeMax [c] - rangeMin [c]) * 0.0001;

    /*
    if (boid.x [c] < rangeMin [c] + margin)
    {
      boid.dx [c] += turnFactor;
    }
    if (boid.x [c] > rangeMax [c] - margin)
    {
      boid.dx [c] -= turnFactor;
    }
    */
    if (boid.x [c] < rangeMin [c]) 
    {
      //boid.x [c] = rangeMax [c];
      boid.dx [c] *= -1;
      
    }
    if (boid.x [c] > rangeMax [c])
    {
      //boid.x [c] = rangeMin [c];
      boid.dx [c] *= -1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类中的Distance方法用于计算Boids算法中两个智能体之间的欧几里得距离。

  1. 初始化“dist”变量用于存储计算出的距离。
  2. 对于每个智能体的坐标，计算它们坐标之间差的平方，并将这个平方值累加到“dist”参数上。
  3. 最后，该方法返回“dist”的平方根，这个值对应于两个智能体之间的欧几里得距离。

这个方法实现了Boids算法中计算智能体之间的距离，这个距离是用来确定智能体之间的相互作用。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_Boids::Distance (S_Boids_Agent &boid1, S_Boids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += pow (boid1.x [c] - boid1.x [c], 2);
  }

  return sqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_Boids类中的Revision方法用于更新Boids算法中的最优解。

  1. 初始化变量“ind”的值为-1。这个变量将用于存储具有最优解智能体的索引。
  2. 对于种群中的每个智能体，都需要检查其适应度函数值“a[i].f”是否小于当前的最优解“fB”。如果是，则将“ind”设置为该智能体的索引。
  3. 如果找到了具有更优解的智能体（即“ind”不等于-1），则使用该智能体的值更新最优解“fB”和最优坐标“cB”。

这个方法实现了Boids算法中最优解的更新，有助于算法专注于解空间中最有前景的区域。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. 测试结果

我希望能够更详细地探讨Boids算法在不同函数集上的结果。在所有的测试函数中，Boids算法的总得分为2.22889，这仅相当于最大可能得分的24.77%。这一结果表明算法的效率较低。基于以上这些，我们可以得出结论：Boids算法在解决各种函数的优化问题方面潜力有限。

Boids|50.0|0.05|0.002|0.01|0.01|0.0001|0.01|0.001|0.0001|
=============================
5 Hilly's; Func runs: 100000; result: 0.43339505349362384
25 Hilly's; Func runs: 100000; result: 0.3058074706767012
500 Hilly's; Func runs: 100000; result: 0.2542539219446322
=============================
5 Forest's; Func runs: 100000; result: 0.35717696198531945
25 Forest's; Func runs: 100000; result: 0.20160005990319796
500 Forest's; Func runs: 100000; result: 0.15708435238635948
=============================
5 Megacity's; Func runs: 100000; result: 0.2784615384615384
25 Megacity's; Func runs: 100000; result: 0.14276923076923081
500 Megacity's; Func runs: 100000; result: 0.09833846153846236
=============================
总分: 2.22889 (24.77%)

在算法排名表中，Boids算法位列第28名，紧挨着它在集群智能系统中的“兄弟”——粒子群优化（Particle Swarm Optimization, PSO）算法。

# AO 说明 Hilly值 Hilly最终值 Forest值 Forest最终值 Megacity (离散) Megacity最终值 最终结果 最大百分比
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA 二进制遗传算法 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O) 进化策略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA 模拟退火算法 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA 种群算法 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
12 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
13 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
14 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
15 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
16 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
17 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
18 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
19 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
20 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
21 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
22 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
23 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
24 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
25 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
26 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
27 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
28 Boids 虚拟生物算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
29 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
30 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
31 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
32 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
33 GWO 灰狼优化算法 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
34 CSS 人工电场算法 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
35 EM 类电磁算法 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


总结

尽管在测试函数上的结果不尽如人意，但值得注意的是，Boids在具有1000个变量的Forest和Megacity函数上，结果相当不错，与表中上半部分算法的结果不相上下。这一点也许说明，在处理大量变量时，Boids算法可能更为高效。总体而言，这些结果表明，不要对Boids算法的潜力抱有过高的期望。

tab

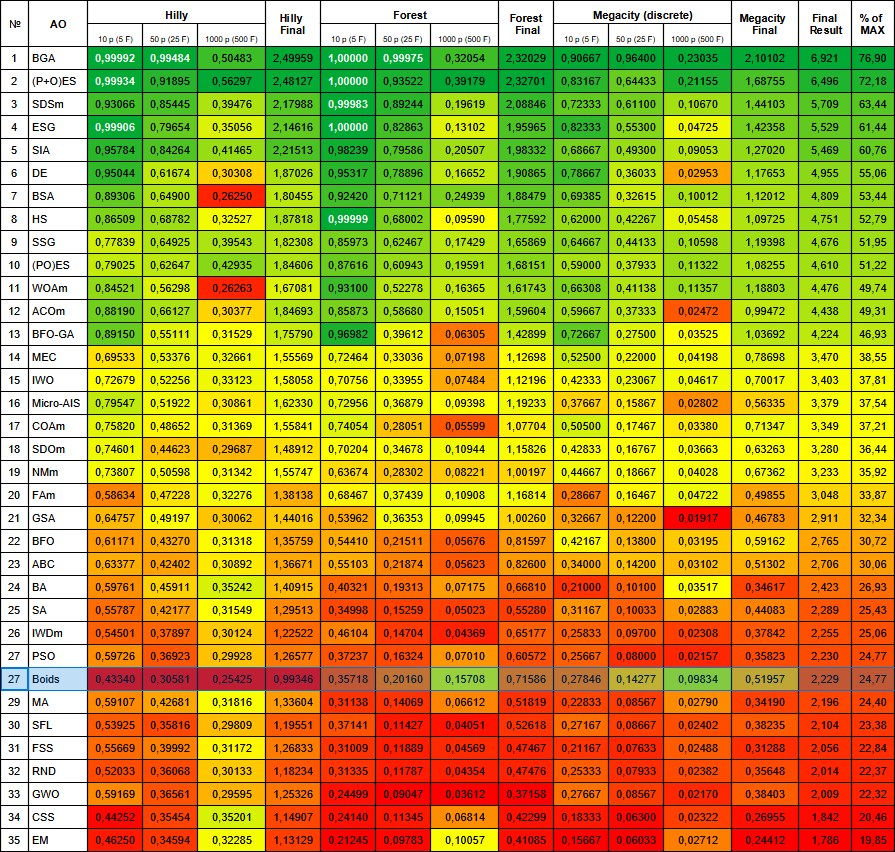
Figure 1. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示

图表

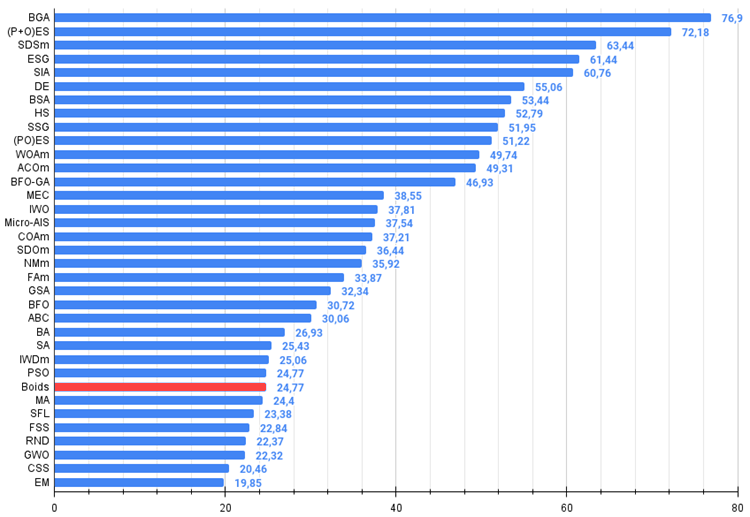
Figure 2. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）。

Boids算法的利与弊

优势：

  1. 逼真的集群行为模拟。

缺点：

  1. 低收敛性。
  2. 计算复杂度高。
  3. 在诸如Hilly等平滑函数上，可扩展性低（高维任务存在问题）。

本文附有一个包含当前代码版本的电子档案。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/14576

附加的文件 |
下载ZIP
Boids.zip (28.61 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
数据科学和机器学习（第 19 部分）：利用 AdaBoost 为您的 AI 模型增压 数据科学和机器学习（第 19 部分）：利用 AdaBoost 为您的 AI 模型增压
AdaBoost，一个强力的提升算法，设计用于提升 AI 模型的性能。AdaBoost 是 Adaptive Boosting 的缩写，是一种复杂的融合学习技术，可无缝集成较弱的学习器，增强它们的集体预测强度。
群体算法的混合 -顺序结构和并行结构 群体算法的混合 -顺序结构和并行结构
在这里，我们将深入探讨优化算法混合的三个主要类型：策略混合、顺序混合和并行混合。我们将结合并测试相关的优化算法进行一系列实验。
分歧问题：深入探讨人工智能的复杂性可解释性 分歧问题：深入探讨人工智能的复杂性可解释性
在这篇文章中，我们将探讨理解人工智能如何工作的挑战。人工智能模型经常会以难以解释的方式做出决策，这就是所谓的 "分歧问题"。这个问题是提高人工智能透明度和可信度的关键。
使用Python和MQL5开发机器人（第一部分）：数据预处理 使用Python和MQL5开发机器人（第一部分）：数据预处理
基于机器学习的交易机器人开发：详细指南本系列文章的第一篇将重点讨论数据的收集与准备以及特征的选择。该项目采用Python编程语言及其相关库，并结合MetaTrader 5平台来实现。