
Алгоритм дендритных клеток — Dendritic Cell Algorithm (DCA)
Содержание
Введение
Продолжая тематику оптимизации инспирированную иммунной системой человека, рассмотрим основной алгоритм дендритных клеток (Dendritic Cell Algorithm, DCA) — метаэвристический метод, вдохновлённый механизмами врождённого иммунитета. Оригинальная версия была разработана Greensmith, Aickelin и Cayzer в 2005 году для задач обнаружения аномалий в компьютерных системах.
Дендритные клетки в биологии выполняют функцию «пограничников» иммунной системы: они собирают сигналы из окружающей среды, накапливают информацию в течение определённого времени, а затем мигрируют в лимфатические узлы, где представляют собранные данные Т-лимфоцитам. Ключевая особенность — клетка не принимает мгновенных решений, а интегрирует множество сигналов во времени, что обеспечивает робастность к шуму и случайным флуктуациям.
В контексте оптимизации DCA интерпретируется иначе: высокий фитнес позиции трактуется как «опасность» (хорошая область для эксплуатации), низкий фитнес — как «безопасность» (область для исследования или покидания). Каждый агент популяции получает значение MCAV (Mature Context Antigen Value), которое накапливается по результатам миграций дендритных клеток и определяет стратегию движения: локальная мутация — для перспективных позиций, глобальный поиск — для неперспективных.
Реализация алгоритма
Дендритные клетки в иммунной системе патрулируют ткани организма, собирая сигналы из окружающей среды. Когда клетка накопила достаточно данных, она мигрирует в лимфатический узел и «докладывает» о том, что обнаружила: опасность или норму, согласно этому дендритная клетка воспринимает четыре типа сигналов:- PAMP (Pathogen-Associated Molecular Pattern) — сигнал явной опасности. В биологии это молекулы, которые встречаются только у патогенов, в оптимизации — признак очень хорошей позиции.
- Danger — сигнал потенциальной опасности. Указывает на повреждение или стресс, но не является абсолютным индикатором угрозы. В оптимизации — позиция лучше среднего.
- Safe — сигнал нормы. Указывает на здоровую, штатную ситуацию, в оптимизации — позиция хуже среднего.
- Inflammation — модулирующий сигнал. Усиливает восприятие остальных сигналов. В оптимизации — разброс значений в популяции.
- CSM (Costimulatory Molecule) — "счётчик жизни" клетки. Все сигналы увеличивают CSM, но с разными весами. Когда CSM достигает порога — клетка мигрирует.
- Semi-mature output — накопленный сигнал «нормы». Увеличивается только от Safe-сигналов.
- Mature output — накопленный сигнал «опасности». Увеличивается от "PAMP" и "Danger", уменьшается от "Safe".
Формула обработки:
Output = (PAMP × Wp + Danger × Wd + Safe × Ws) × (1 + Inflammation)
Воспаление работает как множитель — усиливает все сигналы пропорционально.
Миграция и контекст. Каждая клетка имеет индивидуальный порог миграции. Это критически важно: разные пороги создают «временны́е окна» разной длины. Представьте трёх аналитиков, изучающих рынок акций. Первый принимает решение после часа наблюдений, второй — после дня, а третий — после недели. Они увидят разные паттерны и придут к разным выводам. Комбинация их мнений надёжнее, чем мнение одного.
Когда CSM достигает порога, клетка мигрирует и определяет контекст:
если semi > mature → контекст = 0 (норма)
если mature ≥ semi → контекст = 1 (аномалия)
В оптимизации: контекст = 1 означает «хорошая позиция», контекст = 0 — «плохая позиция».
MCAV (Mature Context Antigen Value) — коллективная память. Каждый агент (точка в пространстве поиска) накапливает статистику по результатам миграций клеток, которые его наблюдали:
MCAV = количество миграций с контекстом 1 / общее количество миграций
MCAV близок к 1 → агент стабильно оценивается как «хороший» MCAV близок к 0 → агент стабильно оценивается как «плохой» MCAV около 0.5 → неопределённость, нужно больше данных. Возьмём на примере рейтинга ресторана на основе отзывов. Один отзыв ненадёжен. Сто отзывов со средней оценкой 4.8 — уже является убедительным сигналом качества данного заведения.
Экспоненциальное затухание. Старые данные постепенно "забываются":
matureSum = matureSum × decay
totalSum = totalSum × decay
При decay = 0.85 информация двухнедельной давности имеет вес около 10% от свежей. Зачем это нужно? Представьте, что ресторан сменил шеф-повара. Старые отзывы больше нерелевантны. Система должна адаптироваться к новой реальности, а не цепляться за устаревшие данные.
Стратегия движения. На основе MCAV агент выбирает стратегию:
MCAV > 0.5 (хорошая позиция) → локальная мутация. Небольшое случайное смещение для тонкой настройки. Вы нашли хороший ресторан. Логично попробовать обойти соседние заведения того же владельца, а не ехать в другой конец города.
MCAV ≤ 0.5 (плохая позиция) → две опции:
- с вероятностью (1 - explorationRate) — движение к лучшему известному решению,
- с вероятностью explorationRate — полная реинициализация в случайной точке.
Ресторан оказался ужасным. Либо идёте в проверенное место (к лучшему решению), либо рискуете и пробуете что-то совершенно новое (реинициализация).
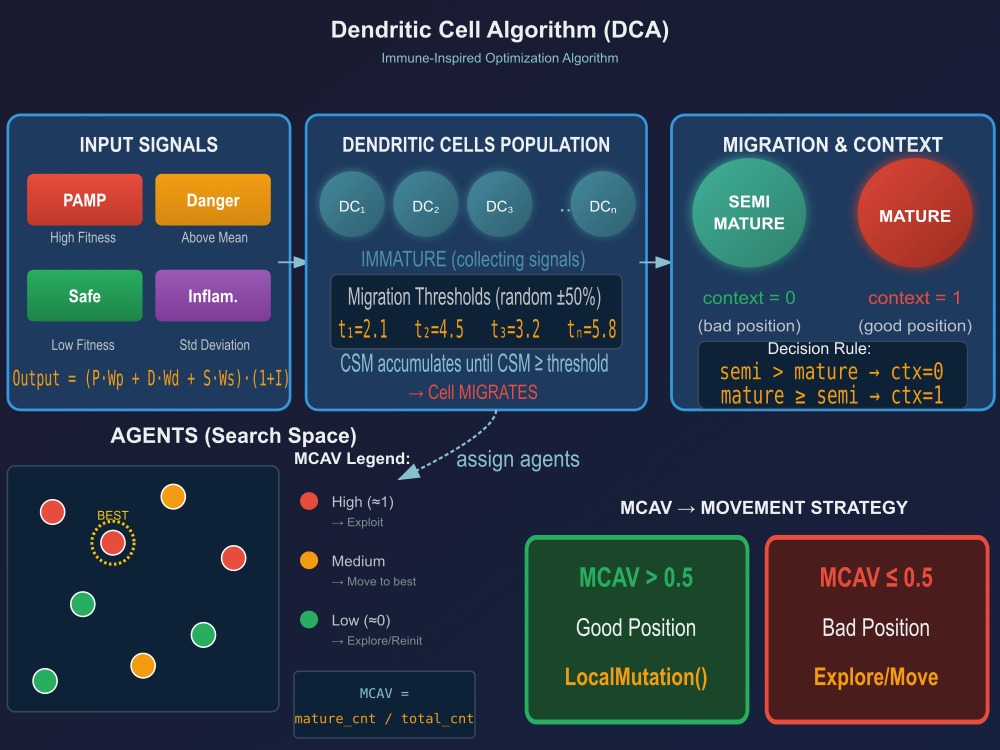
Рисунок 1. Схема процессов в алгоритме DCA
- INPUT SIGNALS — четыре входных сигнала (PAMP, Danger, Safe, Inflammation) с их интерпретацией для оптимизации
- DENDRITIC CELLS POPULATION — популяция незрелых клеток с разными порогами миграции
- MIGRATION & CONTEXT — процесс миграции и определение контекста (semi-mature vs mature)
- AGENTS — агенты в пространстве поиска с цветовой кодировкой по MCAV
- MCAV → MOVEMENT STRATEGY — как значение MCAV определяет стратегию движения

Рисунок 2. Матрица весов, экспоненциальное затухание и цикл алгоритма DCA
WEIGHT MATRIX — матрица весов для преобразования сигналов, MCAV DECAY — экспоненциальное затухание для "забывания" старых данных, ALGORITHM CYCLE — полный цикл алгоритма по шагам.
Переходим к составлению псевдокода алгоритма:
СОЗДАТЬ популяцию агентов:
Для каждого агента:
- Разместить в случайной точке пространства поиска
- Вычислить фитнес в этой точке
- Установить MCAV = 0.5 (нейтральное значение)
- Обнулить счётчики миграций (matureSum = 0, totalSum = 0)
СОЗДАТЬ популяцию дендритных клеток:
Для каждой клетки:
- Установить состояние "незрелая"
- Обнулить накопители сигналов (csm = 0, semi = 0, mature = 0)
- Назначить случайный порог миграции в диапазоне
от (базовый_порог × 0.5) до (базовый_порог × 1.5)
- Очистить список наблюдаемых агентов
ЗАПОМНИТЬ лучшее найденное решение
ПОВТОРЯТЬ пока не исчерпан лимит вычислений фитнеса:
ШАГ 1. Сохранить текущее состояние
Для каждого агента:
- Запомнить текущую позицию как предыдущую
- Запомнить текущий фитнес как предыдущий
ШАГ 2. Обновить статистику популяции
- Найти минимальный фитнес среди всех агентов
- Найти максимальный фитнес среди всех агентов
- Вычислить средний фитнес популяции
ШАГ 3. Применить затухание памяти
Для каждого агента:
- Умножить matureSum на коэффициент затухания
- Умножить totalSum на коэффициент затухания
- Пересчитать MCAV = matureSum / totalSum
(если totalSum близок к нулю, установить MCAV = 0.5)
ШАГ 4. Распределить агентов по клеткам
- Перемешать список агентов случайным образом
- Разделить агентов поровну между клетками
(каждая клетка получает примерно одинаковое количество)
ШАГ 5. Обработать каждую клетку
Для каждой дендритной клетки:
ЕСЛИ клетка незрелая:
Для каждого назначенного агента:
ПОЛУЧИТЬ входные сигналы:
- PAMP = насколько фитнес выше минимального
(нормировано от 0 до 1)
- Safe = насколько фитнес ниже максимального
(нормировано от 0 до 1)
- Danger = 1 если фитнес выше среднего, иначе 0
- Inflammation = стандартное отклонение фитнесов
в популяции (нормировано)
ВЫЧИСЛИТЬ выходные сигналы:
- модификатор = 1 + Inflammation
- csm += (PAMP×2 + Danger×1 + Safe×3) × модификатор
- semi += (Safe×1) × модификатор
- mature += (PAMP×1 + Danger×0.5 - Safe×1.5) × модификатор
ПРОВЕРИТЬ условие миграции:
ЕСЛИ csm >= порог миграции:
ВЫПОЛНИТЬ миграцию клетки
ШАГ 6. Сгенерировать новые позиции
Для каждого агента:
ЕСЛИ MCAV > 0.5 (хорошая позиция):
- Применить локальную мутацию:
новая_позиция = текущая + случайное_смещение
(смещение пропорционально размеру области поиска
и коэффициенту мутации)
ИНАЧЕ (плохая позиция):
- Бросить случайное число от 0 до 1
ЕСЛИ число < вероятность_исследования:
- Переместить в случайную точку пространства
ИНАЧЕ:
- Двигаться к лучшему известному решению:
новая_позиция = текущая +
случайный_шаг × (лучшая_позиция - текущая)
ШАГ 7. Применить границы
Для каждого агента:
- Если позиция вышла за границы, отразить обратно
ШАГ 8. Вычислить фитнес
Для каждого агента:
- Вычислить фитнес в новой позиции
ШАГ 9. Обновить лучшее решение
Для каждого агента:
ЕСЛИ новый фитнес лучше предыдущего:
- Принять новую позицию
ИНАЧЕ:
- Вернуться к предыдущей позиции
ЕСЛИ фитнес агента лучше глобального лучшего:
- Обновить глобальное лучшее решение
ВЕРНУТЬ лучшее найденное решение
Теперь можем приступить к реализации. Перечисление "E_DC_State" определит три возможных состояния дендритной клетки в соответствии с биологической моделью. В процессе работы алгоритма клетка начинает в состоянии "DC_IMMATURE", когда накапливает сигналы, и при достижении порога миграции переходит в одно из двух финальных состояний. После миграции клетка сбрасывается обратно в "DC_IMMATURE" для нового цикла наблюдения.
//———————————————————————————————————————————————————————————————————— enum E_DC_State { DC_IMMATURE, DC_SEMI_MATURE, DC_MATURE }; //————————————————————————————————————————————————————————————————————
Структура "S_SignalWeights" хранит веса для преобразования трёх входных сигналов (PAMP, Danger, Safe) в один выходной. В алгоритме используются три экземпляра этой структуры — по одному для каждого выходного сигнала (CSM, Semi, Mature). Это позволяет компактно представить матрицу весов 3×3 из оригинальной статьи.
//———————————————————————————————————————————————————————————————————— struct S_SignalWeights { double wPAMP; double wDanger; double wSafe; }; //————————————————————————————————————————————————————————————————————
Структура "S_DCA_Cell" представляет одну дендритную клетку со всеми её атрибутами:
- Состояние: могут быть незрелыми или зрелыми (state).
- Привлекательность: имеют метрики (csm, semi, mature), которые влияют на то, будут ли агенты приходить в эту ячейку.
- Порог миграции: определяет, при каких условиях агенты могут покинуть эту ячейку (threshold).
- Вместимость: каждая ячейка имеет ограниченное количество мест для агентов (agentIndices, agentCount, maxAgents из Init).
Структура также предоставляет методы для:
- Init — устанавливает начальное состояние, обнуляет накопители сигналов и выделяет память под массив индексов агентов.
- Reset — сброс ячейки и обновление ее порога. Ключевой момент — новый порог миграции генерируется случайно при каждом сбросе. Это создаёт разнообразие временны́х окон наблюдения между ячейками.
- AddAgent — добавление агента в список ячейки, если есть место. Простая операция с проверкой границ массива. Агенты распределяются по ячейкам равномерно на каждой итерации.
//———————————————————————————————————————————————————————————————————— struct S_DCA_Cell { E_DC_State state; double csm; double semi; double mature; double threshold; int agentIndices []; int agentCount; void Init (double migrationThreshold, int maxAgents) { state = DC_IMMATURE; csm = 0.0; semi = 0.0; mature = 0.0; threshold = migrationThreshold; agentCount = 0; ArrayResize (agentIndices, maxAgents); } void Reset (double newThreshold) { state = DC_IMMATURE; csm = 0.0; semi = 0.0; mature = 0.0; threshold = newThreshold; agentCount = 0; } void AddAgent (int idx) { if (agentCount < ArraySize (agentIndices)) { agentIndices [agentCount++] = idx; } } }; //————————————————————————————————————————————————————————————————————
Структура "S_MCAV" хранит статистику контекстов для одного агента. Метод "Init". Начальное значение 0.5 означает неопределённость — агент ещё не накопил статистику. Метод "AddContext" добавляет результат миграции клетки.
Параметр "ctx" принимает значение 0 (плохая позиция) или 1 (хорошая позиция). При ctx=1 увеличиваются оба счётчика, при ctx=0 - только общий. Метод "ApplyDecay" применяет экспоненциальное затухание. При rate = 0.85 информация десятиитерационной давности имеет вес около 20% от свежей. Это позволяет алгоритму адаптироваться к изменениям ландшафта фитнеса.
Метод "Update" пересчитывает значение "MCAV". Защита от деления на ноль — если статистики недостаточно, возвращается нейтральное значение.
//———————————————————————————————————————————————————————————————————— struct S_MCAV { double matureSum; double totalSum; double value; void Init () { matureSum = 0.0; totalSum = 0.0; value = 0.5; } void AddContext (int ctx) { totalSum += 1.0; if (ctx == 1) matureSum += 1.0; } void ApplyDecay (double rate) { matureSum *= rate; totalSum *= rate; } void Update () { if (totalSum > 0.01) value = matureSum / totalSum; else value = 0.5; } }; //————————————————————————————————————————————————————————————————————
Класс "C_AO_DCA" является реализацией алгоритма Дендритной Клетки (DCA), имитирует работу иммунной системы, используя концепцию дендритных клеток для обнаружения опасностей и принятия решений, наследуется от базового класса "C_AO".
SetParams — метод загружает значения из массива "params" в соответствующие переменные класса. После загрузки, все параметры проходят через ряд проверок, чтобы гарантировать, что они находятся в допустимых пределах. Ограничения предотвращают некорректные конфигурации: минимум 4 агента, минимум 2 клетки, decay в разумных пределах. Init — это ключевая функция инициализации алгоритма DCA. Базовый порог "tMedian" рассчитывается как половина максимально возможного "CSM" за одну итерацию, затем умножить на "lifespanMult". Это обеспечивает, что клетки в среднем живут несколько итераций перед миграцией.Moving — основной метод, выполняющий за один цикл (или "шаг") алгоритма DCA, обработку каждого агента, получение входных сигналов, обновление состояний ячеек (ProcessCell), миграцию агентов между ячейками, применение мутаций и генерацию новых позиций, обновление статистических данных, применение затухания.
Revision — метод используется для извлечения наилучшего решения, найденного алгоритмом.
Приватные методы:
- InitWeights — инициализирует веса для сигналов;
- GetMigrationThreshold — рассчитывает и возвращает порог миграции;
- CalcOutputSignals — рассчитывает выходные сигналы (outCSM, outSemi, outMature) для ячейки на основе входных сигналов (pamp, danger, safe, infl) и весов "wCSM", "wSemi", "wMature";
- GetInputSignals — получает входные сигналы для конкретной ячейки (idx);
- UpdatePopStats — обновляет статистические показатели популяции (tMedian, fMinPop, fMaxPop, fMeanPop);
- AssignAgentsToCells — распределяет агентов по ячейкам, основываясь на силе и привлекательности ячеек;
- ProcessCell — обрабатывает состояние и содержимое одной конкретной ячейки;
- MigrateCell — реализует логику миграции агентов из одной ячейки в другую;
- GeneratePosition — генерирует новую позицию (решение) для агента "idx";
- LocalMutation — применяет мутацию к агенту, изменяя его позицию;
- MoveTowardsBest — перемещает агента в направлении лучшего найденного решения, с учетом силы (strength);
- GlobalReinit — выполняет глобальную переинициализацию агента;
- ApplyBounds — убеждается, что позиция агента находится в допустимых границах.
//———————————————————————————————————————————————————————————————————— class C_AO_DCA : public C_AO { public: //---------------------------------------------------------- ~C_AO_DCA () { } C_AO_DCA () { ao_name = "DCA"; ao_desc = "Dendritic Cell Algorithm"; ao_link = "https://www.mql5.com/ru/articles/20479"; popSize = 50; numCells = 10; lifespanMult = 5.0; decayRate = 0.85; mutationRate = 0.1; explorationRate = 0.3; ArrayResize (params, 6); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "numCells"; params [1].val = numCells; params [2].name = "lifespanMult"; params [2].val = lifespanMult; params [3].name = "decayRate"; params [3].val = decayRate; params [4].name = "mutationRate"; params [4].val = mutationRate; params [5].name = "explorationRate"; params [5].val = explorationRate; } void SetParams () { popSize = (int)params [0].val; numCells = (int)params [1].val; lifespanMult = params [2].val; decayRate = params [3].val; mutationRate = params [4].val; explorationRate = params [5].val; if (popSize < 4) popSize = 4; if (numCells < 2) numCells = 2; if (numCells > popSize) numCells = popSize; if (lifespanMult < 1.0) lifespanMult = 1.0; if (decayRate < 0.5) decayRate = 0.5; if (decayRate > 0.99) decayRate = 0.99; if (mutationRate < 0.001) mutationRate = 0.001; if (mutationRate > 1.0) mutationRate = 1.0; if (explorationRate < 0.0) explorationRate = 0.0; if (explorationRate > 1.0) explorationRate = 1.0; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP); void Moving (); void Revision (); //------------------------------------------------------------------ int numCells; double lifespanMult; double decayRate; double mutationRate; double explorationRate; private: //--------------------------------------------------------- S_DCA_Cell cells []; S_MCAV mcav []; S_SignalWeights wCSM; S_SignalWeights wSemi; S_SignalWeights wMature; double tMedian; double fMinPop; double fMaxPop; double fMeanPop; void InitWeights (); double GetMigrationThreshold (); void CalcOutputSignals (double pamp, double danger, double safe, double infl, double &outCSM, double &outSemi, double &outMature); void GetInputSignals (int idx, double &pamp, double &danger, double &safe, double &infl); void UpdatePopStats (); void AssignAgentsToCells (); void ProcessCell (int cellIdx); void MigrateCell (int cellIdx); void GeneratePosition (int idx); void LocalMutation (int idx); void MoveTowardsBest (int idx, double strength); void GlobalReinit (int idx); void ApplyBounds (int idx); }; //————————————————————————————————————————————————————————————————————
Функция инициализации "Init" для алгоритма дендритных клеток "C_AO_DCA". Она выполняет начальную настройку перед запуском основного алгоритма.
Сначала вызывается стандартная функция инициализации "StandardInit", которая подготавливает необходимые структуры данных и параметры, общие для всех алгоритмов, путем передачи диапазонов входных значений (rangeMinP, rangeMaxP, rangeStepP) и количества эпох "epochsP". Если эта базовая инициализация не удается, функция "Init" также завершает работу с ошибкой.
Вызывается приватный метод "InitWeights", он задает начальные значения для весовых коэффициентов, используемых в алгоритме.
Расчет медианы продолжительности жизни. Сначала вычисляется максимальное значение для сигналов "CSM" (csmMax). Это делается путем суммирования всех весовых коэффициентов, связанных с соответствующими входными сигналами (PAMP, Danger, Safe) из структуры "wCSM". Затем вычисляется "tMedian" (медиана времени жизни). Это значение рассчитывается как половина "csmMax", умноженная на "ifespanMult" (множитель продолжительности жизни).Инициализация клеток. Выделяется память для массива "cells" (который представляет дендритные клетки) на основе значения "numCells" (количества клеток). Рассчитывается максимальное количество агентов, которое может быть помещено в каждую клетку. Это делается путем деления общего количества агентов на количество ячеек и добавления небольшой "форы" (плюс 2) с запасом на неравномерное распределение.
Цикл проходится по каждой ячейке, вызывается метод "Init". При этом ячейке передается порог для миграции, полученный с помощью "GetMigrationThreshold", и максимальное количество агентов, которое она может вместить.
Инициализация агентов. Выделяется память для массива (mcav). Цикл проходится по каждому агенту. Вызывается метод "Init" для каждого агента и проводит начальную настройку.
Функция "Init" подготавливает среду для работы алгоритма дендритных клеток, настраивая дендритные клетки, распределяя их и инициализируя популяцию агентов, а также вычисляя некоторые ключевые параметры.
//———————————————————————————————————————————————————————————————————— bool C_AO_DCA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ InitWeights (); double csmMax = wCSM.wPAMP + wCSM.wDanger + wCSM.wSafe; tMedian = 0.5 * csmMax * lifespanMult; ArrayResize (cells, numCells); int maxAgentsPerCell = (popSize / numCells) + 2; for (int i = 0; i < numCells; i++) { cells [i].Init (GetMigrationThreshold (), maxAgentsPerCell); } ArrayResize (mcav, popSize); for (int i = 0; i < popSize; i++) { mcav [i].Init (); } return true; } //————————————————————————————————————————————————————————————————————
Функция "InitWeights" хранит веса для преобразования трёх входных сигналов (PAMP, Danger, Safe) в один выходной. В алгоритме используются три экземпляра этой структуры — по одному для каждого выходного сигнала (CSM, Semi, Mature). Это позволяет компактно представить матрицу весов 3×3.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::InitWeights () { double W1 = 2.0; double W2 = 1.0; wCSM.wPAMP = W1; wCSM.wDanger = W1 / 2.0; wCSM.wSafe = W1 * 1.5; wSemi.wPAMP = 0.0; wSemi.wDanger = 0.0; wSemi.wSafe = 1.0; wMature.wPAMP = W2; wMature.wDanger = W2 / 2.0; wMature.wSafe = -W2 * 1.5; } //————————————————————————————————————————————————————————————————————Метод "GetMigrationThreshold" возвращает случайное значение порога миграции, которое варьируется в пределах от 50% до 150% от базового значения "tMedian". Такой подход добавляет стохастичности (случайности) в процесс принятия решения о миграции, что часто используется для моделирования биологических процессов, где поведение не всегда детерминировано.
//———————————————————————————————————————————————————————————————————— double C_AO_DCA::GetMigrationThreshold () { return u.RNDfromCI (tMedian * 0.5, tMedian * 1.5); } //————————————————————————————————————————————————————————————————————
Метод "CalcOutputSignals" принимает на вход уровни различных сигналов и коэффициент воспаления, применяет к этим сигналам веса, соответствующие трем различным состояниям и путям обработки (CSM, Semi, Mature), и затем масштабирует результат общим коэффициентом, зависящим от уровня воспаления. В конце, любые отрицательные результаты обрезаются до нуля.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::CalcOutputSignals (double pamp, double danger, double safe, double infl, double &outCSM, double &outSemi, double &outMature) { double amp = 1.0 + infl; outCSM = (pamp * wCSM.wPAMP + danger * wCSM.wDanger + safe * wCSM.wSafe) * amp; outSemi = (pamp * wSemi.wPAMP + danger * wSemi.wDanger + safe * wSemi.wSafe) * amp; outMature = (pamp * wMature.wPAMP + danger * wMature.wDanger + safe * wMature.wSafe) * amp; if (outCSM < 0.0) outCSM = 0.0; if (outSemi < 0.0) outSemi = 0.0; if (outMature < 0.0) outMature = 0.0; } //————————————————————————————————————————————————————————————————————
Метод "UpdatePopStats" проходит по всей популяции, игнорируя неактивные элементы (отмеченные значением -DBL_MAX), и вычисляет минимальное, максимальное и среднее значение для всех активных элементов. Если активных элементов нет, устанавливаются предопределенные значения по умолчанию (0, 0.5, 1.0) для этих статистик. Этот метод, вероятно, вызывается периодически для мониторинга и анализа состояния всей популяции дендритных клеток.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::UpdatePopStats () { fMinPop = DBL_MAX; fMaxPop = -DBL_MAX; fMeanPop = 0.0; int cnt = 0; for (int i = 0; i < popSize; i++) { if (a [i].f != -DBL_MAX) { if (a [i].f > fMaxPop) fMaxPop = a [i].f; if (a [i].f < fMinPop) fMinPop = a [i].f; fMeanPop += a [i].f; cnt++; } } if (cnt > 0) { fMeanPop /= cnt; } else { fMaxPop = 1.0; fMinPop = 0.0; fMeanPop = 0.5; } } //————————————————————————————————————————————————————————————————————
Метод "GetInputSignals" преобразует индивидуальное значение фитнеса в набор сигналов (pamp, danger, safe, infl), которые будут использоваться другими частями модели:
- pamp — отражает положение элемента в популяции по шкале "f" (высокое f означает высокий pamp)
- danger — возрастает, когда "f" элемента значительно превышает среднее по популяции
- safe — имеет более высокое значение, когда фитнес элемента ниже среднего по популяции
- infl — отражает общую "возбужденность" или "разнородность" популяции, основанную на дисперсии значений фитнеса, высокий разброс в популяции — высокий "Inflammation".
Эта логика позволяет отдельным клеткам (или агентам) получать информацию не только о своем собственном состоянии, но и о состоянии всей популяции.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::GetInputSignals (int idx, double &pamp, double &danger, double &safe, double &infl) { double f = a [idx].f; pamp = 0.5; danger = 0.0; safe = 0.5; infl = 0.0; if (f == -DBL_MAX) return; double range = fMaxPop - fMinPop; if (range < 1e-10) return; double fNorm = (f - fMinPop) / range; fNorm = MathMax (0.0, MathMin (1.0, fNorm)); pamp = fNorm; if (f > fMeanPop) { danger = (f - fMeanPop) / range; danger = MathMin (danger * 2.0, 1.0); } safe = 1.0 - fNorm; if (f < fMeanPop) { double belowMean = (fMeanPop - f) / range; safe = MathMin (safe + belowMean, 1.0); } double variance = 0.0; int cnt = 0; for (int i = 0; i < popSize; i++) { if (a [i].f != -DBL_MAX) { variance += (a [i].f - fMeanPop) * (a [i].f - fMeanPop); cnt++; } } if (cnt > 1) { double stdDev = MathSqrt (variance / cnt); infl = MathMin (stdDev / range, 1.0); } } //————————————————————————————————————————————————————————————————————
Этот метод выполняет равномерное цикличное распределение всех агентов популяции по заданному количеству ячеек. При 50 агентах и 10 клетках каждая клетка получает ровно 5 агентов. Это обеспечивает равномерную нагрузку на все клетки.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::AssignAgentsToCells () { for (int c = 0; c < numCells; c++) { cells [c].agentCount = 0; } for (int i = 0; i < popSize; i++) { int cellIdx = i % numCells; cells [cellIdx].AddAgent (i); } } //————————————————————————————————————————————————————————————————————
Метод "Moving" моделирует за один шаг:
- Запоминает состояния агентов до изменений.
- Обновляет общую "среду" или статистику популяции.
- Применяет общие эффекты (затухание).
- Организует агентов (распределение по ячейкам).
- Выполняет локальные взаимодействия и вычисления (обработка ячеек).
- Обновляет вспомогательные структуры (mcav).
- Определяет новое местоположение каждого агента, основываясь на его состоянии, взаимодействиях и глобальных факторах.
- Удерживает агентов в заданных границах.
Этот метод является "ядром" эволюционного процесса, где популяция поведенчески изменяется и адаптируется со временем. Метод реализует полный цикл итерации алгоритма. Сохранение предыдущих позиций необходимо для жадного отбора в методе "Revision".
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::Moving () { if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //------------------------------------------------------------------ for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, coords); a [i].fP = a [i].f; } UpdatePopStats (); for (int i = 0; i < popSize; i++) { mcav [i].ApplyDecay (decayRate); } AssignAgentsToCells (); for (int c = 0; c < numCells; c++) { ProcessCell (c); } for (int i = 0; i < popSize; i++) { mcav [i].Update (); } for (int i = 0; i < popSize; i++) { GeneratePosition (i); ApplyBounds (i); } } //————————————————————————————————————————————————————————————————————
Метод "ProcessCell" выполняет следующие действия:
- Проверяет, что ячейка незрелая и содержит агентов.
- Итерирует по всем агентам в ячейке.
- Получает входные сигналы для каждого агента.
- Вычисляет выходные сигналы для каждого агента.
- Суммирует выходные сигналы от всех агентов.
- Обновляет совокупные значения ячейки на основе сумм сигналов агентов.
- Проверяет, достигло ли совокупное значение csm порога.
- Если порог достигнут, инициирует процесс миграции из этой ячейки.
Этот метод моделирует, как активность агентов внутри ячейки может привести к "созреванию" самой ячейки, подготавливая ее к дальнейшим этапам перераспределения агентов.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::ProcessCell (int cellIdx) { if (cells [cellIdx].state != DC_IMMATURE) return; if (cells [cellIdx].agentCount == 0) return; double totalCSM = 0.0; double totalSemi = 0.0; double totalMature = 0.0; for (int i = 0; i < cells [cellIdx].agentCount; i++) { int agentIdx = cells [cellIdx].agentIndices [i]; if (agentIdx < 0 || agentIdx >= popSize) continue; if (a [agentIdx].f == -DBL_MAX) continue; double pamp, danger, safe, infl; GetInputSignals (agentIdx, pamp, danger, safe, infl); double outCSM, outSemi, outMature; CalcOutputSignals (pamp, danger, safe, infl, outCSM, outSemi, outMature); totalCSM += outCSM; totalSemi += outSemi; totalMature += outMature; } cells [cellIdx].csm += totalCSM; cells [cellIdx].semi += totalSemi; cells [cellIdx].mature += totalMature; if (cells [cellIdx].csm >= cells [cellIdx].threshold) { MigrateCell (cellIdx); } } //————————————————————————————————————————————————————————————————————
Метод "MigrateCell" выполняет следующие функции:
- Классифицирует ячейку после достижения порога: либо как "полузрелую", либо как "полностью зрелую", основываясь на относительных вкладах "semi" и "mature".
- Передает информацию о новом состоянии ячейки (контекст "ctx") всем агентам, находящимся в ней. Это позволяет агентам адаптироваться к новому этапу развития ячейки.
- Переинициализирует ячейку, сбрасывая ее накопленные параметры, чтобы она могла участвовать в последующих циклах "созревания".
Этот метод является важным звеном в модели, где ячейки могут "созревать" и передавать эту информацию своим агентам, влияя на их дальнейшее поведение и развитие. Если за время жизни клетки накопилось больше Safe-сигналов (semi > mature), позиции оцениваются как «плохие». Иначе — как «хорошие». Все агенты, наблюдавшиеся этой клеткой, получают одинаковый контекст.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::MigrateCell (int cellIdx) { int ctx; if (cells [cellIdx].semi > cells [cellIdx].mature) { cells [cellIdx].state = DC_SEMI_MATURE; ctx = 0; } else { cells [cellIdx].state = DC_MATURE; ctx = 1; } for (int i = 0; i < cells [cellIdx].agentCount; i++) { int agentIdx = cells [cellIdx].agentIndices [i]; if (agentIdx >= 0 && agentIdx < popSize) { mcav [agentIdx].AddContext (ctx); } } cells [cellIdx].Reset (GetMigrationThreshold ()); } //————————————————————————————————————————————————————————————————————
Метод "GeneratePosition" реализует стратегию обновления агента, основанную на его текущей "ценности" (m). Для высокоценных агентов (m > 0.5) происходит локальная мутация, направленная на точную настройку или улучшение существующих хороших решений. Для низко- или среднеценных агентов (m <= 0.5):
- Есть вероятность глобальной переинициализации (GlobalReinit), которая зависит от глобального "explorationRate" и текущего "m". Это радикальное исследование (exploration), когда текущее решение не является оптимальным.
- Если глобальной переинициализации не происходит, агент перемещается к лучшему решению (MoveTowardsBest) с силой, зависящей от "m". Это направленное исследование или эксплуатация, когда агент пытается приблизиться к более перспективным областям, но с меньшей агрессивностью, чем если бы было (m > 0.5). Чем ниже MCAV, тем выше вероятность глобальной реинициализации.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::GeneratePosition (int idx) { double m = mcav [idx].value; if (m > 0.5) { LocalMutation (idx); } else { double r = u.RNDfromCI (0.0, 1.0); double reinitProb = explorationRate * (1.0 - m * 2.0); if (reinitProb < 0.0) reinitProb = 0.0; if (r < reinitProb) { GlobalReinit (idx); } else { double strength = 1.0 - m; MoveTowardsBest (idx, strength); } } } //————————————————————————————————————————————————————————————————————
Метод "LocalMutation" выполняет следующее: для каждого измерения пространства (координаты) агента вычисляет случайное изменение (delta). Это изменение пропорционально установленной частоте мутации (mutationRate) и размеру диапазона допустимых значений для данной координаты (range), а так же случайному направлению (от -1 до 1). Применяется это случайное изменение к текущей позиции агента по этой координате.
Этот процесс приводит к небольшим, случайным отклонениям от текущей позиции агента, что является стандартной техникой для локального исследования пространства поиска. При (mutationRate = 0.1) максимальное смещение составляет ±10% от диапазона по каждой координате. Мутация применяется к предыдущей позиции "cP", а не к текущей.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::LocalMutation (int idx) { for (int c = 0; c < coords; c++) { double range = rangeMax [c] - rangeMin [c]; double delta = mutationRate * range * u.RNDfromCI (-1.0, 1.0); a [idx].c [c] = a [idx].cP [c] + delta; } } //————————————————————————————————————————————————————————————————————
Метод "MoveTowardsBest" обновляет позицию агента, комбинируя два компонента:
- Движение к лучшему глобальному решению: агент движется в сторону "cB" (лучшее решение). Степень этого движения контролируется случайным числом "r", которое, в свою очередь, зависит от "strength" и случайности. Чем выше "strength", тем больше вероятность двигаться в направлении "cB". Параметр " strength" регулирует силу притяжения — чем хуже текущая позиция (ниже MCAV), тем сильнее агент стремится к лучшему решению.
- Небольшая точечная мутация. Добавление шума предотвращает преждевременную сходимость.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::MoveTowardsBest (int idx, double strength) { if (fB == -DBL_MAX) { LocalMutation (idx); return; } for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0.0, 1.0) * strength; double range = rangeMax [c] - rangeMin [c]; a [idx].c [c] = a [idx].cP [c] + r * (cB [c] - a [idx].cP [c]) + mutationRate * range * u.RNDfromCI (-0.5, 0.5); } } //————————————————————————————————————————————————————————————————————
Метод "GlobalReinit" предназначен для полной переинициализации позиции агента с индексом "idx". Этот метод вызывается, когда происходит значительное событие, требующее сброса состояния агента. Механизм глобального исследования позволяет алгоритму выбраться из локальных оптимумов.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::GlobalReinit (int idx) { for (int c = 0; c < coords; c++) { a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); } } //————————————————————————————————————————————————————————————————————
Метод "ApplyBounds" использует отражение вместо простого обрезания — это сохраняет «импульс» движения. Если после отражения позиция всё ещё за границами (сильный выброс), применяется случайная реинициализация.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::ApplyBounds (int idx) { for (int c = 0; c < coords; c++) { if (a [idx].c [c] < rangeMin [c]) { a [idx].c [c] = rangeMin [c] + fabs (a [idx].c [c] - rangeMin [c]); if (a [idx].c [c] > rangeMax [c]) a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); } if (a [idx].c [c] > rangeMax [c]) { a [idx].c [c] = rangeMax [c] - fabs (a [idx].c [c] - rangeMax [c]); if (a [idx].c [c] < rangeMin [c]) a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); } a [idx].c [c] = u.SeInDiSp (a [idx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Метод "Revision" делает следующее:
- Пересматривает индивидуальные лучшие позиции агентов: если текущая цель для агента оказалась хуже его лучшей зафиксированной позиции, агент "возвращается" к своей лучшей позиции.
- Находит и обновляет абсолютное глобальное лучшее решение в популяции.
//———————————————————————————————————————————————————————————————————— void C_AO_DCA::Revision () { for (int i = 0; i < popSize; i++) { if (a [i].fP != -DBL_MAX && a [i].fP > a [i].f) { a [i].f = a [i].fP; ArrayCopy (a [i].c, a [i].cP, 0, 0, coords); } } for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, coords); } } } //————————————————————————————————————————————————————————————————————
Результаты тестов
DCA|Dendritic Cell Algorithm|50.0|20.0|5.0|0.5|0.01|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8178926955715087
25 Hilly's; Func runs: 10000; result: 0.4463156865164426
500 Hilly's; Func runs: 10000; result: 0.276079330277272
=============================
5 Forest's; Func runs: 10000; result: 0.6916302728114128
25 Forest's; Func runs: 10000; result: 0.3490153259275664
500 Forest's; Func runs: 10000; result: 0.19980310116079952
=============================
5 Megacity's; Func runs: 10000; result: 0.4492307692307693
25 Megacity's; Func runs: 10000; result: 0.22399999999999992
500 Megacity's; Func runs: 10000; result: 0.10461538461538558
=============================
All score: 3.55858 (39.54%)
На функциях малой размерности слабые показатели сходимости, особенно на дискретной "Megacity".
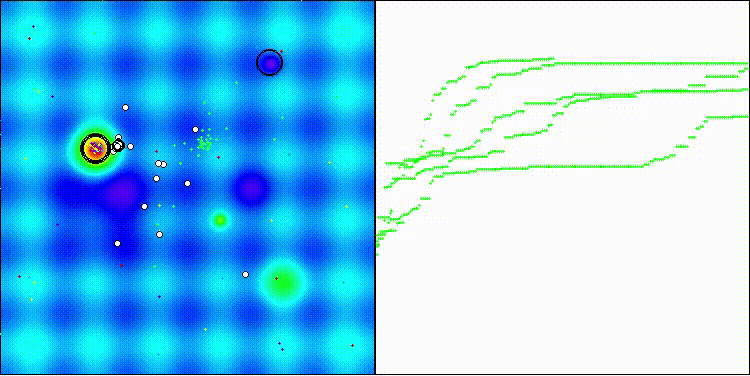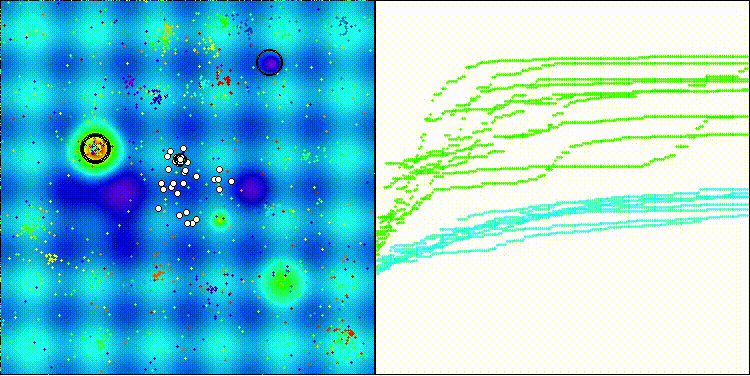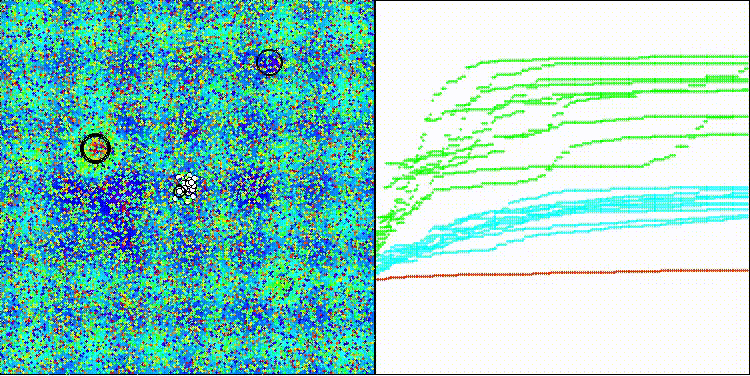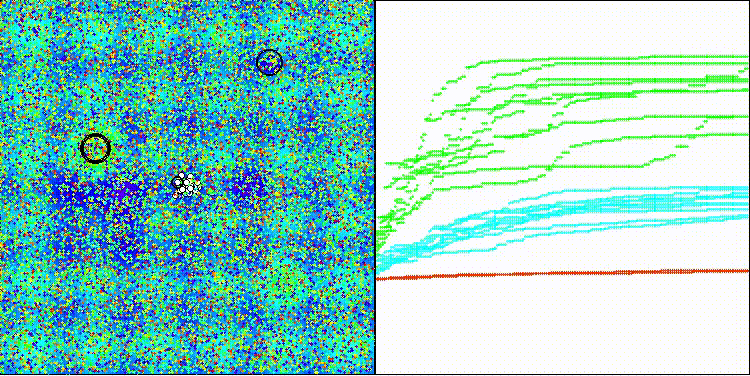
DCA на тестовой функции Hilly
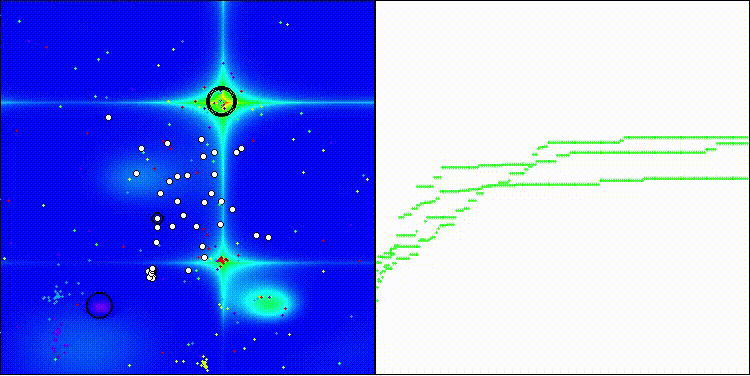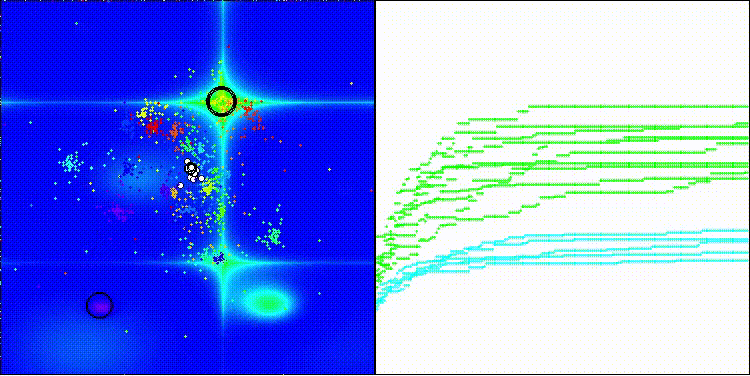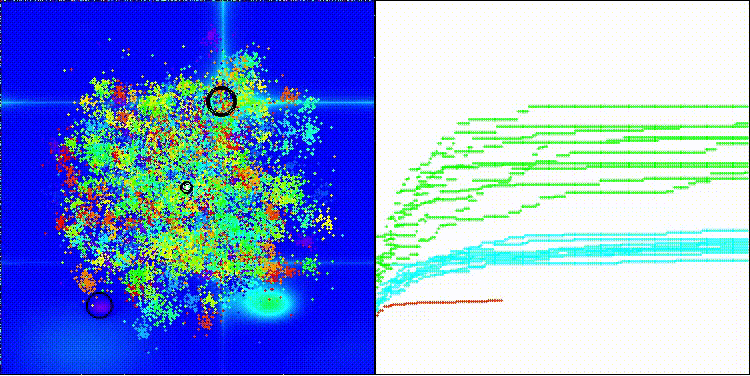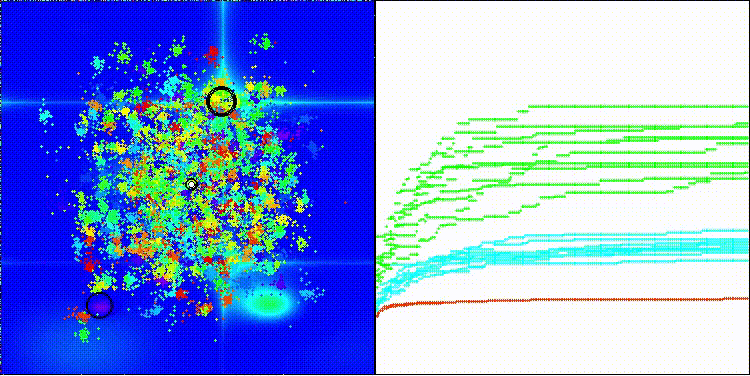
DCA на тестовой функции Forest

DCA на тестовой функции Megacity
Для задач на стандартных тестовых функциях алгоритм DCA хорошо себя показывает, более простые функции "одолеть" не составляет труда.
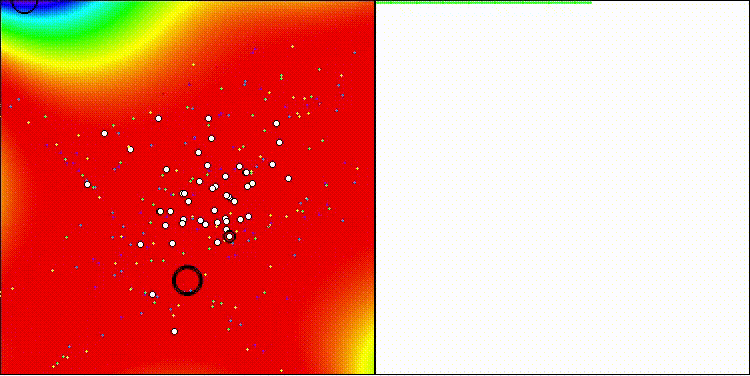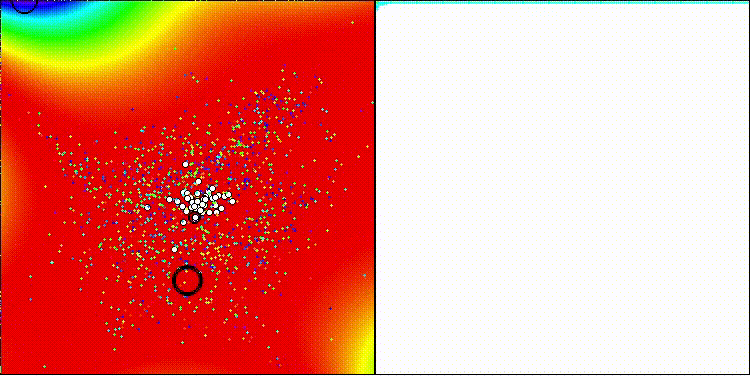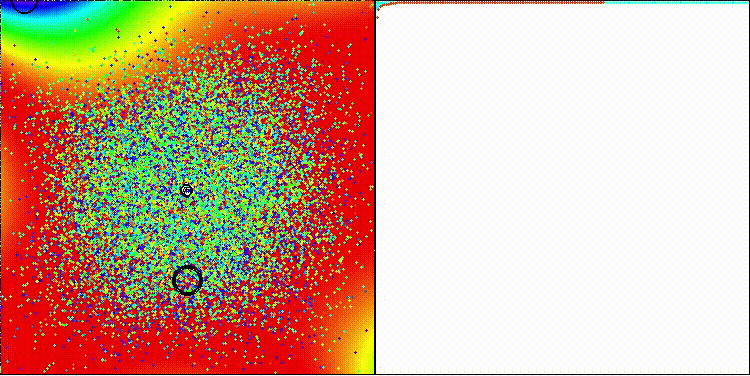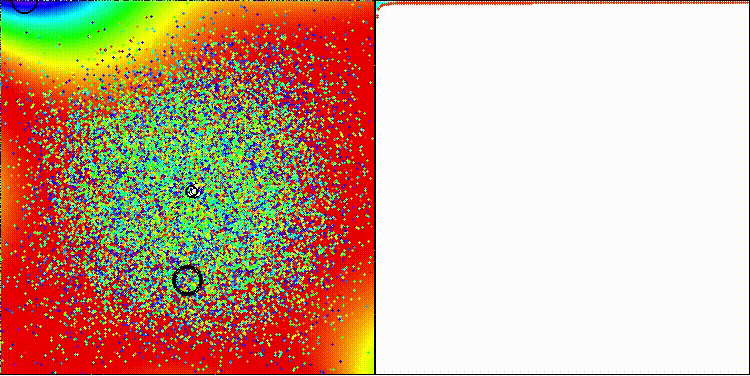
DCA на стандартной тестовой функции GoldsteinPrice
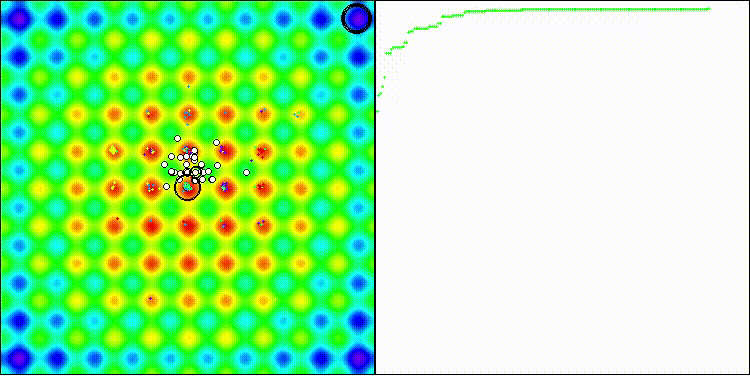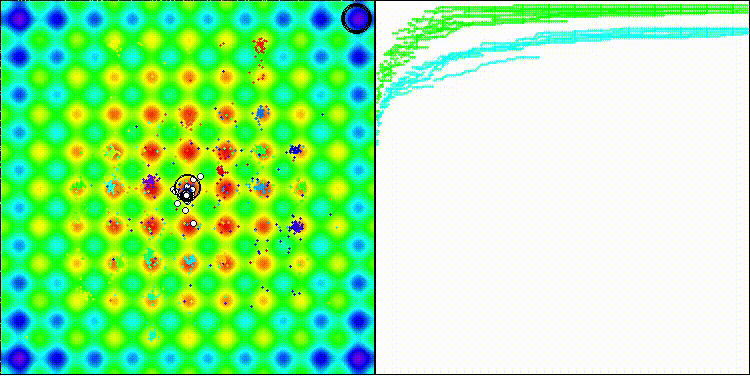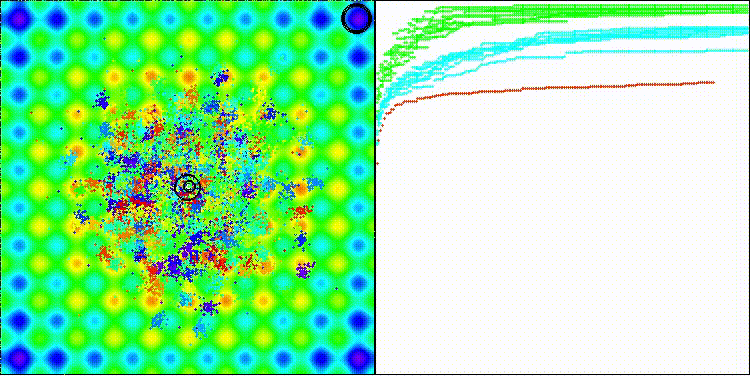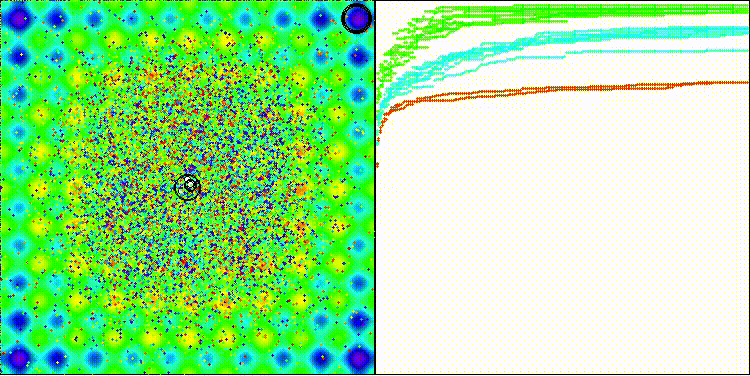
DCA на стандартной тестовой функции Rastrigin
В рейтинговой таблице популяционных методов оптимизации алгоритм DCA представлен ознакомительно.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 5 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 6 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 7 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 8 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | BO | bonobo_optimizer | 0,77565 | 0,63805 | 0,32908 | 1,74278 | 0,88088 | 0,76344 | 0,25573 | 1,90005 | 0,61077 | 0,49846 | 0,14246 | 1,25169 | 4,895 | 54,38 |
| 26 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 27 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 28 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 29 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 30 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 31 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 32 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 33 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 34 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 35 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 36 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 37 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 38 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 39 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 40 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 41 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 42 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 43 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 44 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 45 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| DCA | dendritic_cell_algorithm | 0,81789 | 0,44631 | 0,27607 | 1,54027 | 0,69163 | 0,34901 | 0,19980 | 1,24044 | 0,44923 | 0,22399 | 0,10461 | 0,77783 | 3,559 | 39,54 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Алгоритм дендритных клеток (DCA) представляет собой интересный пример адаптации иммунологической модели для задач оптимизации. Проведённое тестирование на стандартном наборе функций позволило выявить как сильные, так и слабые стороны данного подхода. На простых стандартных функциях DCA демонстрирует уверенную работу. Механизм накопления контекста через MCAV эффективно разделяет перспективные и бесперспективные области поиска, а адаптивный выбор стратегии движения обеспечивает разумный баланс между эксплуатацией и исследованием.
Однако на сложных задачах, особенно при малой размерности пространства поиска, алгоритм показывает слабую сходимость. Наиболее проблемными оказались дискретные функции, где DCA существенно уступает конкурентам. По совокупности результатов алгоритм не набрал достаточно баллов для включения в рейтинговую таблицу.
Оригинальный DCA проектировался для задач обнаружения аномалий, где временно́е окно наблюдения измеряется сотнями и тысячами событий. В оптимизации бюджет вычислений фитнеса ограничен, и клетки не успевают накопить статистически значимую информацию. Порог миграции приходится занижать, что приводит к «шумным» оценкам контекста.
Сложная система из четырёх входных сигналов, матрицы весов и накопителей MCAV оправдана для многомерных пространств с богатой структурой. На функциях малой размерности эта избыточность превращается в накладные расходы без соответствующего выигрыша в качестве поиска.
Механизм локальной мутации генерирует смещения, пропорциональные диапазону переменной. На дискретных функциях с крупным шагом многие мутации «схлопываются» в одну и ту же точку после округления, что резко снижает эффективность эксплуатации.
Экспоненциальное затухание с типичным коэффициентом 0.85 означает, что информация «помнится» около 10 итераций. На быстро меняющемся ландшафте (когда популяция активно перемещается) старые оценки могут вводить в заблуждение. На медленно меняющемся —память оказывается слишком короткой для надёжной статистики.
Все агенты, назначенные одной клетке, получают одинаковый контекст при миграции. Это усреднение размывает информацию об индивидуальном качестве позиций, особенно когда в одной клетке оказываются агенты с сильно различающимися фитнесами.
Алгоритм дендритных клеток представляет академический интерес как пример переноса иммунологических концепций в область оптимизации. Механизм мультисенсорного слияния сигналов, временны́е окна наблюдения и коллективная память через MCAV — элегантные идеи, имеющие биологическое обоснование. Однако в текущей реализации DCA не достигает уровня производительности, необходимого для практического применения в качестве универсального оптимизатора. Алгоритм может рассматриваться как отправная точка для разработки более специализированных методов, или как компонент гибридных схем.
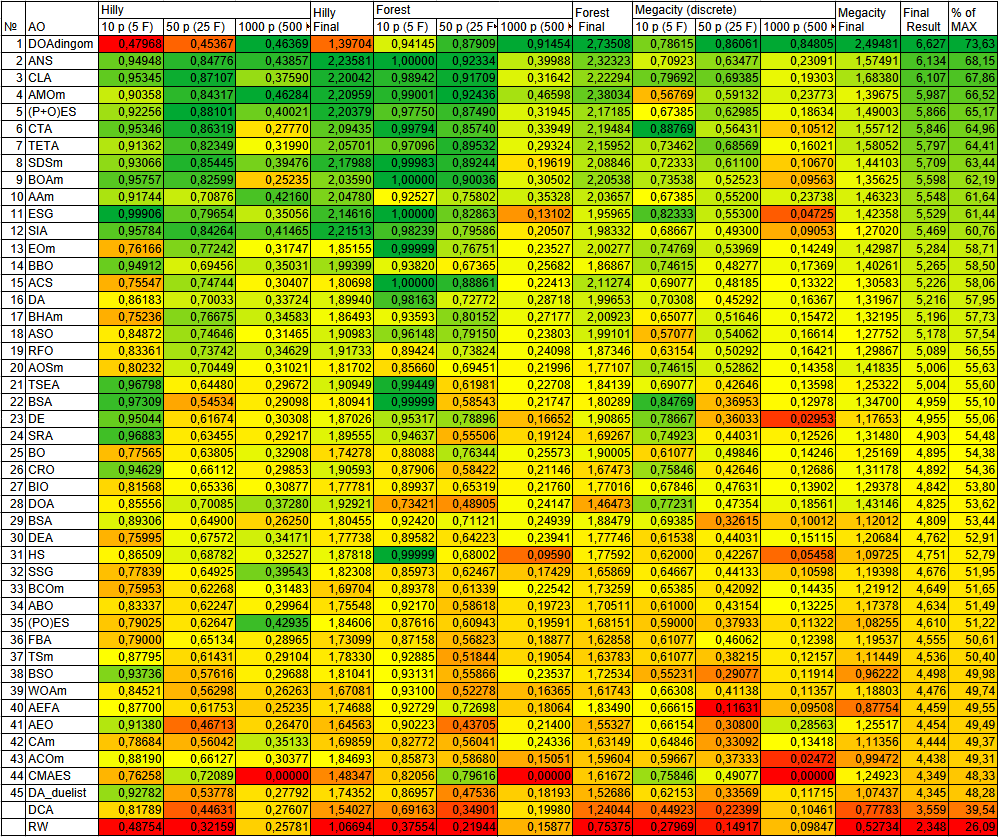
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам
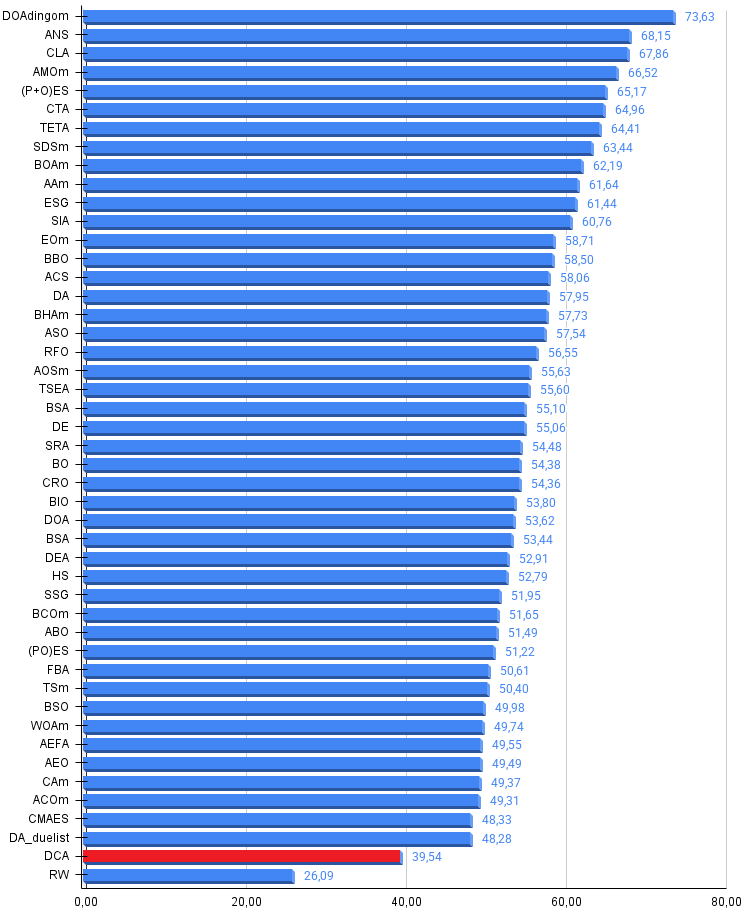
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма DCA:
Плюсы:
- Быстрый.
- Лучшие результаты на функциях средней и большой размерности.
Минусы:
- Более слабые результаты на функциях малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_DCA.mq5 | Скрипт | Испытательный стенд для DCA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Знакомство с языком MQL5 (Часть 20): Введение в гармонические паттерны
Знакомство с языком MQL5 (Часть 20): Введение в гармонические паттерны
 Нейросети в трейдинге: Двусторонняя адаптивная временная корреляция (Окончание)
Нейросети в трейдинге: Двусторонняя адаптивная временная корреляция (Окончание)
 Возможности Мастера MQL5, которые вам нужно знать (Часть 56): Фракталы Билла Вильямса
Возможности Мастера MQL5, которые вам нужно знать (Часть 56): Фракталы Билла Вильямса
 Знакомство с MQL5 (Часть 19): Автоматизация обнаружения волн Вульфа
Знакомство с MQL5 (Часть 19): Автоматизация обнаружения волн Вульфа
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования