Знакомство с языком MQL5 (Часть 20): Введение в гармонические паттерны

Введение

И снова приветствуем вас в Части 20 серии "Знакомство с языком MQL5"! В этой части мы рассмотрим еще один продвинутый тип графических паттернов – гармонические паттерны. Эти паттерны основываются на точных коэффициентах Фибоначчи для определения потенциальных зон разворота и широко признаны в техническом анализе.

Если вы пытались глубже понять эту концепцию, эта статья для вас. В этой статье вы познакомитесь с концепцией структуры гармонических паттернов, а также с основными инструментами расширения и коррекции Фибоначчи, используемыми для их определения.

Мы исследуем основные элементы некоторых наиболее известных гармонических структур, включая такие паттерны, как Гартли, летучая мышь, бабочка и краб, а также точные измерения Фибоначчи, которые их определяют. Поскольку даже незначительное отклонение может сделать сетап недействительным, важно понимать эти соотношения. В следующей статье мы сконцентрируемся на применении этих знаний в виде программ на языке MQL5, что позволит автоматически выявлять как медвежьи, так и бычьи гармонические паттерны.

В этой статье вы узнаете:

• Основы гармонических паттернов и их применение в торговле.
• Математические концепции, лежащие в основе уровней Фибоначчи, и почему они важны для идентификации паттернов.
• Как работают расширения Фибоначчи, и их роль в определении потенциальных ценовых целей.
• Реализация обнаружения гармонических паттернов на языке MQL5, включая использование коэффициентов Фибоначчи в программах.
• Структура различных гармонических паттернов, и как их распознать на графике.

Расширение и коррекция Фибоначчи

Прежде чем мы сможем обсудить концепцию гармонических паттернов, вы должны понять инструменты расширения и коррекции Фибоначчи. Объекты коррекции Фибоначчи и расширения Фибоначчи, вероятно, знакомы вам по вашему инструментарию MetaTrader 5, но задумывались ли вы когда-нибудь о математических формулах, используемых для определения этих уровней?

Если да – прекрасно, и этот раздел поможет вам узнать больше. Если нет, не переживайте, я позабочусь об этом. К концу этого обсуждения вы будете точно знать, как определяются эти уровни Фибоначчи, и почему они имеют решающее значение для распознания гармонических паттернов.

Коррекция Фибоначчи

И коррекция, и расширение Фибоначчи работают с процентными соотношениями. Представьте это как измерение того, на какую часть движения рынок "откатился" или "продолжился". Воспользуемся простым примером. Представьте, что рынок делает четкий свинг: сначала минимум, затем максимум.

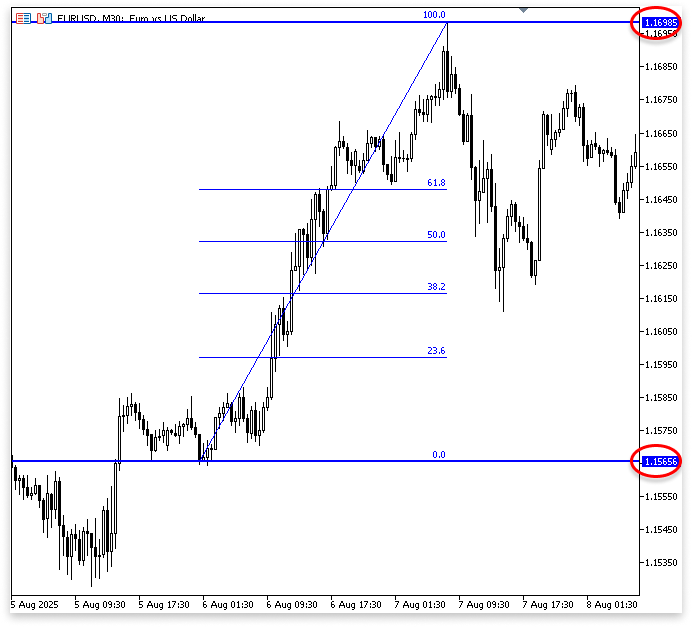
Чтобы рассчитать уровни коррекции Фибоначчи, мы берем разницу между этими двумя точками (высота движения).

Пример:

double price_differecence;
double swing_high;
double swing_low;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   swing_high =  1.16985;
   swing_low = 1.15656;

   price_differecence = swing_high - swing_low;

  }

Всегда вычитайте swing_low из swing_high, чтобы получить положительную разницу в цене. Обратный порядок дает отрицательное значение. 

Что произойдет, если рынок изменит направление на середине от этого движения? Это будет коррекция 50%. Это указывает на то, что произошел откат, равный половине восходящего движения цены.

Пример:

double price_diff_50_percent;

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---

   swing_high =  1.16985;
   swing_low = 1.15656;

   price_differecence = swing_high - swing_low;

   price_diff_50_percent = (50.0/100.0) * price_differecence; // (Fibonacci Retracement level / 100) * Price Difference

  }

Эта строка рассчитывает 50% от общей разницы в цене, и расчет выполняется как деление с плавающей точкой, поскольку используются 50,0 и 100,0, а не просто целочисленные значения. Это важно, поскольку деление с плавающей точкой дает точное десятичное значение. Если мы выразим это в целочисленных значениях, некоторые языки программирования будут рассматривать 50/100 как целочисленное деление.

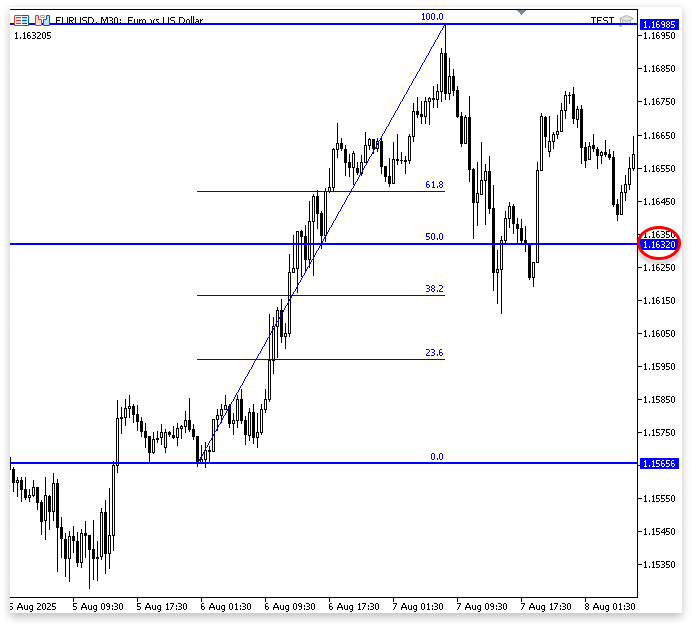
Можно представить это как подъем на десять ступенек лестницы. Если сделаете пять шагов назад, то это будет коррекция на половину от восходящего движения. В коррекции Фибоначчи вы можете рассмотреть несколько процентных уровней. На этих уровнях, которые часто функционируют как невидимые зоны поддержки или сопротивления, цена может приостановиться или развернуться. Согласно пропорциям Фибоначчи, когда вы слышите "рынок откатился до уровня 61,8%", это просто означает, что цена откатилась почти на две трети пути от максимума свинга до минимума свинга.

Расширение Фибоначчи

Расширение Фибоначчи нацелено на оценку того, насколько далеко следующее движение может выйти за пределы изначального свинга, в то время как коррекция Фибоначчи в основном используется для оценки того, насколько рынок откатился от предыдущего движения. Хотя оба эти инструмента выражены в процентах, уровни расширения превышают изначальный свинг на 100 процентов.

Если вы хотите что-то измерить на рынке, вы можете использовать расширения Фибоначчи двумя разными способами.

Первый сценарий (стандартное использование с коррекцией):

При обычном применении инструмент расширения Фибоначчи требует, чтобы рынок откатился, прежде чем будут построены уровни расширения. Здесь вы будете использовать три якоря:

• Первый якорь размещается в точке X.
• Второй якорь размещается в точке A.
• Третий якорь размещается в точке B, где B является коррекцией движения XA.

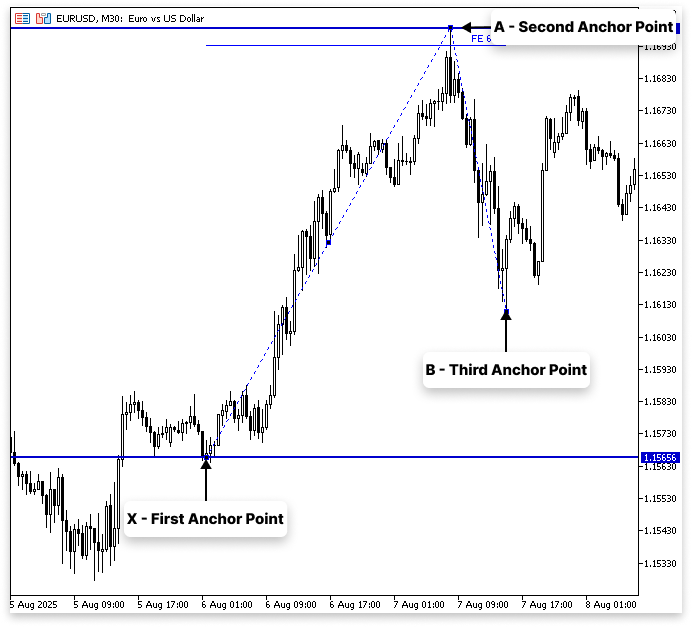
В первом сценарии расширения Фибоначчи мы начинаем с ценового свинга, который мы называем XA. В этом случае X и A обозначают начальную и конечную точки движения, соответственно. После этого первого движения цены рынок обычно возвращается к точке B, которая расположена посередине между X и A. X, A и B – это три опоры, которые мы используем для вычисления расширений Фибоначчи. Инструмент расширения дает вам представление о том, куда может пойти рынок, как только коррекция завершится, проецируя возможные ценовые цели за пределами точки A.

С математической точки зрения, сначала мы вычисляем разницу в цене между X и A:

price difference=A−X

Это дает общий размер движения XA. Затем мы берем выбранное соотношение расширения Фибоначчи, например, 61,8%, и выражаем его в десятичном виде, деля на 100:

fibo ratio= 61.8/100.0

Теперь мы умножаем это соотношение на разницу в цене, чтобы определить, насколько далеко расширение выйдет за пределы точки A:

extension distance = fibo ratio×price difference

Наконец, мы добавляем это расстояние расширения к точке B, чтобы получить уровень расширения Фибоначчи:

fibo extension = B+extension distance

Фактически это означает, что инструмент расширения предсказывает, где может закончиться следующий бычий отрезок за пределами A, если XA является бычьим движением, а B – коррекцией этого движения. Аналогично, на медвежьем рынке инструмент расширения помогает находить возможные цели снижения за пределами A. Благодаря этой математической процедуре расширения Фибоначчи гарантированно выступают в качестве систематических прогнозов, основанных на пропорциональных соотношениях внутри ценового свинга, а не просто случайными линиями на графике.

Второй сценарий (непосредственное использование в гармонических паттернах):

При работе с гармоническими паттернами расширение Фибоначчи применяется иначе, чем обычное коррекционное движение. Первый якорь располагаются в точке X, а второй и третий якоря располагаются в точке A вместо наложения инструмента на коррекцию. Вместо измерения коррекций, этот сетап сосредоточен на оценке будущих ценовых целей.

Хотя расширение и коррекция Фибоначчи в этом случае могут показаться сопоставимыми, это не так. Если точка A является максимумом свинга, мы часто вычитаем из нее процентное соотношение Фибоначчи от отрезка XA; если это минимум свинга, мы добавляем его. Но с расширениями мы добавляем значение, а не вычитаем его, когда точка A является максимумом свинга; таким образом, это расширение, а не коррекция.

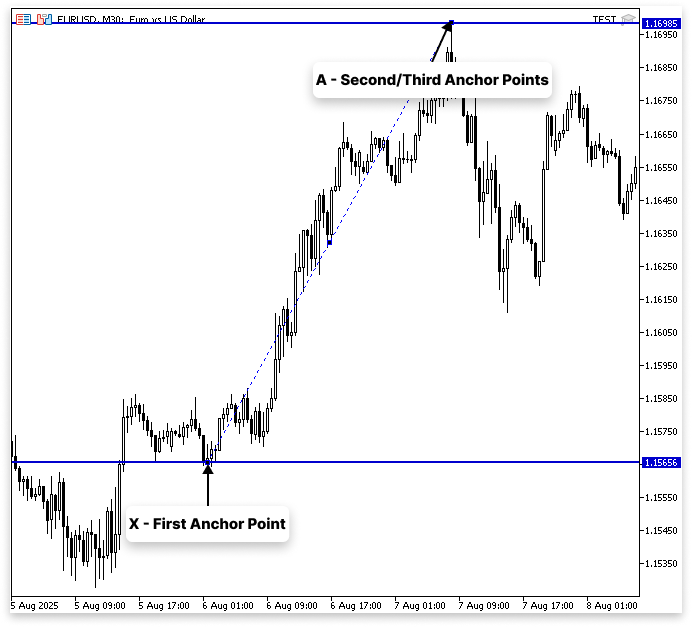
Пример:

double price_differecence;
double swing_high; //A
double swing_low;  //X
double price_diff_161_8_percent;
double fibo_extension_161_8;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---

   swing_high =  1.16985;
   swing_low = 1.15656;

   price_differecence = swing_high - swing_low;

   price_diff_161_8_percent = (61.8/100.0) * price_differecence;
   fibo_extension_161_8 = swing_high + price_diff_161_8_percent;


  }

Пусть расстояние от X до A рассматривается как 100%. Уровень Фибоначчи для XA составляет 61,8%, что дает нам расширение за пределы точки A. Когда значение добавляется к точке A, а не вычитается, полученный уровень составляет 161,8. По этой причине такие расширения, как 127,2 или 161,8, часто используются в гармонических паттернах; они не являются коррекциями для первоначального движения XA, а скорее проекцией за его пределы.

Этот метод устраняет необходимость в фактическом откате от XA и упрощает выявление вероятного местоположения последующего свинга в гармонических паттернах. Движение цены от X до A скорее математически растягивается, и эти проекции помогают определить ключевые точки, в которых рынок может развернуться или завершить гармоническую структуру.

Гармонический паттерн

Гармонические паттерны гораздо проще обсуждать после прояснения концепций коррекции и расширения Фибоначчи. Это связано с тем, что коэффициенты Фибоначчи являются основой всех гармонических паттернов. На самом деле, степень, в которой отрезки цены соответствуют определенным уровням коррекции и расширения Фибоначчи, а также внешний вид паттерна на графике – это и есть отличительная черта любого гармонического паттерна.

Геометрические ценовые структуры, которые повторяются на различных временных интервалах, известны как гармонические паттерны. Они состоят из последовательных свингов (отрезков), таких как XA, AB, BC и CD, и для валидации паттерна каждый отрезок должен удовлетворять точным требованиям Фибоначчи. Гармонические паттерны являются более отчетливыми и объективными, чем простые графические паттерны, такие как треугольники или флаги, поскольку они в значительной степени опираются на математические соотношения.

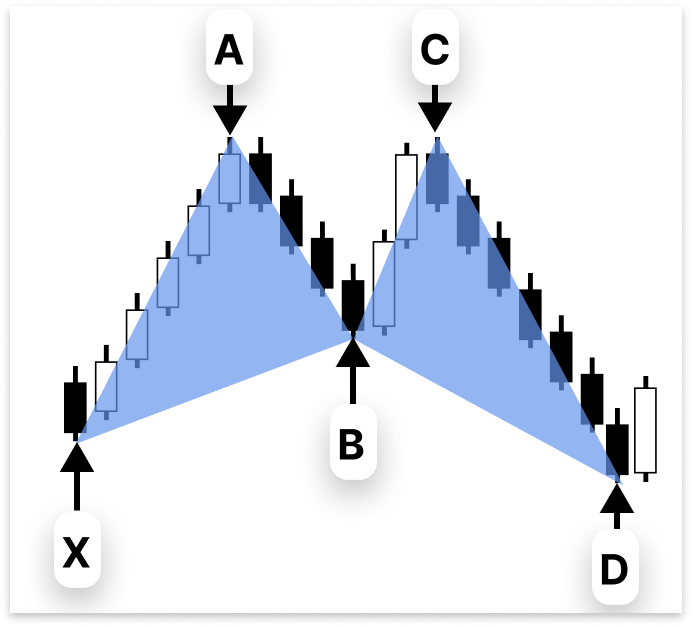
Такие гармонические паттерны, как Гартли, летучая мышь, бабочка и краб, являются одними из наиболее популярных. Взаимосвязи между отрезками определяются уникальным "рецептом" Фибоначчи для каждого из этих паттернов. Например, чтобы паттерн считался действительным, откат AB относительно XA или расширение CD относительно BC должны находиться в определенных диапазонах Фибоначчи и не быть произвольными.

Гармонический паттерн "бабочка"

В типичном паттерне "бабочка" первый отрезок идет от точки X до A и формирует изначальное ценовое движение.

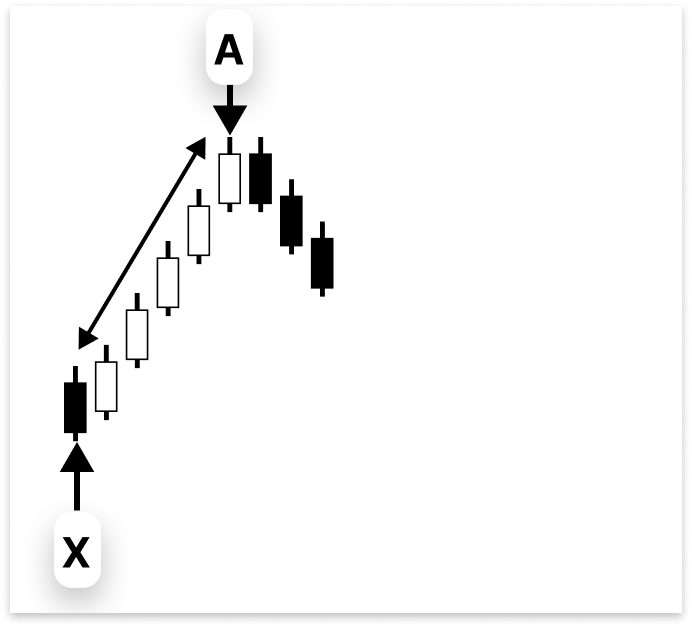
Точка B должна повторить отрезок A-B в соотношении от 76% до 79% относительно отрезка X-A. Хотя 78,6% часто упоминается как "идеальная" коррекция, цена редко достигает этого точного уровня. По этой причине использование диапазона вместо фиксированной точки безопаснее.

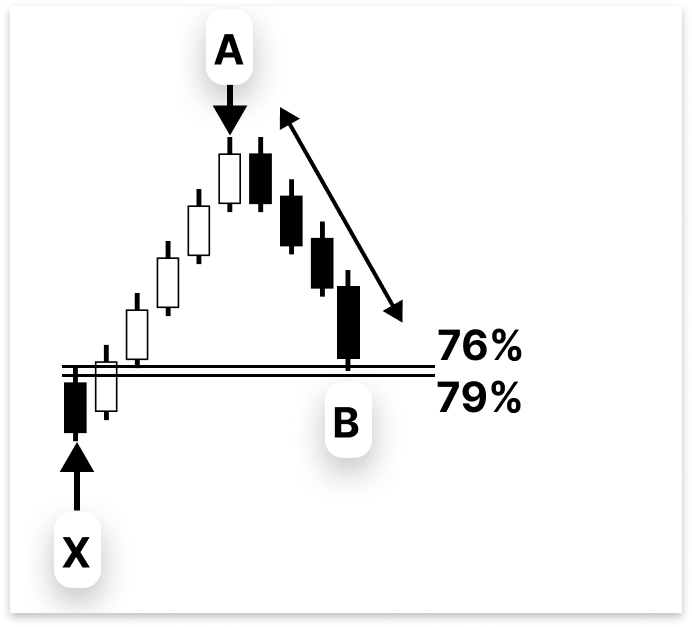
Пример:

double swing_low_x;  //X
double swing_high_x; //A
double price_differecence;
double fib_ret_79;
double fib_ret_76;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---


   swing_low_x = 1.15656;
   swing_high_x =  1.16985;

   price_differecence = swing_high_a - swing_low_x;

   fib_ret_79 = swing_high_x - ((79.0/100.0) * price_differecence);
   fib_ret_76 = swing_high_x - ((76.0/100.0) * price_differecence);


   /*
      if(B <= fib_ret_76 && B>= fib_ret_79)
      {



      }

    */
  }

Пояснение:

Этот алгоритм вычисляет уровни коррекции Фибоначчи между точками свинга X и A, закладывая основу для нахождения точки B в гармоническом паттерне "летучая мышь". Определяется разница в цене, и рассчитываются уровни коррекции 79% и 76%, чтобы указать диапазон, в пределах которого точка должна сформироваться B.

После расчета уровней коррекции мы можем сравнить цену точки B с этим диапазоном. В закомментированном блоке:

if(B <= fib_ret_76 && B >= fib_ret_79) { }

Это условие определяет, находится ли точка B в пределах указанного диапазона коррекции относительно отрезка XA. Точка B соответствует правилам гармонического паттерна "летучая мышь", если это условие истинно, и в этом случае мы можем перейти к дополнительной проверке для точек C и D.

Обычно сегмент B-C откатывается примерно на расстояние от 38,2% до почти 88,6% относительно предыдущего движения A-B. Этому сегменту присуща некоторая гибкость по сравнению с другими. Пока этот откат остается в ожидаемых пределах, весь паттерн считается правильным.

Пример:

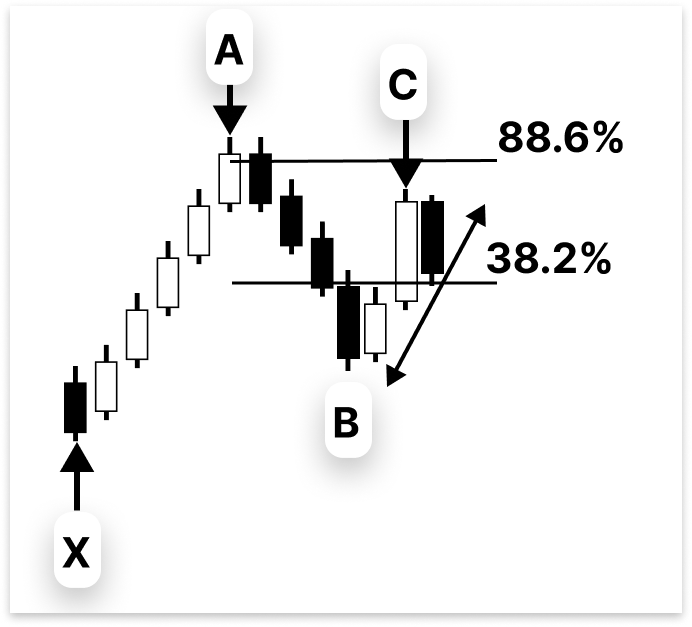
double swing_low_x;  //X
double swing_high_a; //A
double price_differecence;
double fib_ret_79;
double fib_ret_76;

double swing_low_b;  //B
double price_differecence_ab;
double fib_ret_88_6_ab;
double fib_ret_38_2_ab;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---


   swing_low_x = 1.15656;
   swing_high_a =  1.16985;

   price_differecence = swing_high_a - swing_low_x;
   fib_ret_79 = swing_high_a - ((79.0/100.0) * price_differecence);
   fib_ret_76 = swing_high_a - ((76.0/100.0) * price_differecence);

   price_differecence_ab = swing_high_a - swing_low_b;
   fib_ret_88_6_ab = swing_low_b + ((88.6/100.0) * price_differecence_ab);
   fib_ret_38_2_ab = swing_low_b + ((38.2/100.0) * price_differecence_ab);


   /*
     if(B <= fib_ret_76 && B>= fib_ret_79 && C >= fib_ret_38_2_ab && C <= fib_ret_88_6_ab)
     {



     }

   */

  }

Пояснение:

В этом разделе рассчитывается общее движение цены между двумя значимыми точками рынка. На основе этого движения вычисляются определенные уровни коррекции Фибоначчи, которые показывают возможные места для разворота цены или нахождения поддержки и сопротивления. Уровень 38,2% использует меньшую долю движения цены, которая добавляется к той же точке, в то время как уровень коррекции 88,6% находит два эталонных уровня для анализа, принимая большую часть всего движения цены и добавляя его к точке минимума.

Эти уровни помогают определить потенциальные зоны отскока цены во время коррекционного движения. Наконец, в рамках логики подтверждения паттерна закомментированное условие if определяет, находится ли точка B между двумя определенными уровнями коррекции, и находится ли точка C также внутри указанного диапазона Фибоначчи.

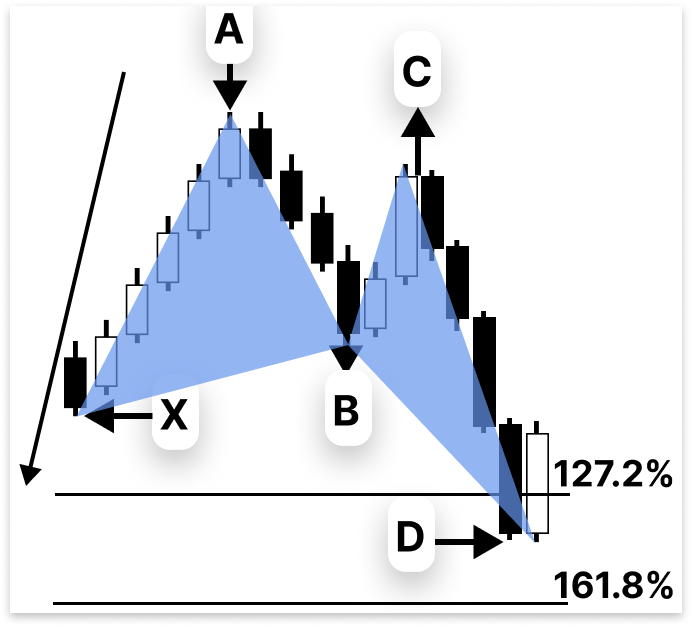
Наконец, отрезок C-D, который обозначает потенциальную зону разворота (PRZ), является наиболее важным компонентом паттерна "бабочка". Точка D в действительной "бабочке" растягивается на расстояние от 127,2% до 161,8% от оригинального отрезка X-A. Зона завершения, где трейдеры ищут возможные признаки разворота, формируется этим расширением. При условии, что X-A составляет 100%, D будет находится на уровне примерно 161,8% от X-A после расширения на 61,8%.

Пример:

double swing_low_x;  //X
double swing_high_a; //A
double price_differecence;
double fib_ret_79;
double fib_ret_76;

double swing_low_b;  //B
double price_differecence_ab;
double fib_ret_88_6_ab;
double fib_ret_38_2_ab;

double xa_price_differecence;
double fib_ext_127_2_xa;
double fib_ext_161_8_xa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---

   swing_low_x = 1.15656;
   swing_high_a =  1.16985;

   price_differecence_ab = swing_high_a - swing_low_b;
   fib_ret_79 = swing_high_a - ((79.0/100.0) * price_differecence);
   fib_ret_76 = swing_high_a - ((76.0/100.0) * price_differecence);

   fib_ret_88_6_ab = swing_low_b + ((88.6/100.0) * price_differecence_ab);
   fib_ret_38_2_ab = swing_low_b + ((38.2/100.0) * price_differecence_ab);

   xa_price_differecence = swing_high_a - swing_low_x;
   fib_ext_127_2_xa = MathAbs(swing_low_x - ((127.2/100.0) * xa_price_differecence));
   fib_ext_161_8_xa = MathAbs(swing_low_x - ((161.8/100.0) * xa_price_differecence));

   /*
     if(B <= fib_ret_76 && B>= fib_ret_79 && C >= fib_ret_38_2_ab && C <= fib_ret_88_6_ab && D <= fib_ext_127_2_xa && D >= fib_ext_161_8_xa)
     {

     }

   */

  }

Пояснение:

Эта часть кода вычисляет расстояние между двумя важными точками свинга в рыночном паттерне. Затем движение цены используется для определения уровней расширения Фибоначчи для этого паттерна. Вычисляя разницу между начальной и конечной точками свинга и используя уровни Фибоначчи 127,2% и 161,8%, этот фрагмент по сути прогнозирует, до куда цена может продолжить движение. Чтобы обеспечить работу вычислений для движений как вверх, так и вниз, код использует функцию, которая преобразует любой результат в положительное целочисленное значение. Затем эти соотношения применяются к изначальному движению цены, либо добавляя, либо вычитая их в зависимости от направления движения, чтобы получить прогнозируемые уровни расширения.

Теперь вам должны быть хорошо понятны математический фундамент расширений и коррекций Фибоначчи, а также их применение в языке MQL5. Теперь мы знаем, как использовать соотношения Фибоначчи, вычислять ценовые различия между точками свинга и определять важные уровни для проверки гармонических паттернов. Логику, которую мы использовали здесь, можно применять и для других гармонических паттернов, так как все они используют аналогичные расчеты на основе Фибоначчи для выявления потенциальных зон разворота и продолжения. Теперь, когда у нас есть эта система, мы можем с уверенностью рассмотреть больше гармонических паттернов. Эти идеи будут применены для выявления потенциальных торговых возможностей на основе ценового действия и соотношений Фибоначчи.

Паттерн Гартли: Паттерн Гартли состоит из отрезков XA, AB, BC и CD. Точка D расположена внутри расширения XA на уровнях 127,2%-161.8%, точка B откатывается примерно на 61,8% от XA, а точка C откатывается на 38,2%-88,6% от AB. Это указывает на возможную зону разворота торговли.

Паттерн "летучая мышь": Определенные соотношения Фибоначчи задают гармоническую структуру, известную как паттерн "летучая мышь". Точка D, обычно находящаяся в зоне коррекции 88,6% от XA, обозначает завершение паттерна, при этом точка B откатывается на расстояние от 38,2% до 50% от отрезка XA.

Заключение

В этой статье были рассмотрены принципы гармонических паттернов и их использование в торговле. Теперь вы понимаете, как применять уровни коррекции и расширения Фибоначчи в языке MQL5, и изучили математические принципы, лежащие в их основе. В следующей статье мы перейдем от теории к практике, используя гармонические паттерны для создания полнофункционального советника. Кроме того, вы узнаете, как визуально распознавать и выделять эти паттерны на ваших торговых графиках, используя графические элементы языка MQL5. В конце следующей статьи у вас будут информация и ресурсы, необходимые для успешной автоматизации торговых стратегий на основе гармонических паттернов.