
Знакомство с языком MQL5 (Часть 22): Создание советника для торговли по паттерну 5-0
Введение
И снова приветствуем вас в Части 22 серии "Знакомство с языком MQL5"! В предыдущей статье мы рассмотрели, как автоматизировать обнаружение таких гармонических паттернов, как формация Гартли, на языке MQL5. В этом продолжении мы сосредоточимся на другой увлекательной, но менее распространенной структуре, известной как гармонический паттерн 5-0. Этот паттерн выделяется тем, что, в отличие от большинства гармоничных сетапов, которые начинаются с коррекции, паттерн 5-0 начинается с резкого движения против тренда, за которым следует структурированная коррекция, предоставляющая ценные торговые возможности.
Эта статья научит вас автоматически распознавать паттерн 5-0 в советнике и обнаруживать его программно. Вы научитесь определять основные точки разворота структуры 5-0 (0, X, A, B, C и D), рассчитывать и проверять коэффициенты Фибоначчи, характерные для нее, и визуально представлять паттерн на графике. К концу этой статьи вы узнаете, как преобразовать техническую идею, лежащую в основе паттерна 5-0, в функциональный код на языке MQL5, который сможет автоматически анализировать ценовое действие.
Гармонический паттерн 5-0
Гармонический паттерн 5-0 является разворотной формацией, которая обычно возникает после значительного и продолжительного движения цены. Рассматривается скорее как паттерн перехода от продолжения к развороту, чем как чистый сетап разворота, и указывает на возможное изменение направления тренда. Четыре отрезка (XA, AB, BC и CD) формируются шестью основными точками паттерна: 0, X, A, B, C и D. Выделяющаяся начальная точка и структура гармонического паттерна 5-0 выделяют его среди других гармонических паттернов. В отличие от большинства гармонических паттернов, которые начинаются с максимума или минимума свинга, гармонический паттерн 5-0 начинается с коррекционного движения, которое часто происходит после завершения предыдущего тренда или паттерна. Это отличает его, поскольку он нацелен на захват истощения контртрендового движения, а не на начало нового импульса.
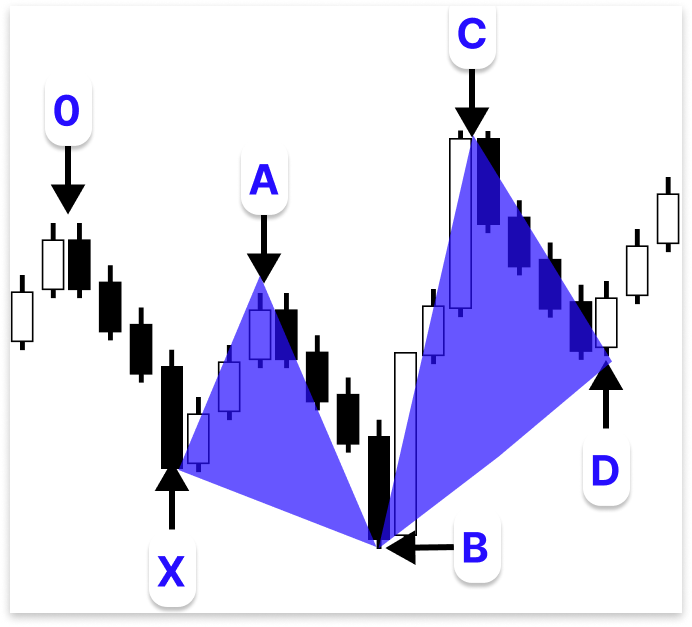
Точка 0, которая создает четкий максимум свинга на графике, является началом бычьего паттерна 5-0. Рынок падает от этого уровня, формируя точку X, которая является первым значительным медвежьим отрезком структуры. Корректирующий откат к этому снижению представлен последующим движением от точки X до точки A. Хотя для этого отката нет установленного уровня Фибоначчи, точка A должна находиться ниже точки 0, указывая на то, что тренд в целом все еще медвежий.
После установления точки A рынок продолжает снижаться, образуя точку B, которая располагается между уровнями 113% и 161,8% расширения Фибоначчи для отрезка XA. Данный отрезок часто представляет этап истощения текущего нисходящего тренда. Рынок разворачивается вверх от точки B, чтобы сформировать точку C, которая обычно составляет от 161,8% до 224% длины отрезка AB. Внутри паттерна это движение демонстрирует мощную коррекционную реакцию. Структура завершается в точке D, где рынок снова откатывается. Рекомендуется, чтобы точка D откатилась на расстояние от 50% до 55% длины отрезка BC. Эта зона коррекции является зоной потенциальной покупки.
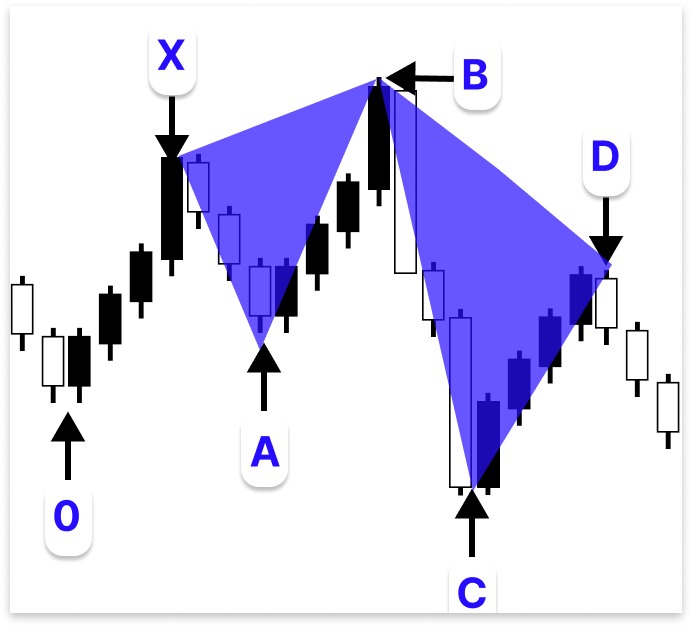
Точка 0 устанавливает выразительный минимум свинга на графике и знаменует начало медвежьего паттерна 5-0. Первый бычий отрезок паттерна устанавливается, когда рынок поднимается от этой точки, чтобы установить точку X. Хотя последующее движение от точки X до точки A является коррекционным откатом, точное соответствие какому-либо уровню коррекции Фибоначчи для этого отрезка не требуется. Чтобы гарантировать, что общий тренд в настоящее время все еще положительный, точка A должна быть выше точки 0.
Точка B, которая должна находиться в диапазоне от 113% до 161,8% расширения Фибоначчи для отрезка XA, устанавливается, когда цена снова поднимается после формирования точки A. Обычно этот уровень указывает на то, что бычий тренд достиг своего предела. После этого рынок снова поворачивает вниз, чтобы сформировать точку C, которая должна представлять собой значимую коррекцию паттерна и соответствовать от 161,8% до 224% длины отрезка AB. Структура завершается, когда цена снова поднимается, достигая точки D. Рекомендуется, чтобы точка D откатилась на расстояние от 50% до 55% длины отрезка BC. Эта область коррекции служит точкой потенциальной продажи.
Выявление 0XAB
Теперь, когда мы осведомлены о значении паттерна 5-0 и основных принципах соотношений внутри него, следующим шагом является программная реализация паттерна 5-0 на языке MQL5. Это подразумевает воплощение идеи на практике путем сбора и обновления свечных данных, точного выявления точек свинга, составления потенциальных последовательностей для точек 0, X, A, B, C и D, проверки каждого отрезка в соответствии с требованиями к соотношениям внутри паттерна и маркировки проверенных паттернов на графике.
На практике мы будем следовать простому процессу: копировать недавние бары в массивы, находить важные опорные точки с помощью надежной техники обнаружения свингов, а затем проходить через эти опорные точки, чтобы построить потенциальные отрезки 0X, XA, AB и BC. Критерии расширения и коррекции Фибоначчи будут затем использоваться для проверки корректности точек B, C и D. Если все требования будут выполнены, далее мы свяжем логику обнаружения с выполнением сделок и нарисуем паттерн и треугольники для визуального подтверждения. Хотя основным фокусом этой статьи будет выявление бычьего гармонического паттерна 5-0, следует отметить, что с несколькими незначительными изменениями в части направления тот же подход и процедура обнаружения могут также быть использованы для выявления медвежьего паттерна 5-0.
Первым этапом в разработке алгоритма обнаружения паттерна 5-0 является копирование свечных данных и нахождение структуры 0XAB. Начинается этот этап со сбора недавних рыночных данных, включая цены открытия, закрытия, максимума, минимума и время, с помощью встроенных в язык MQL5 функции Copy. Компьютер может получать доступ к историческим ценовым движений через эти массивы данных, что имеет решающее значение для выявления значимых максимумов и минимумов свинга.
Как только данные становятся доступными, программа использует логику выявления свингов для определения потенциальных точек разворота в ценовом действии. Советник использует эти точки свинга для определения потенциальных точек 0, X, A и B, которые составляют основу паттерна 5-0. Значительный максимум свинга представлен точкой 0, а минимум свинга представлен точкой X. Затем точка B выходит за пределы точки X в соответствии с диапазоном расширения Фибоначчи (на расстояние от 113% до 161,8% длины отрезка XA), в то время как точка A появляется как более низкий максимум, ниже точки 0. Поскольку точки C и D определяют, может ли паттерн перейти в действительный бычий сетап 5-0, решающее значение при подтверждении точек C и D в будущем имеет корректное определение первых четырех точек.
Пример:input ENUM_TIMEFRAMES timeframe = PERIOD_CURRENT; datetime time_bar; int bars_check = 400; int total_symbol_bars; double open[]; double close[]; double low[]; double high[]; datetime time[]; int z = 4; double O; datetime O_time; string O_line; string O_letter; double X; datetime X_time; string X_letter; double A; datetime A_time; string A_letter; double B; datetime B_time; string B_line; string B_letter; double C; datetime C_time; string C_line; string C_letter; double D; datetime D_time; string D_line; string D_letter; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- total_symbol_bars = Bars(_Symbol, timeframe); time_bar = iTime(_Symbol, timeframe, 0); CopyOpen(_Symbol, timeframe, time_bar, bars_check, open); CopyClose(_Symbol, timeframe, time_bar, bars_check, close); CopyLow(_Symbol, timeframe, time_bar, bars_check, low); CopyHigh(_Symbol, timeframe, time_bar, bars_check, high); CopyTime(_Symbol, timeframe, time_bar, bars_check, time); } //+------------------------------------------------------------------+ //| FUNCTION FOR SWING LOW | //+------------------------------------------------------------------+ bool IsSwingLow(const double &low_price[], int index, int lookback) { for(int i = 1; i <= lookback; i++) { if(low_price[index] > low_price[index - i] || low_price[index] > low_price[index + i]) return false; } return true; } //+------------------------------------------------------------------+ //| FUNCTION FOR SWING HIGH | //+------------------------------------------------------------------+ bool IsSwingHigh(const double &high_price[], int index, int lookback) { for(int i = 1; i <= lookback; i++) { if(high_price[index] < high_price[index - i] || high_price[index] < high_price[index + i]) return false; // If the current high is not the highest, return false. } return true; }
Пояснение:
input ENUM_TIMEFRAMES timeframe = PERIOD_CURRENT;
Здесь указан таймфрейм графика, который советник будет анализировать. Хотя по умолчанию используется таймфрейм текущего графика, трейдеры могут легко изменить его, чтобы протестировать советник на других таймфреймах, включая M15, H1 или D1, не изменяя основной код.
Затем для управления свечными данными и общей информацией графика объявляется ряд глобальных переменных:
datetime time_bar; int bars_check = 400; int total_symbol_bars; double open[]; double close[]; double low[]; double high[]; datetime time[];
Эти переменные хранят рыночные данные. Количество баров (свечей), которые советник должен проверить, задается переменной bars_check; в нашем примере это последние 400 свечей. Данные свечей графика, попадающих в этот диапазон, будут загружены в массивы. Поскольку эти массивы данных содержат историю цен, исходя из которой будут определяться максимумы и минимумы свинга, они имеют решающее значение.
Программа определяет ряд переменных для хранения характеристик каждой значимой точки в паттерне 5-0 после объявления основных контейнеров данных:
double O; datetime O_time; string O_line; string O_letter; double X; datetime X_time; string X_letter; double A; datetime A_time; string A_letter; double B; datetime B_time; string B_line; string B_letter; double C; datetime C_time; string C_line; string C_letter; double D; datetime D_time; string D_line; string D_letter;
Каждая точка свинга имеет закрепленный за ней уникальный набор переменных. Например, переменная O_time фиксирует время, в которое произошла точка O, в то время как переменная O хранит цену точки O. Переменные O_line и O_letter делают возможными отметку точки и отрисовку визуальных маркеров на графике. С точками свинга применяется та же процедура. Благодаря этой структуре, которая позволяет программе записывать координаты каждой точки, становится возможным построение всего паттерна 5-0 на графике, когда все отрезки будут проверены.
Чтобы определить минимум свинга, функция IsSwingLow проверяет, меньше ли минимальная цена свечи по указанному индексу минимальных значений свечей, которые ее окружают. Параметр интервала проверки lookback регулирует количество свечей до и после текущей, с которыми осуществляется сравнение. Минимум свинга подтверждается, если минимум свечи на самом деле является наименьшим по сравнению с минимумами ее соседей. Минимумы свинга имеют решающее значение для определения точек разворота, которые могут заложить основу паттерна – точки 0 или X. В пределах указанного интервала проверки функция IsSwingHigh дополнительно проверяет, выше ли максимум свечи максимумов ближайших свечей.
Следующим шагом после установления основной системы для управления рыночными данными и выявления точек свинга является нахождение формации 0XAB. Поиск значимых максимумов и минимумов свинга, которые соответствуют волнам бычьего гармонического паттерна 5-0, включает в себя анализ исторических свечных данных. Точка X распознается как минимум свинга, а точка 0 – как значимый максимум свинга. Следующая за ними точка B должна выходить за пределы точки X и находиться в диапазоне расширения Фибоначчи от 113% до 161,8% для отрезка XA, после чего должна сформироваться точка A как более низкий максимум под точкой 0.
Пример:
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- total_symbol_bars = Bars(_Symbol, timeframe); time_bar = iTime(_Symbol, timeframe, 0); CopyOpen(_Symbol, timeframe, time_bar, bars_check, open); CopyClose(_Symbol, timeframe, time_bar, bars_check, close); CopyLow(_Symbol, timeframe, time_bar, bars_check, low); CopyHigh(_Symbol, timeframe, time_bar, bars_check, high); CopyTime(_Symbol, timeframe, time_bar, bars_check, time); if(total_symbol_bars >= bars_check) { for(int i = z ; i < bars_check - z; i++) { if(IsSwingHigh(high, i, z)) { for(int j = i; j < bars_check - z; j++) { if(IsSwingLow(low, j, z) && low[j] < high[i]) { X = low[j]; X_time = time[j]; X_letter = StringFormat("X %d",j); for(int a = j; a >= i; a--) { if(IsSwingHigh(high, a, z) && high[a] > X) { O = high[a]; O_time = time[a]; O_letter = StringFormat("0 %d",a); for(int k = j; k < bars_check - z; k++) { if(IsSwingHigh(high, k, z) && high[k] > X) { A = high[k]; A_time = time[k]; A_letter = StringFormat("A %d",k); for(int l = k; l < bars_check - z; l++) { if(IsSwingLow(low, l, z) && low[l] < X) { B = low[l]; B_time = time[l]; B_letter = StringFormat("B %d",l); break; } } break; } } break; } } break; } } } } } }
Пояснение:
Программа начинается с проверки, достаточно ли имеется баров для анализа. Поиск не начинается, если в целом доступно меньше баров, чем необходимо для анализа. Это похоже на проверку того, что ваш книжный шкаф заполнен, прежде чем искать в нем раскладывать книги в нем в определенной последовательности, потому что если вы этого не сделаете, вы можете сделать выводы слишком рано и упустить полный паттерн.
Затем программа начинает искать первый максимум свинга на графике. Чтобы определить, является ли бар в конкретном месте локальным максимумом, внешний цикл проверяет каждый бар с помощью функции IsSwingHigh(). Когда это требование выполняется, это место становится возможной начальной точкой для структуры 5-0.
После выявления максимума свинга программа ищет минимум свинга, который можно использовать в качестве точки X. Для достижения этой цели используется другой цикл, который начинается с максимума и проходит по барам в поисках точки минимума, которая ниже предыдущего максимума. Когда критерии выполнены, минимальная цена, метка времени и метка для отображения на графике сохраняются в соответствующих переменных для точки X. Вы отметили следующую книгу в вашей потенциальной последовательности после того, как нашли немного дальше на полке книгу меньшего размера.
Алгоритм находит правильную точку 0, двигаясь назад от точки X после ее обнаружения. Чтобы найти наибольший максимум, который выше X, он меняет направление сканирования между точкой X и начальным максимумом. Первая такая вершина, которая будет обнаружена, превращается в точку 0, при этом записываются ее цена, время и метка. Поиск выполняется в обратном порядке, чтобы гарантировать, что точка 0 будет самым последним максимумом перед точкой X.
После выявления точек 0 и X алгоритм снова приступает к поиску точки A. Когда следующий максимум свинга пересекает уровень X, он находит его и отмечает как точку A. Точка A обозначает начало нового ценового ралли внутри развивающегося паттерна, представляя собой новый пик после первоначального падения. Это указывает на то, что ваша последовательность книг все еще формируется в ожидаемом альтернативном порядке, подобно тому, как в примере с книжной полкой вы видите книгу среднего размера после маленькой.
Следующим этапом является нахождение точки B. Чтобы найти минимум свинга, который находится ниже точки X, код продолжает сканирование данных после точки A. После нахождения такого минимума свинга цена, время и метка его бара отмечаются как точка B. Затем код отмечает точку B как последнюю точку последовательности 0XAB и прекращает поиск дополнительных минимумов. В аналогии с книжной полкой теперь завершена группа из четырех книг, которая характеризует раннюю структуру паттерна 5-0, так как вы обнаружили еще одну маленькую книгу, которая даже меньше, чем предшествующая короткая.
Все внутренние циклы этой последовательности задействуют команды break для завершения, когда найдена действительная точка. Это позволяет сделать обнаружение целенаправленным и эффективным, гарантируя, что алгоритм не сгенерирует много перекрывающих друг друга сетапов в одном и том же регионе. Когда вы собрали корректный набор книг, который соответствует указаниям по высоте и порядку, вы прекращаете сканирование соответствующего раздела и переходите к следующему. После этих вложенных циклов программа корректно находит и сохраняет первые четыре ключевые точки 0, X, A и B вместе с их значениями времени и метками.
Как я уже упоминал, максимум свинга A, который является коррекцией отрезка 0X, должен быть выше точки X и ниже точки 0, а максимум свинга 0 должен быть выше точки X. Но для точки A не требуется никакой конкретный % коррекции Фибоначчи. Точка B должна находиться между уровнями 113,0% и 161,8% расширения Фибоначчи для отрезка XA. Как только алгоритм подтвердит выполнение этих условий, мы должны создать объект на графике, чтобы визуально обозначить развитие этого паттерна.
Пример:
input ENUM_TIMEFRAMES timeframe = PERIOD_CURRENT; input double b_xa_max = 161.8; // MAX B EXTENSION LEVEL FOR XA input double b_xa_min = 113.0; // MIN B EXTENSION LEVEL FOR XA
double fib_ext_b_161; double fib_ext_b_113; string fib_xa_ext_obj; string fib_xa_ext_lvl; string ox_line; string xa_line; string ab_line; ulong chart_id = ChartID();
for(int l = k; l < bars_check - z; l++) { if(IsSwingLow(low, l, z) && low[l] < X) { B = low[l]; B_time = time[l]; B_letter = StringFormat("B %d",l); fib_ext_b_113 = MathAbs((((A - X) / 100) * (b_xa_min - 100)) - X); fib_ext_b_161 = MathAbs((((A - X) / 100) * (b_xa_max - 100)) - X); if(X < O && A > X && A < O && B <= fib_ext_b_113 && B >= fib_ext_b_161) { ObjectCreate(chart_id,O_letter,OBJ_TEXT,0,O_time,O); ObjectSetString(chart_id,O_letter,OBJPROP_TEXT,"0"); ObjectSetInteger(chart_id,O_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectSetInteger(chart_id,X_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); ObjectSetInteger(chart_id,A_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectSetInteger(chart_id,B_letter,OBJPROP_COLOR,clrBlue); ox_line = StringFormat("0X Line %d",i); xa_line = StringFormat("XA Line %d",i); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ox_line,OBJ_TREND,0, O_time, O,X_time,X); ObjectSetInteger(chart_id,ox_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,xa_line,OBJ_TREND,0, X_time, X,A_time,A); ObjectSetInteger(chart_id,xa_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,ab_line,OBJ_TREND,0, A_time, A,B_time,B); ObjectSetInteger(chart_id,ab_line,OBJPROP_COLOR,clrBlue); fib_xa_ext_obj = StringFormat("XA Expansion %d",i); ObjectCreate(chart_id,fib_xa_ext_obj,OBJ_EXPANSION,0,A_time,A,X_time,X,A_time,A); ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_xa_ext_lvl = StringFormat("XA Expansion Levels %d",i); ObjectCreate(chart_id,fib_xa_ext_lvl,OBJ_RECTANGLE,0,X_time,fib_ext_b_113,B_time,fib_ext_b_161); ObjectSetInteger(chart_id,fib_xa_ext_lvl,OBJPROP_COLOR,clrBlue); } break; } }
Вывод:
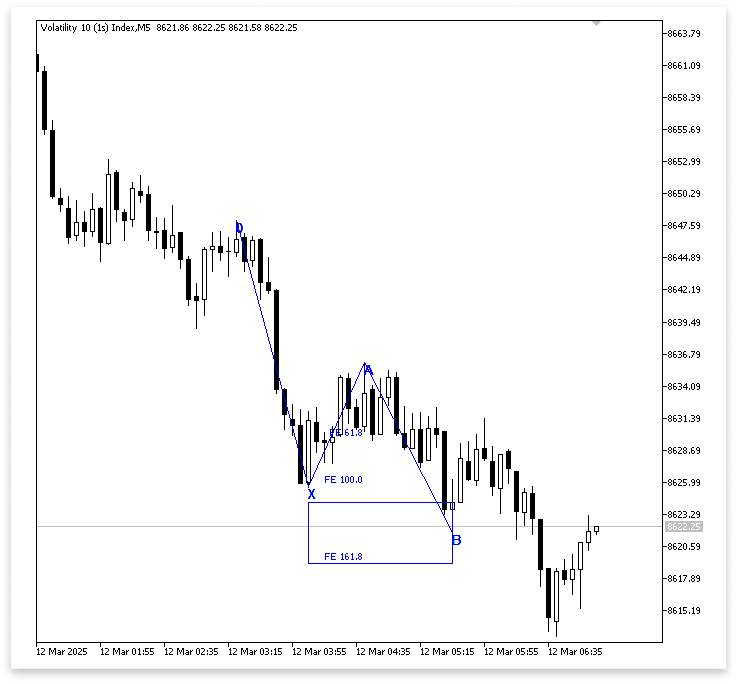
Пояснение:
Код сначала объявляет несколько входных переменных. Программа будет автоматически использовать тот же таймфрейм, который выставлен у графика, к которому она применяется. Диапазон расширения Фибоначчи для отрезка XA представлен двумя входными переменными. Чтобы паттерн был действительным, точка B должна находиться внутри диапазона, определенного этими значениями.
Вычисленные значения и имена объектов затем сохраняются в коллекции переменных. Ценовые уровни расширения Фибоначчи, рассчитанные как 113% и 161,8% для отрезка XA, впоследствии будут сохранены в переменных fib_ext_b_113 и fib_ext_b_161. Различные графические компоненты, которые будут изображены на графике для иллюстрации выявленного паттерна, именуются с помощью переменных fib_xa_ext_obj, fib_xa_ext_lvl, ox_line, xa_line и ab_line. Чтобы убедиться, что все действия рисования происходят в соответствующем окне графика, переменная chart_id получает идентификатор активного графика.
После объявления этих переменных компьютер вычисляет уровни расширения Фибоначчи, используя математические соотношения между точками A и X. Он определяет ценовые точки, соответствующие 113% и 161,8% расширения отрезка XA. Чтобы лучше понять это, рассмотрите аналогию с измерением расстояния между точками X и A на книжной полке. Первый отрезок XA представлен базовым расстоянием (100%), а расширение следующей точки за его пределами представлено уровнями расширения 113% и 161,8%. Чтобы паттерн был действительным, точка B должна находиться внутри этого допустимого диапазона, определенного этими рассчитанными уровнями.
В следующей строке кода вводится условное выражение, которое гарантирует выполнение всех необходимых геометрических соотношений и соотношений Фибоначчи для паттерна 5-0. Определяя, находится ли точка X ниже точки 0, это выражений поддерживает переходную ценовую структуру от медвежьей к бычьей. Кроме того, это подтверждает, что точка A остается в допустимой зоне, совершая коррекцию вверх от точки X, но не превышая точку 0. Наконец, проверяется, находится ли точка B в пределах диапазона от 113% до 161,8% для отрезка XA, что является допустимым диапазоном расширения Фибоначчи.
Затем, как только все эти требования выполнены, алгоритм рисует выявленную структуру на графике. Сначала с помощью текстовых объектов обозначаются важные точки свинга (0, X, A и B). Чтобы они были легко видны, каждому текстовому элементу присваивается синий цвет. Эти обозначения позволяют трейдерам проще выявлять основную структуру паттерна.
Код отмечает расположение отрезков 0X, XA и AB, а затем соединяет их трендовыми линиями. Каждая из этих линий является графическим представлением движения ценовых свингов, которые служат основой для паттерна 5-0. Обозначение каждой линии (например, "0X Line" или "XA Line") гарантирует, что каждый элемент на графике останется отличимым и простым для распознавания.
После этого потенциальные зоны расширения визуально проецируются на отрезок XA с помощью инструмента расширения Фибоначчи. Это расширение укрепляет связь, которая устанавливает правильность точки B, демонстрируя трейдерам, насколько далеко цена могла выйти за пределы отрезка XA. Наконец, чтобы визуально подчеркнуть область между уровнями расширения 113% и 161,8%, рисуется объект "прямоугольник". Эта прямоугольная область ясно иллюстрирует ожидаемое формирование точки B, выступая в качестве выделенной части книжной полки. Точка B поможет вам визуально подтвердить гармонический сетап на графике, указывая подходящую зону расширения для возможного паттерна 5-0, если точка попадает в этот диапазон.
Выявление точки C
После того, как точки 0, X, A и B будут корректно расставлены, нахождение точек C и D завершит структуру паттерна 5-0. Поскольку они устанавливают, развивается ли обнаруженный сетап в действительную гармоническую формацию, эти две точки являются крайне важными. В зависимости от того, как цена отреагирует на точку B, точка C может образоваться как расширение либо как коррекция для отрезка AB. В случае медвежьего паттерна 5-0 ожидается, что точка C будет поставлена в диапазоне от 161,8% до 224% расширения Фибоначчи для отрезка AB. Это указывает на то, что цена после достижения точки B должна выйти за конец отрезка AB на расстояние AB, умноженное на коэффициент примерно от 1,618 до 2,24.
Иными словами, представьте, что отрезок AB – это секция полки. Размещение новой книги (C) дальше по полке, не слишком близко к точке B (менее 161,8%) и не слишком далеко (более 224%), происходит, когда цена превышает B. Эта зона, которая указывает на то, что рынок расширился достаточно, чтобы сохранить гармоничное равновесие, не выходя за его пределы, является идеальной областью для формирования точки C.
После определения точки C структура будет завершена определением точки D как коррекции для отрезка BC. Проверка медвежьего сетапа 5-0 перед применением любой логики подтверждения сделок или алертов требует, чтобы как точка C, так и точка D были расставлены корректно, чтобы паттерн сохранил свою гармоническую симметрию.
Пример:
input double c_ab_max = 224.0; // MAX C EXTENSION LEVEL FOR AB input double c_ab_min = 161.8; // MIN C EXTENSION LEVEL FOR AB
double fib_ext_c_161; double fib_ext_c_224; string fib_ab_ext_obj; string fib_ab_ext_lvl; string bc_line;
if(total_symbol_bars >= bars_check) { for(int i = z ; i < bars_check - z; i++) { if(IsSwingHigh(high, i, z)) { for(int j = i; j < bars_check - z; j++) { if(IsSwingLow(low, j, z) && low[j] < high[i]) { X = low[j]; X_time = time[j]; X_letter = StringFormat("X %d",j); for(int a = j; a >= i; a--) { if(IsSwingHigh(high, a, z) && high[a] > X) { O = high[a]; O_time = time[a]; O_letter = StringFormat("0 %d",a); for(int k = j; k < bars_check - z; k++) { if(IsSwingHigh(high, k, z) && high[k] > X) { A = high[k]; A_time = time[k]; A_letter = StringFormat("A %d",k); for(int l = k; l < bars_check - z; l++) { if(IsSwingLow(low, l, z) && low[l] < X) { B = low[l]; B_time = time[l]; B_letter = StringFormat("B %d",l); for(int m = l; m < bars_check - z; m++) { if(IsSwingHigh(high, m, z) && high[m] > A) { C = high[m]; C_time = time[m]; C_letter = StringFormat("C %d",m); fib_ext_b_113 = MathAbs((((A - X) / 100) * (b_xa_min - 100)) - X); fib_ext_b_161 = MathAbs((((A - X) / 100) * (b_xa_max - 100)) - X); fib_ext_c_161 = MathAbs((((A - B) / 100) * (c_ab_min - 100)) + A); fib_ext_c_224 = MathAbs((((A - B) / 100) * (c_ab_max - 100)) + A); if(X < O && A > X && A < O && B <= fib_ext_b_113 && B >= fib_ext_b_161 && C >= fib_ext_c_161 && C <= fib_ext_c_224) { ObjectCreate(chart_id,O_letter,OBJ_TEXT,0,O_time,O); ObjectSetString(chart_id,O_letter,OBJPROP_TEXT,"0"); ObjectSetInteger(chart_id,O_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectSetInteger(chart_id,X_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); ObjectSetInteger(chart_id,A_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectSetInteger(chart_id,B_letter,OBJPROP_COLOR,clrBlue); ox_line = StringFormat("0X Line %d",i); xa_line = StringFormat("XA Line %d",i); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ox_line,OBJ_TREND,0, O_time, O,X_time,X); ObjectSetInteger(chart_id,ox_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,xa_line,OBJ_TREND,0, X_time, X,A_time,A); ObjectSetInteger(chart_id,xa_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,ab_line,OBJ_TREND,0, A_time, A,B_time,B); ObjectSetInteger(chart_id,ab_line,OBJPROP_COLOR,clrBlue); fib_xa_ext_obj = StringFormat("XA Expansion %d",i); ObjectCreate(chart_id,fib_xa_ext_obj,OBJ_EXPANSION,0,A_time,A,X_time,X,A_time,A); ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_xa_ext_lvl = StringFormat("XA Expansion Levels %d",i); ObjectCreate(chart_id,fib_xa_ext_lvl,OBJ_RECTANGLE,0,X_time,fib_ext_b_113,B_time,fib_ext_b_161); ObjectSetInteger(chart_id,fib_xa_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ObjectSetInteger(chart_id,C_letter,OBJPROP_COLOR,clrBlue); bc_line = StringFormat("BC Line %d",i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0, B_time, B,C_time,C); ObjectSetInteger(chart_id,bc_line,OBJPROP_COLOR,clrBlue); fib_ab_ext_obj = StringFormat("AB Expansion %d",i); ObjectCreate(chart_id,fib_ab_ext_obj,OBJ_EXPANSION,0,B_time,B,A_time,A,B_time,B); ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_ab_ext_lvl = StringFormat("AB Expansion Levels %d",i); ObjectCreate(chart_id,fib_ab_ext_lvl,OBJ_RECTANGLE,0,A_time,fib_ext_c_161,C_time,fib_ext_c_224); ObjectSetInteger(chart_id,fib_ab_ext_lvl,OBJPROP_COLOR,clrBlue); } break; } } break; } } break; } } break; } } break; } } } } }
Вывод:
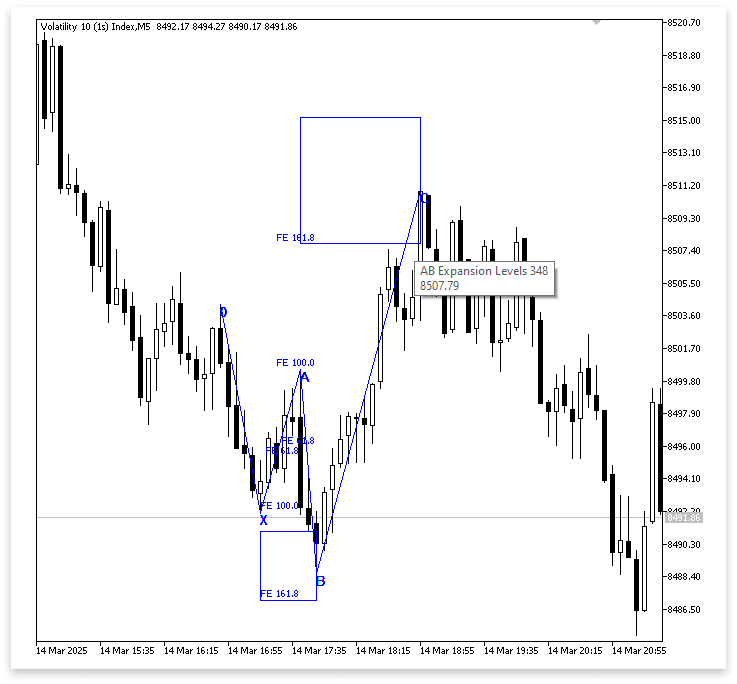
Пояснение:
Чтобы предотвратить слишком большое расширение точки C за пределы расстояния AB, установлен максимально допустимый уровень расширения Фибоначчи для отрезка AB, равный 224%. Чтобы предотвратить образование точки C слишком близко к точке B, также установлен минимальный уровень расширения Фибоначчи, равный 161,8%. Эти два уровня совместно определяют корректную ценовую зону, где ожидается возникновение точки C. Кроме того, к расчету и отображению готовы несколько переменных. Для улучшения ясности структуры паттерна они создают трендовую линию, соединяющую точки B и C, сохраняют вычисленные уровни расширения Фибоначчи и управляют расширением Фибоначчи и его сопутствующим визуальным представлением на графике.
Когда программа обнаруживает возможный максимум свинга, который соответствует критериям для точки C, она записывает его цену, время и метку для обращения в будущем. Затем, чтобы подтвердить корректность диапазона для точки B и определить ожидаемую ценовую зону для точки C, уровни расширения Фибоначчи пересчитываются. Эти вычисления определяют уровни расширения 161,8% и 224%, которые указывают, где точка C должна появляться в идеале в зависимости от разницы между точками A и B. С помощью этой процедуры советник может проверить, действительно ли обнаруженный свинг попадает в допустимые для паттерна 5-0 границы.
Затем компьютер использует условное выражение для определения, корректно ли расположены все точки паттерна. Точка A должна быть выше точки X, но ниже точки O, точка B должна находиться между уровнями 113% и 161,8% для отрезка XA, а точка C должна находиться между уровнями 161,8% и 224% расширения Фибоначчи для отрезка AB. Это подтверждает, что точка X находится ниже точки O. Если все эти геометрические правила и соотношения Фибоначчи выполнены, подтверждается действительность структуры 0XABC для потенциального бычьего паттерна 5-0.
После выполнения этого требования советник отображает паттерн на графике. После создания текстовой метки для точки C и рисования линии, соединяющей точки B и C, отображается зона расширения для точки C путем добавления прямоугольника и объекта расширения Фибоначчи. Прямоугольник показывает трейдерам точное местоположение точки C относительно AB, выделяя диапазон от 161,8% до 224%.
Выявление точки D
Точка D является финальной волной в бычьем гармоническом паттерне 5-0, завершая всю структуру. Обнаружение точки D внутри корректного диапазона коррекции Фибоначчи является последним шагом после выявления и валидации точек 0, X, A, B и C. Точка D является зоной завершения паттерна и часто обозначает область, в которой трейдеры ожидают возможный бычий разворот.
Чтобы бычий сетап 5-0 считался действительным, точка D должна достичь уровня от 50% до 55% коррекции Фибоначчи для отрезка BC. Эта зона коррекции обеспечивает гармонический баланс, который определяет структуру паттерна. Другими словами, точка D должна пройти около половины отрезка BC, указывая на то, что нисходящая коррекция от точки C может подходить к концу.
Пример:
input double d_bc_max = 55.0; // MAX D RETRACEMENT LEVEL FOR BC input double d_bc_min = 50.0; // MIN D RETRACEMENT LEVEL FOR BC
double fib_ret_d_50; double fib_ret_d_55; string fib_bc_ret_lvl; string cd_line;
for(int n = m; n < bars_check - z; n++) { if(IsSwingLow(low, n, z) && low[n] < C) { D = low[n]; D_time = time[n]; D_letter = StringFormat("D %d",l); cd_line = StringFormat("CD %d",i); fib_ext_b_113 = MathAbs((((A - X) / 100) * (b_xa_min - 100)) - X); fib_ext_b_161 = MathAbs((((A - X) / 100) * (b_xa_max - 100)) - X); fib_ext_c_161 = MathAbs((((A - B) / 100) * (c_ab_min - 100)) + A); fib_ext_c_224 = MathAbs((((A - B) / 100) * (c_ab_max - 100)) + A); fib_ret_d_50 = C - ((d_bc_min / 100) * (C - B)); fib_ret_d_55 = C - ((d_bc_max / 100) * (C - B)); if(X < O && A > X && A < O && B <= fib_ext_b_113 && B >= fib_ext_b_161 && C >= fib_ext_c_161 && C <= fib_ext_c_224 && D <= fib_ret_d_50 && D >= fib_ret_d_55) { ObjectCreate(chart_id,O_letter,OBJ_TEXT,0,O_time,O); ObjectSetString(chart_id,O_letter,OBJPROP_TEXT,"0"); ObjectSetInteger(chart_id,O_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectSetInteger(chart_id,X_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); ObjectSetInteger(chart_id,A_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectSetInteger(chart_id,B_letter,OBJPROP_COLOR,clrBlue); ox_line = StringFormat("0X Line %d",i); xa_line = StringFormat("XA Line %d",i); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ox_line,OBJ_TREND,0, O_time, O,X_time,X); ObjectSetInteger(chart_id,ox_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,xa_line,OBJ_TREND,0, X_time, X,A_time,A); ObjectSetInteger(chart_id,xa_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,ab_line,OBJ_TREND,0, A_time, A,B_time,B); ObjectSetInteger(chart_id,ab_line,OBJPROP_COLOR,clrBlue); fib_xa_ext_obj = StringFormat("XA Expansion %d",i); ObjectCreate(chart_id,fib_xa_ext_obj,OBJ_EXPANSION,0,A_time,A,X_time,X,A_time,A); ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_xa_ext_lvl = StringFormat("XA Expansion Levels %d",i); ObjectCreate(chart_id,fib_xa_ext_lvl,OBJ_RECTANGLE,0,X_time,fib_ext_b_113,B_time,fib_ext_b_161); ObjectSetInteger(chart_id,fib_xa_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ObjectSetInteger(chart_id,C_letter,OBJPROP_COLOR,clrBlue); bc_line = StringFormat("BC Line %d",i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0, B_time, B,C_time,C); ObjectSetInteger(chart_id,bc_line,OBJPROP_COLOR,clrBlue); fib_ab_ext_obj = StringFormat("AB Expansion %d",i); ObjectCreate(chart_id,fib_ab_ext_obj,OBJ_EXPANSION,0,B_time,B,A_time,A,B_time,B); ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_ab_ext_lvl = StringFormat("AB Expansion Levels %d",i); ObjectCreate(chart_id,fib_ab_ext_lvl,OBJ_RECTANGLE,0,A_time,fib_ext_c_161,C_time,fib_ext_c_224); ObjectSetInteger(chart_id,fib_ab_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); ObjectSetInteger(chart_id,D_letter,OBJPROP_COLOR,clrBlue); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0, C_time, C,D_time,D); ObjectSetInteger(chart_id,cd_line,OBJPROP_COLOR,clrBlue); fib_bc_ret_lvl = StringFormat("BC RETRACEMENT Levels %d",i); ObjectCreate(chart_id,fib_bc_ret_lvl,OBJ_RECTANGLE,0,B_time,fib_ret_d_50,D_time,fib_ret_d_55); ObjectSetInteger(chart_id,fib_bc_ret_lvl,OBJPROP_COLOR,clrBlue); } break; } }
Вывод:
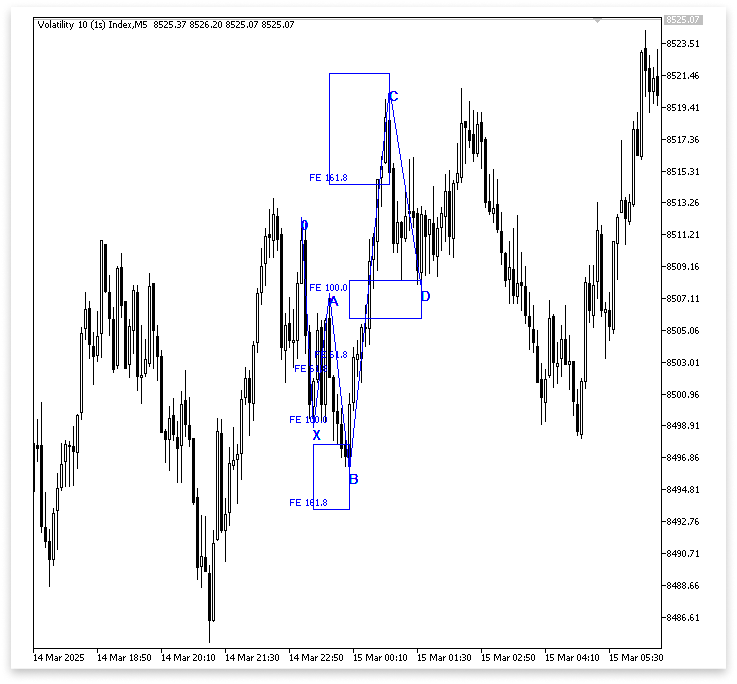
Пояснение:
Переменные fib_ret_d_50 и fib_ret_d_55 используются для определения точных уровней коррекции, в пределах которых может быть установлена точка D. В процессе вычисления разница между точками C и B умножается на десятичное представление процента коррекции, а затем результат вычитается из цены точки C. Это дает ценовые уровни, которые очерчивают зону коррекции для точки D. Формула гарантирует правильное размещение точки D в пределах ожидаемого диапазона уровней коррекции Фибоначчи.
После определения уровней коррекции программа определяет, удовлетворяет ли вся структура паттерна 5-0 необходимым гармоническим требованиям. Точка D находится внутри диапазона коррекции от 50% до 55% для отрезка BC, в то время как точки B и C находятся между уровнями 113% и 161,8% расширения для отрезка XA, точка C находится между уровнями 161,8% и 224% расширения для отрезка AB, а точка X находится ниже точки O, сообразно обстоятельствам. Структура считается действительным паттерном 5-0 только тогда, когда все эти соотношения соблюдены.
После проверки компьютер использует график для визуального отображения структуры. На позиции точки D размещается текстовая метка "D", чтобы указать местоположение точки. Последняя секция паттерна, очевидно, отображается, когда отрисовывается линия, соединяющая точки C и D, образуя отрезок CD. Чтобы визуально обозначить возможную зону завершения для точки D, также создается прямоугольник, чтобы выделить область коррекции от 50% до 55%. Это позволяет трейдерам проще замечать потенциальные развороты или завершения в реальном времени.
Следующим шагом является проверка того, что каждая идентифицированная точка точно отображает преобладающий свинг внутри соответствующего отрезка. Поскольку небольшие изменения цены могут исказить общую структуру паттерна и вызвать путаницу или вводящие в заблуждение сигналы, недостаточно просто записывать максимумы и минимумы. Чтобы сохранить точность, необходимо разработать четкие указания для проверки каждой точки свинга.
Это должен быть наибольший максимум между точками 0 и X, начиная с точки 0. Это гарантирует, что начало первого нисходящего отрезка (0X) обозначено настоящим максимумом свинга, а не незначительным повышением цены. При этом между точками X и A точка X должна быть наименьшим минимумом. Это демонстрирует, что отрезок XA начинается с истинного минимума свинга, а не с незначительного падения.
В аналогичном ключе, чтобы гарантировать, что отрезок AB отражает действительный максимум свинга, точка A должна быть наибольшим максимумом между точками A и B. Затем отрезок BC должен откатиться от доминирующего минимума, если точка B является наименьшим минимумом между точками B и C. Чтобы гарантировать, что отрезок CD начинается от истинного максимума свинга, точка C должна быть наибольшим максимумом между точками C и D.
Пример:int c_d_bars; int c_highest_index; double c_d_hh; datetime c_d_hh_t; int b_c_bars; int b_lowest_index; double b_c_ll; datetime b_c_ll_t; int a_b_bars; int a_highest_index; double a_b_hh; datetime a_b_hh_t; int x_a_bars; int x_lowest_index; double x_a_ll; datetime x_a_ll_t; int o_x_bars; int o_highest_index; double o_x_hh; datetime o_x_hh_t;
for(int n = m; n < bars_check - z; n++) { if(IsSwingLow(low, n, z) && low[n] < C) { D = low[n]; D_time = time[n]; D_letter = StringFormat("D %d",l); cd_line = StringFormat("CD %d",i); c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time); c_highest_index = ArrayMaximum(high,m,c_d_bars); c_d_hh = high[c_highest_index]; c_d_hh_t = time[c_highest_index]; b_c_bars = Bars(_Symbol,PERIOD_CURRENT,B_time,c_d_hh_t); b_lowest_index = ArrayMinimum(low,l,b_c_bars); b_c_ll = low[b_lowest_index]; b_c_ll_t = time[b_lowest_index]; a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_ll_t); a_highest_index = ArrayMaximum(high,k,a_b_bars); a_b_hh = high[a_highest_index]; a_b_hh_t = time[a_highest_index]; x_a_bars = Bars(_Symbol,PERIOD_CURRENT,X_time,a_b_hh_t); x_lowest_index = ArrayMinimum(low,j,x_a_bars); x_a_ll = low[x_lowest_index]; x_a_ll_t = time[x_lowest_index]; o_x_bars = Bars(_Symbol,PERIOD_CURRENT,O_time,x_a_ll_t); o_highest_index = ArrayMaximum(high,a,o_x_bars); o_x_hh = high[o_highest_index]; o_x_hh_t = time[o_highest_index]; fib_ext_b_113 = MathAbs((((a_b_hh - x_a_ll) / 100) * (b_xa_min - 100)) - x_a_ll); fib_ext_b_161 = MathAbs((((a_b_hh - x_a_ll) / 100) * (b_xa_max - 100)) - x_a_ll); fib_ext_c_161 = MathAbs((((a_b_hh - b_c_ll) / 100) * (c_ab_min - 100)) + a_b_hh); fib_ext_c_224 = MathAbs((((a_b_hh - b_c_ll) / 100) * (c_ab_max - 100)) + a_b_hh); fib_ret_d_50 = c_d_hh - ((d_bc_min / 100) * (c_d_hh - b_c_ll)); fib_ret_d_55 = c_d_hh - ((d_bc_max / 100) * (c_d_hh - b_c_ll)); if(x_a_ll < o_x_hh && a_b_hh > x_a_ll && a_b_hh < o_x_hh && b_c_ll <= fib_ext_b_113 && b_c_ll >= fib_ext_b_161 && c_d_hh >= fib_ext_c_161 && c_d_hh <= fib_ext_c_224 && D <= fib_ret_d_50 && D >= fib_ret_d_55) { ObjectCreate(chart_id,O_letter,OBJ_TEXT,0,o_x_hh_t,o_x_hh); ObjectSetString(chart_id,O_letter,OBJPROP_TEXT,"0"); ObjectSetInteger(chart_id,O_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_ll_t,x_a_ll); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectSetInteger(chart_id,X_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_hh_t,a_b_hh); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); ObjectSetInteger(chart_id,A_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_ll_t,b_c_ll); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectSetInteger(chart_id,B_letter,OBJPROP_COLOR,clrBlue); ox_line = StringFormat("0X Line %d",i); xa_line = StringFormat("XA Line %d",i); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ox_line,OBJ_TREND,0, o_x_hh_t, o_x_hh,x_a_ll_t,x_a_ll); ObjectSetInteger(chart_id,ox_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,xa_line,OBJ_TREND,0, x_a_ll_t, x_a_ll,a_b_hh_t,a_b_hh); ObjectSetInteger(chart_id,xa_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,ab_line,OBJ_TREND,0, a_b_hh_t, a_b_hh,b_c_ll_t,b_c_ll); ObjectSetInteger(chart_id,ab_line,OBJPROP_COLOR,clrBlue); fib_xa_ext_obj = StringFormat("XA Expansion %d",i); ObjectCreate(chart_id,fib_xa_ext_obj,OBJ_EXPANSION,0,a_b_hh_t,a_b_hh,x_a_ll_t,x_a_ll,a_b_hh_t,a_b_hh); ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_xa_ext_lvl = StringFormat("XA Expansion Levels %d",i); ObjectCreate(chart_id,fib_xa_ext_lvl,OBJ_RECTANGLE,0,x_a_ll_t,fib_ext_b_113,b_c_ll_t,fib_ext_b_161); ObjectSetInteger(chart_id,fib_xa_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_hh_t,c_d_hh); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ObjectSetInteger(chart_id,C_letter,OBJPROP_COLOR,clrBlue); bc_line = StringFormat("BC Line %d",i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0, b_c_ll_t, b_c_ll,c_d_hh_t,c_d_hh); ObjectSetInteger(chart_id,bc_line,OBJPROP_COLOR,clrBlue); fib_ab_ext_obj = StringFormat("AB Expansion %d",i); ObjectCreate(chart_id,fib_ab_ext_obj,OBJ_EXPANSION,0,b_c_ll_t,b_c_ll,a_b_hh_t,a_b_hh,b_c_ll_t,b_c_ll); ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_ab_ext_lvl = StringFormat("AB Expansion Levels %d",i); ObjectCreate(chart_id,fib_ab_ext_lvl,OBJ_RECTANGLE,0,a_b_hh_t,fib_ext_c_161,c_d_hh_t,fib_ext_c_224); ObjectSetInteger(chart_id,fib_ab_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); ObjectSetInteger(chart_id,D_letter,OBJPROP_COLOR,clrBlue); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0, C_time, C,D_time,D); ObjectSetInteger(chart_id,cd_line,OBJPROP_COLOR,clrBlue); fib_bc_ret_lvl = StringFormat("BC RETRACEMENT Levels %d",i); ObjectCreate(chart_id,fib_bc_ret_lvl,OBJ_RECTANGLE,0,b_c_ll_t,fib_ret_d_50,D_time,fib_ret_d_55); ObjectSetInteger(chart_id,fib_bc_ret_lvl,OBJPROP_COLOR,clrBlue); } break; } }
Пояснение:
Чтобы убедиться, что каждая точка точно отражает рыночный свинг, используется та же проверка для остальных отрезков. Алгоритм определяет минимум между точками X и A для отрезка XA, таким образом подтверждая, что точка X является минимумом свинга. Чтобы гарантировать, что точка 0 представляет собой максимум свинга в начале паттерна, на отрезке 0X аналогично осуществляется поиск наибольшего максимума между точками 0 и X. Этот метод оценки каждой точки поддерживает стабильности и надежность структуры паттерна, устраняя ложные свинги, которые могут исказить точность идентификации.
После проверки каждой доминирующей точки свинга программа обеспечивает включение всех проверенных максимумов и минимумов в последующие вычисления. Это улучшение позволяет более точно пересчитывать уровни расширения Фибоначчи и коррекции, гарантируя, что пропорции каждого отрезка соответствуют фактическим колебаниям рынка. После завершения этой перекалибровки программа проверяет, что каждая из точек в бычьем паттерне 5-0 по-прежнему имеет правильный порядок и соотношения. Как только все геометрические и Фибоначчи требования будут выполнены, метод подтвердит, что на графике развилась действительная структура 5-0.
Исполнение сделок
После подтверждения того, что бычий гармонический паттерн 5-0 был корректно идентифицирован, следующим шагом является исполнение сделок на основе этой структуры. В данном сетапе вход в сделку происходит, когда цена достигает точки D, которая представляет собой потенциальное завершение паттерна и возможную бычью зону разворота. На языке MQL5 это можно реализовать путем проверки, находится ли текущая цена вблизи точки D, а затем открывая ордер на покупку с заранее определенными параметрами, такими как размер лота, стоп-лосс и тейк-профит.
Пример:
#include <Trade/Trade.mqh> CTrade trade; input double lot_size = 0.6;
datetime time_price[]; double ask_price; double take_p; datetime last_trade_time = 0; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ArraySetAsSeries(time_price,true); //--- return(INIT_SUCCEEDED); }
CopyTime(_Symbol, timeframe, 0, 2, time_price); ask_price = SymbolInfoDouble(_Symbol,SYMBOL_ASK); datetime current_bar_time = iTime(_Symbol,timeframe,0);
if(x_a_ll < o_x_hh && a_b_hh > x_a_ll && a_b_hh < o_x_hh && b_c_ll <= fib_ext_b_113 && b_c_ll >= fib_ext_b_161 && c_d_hh >= fib_ext_c_161 && c_d_hh <= fib_ext_c_224 && D <= fib_ret_d_50 && D >= fib_ret_d_55) { ObjectCreate(chart_id,O_letter,OBJ_TEXT,0,o_x_hh_t,o_x_hh); ObjectSetString(chart_id,O_letter,OBJPROP_TEXT,"0"); ObjectSetInteger(chart_id,O_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_ll_t,x_a_ll); ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X"); ObjectSetInteger(chart_id,X_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_hh_t,a_b_hh); ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A"); ObjectSetInteger(chart_id,A_letter,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_ll_t,b_c_ll); ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B"); ObjectSetInteger(chart_id,B_letter,OBJPROP_COLOR,clrBlue); ox_line = StringFormat("0X Line %d",i); xa_line = StringFormat("XA Line %d",i); ab_line = StringFormat("AB Line %d",i); ObjectCreate(chart_id,ox_line,OBJ_TREND,0, o_x_hh_t, o_x_hh,x_a_ll_t,x_a_ll); ObjectSetInteger(chart_id,ox_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,xa_line,OBJ_TREND,0, x_a_ll_t, x_a_ll,a_b_hh_t,a_b_hh); ObjectSetInteger(chart_id,xa_line,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,ab_line,OBJ_TREND,0, a_b_hh_t, a_b_hh,b_c_ll_t,b_c_ll); ObjectSetInteger(chart_id,ab_line,OBJPROP_COLOR,clrBlue); fib_xa_ext_obj = StringFormat("XA Expansion %d",i); ObjectCreate(chart_id,fib_xa_ext_obj,OBJ_EXPANSION,0,a_b_hh_t,a_b_hh,x_a_ll_t,x_a_ll,a_b_hh_t,a_b_hh); ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_xa_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_xa_ext_lvl = StringFormat("XA Expansion Levels %d",i); ObjectCreate(chart_id,fib_xa_ext_lvl,OBJ_RECTANGLE,0,x_a_ll_t,fib_ext_b_113,b_c_ll_t,fib_ext_b_161); ObjectSetInteger(chart_id,fib_xa_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_hh_t,c_d_hh); ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C"); ObjectSetInteger(chart_id,C_letter,OBJPROP_COLOR,clrBlue); bc_line = StringFormat("BC Line %d",i); ObjectCreate(chart_id,bc_line,OBJ_TREND,0, b_c_ll_t, b_c_ll,c_d_hh_t,c_d_hh); ObjectSetInteger(chart_id,bc_line,OBJPROP_COLOR,clrBlue); fib_ab_ext_obj = StringFormat("AB Expansion %d",i); ObjectCreate(chart_id,fib_ab_ext_obj,OBJ_EXPANSION,0,b_c_ll_t,b_c_ll,a_b_hh_t,a_b_hh,b_c_ll_t,b_c_ll); ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_COLOR,clrBlue); for(int i = 0; i <= 2; i++) { ObjectSetInteger(chart_id,fib_ab_ext_obj,OBJPROP_LEVELCOLOR,i,clrBlue); } fib_ab_ext_lvl = StringFormat("AB Expansion Levels %d",i); ObjectCreate(chart_id,fib_ab_ext_lvl,OBJ_RECTANGLE,0,a_b_hh_t,fib_ext_c_161,c_d_hh_t,fib_ext_c_224); ObjectSetInteger(chart_id,fib_ab_ext_lvl,OBJPROP_COLOR,clrBlue); ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D); ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D"); ObjectSetInteger(chart_id,D_letter,OBJPROP_COLOR,clrBlue); cd_line = StringFormat("CD Line %d",i); ObjectCreate(chart_id,cd_line,OBJ_TREND,0, c_d_hh_t, c_d_hh,D_time,D); ObjectSetInteger(chart_id,cd_line,OBJPROP_COLOR,clrBlue); fib_bc_ret_lvl = StringFormat("BC RETRACEMENT Levels %d",i); ObjectCreate(chart_id,fib_bc_ret_lvl,OBJ_RECTANGLE,0,b_c_ll_t,fib_ret_d_50,D_time,fib_ret_d_55); ObjectSetInteger(chart_id,fib_bc_ret_lvl,OBJPROP_COLOR,clrBlue); if(time[n+z] == time_price[1] && close[n+z] > D && current_bar_time != last_trade_time) { take_p = ask_price + (MathAbs(ask_price - D) * 3); trade.Buy(lot_size,_Symbol,ask_price,D,take_p); last_trade_time = current_bar_time; } }
Вывод:
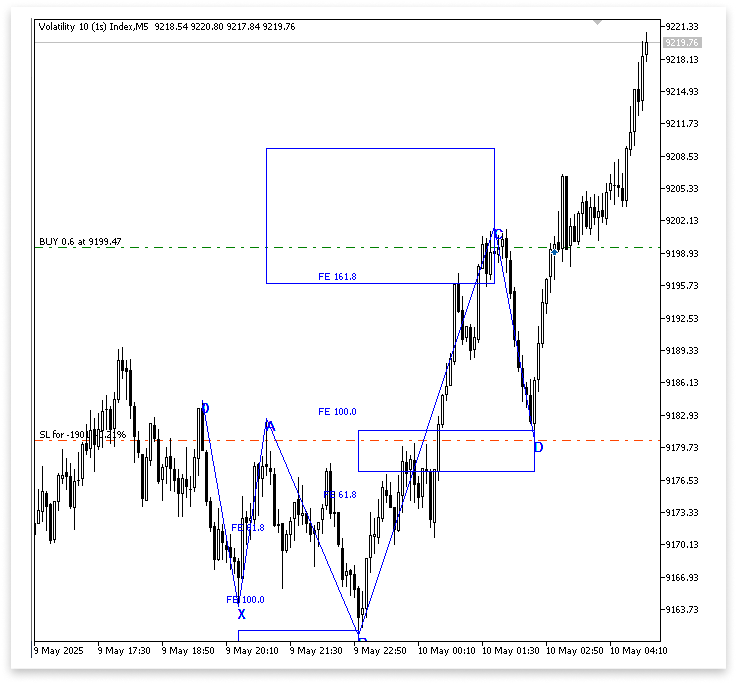
Пояснение:
Этот раздел программы осуществляет исполнение сделки после подтверждения бычьего гармонического паттерна 5-0. Торговая библиотека MQL5, которая предоставляет класс CTrade, необходимый для передачи торговых ордеров брокеру, импортируется в первой строке: #include <Trade/Trade.mqh>. Создавая экземпляр этого класса, строка CTrade trade; позволяет программе выполнять торговые операции, такие как покупка и продажа. В каждой открываемой сделке будет использоваться объем 0,6 лота, определяемый входной переменной lot_size = 0.6.
Для контроля исполнения сделок и предотвращения дублирования записей программа определяет ряд переменных. Переменная ask_price хранит текущую рыночную цену Ask, take_p используется для определения цели для фиксации прибыли, last_trade_time фиксирует время последней сделки, а массив time_price[] отслеживает значения времени свечей. Чтобы соответствовать требованиям языка MQL5 в части обработки временных рядов, массив time_price инициализируется в порядке от новейшего элемента к старейшему. Программа извлекает значения времени самых последних свечей и рыночную цену для каждого тика.
Время текущей свечи должно совпадать с самым последним скопированным временем, цена закрытия должна быть выше точки D, и не должно быть ранее исполненных сделок на этой же свече. Затем эти критерии проверяются, чтобы определить, следует ли открывать сделку. Чтобы избежать множественных входов в пределах одного бара, компьютер осуществляет покупку, если выполнены эти требования, устанавливает тейк-профит на уровне, в три раза превышающем расстояние между текущей ценой Ask и точкой D, и записывает время сделки.
Заключение
В этой статье объясняется, как создать советник, который обнаруживает гармонический паттерн 5-0 и торгует по нему. В статье рассмотрено, как выявлять и валидировать каждую точку свинга, подтверждать структуру паттерна, исполнять сделки автоматически и отображать паттерн на графике с помощью графических объектов, таких как трендовые линии и метки. Это заключительная статья из серии о продвинутых графических паттернах. В следующей части будут исследованы новые аспекты языка MQL5.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/19856
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Разностное моделирование рыночной микроструктуры (EDCFlow)
Нейросети в трейдинге: Разностное моделирование рыночной микроструктуры (EDCFlow)
 Нейросети в трейдинге: Сеточная аппроксимация событийного потока как инструмент анализа ценовых паттернов (Окончание)
Нейросети в трейдинге: Сеточная аппроксимация событийного потока как инструмент анализа ценовых паттернов (Окончание)
 От новичка до эксперта: Раскрытие секретов теней свечей
От новичка до эксперта: Раскрытие секретов теней свечей
 Объединяем 3D-бары, квантовые вычисления и машинное обучение в единую торговую систему
Объединяем 3D-бары, квантовые вычисления и машинное обучение в единую торговую систему
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Волны Элиота?
Да, это волны Элиота. И не надо изобретать новых сущностей, Уильям Оккам не одобряет.
Элиот машет руками?
Да, это волны Элиота. И не придумывайте новых сущностей, Уильям Оккам не одобряет.