
Алгоритм дифференциального поиска — Differential Search Algorithm (DSA)
Содержание
Введение
В данной статье рассмотрим Differential Search Algorithm — алгоритм оптимизации, имитирующий миграцию суперорганизма (стаи) в поисках лучших условий. DSA был предложен Pinar Civicioglu в 2012 году как альтернатива классическим алгоритмам, таким как PSO (Particle Swarm Optimization) и DE (Differential Evolution). Он моделирует поведение популяции организмов, которые перемещаются в пространстве решений, имитируя естественную миграцию с элементами случайности и направленного поиска. Вот одна из публикаций этого алгоритма.
Реализация алгоритма
DSA имитирует миграцию суперорганизма (стаи, роя) в поисках лучших условий обитания. Представьте стаю птиц, которая перелетает с места на место в поисках пищи, это популяция решений движется в пространстве поиска. На каждой итерации каждая особь выбирает направление — куда двигаться (к случайной особи, к лучшим, или к самому лучшему), делает шаг — размер шага определяется гамма-распределением, что даёт много мелких шагов и редкие большие прыжки.
Шаг может быть отрицательным — тогда особь движется в противоположную сторону. Когда частично откатывается — случайно выбранные координаты возвращаются к прежним значениям. Это сохраняет хорошие гены и позволяет точно настраивать отдельные параметры. Принимает решение — если новая позиция лучше старой, особь остаётся, иначе возвращается назад.
1. Суперорганизм (Популяция). Это набор особей (решений). Каждая особь — это точка в пространстве поиска.
Пример: Ищем оптимум функции f(x, y). Популяция из 5 особей:
Особь 0: (2.5, 3.1) фитнес = 0.65
Особь 1: (1.2, 4.0) фитнес = 0.42
Особь 2: (3.8, 2.5) фитнес = 0.78 ← лучшая
Особь 3: (0.5, 1.0) фитнес = 0.31
Особь 4: (2.0, 2.0) фитнес = 0.55
2. Направление миграции (Direction). Куда будет двигаться каждая особь? Есть 4 стратегии:
B-DSA (Bijective) — Случайная перестановка. Каждая особь движется к случайной другой особи.Пример: Перестановка индексов: [0,1,2,3,4] → [3,0,4,2,1]
Особь 0 → движется к особи 3: направление = (0.5, 1.0)
Особь 1 → движется к особи 0: направление = (2.5, 3.1)
Особь 2 → движется к особи 4: направление = (2.0, 2.0)
Особь 3 → движется к особи 2: направление = (3.8, 2.5)
Особь 4 → движется к особи 1: направление = (1.2, 4.0)
S-DSA (Surjective) — К случайным лучшим. Каждая особь движется к случайному решению из топ-N лучших.
Пример: Сортировка по фитнесу: [2, 0, 4, 1, 3] (от лучшего к худшему)
Для особи 0: случайно выбираем из топ-3 → выбрали особь 2
Для особи 1: случайно выбираем из топ-2 → выбрали особь 0 и т.д.
E1-DSA (Elitist #1) — Все особи двигаются к одному случайному лидеру. Выбирается один случайный лидер из топа, и все перемещаются в его сторону.
Случайно выбрали из топ-2: особь 0; все особи движутся к (2.5, 3.1)
Пример: Лучшая особь: #2 с координатами (3.8, 2.5). Все особи движутся к (3.8, 2.5)
E2-DSA (Elitist #2) — Все особи движутся к самому лучшему решению.
Пример: Лучшая особь: #2 с координатами (3.8, 2.5) Все особи движутся к (3.8, 2.5)
3. Фактор масштаба (Scale Factor). Определяет размер шага при движении. Вычисляется по формуле: Scale = Gamma(2·rand) × (rand - rand)
Пример вычисления: rand1 = 0.7 → shape = 2 × 0.7 = 1.4 Gamma(1.4) ≈ 0.89; rand2 = 0.8 rand3 = 0.3 Scale = 0.89 × (0.8 - 0.3) = 0.89 × 0.5 = 0.445
Scale может быть отрицательным, что позволяет двигаться в противоположном направлении. rand2 = 0.2, rand3 = 0.9; Scale = 0.89 × (0.2 - 0.9) = 0.89 × (-0.7) = -0.623
4. Вычисление Stopover (промежуточной позиции). Формула движения: stopover = current + scale × (direction - current)
Пример для особи 0: current = (2.5, 3.1); direction = (0.5, 1.0) ← из B-DSA; scale = 0.445
stopover_x = 2.5 + 0.445 × (0.5 - 2.5) = 2.5 + 0.445 × (-2.0) = 2.5 - 0.89 = 1.61
stopover_y = 3.1 + 0.445 × (1.0 - 3.1) = 3.1 + 0.445 × (-2.1) = 3.1 - 0.93 = 2.17 stopover = (1.61, 2.17)
С отрицательным scale: scale = -0.623
stopover_x = 2.5 + (-0.623) × (0.5 - 2.5) = 2.5 + (-0.623) × (-2.0) = 2.5 + 1.25 = 3.75
stopover_y = 3.1 + (-0.623) × (1.0 - 3.1) = 3.1 + (-0.623) × (-2.1) = 3.1 + 1.31 = 4.41
stopover = (3.75, 4.41) ← движение в противоположную сторону!
5. Карта мутации (Map). Определяет, какие координаты изменить, а какие оставить
map[i] = 0 → координата i БУДЕТ изменена
map[i] = 1 → координата i ОСТАНЕТСЯ прежней
Стратегия 1: Random-mutation #1. Каждая координата независимо решает: меняться или нет
Пример (2D): Особь 0: map = [0, 1] → x меняется, y остается; Особь 1: map = [1, 0] → x остается, y меняется; Особь 2: map = [0, 0] → обе координаты меняются; Особь 3: map = [1, 1] → обе остаются (нет изменений)
Стратегия 2: Differential-mutation. Меняется только одна случайная координата
Пример (5D): Особь 0: случайный индекс = 2 → map = [1, 1, 0, 1, 1]; Особь 1: случайный индекс = 0 → map = [0, 1, 1, 1, 1]; Особь 2: случайный индекс = 4 → map = [1, 1, 1, 1, 0]
Стратегия 3: Random-mutation #2. Меняется несколько случайных координат (количество зависит от p2)
Пример (5D, p2=0.3, numModify = ceil(0.15 × 5) = 1). Особь 0: случайные индексы = [2] → map = [1, 1, 0, 1, 1]; Особь 1: случайные индексы = [0, 3] → map = [0, 1, 1, 0, 1]
6. Применение карты
Пример: current = (2.5, 3.1); stopover = (1.61, 2.17); map = [0, 1]
Результат: x: map[0]=0 → берем stopover_x = 1.61 y: map[1]=1 → берем current_y = 3.1 Финальная позиция = (1.61, 3.1)
7. Селекция. После вычисления фитнеса новой позиции, решаем, принять её или нет
Особь 0: старая позиция: (2.5, 3.1), фитнес = 0.65 новая позиция: (1.61, 3.1), фитнес = 0.72 0.72 > 0.65 → ПРИНИМАЕМ новую позицию
Особь 1: старая позиция: (1.2, 4.0), фитнес = 0.42 новая позиция: (0.8, 3.5), фитнес = 0.38 0.38 < 0.42 → ОТКЛОНЯЕМ, остаемся на старой позиции
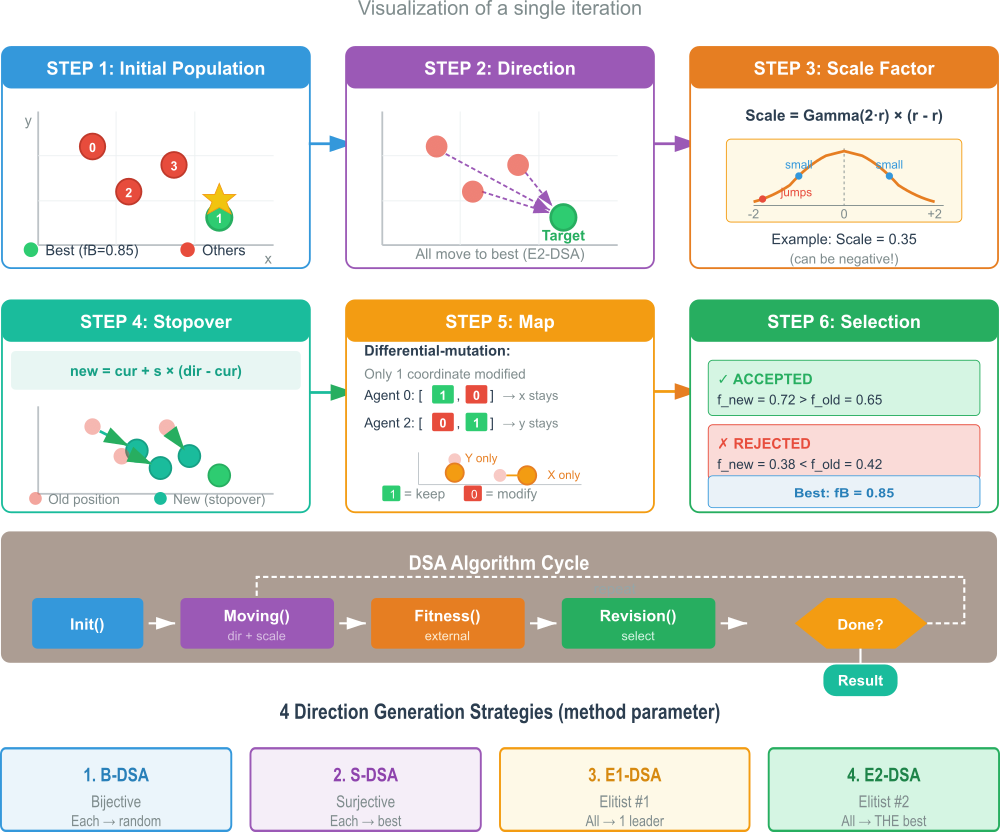
Рисунок 1. Схема работы алгоритма DSA
На иллюстрации показано 6 шагов одной итерации: исходная популяция — это точки в пространстве поиска, лучшая отмечена зелёным цветом, генерация направления (E2-DSA), когда все особи движутся к лучшей, показаны стрелки направлений, Scale Factor — график распределения размера шага: много мелких шагов, редкие большие прыжки, вычисление Stopover — формула и визуализация движения точек к новым позициям, применение Map, показано, как маска определяет какие координаты менять (0=изменить, 1=оставить), селекция — примеры принятия и отклонения новых позиций.
Так же дополнительно показан цикл алгоритма — последовательность вызовов: Init → Moving → CalcFitness → Revision → повтор и в конце, 4 стратегии направления — краткое описание методов B-DSA, S-DSA, E1-DSA, E2-DSA.
Переходим к написанию псевдокода алгоритма.
1. ИНИЦИАЛИЗАЦИЯ
ДЛЯ каждой особи i = 1..popSize
x[i] = случайная точка в пределах bounds
f[i] = вычислить фитнес(x[i])
КОНЕЦ ДЛЯ
xBest = лучшая особь
fBest = лучший фитнес
2. ГЛАВНЫЙ ЦИКЛ (iter = 1..maxIter)
2.1. Сохранить текущее состояние
xPrev = x
fPrev = f
2.2. ДЛЯ каждой особи i
a) Выбрать направление (зависит от method):
- B-DSA (1): direction = случайная другая особь
- S-DSA (2): direction = случайная из топ-лучших
- E1-DSA (3): direction = один случайный лидер (для всех одинаковый)
- E2-DSA (4): direction = самая лучшая особь (для всех одинаковый)
b) Вычислить масштаб:
scale = Gamma(2·rand) × (rand - rand)
c) Вычислить промежуточную позицию:
stopover[d] = xPrev[i][d] + scale × (direction[d] - xPrev[i][d])
для всех координат d = 1..dim
d) Сгенерировать карту мутации:
prob = случайное число [0, 1]
ЕСЛИ prob < p1 ТОГДА
// Random-mutation #1: каждая координата ~50% меняется
map[d] = случайно 0 или 1
ИНАЧЕ ЕСЛИ prob > (1 - p1) ТОГДА
// Differential-mutation: только ОДНА координата
randomCoord = случайный индекс
map[d] = 1 для всех d, кроме randomCoord
map[randomCoord] = 0
ИНАЧЕ
// Random-mutation #2: несколько координат
numModify = ceil(rand × p2 × dim)
map = все 1
выбрать numModify случайных координат и поставить 0
КОНЕЦ ЕСЛИ
e) Применить карту:
ДЛЯ d = 1..dim
ЕСЛИ map[d] == 0 ТОГДА
x[i][d] = stopover[d] // изменить
ИНАЧЕ
x[i][d] = xPrev[i][d] // оставить старое
КОНЕЦ ЕСЛИ
КОНЕЦ ДЛЯ
f) Проверить границы:
ДЛЯ d = 1..dim
ЕСЛИ x[i][d] выходит за bounds ТОГДА
ЕСЛИ rand < 0.5 ТОГДА
x[i][d] = случайное в пределах bounds
ИНАЧЕ
x[i][d] = ближайшая граница
КОНЕЦ ЕСЛИ
КОНЕЦ ЕСЛИ
КОНЕЦ ДЛЯ
КОНЕЦ ДЛЯ
2.3. Вычислить фитнес для всех новых позиций
ДЛЯ i = 1..popSize
f[i] = фитнес(x[i])
КОНЕЦ ДЛЯ
2.4. Селекция (жадный отбор)
ДЛЯ i = 1..popSize
ЕСЛИ f[i] > fPrev[i] ТОГДА
// принять новую позицию (уже в x[i])
ИНАЧЕ
// откатиться к старой
x[i] = xPrev[i]
f[i] = fPrev[i]
КОНЕЦ ЕСЛИ
КОНЕЦ ДЛЯ
2.5. Обновить глобальное лучшее
ЕСЛИ max(f) > fBest ТОГДА
xBest = x[индекс max(f)]
fBest = max(f)
КОНЕЦ ЕСЛИ
КОНЕЦ ЦИКЛА
ВЕРНУТЬ xBest, fBest
Теперь можем приступить к самой реализации в коде. Структура данных под названием "S_DSA_Map" служит для управления информацией об "активных" объектах, связанных с определенным количеством "координат". Основной частью этой структуры является массив, который называется "active". Размер этого массива не фиксирован при объявлении, что позволяет ему адаптироваться. По сути, каждый элемент этого массива будет соответствовать одной "координате". Информация, хранящаяся в каждом элементе "active", изначально равна нулю, что подразумевает неактивное состояние по умолчанию.
Структура также содержит функцию "Init", которая служит для инициализации. При вызове функции, ей передается число, представляющее общее количество "координат", затем она настраивает массив "active" так, чтобы он имел соответствующий размер, то есть количество элементов будет равно переданному значению "координат". После чего, она гарантирует, что все элементы этого массива будут установлены в значение ноль.
//—————————————————————————————————————— —————————————————————————————— struct S_DSA_Map { int active []; // map of active individuals for each coordinate void Init (int coords) { ArrayResize (active, coords); ArrayInitialize (active, 0); } }; //————————————————————————————————————————————————————————————————————
Класс "C_AO_DSA" является производным от базового класса "C_AO" и предназначен для реализации алгоритма дифференциального поиска.
Параметры алгоритма:
- popSize — размер популяции.
- method — выбор используемого метода дифференциального поиска. По умолчанию установлен в 1, что соответствует методу "B-DSA". Возможны значения: 1 (B-DSA), 2 (S-DSA), 3 (E1-DSA), 4 (E2-DSA).
- p1 — контрольный параметр для стратегии мутации.
- p2 — второй контрольный параметр для стратегии мутации.
Конструктор класса инициализирует внутреннюю структуру "params", в которую записываются имена и текущие значения "popSize", "method", "p1" и "p2". Метод "SetParams" отвечает за обновление значений параметров выше данных на основе структуры "params". После получения новых значений, метод производит проверку и корректировку параметров, чтобы они находились в допустимых пределах.
Основные методы:
- Init— для инициализации алгоритма. Он принимает диапазоны и шаг поиска, а также количество эпох (итераций),
- Moving — отвечает за перемещение и обновление объектов в рамках алгоритма,
- Revision — используется для пересмотра или коррекции решений.
Приватные данные и методы:
- direction— массив, хранящий информацию об "агентах" (элементах популяции) и их направлениях,
- mapArray— массив структур "S_DSA_Map", которые, как описано в предыдущем разделе, предназначены для управления состоянием активных элементов по координатам,
- InitializePopulation— метод для создания начальной популяции,
- GenerateDirection— метод для генерации направлений движения агентов, зависящий от выбранного "methodType",
- GenerateMap— метод для генерации карты "S_DSA_Map",
- GenerateScaleFactor — метод для генерации масштабирующего фактора, который используется в мутациях,
- GammaRandom— метод для генерации случайных чисел из гамма-распределения с заданными параметрами формы и масштаба,
- BoundaryControl— метод для контроля выхода объектов за установленные границы, с применением указанного индекса.
В целом, "C_AO_DSA" представляет собой реализацию алгоритма дифференциального поиска, позволяющую настраивать различные аспекты его работы, такие как размер популяции, применяемый метод мутации и параметры контролирующих переменных.
//———————————————————————————————————————————————————————————————————— class C_AO_DSA : public C_AO { public: ~C_AO_DSA () { } C_AO_DSA () { ao_name = "DSA"; ao_desc = "Differential Search Algorithm"; ao_link = "https://www.mql5.com/ru/articles/20346"; popSize = 50; method = 1; // 1-B-DSA, 2-S-DSA, 3-E1-DSA, 4-E2-DSA p1 = 0.3; // mutation strategy control [0.0, 0.3] p2 = 0.3; // mutation strategy control [0.0, 0.3] ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "method"; params [1].val = method; params [2].name = "p1"; params [2].val = p1; params [3].name = "p2"; params [3].val = p2; } void SetParams () { popSize = (int)params [0].val; method = (int)params [1].val; p1 = params [2].val; p2 = params [3].val; if (method < 1) method = 1; if (method > 4) method = 4; if (p1 < 0.0) p1 = 0.0; if (p1 > 0.3) p1 = 0.3; if (p2 < 0.0) p2 = 0.0; if (p2 > 0.3) p2 = 0.3; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP); void Moving (); void Revision (); //------------------------------------------------------------------ int method; double p1; double p2; private: //--------------------------------------------------------- S_AO_Agent direction []; S_DSA_Map mapArray []; void InitializePopulation (); void GenerateDirection (int methodType); void GenerateMap (); double GenerateScaleFactor (); double GammaRandom (double shape, double scale); void BoundaryControl (int idx); }; //————————————————————————————————————————————————————————————————————
Функция инициализации "Init" для класса "C_AO_DSA". Сначала вызывается функция "StandardInit" которая, выполняет общие шаги инициализации, необходимые для всех алгоритмов, основанных на "C_AO". Если эта базовая инициализация завершается неудачно, функция класса немедленно прекращает работу и возвращает ложное значение.
Инициализация массива направлений. Создается массив "direction", размер которого определяется переменной "popSize" (размер популяции). Затем, для каждого элемента в этом массиве "direction", вызывается его собственный метод "Init". При этом каждому элементу передается значение "coords", которое представляет количество "координат", используемых в алгоритме.
Инициализация массива карт. Создается массив "mapArray", также имеющий размер, равный "popSize". Аналогично массиву "direction", для каждого элемента в "mapArray" вызывается его метод "Init". И в этом случае передается значение "coords", что позволяет правильно настроить структуру "S_DSA_Map" для каждого элемента. Если все предыдущие шаги успешно выполнены, функция "Init" возвращает истинное значение.
//———————————————————————————————————————————————————————————————————— bool C_AO_DSA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ ArrayResize (direction, popSize); for (int i = 0; i < popSize; i++) direction [i].Init (coords); ArrayResize (mapArray, popSize); for (int i = 0; i < popSize; i++) mapArray [i].Init (coords); return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" класса "C_AO_DSA" отвечает за основную логику движения агентов (представителей популяции) в процессе работы алгоритма дифференциального поиска.
Инициализация популяции (при первой итерации). Если флаг "revision" установлен в ложное значение (что означает, что это первая итерация), то вызывается метод "InitializePopulation" для создания начальной популяции агентов. После этого флаг "revision" устанавливается в истинное значение, и выполнение метода завершается до следующей итерации.
Сохранение текущего состояния. На каждой последующей итерации (когда "revision" истинно) происходит сохранение текущих координат "c" и их значений функции приспособленности "f" для каждого агента. Сохраненные координаты помещаются в массив "cP" (предыдущие координаты), а значения приспособленности — в "fP".
Генерация направления и масштабирующего коэффициента. Вызывается метод "GenerateDirection", он определяет "направление" для каждого агента. Выбор конкретной стратегии генерации направления осуществляется на основе параметра "method". Затем вызывается метод "GenerateScaleFactor" для получения масштабирующего коэффициента. Этот коэффициент влияет на величину шага смещения.
Вычисление новой позиции (предварительное). Для каждого агента и каждой координаты происходит вычисление новой предварительной позиции. Новая координата рассчитывается как: (предыдущая координата) + (масштабирующий коэффициент) * (разница между направлением и предыдущей координатой). Этот этап фактически формирует "кандидатскую" новую позицию.
Генерация карты активных/пассивных координат. Вызывается метод "GenerateMap". Этот метод, как было упомянуто ранее, создает структуру "mapArray", которая для каждого агента указывает, какие координаты являются "активными" (требуют обновления) и какие "пассивными" (должны оставаться неизменными).
Корректировка позиции с учетом карты и границ. Для каждого агента происходит проверка карты активных/пассивных координат. Если координата помечена как "активная", то ее новая позиция устанавливается обратно в значение предыдущей координаты. То есть, эта координата не обновляется. Если координата "пассивная", то новое значение, вычисленное на шаге 4, сохраняется. После корректировки координат вызывается метод "BoundaryControl" для каждого агента, чтобы убедиться, что все координаты находятся в допустимых пределах поиска.
Таким образом, метод "Moving" моделирует один шаг эволюции популяции, где агенты генерируют новые потенциальные позиции, которые затем модифицируются и ограничиваются в соответствии с заданными правилами и параметрами алгоритма.
//———————————————————————————————————————————————————————————————————— void C_AO_DSA::Moving () { //------------------------------------------------------------------ // Первая итерация: инициализация популяции if (!revision) { InitializePopulation (); revision = true; return; } //------------------------------------------------------------------ // Сохраняем текущие координаты и фитнес в cP и fP for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, coords); a [i].fP = a [i].f; } //------------------------------------------------------------------ // Генерация направления на основе cP (старых координат) GenerateDirection (method); // Генерация Scale-Factor double scale = GenerateScaleFactor (); //------------------------------------------------------------------ // Вычисляем stopover site и записываем в c for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double diff = direction [i].c [c] - a [i].cP [c]; a [i].c [c] = a [i].cP [c] + scale * diff; } } //------------------------------------------------------------------ // Генерация карты активных/пассивных координат GenerateMap (); //------------------------------------------------------------------ // Восстанавливаем координаты где map > 0 (сохранить оригинальные) for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (mapArray [i].active [c] > 0) { a [i].c [c] = a [i].cP [c]; } } // Контроль границ BoundaryControl (i); } } //————————————————————————————————————————————————————————————————————
Метод "InitializePopulation" класса "C_AO_DSA". Его основная задача — создать и инициализировать начальное состояние популяции агентов. Метод проходит по каждому агенту в популяции, от первого до последнего (количество агентов определяется переменной "popSize"). Для каждого агента метод последовательно обрабатывает все его координаты. Для каждой координаты текущего агента генерируется случайное число в пределах заданного диапазона (от "rangeMin" до "rangeMax"). Это делается с помощью функции "u.RNDfromCI".
Полученное случайное значение затем проходит дополнительную корректировку с помощью функции "u.SeInDiSp". Скорректированное значение присваивается соответствующей координате "c" текущего агента. Таким образом, "InitializePopulation" отвечает за генерацию начальной, случайной, но при этом корректной (в рамках заданных диапазонов и шагов) конфигурации каждого агента в популяции, готовя ее к дальнейшей работе алгоритма.
//———————————————————————————————————————————————————————————————————— void C_AO_DSA::InitializePopulation () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Следующий метод "GenerateDirection" класса "C_AO_DSA" отвечает за определение вектора направления для каждого агента в популяции. Метод принимает параметр "methodType", который определяет, какой именно алгоритм поиска направления будет использован. Различные стратегии генерации направления (в зависимости от "methodType"):
Тип 1: B-DSA (Bijective) - Случайная перестановка:- Создается массив индексов, соответствующий всем агентам.
- Применяется алгоритм перемешивания Фишера-Йетса, чтобы случайно переупорядочить эти индексы.
- Для каждого агента в популяции его вектор направления "direction" устанавливается равным координатам агента, чей индекс оказался на соответствующей позиции после случайной перестановки.
- Цель: каждый агент "смотрит" в сторону другого случайного агента.
- Создается массив индексов агентов.
- Агенты сортируются в порядке убывания их приспособленности "fP".
- Для каждого агента случайным образом определяется число "лучших" агентов (topCount), из которых будет выбран кандидат. Из этой группы "лучших" случайным образом выбирается один агент. Вектор направления текущего агента устанавливается равным предыдущим координатам (cP) выбранного "лучшего" агента.
- Цель: агенты "стремятся" к случайным выборам из более успешных агентов.
- Аналогично типу 2, агенты сортируются по убыванию приспособленности.
- Случайным образом определяется группа "лучших" агентов (topCount).
- Из этой группы выбирается один случайный "лучший" агент.
- Все агенты популяции устанавливают свой вектор направления равным предыдущим координатам этого единственного выбранного "лучшего" агента.
- Цель: все агенты "ориентируются" на случайно выбранного, но все еще из лучших, агента.
- Находится агент с наилучшей приспособленностью (bestIdx).
- Все агенты популяции устанавливают свой вектор направления равным предыдущим координатам этого абсолютно-лучшего агента.
- Цель: все агенты "копируют" или "стремятся" к самому сильному представителю популяции.
Таким образом, метод "GenerateDirection" реализует различные стратегии "обмена информацией" или "ориентации" между агентами, позволяя алгоритму исследовать пространство поиска, опираясь на информацию о лучших или случайно выбранных участниках популяции.
//———————————————————————————————————————————————————————————————————— void C_AO_DSA::GenerateDirection (int methodType) { // Используем cP (старые координаты) для генерации направления switch (methodType) { case 1: // B-DSA (Bijective) - случайная перестановка { int indices []; ArrayResize (indices, popSize); for (int i = 0; i < popSize; i++) indices [i] = i; // Fisher-Yates shuffle for (int i = popSize - 1; i > 0; i--) { int j = u.RNDminusOne (i + 1); int temp = indices [i]; indices [i] = indices [j]; indices [j] = temp; } for (int i = 0; i < popSize; i++) { ArrayCopy (direction [i].c, a [indices [i]].cP, 0, 0, coords); } break; } case 2: // S-DSA (Surjective) - к случайным лучшим { int sortedIdx []; ArrayResize (sortedIdx, popSize); for (int i = 0; i < popSize; i++) sortedIdx [i] = i; // Сортировка по fP (старому фитнесу) по убыванию for (int i = 0; i < popSize - 1; i++) { for (int j = 0; j < popSize - i - 1; j++) { if (a [sortedIdx [j]].fP < a [sortedIdx [j + 1]].fP) { int temp = sortedIdx [j]; sortedIdx [j] = sortedIdx [j + 1]; sortedIdx [j + 1] = temp; } } } for (int i = 0; i < popSize; i++) { int topCount = (int)MathCeil (u.RNDfromCI (0.0, 1.0) * popSize); if (topCount < 1) topCount = 1; int selectedIdx = sortedIdx [u.RNDminusOne (topCount)]; ArrayCopy (direction [i].c, a [selectedIdx].cP, 0, 0, coords); } break; } case 3: // E1-DSA (Elitist #1) - к одному случайному из лучших { int sortedIdx []; ArrayResize (sortedIdx, popSize); for (int i = 0; i < popSize; i++) sortedIdx [i] = i; for (int i = 0; i < popSize - 1; i++) { for (int j = 0; j < popSize - i - 1; j++) { if (a [sortedIdx [j]].fP < a [sortedIdx [j + 1]].fP) { int temp = sortedIdx [j]; sortedIdx [j] = sortedIdx [j + 1]; sortedIdx [j + 1] = temp; } } } int topCount = (int)MathCeil (u.RNDfromCI (0.0, 1.0) * popSize); if (topCount < 1) topCount = 1; int bestIdx = sortedIdx [u.RNDminusOne (topCount)]; for (int i = 0; i < popSize; i++) { ArrayCopy (direction [i].c, a [bestIdx].cP, 0, 0, coords); } break; } case 4: // E2-DSA (Elitist #2) - к самому лучшему { int bestIdx = 0; double bestFit = a [0].fP; for (int i = 1; i < popSize; i++) { if (a [i].fP > bestFit) { bestFit = a [i].fP; bestIdx = i; } } for (int i = 0; i < popSize; i++) { ArrayCopy (direction [i].c, a [bestIdx].cP, 0, 0, coords); } break; } } } //————————————————————————————————————————————————————————————————————
Метод "GenerateMap" предназначен для создания "карты" мутаций, которые будут применяться к популяции агентов. Эта карта определяет, какие координаты каких агентов будут подвержены изменениям. Генерируются две случайные переменные. Перед определением специфических мутаций, для всех мест в "карте" устанавливается значение "0".
Основное условие выбора стратегии мутации. Сравнивается два случайных числа, генерируемых в диапазоне [0.0, 1.0] одно с другим. Вероятность выполнения основного условия (т.е. "true") составляет 0.5, это означает, что выбор между двумя основными ветками алгоритма (первая с двумя под-ветками "Random-mutation #1" и "Differential-mutation", и вторая "Random-mutation #2") происходит случайным образом с вероятностью 50%.
Случай 1: Random-mutation #1. Для каждого агента и каждой его координаты, генерируется еще одно случайное число. Если оно меньше другого случайного числа, то "mapArray [i].active [c]" устанавливается в "1". Опять же, сравнение двух случайных чисел означает, что активация каждой отдельной координаты происходит с вероятностью 0.5. Цель: случайным образом активировать (помечать для мутации) отдельные координаты у разных агентов.
-
Differential-mutation (иначе): Для каждого агента "mapArray [i].active" целиком инициализируется как "1" (все координаты активны для мутации). Затем случайным образом выбирается одна координата (modifyCoord) у каждого агента, и для этой конкретной координаты "mapArray [i].active [modifyCoord]" устанавливается в "0" (отключается). Цель: у каждого агента мутирует только одна, случайно выбранная координата.
Случай 2: Random-mutation #2. Определяется количество координат (numModify) для мутации для каждого агента. Оно зависит от "p2_iter" и общего количества координат. Количество ограничивается в разумных пределах (от "1" до "coords"). Для каждого агента "mapArray [i].active" целиком инициализируется как "1". Затем "numModify" раз случайно выбираются координаты, и для них "mapArray [i].active [modifyCoord]" устанавливается в "0". Цель: у каждого агента мутирует фиксированное (но случайное) количество координат.
Метод GenerateMap отвечает за установку масок мутаций. Он генерирует структуру "mapArray", которая для каждого агента содержит информацию о том, какие его координаты должны быть изменены. Алгоритм предлагает несколько различных стратегий для создания этой маски, что позволяет варьировать процесс исследования пространства поиска — от случайного применения мутаций к отдельным координатам до более целенаправленных изменений.
//———————————————————————————————————————————————————————————————————— void C_AO_DSA::GenerateMap () { double p1_iter = u.RNDfromCI (0.0, p1); double p2_iter = u.RNDfromCI (0.0, p2); for (int i = 0; i < popSize; i++) { ArrayInitialize (mapArray [i].active, 0); } if (u.RNDfromCI (0.0, 1.0) < u.RNDfromCI (0.0, 1.0)) { if (u.RNDfromCI (0.0, 1.0) < p1_iter) { // Random-mutation #1 for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDfromCI (0.0, 1.0) < u.RNDfromCI (0.0, 1.0)) { mapArray [i].active [c] = 1; } } } } else { // Differential-mutation for (int i = 0; i < popSize; i++) { ArrayInitialize (mapArray [i].active, 1); int modifyCoord = u.RNDminusOne (coords); mapArray [i].active [modifyCoord] = 0; } } } else { // Random-mutation #2 int numModify = (int)MathCeil (p2_iter * coords); if (numModify < 1) numModify = 1; if (numModify > coords) numModify = coords; for (int i = 0; i < popSize; i++) { ArrayInitialize (mapArray [i].active, 1); for (int k = 0; k < numModify; k++) { int modifyCoord = u.RNDminusOne (coords); mapArray [i].active [modifyCoord] = 0; } } } } //————————————————————————————————————————————————————————————————————
Функция "GenerateScaleFactor" класса "C_AO_DSA" генерирует масштабный коэффициент (scale factor). Этот метод генерирует масштабирующий множитель, который, используется для контроля "длины" шага, совершаемого агентами. Использование распределения Гамма и случайных чисел позволяет ввести разнообразие в величину и направление этого шага, что может помочь алгоритму более эффективно исследовать пространство поиска, избегая локальных минимумов и находить глобальный оптимум.
- rand1 — влияет на "форму" распределения Гамма, делая его более "широким" или "узким" в зависимости от его значения.
- gamma_val — само по себе является случайным положительным числом, распределение которого зависит от "rand1".
- rand2 - rand3 — определяет знак и относительную величину масштабирующего коэффициента. Результат может быть положительным (если rand2 > rand3) или отрицательным (если rand2 < rand3).
В итоге "GenerateScaleFactor" выдает "случайный по величине и направлению" множитель, который применяется к вектору направления для формирования вектора шага.
//———————————————————————————————————————————————————————————————————— double C_AO_DSA::GenerateScaleFactor () { double rand1 = u.RNDfromCI (0.0, 1.0); double rand2 = u.RNDfromCI (0.0, 1.0); double rand3 = u.RNDfromCI (0.0, 1.0); double shape = 2.0 * rand1; double gamma_val = GammaRandom (shape, 1.0); return gamma_val * (rand2 - rand3); } //————————————————————————————————————————————————————————————————————
Далее идет реализация функции "GammaRandom", которая генерирует случайные числа, распределенные по гамма-распределению (Gamma distribution). Распределение Гамма является важным распределением вероятностей, оно моделирует время ожидания до завершения некоторого числа независимых событий, каждое из которых происходит с некоторой средней скоростью. Оно имеет два параметра:
- shape (форма) — определяет форму распределения,
- scale (масштаб) — определяет, насколько "растянуто" распределение.
В DSA используется для создания псевдо-стабильного блуждания — специального паттерна движения, где часто встречаются маленькие шаги и редко — большие прыжки. Функция "GammaRandom" реализует Алгоритм реализации (Marsaglia-Tsang, 2000). Метод отбора-отклонения (Rejection Sampling).
Назначение "GammaRandom"— эта функция является вспомогательной для алгоритма DSA, которая требует генерации чисел из распределения Гамма. Как было сказано ранее, в DSA распределение Гамма может использоваться при генерации масштабного коэффициента, что позволяет контролировать степень и направление шага агентов в пространстве поиска.
Рекурсивно вызываем функцию "с" (shape+1), затем умножаем на случайное число в степени (1/shape). Это уменьшает результат и смещает распределение к нулю. Случай 2: shape ≥ 1. Метод отбора-отклонения: вычисляем вспомогательные константы "d" и "c" из "shape", генерируем кандидата "x" из нормального распределения N(0,1), вычисляем v = (1 + c·x)³. Проверяем, можем ли принять кандидата. Быстрый тест: сравниваем случайное число с простым выражением. Точный тест: сравниваем логарифмы. Если принят — возвращаем (d·v·scale). Если отклонён — повторяем с шага 2. Защиты:
- минимальный shape = 0.01 (избегаем деления на ноль)
- проверка v > 0 перед возведением в куб
- защита от log(0)
- максимум 100 итераций (на случай невезения)
//———————————————————————————————————————————————————————————————————— double C_AO_DSA::GammaRandom (double shape, double scale) { if (shape <= 0.0) return 1.0; if (shape < 0.01) shape = 0.01; if (shape < 1.0) { double gamma = GammaRandom (1.0 + shape, scale); double u_rand = u.RNDfromCI (1e-10, 1.0); return gamma * MathPow (u_rand, 1.0 / shape); } double d = shape - 1.0 / 3.0; double c = 1.0 / MathSqrt (9.0 * d); int maxIter = 100; int iter = 0; while (iter < maxIter) { iter++; double x, v; do { x = u.GaussDistribution (0.0, 1.0, -10.0, 10.0); v = 1.0 + c * x; } while (v <= 0.0); v = v * v * v; double u_rand = u.RNDfromCI (1e-10, 1.0); double x_sq = x * x; if (u_rand < 1.0 - 0.0331 * x_sq * x_sq) { return scale * d * v; } if (MathLog (u_rand) < 0.5 * x_sq + d * (1.0 - v + MathLog (v))) { return scale * d * v; } } return scale * d; } //————————————————————————————————————————————————————————————————————
Функция "BoundaryControl" предназначена для контроля границ (boundary control) для конкретного агента. Ее цель — убедиться, что координаты каждого агента остаются в пределах допустимого диапазона.
Зачем нужна такая обработка границ?
В алгоритмах оптимизации, особенно основанных на популяциях (как DSA), агенты перемещаются в пространстве поиска. Нередко при вычислении нового положения агента, его координаты могут выйти за пределы допустимого диапазона, который определяется постановкой задачи. Функция "BoundaryControl" гарантирует, что:
- агенты остаются в физически или логически допустимой области;
- предотвращаются некорректные вычисления в последующих итерациях, которые могут быть вызваны выходом за пределы;
- наличие вероятностной подстановки (u.RNDfromCI (rangeMin [c], rangeMax [c])) вместо простого "отражения" или "срезания" может помочь избежать образования "кластеров" агентов именно на границах, способствуя более полному исследованию пространства.
//———————————————————————————————————————————————————————————————————— void C_AO_DSA::BoundaryControl (int idx) { for (int c = 0; c < coords; c++) { if (a [idx].c [c] < rangeMin [c]) { if (u.RNDprobab () < 0.5) { a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { a [idx].c [c] = rangeMin [c]; } } if (a [idx].c [c] > rangeMax [c]) { if (u.RNDprobab () < 0.5) { a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); } else { a [idx].c [c] = rangeMax [c]; } } a [idx].c [c] = u.SeInDiSp (a [idx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Функция "Revision" выполняет два основных шага после генерации новых положений для агентов в алгоритме: селекцию для определения, какие из новых положений будут сохранены, и обновление глобального лучшего решения.
Шаг 1: Селекция (Оценка новых решений). Для каждого агента в популяции сравнивается значение его новой позиции (насколько она "хороша" или "приспособлена") со значением его предыдущей позиции. Если новая позиция оказалась не лучше (то есть, либо равна по качеству, либо хуже) предыдущей, то агент возвращается к своему старому, более выгодному положению. Это означает, что сохраняются только те шаги, которые привели к улучшению. Если у агента не было валидного предыдущего положения, это условие не применяется.
Шаг 2: Обновление глобального лучшего. После того как все агенты определились, какое положение им сохранить, функция ищет среди всех текущих позиций агентов ту, которая обладает наилучшим качеством (наивысшим показателем приспособленности). Затем это качество сравнивается с наилучшим качеством, которое было зафиксировано за всё время работы алгоритма. Если текущая лучшая позиция в популяции превосходит ранее найденное абсолютное лучшее решение, оно становится новым глобальным лучшим решением, и местоположение этого лучшего решения запоминается.
//———————————————————————————————————————————————————————————————————— void C_AO_DSA::Revision () { //------------------------------------------------------------------ // Селекция: принять только если новый фитнес лучше старого for (int i = 0; i < popSize; i++) { // Если новый фитнес (f) НЕ лучше старого (fP) - восстанавливаем if (a [i].f <= a [i].fP && a [i].fP != -DBL_MAX) { a [i].f = a [i].fP; ArrayCopy (a [i].c, a [i].cP, 0, 0, coords); } } //------------------------------------------------------------------ // Обновление глобального лучшего int bestIdx = 0; double bestFit = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f > bestFit) { bestFit = a [i].f; bestIdx = i; } } if (bestFit > fB) { fB = bestFit; ArrayCopy (cB, a [bestIdx].c, 0, 0, coords); } } //————————————————————————————————————————————————————————————————————
Результаты тестов
В результатах показываем возможности всех 4 методов, которые у нас присутствуют в настройках. Как можно заметить, второй метод набирает наибольшее значение, когда каждая особь движется к случайному решению из топ-N лучших.
DSA|Differential Search Algorithm|50.0|1.0|0.3|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.6982999549366771
25 Hilly's; Func runs: 10000; result: 0.4112441157981344
500 Hilly's; Func runs: 10000; result: 0.26639110224055546
=============================
5 Forest's; Func runs: 10000; result: 0.7546811566849957
25 Forest's; Func runs: 10000; result: 0.33583122216029415
500 Forest's; Func runs: 10000; result: 0.18324446089620824
=============================
5 Megacity's; Func runs: 10000; result: 0.5538461538461539
25 Megacity's; Func runs: 10000; result: 0.2156923076923077
500 Megacity's; Func runs: 10000; result: 0.10643076923077019
=============================
All score: 3.52566 (39.17%)
1 (B-DSA)
DSA|Differential Search Algorithm|50.0|2.0|0.3|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.75651834013058
25 Hilly's; Func runs: 10000; result: 0.420539560652641
500 Hilly's; Func runs: 10000; result: 0.2673297720453783
=============================
5 Forest's; Func runs: 10000; result: 0.8226119802254519
25 Forest's; Func runs: 10000; result: 0.3408987112971432
500 Forest's; Func runs: 10000; result: 0.18471282959506144
=============================
5 Megacity's; Func runs: 10000; result: 0.5323076923076923
25 Megacity's; Func runs: 10000; result: 0.22153846153846152
500 Megacity's; Func runs: 10000; result: 0.10521538461538557
=============================
All score: 3.65167 (40.57%)
2 (S-DSA)
DSA|Differential Search Algorithm|50.0|3.0|0.3|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.704394194121553
25 Hilly's; Func runs: 10000; result: 0.415864841547213
500 Hilly's; Func runs: 10000; result: 0.26675670523279044
=============================
5 Forest's; Func runs: 10000; result: 0.8200531047825427
25 Forest's; Func runs: 10000; result: 0.3345381783754753
500 Forest's; Func runs: 10000; result: 0.18518322851491886
=============================
5 Megacity's; Func runs: 10000; result: 0.49846153846153846
25 Megacity's; Func runs: 10000; result: 0.21846153846153848
500 Megacity's; Func runs: 10000; result: 0.1064307692307701
=============================
All score: 3.55014 (39.45%)
3 (E1-DSA)
DSA|Differential Search Algorithm|50.0|4.0|0.3|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.7184577016736993
25 Hilly's; Func runs: 10000; result: 0.4114617093550586
500 Hilly's; Func runs: 10000; result: 0.2650947599954659
=============================
5 Forest's; Func runs: 10000; result: 0.8159647894070122
25 Forest's; Func runs: 10000; result: 0.3307842077432657
500 Forest's; Func runs: 10000; result: 0.18482144990330598
=============================
5 Megacity's; Func runs: 10000; result: 0.4800000000000001
25 Megacity's; Func runs: 10000; result: 0.20769230769230776
500 Megacity's; Func runs: 10000; result: 0.10500000000000091
=============================
All score: 3.51928 (39.10%)
4 (E2-DSA)
На визуализации алгоритм DSA работает достаточно кучно, без сильного разброса, качество сходимости хотелось бы видеть лучшим на функциях малой размерности.

DSA на тестовой функции Hilly

DSA на тестовой функции Forest

DSA на тестовой функции Megacity
Для задач на стандартных тестовых функциях алгоритм хорошо себя показывает, высокая сходимость и небольшой разброс результатов.

DSA на стандартной тестовой функции Paraboloid

DSA на стандартной тестовой функции GoldsteinPrice
В рейтинговой таблице алгоритм DSA представлен ознакомительно.
| Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||
| dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| bonobo_optimizer | 0,77565 | 0,63805 | 0,32908 | 1,74278 | 0,88088 | 0,76344 | 0,25573 | 1,90005 | 0,61077 | 0,49846 | 0,14246 | 1,25169 | 4,895 | 54,38 |
| chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| differential _search_algorithm | 0,75651 | 0,42054 | 0,26733 | 1,44438 | 0,82261 | 0,34090 | 0,18471 | 1,34822 | 0,53231 | 0,22154 | 0,10521 | 0,85906 | 3,652 | 40,57 |
| random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 |
Выводы
Алгоритм дифференциального поиска DSA демонстрирует среднюю результативность на тестовых задачах оптимизации. При использовании стратегии S-DSA, где каждая особь движется к случайному решению из топ-N лучших, алгоритм набирает чуть более 40% производительности относительно эталонных значений. Данная стратегия обеспечивает наилучший баланс между исследованием пространства поиска и эксплуатацией найденных решений. Остальные три стратегии генерации направления показывают незначительно худшие результаты с отставанием в пределах 1.5%, что говорит об относительной устойчивости алгоритма к выбору параметров.
При тестировании на задачах малой, средней и высокой размерности алгоритм, к сожалению, не набирает достаточного количества баллов для попадания в рейтинговую таблицу лучших методов оптимизации. Тем не менее DSA показывает стабильную и надёжную работу, уверенно справляясь со стандартными тестовыми функциями и находя решения приемлемого качества.
Средняя производительность DSA может объясняться несколькими факторами. Во-первых, использование гамма-распределения для генерации размера шага, хотя и обеспечивает теоретически обоснованное псевдо-стабильное блуждание, на практике может приводить к недостаточно агрессивному исследованию пространства поиска на ранних итерациях. Во-вторых, механизм частичного изменения координат через карту мутации, меняя лишь одну или несколько координат за итерацию, замедляет сходимость в многомерных пространствах, где для достижения оптимума требуется одновременная коррекция множества переменных. В-третьих, жадный отбор, при котором любое ухудшение решения отклоняется, может приводить к преждевременной сходимости и застреванию в локальных оптимумах.
К достоинствам алгоритма следует отнести концептуальную простоту и интуитивно понятную метафору миграции суперорганизма, небольшое количество настраиваемых параметров, устойчивость результатов при различных настройках, а также гарантированное сохранение лучших найденных решений благодаря элитарной селекции.
Алгоритм может быть рекомендован для практических задач, где не требуется максимальная точность, а важны простота реализации и предсказуемость поведения. DSA хорошо подходит для предварительной оптимизации с последующим уточнением другими методами, для задач с ограниченным вычислительным бюджетом, где важна стабильность результата, а также для образовательных целей, как наглядный пример метаэвристического алгоритма с чётко разделёнными компонентами исследования и эксплуатации.
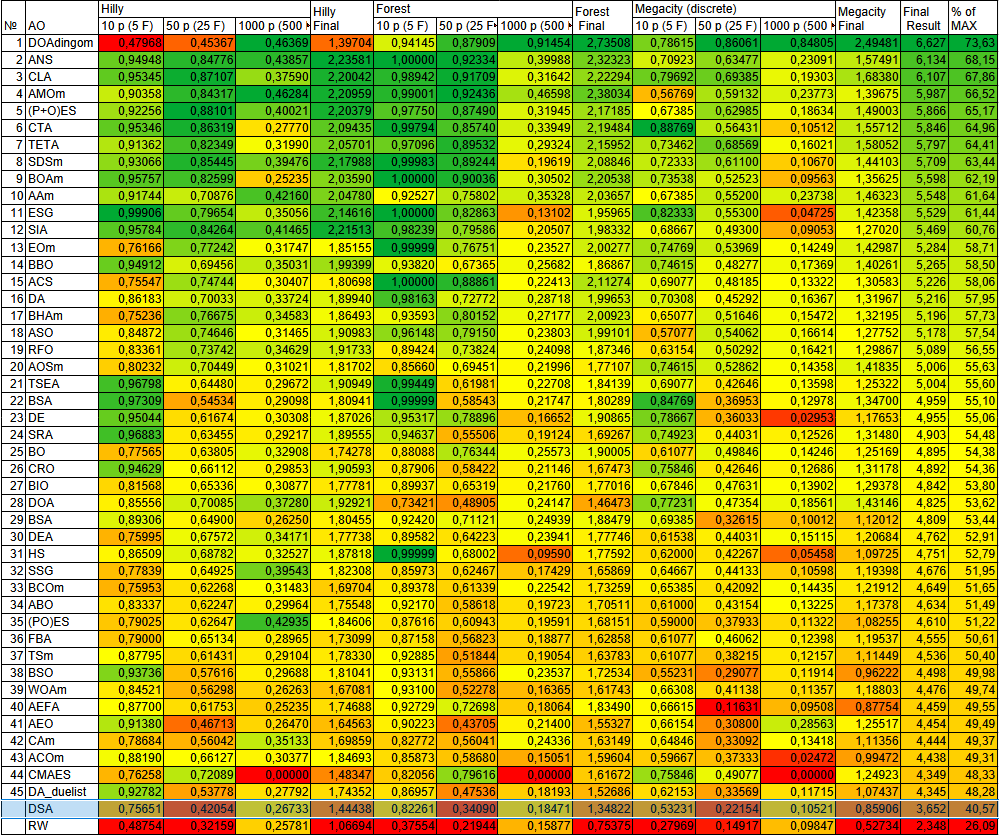
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
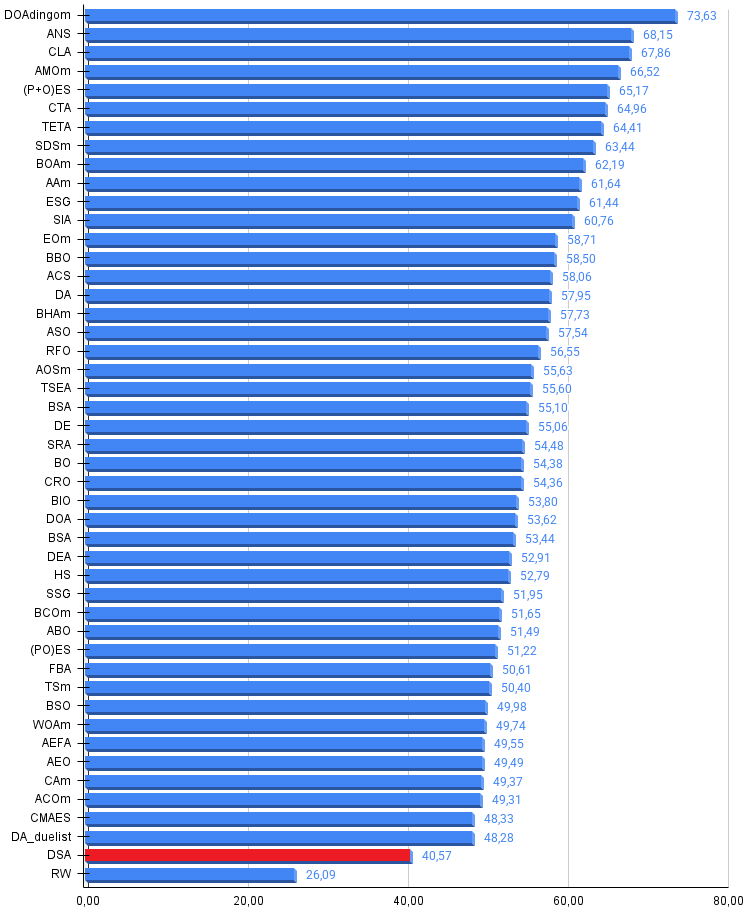
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма DSA:
Плюсы:
- Быстрый.
- Небольшой разброс результатов по запускам.
- Лучшие результаты на функциях средней и большой размерности.
Минусы:
- Более слабые результаты на функциях малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_DSA.mq5 | Скрипт | Испытательный стенд для DSA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Знакомство с языком MQL5 (Часть 15): Руководство для начинающих по созданию пользовательских индикаторов (IV)
Знакомство с языком MQL5 (Часть 15): Руководство для начинающих по созданию пользовательских индикаторов (IV)
 Знакомство с языком MQL5 (Часть 14): Руководство для начинающих по созданию пользовательских индикаторов (III)
Знакомство с языком MQL5 (Часть 14): Руководство для начинающих по созданию пользовательских индикаторов (III)
 Нейросети в трейдинге: Пространственно-временная модель состояния для анализа финансовых данных (STSSM-блок)
Нейросети в трейдинге: Пространственно-временная модель состояния для анализа финансовых данных (STSSM-блок)
 Моделирование рынка (Часть 16): Сокеты (X)
Моделирование рынка (Часть 16): Сокеты (X)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования