MetaTrader 5 / Трейдинг
preview
Детерминированный алгоритм дендритных клеток — Deterministic Dendritic Cell Algorithm (dDCA)

Детерминированный алгоритм дендритных клеток — Deterministic Dendritic Cell Algorithm (dDCA)

MetaTrader 5 — Трейдинг |
141 0
Andrey Dik
Andrey Dik

Содержание

  1. Введение
  2. Реализация алгоритма
  3. Результаты тестов
  4. Выводы


Введение

В данной работе предлагается адаптация Deterministic Dendritic Cell Algorithm для задач непрерывной оптимизации. Оригинальный dDCA применяется для обнаружения аномалий. Основная идея — переосмысление иммунологических концепций в терминах поиска.

Дендритные клетки становятся агентами, исследующими пространство решений. Сигналы опасности и безопасности отражают качество найденных решений. Механизм созревания определяет баланс между исследованием новых областей и эксплуатацией перспективных регионов. Предложенный подход сохраняет ключевые особенности оригинального dDCA — детерминированное распределение времени жизни, централизованную обработку сигналов и формулы расчёта контекста — адаптируя их для навигации в многомерном пространстве поиска.

Иммунная система человека — одна из наиболее эффективных адаптивных систем, созданных природой. Особый интерес среди её компонентов представляют дендритные клетки — специализированные клетки врождённого иммунитета. Они патрулируют ткани, накапливают сигналы из окружающей среды и принимают решения о характере обнаруженных объектов. Эта способность к интеграции разнородной информации легла в основу алгоритма дендритных клеток (Dendritic Cell Algorithm, DCA), предложенного Greensmith и коллегами в 2005 году.

Теоретическим фундаментом DCA служит Теория Опасности, сформулированная P. Matzinger в 1994 году. В отличие от классической парадигмы «своё-чужое», эта теория утверждает, что иммунная система реагирует не на чужеродность объекта, а на сигналы опасности от повреждённых клеток. Это объясняет толерантность к полезным бактериям кишечника (чужие, но безопасные) и аутоиммунные реакции (свои, но опасные).

Детерминированная версия алгоритма (dDCA), разработанная J. Greensmith and U. Aickelin в 2008 году, устранила стохастические элементы оригинала, обеспечив воспроизводимость результатов.



Реализация алгоритма

Дендритные клетки циркулируют по тканям организма, собирая два типа сигналов:

  • Сигналы опасности (Danger, D)  — молекулы, выделяемые повреждёнными или умирающими клетками. Представьте дым или звук разбитого стекла — это явные признаки проблемы.
  • Сигналы безопасности (Safe, S)  — молекулы, характерные для нормального функционирования тканей. Можно описать спокойной музыкой и обычным шумом толпы в торговом центре.

После накопления достаточного количества сигналов, дендритная клетка «созревает» и мигрирует в лимфоузел, где передаёт собранную информацию T-лимфоцитам. Критически важно, чтобы клетка созревала в одном из двух состояний:

  • Зрелая (Mature)  — если преобладали сигналы опасности. Такая клетка активирует иммунный ответ.
  • Полузрелая (Semi-mature)  — если преобладали сигналы безопасности. Такая клетка способствует толерантности.

Классическая иммунология учила, что иммунная система различает «своё» и «чужое». Однако это не объясняет многих явлений: почему бактерии в кишечнике не вызывают иммунного ответа (они чужие), а раковые клетки организм часто игнорирует (они свои)? Теория Опасности предлагает иной взгляд: иммунная система реагирует не на чужеродность, а на опасность. Главный вопрос не «Это своё или чужое?», а «Это опасно или безопасно?».

Простой пример: занозу в пальце организм воспринимает как угрозу не потому, что дерево «чужое», а потому, что повреждённые клетки вокруг занозы выделяют сигналы опасности. Те же молекулы дерева в виде бумаги, которую мы держим в руках, не вызывают реакции —нет повреждения, нет сигналов опасности.

Для адаптации dDCA к задачам оптимизации необходимо установить соответствие между иммунологическими и оптимизационными понятиями:

Иммунология
Оптимизация
Дендритная клетка
Агент поиска
Антиген (исследуемый объект)
Кандидатное решение
Сигнал опасности D
Индикатор плохого качества
Сигнал безопасности S
Индикатор хорошего качества
Созревание в Mature
Переход к локальному поиску
Созревание в Semi-mature
Переход к глобальному поиску
Время жизни клеткиПериод накопления статистики

Ключевая идея адаптации: качество решения определяет баланс сигналов D и S. Хорошие решения генерируют больше сигналов безопасности, плохие — больше сигналов опасности. Накопив статистику за несколько итераций, агент «понимает», находится ли он в перспективном регионе (стоит исследовать локально) или в бесперспективном (стоит переместиться в другое место).

Представьте, что вы ищете лучший ресторан в незнакомом городе. У вас есть команда из 50 друзей, каждый исследует свой район. Друг, попавший в район с хорошими ресторанами, получает положительные сигналы: приятные запахи, довольные посетители, высокие рейтинги в витринах. Он накапливает «безопасные» впечатления и решает исследовать этот район подробнее — заглянуть в соседние переулки, попробовать разные заведения поблизости.

Друг, оказавшийся в промышленной зоне, получает негативные сигналы: нет ресторанов, пустые улицы, неприятные запахи. Он накапливает «опасные» впечатления и решает покинуть этот район — переехать в совершенно другую часть города. Важно, что решение принимается не мгновенно, а после накопления опыта. Один плохой ресторан в хорошем районе не заставит вашего друга уехать. Аналогично, один случайно найденный приличный ресторан в плохом районе не означает, что весь район перспективен.

Каждый агент (дендритная клетка) характеризуется набором параметров Агент i:

  • c[i] — текущая позиция (кандидатное решение)
  • f[i] — значение фитнес-функции
  • lifespan — оставшееся время жизни
  • k_acc — накопленный контекст
  • iterations — количество пройденных итераций

Одна из ключевых особенностей dDCA — детерминированное назначение времени жизни клеткам. В отличие от случайного распределения, время жизни назначается равномерно:

lsi = i × lsmax / N, i = 1, 2, …, N; где N — размер популяции, lsmax — максимальное время жизни.

Пример. При N = 50 и lsmax = 20:

  • Агент 1: время жизни = 0.4
  • Агент 10: время жизни = 4.0
  • Агент 25: время жизни = 10.0
  • Агент 50: время жизни = 20.0

Это обеспечивает равномерное распределение моментов созревания во времени. В любой момент часть агентов только начала накапливать информацию, часть находится в середине цикла, а часть готова принять решение. Такая асинхронность может повысить устойчивость алгоритма.

На каждой итерации для каждого агента вычисляются сигналы на основе нормализованной приспособленности:

fnorm = (fi − fmin) / (fmax − fmin); где fmin и fmax — минимальное и максимальное значения фитнеса в текущей популяции.

Важно: предполагается задача минимизации. Агент с fnorm = 0 имеет лучшее решение в популяции, агент с fnorm = 1 - худшее. Сигналы опасности и безопасности: Di = fnorm × 50 Si = (1 − fnorm) × 50. Интерпретация: агент с худшим решением (fnorm = 1) получает D = 50, S = 0 - максимум опасности. Агент с лучшим решением (fnorm = 0) получает D = 0, S = 50 - максимум безопасности. Коэффициент 50 выбран для удобства: сумма сигналов всегда равна 100, что упрощает интерпретацию.

Контекст и созревание. Выходной сигнал (контекст) определяет характер созревания:

ki = Di − ws × Si; где ws — вес безопасного сигнала (по умолчанию 2.0).

fnorm
DSk (при ws = 2)
Интерпретация
0.0
0
50
−100
Лучший агент, сильно отрицательный k
0.33
16.5
33.5
−50.5
Хороший агент
0.67
33.5
16.5
0.5
Порог: k становится положительным
1.0
50
0
50
Худший агент, максимальный k

При ws = 2 порог находится на уровне fnorm = 2/3 ≈ 0.67. Это означает, что только худшие 33% популяции имеют положительный контекст. 

Контекст накапливается на протяжении жизни агента: kacc = kacc + ki; k̄ = kacc / iterations. Среднее значение k̄ сглаживает случайные флуктуации и даёт устойчивую оценку качества региона.

Стратегии перемещения. После вычисления накопленного контекста агент выбирает одну из трёх стратегий перемещения.

1. Локальная мутация (Mature). Если k̄ > 0, агент находится в перспективном регионе и выполняет локальный поиск: cnew = cold + μ × range × rand(−1, 1), где μ — коэффициент мутации (0.01), range — размах области поиска. Аналогия: вы нашли хороший район с ресторанами, теперь вы не уезжаете далеко, а обходите соседние улицы в поисках ещё лучшего заведения.

2. Направленное перемещение (Semi-mature, вариант 1). Если k̄ ≤ 0, агент склонен к исследованию.

С вероятностью (1 − preinit) выполняется направленное перемещение к лучшему известному решению: cnew = cold + r × (cbest − cold) + noise, где r ∈ [0, 1] — случайный коэффициент. Аналогия: ваш район оказался неудачным, но друг сообщил об отличном ресторане в другой части города, и вы движетесь в том направлении, попутно осматривая окрестности.

3. Глобальная реинициализация (Semi-mature, вариант 2). С вероятностью preinit = min(|k̄| / 50, 0.5) агент полностью реинициализируется: cnew = rand(cmin, cmax). Вероятность реинициализации пропорциональна силе негативного сигнала: чем хуже регион, тем выше шанс полного перезапуска. Аналогия: район настолько плох, что нет смысла двигаться постепенно, вы садитесь в такси и едете в случайную точку города, надеясь на удачу.

dDCA

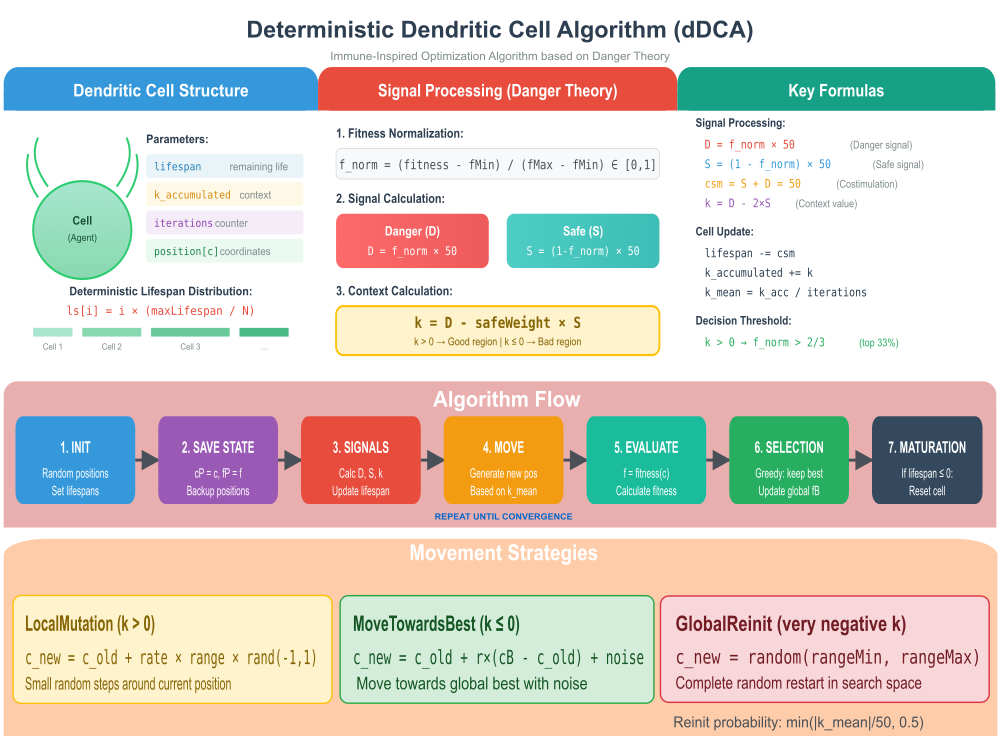
Рисунок 1. Иллюстрация работы алгоритма dDCA

На иллюстрации отображено:

  • Cell Structure — структура дендритной клетки с параметрами и визуализация детерминированного распределения lifespan,
  • Signal Processing — расчёт сигналов Danger/Safe и контекста k по Danger Theory,
  • Key Formulas — все ключевые формулы алгоритма,
  • Algorithm Flow — пошаговая схема работы,
  • Movement Strategies — три стратегии перемещения с формулами.

Переходим к написанию псевдокода алгоритма dDCA.

ИНИЦИАЛИЗАЦИЯ:
    Для каждой клетки i = 1..N:
        lifespan[i] = i × (maxLifespan / N)    // равномерное распределение
        k_accumulated[i] = 0
        позиция[i] = случайная в пространстве поиска

ОСНОВНОЙ ЦИКЛ:
    Для каждой клетки i:
        // Сохранение предыдущего состояния
        предыдущая_позиция[i] = позиция[i]
        предыдущий_фитнес[i] = фитнес[i]
    
    // Централизованный расчёт статистики
    fMin = min(фитнес всех клеток)
    fMax = max(фитнес всех клеток)
    
    Для каждой клетки i:
        // Нормализация и расчёт сигналов
        f_norm = (фитнес[i] - fMin) / (fMax - fMin)
        D = f_norm × 50
        S = (1 - f_norm) × 50
        k = D - safeWeight × S
        
        // Обновление состояния клетки
        lifespan[i] -= 50                      // csm = 50 (константа)
        k_accumulated[i] += k
        iterations[i]++
    
    Для каждой клетки i:
        // Средний контекст за время жизни
        k_mean = k_accumulated[i] / iterations[i]
        
        // Генерация новой позиции
        ЕСЛИ k_mean > 0:
            LocalMutation(i)                   // Эксплуатация
        ИНАЧЕ:
            reinit_prob = min(|k_mean| / 50, 0.5)
            ЕСЛИ random < reinit_prob:
                GlobalReinit(i)                // Глобальное исследование
            ИНАЧЕ:
                MoveTowardsBest(i)             // Направленное исследование
        
        // Проверка созревания
        ЕСЛИ lifespan[i] ≤ 0:
            Сброс клетки (lifespan, k_accumulated, iterations)
        
        Контроль границ(i)
    
    // Жадная селекция
    Для каждой клетки i:
        ЕСЛИ предыдущий_фитнес[i] > фитнес[i]:
            Восстановить предыдущую позицию и фитнес
    
    Обновить глобальное лучшее решение

Можем приступить к написанию кода алгоритма. Структура "Дендритная клетка" (S_dDCA_Cell) моделирует отдельную "дендритную клетку", представляющую собой элемент системы, обладающий специфическими свойствами и жизненным циклом. 

Основные характеристики клетки:

  • lifespan (время жизни) — текущее количество времени, которое клетка еще может существовать или функционировать. Этот показатель убывает со временем.
  • k_accumulated (накопленный контекст) — значение, отражающее накопленную внутри клетки информацию или "контекст".
  • initial_lifespan (начальное время жизни) — изначальное значение времени жизни клетки. Используется для сброса клетки в исходное состояние.
  • iterations (счетчик итераций) — отслеживает, сколько раз клетка прошла через полный цикл обработки или "инкарнацию" с момента последнего сброса.

Методы (действия) клетки:

  • Init () Инициализация:

    • Устанавливает начальные значения параметров клетки при ее создании.
    • lifespan и initial_lifespan — устанавливаются равными переданному значению "ls" (начальное время жизни).
    • k_accumulated — обнуляется (начинаем с чистого листа).
    • iterations — обнуляется, так как это первая "инкарнация".

  • Reset () Сброс:

    • Возвращает клетку в ее исходное состояние.
    • lifespan — восстанавливается до значения "initial_lifespan".
    • k_accumulated — сбрасывается на ноль.
    • iterations — также сбрасывается на ноль, готовясь к новому циклу работы.
//————————————————————————————————————————————————————————————————————
// Структура дендритной клетки
struct S_dDCA_Cell
{
    double lifespan;          // Текущее время жизни
    double k_accumulated;     // Накопленный контекст
    double initial_lifespan;  // Начальное время жизни (для сброса)
    int    iterations;        // Счётчик итераций в текущей инкарнации

    void Init (double ls)
    {
      lifespan         = ls;
      initial_lifespan = ls;
      k_accumulated    = 0.0;
      iterations       = 0;
    }

    void Reset ()
    {
      lifespan      = initial_lifespan;
      k_accumulated = 0.0;
      iterations    = 0;
    }
};
//————————————————————————————————————————————————————————————————————

Класс "C_AO_dDCA" представляет собой реализацию детерминированного алгоритма дендритных клеток (dDCA) для решения задач поиска оптимальных решений. Он наследуется от базового класса "C_AO", который предоставляет общую структуру для оптимизационных алгоритмов. 

Открытые (public) члены класса: 

Конструктор C_AO_dDCA () —

  • инициализирует основные атрибуты алгоритма,
  • устанавливает параметры по умолчанию,
  • создает массив "params" для хранения параметров с их именами и текущими значениями.
SetParams () Установка параметров —
  • метод для обновления внутренних параметров алгоритма на основе значений, хранящихся в массиве "params",
  • после установки значений, проводит проверку (контроль границ) для обеспечения их корректности, устанавливая минимальные и максимальные допустимые значения.
Init () Инициализация —
  • публичный метод для инициализации алгоритма — принимает интервалы поиска (rangeMinP, rangeMaxP, rangeStepP) и количество эпох (epochsP),
  • вызывает стандартную процедуру инициализации (StandardInit) и, если она успешна, выполняет специфическую для dDCA инициализацию:
    • создает массив "клеток" (cells) с размером, равным "popSize";
    • инициализирует каждую клетку с помощью метода "Init", устанавливая их начальное время жизни (lifespan) равномерно распределенным в пределах от 0 до maxLifespan, что создает разнообразие в "возрасте" клеток, как описано в исходной статье авторов;
    • инициализирует переменные для отслеживания минимального (fMin_pop) и максимального (fMax_pop) значения фитнес-функции в популяции.

Moving () Перемещение — публичный метод, отвечающий за основной цикл работы алгоритма, где клетки "движутся" или обновляются в пространстве поиска.

Revision () Ревизия — публичный метод, выполняющий корректирующие и оценочные действия по завершении этапа "Moving".

Открытые (public) члены данных:

  • maxLifespan (максимальное время жизни) — максимальное значение времени жизни для клеток,
  • safeWeight (вес "Safe" сигнала) — параметр, влияющий на расчет контекста клетки,
  • mutationRate (скорость мутации) — параметр, определяющий силу и вероятность локальных мутаций.

Закрытые (private) члены класса:

  • cells [] (массив клеток) — массив, содержащий объекты типа "S_dDCA_Cell", представляющие собой популяцию дендритных клеток,
  • fMin_pop (минимальный фитнес в популяции) — хранит минимальное значение фитнес-функции, найденное среди всех клеток в текущей популяции,
  • fMax_pop (максимальный фитнес в популяции) — хранит максимальное значение фитнес-функции, найденное среди всех клеток в текущей популяции.

Закрытые (private) методы:

  • CalculateSignals () (расчет сигналов) — метод для вычисления различных сигналов (например, "Danger" (D), "Safe" (S), "ClonalSelectionMarker" (csm), "Context" (k)) на основе нормализованного фитнес-значения (f_norm);
  • GenerateNewPosition () (генерация новой позиции) — метод для определения нового положения клетки в пространстве поиска, на основе среднего контекста популяции (k_mean);
  • LocalMutation () (локальная мутация) — применяет небольшие случайные изменения к параметрам клетки (ее "позиции");
  • MoveTowardsBest () (движение к лучшему) — перемещает клетку в направлении лучшей найденной на данный момент позиции;
  • GlobalReinit () (глобальная реинициализация) — полностью перезапускает клетку;
  • BoundaryControl () (контроль границ) — обеспечивает, чтобы параметры клетки оставались в пределах допустимых границ поиска;
  • GetNormalizedFitness() (получение нормализованного фитнеса) — преобразует значение фитнес-функции к нормализованному диапазону, необходимо для корректного расчета сигналов.
//————————————————————————————————————————————————————————————————————
class C_AO_dDCA : public C_AO
{
  public:
  ~C_AO_dDCA () { }

  C_AO_dDCA ()
  {
    ao_name = "dDCA";
    ao_desc = "Deterministic Dendritic Cell Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/20430";

    popSize      = 50;
    maxLifespan  = 20.0;    // Максимальный лимит времени жизни
    safeWeight   = 2.0;     // Вес Safe сигнала: k = D - safeWeight*S
    mutationRate = 0.01;    // Сила локальной мутации

    ArrayResize (params, 4);
    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "maxLifespan";  params [1].val = maxLifespan;
    params [2].name = "safeWeight";   params [2].val = safeWeight;
    params [3].name = "mutationRate"; params [3].val = mutationRate;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    maxLifespan  = params      [1].val;
    safeWeight   = params      [2].val;
    mutationRate = params      [3].val;

    if (popSize < 2) popSize = 2;
    if (maxLifespan < 1.0) maxLifespan = 1.0;
    if (safeWeight < 0.0) safeWeight = 0.0;
    if (mutationRate < 0.0) mutationRate = 0.0;
    if (mutationRate > 1.0) mutationRate = 1.0;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP);

  void Moving   ();
  void Revision ();

  //------------------------------------------------------------------
  double maxLifespan;
  double safeWeight;
  double mutationRate;

  private: //---------------------------------------------------------
  S_dDCA_Cell cells [];

  double fMin_pop;        // Минимальный фитнес в популяции
  double fMax_pop;        // Максимальный фитнес в популяции

  void   CalculateSignals     (double f_norm, double &D, double &S, double &csm, double &k);
  void   GenerateNewPosition  (int idx, double k_mean);
  void   LocalMutation        (int idx);
  void   MoveTowardsBest      (int idx);
  void   GlobalReinit         (int idx);
  void   BoundaryControl      (int idx);
  double GetNormalizedFitness (double f);
};
//————————————————————————————————————————————————————————————————————

Метод "Init" класса "C_AO_dDCA" отвечает за первоначальную настройку и подготовку алгоритма к работе. Он получает информацию о диапазоне поиска параметров, шагах поиска и количестве обучающих эпох. Первым шагом вызывается метод "StandardInit", который выполняет общую инициализацию, необходимую для всех оптимизационных алгоритмов.

Размер массива "cells" хранит все "дендритные клетки", устанавливается равным "popSize" — значению, определяющему количество клеток в популяции. Рассчитывается "lifespanIncrement" — величина, на которую будет увеличиваться время жизни каждой последующей клетки. Это делается путем деления максимального времени жизни (maxLifespan) на общее количество клеток (popSize).

В цикле для каждой клетки происходит следующее: вычисляется начальное время жизни для текущей клетки, каждая клетка получает свое уникальное начальное время жизни, равномерно распределенное в интервале от "lifespanIncrement" до "maxLifespan", вызывается метод "Init" для текущей клетки, передавая ей рассчитанное значение "ls". Это настраивает клетку с ее индивидуальным временем жизни, обнуляет накопленный контекст и счетчик итераций.

Такое дробление времени жизни на разные интервалы позволяет клеткам иметь различные "окна наблюдения" или "периоды активности" в процессе работы алгоритма, что соответствует одной из ключевых идей оригинальной статьи по dDCA.

В конце метода возвращается "true", инициализация алгоритма прошла успешно.
//————————————————————————————————————————————————————————————————————
bool C_AO_dDCA::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //------------------------------------------------------------------
  // Инициализация клеток с равномерным распределением lifespan
  // Это обеспечивает разные "временные окна" как в статье авторов
  //------------------------------------------------------------------
  ArrayResize (cells, popSize);

  double lifespanIncrement = maxLifespan / popSize;

  for (int i = 0; i < popSize; i++)
  {
    double ls = (i + 1) * lifespanIncrement;
    cells [i].Init (ls);
  }

  //------------------------------------------------------------------

  return true;
}
//————————————————————————————————————————————————————————————————————

Метод "Moving" является основным рабочим циклом алгоритма dDCA. Он представляет собой последовательность шагов, моделирующих поведение дендритных клеток в процессе поиска решения.

Итерация 1. Случайная инициализация популяции.

  • Если переменная "revision" имеет значение "false" (что указывает на первую итерацию), происходит случайное распределение начальных позиций всех клеток в пределах заданных диапазонов (rangeMin, rangeMax).
  • Метод "u.RNDfromCI" генерирует случайное значение в указанном интервале.
  • Метод "u.SeInDiSp" приводит сгенерированное значение к заданному шагу (rangeStep), обеспечивая дискретность поиска.
  • После инициализации "revision" устанавливается в "true", и метод завершает выполнение, готовясь к основной обработке на следующей итерации.

Сохранение текущих координат и фитнес-значения. Этот шаг выполняется перед любыми дальнейшими расчетами.

  • Для каждой клетки текущие координаты копируются в предыдущие координаты, текущий фитнес копируется в предыдущий фитнес.
  • Важно: это критически важный шаг, так как он сохраняет состояние популяции на момент начала текущей итерации, которое будет использоваться для расчетов на этой итерации.

Обновление статистики популяции для нормализации:

  • инициализируются переменные "fMin_pop" (минимальный фитнес) и fMax_pop (максимальный фитнес) с экстремальными значениями;
  • итерируя по всем клеткам, происходит поиск истинных минимального и максимального значений фитнес-функции среди всех клеток, которые не имеют значения "-DBL_MAX" (фитнес еще не вычислен);
  • защита от невалидных значений — если после обхода популяции "fMax_pop" остается "-DBL_MAX" или "fMin_pop" остается "DBL_MAX" (что может произойти, если все фитнес-значения некорректны или популяция не инициализирована), устанавливаются значения по умолчанию (1.0 и 0.0 соответственно), чтобы избежать ошибок при дальнейшей нормализации.

Обработка сигналов и обновление состояния клеток. Этот блок моделирует "чувствительность" и "распространение сигналов" в популяции дендритных клеток.

  • Для каждой клетки вычисляется нормализованное значение фитнес-функции с использованием метода "GetNormalizedFitness", вызывается метод "CalculateSignals" для определения сигналов "Danger" (D), "Safe" (S), "Clonal Selection Marker" (csm) и "Context" (k). Эти сигналы отражают "опасность" текущего окружения (D), "безопасность" (S), маркер для клонального отбора (csm) и "контекст" (k) – внутреннее состояние клетки. Далее:
    • Обновление состояния клетки:
      • cells[i].lifespan -= csm: Уменьшается время жизни клетки пропорционально маркеру клонального отбора.
      • cells[i].k_accumulated += k: Накапливается значение сигнала "Context" (k) в  k_accumulated  клетки.
      • cells[i].iterations++: Увеличивается счетчик итераций клетки.

Генерация новых позиций. На этом этапе происходит принятие решений о дальнейшем поведении каждой клетки.

Для каждой клетки:

  • расчет среднего контекста — вычисляется среднее значение накопленного контекста  "k_mean" клетки за все ее итерации;
  • если клетка "созрела", принимается решение на основе ее накопленного контекста;
  • если клетка не созрела, исследование продолжается с текущей стратегией, которая также зависит от накопленного контекста;
  • в обоих случаях (созревшая или нет) вызывается метод "GenerateNewPosition";
  • после определения новой позиции, метод "BoundaryControl" гарантирует, что координаты клетки останутся в пределах допустимых границ поиска (rangeMin, rangeMax).

В целом, метод "Moving" моделирует:

  • первую фазу — случайное распределение начальных точек,
  • сохранение состояния — фиксация лучших достижений перед началом изменений,
  • оценку популяции — определение текущего диапазона качества решений,
  • обработку сигналов — каждая клетка "чувствует" окружение (представленное ее фитнес-значением) и генерирует внутренние сигналы (D, S, csm, k),
  • управление временем жизни — время жизни клетки регулируется сигналом "csm",
  • накопление контекста — информация о "здоровье" и "опасности" окружения накапливается в "k_accumulated",
  • принятие решения — зрелые клетки принимают более радикальные решения, в то время как молодые клетки продолжают исследование,
  • использование стратегии — новая позиция генерируется на основе накопленного контекста (k_mean), что позволяет клеткам адаптироваться к локальной или глобальной обстановке.
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::Moving ()
{
  //------------------------------------------------------------------
  // Итерация 1: случайная инициализация популяции
  //------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //------------------------------------------------------------------
  // ШАГ 1: Сохраняем текущие координаты и фитнес
  // ВАЖНО: это нужно сделать первым, до любых расчётов!
  // a[i].f содержит фитнес, вычисленный после предыдущего Moving()
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    ArrayCopy (a [i].cP, a [i].c, 0, 0, coords);
    a [i].fP = a [i].f;
  }

  //------------------------------------------------------------------
  // ШАГ 2: Обновляем статистику популяции для нормализации
  // Используем fP (только что сохранённый актуальный фитнес)
  //------------------------------------------------------------------
  fMin_pop =  DBL_MAX;
  fMax_pop = -DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].fP != -DBL_MAX)  // Проверка на инициализацию
    {
      if (a [i].fP > fMax_pop) fMax_pop = a [i].fP;
      if (a [i].fP < fMin_pop) fMin_pop = a [i].fP;
    }
  }

  // Защита от невалидных значений
  if (fMax_pop == -DBL_MAX || fMin_pop == DBL_MAX)
  {
    fMax_pop = 1.0;
    fMin_pop = 0.0;
  }

  //------------------------------------------------------------------
  // ШАГ 3: Обработка сигналов и обновление состояния клеток
  // Централизованная обработка как в оригинальном dDCA
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    // Нормализация фитнеса
    double f_norm = GetNormalizedFitness (a [i].fP);

    // Расчёт сигналов
    double D, S, csm, k;
    CalculateSignals (f_norm, D, S, csm, k);

    // Обновление состояния клетки
    cells [i].lifespan -= csm;
    cells [i].k_accumulated += k;
    cells [i].iterations++;
  }

  //------------------------------------------------------------------
  // ШАГ 4: Генерация новых позиций
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    // Средний контекст за время жизни
    double k_mean = cells [i].k_accumulated / MathMax (cells [i].iterations, 1);

    // Проверка на созревание
    if (cells [i].lifespan <= 0.0)
    {
      // Клетка созрела - принимаем решение на основе накопленного контекста
      GenerateNewPosition (i, k_mean);
      cells [i].Reset ();
    }
    else
    {
      // Клетка не созрела - продолжаем исследование с текущей стратегией
      // Стратегия зависит от накопленного контекста
      GenerateNewPosition (i, k_mean);
    }

    BoundaryControl (i);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "GetNormalizedFitness" отвечает за масштабирование (нормализацию) значения фитнес-функции в стандартный диапазон от 0 до 1. Это важно для того, чтобы различные фитнес-функции или фитнес-значения, полученные в разных состояниях поиска, могли быть корректно сравнены и использованы в дальнейших расчетах.

//————————————————————————————————————————————————————————————————————
// Нормализация фитнеса в диапазон [0, 1]
//————————————————————————————————————————————————————————————————————
double C_AO_dDCA::GetNormalizedFitness (double f)
{
  if (f == -DBL_MAX) return 0.5;

  double range = fMax_pop - fMin_pop;
  if (range < 1e-10) return 0.5;

  double norm = (f - fMin_pop) / range;

  // Ограничение в [0, 1]
  if (norm < 0.0) norm = 0.0;
  if (norm > 1.0) norm = 1.0;

  return norm;
}
//————————————————————————————————————————————————————————————————————

Метод "CalculateSignals" берёт показатель "приспособленности" какого-либо элемента, который уже был приведен к универсальному масштабу. На основе этого показателя он рассчитывает четыре новых характеристики, которые отражают:

  • (S) — показывает, насколько этот элемент является "перспективным" или "привлекательным",
  • (D) — показывает, насколько элемент является "неперспективным" или "менее привлекательным".

"Совместную стимуляцию" (csm). Это общее значение, которое учитывает как "опасность", так и "безопасность" вместе. В конкретной реализации оно всегда будет равно 50, если исходный показатель приемлемости был приведен к диапазону от 0 до 50.

"Контекст" (k). Это более сложное значение, которое учитывает "опасность", но с учетом того, насколько "безопасность" может её подавлять. Оно помогает оценить, насколько действительно стоит полагаться на "опасный" сигнал, учитывая наличие "безопасных" факторов.

Таким образом, метод преобразует один входной показатель качества в несколько новых, которые более детально описывают его "привлекательность" и "отталкивающие" свойства, учитывая разные аспекты для принятия решений.

//————————————————————————————————————————————————————————————————————
// Расчёт сигналов D и S
//
// Формулы из статьи (с нормализацией в [0, 50] как в эксперименте):
//   csm = S + D      (1) - costimulation
//   k = D - 2*S      (4) - context (или D - safeWeight*S)
//
// Интерпретация для оптимизации:
//   D  = низкий фитнес = нужно уходить
//   S  = высокий фитнес = перспективный регион
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::CalculateSignals (double f_norm, double &D, double &S, double &csm, double &k)
{
  // Нормализация в диапазон [0, 50] как в статье
  D = f_norm * 50.0;
  S = (1.0 - f_norm) * 50.0;

  // Формула (1): csm = S + D = 50 (константа при данной нормализации)
  csm = S + D;

  // Формула (4): k = D - safeWeight * S
  k = D - safeWeight * S;
}
//————————————————————————————————————————————————————————————————————

Метод "GenerateNewPosition" определяет, каким образом будет генерироваться новая позиция (или решение) для определенного агента в алгоритме, основываясь на "контексте" текущей ситуации. Контекст этот описывается средней величиной "k_mean".

Если "k_mean" положительный — это означает, что текущая область поиска считается "хорошей" или "перспективной". В этом случае метод выбирает стратегию эксплуатации, то есть локальной мутации. Агент остается вблизи своего текущего положения и вносит небольшие, точечные изменения, как бы "дорабатывая" или "исследуя" мельчайшие детали в этой хорошей области.

Если "k_mean" неположительный — это указывает на то, что текущая область поиска считается "плохой" или "менее перспективной". Здесь алгоритм переходит к стратегии исследования, призванной выбраться из этой зоны:

Вероятность переинициализации. Метод сначала генерирует случайное число. Это число сравнивается с вероятностью переинициализации (reinit_prob). Эта вероятность тем выше, чем более отрицательным является "k_mean" (чем хуже контекст) и ограничена сверху (например, 0.5, то есть не более 50% случаев).

Если случайное число меньше вероятности переинициализации. Выполняется глобальная переинициализация. Это означает, что агент полностью "сбрасывается" и помещается в совершенно новую, случайную позицию в пространстве поиска. Это как начать все сначала в другой части поиска.

В противном случае(если случайное число больше вероятности переинициализации). Выполняется движение к лучшему решению. Это означает, что агент пытается направиться к уже найденному наилучшему решению, надеясь, что это приведет его к лучшему участку пространства поиска, минуя текущую плохую область.

Таким образом, метод "GenerateNewPosition" действует как "умный" способ генерации новых решений:

  • вознаграждает "хорошие" области, позволяя агентам детально их исследовать;
  • выводит агентов из "плохих" областей, либо давая им шанс на "счастливую случайность" (глобальная переинициализация), либо направляя их к уже найденному успеху (движение к лучшему).
//————————————————————————————————————————————————————————————————————
// Генерация новой позиции на основе контекста
//
// k > 0: хороший регион (аналог "mature" в dDCA)
//   ? локальная мутация (эксплуатация)
//
// k <= 0: плохой регион (аналог "semi-mature" в dDCA)
//   ? движение к лучшему или переинициализация (исследование)
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::GenerateNewPosition (int idx, double k_mean)
{
  if (k_mean > 0.0)
  {
    // Положительный контекст - хороший регион
    // Локальное исследование вокруг текущей позиции
    LocalMutation (idx);
  }
  else
  {
    // Отрицательный контекст - плохой регион
    // Нужно уходить: либо к лучшему, либо случайно

    double r = u.RNDfromCI (0.0, 1.0);

    // Чем хуже контекст (более отрицательный k), тем выше шанс переинициализации
    double reinit_prob = MathMin (MathAbs (k_mean) / 50.0, 0.5);

    if (r < reinit_prob)
    {
      // Глобальная переинициализация
      GlobalReinit (idx);
    }
    else
    {
      // Движение к лучшему решению
      MoveTowardsBest (idx);
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "LocalMutation" вносит небольшие, случайные изменения в каждую координату текущей позиции элемента. Эти изменения происходят в пределах установленных границ рабочей области для каждой координаты и зависят от общей "скорости мутации", что позволяет исследовать "соседние" решения относительно текущего.

//————————————————————————————————————————————————————————————————————
// Локальная мутация - исследование окрестности текущей позиции
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::LocalMutation (int idx)
{
  for (int c = 0; c < coords; c++)
  {
    double range    = rangeMax [c] - rangeMin [c];
    double mutation = mutationRate * range * u.RNDfromCI (-1.0, 1.0);

    a [idx].c [c] = a [idx].cP [c] + mutation;
  }
}
//————————————————————————————————————————————————————————————————————

Метод "MoveTowardsBest" описывает стратегию, при которой агент пытается приблизиться к наилучшему известному решению, добавляя при этом некоторый случайный "шум" для поддержания исследовательских свойств. Метод балансирует между эксплуатацией (стремление к лучшему найденному решению) и исследованием (внезапные, небольшие случайные отклонения вокруг движущейся траектории). Это позволяет элементу эффективно перемещаться в направлении перспективных областей, но при этом не "застревать" слишком сильно в одной точке и сохранять способность находить новые, возможно, даже лучшие решения.

//————————————————————————————————————————————————————————————————————
// Движение к лучшему известному решению с шумом
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::MoveTowardsBest (int idx)
{
  // Проверка: если cB ещё не инициализирован, делаем локальную мутацию
  if (fB == -DBL_MAX)
  {
    LocalMutation (idx);
    return;
  }

  for (int c = 0; c < coords; c++)
  {
    double r     = u.RNDfromCI (0.0, 1.0);
    double range = rangeMax [c] - rangeMin [c];

    // Движение к лучшему + случайный шум
    a [idx].c [c] = a [idx].cP [c]
                    + r * (cB [c] - a [idx].cP [c])
                    + mutationRate * range * u.RNDfromCI (-1.0, 1.0);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "GlobalReinit" помещает элемент в абсолютно новую, случайно выбранную точку в пространства поиска. Это действует как "полный сброс" или "прыжок" в совершенно другую часть пространства решений. Такой подход может быть полезен, если текущий алгоритм застрял в локальном оптимуме и нужно "вытолкнуть" его оттуда, чтобы начать исследование с чистого листа.

//————————————————————————————————————————————————————————————————————
// Глобальная переинициализация - полностью случайная позиция
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::GlobalReinit (int idx)
{
  for (int c = 0; c < coords; c++)
  {
    a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
  }
}
//————————————————————————————————————————————————————————————————————

Метод предназначен для удержания элемента (агента, частицы) в пределах заданных допустимых границ для его координат. Если элемент оказывается за пределами этих границ, метод пытается вернуть его обратно, используя различные стратегии.

Метод BoundaryControl является корректирующим механизмом. Он гарантирует, что элементы не выходят за пределы определяемого пространства поиска. Стратегия "отражения" позволяет элементу "оттолкнуться" от границы и вернуться в допустимую область, сохраняя при этом некоторую информацию о своем движении. Дополнительная рандомизация при пересечении границы помогает избежать застреваний. И наконец, последняя строка гарантирует, что позиция соответствует дискретным правилам пространства.

//————————————————————————————————————————————————————————————————————
// Контроль границ с отражением
//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::BoundaryControl (int idx)
{
  for (int c = 0; c < coords; c++)
  {
    if (a [idx].c [c] < rangeMin [c])
    {
      a [idx].c [c] = rangeMin [c] + MathAbs (a [idx].c [c] - rangeMin [c]);

      if (a [idx].c [c] > rangeMax [c])
      {
        a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      }
    }

    if (a [idx].c [c] > rangeMax [c])
    {
      a [idx].c [c] = rangeMax [c] - MathAbs (a [idx].c [c] - rangeMax [c]);

      if (a [idx].c [c] < rangeMin [c])
      {
        a [idx].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      }
    }

    a [idx].c [c] = u.SeInDiSp (a [idx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "Revision" выполняет две ключевые функции:

  1. селекция (отбор) — он определяет, стоит ли сохранять новую (потенциально улучшенную) позицию агента или вернуться к предыдущей лучшей,
  2. обновление глобальных лучшего — он отслеживает наилучшую и наихудшую найденные позиции среди всех агентов и сохраняет эту информацию.

Селекция: жадный выбор. Суть селекции. Этот блок реализует "жадную" стратегию. Если новое положение агента оказалось хуже, чем его собственное лучшее известное положение, агент "никогда не забудет" свое предыдущее лучшее положение и вернется к нему.

Метод "Revision" используется для стабилизации и отслеживания прогресса популяции. Он обеспечивает, что каждый агент не теряет свои лучшие найденные решения (благодаря жадной селекции) и помогает определить общее лучшее найденное решение во всей популяции. Алгоритм основан на задачах максимизации, то "fB" и "cB" будут хранить наилучшие результаты.

//————————————————————————————————————————————————————————————————————
void C_AO_dDCA::Revision ()
{
  //------------------------------------------------------------------
  // Селекция: жадный выбор - сохраняем позицию если она лучше
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    // Если предыдущий фитнес лучше текущего - возвращаемся
    if (a [i].fP > a [i].f && a [i].fP != -DBL_MAX)
    {
      a [i].f = a [i].fP;
      ArrayCopy (a [i].c, a [i].cP, 0, 0, coords);
    }
  }

  //------------------------------------------------------------------
  // Обновление глобального лучшего 
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, coords);
    }
  }
}
//————————————————————————————————————————————————————————————————————


Результаты тестов

Теперь можем познакомиться с результатами тестирования алгоритма на наших тестовых функциях, алгоритм набирает 41%, слабее всего чувствует себя на дискретных функциях.

dDCA|Deterministic Dendritic Cell Algorithm|50.0|20.0|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.8798800651743539
25 Hilly's; Func runs: 10000; result: 0.4788852312258377
500 Hilly's; Func runs: 10000; result: 0.27717376068435823
=============================
5 Forest's; Func runs: 10000; result: 0.6340906667281795
25 Forest's; Func runs: 10000; result: 0.3689169839474446
500 Forest's; Func runs: 10000; result: 0.21510602459276465
=============================
5 Megacity's; Func runs: 10000; result: 0.5292307692307692
25 Megacity's; Func runs: 10000; result: 0.2163076923076923
500 Megacity's; Func runs: 10000; result: 0.10510769230769328
=============================
All score: 3.70470 (41.16%)

На визуализации заметен разброс результатов на функциях малой размерности и на дискретной функции "Megacity" низкие показатели сходимости. Популяция разбивается на группы клеток агентов, исследуя перспективные области, но этого не достаточно с точки зрения общего поиска ко всему пространству решений.

Hilly

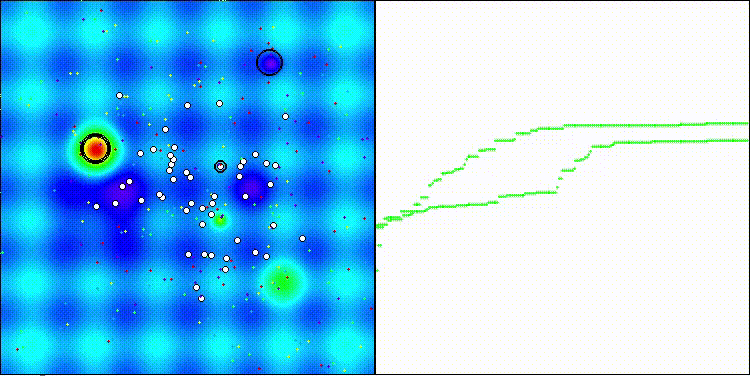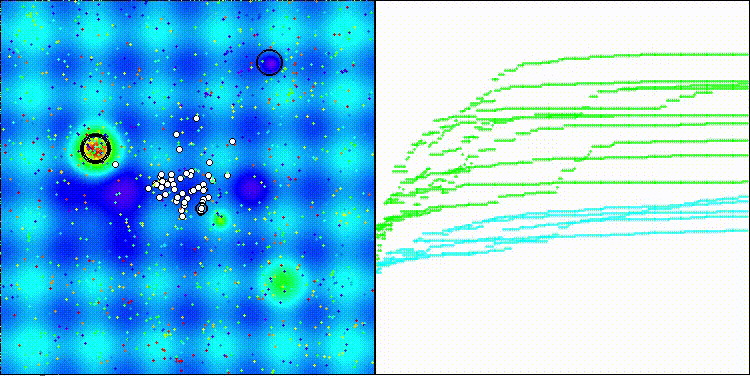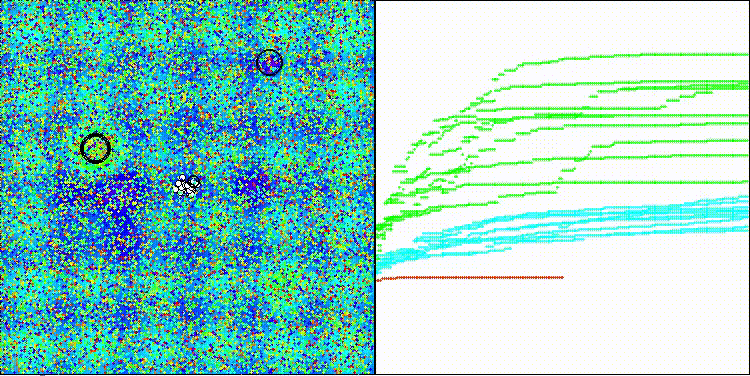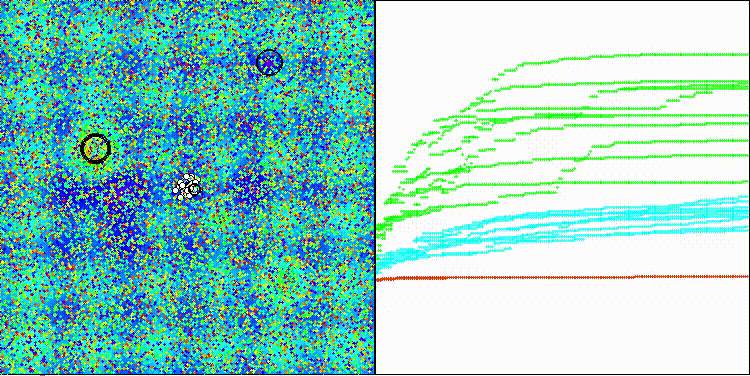
dDCA на тестовой функции Hilly

Forest

dDCA на тестовой функции Forest

Megacity

dDCA на тестовой функции Megacity

Для общего ознакомления с работой алгоритма dDCA, посмотрим его поведение на стандартных тестовых функциях, которые не участвуют в нашем тестировании, но имеют свои поставленные задачи. Разброс значений менее заметен.

Ackley

dDCA на стандартной тестовой функции Ackley

Shaffer

dDCA на стандартной тестовой функции Shaffer

Paraboloid

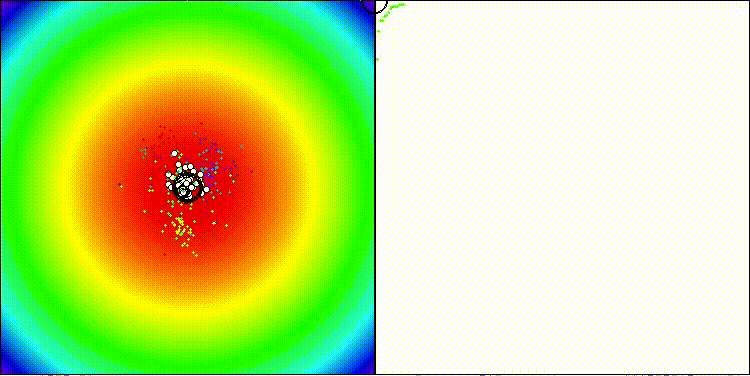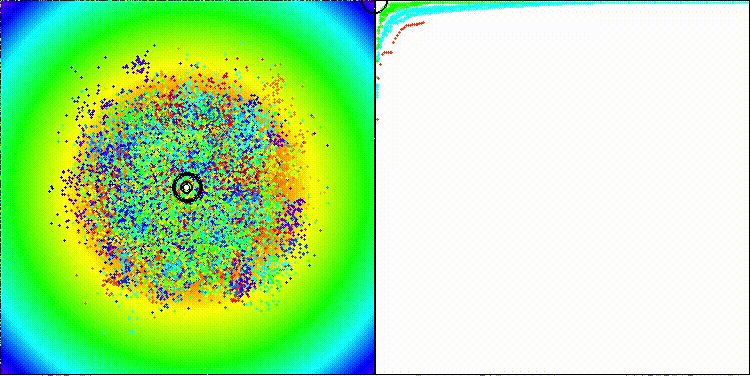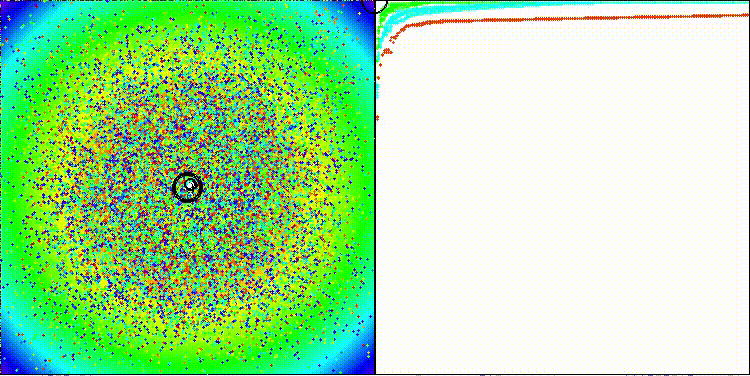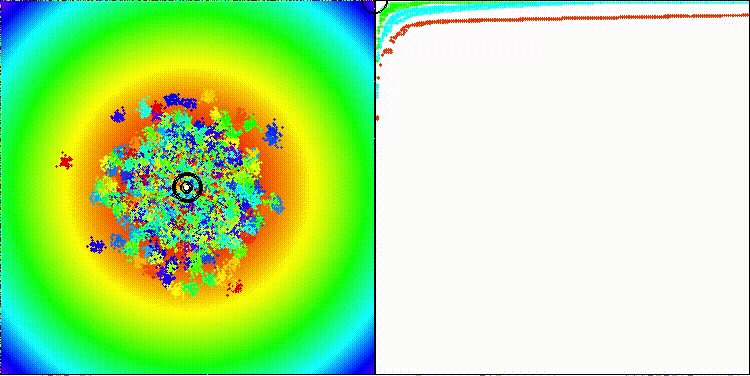
dDCA на стандартной тестовой функции Paraboloid

Алгоритм dDCA представлен в нашей рейтинговой таблице лучших популяционных методов оптимизации ознакомительно.

№ AO Description Hilly Hilly
Final 		Forest Forest
Final 		Megacity (discrete) Megacity
Final 		Final
Result 		% of
MAX
10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)10 p (5 F)50 p (25 F)1000 p (500 F)
1DOAdingomdingo_optimization_algorithm_M0,479680,453670,463691,397040,941450,879090,914542,735080,786150,860610,848052,494816,62773,63
2ANSacross neighbourhood search0,949480,847760,438572,235811,000000,923340,399882,323230,709230,634770,230911,574916,13468,15
3CLAcode lock algorithm (joo)0,953450,871070,375902,200420,989420,917090,316422,222940,796920,693850,193031,683806,10767,86
4AMOmanimal migration ptimization M0,903580,843170,462842,209590,990010,924360,465982,380340,567690,591320,237731,396755,98766,52
5(P+O)ES(P+O) evolution strategies0,922560,881010,400212,203790,977500,874900,319452,171850,673850,629850,186341,490035,86665,17
6CTAcomet tail algorithm (joo)0,953460,863190,277702,094350,997940,857400,339492,194840,887690,564310,105121,557125,84664,96
7TETAtime evolution travel algorithm (joo)0,913620,823490,319902,057010,970960,895320,293242,159520,734620,685690,160211,580525,79764,41
8SDSmstochastic diffusion search M0,930660,854450,394762,179880,999830,892440,196192,088460,723330,611000,106701,441035,70963,44
9BOAmbilliards optimization algorithm M0,957570,825990,252352,035901,000000,900360,305022,205380,735380,525230,095631,356255,59862,19
10AAmarchery algorithm M0,917440,708760,421602,047800,925270,758020,353282,036570,673850,552000,237381,463235,54861,64
11ESGevolution of social groups (joo)0,999060,796540,350562,146161,000000,828630,131021,959650,823330,553000,047251,423585,52961,44
12SIAsimulated isotropic annealing (joo)0,957840,842640,414652,215130,982390,795860,205071,983320,686670,493000,090531,270205,46960,76
13EOmextremal_optimization_M0,761660,772420,317471,851550,999990,767510,235272,002770,747690,539690,142491,429875,28458,71
14BBObiogeography based optimization0,949120,694560,350311,993990,938200,673650,256821,868670,746150,482770,173691,402615,26558,50
15ACSartificial cooperative search0,755470,747440,304071,806981,000000,888610,224132,112740,690770,481850,133221,305835,22658,06
16DAdialectical algorithm0,861830,700330,337241,899400,981630,727720,287181,996530,703080,452920,163671,319675,21657,95
17BHAmblack hole algorithm M0,752360,766750,345831,864930,935930,801520,271772,009230,650770,516460,154721,321955,19657,73
18ASOanarchy society optimization0,848720,746460,314651,909830,961480,791500,238031,991010,570770,540620,166141,277525,17857,54
19RFOroyal flush optimization (joo)0,833610,737420,346291,917330,894240,738240,240981,873460,631540,502920,164211,298675,08956,55
20AOSmatomic orbital search M0,802320,704490,310211,817020,856600,694510,219961,771070,746150,528620,143581,418355,00655,63
21TSEAturtle shell evolution algorithm (joo)0,967980,644800,296721,909490,994490,619810,227081,841390,690770,426460,135981,253225,00455,60
22BSAbacktracking_search_algorithm0,973090,545340,290981,809410,999990,585430,217471,802890,847690,369530,129781,347004,95955,10
23DEdifferential evolution0,950440,616740,303081,870260,953170,788960,166521,908650,786670,360330,029531,176534,95555,06
24SRAsuccessful restaurateur algorithm (joo)0,968830,634550,292171,895550,946370,555060,191241,692670,749230,440310,125261,314804,90354,48
25BObonobo_optimizer0,775650,638050,329081,742780,880880,763440,255731,900050,610770,498460,142461,251694,89554,38
26CROchemical reaction optimisation0,946290,661120,298531,905930,879060,584220,211461,674730,758460,426460,126861,311784,89254,36
27BIOblood inheritance optimization (joo)0,815680,653360,308771,777810,899370,653190,217601,770160,678460,476310,139021,293784,84253,80
28DOAdream_optimization_algorithm0,855560,700850,372801,929210,734210,489050,241471,464730,772310,473540,185611,431464,82553,62
29BSAbird swarm algorithm0,893060,649000,262501,804550,924200,711210,249391,884790,693850,326150,100121,120124,80953,44
30DEAdolphin_echolocation_algorithm0,759950,675720,341711,777380,895820,642230,239411,777460,615380,440310,151151,206844,76252,91
31HSharmony search0,865090,687820,325271,878180,999990,680020,095901,775920,620000,422670,054581,097254,75152,79
32SSGsaplings sowing and growing0,778390,649250,395431,823080,859730,624670,174291,658690,646670,441330,105981,193984,67651,95
33BCOmbacterial chemotaxis optimization M0,759530,622680,314831,697040,893780,613390,225421,732590,653850,420920,144351,219124,64951,65
34ABOafrican buffalo optimization0,833370,622470,299641,755480,921700,586180,197231,705110,610000,431540,132251,173784,63451,49
35(PO)ES(PO) evolution strategies0,790250,626470,429351,846060,876160,609430,195911,681510,590000,379330,113221,082554,61051,22
36FBAfractal-based Algorithm0,790000,651340,289651,730990,871580,568230,188771,628580,610770,460620,123981,195374,55550,61
37TSmtabu search M0,877950,614310,291041,783300,928850,518440,190541,637830,610770,382150,121571,114494,53650,40
38BSObrain storm optimization0,937360,576160,296881,810410,931310,558660,235371,725340,552310,290770,119140,962224,49849,98
39WOAmwale optimization algorithm M0,845210,562980,262631,670810,931000,522780,163651,617430,663080,411380,113571,188034,47649,74
40AEFAartificial electric field algorithm0,877000,617530,252351,746880,927290,726980,180641,834900,666150,116310,095080,877544,45949,55
41AEOartificial ecosystem-based optimization algorithm0,913800,467130,264701,645630,902230,437050,214001,553270,661540,308000,285631,255174,45449,49
42CAmcamel algorithm M0,786840,560420,351331,698590,827720,560410,243361,631490,648460,330920,134181,113564,44449,37
43ACOmant colony optimization M0,881900,661270,303771,846930,858730,586800,150511,596040,596670,373330,024720,994724,43849,31
44CMAEScovariance_matrix_adaptation_evolution_strategy0,762580,720890,000001,483470,820560,796160,000001,616720,758460,490770,000001,249234,34948,33
45DA_duelistduelist_algorithm0,927820,537780,277921,743520,869570,475360,181931,526860,621530,335690,117151,074374,34548,28
dDCAdeterministic_dendritic_cell_algorithm0,879880,478880,277171,635930,634090,368910,215101,218100,529230,216300,105100,850633,70541,16
RWrandom walk0,487540,321590,257811,066940,375540,219440,158770,753750,279690,149170,098470,527342,34826,09


Выводы

Предложенная адаптация детерминированного алгоритма дендритных клеток (dDCA) для задач непрерывной оптимизации продемонстрировала работоспособность подхода, однако не достигла уровня лучших популяционных методов. В ходе тестирования на стандартном наборе функций алгоритм набрал 41%, что ниже порогового значения 48% для включения в рейтинговую таблицу.

Анализ результатов выявил характерную особенность: алгоритм показывает наиболее слабые результаты на дискретных функциях. Это объясняется природой механизма сигналов — плавная нормализация фитнеса плохо отражает резкие переходы в дискретных ландшафтах, где соседние решения могут иметь кардинально различное качество.

Несмотря на общий результат, ряд компонентов алгоритма представляет самостоятельный интерес:

  • детерминированное распределение времени жизни обеспечивает равномерную асинхронность популяции без введения дополнительной стохастичности;
  • механизм накопления контекста позволяет принимать решения на основе статистики нескольких итераций, что повышает устойчивость к шуму фитнес-функции;
  • адаптивный баланс исследования и эксплуатации на основе коллективного контекста популяции может служить альтернативой классическим схемам с явным параметром.

Данные компоненты могут быть использованы как составные элементы гибридных алгоритмов или адаптированы для специализированных задач, где важна устойчивость к зашумленным оценкам качества решений.

tab

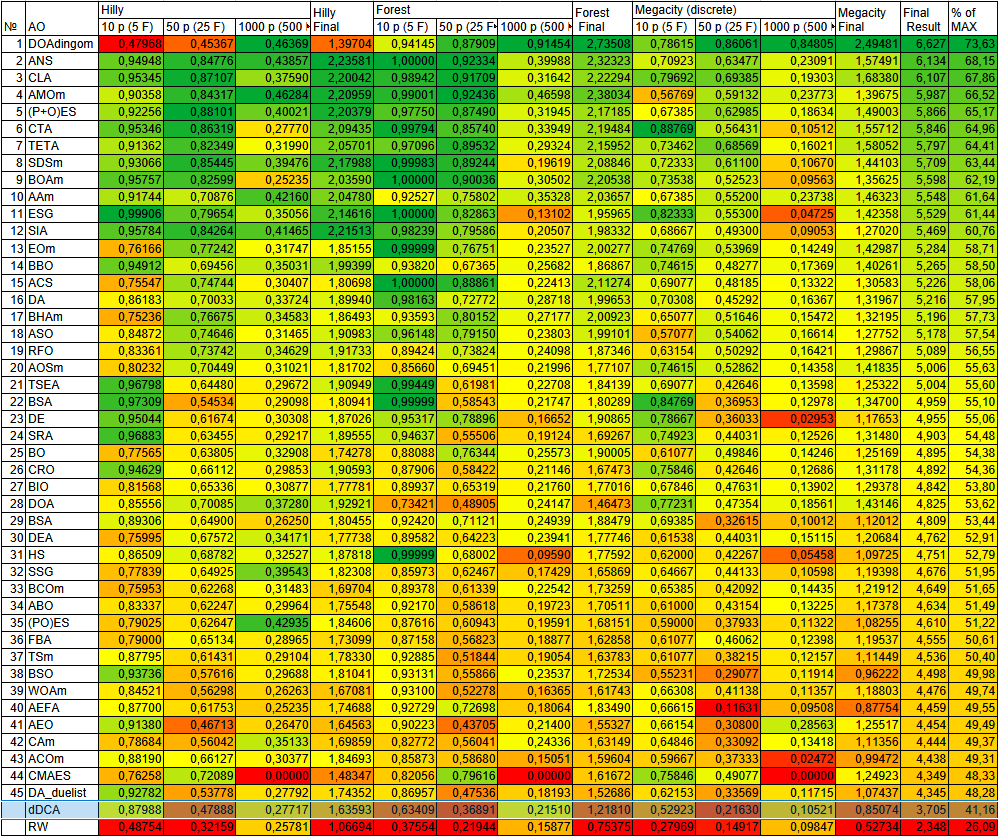
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам

chart

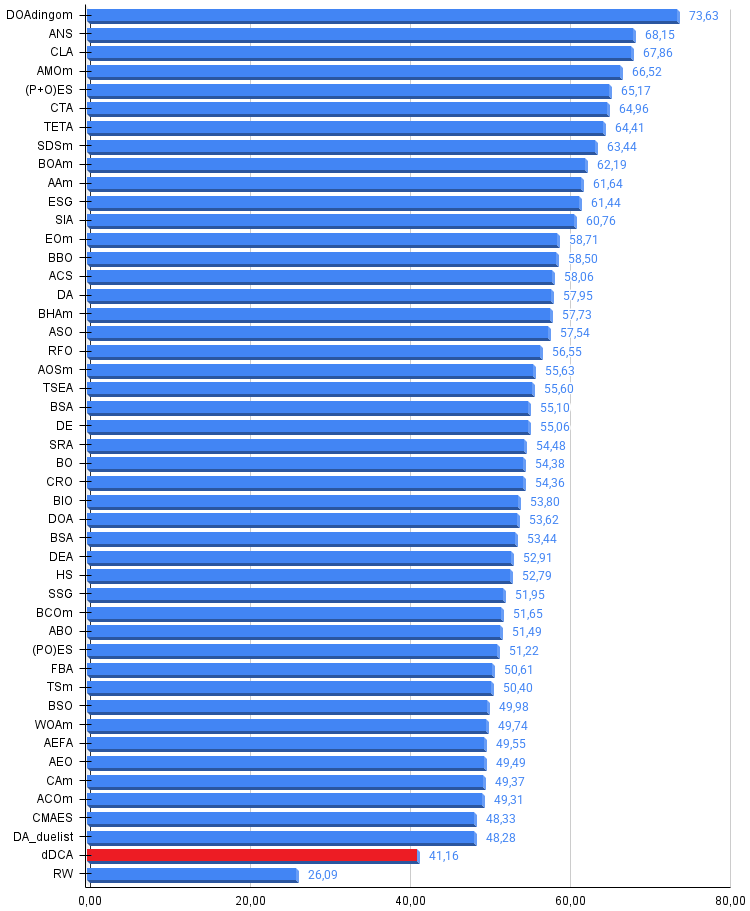
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

Плюсы и минусы алгоритма dDCA:

Плюсы:

  1. Быстрый.

Минусы:

  1. Более слабые результаты на дискретных функциях.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.



Программы, используемые в статье

#ИмяТипОписание
1#C_AO.mqh
Включаемый файл
Родительский класс популяционных алгоритмов оптимизации
2#C_AO_enum.mqh
Включаемый файл
Перечисление популяционных алгоритмов оптимизации
3TestFunctions.mqh
Включаемый файл
Библиотека тестовых функций
4
TestStandFunctions.mqh
Включаемый файл
Библиотека функций тестового стенда
5
Utilities.mqh
Включаемый файл
Библиотека вспомогательных функций
6
CalculationTestResults.mqh
Включаемый файл
Скрипт для расчета результатов в сравнительную таблицу
7
Testing AOs.mq5
СкриптЕдиный испытательный стенд для всех популяционных алгоритмов оптимизации
8
Simple use of population optimization algorithms.mq5
Скрипт
Простой пример использования популяционных алгоритмов оптимизации без визуализации
9
Test_AO_dDCA.mq5
СкриптИспытательный стенд для dDCA
Прикрепленные файлы |
Загрузить ZIP
dDCA.zip (378.2 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Знакомство с MQL5 (Часть 19): Автоматизация обнаружения волн Вульфа Знакомство с MQL5 (Часть 19): Автоматизация обнаружения волн Вульфа
Эта статья описывает, как программно выявлять бычьи и медвежьи паттерны волн Вульфа и торговать на их основе с помощью языка MQL5. Мы рассмотрим, как выявлять структуры волн Вульфа программным образом и исполнять сделки на их основе с помощью языка MQL5. Это включает в себя обнаружение ключевых точек свинга, проверку правил паттерна и подготовку советника к действию на основе найденных сигналов.
Нейросети в трейдинге: Двусторонняя адаптивная временная корреляция (Основные компоненты) Нейросети в трейдинге: Двусторонняя адаптивная временная корреляция (Основные компоненты)
В этой статье мы продолжаем реализацию фреймворка BAT средствами MQL5, показывая, как двунаправленная корреляция и модуль SATMA позволяют анализировать динамику рынка в контексте текущего состояния. Представлены ключевые архитектурных решения, позволяющие адаптировать фреймворк к анализу финансовых данных.
Нейросети в трейдинге: Двусторонняя адаптивная временная корреляция (Окончание) Нейросети в трейдинге: Двусторонняя адаптивная временная корреляция (Окончание)
Фреймворк BAT превращает хаотичный поток рыночных данных в точные прогнозы и взвешенные торговые решения. Тесты на исторических данных показывают стабильный рост капитала при контролируемых рисках. Архитектура модели проста, масштабируема и готова к дальнейшей оптимизации.
Знакомство с языком MQL5 (Часть 18): Введение в паттерн "Волны Вульфа" Знакомство с языком MQL5 (Часть 18): Введение в паттерн "Волны Вульфа"
В этой статье подробно объясняется паттерн волн Вульфа – как медвежьи, так и бычьи его вариации. В статье также проводится пошаговый разбор логики, используемой для выявления действительных сетапов на покупку и продажу на основе этого продвинутого графического паттерна.