
Алгоритм эволюции элитных кристаллов — Elite Crystal Evolution Algorithm (CEO-inspired): Практика
Содержание
Реализация алгоритма
Мы продолжаем описание специфических методов алгоритма оптимизации ECEA, идея которого представлена в предыдущей статье. Напомню, что разработанный алгоритм оперирует популяцией из кристаллов, динамически разделяемых на две группы: элитные (аналог замёрзших) и обычные (аналог незамёрзших). Элитные кристаллы выполняют интенсивный локальный поиск с адаптивно уменьшающимся шагом, обеспечивая эксплуатацию найденных перспективных областей. Обычные кристаллы используют три стратегии движения с вероятностями сорок-тридцать-тридцать процентов: направленное движение к глобально лучшему решению (эксплуатация), движение к ближайшему элитному и центру масс элитной группы (умеренная эксплуатация), исследовательские случайные прыжки двух масштабов (исследование). Периодический эффект "ветра" с вероятностью десять процентов регенерирует худшие неэлитные кристаллы, обеспечивая диверсификацию популяции. Итак, едем дальше.
Функция "MoveTowardsEliteCluster" предназначена для перемещения неэлитного агента (кристалла) в направлении группы лучших (элитных) агентов.
Определение ближайшего элитного агента: сначала вызывается функция "FindNearestElite (idx)", чтобы найти индекс ближайшего к текущему агенту (idx) элитного агента. Если элитных агентов нет (nearestElite < 0), функция завершается, так как перемещаться не к чему.
Перемещение по каждому измерению (координате): метод затем проходит по всем измерениям (координатам "c") текущего агента. Вычисляются два вектора направления:
- toElite — это разница между координатой ближайшего элитного агента и текущей координатой агента, указывает на ближайшего элитного агента.
- toCenter — это разница между координатой "центра масс" всех элитных агентов и текущей координатой агента, указывает на усредненное положение элитных агентов.
Генерируются два случайных числа "r1" и "r2" между 0.0 и 1.0. Эти числа используются для взвешивания влияния каждого из двух направлений (к ближайшему элитному и к центру масс элитных). Обновляется текущая координата агента путем добавления следующего:
- r1 * 0.3 * toElite — часть движения, направленная к ближайшему элитному агенту. Фиксированный коэффициент 0.3 определяет, насколько сильно агент будет стремиться к ближайшему элитному.
- r2 * 0.2 * toCenter — часть движения, направленная к центру масс элитных агентов. Фиксированный коэффициент 0.2 определяет, насколько сильно агент будет стремиться к усредненному положению элитных.
После суммирования этих компонентов, новое значение координаты пропускается через функцию "u.SeInDiSp". Эта функция, как и ранее, гарантирует, что значение координаты остается в пределах дозволенных границ и соответствует установленному шагу.
Метод помогает неэлитным агентам "подтягиваться" к областям, где уже найдены хорошие решения. Агент не просто движется в одном направлении, а комбинирует движение к ближайшему сильному примеру с движением к общему "центру притяжения" всех сильных примеров. Случайные весовые коэффициенты "r1" и "r2" добавляют элемент стохастичности, чтобы избежать застревания в одном и том же месте.
//———————————————————————————————————————————————————————————————————— void C_AO_ECEA::MoveTowardsEliteCluster (int idx) { int nearestElite = FindNearestElite (idx); if (nearestElite < 0) return; for (int c = 0; c < coords; c++) { // Движение к ближайшему элитному double toElite = a [nearestElite].c [c] - a [idx].c [c]; // Движение к центру масс элитных double toCenter = centerMass [c] - a [idx].c [c]; double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); a [idx].c [c] = a [idx].c [c] + r1 * 0.3 * toElite + r2 * 0.2 * toCenter; a [idx].c [c] = u.SeInDiSp (a [idx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Процедура "ExploratoryMove" предназначена для осуществления случайного перемещения агента с целью исследования пространства решений.
Индекс агента "idx" будет совершать случайное перемещение. Метод итерирует по всем измерениям (координатам "c") текущего агента, и для каждой координаты вычисляется "range" — полный диапазон допустимых значений этой координаты, от минимума (rangeMin [c]) до максимума (rangeMax [c]). Генерируется случайное число "r" в диапазоне от 0.0 до 1.0. Это число определяет, какой тип исследования будет предпринят:
- Если "r" меньше 0.7 (70% случаев), агент совершает небольшой шаг, который способствует локальному исследованию некоторой области пространства решений. Величина этого шага определяется как случайное значение от -1.0 до 1.0, умноженное на полный диапазон "range", на коэффициент "explorationRate" (который, контролирует общую интенсивность исследования) и на 0.1 (чтобы сделать шаг относительно небольшим).
- Иначе (30% случаев), агент совершает большой прыжок, который способствует глобальному исследованию больших участков пространства решений. Величина этого шага определяется аналогично, но умножается на 0.5 (что делает прыжок существенно большим, чем при локальном исследовании).
Текущее значение координаты агента (a [idx].c [c]) обновляется путем добавления вычисленного "move", и далее оно пропускается через функцию "u.SeInDiSp".
Метод вводит элемент случайности в поведение агента, позволяя ему покидать уже исследованные области и находить новые, потенциально лучшие решения. Процедура обеспечивает сбалансированное исследование: в большинстве случаев агент делает небольшие шаги для тонкой настройки вблизи текущих решений, но периодически совершает большие прыжки для охвата более широких просторов пространства поиска. Коэффициент "explorationRate" позволяет управлять общей активностью исследовательских перемещений.
//———————————————————————————————————————————————————————————————————— void C_AO_ECEA::ExploratoryMove (int idx) { for (int c = 0; c < coords; c++) { double range = rangeMax [c] - rangeMin [c]; // Простой но эффективный метод для исследования double r = u.RNDfromCI (0.0, 1.0); double move; if (r < 0.7) { // 70% - небольшие шаги (локальное исследование) move = u.RNDfromCI (-1.0, 1.0) * range * explorationRate * 0.1; } else { // 30% - большие прыжки (глобальное исследование) move = u.RNDfromCI (-1.0, 1.0) * range * explorationRate * 0.5; } a [idx].c [c] = a [idx].c [c] + move; a [idx].c [c] = u.SeInDiSp (a [idx].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Следующий метод описывает эффект "ветра", который является механизмом перемещения наихудшего неэлитного агента (кристалла) с целью обновления его позиции и потенциального нахождения лучшего решения.
Поиск наихудшего неэлитного агента: инициализируется переменная "worstNonElite" значением -1 (худший агент еще не найден) и "worstFitness" максимально возможным значением (DBL_MAX). Функция итерирует по всем агентам в популяции "popSize". Для каждого агента проверяется, является ли он неэлитным и имеет ли он более плохую приспособленность (a [i].f) по сравнению с текущим наихудшим "worstFitness". Если оба условия выполняются, то этот агент становится новым "худшим" (обновляются "worstFitness" и "worstNonElite).
Проверка наличия худшего агента: если "worstNonElite" осталось равным -1, это означает, что, либо нет неэлитных агентов, либо все они обладают одинаково "хорошей" (или "плохой" в зависимости от интерпретации) приспособленностью, на основании которой нельзя выделить худшего. В этом случае функция завершается.
Перемещение худшего агента: генерируется случайное число "strategy" в диапазоне от 0.0 до 1.0, которое определяет, как именно будет перемещаться худший агент.
Если strategy меньше 0.5 (50% случаев), агент перемещается около лучшего. Для каждой координаты "c":
- вычисляется диапазон (range) для данной координаты,
- генерируется небольшой случайный "шум" (noise) в пределах ±30% от полного диапазона,
- новая позиция агента устанавливается как (cB [c] + noise),
- значение координаты принудительно ограничивается допустимыми минимальным (rangeMin [c]) и максимальным (rangeMax [c]) значениями,
- финальная коррекция значения координаты выполняется с помощью "u.SeInDiSp", чтобы обеспечить соответствие шагу "rangeStep [c]" и границам.
Иначе (50% случаев), агент перемещается в полностью случайное место в пределах допустимых границ. Для каждой координаты "c":
- генерируется случайное число "xi" от 0.0 до 1.0,
- новая позиция устанавливается как: rangeMin [c] + xi * (rangeMax [c] - rangeMin [c]) — это гарантирует, что значение будет равномерно распределено между минимумом и максимумом,
- финальная коррекция значения координаты выполняется с помощью u.SeInDiSp.
Механизм "ветра" стремится "встряхнуть" систему, удаляя наименее успешных неэлитных агентов и помещая их в новые, потенциально более перспективные позиции. Это помогает избежать стагнации, когда популяция состоит в основном из похожих, не очень эффективных решений. Перемещение может быть либо локальным, вблизи текущего лучшего найденного решения, либо совершенно случайным, что дает шанс найти совершенно новую область поиска.
//———————————————————————————————————————————————————————————————————— void C_AO_ECEA::WindEffect () { // "Ветер" разрушает худшие не-элитные и переносит их int worstNonElite = -1; double worstFitness = DBL_MAX; for (int i = 0; i < popSize; i++) { if (!crystalData [i].isElite && a [i].f < worstFitness) { worstFitness = a [i].f; worstNonElite = i; } } if (worstNonElite < 0) return; // Перемещаем в новое место double strategy = u.RNDfromCI (0.0, 1.0); if (strategy < 0.5) { // Около лучшего for (int c = 0; c < coords; c++) { double range = rangeMax [c] - rangeMin [c]; double noise = u.RNDfromCI (-1.0, 1.0) * range * 0.3; a [worstNonElite].c [c] = cB [c] + noise; if (a [worstNonElite].c [c] < rangeMin [c]) a [worstNonElite].c [c] = rangeMin [c]; if (a [worstNonElite].c [c] > rangeMax [c]) a [worstNonElite].c [c] = rangeMax [c]; a [worstNonElite].c [c] = u.SeInDiSp (a [worstNonElite].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } else { // Полностью случайно for (int c = 0; c < coords; c++) { double xi = u.RNDfromCI (0.0, 1.0); a [worstNonElite].c [c] = rangeMin [c] + xi * (rangeMax [c] - rangeMin [c]); a [worstNonElite].c [c] = u.SeInDiSp (a [worstNonElite].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Функция "FindNearestElite" находит индекс ближайшего "элитного" агента (кристалла) к заданному агенту. Индекс агента "idx", для которого мы ищем ближайшего элитного соседа. Инициализируются переменные:
- nearest — значением -1 (что означает, что ближайший элитный агент еще не найден);
- minDist — максимально возможным значением (DBL_MAX), чтобы любая найденная дистанция была меньше.
- Игнорирование самого себя: если "i" совпадает с "idx" (то есть, это тот же самый агент, для которого мы ищем соседа), то этот агент пропускается (continue).
- Проверка элитности: если агент "i" не является элитным, то он пропускается. Мы ищем только среди элитных агентов.
Если агент "i" является элитным и не совпадает с "idx", вычисляется евклидово расстояние между агентом "idx" и агентом "i". Для каждой координаты "c" вычисляется разница (diff) между соответствующими координатами агентов. Квадрат этой разницы (diff * diff) добавляется к общей сумме квадратов разниц "dist". После прохода по всем координатам, к "dist" применяется операция квадратного корня, чтобы получить фактическое евклидово расстояние.
Если рассчитанное расстояние "dist" меньше текущего минимального расстояния "minDist", значит мы нашли нового ближайшего элитного агента. Обновляются "minDist" (текущее минимальное расстояние) и "nearest" (индекс этого нового ближайшего элитного агента). После полного перебора всех агентов, функция возвращает индекс (nearest) ближайшего элитного агента. Если элитных агентов в популяции не найдено, функция вернет -1.
Эта функция является вспомогательной и используется для определения, к какому "элитному" решению (наиболее успешному агенту) должен приблизиться другой агент.
//———————————————————————————————————————————————————————————————————— int C_AO_ECEA::FindNearestElite (int idx) { int nearest = -1; double minDist = DBL_MAX; for (int i = 0; i < popSize; i++) { if (i == idx) continue; if (!crystalData [i].isElite) continue; double dist = 0.0; for (int c = 0; c < coords; c++) { double diff = a [idx].c [c] - a [i].c [c]; dist += diff * diff; } dist = MathSqrt (dist); if (dist < minDist) { minDist = dist; nearest = i; } } return nearest; } //————————————————————————————————————————————————————————————————————
Функция "CalculateEliteRadii" вычисляет радиус влияния для каждого "элитного" агента (кристалла) на основе расстояний до других элитных агентов. Функция перебирает всех агентов в популяции, обрабатываются только те агенты, которые помечены как элитные.
Поиск ближайшего другого элитного агента. Для каждого элитного агента "i", инициализируется переменная "minDistToOtherElite" максимально возможным значением (DBL_MAX), чтобы найти минимальное расстояние. Запускается вложенный цикл, который снова перебирает всех агентов "j" в популяции. Проверяется, что мы не сравниваем агента самого с собой (i == j) и что другой агент "j" также является элитным (crystalData[j].isElite). Вычисляется евклидово расстояние между элитным агентом "i" и другим элитным агентом "j" по всем координатам. Если найденное расстояние "dist" меньше текущего минимального расстояния "minDistToOtherElite", то "minDistToOtherElite" обновляется.
Вычисление радиуса и сохранение. После внутреннего цикла (в котором было найдено минимальное расстояние до другого элитного агента), радиус для текущего элитного агента "i" вычисляется как половина этого минимального расстояния (minDistToOtherElite/2.0). Этот вычисленный радиус сохраняется в структуре данных, связанной с агентом "i" (crystalData [i].radius).
Этот механизм предназначен для определения "области влияния" каждого элитного решения. Радиус выбирается таким образом, чтобы он был меньше половины расстояния до ближайшего соседа. Это означает, что области влияния разных элитных агентов не должны перекрываться. Это может быть полезно для поддержания разнообразия в популяции, гарантируя, что разные элитные решения действительно представляют собой отдельные, отличные от других, области поиска.
//———————————————————————————————————————————————————————————————————— void C_AO_ECEA::CalculateEliteRadii () { // Вычисляем радиусы влияния элитных на основе их взаимных расстояний for (int i = 0; i < popSize; i++) { if (!crystalData [i].isElite) continue; double minDistToOtherElite = DBL_MAX; for (int j = 0; j < popSize; j++) { if (i == j) continue; if (!crystalData [j].isElite) continue; double dist = 0.0; for (int c = 0; c < coords; c++) { double diff = a [i].c [c] - a [j].c [c]; dist += diff * diff; } dist = MathSqrt (dist); if (dist < minDistToOtherElite) { minDistToOtherElite = dist; } } crystalData [i].radius = minDistToOtherElite / 2.0; } } //————————————————————————————————————————————————————————————————————
Функция "GetDynamicExplorationRate" динамически регулирует уровень исследования на основе текущего хода выполнения алгоритма. Основная цель этой функции — уменьшать интенсивность исследования "exploration rate" по мере выполнения алгоритма. На начальных этапах алгоритма важно исследовать новые области, а по мере приближения к оптимальному решению, фокус смещается на более точную доводку найденных решений.
Вычисляется переменная "progress" (прогресс выполнения). Он определяется как отношение текущего количества итераций (iterationCount) к фиксированному максимальному значению (100.0). Если "progress" превышает 1.0 (то-есть, выполнено более 100 итераций), он обрезается до 1.0, чтобы гарантировать, что максимальный коэффициент уменьшения составит 0.7. Возвращаемое значение — это результат умножения базовой ставки исследования (explorationRate) на коэффициент уменьшения (1.0 - 0.7 * progress).
На начальных этапах "progress" близок к 0. По мере увеличения "progress" (приближения "progress" к 1.0), коэффициент будет уменьшаться. Например, когда "progress" равен 1.0, коэффициент составит 1.0 - 0.7 * 1.0 = 0.3. Это означает, что ставка исследования уменьшится до 30% от своей базовой величины.
Представьте, что у вас есть "ручка" для регулировки исследования. Эту ручку в начале алгоритма ставят на максимум. Функция "GetDynamicExplorationRate" постепенно поворачивает эту ручку, уменьшая интенсивность исследования. Таким образом, на поздних стадиях алгоритм меньше "блуждает", а больше сосредоточен на улучшении найденных решений.
//———————————————————————————————————————————————————————————————————— double C_AO_ECEA::GetDynamicExplorationRate () { // Адаптивная интенсивность исследования // Начинаем с высокой, уменьшаем со временем double progress = (double)iterationCount / 100.0; if (progress > 1.0) progress = 1.0; return explorationRate * (1.0 - 0.7 * progress); } //————————————————————————————————————————————————————————————————————
Метод "Revision" обновляет информацию о лучшем обнаруженном решении и отслеживает стагнацию (отсутствие улучшения). Перед возможным обновлением, текущее лучшее значение функции (обозначаемое "fB") сохраняется в переменной "prevBest". Это нужно для последующего сравнения. Вызывается другая функция (UpdateEliteStatus), которая пересматривает и при необходимости изменяет статус "элитности" для агентов в популяции.
Обновление лучшего решения. Наличие "a [0]" предполагает, что агенты сортируются или обрабатываются таким образом, что "a [0]" всегда содержит самое лучшее текущее решение. Значение функции для лучшего агента (a [0].f) присваивается "fB". Координаты этого лучшего решения "a [0].c" копируются в "cB" (переменная для хранения координат лучшего известного решения).
Отслеживание стагнации. Сравнивается текущее лучшее значение функции (fB) с сохраненным предыдущим лучшим значением (prevBest). Если разница между ними очень мала (меньше 1e-10, что указывает на отсутствие существенного улучшения), счетчик стагнации (noImprovementCount) увеличивается на единицу. Если же улучшение произошло (разница больше 1e-10), счетчик стагнации сбрасывается в ноль.
Эта функция выполняет периодическую "ревизию" состояния алгоритма:
- определяет, кто из агентов остается "элитным";
- фиксирует самое лучшее решение, найденное на данный момент;
- контролирует, продолжает ли алгоритм находить новые, лучшие решения, или же он "застрял" на одном месте (стагнация).
//———————————————————————————————————————————————————————————————————— void C_AO_ECEA::Revision () { double prevBest = fB; // Обновляем статус элитных кристаллов UpdateEliteStatus (); fB = a [0].f; ArrayCopy (cB, a [0].c, 0, 0, coords); // Отслеживаем стагнацию if (MathAbs (fB - prevBest) < 1e-10) noImprovementCount++; else noImprovementCount = 0; } //————————————————————————————————————————————————————————————————————
Результаты тестов
ECEA|Elite Crystal Evolution Algorithm|50.0|10.0|0.5|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.6824547309245615
25 Hilly's; Func runs: 10000; result: 0.4467067359108001
500 Hilly's; Func runs: 10000; result: 0.29066242412735266
=============================
5 Forest's; Func runs: 10000; result: 0.6110808506476546
25 Forest's; Func runs: 10000; result: 0.36838637212724284
500 Forest's; Func runs: 10000; result: 0.20596535563655824
=============================
5 Megacity's; Func runs: 10000; result: 0.36
25 Megacity's; Func runs: 10000; result: 0.2033846153846154
500 Megacity's; Func runs: 10000; result: 0.11233846153846264
=============================
All score: 3.28098 (36.46%)
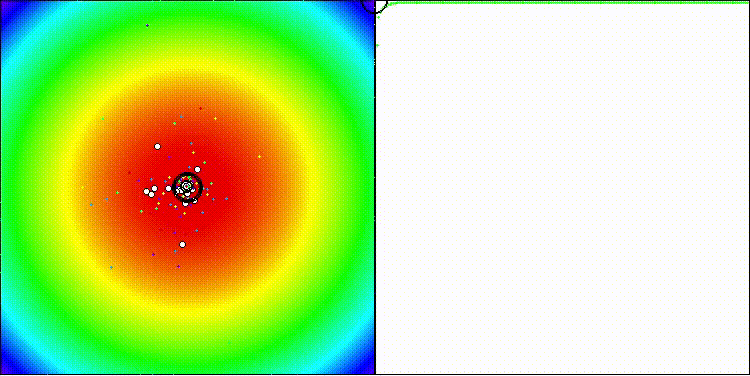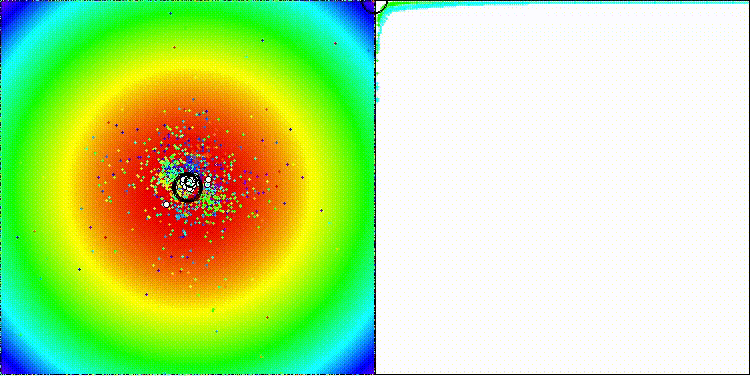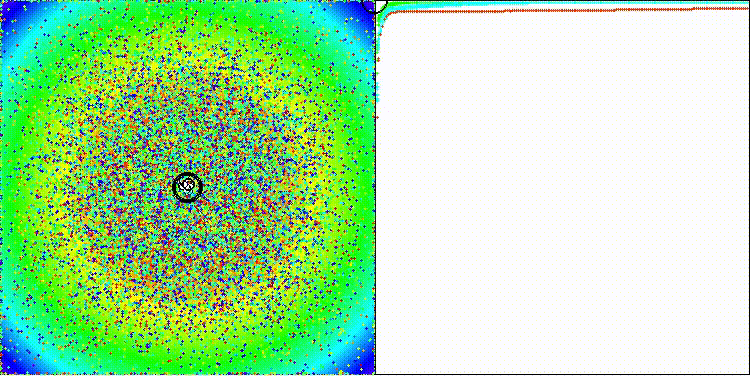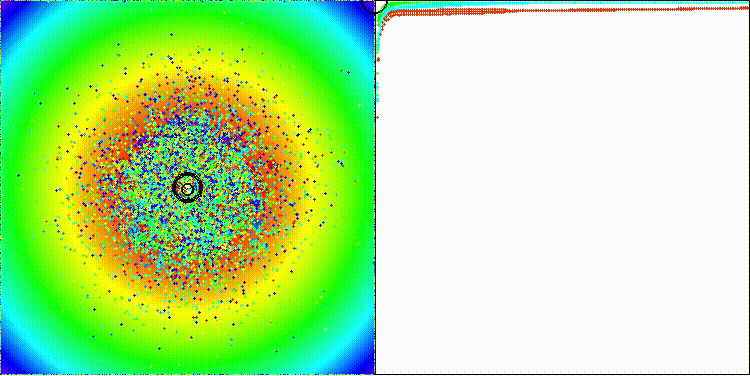
На визуализации заметны объекты кристаллизации, поисковые способности алгоритма лучше проявляются на функциях средней размерности.
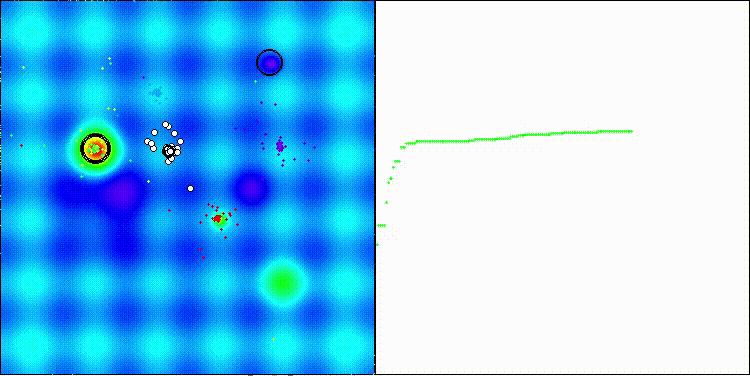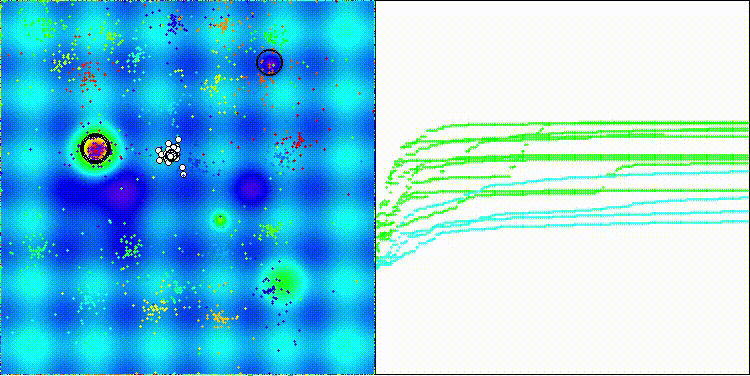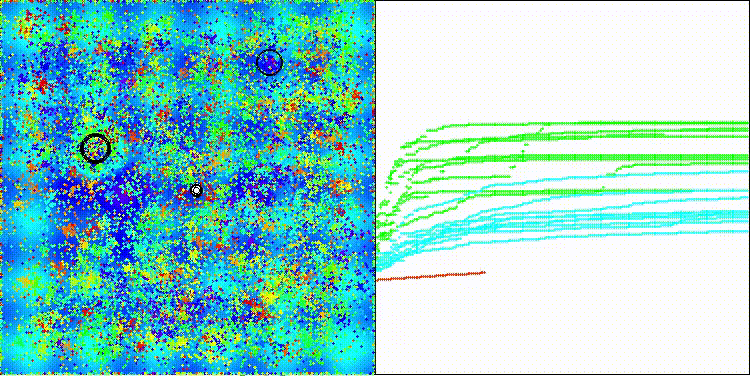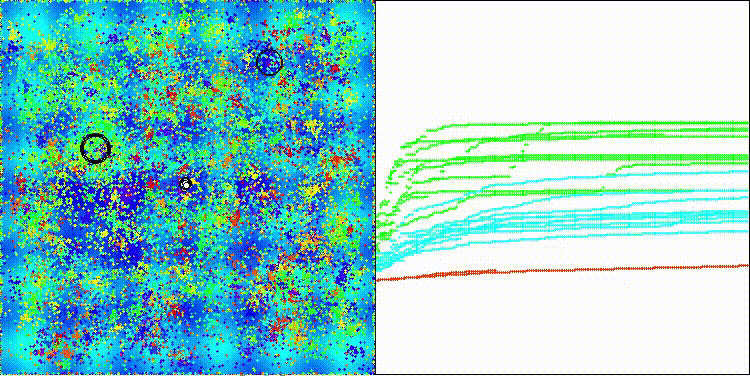
ECEA на тестовой функции Hilly
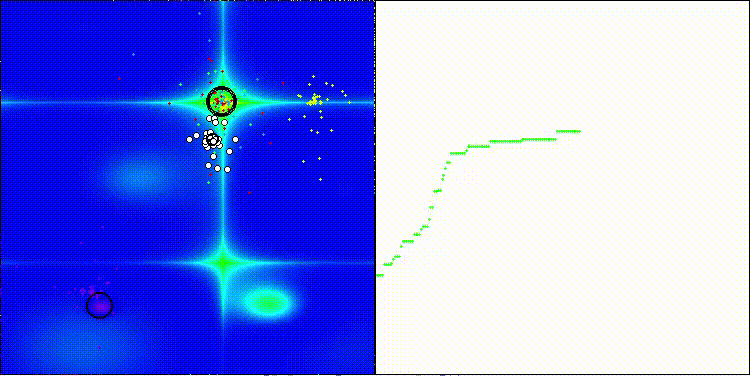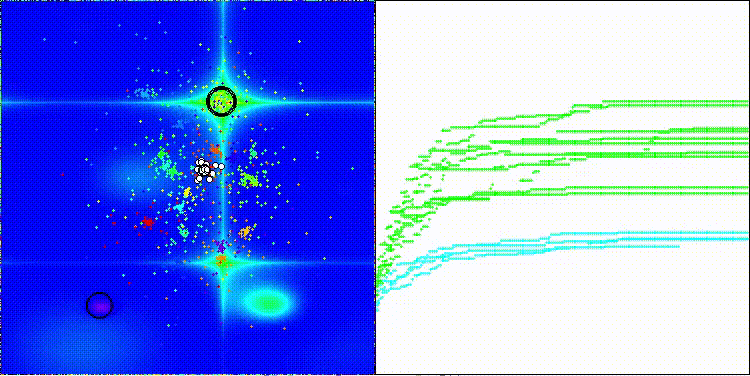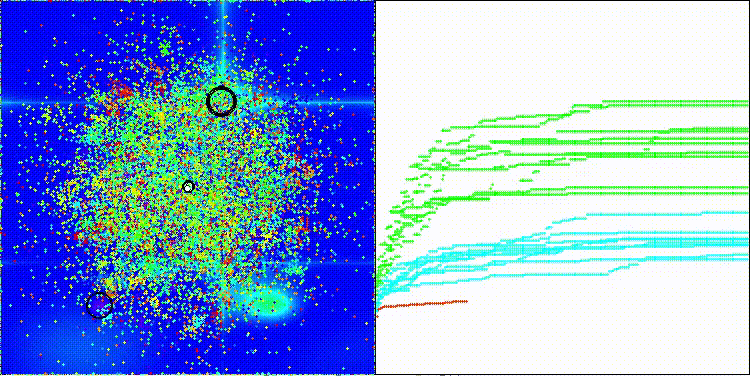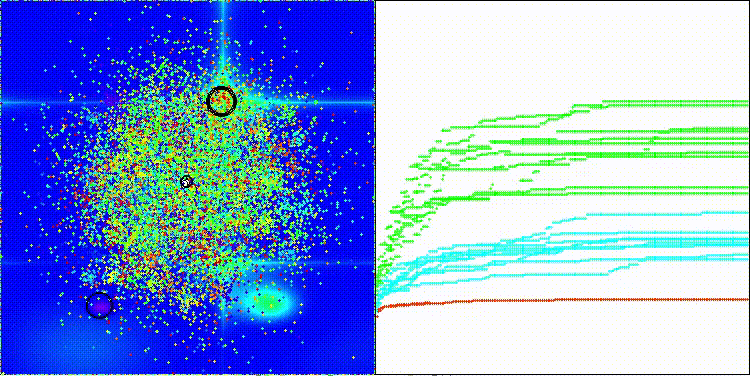
ECEA на тестовой функции Forest
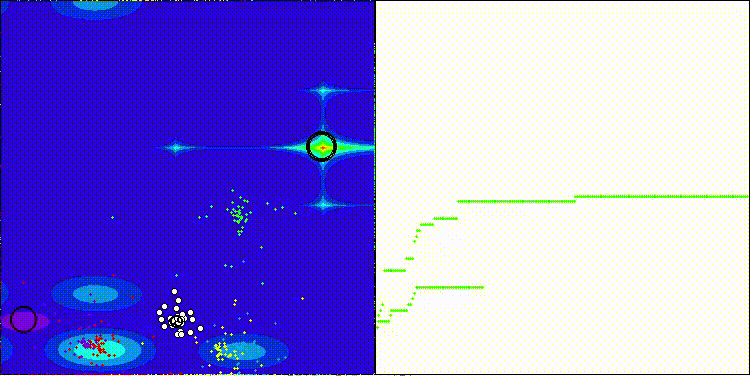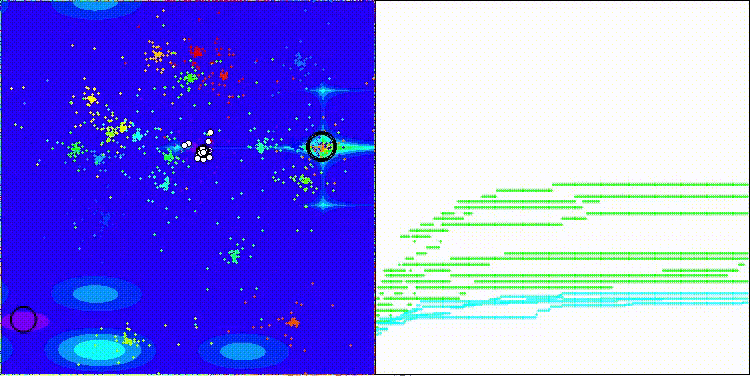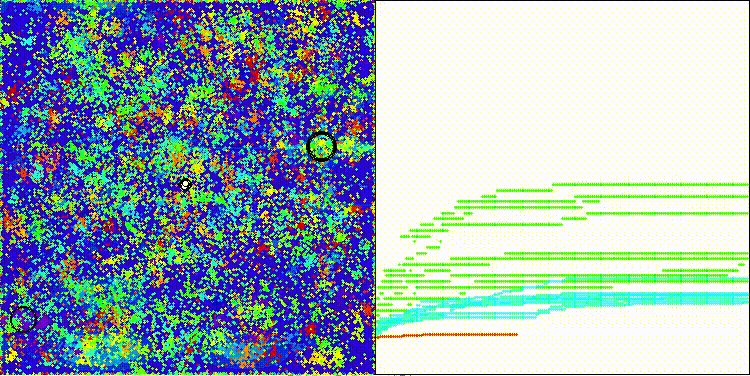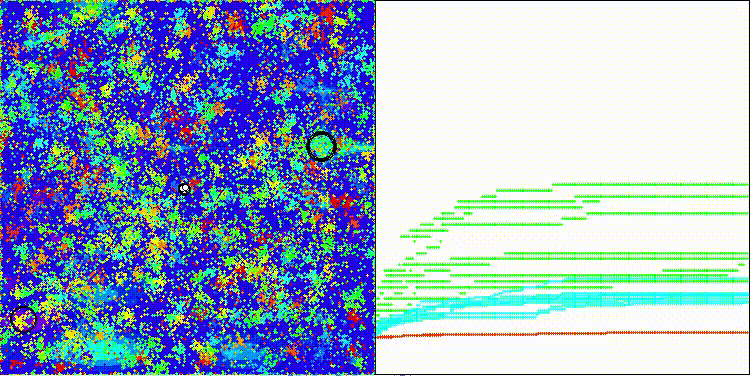
ECEA на тестовой функции Forest
Давайте еще посмотрим, как работает алгоритма ECEA на стандартных функциях, которые не участвуют в определении нашего рейтинга популяционных алгоритмов, но являются общепринятыми для тестирования. На таких видах задач, как можно заметить, алгоритм имеет очень высокие показатели сходимости, следовательно, каждый алгоритм нужно тестировать на различных типах функций, чтобы определить наилучший его потенциал для работы.
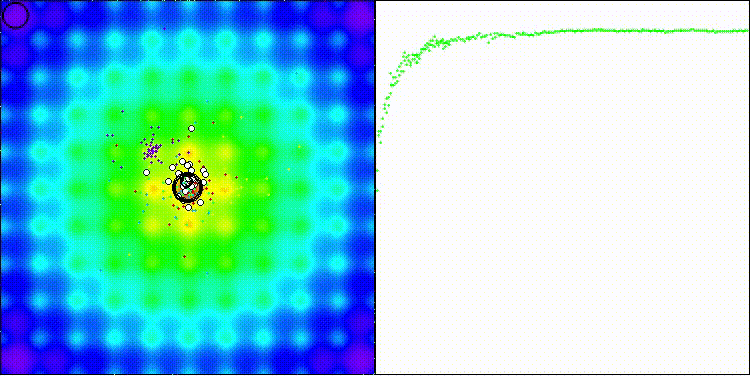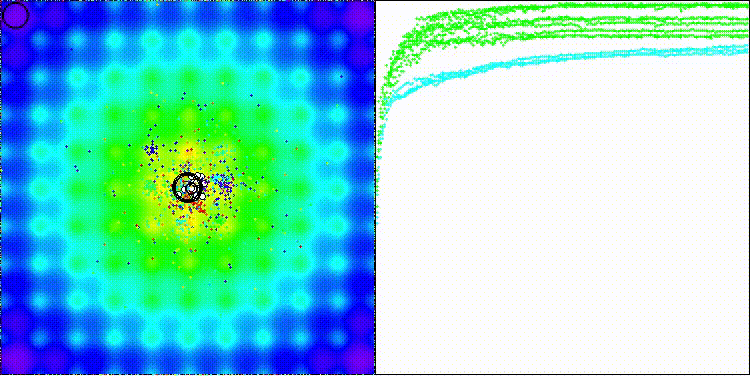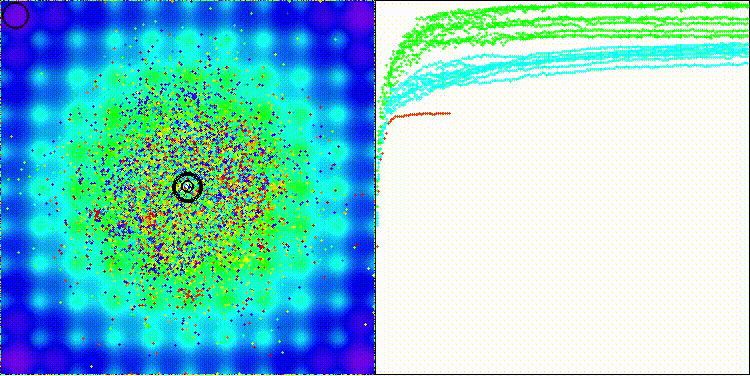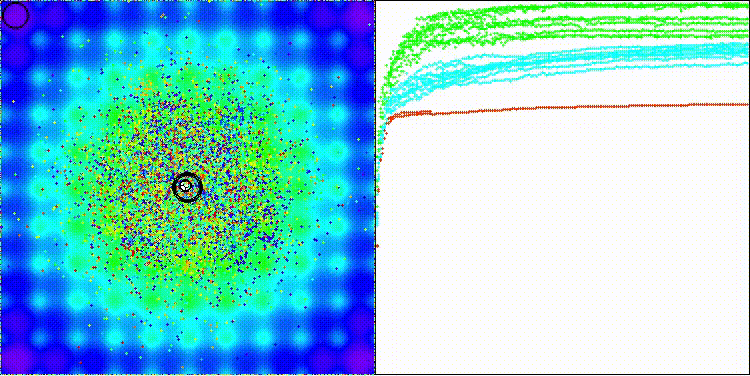
ECEA на стандартной тестовой функции Ackley
ECEA на стандартной тестовой функции Paraboloid
В рейтинговой таблице алгоритм ECEA представлен ознакомительно.
№ | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 5 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 6 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 7 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 8 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 26 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 27 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 28 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 29 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 30 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 31 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 32 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 33 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 34 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 35 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 36 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 37 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 38 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 39 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 40 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 41 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 42 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 43 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 44 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| 45 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| ECEA | Elite crystal_evolution_algorithm | 0,68245 | 0,44671 | 0,29066 | 1,41982 | 0,61108 | 0,36838 | 0,20597 | 1,18543 | 0,36000 | 0,20338 | 0,11233 | 0,67571 | 3,281 | 36,46 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Алгоритм ECEA представляет собой попытку адаптации концепции кристаллизации из оригинального алгоритма Crystal Energy Optimizer, разработанного для комбинаторных задач, к области непрерывной оптимизации в многомерных вещественных пространствах. Экспериментальное исследование на наших бенчмарк-функциях показало, что разработанный алгоритм демонстрирует результат в 36%, что превышает эффективность случайного поиска. Этот результат свидетельствует о том, что алгоритм действительно работает и обладает осмысленной поисковой способностью, превосходящей примитивные методы, однако он не достигает порогового значения, необходимого для включения в число лучших алгоритмов оптимизации.
Анализ причин полученных результатов указывает на сложность прямой адаптации алгоритмов из комбинаторной области в непрерывную. Оригинальный CEO основывается на специфических механизмах, имеющих смысл только для дискретных структур, таких как граф связей между решениями-маршрутами в задаче коммивояжёра, физические формулы теплопередачи с влиянием центра озера обратно пропорциональны расстоянию, взаимодействие между парами связанных замёрзших кристаллов через треугольные расстояния, процесс осаждения новых кристаллов в позиции между существующими соседями с разрывом и созданием новых связей. В процессе адаптации ECEA все эти уникальные механизмы были радикально упрощены, поскольку они не имеют прямых аналогов в геометрии непрерывного пространства. В итоге от оригинального алгоритма остались концептуальные идеи верхнего уровня: разделение популяции на элитные и обычные агенты, наличие центрального аттрактора, периодическая диверсификация через эффект ветра и баланс между исследованием и эксплуатацией.
Несмотря на ограничения, работа по созданию ECEA имеет определённую научную и практическую ценность. Созданная реализация является полностью работоспособной, стабильной, не содержит ошибок и может использоваться как базовая версия для дальнейших исследований и улучшений. Простота алгоритма со всего четырьмя настраиваемыми параметрами делает его понятным и легко модифицируемым, что полезно в образовательных целях и для быстрого прототипирования идей.
Перспективы улучшения алгоритма связаны с несколькими направлениями. Добавление механизма оппозиционного обучения, когда для каждого кристалла рассматривается также его противоположная точка в пространстве поиска, может помочь избежать ситуаций, когда вся популяция сосредотачивается в неправильной области. Периодическая мутация элитных кристаллов с небольшой вероятностью может предотвратить их застревание в локальных оптимумах.
В заключение следует отметить, что эксперимент по адаптации CEO для непрерывной оптимизации можно считать успешным с точки зрения научного исследования, поскольку он выявил и продемонстрировал ключевые проблемы такой адаптации и показал, что прямой перенос комбинаторных алгоритмов в непрерывную область требует не просто замены операторов, но переосмысления базовых механизмов. С практической точки зрения результат является промежуточным: алгоритм работает стабильно и превосходит случайный поиск, но не достигает производительности лучших популяционных методов оптимизации.
ECEA может быть рекомендован как учебный пример адаптации природно-вдохновлённых алгоритмов, как отправная точка для дальнейших улучшений, или как простой и понятный метод. Основной вклад работы заключается не столько в создании высокоэффективного алгоритма, сколько в систематическом исследовании процесса междоменной адаптации метаэвристик.
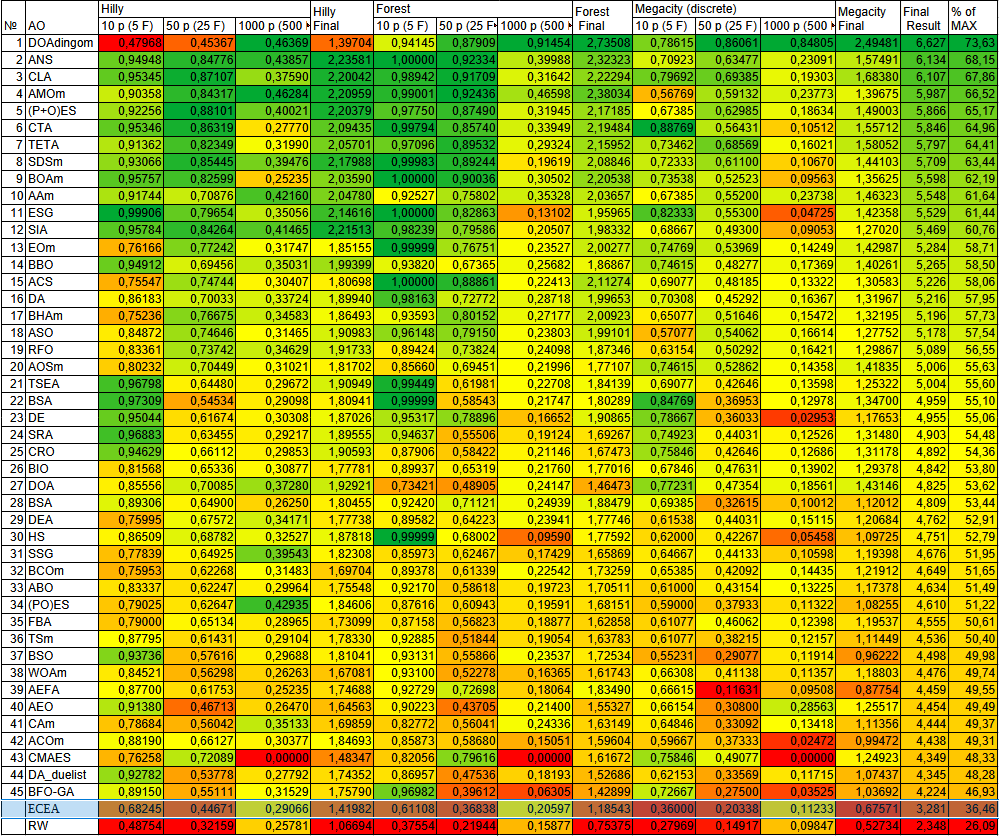
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
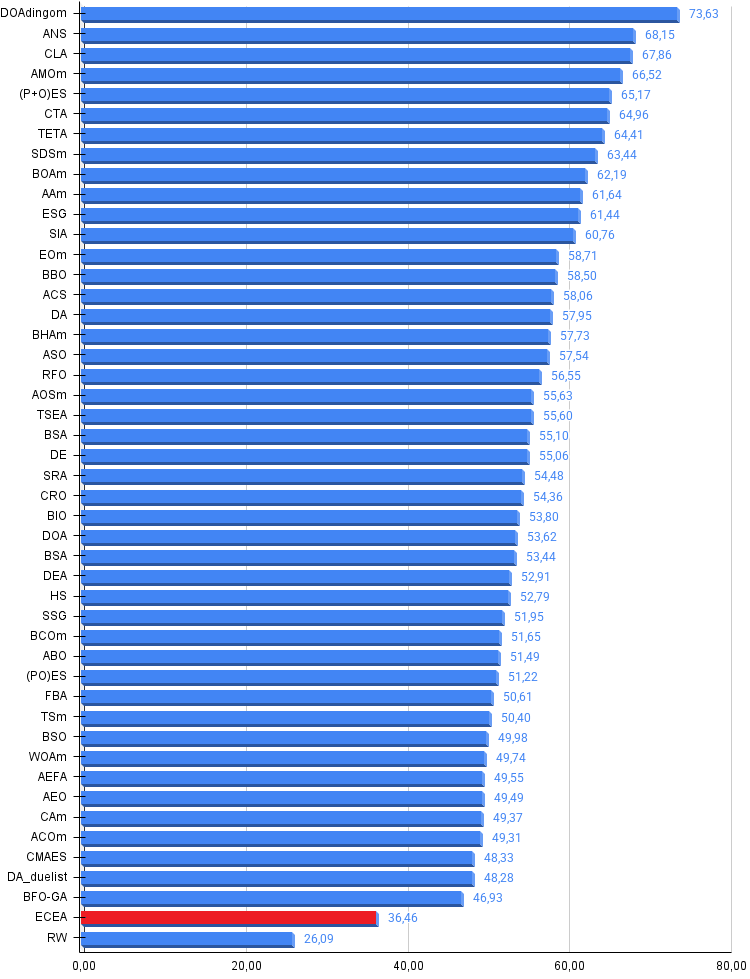
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма ECEA:
Плюсы:
- Быстрый.
- Лучшие результаты на функциях средней и большой размерности.
Минусы:
- Более слабые результаты на функциях малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_ECEA.mq5 | Скрипт | Испытательный стенд для ECEA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Рекуррентное моделирование микродвижений рынка (Окончание)
Нейросети в трейдинге: Рекуррентное моделирование микродвижений рынка (Окончание)
 Моделирование рынка (Часть 12): Сокеты (VI)
Моделирование рынка (Часть 12): Сокеты (VI)
 Инженерия признаков с Python и MQL5 (Часть III): Угол наклона цены (2) Полярные координаты
Инженерия признаков с Python и MQL5 (Часть III): Угол наклона цены (2) Полярные координаты
 Машинное обучение и Data Science (Часть 33): Pandas Dataframe в MQL5, упрощаем сбор данных для машинного обучения
Машинное обучение и Data Science (Часть 33): Pandas Dataframe в MQL5, упрощаем сбор данных для машинного обучения
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования