Redes neuronales en el trading: Aprendizaje contextual aumentado por la memoria (MacroHFT)

Introducción

Los mercados financieros atraen a un gran número de inversores debido a su amplia accesibilidad y a su rentabilidad potencialmente elevada. Entre todos los activos disponibles, las criptomonedas destacan por su extraordinaria volatilidad, que abre oportunidades únicas para obtener importantes beneficios en poco tiempo. Una ventaja adicional es el modo de funcionamiento ininterrumpido, que permite a los tráders reaccionar rápidamente a los cambios en la situación del mercado. Sin embargo, una volatilidad tan elevada no solo conlleva beneficios, sino también importantes riesgos, que requieren estrategias de gestión más sofisticadas.

El trading de alta frecuencia (HFT), una forma de trading algorítmico basada en la ejecución ultrarrápida de las transacciones, se utiliza cada vez más en los mercados de criptomonedas para maximizar los beneficios. El HFT ha ocupado durante mucho tiempo una posición de liderazgo en los mercados financieros tradicionales, y recientemente también se ha aplicado de forma activa en el ámbito de las criptomonedas. El trading de alta frecuencia se caracteriza no solo por su velocidad de ejecución, sino también por su capacidad para procesar enormes cantidades de datos en tiempo real, lo cual lo hace indispensable en unos mercados de criptomonedas muy dinámicos.

Los métodos de aprendizaje por refuerzo (RL) son cada vez más populares en finanzas porque pueden resolver complejos problemas secuenciales de toma de decisiones. Los algoritmos de RL son capaces de gestionar datos multidimensionales, considerar distintos parámetros y adaptarse a condiciones cambiantes. Sin embargo, a pesar de los avances en el trading de baja frecuencia, aún se están desarrollando algoritmos eficientes para los mercados de criptomonedas de alta frecuencia. Las peculiaridades de los mercados de criptomonedas son su alta volatilidad, inestabilidad y la necesidad de considerar horizontes comerciales a largo plazo junto con una respuesta rápida.

Los algoritmos de HFT existentes para criptomonedas se enfrentan a una serie de retos que limitan su eficacia. En primer lugar, el mercado suele tratarse como un único sistema estacionario y muchos algoritmos se limitan al análisis de tendencias, ignorando la volatilidad. Este planteamiento complica la gestión de riesgos y reduce la precisión de las previsiones. En segundo lugar, muchas estrategias son propensas al sobreentrenamiento debido a un enfoque excesivo en un conjunto reducido de características del mercado. Y esto provoca una reducción de su capacidad para adaptarse a las nuevas condiciones del mercado. Por último, las políticas comerciales individuales de los agentes carecen a menudo de la flexibilidad necesaria para responder con rapidez a cambios bruscos, lo que resulta especialmente crítico en mercados con alta frecuencia de datos.

Una de las opciones para resolver los problemas anteriores se presenta en el artículo "MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading". Sus autores proponen el framework MacroHFT, un enfoque innovador basado en el aprendizaje por refuerzo dependiente del contexto. Este framework está diseñado específicamente para el trading de criptomonedas de alta frecuencia en un framework temporal de minutos. MacroHFT usa la información macroeconómica y otros datos contextuales para mejorar la toma de decisiones. El proceso consta de dos pasos fundamentales. En el primero, el mercado se clasifica según los indicadores de tendencia y volatilidad. Los subagentes especializados reciben formación para cada categoría de condiciones de mercado y ajustan sus estrategias según la situación actual. Dichos subagentes aportan flexibilidad y capacidad para adaptarse a las condiciones del mercado local.

En el segundo paso, se crea un hiperagente que integra las estrategias de los subagentes y optimiza su uso en función de la dinámica del mercado. El hiperagente está equipado con un módulo de memoria que tiene en cuenta la experiencia reciente y permite desarrollar estrategias comerciales estables y adaptables. Esto garantiza que el sistema resulte muy resistente a los cambios repentinos en las condiciones del mercado y ayuda a minimizar los riesgos.

El algoritmo MacroHFT

El framework MacroHFT supone una innovadora plataforma comercial algorítmica diseñada específicamente para los mercados de criptomonedas, con su alta volatilidad y sus rápidos cambios. El framework se basa en métodos de aprendizaje por refuerzo que permiten crear algoritmos adaptativos capaces de analizar las condiciones del mercado y predecir sus cambios. La idea principal consiste en integrar subagentes especializados, cada uno optimizado para un escenario de mercado específico, y un hiperagente que coordine su trabajo, garantizando la coherencia y eficacia del sistema en su conjunto.

En un entorno de mercado altamente volátil y en constante cambio, el uso de un único agente de aprendizaje por refuerzo (RL) se revela insuficientemente eficaz. Esto se debe a que las condiciones del mercado pueden cambiar con demasiada rapidez y de forma imprevisible, y un único algoritmo no tiene tiempo de adaptarse a cada nueva situación. Para resolver este problema, los autores del framework MacroHFT proponen crear varios subagentes especializados, cada uno de los cuales está entrenado en determinadas condiciones de mercado, lo cual permite construir un sistema más flexible y adaptable.

La idea básica es segmentar y clasificar los datos del mercado usando dos parámetros clave: la tendencia y la volatilidad. Para el análisis, los datos de mercado se desglosan en bloques de longitud fija. Estas unidades se usan tanto para el entrenamiento como para las pruebas. Después, a cada bloque se le asignan etiquetas que ayudan a identificar a qué tipo de condiciones de mercado pertenece, lo cual facilita su aprendizaje por parte de los subagentes.

El proceso de etiquetado de datos se divide en dos pasos:

1. Definición de las etiquetas de tendencia. Para identificar la tendencia del mercado, se usan los datos de cada bloque, que se pasan por un filtro de baja frecuencia. Esto permite eliminar el ruido y destacar la dirección principal del movimiento de los precios. Luego se aplica una regresión lineal: la inclinación de la línea resultante sirve como indicador de tendencia. A partir de ahí, las tendencias se clasificarán en positivas (mercado alcista), neutras (planas) o negativas (mercado bajista).
2. Identificación de las etiquetas de volatilidad. Para evaluar el nivel de volatilidad, se calculará el valor medio de las variaciones de precios dentro de cada bloque. Los valores resultantes se clasificarán en tres categorías: volatilidad alta, volatilidad media y volatilidad baja. La clasificación se basa en la distribución de los datos y el uso de cuantiles para determinar los límites de las categorías.

Así, cada bloque de datos obtiene dos etiquetas: tendencia y volatilidad. Todos los datos se dividen en seis categorías que se corresponden con las combinaciones de los tipos de tendencia (alcista, neutra, bajista) y niveles de volatilidad (alta, media, baja). De este modo se crean seis subconjuntos de datos de entrenamiento, cada uno diseñado para formar a subagentes para condiciones de mercado específicas. A continuación, se aplica un etiquetado similar a los datos de prueba, que utiliza umbrales calculados a partir de la muestra de entrenamiento. Este enfoque garantiza que el rendimiento de cada subagente se valore de forma justa.

Cada subagente se entrena con uno de los seis subconjuntos de datos. Luego se comprueba su rendimiento con el conjunto de pruebas correspondiente a su categoría. Esto permite crear subagentes especializados, cada uno optimizado para unas condiciones de mercado concretas. Por ejemplo, un subagente resultará más eficaz en un mercado alcista con alta volatilidad y otro será más eficaz en un mercado bajista con baja volatilidad. Esta estructura modular permite al sistema adaptarse de forma flexible a las condiciones cambiantes y mejorar su eficacia.

Para entrenar a los subagentes, los autores del framework proponen utilizar el método Double Deep Q-Network(DDQN) con una arquitectura dual que considera las lecturas de mercado, las características contextuales y la posición del tráder. Estos datos son procesados por las distintas capas de la red neuronal y después se combinan en una visión global. La representación resultante se adapta usando el Adaptive Layer Norm Block, que permite tener en cuenta las condiciones específicas del mercado, ofreciendo flexibilidad y precisión en la toma de decisiones.

MacroHFT prevé la creación de seis subagentes, cada uno especializado en condiciones de mercado específicas. Las estrategias finales son combinadas por el hiperagente, que garantiza la eficacia y adaptabilidad del sistema en el volátil mercado de las criptomonedas.

El hiperagente reúne los resultados de los subagentes para formar una política flexible y eficaz capaz de adaptarse a los cambios dinámicos del mercado. Asimismo, integra sus soluciones de subagentes utilizando una metapolítica basada en el modelo de ponderación SoftMax. Este planteamiento minimiza el riesgo de dependencia excesiva de un único subagente y considera los puntos de vista de todos los componentes del sistema.

Una de las principales ventajas del hiperagente es el uso de indicadores técnicos de tendencia y volatilidad para tomar decisiones rápidas. Esto le permite responder rápidamente a los cambios en las condiciones del mercado. Sin embargo, los métodos tradicionales de aprendizaje basados en MDP de alto nivel tienen sus propias complicaciones: una alta variabilidad en las recompensas y raros cambios extremos del mercado. Para resolver estos problemas, en el hiperagente se integra un módulo de memoria.

El módulo de memoria se implementa como una tabla de tamaño limitado que almacena los vectores clave de los estados y acciones. Las nuevas experiencias se añaden a la memoria calculando su valor a partir de una puntuación Q de un paso. Cuando la tabla se rellena, los registros antiguos se borran para mantener los datos más actuales. Durante la búsqueda, el hiperagente encuentra los registros más relevantes calculando la distancia L2 entre el estado actual y las claves almacenadas. El valor total se calcula como una suma ponderada de los datos de la memoria.

El módulo de memoria también se usa para mejorar la evaluación de las acciones del hiperagente. Esto se logra modificando la función de pérdida, que añade un nuevo componente para conciliar las estimaciones de la memoria con las predicciones actuales del hiperagente. Este enfoque permite entrenar estrategias comerciales más estables que pueden responder eficazmente a los cambios repentinos en las condiciones del mercado.

MacroHFT se caracteriza por una arquitectura bien pensada que lo convierte en una herramienta versátil para operar en diversos mercados. Aunque principalmente se desarrolló para las criptomonedas, sus planteamientos y algoritmos pueden adaptarse para su uso en otros mercados financieros, incluidos los mercados bursátiles o de materias primas.

A continuación le mostramos la visualización del framework MacroHFT realizada por el autor.

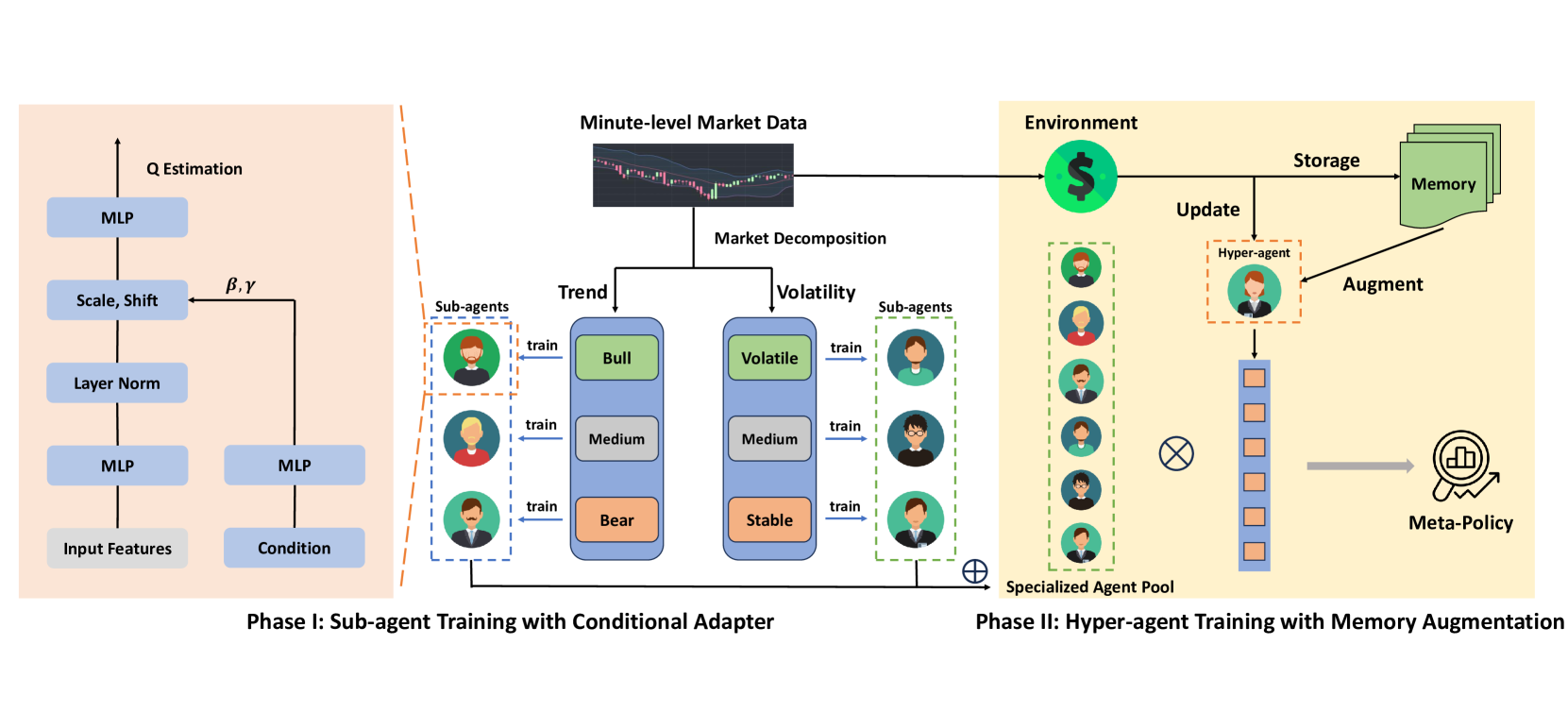
Implementación con la ayuda de MQL5

Tras analizar los aspectos teóricos del framework MacroHFT, pasaremos a la parte práctica de nuestro artículo, donde implementaremos nuestra propia visión de los enfoques propuestos utilizando herramientas MQL5.

En la aplicación presentada, mantendremos el concepto básico de construcción de modelos jerárquicos, pero introduciendo cambios significativos en la arquitectura de los componentes y en el proceso de aprendizaje. En primer lugar, abandonaremos la división manual de las muestras de entrenamiento y prueba en bloques con etiquetas de tendencia y nivel de volatilidad. En segundo lugar, el proceso de aprendizaje del modelo no se separará en dos fases distintas. En su lugar, implementaremos el entrenamiento simultáneo del hiperagente y los subagentes en un único proceso iterativo. Podemos suponer que durante el entrenamiento, el hiperagente será capaz de categorizar de forma independiente los estados del entorno y asignar funciones a los agentes.

Asimismo, hemos abandonado el uso de tablas para organizar la memoria del hiperagente, sustituyéndola por el objeto de memoria de tres niveles desarrollado como parte de nuestro trabajo con el framework FinCon. Además, hemos decidido integrar un agente analítico con una arquitectura más compleja y avanzada para implementar de forma más eficaz la funcionalidad de los subagentes. Así, comenzaremos nuestro trabajo de implementación de los componentes del framework MacroHFT creando un hiperagente.

Construyendo un hiperagente

La descripción de la funcionalidad del Hiperagente ofrecida por los autores del framework MacroHFT afirma que analiza el estado actual del entorno, lo mapea a objetos en memoria y devuelve la distribución de probabilidad de la clasificación del estado analizado. Puede tratarse de una clasificación de la tendencia o de la volatilidad del movimiento del mercado. La distribución de probabilidades resultante se usará para calcular la contribución de cada subagente a la decisión final sobre la ejecución de una transacción comercial, lo cual se logrará ponderando las decisiones de los subagentes según su relevancia para las condiciones actuales del mercado. Este planteamiento permitirá adaptar la solución global en función de los factores dominantes.

En otras palabras, tendremos que crear un componente de clasificación del estado del entorno analizado que considere el contexto de los estados anteriores almacenados en la memoria. Esto se consigue analizando la secuencia de cambios en los parámetros del mercado y su correlación con la situación actual. Los estados anteriores ayudarán a identificar tendencias a largo plazo y los patrones ocultos, lo cual permitirá tomar decisiones más informadas a la hora de categorizar la situación actual del mercado.

Crearemos dicho hiperagente dentro del objeto CNeuronMacroHFTHyperAgent, cuya estructura mostramos a continuación.

class CNeuronMacroHFTHyperAgent  :  public CNeuronSoftMaxOCL
  {
protected:
   CNeuronMemoryDistil  cMemory;
   CNeuronRMAT          cStatePrepare;
   CNeuronTransposeOCL  cTranspose;
   CNeuronConvOCL       cScale;
   CNeuronBaseOCL       cMLP[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFTHyperAgent(void) {};
                    ~CNeuronMacroHFTHyperAgent(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint agents, uint stack_size,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFTHyperAgent; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  };

Como clase padre, se usará la implementación de la capa SoftMax. Esta función fue propuesta por los autores del framework para calcular la distribución de probabilidad, y desempeña un papel clave en la determinación de la contribución de cada subagente a la decisión final, garantizando la precisión y adaptabilidad del modelo.

La estructura del hiperagente presenta un conjunto estándar de métodos virtuales y varios objetos internos que suponen la base para construir un algoritmo que analice el estado actual del entorno. Aprenderemos más sobre su funcionalidad durante la implementación de los métodos de la clase de hiperagente.

Todos los objetos internos se declararán estáticamente, lo cual nos permitirá dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización de los objetos declarados y heredados se realizará en el método Init. En los parámetros de este método se transmitirán varias constantes que permiten definir inequívocamente la arquitectura del objeto creado.

bool CNeuronMacroHFTHyperAgent::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint window, uint window_key, uint units_count,
                                     uint heads, uint layers, uint agents, uint stack_size,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, agents, optimization_type, batch))
      return false;
   SetHeads(1);
//---
   int index = 0;

En el cuerpo del método, como viene siendo habitual, primero llamaremos al método homónimo de la clase padre. En este caso, hablamos de la capa de características SoftMax. Esperamos que el tamaño del vector de resultados sea igual al número de subagentes usados. Obtendremos el valor requerido del programa que realiza la llamada, en los parámetros del método.

A continuación, inicializaremos los objetos internos. En primer lugar, inicializaremos el módulo de memoria.

   int index = 0;
   if(!cMemory.Init(0, 0, OpenCL, window, window_key, units_count, heads, stack_size,
                                                                optimization, iBatch))
      return false;

Tenemos previsto buscar las dependencias en los datos del estado del entorno analizado usando un transformador con codificación relativa.

   index++;
   if(!cStatePrepare.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                                                                     optimization, iBatch))
      return false;

El siguiente paso consistirá en proyectar el estado del entorno analizado en un subespacio con una dimensionalidad igual al número de subagentes. Esto requerirá un mecanismo de proyección eficaz que preserve todas las características clave de los datos. A primera vista, podemos utilizar una capa estándar completamente conectada o convolucional. Sin embargo, dada la especificidad de las series temporales multimodales, deberemos considerar la conservación de la estructura de las secuencias unitarias, que contiene información importante. Estos datos pueden perderse en la adición de datos redundantes.

Antes utilizábamos el transformador de codificación relativa para analizar las dependencias entre pasos temporales, pero ahora debemos complementar este proceso conservando los detalles de las secuencias unitarias individuales. Para ello, primero realizaremos una transposición de los datos, lo que facilitará el procesamiento posterior de las secuencias unitarias.

   index++;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

A continuación, utilizaremos la capa convolucional para extraer las características espaciales y temporales de las secuencias unitarias, mejorando su interpretación. La no linealidad de la operación se logrará utilizando una tangente hiperbólica como función de activación.

   index++;
   if(!cScale.Init(4 * agents, index, OpenCL, 3, 1, 1, units_count - 2, window, optimization, iBatch))
      return false;
   cScale.SetActivationFunction(TANH);

Después de esta etapa viene el punto clave de la compresión de datos. Aquí se utilizará una arquitectura de MLP de dos capas para reducir la dimensionalidad. La primera capa se encargará de la reducción inicial del volumen de datos eliminando las correlaciones y el ruido excesivos. En esto nos ayudará el uso de la función de activación LReLU, que evitará la linealidad de las transformaciones. La segunda capa completará el proceso de compresión, optimizando los datos para su posterior análisis.

   index++;
   if(!cMLP[0].Init(agents, index, OpenCL, 4 * agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(LReLU);
   index++;
   if(!cMLP[1].Init(0, index, OpenCL, agents, optimization, iBatch))
      return false;
   cMLP[0].SetActivationFunction(None);
//---
   return true;
  }

Este enfoque logra un equilibrio entre la preservación de la información útil y la simplificación del modelo, que resulta fundamental para un rendimiento eficaz del hiperagente en un entorno de trading de alta frecuencia.

Tenemos previsto transferir los datos obtenidos al dominio de la probabilidad usando la clase padre inicializada anteriormente. Por ello, en este punto podremos devolver un resultado lógico al programa que realiza la llamada y finalizar el método de inicialización.

Una vez finalizado el trabajo de inicialización de objetos, pasaremos a construir el algoritmo de pasada directa dentro del método feedForward. Aquí todo será bastante sencillo y lineal.

bool CNeuronMacroHFTHyperAgent::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cMemory.FeedForward(NeuronOCL))
      return false;

En los parámetros del método, obtendremos el puntero al objeto de datos de origen que contiene el tensor multimodal que describe el estado del entorno analizado. Este puntero se transmitirá directamente al método homónimo del módulo de memoria. Aquí, la descripción estática del estado del entorno se enriquecerá con información sobre la dinámica reciente para crear una representación más completa y pertinente para el análisis posterior. La integración de estos datos posibilitará un seguimiento más preciso de los cambios producidos en el sistema y ayudará a mejorar la eficacia de los algoritmos de procesamiento.

Los datos procesados en la etapa anterior se transferirán al bloque de atención, donde se determinarán las interdependencias entre los puntos temporales individuales de las series temporales analizadas. Esto permitirá revelar dependencias ocultas y mejorar la precisión de las previsiones posteriores de la dinámica del movimiento de precios.

   if(!cStatePrepare.FeedForward(cMemory.AsObject()))
      return false;

Después, procederemos a la compresión de los datos. En primer lugar, transpondremos los resultados del análisis anterior.

   if(!cTranspose.FeedForward(cStatePrepare.AsObject()))
      return false;

A continuación, primero comprimiremos los datos de secuencias unitarias individuales usando una capa de convolución, lo que nos permitirá preservar la información sobre su estructura.

   if(!cScale.FeedForward(cTranspose.AsObject()))
      return false;

Luego proyectaremos el estado del entorno analizado en un subespacio de un tamaño determinado usando un MLP.

   if(!cMLP[0].FeedForward(cScale.AsObject()))
      return false;
   if(!cMLP[1].FeedForward(cMLP[0].AsObject()))
      return false;

Ahora tendremos que transferir los valores obtenidos al dominio de la probabilidad. Para ello utilizaremos los recursos de la clase padre SoftMax. Bastará con llamar al método homónimo de la clase padre, transmitiéndole los resultados del trabajo anterior.

   return CNeuronSoftMaxOCL::feedForward(cMLP[1].AsObject());
  }

Después retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.

Como habrá notado, antes le hemos presentado el algoritmo de hiperagente lineal. Los algoritmos de los métodos de pasada inversa tendrán una naturaleza lineal similar, así que serán relativamente fáciles de aprender por uno mismo.

Así, le propongo concluir el análisis de los principios del funcionamiento del hiperagente. Encontrará el código completo de la clase presentada, incluidos todos sus métodos, en el archivo adjunto. Podrá estudiarlo en profundidad y aplicarlo en la práctica por su cuenta. Continuemos. El siguiente paso consistirá en unificar los agentes en un único framework.

Creación del framework MacroHFT

En esta fase tenemos los objetos de subagente e hiperagente separados. Ha llegado el momento de combinarlos en una única estructura coherente en la que se construirán los algoritmos para el intercambio de datos entre los componentes del modelo. Esta tarea se realizará en el marco del objeto CNeuronMacroHFT, que permitirá optimizar el procesamiento de los datos. Más abajo resumimos la estructura del nuevo objeto.

class CNeuronMacroHFT   :  public CNeuronBaseOCL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   CNeuronFinConAgent   caAgetnts[6];
   CNeuronMacroHFTHyperAgent  cHyperAgent;
   CNeuronBaseOCL       cConcatenated;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMacroHFT(void) {};
                    ~CNeuronMacroHFT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count,
                          uint heads, uint layers, uint stack_size, uint nactions,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMacroHFT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      Clear(void) override;
  }; 

La estructura del nuevo objeto contendrá el conjunto habitual de métodos virtuales redefinidos, lo cual ofrecerá flexibilidad a la hora de implementar su funcionalidad. Las entidades internas incluyen un hiperagente, que desempeña un papel central en la gestión, y un conjunto de seis subagentes, cada uno responsable de manejar determinados aspectos de los datos. La descripción detallada de la funcionalidad de los objetos internos y la lógica de su interacción se tendrán en cuenta durante la construcción de los métodos del nuevo objeto.

Todos los objetos internos se declararán estáticamente, lo cual nos permitirá dejar el constructor y el destructor de la clase vacíos. La inicialización de los objetos declarados y heredados se realizará en el método Init. En los parámetros de este método, obtendremos una serie de constantes que nos darán una idea inequívoca de la arquitectura del objeto creado.

bool CNeuronMacroHFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window, uint window_key, uint units_count,
                           uint heads, uint layers, uint stack_size, uint nactions,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, nactions, optimization_type, batch))
      return false;

En el cuerpo del método, como viene siendo habitual, primero llamaremos al método homónimo de la clase padre, en el que ya se ha implementado el proceso de inicialización de los objetos e interfaces heredados. En este caso, se trata de una capa totalmente conectada de la que solo necesitaremos las interfaces básicas para interactuar con los objetos externos del modelo. A la salida de nuestra nuevo objeto, esperamos obtener el modelo final del tensor de acción según las condiciones de mercado analizadas. Por consiguiente, especificaremos la dimensionalidad del espacio de acciones de nuestro Agente en los parámetros del método de la clase padre.

La organización de subagentes presentada por los autores sugiere dividir estos según la tendencia y la volatilidad del mercado. Nosotros, en cambio, hemos decidido utilizar la división según el ángulo de visión del mercado. Nuestros subagentes recibirán diferentes proyecciones de los datos de mercado analizados. Para generar dichas proyecciones se utilizará una capa de transposición de datos.

   int index = 0;
   if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
      return false;

A continuación, realizaremos la inicialización de los subagentes. La primera mitad de los subagentes analizará los datos de origen en la representación recibida del programa externo, mientras que la última mitad analizará la forma transpuesta de los datos. Para llevar a cabo el proceso de inicialización, organizaremos 2 ciclos consecutivos con el número de iteraciones necesario.

   uint half = (caAgetnts.Size() + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, window, window_key, units_count, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }
   for(uint i = half; i < caAgetnts.Size(); i++)
     {
      index++;
      if(!caAgetnts[i].Init(0, index, OpenCL, units_count, window_key, window, heads,
                            stack_size, nactions, optimization, iBatch))
         return false;
     }

A continuación, inicializaremos el objeto de hiperagente. También analizaremos los datos de origen en su presentación primaria.

   index++;
   if(!cHyperAgent.Init(0, index, OpenCL, window, window_key, units_count, heads, layers,
                        caAgetnts.Size(), stack_size, optimization, iBatch))
      return false;

Después, según el algoritmo del framework MacroHFT, tendremos que realizar la suma ponderada de los resultados de los subagentes. En este caso, los pesos serán generados por el hiperagente. Esta operación se realizará fácilmente multiplicando la matriz de resultados del subagente por el vector de pesos obtenido del hiperagente, solo que en nuestro caso, los resultados de los subagentes se almacenarán en objetos separados. Asimismo, crearemos un objeto para concatenar los vectores necesarios en una única matriz.

   index++;
   if(!cConcatenated.Init(0, index, OpenCL, caAgetnts.Size()*nactions, optimization, iBatch))
      return false;
//---
   return true;
  }

La multiplicación directa de matrices se realizará en el proceso de pasada directa. Ahora devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método de inicialización.

Nuestro siguiente paso será construir el algoritmo de pasada directa dentro del método feedForward. Al igual que antes, en los parámetros del método obtendremos el puntero al objeto de datos de origen, que transpondremos directamente.

bool CNeuronMacroHFT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

A continuación, una mitad de los subagentes trabajará con la representación original del estado del entorno analizado, mientras que la otra mitad lo hará con la proyección transpuesta.

   uint total = caAgetnts.Size();
   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
      if(!caAgetnts[i].FeedForward(NeuronOCL))
         return false;

   for(uint i = half; i < total; i++)
      if(!caAgetnts[i].FeedForward(cTranspose.AsObject()))
         return false;

Ahí es donde nuestro hiperagente analizará los datos de origen.

   if(!cHyperAgent.FeedForward(NeuronOCL))
      return false;

Ahora tendremos que reunir la información de todos los subagentes en una única matriz.

   if(!Concat(caAgetnts[0].getOutput(), caAgetnts[1].getOutput(), caAgetnts[2].getOutput(),
              caAgetnts[3].getOutput(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
              Neurons(), Neurons(), 1) ||
      !Concat(cConcatenated.getPrevOutput(), caAgetnts[4].getOutput(), caAgetnts[5].getOutput(),
              cConcatenated.getOutput(), 4 * Neurons(), Neurons(), Neurons(), 1))
      return false;

En la salida, obtendremos una matriz en la que cada fila individual representará los resultados de un subagente. Para obtener correctamente la suma ponderada, deberemos multiplicar el vector de pesos por la matriz resultante.

   if(!MatMul(cHyperAgent.getOutput(), cConcatenated.getOutput(), Output, 1, total, Neurons(), 1))
      return false;
//---
   return true;
  }

Luego escribiremos los resultados de la multiplicación en el búfer de interfaces externas heredado de la clase padre y finalizaremos el método, retornando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

Aquí cabe destacar que, a pesar de haber experimentado algunos cambios en el diseño, el algoritmo de pasada directa ha conservado íntegramente la idea original de los autores del framework MacroHFT. Sin embargo, este no es el caso del proceso de entrenamiento que hemos construido, y que se analizaremos a continuación.

Como ya hemos indicado, los autores del framework dividen la muestra de entrenamiento en bloques separados según la tendencia y la volatilidad del mercado. Cada subagente se entrena con una submuestra distinta. No obstante, tenemos previsto entrenar a todos los agentes al mismo tiempo. Y este es exactamente el tipo de proceso que construiremos en los métodos de pasada inversa de nuestra clase.

Comenzamos la implementación de los procesos de pasada inversa construyendo un algoritmo para distribuir los gradientes de error entre los objetos internos de nuestra clase y los datos de entrada según su influencia en la salida del modelo. Este trabajo se realizará como parte del método calcInputGradients.

bool CNeuronMacroHFT::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

En los parámetros del método, obtendremos el puntero al mismo objeto de datos de origen que hemos obtenido en la pasada directa, solo que esta vez tendremos que transmitirle el gradiente de error correspondiente. Y en el cuerpo del método comprobaremos directamente la relevancia del puntero recibido, porque de lo contrario simplemente no podremos escribir información en un objeto inexistente. Y en ese caso, todas las operaciones posteriores carecerán de sentido.

Como ya sabe, el flujo de información de la distribución del gradiente de error es exactamente el mismo que el de las operaciones de pasada directa, solo que dirigido en sentido contrario. Y, puesto que la pasada directa la hemos completado con la operación de multiplicación de la matriz de resultados por el vector de pesos, la pasada inversa comenzará distribuyendo el gradiente de error mediante esta operación.

   uint total = caAgetnts.Size();
   if(!MatMulGrad(cHyperAgent.getOutput(), cHyperAgent.getGradient(), cConcatenated.getOutput(),
                                 cConcatenated.getGradient(), Gradient, 1, total, Neurons(), 1))
      return false;

Aquí cabe señalar que, como resultado de esta operación, hemos dividido el gradiente de error en 2 flujos de información. Uno será el flujo de información del hiperagente. Gracias a este, podremos transmitir directamente el error al nivel de los datos de origen.

   if(!NeuronOCL.calcHiddenGradients(cHyperAgent.AsObject()))
      return false;

El segundo flujo de información se refiere a los subagentes. Al distribuir el gradiente de error mediante una operación de multiplicación de matrices, hemos obtenido valores de error al nivel del objeto concatenado. Creo que aquí resulta obvio que el subagente con el máximo impacto en la salida del modelo ha obtenido la mayor cantidad de errores. Esto nos permitirá implementar la distribución de funciones entre los subagentes durante el entrenamiento basado en la clasificación de los estados del entorno analizados realizada por el hiperagente.

Ahora tendremos que distribuir los valores resultantes entre los respectivos subagentes. Para ello, realizaremos operaciones de desconcatenación de datos.

   if(!DeConcat(cConcatenated.getPrevOutput(), caAgetnts[4].getGradient(), caAgetnts[5].getGradient(),
                cConcatenated.getGradient(), 4 * Neurons(), Neurons(), Neurons(), 1) ||
      !DeConcat(caAgetnts[0].getGradient(), caAgetnts[1].getGradient(), caAgetnts[2].getGradient(),
                caAgetnts[3].getGradient(), cConcatenated.getPrevOutput(), Neurons(), Neurons(),
                Neurons(), Neurons(), 1))
      return false;

A continuación, podremos pasar el gradiente de error al nivel de los datos de origen por la línea troncal de cada subagente individual. Pero deberemos prestar atención a dos puntos. En primer lugar, el búfer de gradiente del objeto de datos de origen ya contiene información obtenida del hiperagente, y tenemos que preservar esta. Para ello, como hacemos siempre, utilizaremos las operaciones de sustitución de punteros del búfer de datos, sustituyendo el búfer de gradiente de error del objeto de datos de origen por otro libre.

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!temp ||
      !NeuronOCL.SetGradient(cTranspose.getPrevOutput(), false))
      return false;

Además, no todos nuestros subagentes trabajan directamente con la entidad de datos de origen. La mitad de ellos analizan datos transpuestos. Por ello, deberemos tener esto en cuenta durante la distribución del gradiente de error. Como sucede con la pasada directa, organizaremos 2 ciclos consecutivos. En el primero, trabajaremos con los subagentes de interacción directa. Aquí haremos descender el gradiente de error al nivel de los datos de origen y sumaremos los datos resultantes con los acumulados anteriormente.

   uint half = (total + 1) / 2;
   for(uint i = 0; i < half; i++)
     {
      if(!NeuronOCL.calcHiddenGradients(caAgetnts[i].AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

El segundo ciclo será similar al primero, pero se añadirá un paso de transmisión del gradiente de error a través de la capa de transposición de datos. Aquí se procesará la otra mitad de los subagentes.

   for(uint i = half; i < total; i++)
     {
      if(!cTranspose.calcHiddenGradients(caAgetnts[i].AsObject()) ||
         !NeuronOCL.calcHiddenGradients(cTranspose.AsObject()))
         return false;
      if(!SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
         return false;
     }

Una vez completadas con éxito todas las iteraciones de los ciclos anteriores, devolveremos a su estado inicial los punteros a los búferes de datos. Y finalizaremos el método, pasando previamente el resultado lógico de las operaciones al programa que realiza la llamada.

Con esto concluirá nuestra revisión de los algoritmos para construir los métodos de nuestro nuevo objeto de organización del framework MacroHFT. Podrá ver el código completo de la clase presentada y todos sus métodos en el archivo adjunto.

Casi hemos llegado al final del artículo, pero nuestro trabajo aún no ha terminado. Le propongo tomarnos un breve descanso y terminar en el próximo artículo el trabajo iniciado. También evaluaremos los enfoques aplicados con datos históricos reales.

Conclusión

En este artículo, nos hemos familiarizado con el framework MacroHFT, una solución prometedora para el trading de alta frecuencia en los mercados de criptomonedas. Este framework considera los contextos macroeconómicos y la dinámica de los mercados locales, lo cual lo convierte en una poderosa herramienta para los tráders profesionales que buscan maximizar sus beneficios en condiciones de mercado difíciles y volátiles.

En la parte práctica, hemos implementado nuestra visión de los componentes principales del framework considerado usando MQL5. En el próximo artículo llevaremos el trabajo iniciado a su conclusión lógica, comprobando además la eficacia de los enfoques aplicados con datos históricos reales.

Enlaces

• MacroHFT: Memory Augmented Context-aware Reinforcement Learning On High Frequency Trading
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL