Redes neuronales en el trading: Transformador con codificación relativa
218
0
Introducción
La previsión de los precios y las tendencias del mercado resulta fundamental para el éxito del trading y la gestión del riesgo. Las previsiones de alta calidad sobre la evolución de los precios ayudan a los tráders a tomar decisiones oportunas y evitar pérdidas financieras. No obstante, en mercados muy volátiles, los modelos tradicionales de aprendizaje automático pueden ver limitadas sus capacidades.
Pasar del entrenamiento de modelos desde cero al preentrenamiento con grandes conjuntos de datos sin etiquetar, seguido de un ajuste fino para tareas específicas, permite obtener una gran precisión de predicción sin necesidad de recopilar enormes cantidades de datos nuevos. Por ejemplo, los modelos basados en la arquitectura del Transformer adaptada a los datos financieros pueden utilizar información sobre correlaciones entre activos, las dependencias temporales y otros factores para hacer predicciones más precisas. La introducción de mecanismos de atención alternativos ayuda a considerar importantes dependencias del mercado, lo que mejora significativamente el rendimiento del modelo. Esto abre nuevas oportunidades para crear estrategias comerciales minimizando los ajustes manuales y los complejos modelos basados en reglas.
Uno de estos algoritmos de atención alternativos se presentó en el artículo "Relative Molecule Self-Attention Transformer". Los autores del artículo han desarrollado una nueva formulación de la Self-Attention para grafos moleculares que procesa cuidadosamente diferentes funciones de entrada para obtener una mayor precisión y robustez en muchos dominios químicos. El Relative Molecule Attention Transformer (R-MAT) es un modelo preentrenado basado en el Transformer. Se trata de una nueva variante de Self-Attention relativa que permite combinar eficazmente la información sobre distancia y vecindad. El R-MAT ofrece un rendimiento vanguardista y competitivo en una amplia gama de aplicaciones.
1. Algoritmo R-MAT
En el procesamiento del lenguaje natural, la capa de Self-Attention vainilla no tiene en cuenta la información posicional de los tokens de entrada, es decir, si se reordenan los datos de entrada, el resultado seguirá siendo el mismo. Para añadir información posicional a los datos de origen, el Transformer vainilla los enriquece con la codificación de posición absoluta. Por otro lado, la codificación posicional relativa añade una distancia relativa entre cada par de tokens, lo que permite obtener beneficios significativos en algunas tareas. El algoritmo R-MAT usa la codificación de posición relativa de los tokens.
La idea principal consiste en aumentar la flexibilidad del procesamiento de la información sobre grafos y distancias. Los autores del método R-MAT han adaptado la codificación relativa posicional para enriquecer el bloque de Self-Attention con información que representara eficazmente las posiciones relativas de los elementos en la secuencia original.
La disposición mutua de dos átomos en una molécula se caracteriza por tres factores interrelacionados:
- su distancia relativa,
- la distancia en el grafo molecular,
- su relación fisicoquímica.
Dos átomos están representados por los vectores 𝒙i, 𝒙j con una dimensionalidad D. Los autores proponen codificar su relación incrustando las relaciones de los átomos 𝒃ij de dimensionalidad D′. Este archivo adjunto se usará en el módulo de Self-Attention después de la capa de proyección.
En primer lugar, el orden de vecindad entre dos átomos se codifica con información sobre cuántos otros nodos hay entre los nodos i y j en el grafo molecular original. A continuación, se usa la codificación de base radial de las distancias. Y, por último, cada enlace se destaca para reflejar la relación física entre pares de átomos.
Los autores del método señalan que, aunque estas características puedan aprenderse fácilmente en el entrenamiento previo, este diseño puede resultar muy útil para entrenar el R-MAT con conjuntos de datos pequeños.
El token 𝒃ij obtenido para cada par de átomos de la molécula se utiliza para definir una nueva capa de Self-Attention que los autores del método han denominado Self-Attention de la molécula (Relative Molecule Self-Attention).
En la nueva arquitectura, los autores del método reflejan el diseño Query-Key-Value de Self-Attention vainilla; el token 𝒃ij se transforma en vectores específicos para la clase y el valor 𝒃ijV, 𝒃ijK con uso de dos redes neuronales φV y φK. Cada red neuronal consta de dos capas. Una capa oculta común a todas las cabezas de atención y una capa de salida que crea una incorporación relativa separada para las diferentes cabezas de atención. La Self-Attention relativa puede expresarse de la siguiente manera:
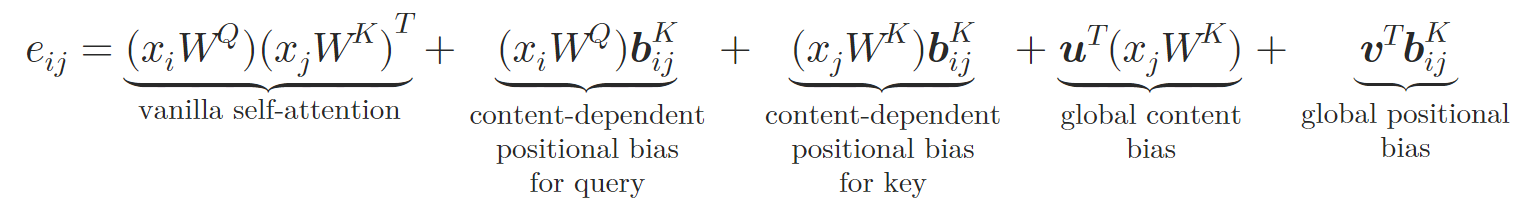
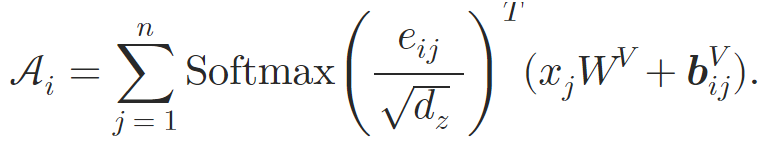
donde 𝒖, 𝒗 son los vectores de entrenamiento.
Así, los autores del método enriquecen el bloque de Self-Attention incorporando relaciones atómicas. En el paso de cálculo de los pesos de atención, se suman y calculan el desplazamiento posicional dependiente del contenido, el desplazamiento contextual global y el desplazamiento posicional global basados en 𝒃ijK. Entonces, durante el cálculo de la atención media ponderada, los autores del método incluyen igualmente información sobre la otra incorporación 𝒃ijV.
El bloque de Self-Attention relativa se utiliza para crear la arquitectura del Transformer de atención molecular relativa (Relative Molecule Attention Transformer — R-MAT).
Los datos de origen se pasan como una matriz de tamaño Nátomos×36, que se procesan utilizando una pila de N capas de atención Relative Molecule Self-Attention. A cada capa de atención le sigue un MLP con un enlace residual, similar al modelo del Transformer vainilla.
Tras procesar los datos de origen usando las capas de atención, los autores del método fusionan la representación en un vector de tamaño fijo. Para ello se usa una agrupación de Self-Attention.
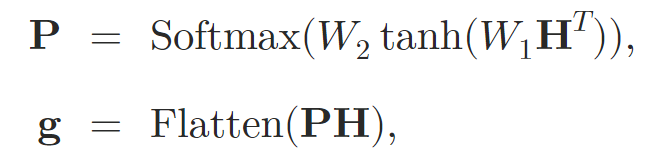
donde 𝐇 es el estado latente obtenido de las capas de Self-Attention, mientras que W1 y W2 son los pesos de agrupación de la atención.
El gráfico incorporado 𝐠 se pasa entonces a un MLP de dos niveles con una función de activación leaky-ReLU, a cuya salida obtendremos los valores predichos.
A continuación le presentamos la visualización del método por parte del autor.
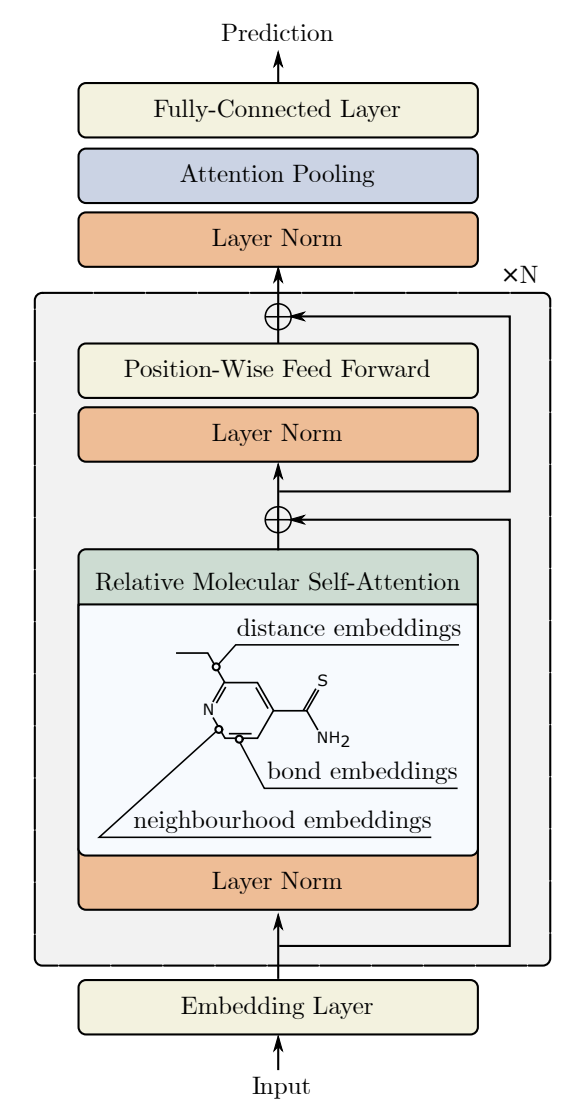
2. Implementación con MQL5
Tras repasar los aspectos teóricos del método Relative Molecule Attention Transformer (R-MAT) propuesto, procederemos a construir nuestra visión de los enfoques propuestos usando MQL5. Y de entrada quiero decir que hemos decidido dividir la construcción del algoritmo propuesto en bloques. Primero crearemos un objeto separado para implementar el algoritmo de Self-Attention relativa, y luego montaremos el modelo R-MAT en una clase de nivel superior separada.
2.1 Módulo de Self-Attention relativa
Como sabe, introduciremos el grueso de los cálculos en el contexto de OpenCL. Por ello, al empezar a implementar un nuevo algoritmo, deberemos añadir los kernels que faltan a nuestro programa OpenCL. Lo primero que haremos será crear el kernel de pasada directa MHRelativeAttentionOut. Aunque basamos este kernel en las implementaciones del algoritmo de Self-Attention discutidas anteriormente, es fácil notar aquí un aumento significativo en el número de búferes globales cuyo propósito conoceremos en el proceso de construcción del algoritmo.
__kernel void MHRelativeAttentionOut(__global const float *q, ///<[in] Matrix of Querys __global const float *k, ///<[in] Matrix of Keys __global const float *v, ///<[in] Matrix of Values __global const float *bk, ///<[in] Matrix of Positional Bias Keys __global const float *bv, ///<[in] Matrix of Positional Bias Values __global const float *gc, ///<[in] Global content bias vector __global const float *gp, ///<[in] Global positional bias vector __global float *score, ///<[out] Matrix of Scores __global float *out, ///<[out] Matrix of attention const int dimension ///< Dimension of Key ) { //--- init const int q_id = get_global_id(0); const int k_id = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2);
Planeamos implementar este kernel en un espacio de tareas tridimensional, cada una correspondiente a las dimensiones Query, Kye y Heads. En la segunda dimensión, creamos grupos de trabajo.
En el cuerpo del kernel, identificamos directamente el flujo actual en todas las dimensiones del espacio de tareas, y también definimos sus límites. A continuación, definimos las constantes de desplazamiento en los búferes de datos para acceder a los elementos necesarios.
const int shift_q = dimension * (q_id * heads + h); const int shift_kv = dimension * (heads * k_id + h); const int shift_gc = dimension * h; const int shift_s = kunits * (q_id * heads + h) + k_id; const int shift_pb = q_id * kunits + k_id; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
Aquí es donde creamos un array en memoria local, para compartir información dentro del grupo de trabajo.
__local float temp[LOCAL_ARRAY_SIZE];
Después, según el algoritmo de Self-Attention relativa, debemos calcular los coeficientes de atención. Para ello, tenemos que calcular el producto escalar de varios vectores y sumar los resultados. Aquí aprovecharemos la propiedad de que las dimensionalidades de todos los vectores multiplicados son iguales. Por lo tanto, solo necesitaremos un ciclo para multiplicar todos los vectores necesarios.
//--- score float sc = 0; for(int d = 0; d < dimension; d++) { float val_q = q[shift_q + d]; float val_k = k[shift_kv + d]; float val_bk = bk[shift_kv + d]; sc += val_q * val_k + val_q * val_bk + val_k * val_bk + gc[shift_q + d] * val_k + gp[shift_q + d] * val_bk; }
El siguiente paso consiste en normalizar los coeficientes de dependencia obtenidos como Query individuales. Para la normalización, utilizaremos la función SoftMax de forma similar al algoritmo vainilla. Por lo tanto, el algoritmo de normalización también se ha copiado de desarrollos existentes sin modificaciones. Aquí calcularemos primero el valor exponencial del coeficiente.
sc = exp(sc / koef); if(isnan(sc) || isinf(sc)) sc = 0;
Y luego sumaremos los coeficientes obtenidos dentro del grupo de trabajo utilizando el array creado anteriormente en la memoria local.
//--- sum of exp for(int cur_k = 0; cur_k < kunits; cur_k += ls) { if(k_id >= cur_k && k_id < (cur_k + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_k == 0 ? 0 : temp[shift_local]) + sc; } barrier(CLK_LOCAL_MEM_FENCE); } uint count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k_id < ls) temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0); if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Ahora podemos dividir el coeficiente obtenido anteriormente por la suma total y almacenar el valor normalizado en el búfer global correspondiente.
//--- score float sum = temp[0]; if(isnan(sum) || isinf(sum) || sum <= 1e-6f) sum = 1; sc /= sum; score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Tras calcular los coeficientes de dependencia normalizados, podremos calcular el resultado de la operación de atención. Aquí el algoritmo resulta muy parecido al algoritmo vainilla. Solo añadiremos la suma de los vectores Value y bijV antes de multiplicar por el factor de atención.
//--- out for(int d = 0; d < dimension; d++) { float val_v = v[shift_kv + d]; float val_bv = bv[shift_kv + d]; float val = sc * (val_v + val_bv); if(isnan(val) || isinf(val)) val = 0; //--- sum of value for(int cur_v = 0; cur_v < kunits; cur_v += ls) { if(k_id >= cur_v && k_id < (cur_v + ls)) { int shift_local = k_id % ls; temp[shift_local] = (cur_v == 0 ? 0 : temp[shift_local]) + val; } barrier(CLK_LOCAL_MEM_FENCE); } //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k_id < count && (k_id + count) < kunits) temp[k_id] += temp[k_id + count]; if(k_id + count < ls) temp[k_id + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- if(k_id == 0) out[shift_q + d] = (isnan(temp[0]) || isinf(temp[0]) ? 0 : temp[0]); } }
Probablemente merezca la pena recordar de nuevo la precisión del uso de barreras para sincronizar operaciones entre los flujos de los grupos de trabajo. Su disposición segun código de kernel debe hacerse de tal manera que cada flujo individual del grupo de trabajo se acerque a la barrera el mismo número de veces. En el código no deberán darse rodeos de barreras y salidas anticipadas antes de que se hayan visitado todos los puntos de sincronización. De lo contrario, correremos el riesgo de que el kernel se cuelgue cuando los flujos individuales esperen a que un flujo que ha completado sus operaciones antes se acerque a la barrera.
El algoritmo de pasada inversa se ha implementado en el kernel MHRelativeAttentionInsideGradients. Su implementación invierte completamente las operaciones del kernel de pasada directa discutido anteriormente y toma prestado en gran medida de las implementaciones previamente analizadas. Por lo tanto, le sugiero que se familiarice con él por su cuenta. En el archivo adjunto figura el código completo de todos los programas OpenCL.
Ahora comenzaremos a trabajar en el programa principal. Aquí crearemos la clase CNeuronRelativeSelfAttention, en la que implementaremos el algoritmo de Self-Attention relativa. Pero antes de proceder a su aplicación, deberemos discutir algunos aspectos de la codificación posicional relativa.
Los autores del marco R-MAT propusieron su algoritmo para resolver problemas en la industria química. Y construyeron un algoritmo de descripción posicional de átomos moleculares basado en las especificidades de los problemas a resolver. Para nosotros, la distancia entre las velas y sus signos también importa, pero hay un matiz a considerar. Además de la distancia, también nos importará la dirección. Solo los movimientos unidireccionales de los precios forman tendencias que se convierten en tendencias.
El segundo punto es el tamaño de la secuencia a analizar. El número de átomos de una molécula suele limitarse a un número bastante reducido. Y en ese caso podemos calcular el vector de desviación para cada par de átomos. En nuestro caso, sin embargo, el volumen de la historia analizada puede ser bastante grande. Así que calcular y almacenar vectores de desviación independientes para cada par de velas analizadas puede ser una tarea que consuma muchos recursos.
Por ello, hemos decidido abandonar la metodología propuesta por los autores para calcular las desviaciones entre elementos individuales de la secuencia. En busca de un mecanismo alternativo, hemos usado una solución bastante sencilla: multiplicar la matriz de datos original por su copia transpuesta. Matemáticamente, la multiplicación de 2 vectores será igual al producto de las longitudes escalares de los vectores dados por el coseno del ángulo entre ellos. Por consiguiente, el producto de los vectores perpendiculares será 0. En este caso, los vectores unidireccionales dan un valor positivo, mientras que los vectores multidireccionales dan un valor negativo. Por lo tanto, al comparar un vector con otros vectores, el valor del producto de los vectores aumentará a medida que disminuya el ángulo entre los vectores y aumente la longitud del segundo vector.
Y ahora que hemos decidido la metodología a usar, podemos pasar a la construcción de nuestro nuevo objeto, cuya estructura se indica a continuación.
class CNeuronRelativeSelfAttention : public CNeuronBaseOCL { protected: uint iWindow; uint iWindowKey; uint iHeads; uint iUnits; int iScore; //--- CNeuronConvOCL cQuery; CNeuronConvOCL cKey; CNeuronConvOCL cValue; CNeuronTransposeOCL cTranspose; CNeuronBaseOCL cDistance; CLayer cBKey; CLayer cBValue; CLayer cGlobalContentBias; CLayer cGlobalPositionalBias; CLayer cMHAttentionPooling; CLayer cScale; CBufferFloat cTemp; //--- virtual bool AttentionOut(void); virtual bool AttentionGraadient(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronRelativeSelfAttention(void) : iScore(-1) {}; ~CNeuronRelativeSelfAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronRelativeSelfAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Como podemos ver, hay bastantes objetos internos en la estructura presentada de la nueva clase. Nos familiarizaremos con su funcionalidad durante la implementación de los algoritmos de los métodos de la clase. Y ahora es importante para nosotros que todos los objetos se declaren de forma estática. Por ello, podemos dejar el constructor y el destructor de la clase vacíos. La inicialización de todos los objetos declarados y heredados se realizará, como siempre, en el método Init. En los parámetros de este método, obtendremos constantes que nos permitirán definir con precisión la arquitectura del objeto que se va a crear. Resulta fácil ver que todos los parámetros del método se han copiado de la Multi-Head Self-Attention vainilla sin ningún cambio. Solo el parámetro de especificación del número de capas interiores se "ha perdido por el camino". Se trata de un paso intencionado, ya que en esta implementación el número de capas será determinado por el objeto de nivel superior mediante la creación de suficientes objetos internos.
bool CNeuronRelativeSelfAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
En el cuerpo del método llamamos inmediatamente al método homónimo de la clase padre transmitiéndole una parte de los parámetros recibidos. Como sabrá usted, el método de la clase padre ya implementa los algoritmos necesarios para realizar un control mínimo de los parámetros recibidos y la inicialización de los objetos heredados. Así que solo verificaremos el resultado lógico de la realización de estas operaciones.
A continuación, almacenaremos las constantes resultantes en las variables internas de la clase para su uso posterior.
iWindow = window; iWindowKey = window_key; iUnits = units_count; iHeads = heads;
Y procederemos a inicializar los objetos internos declarados. En primer lugar, se inicializan las capas de generación convolucional de las entidades Query, Key y Value en los objetos internos homónimos. Usaremos parámetros idénticos para las tres capas.
int idx = 0; if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; idx++; if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; idx++; if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false;
A continuación deberemos preparar los objetos para calcular nuestra matriz de distancias. Para ello, primero crearemos un objeto de transposición de datos de origen.
idx++; if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch)) return false;
Y luego crearemos un objeto para registrar los resultados. La propia operación de multiplicación de arrays ya ha sido implementada en la clase padre.
idx++; if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnits, optimization, iBatch)) return false;
A continuación tendremos que organizar el proceso de generación de los tensores BK y BV. Como se menciona en la descripción teórica del método, se usará un MLP de 2 capas para generarlas. La primera capa es común a todas las cabezas de atención, mientras que la segunda generará tokens individuales para cada cabeza de atención. En nuestra implementación, usaremos dos capas convolucionales consecutivas para cada entidad. Y estableceremos una tangente hiperbólica para crear no linealidad entre las capas.
idx++; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) || !cBKey.Add(conv)) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) || !cBKey.Add(conv)) return false;
idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnits, 1, optimization, iBatch) || !cBValue.Add(conv)) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch) || !cBValue.Add(conv)) return false;
También necesitaremos vectores de contexto global y de cambio de posición entrenables. Para crearlos, usaremos el planteamiento que hemos empleado en trabajos anteriores. Hablamos de crear un MLP de dos capas. Una será estática y contendrá "1", mientras que la otra será entrenable y generará el tensor deseado. Almacenaremos los punteros a los objetos creados en los arrays cGlobalContentBias y cGlobalPositionalBias.
idx++; CNeuronBaseOCL *neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) || !cGlobalContentBias.Add(neuron)) return false; idx++; CBufferFloat *buffer = neuron.getOutput(); buffer.BufferInit(1, 1); if(!buffer.BufferWrite()) return false; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cGlobalContentBias.Add(neuron)) return false;
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) || !cGlobalPositionalBias.Add(neuron)) return false; idx++; buffer = neuron.getOutput(); buffer.BufferInit(1, 1); if(!buffer.BufferWrite()) return false; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cGlobalPositionalBias.Add(neuron)) return false;
En esta fase, hemos preparado todos los objetos para acondicionar correctamente los datos de entrada de nuestro módulo de atención relativa. A continuación, pasaremos a los resultados del procesamiento de los objetos de atención. En primer lugar, crearemos un objeto de registro de resultados de atención multicabeza y a añadiremos su puntero al array cMHAttentionPooling.
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHAttentionPooling.Add(neuron) ) return false;
A continuación, añadiremos un MLP de operaciones de agrupación.
idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cMHAttentionPooling.Add(conv) ) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iHeads, iUnits, 1, optimization, iBatch) || !cMHAttentionPooling.Add(conv) ) return false;
Y añadiremos una capa SoftMax en la salida.
idx++; conv.SetActivationFunction(None); CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL(); if(!softmax || !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) || !cMHAttentionPooling.Add(conv) ) return false; softmax.SetHeads(iUnits);
Obsérvese que en la salida del MLP de la agrupación obtenemos coeficientes normalizados de la influencia de las cabezas de atención para cada elemento individual de la secuencia. Ahora solo tendremos que multiplicar los vectores obtenidos por los resultados correspondientes del bloque de atención múltiple para obtener los resultados finales. Solo que el tamaño del vector de descripción de un elemento de la secuencia será igual a nuestra dimensionalidad intrínseca. Por lo tanto, añadiremos más objetos para escalar los resultados al nivel de los datos de origen.
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iUnits, optimization, iBatch) || !cScale.Add(neuron) ) return false; idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) || !cScale.Add(conv) ) return false; conv.SetActivationFunction(LReLU); idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) || !cScale.Add(conv) ) return false; conv.SetActivationFunction(None);
Ahora solo tendremos que intercambiar los búferes de datos para evitar operaciones de copiado innecesarias y retornar el resultado lógico de las operaciones del método al programa que realiza la llamada.
//--- if(!SetGradient(conv.getGradient(), true)) return false; //--- SetOpenCL(OpenCL); //--- return true; }
Nótese que en este caso solo estaremos intercambiando al puntero del búfer de gradiente. Esto se debe a la creación de enlaces residuales dentro de la unidad de atención. Pero discutiremos este tema cuando implementemos el método feedForward.
En los parámetros del método de pasada directa obtendremos el puntero al objeto de datos fuente, que pasaremos inmediatamente al método homónimo de objetos internos para generar las entidades Query, Key y Value.
bool CNeuronRelativeSelfAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cQuery.FeedForward(NeuronOCL) || !cKey.FeedForward(NeuronOCL) || !cValue.FeedForward(NeuronOCL) ) return false;
Tenga en cuenta que no comprobaremos la relevancia del puntero al objeto de datos de origen recibido del programa externo. Al fin y al cabo, esta operación ya está implementada en los métodos de los objetos internos. Por consiguiente, ese punto de control será innecesario en este caso.
A continuación, pasaremos a la generación de entidades para determinar las distancias entre los objetos analizados. Luego transpondremos el tensor de los datos de origen.
if(!cTranspose.FeedForward(NeuronOCL) || !MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnits, iWindow, iUnits, 1) ) return false;
E inmediatamente realizaremos una multiplicación matricial del tensor de los datos de origen por su copia transpuesta. Utilizaremos el resultado de la operación para generar las entidades BK y BV. Para ello, organizaremos ciclos de enumeración de las capas de los modelos internos correspondientes.
if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) || !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject()) ) return false; for(int i = 1; i < cBKey.Total(); i++) if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1])) return false; for(int i = 1; i < cBValue.Total(); i++) if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1])) return false;
A continuación, organizaremos los ciclos para generar entidades de compensación globales.
for(int i = 1; i < cGlobalContentBias.Total(); i++) if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1])) return false; for(int i = 1; i < cGlobalPositionalBias.Total(); i++) if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1])) return false;
Y con esto concluirá la fase preparatoria del trabajo. Luego llamaremos al método de envoltorio del kernel de pasada directa de atención relativa anteriormente creado.
if(!AttentionOut()) return false;
Después procederemos al procesamiento de los resultados. En primer lugar, utilizaremos el MLP de la agrupación para generar el tensor de la influencia de las cabezas de atención.
for(int i = 1; i < cMHAttentionPooling.Total(); i++) if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1])) return false;
Y luego multiplicaremos los vectores resultantes por los resultados de la atención multicabeza.
if(!MatMul(((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).getOutput(), ((CNeuronBaseOCL*)cMHAttentionPooling[0]).getOutput(), ((CNeuronBaseOCL*)cScale[0]).getOutput(), 1, iHeads, iWindowKey, iUnits) ) return false;
Ahora solo nos quedará escalar los valores resultantes utilizando el escalado MLP.
for(int i = 1; i < cScale.Total(); i++) if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1])) return false;
Luego sumaremos los resultados obtenidos con los datos de origen, y escribiremos el resultado en el búfer de resultados de nivel superior heredado de la clase padre. Para realizar esta operación necesitábamos dejar el puntero al búfer de resultados sin sustituir.
if(!SumAndNormilize(NeuronOCL.getOutput(), ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Después de implementar el método de pasada directa, normalmente pasamos a construir los algoritmos de pasada inversa, que organizamos en los métodos calcInputGradients y updateInputWeights. En la primera, se realizará la distribución de gradientes de error a todos los elementos del modelo según su influencia en el resultado final. Y en el segundo, se ajustarán los parámetros del modelo para reducir el error del mismo. Le sugiero que se familiarice con los métodos mencionados en el anexo. Allí también encontrará el código completo de esta clase y todos sus métodos. Ahora pasaremos a la siguiente fase de nuestro trabajo: la construcción de un objeto de alto nivel con la implementación del marco R-MAT.
2.2 aplicación del marco R-MAT
Para organizar el algoritmo de nivel superior del marco R-MAT, crearemos una nueva clase CNeuronRMAT. Su estructura se resumirá a continuación.
class CNeuronRMAT : public CNeuronBaseOCL { protected: CLayer cLayers; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronRMAT(void) {}; ~CNeuronRMAT(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronRMAT; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Y a diferencia de la clase anterior, solo contendrá un objeto de array dinámico anidado. A primera vista, esto podría no bastar para implementar una arquitectura tan completa. No obstante, hemos declarado un array dinámico en la que escribiremos punteros a los objetos necesarios para construir el algoritmo.
Hemos declarado el array dinámico como estático, y esto nos permitirá dejar el constructor y destructor de la clase vacíos. La inicialización de los objetos internos y heredados se realizará en el método Init.
bool CNeuronRMAT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
En los parámetros del método de inicialización, obtendremos constantes que nos permitirán interpretar sin ambigüedades los deseos del usuario respecto al objeto que se va a crear. Y aquí vemos el conjunto habitual de parámetros del bloque de atención, incluido el número de capas internas.
Y la primera operación que realizaremos es la consabida llamada al método homónimo de la clase padre. Luego prepararemos las variables locales
cLayers.SetOpenCL(OpenCL); CNeuronRelativeSelfAttention *attention = NULL; CResidualConv *conv = NULL;
Y organizaremos un ciclo con un número de iteraciones igual al número de capas internas a crear.
for(uint i = 0; i < layers; i++) { attention = new CNeuronRelativeSelfAttention(); if(!attention || !attention.Init(0, i * 2, OpenCL, window, window_key, units_count, heads, optimization, iBatch) || !cLayers.Add(attention) ) { delete attention; return false; }
En el cuerpo del ciclo, primero crearemos una nueva instancia del objeto de atención relativa implementado anteriormente y lo inicializaremos, pasándole las constantes recibidas del programa externo.
Como recordará, en el método de pasada directa de la clase de atención relativa, organizamos un flujo de enlaces residuales. Por lo tanto, podremos omitir esta operación en este nivel y seguir adelante.
El siguiente paso consistirá en crear un bloque FeedForward similar al Transformer vainilla. Sin embargo, para implementar la aparente simplicidad del objeto de nivel superior, hemos decidido cambiar un poco la arquitectura de bloques. E inicializar en su lugar un bloque de convolución con un enlace residual CResidualConv. Como podrá adivinar por el nombre, este bloque también contiene enlaces residuales y elimina la necesidad de implementarlos en una clase de nivel superior.
conv = new CResidualConv(); if(!conv || !conv.Init(0, i * 2 + 1, OpenCL, window, window, units_count, optimization, iBatch) || !cLayers.Add(conv) ) { delete conv; return false; } }
Así, solo necesitaremos crear 2 objetos para organizar una capa de atención relativa. Luego añadiremos a nuestro array dinámico los punteros a los objetos creados en el orden en que son llamados posteriormente y pasaremos a la siguiente iteración del ciclo interno de generación de la capa de atención.
Una vez que todas las iteraciones del ciclo se hayan ejecutado correctamente, sustituiremos los punteros a los búferes de datos de nuestra última capa interna en los correspondientes búferes de la capa superior.
SetOutput(conv.getOutput(), true); SetGradient(conv.getGradient(), true); //--- return true; }
Después transmitiremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
Como podemos ver, dividiendo el algoritmo del marco R-MAT en bloques separados, hemos podido construir un objeto de nivel superior bastante conciso.
Aquí debemos decir que podemos observar una brevedad similar en otros métodos de la clase. Tomemos, por ejemplo, el método feedForward. En los parámetros, el método obtiene un puntero al objeto de datos de origen.
bool CNeuronRMAT::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *neuron = cLayers[0]; if(!neuron.FeedForward(NeuronOCL)) return false;
En el cuerpo del método, primero llamaremos al método homónimo del primer objeto anidado. Y luego organizaremos un ciclo de enumeración consecutiva de todos los objetos anidados con la llamada de los métodos homónimos. En este caso, transmitiremos un puntero al objeto anterior como entrada.
for(int i = 1; i < cLayers.Total(); i++) { neuron = cLayers[i]; if(!neuron.FeedForward(cLayers[i - 1])) return false; } //--- return true; }
Y una vez completadas todas las iteraciones del ciclo, ni siquiera necesitaremos copiar los datos, ya que antes hemos organizado la sustitución de los búferes de datos. Por lo tanto, simplemente finalizaremos el método transmitiendo el resultado lógico de las operaciones al programa que realiza la llamada.
La situación será similar con los métodos de pasada inversa; le sugiero que los aprenda por su cuenta. Con esto concluirá la revisión de algoritmos para implementar el marco R-MAT utilizando herramientas MQL5. Encontrará el código completo de las clases presentadas en este artículo y todos sus métodos en el archivo adjunto.
Allí encontrará también el código completo de los programas de interacción con el entorno y de entrenamiento de modelos. Se han tomado íntegramente de los artículos anteriores sin modificaciones. En cuanto a la arquitectura del modelo, solo hemos realizado modificaciones puntuales para sustituir una capa en el Codificador de estados del entorno.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRMAT; descr.window=BarDescr; descr.count=HistoryBars; descr.window_out = EmbeddingSize/2; // Key Dimension descr.layers = 5; // Layers descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
En el archivo adjunto figura una descripción completa de la arquitectura de los modelos entrenados.
3. Simulación
Hemos trabajado seriamente en la implementación del marco R-MAT usando MQL5. Ahora pasaremos a la parte final de nuestro trabajo: el entrenamiento de los modelos y la prueba de la política resultante. En este artículo, nos ceñiremos al algoritmo de entrenamiento de modelos descrito anteriormente. En este caso, entrenaremos los 3 modelos simultáneamente: El Codificador del estado de la cuenta, el Actor y el Crítico. El primer modelo realizará el trabajo preparatorio de interpretación de la situación del mercado. El Actor tomará la decisión de negociar basándose en la política aprendida. Y el Crítico evaluará las acciones del Actor e indicará la dirección del ajuste de la política.
Al igual que antes, el entrenamiento del modelo se llevará a cabo sobre datos históricos reales del instrumento financiero EURUSD, con el marco temporal H1 para todo el año 2023. Los parámetros de todos los indicadores analizados se han usado por defecto.
Los modelos se entrenarán de forma iterativa con actualizaciones periódicas de la muestra de entrenamiento.
Comprobaremos la eficacia de la política entrenada con los datos históricos de enero de 2024. A continuación resumiremos los resultados de las pruebas.
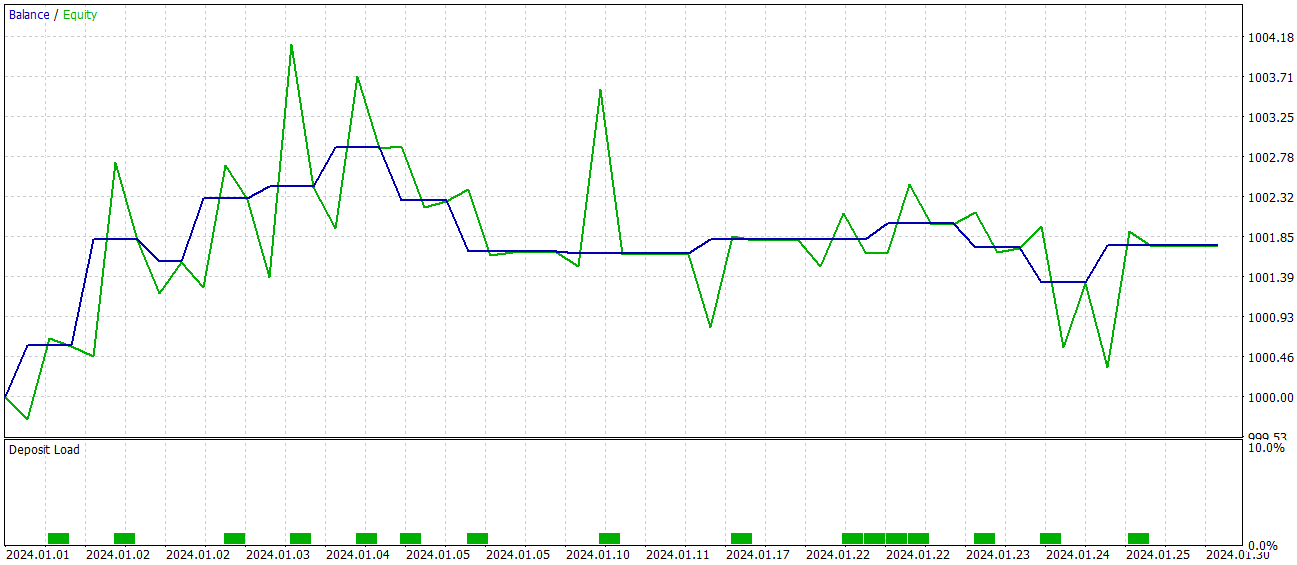
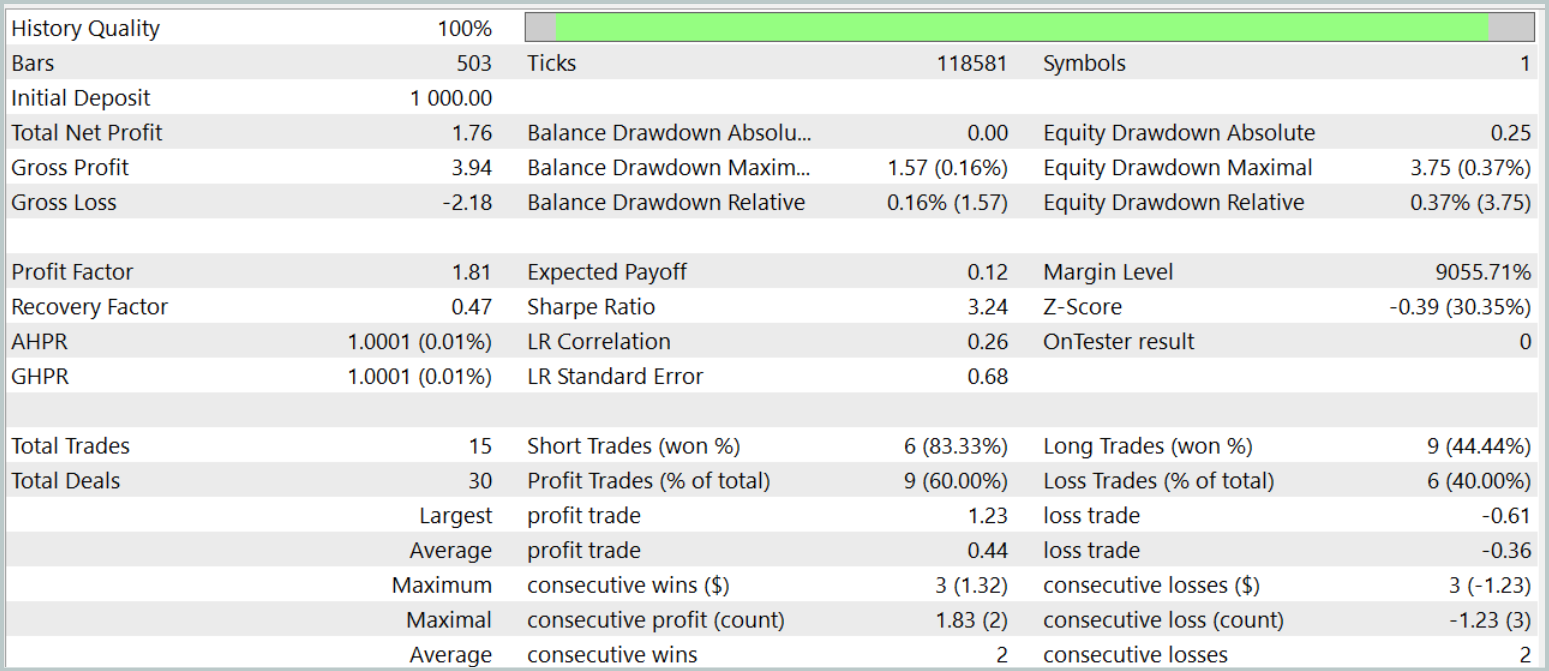
Como podemos ver, según los resultados de las pruebas, el modelo ha alcanzado el nivel del 60% de transacciones rentables. Al mismo tiempo, tanto de la posición media como la máxima rentable superan el indicador similar de transacciones no rentables.
Sin embargo, hay un momento negativo en estos resultados "ideales". Durante el periodo de prueba, el modelo solo ha realizado 15 transacciones comerciales. Y el gráfico del balance muestra que los principales ingresos se han obtenido a principios de mes. Y luego vemos un flat (movimiento lateral). Por lo tanto, en este caso, solo podemos hablar del potencial del modelo: necesitaremos trabajar con él durante un intervalo de tiempo más largo.
Conclusión
El modelo Relative Molecule Attention Transformer (R-MAT) representa un importante paso adelante en la predicción de propiedades complejas. En el contexto del trading, el R-MAT puede considerarse una potente herramienta para analizar las complejas relaciones entre los distintos factores del mercado, teniendo en cuenta tanto sus distancias relativas como sus dependencias temporales.
En la parte práctica, hemos implementado nuestra visión de los enfoques propuestos utilizando herramientas MQL5, y también hemos entrenado los modelos obtenidos con datos reales. Los resultados de las pruebas nos permiten hablar del potencial de la solución propuesta. Sin embargo, el modelo deberá perfeccionarse antes de poder utilizarse en el comercio real.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16097
Creación de un asesor experto integrado de MQL5 y Telegram (Parte 5): Envío de comandos desde Telegram a MQL5 y recepción de respuestas en tiempo real
Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte III): Descifrando el algoritmo del Boom 1000
Redes neuronales en el trading: Análisis de la situación del mercado usando el Transformador de patrones
Algoritmo de optimización basado en ecosistemas artificiales — Artificial Ecosystem-based Optimization (AEO)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso