Знакомство с языком MQL5 (Часть 21): Автоматическое обнаружение паттернов Гартли

Введение

И снова приветствуем вас в Части 21 серии "Знакомство с языком MQL5"! В Части 20 я познакомил вас с гармоническими паттернами и объяснил математические концепции, лежащие в основе уровней Фибоначчи и их расширений, а также как их реализовать на языке MQL5. В этой статье мы сделаем шаг вперед, сосредоточившись на автоматизации обнаружения гармонического паттерна Гартли.

Вы научитесь распознавать возможные паттерны Гартли программным способом на ваших графиках, используя уровни Фибоначчи, ценовые свинги и графические объекты. Логика и методы, которые мы обсуждаем здесь, могут быть применены к другим гармоническим паттернам, таким как "летучая мышь", "бабочка", "краб" и "глубокий краб", но ради простоты мы сосредоточимся на паттерне Гартли.

Отличительная особенность этой статьи заключается в том, что она написана на понятном для начинающих языке, а также в том, как мы упрощаем сложные идеи, разбивая их на управляемые этапы. Вместо того чтобы перегружать вас теорией, мы будем работать над проектно-ориентированной стратегией, в рамках которой мы создадим советник, способный автоматически распознавать паттерн Гартли.

Настройка проекта

Цель этого проекта заключается в создании советника, который сможет автоматически распознавать гармонические паттерны Гартли на графике. На основе заранее определенных критериев советник будет оценивать свинги цен, рассчитывать важные уровни коррекции и расширения Фибоначчи, а также выявлять возможные формации Гартли.

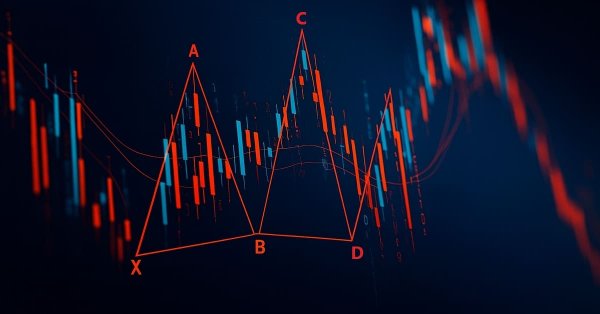
Паттерн Гартли определяют четыре основных отрезка (XA, AB, BC и CD) и определенные соотношения Фибоначчи: точка B должна откатиться примерно на 78,6 процента от отрезка XA, точка C должна откатиться на расстояние от 38,2 до 88,6 процента от отрезка AB, а точка D должна откатиться примерно на 78,6 процента от отрезка XA. Наш советник адаптируемый и простой в использовании для начинающих, поскольку позволяет трейдерам изменять диапазоны коррекции и расширения Фибоначчи в зависимости от их стиля торговли.

Логика для покупки

Чтобы обнаружить бычий паттерн Гартли, советник выполнит следующие шаги:

• Выявление X как точки минимума свинга.
• Обнаружение точки A как значимого максимума свинга после X.
• Нахождение точки B, которая должна совершить откат в пределах определенного диапазона отрезка XA.
• Подтверждение точки C, которая совершает откат в пределах определенного диапазона отрезка AB.
• Расчет потенциальной точки D, которая должна попадать в определенный диапазон коррекции относительно отрезка XA.
• Проверка, что все отрезки соответствуют необходимым соотношениям Фибоначчи, для подтверждения действительности структуры Гартли.
• Как только точка D будет подтверждена, советник сгенерирует сигнал на покупку, ожидая, что цена развернется вверх от этого уровня.
• Кроме того, советник предоставит пользователям возможность настраивать все уровни коррекции и расширения Фибоначчи через входные настройки, обеспечивая тем самым гибкость в зависимости от различных рыночных условий.

Как только советник найдет подтверждение действительного бычьего паттерна Гартли:

• Вход: сделка на покупку открывается в точке D, сразу после завершения паттерна.
• Стоп-лосс (SL): размещается на минимуме свинга, образовавшим точку D.
• Тейк-профит (TP): устанавливает соотношение риска к вознаграждению 1:3, то есть расстояние до тейк-профита будет в три раза больше расстояния до стоп-лосса.

Логика для продажи

Чтобы обнаружить медвежий паттерн Гартли, советник выполнит следующие шаги:

• Выявление X как точки максимума свинга.
• Обнаружение точки A как значимого минимума свинга после X.
• Нахождение точки B, которая должна совершить откат в пределах определенного диапазона отрезка XA.
• Подтверждение точки C, которая совершает откат в пределах определенного диапазона отрезка AB.
• Расчет потенциальной точки D, которая должна попадать в определенный диапазон относительно отрезка XA.
• Проверка, что все отрезки соответствуют необходимым соотношениям Фибоначчи, для подтверждения действительности структуры Гартли.
• Как только точка D будет подтверждена, советник сгенерирует сигнал на продажу, ожидая, что цена развернется вниз от этого уровня.
• Кроме того, советник предоставит пользователям возможность настраивать все уровни коррекции и расширения Фибоначчи через входные настройки, обеспечивая тем самым гибкость в зависимости от различных рыночных условий.

Как только советник подтвердит действительный медвежий паттерн Гартли:

• Вход: сразу после завершения паттерна в точке D открывается сделка на продажу.
• Стоп-лосс (SL): размещен на максимуме свинга, образовавшем точку D.
• Тейк-профит (TP): устанавливает соотношение риска к вознаграждению 1:3, то есть расстояние до тейк-профита будет в три раза больше расстояния до стоп-лосса.

Выявление медвежьего паттерна Гартли

В последней статье я подробно объяснил разницу между бычьими и медвежьими гармоническими паттернами. Как я всегда говорю, когда вы работаете с графическими паттернами, вам понадобятся данные свечей, и вы должны уметь выявлять максимумы и минимумы свинга. Начальная точка X для медвежьего паттерна Гартли должна быть максимумом свинга. Затем структура должна следовать необходимым уровням коррекции и расширения Фибоначчи, развиваясь в отрезки XA, AB, BC и CD. Советник может определить структуру XABCD и выяснить, соответствует ли она параметрам медвежьего Гартли, с точностью выявляя эти свинги.

Пример:

input ENUM_TIMEFRAMES timeframe = PERIOD_CURRENT; // TIMEFRAME


double open[];
double close[];
double low[];
double high[];
datetime time[];

datetime time_bar;
int bars_check = 500;
int total_symbol_bars;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {

   total_symbol_bars = Bars(_Symbol, timeframe);
   time_bar = iTime(_Symbol, timeframe, 0);

   CopyOpen(_Symbol, timeframe, time_bar, bars_check, open);
   CopyClose(_Symbol, timeframe, time_bar, bars_check, close);
   CopyLow(_Symbol, timeframe, time_bar, bars_check, low);
   CopyHigh(_Symbol, timeframe, time_bar, bars_check, high);
   CopyTime(_Symbol, timeframe, time_bar, bars_check, time);

  }

//+------------------------------------------------------------------+
//| FUNCTION FOR SWING LOW                                           |
//+------------------------------------------------------------------+
bool IsSwingLow(const double &low_price[], int index, int lookback)
  {
   for(int i = 1; i <= lookback; i++)
     {
      if(low_price[index] > low_price[index - i] || low_price[index] > low_price[index + i])
         return false;
     }
   return true;
  }

//+------------------------------------------------------------------+
//| FUNCTION FOR SWING HIGH                                          |
//+------------------------------------------------------------------+
bool IsSwingHigh(const double &high_price[], int index, int lookback)
  {
   for(int i = 1; i <= lookback; i++)
     {
      if(high_price[index] < high_price[index - i] || high_price[index] < high_price[index + i])
         return false; // If the current high is not the highest, return false.
     }
   return true;
  }

Пояснение:

Первым шагом процесса является установка таймфрейма советника в соответствии с графиком, на котором он работает. Массивы объявлены для записи исторических свечных данных, включая цены открытия, закрытия, максимума, минимума и время. Остальные переменные отслеживают временную метку самого последнего бара, общее количество доступных баров и количество баров для анализа. Впоследствии рыночные данные будут храниться в этих массивах для проведения детального анализа ценовых колебаний.

Программа получает время последнего бара и определяет, сколько баров доступно для каждого обновления рынка. Чтобы гарантировать, что анализ всегда основывается на состоянии рынка, советник затем собирает самые последние данные о ценах и времени. Это обеспечивает надежную основу для дополнительных вычислений, а также для выявления технических трендов в ценовых данных.

Сравнивая каждый бар с соседними, пользовательские функции выявляют значимые максимумы и минимумы. Одна функция проверяет отчетливый минимум, в то время как другая проверяет отчетливый максимум. Бычьи и медвежьи сетапы Гартли являются примерами гармонических паттернов, которые компьютер стабильно обнаруживает, просто отслеживая эти точки, когда формируется новая свеча.

Выявление точки X

Нахождение точки X является первым шагом в выявлении медвежьего паттерна Гартли. Точка X должна быть максимумом свинга на графике, чтобы сетап был медвежьим. Это подразумевает, что она должна быть очевидным пиком, в котором цена увеличивается перед снижением.

Пример:

double X;
datetime X_time;
string X_letter;
int z = 4;
long chart_id = ChartID();

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {

   total_symbol_bars = Bars(_Symbol, timeframe);
   time_bar = iTime(_Symbol, timeframe, 0);

   CopyOpen(_Symbol, timeframe, time_bar, bars_check, open);
   CopyClose(_Symbol, timeframe, time_bar, bars_check, close);
   CopyLow(_Symbol, timeframe, time_bar, bars_check, low);
   CopyHigh(_Symbol, timeframe, time_bar, bars_check, high);
   CopyTime(_Symbol, timeframe, time_bar, bars_check, time);

   if(total_symbol_bars >= bars_check)
     {

      for(int i = z ; i < bars_check - z; i++)
        {

         if(IsSwingHigh(high, i, z))
           {

            X = high[i];
            X_time = time[i];
            X_letter = StringFormat("X  %d",i);

            ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
            ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

           }
        }
     }
  }

Пояснение:

Чтобы обеспечить наличие достаточного количества свечей для исследования, программа начинает с проверки безопасности. Она обеспечивает наличие как минимум 500 баров на графике перед продолжением, так как требуется именно это количество. Таким образом предотвращаются ошибки, и советник точно будет использовать только полноценные рыночные данные благодаря этой мере предосторожности. После этой проверки программа задействует цикл и окно обратного просмотра (z), чтобы пройтись по свечам и сравнить каждую из них с соседними. К примеру, чтобы избежать ошибок выхода за пределы диапазона и точно определять точки свинга, переменной z присваивается значение 4, чтобы каждая свеча сравнивалась с четырьмя свечами, которые предшествовали ей и следовали за ней.

Алгоритм, осуществляя поиск максимума свинга, устанавливает точку X, первый якорь медвежьего паттерна Гартли, в этом цикле. Когда максимум свинга идентифицирован, цена, время и индекс сохраняются, и график немедленно помечается текстовой меткой с надписью "X". В дополнение к выделению ключевой точки свинга, этот визуальный маркер создает четкую точку отсчета для последующих этапов по определению остальных частей паттерна Гартли.

Выявление точки A

Следующим этапом после того, как точка X корректно отмечена как действительный максимум свинга, является поиск точки A. Точка A обычно является минимумом свинга, который формируется после точки X в медвежьем гармоническом паттерне. Чтобы найти его, советник продвигается вперед от бара, где была обнаружена точка X. Аналогично тому, как мы использовали IsSwingHigh для точки X, советник использует функцию IsSwingLow для поиска минимума свинга, проверяя каждую свечу в диапазоне.

Пример:

double A;
datetime A_time;
string A_letter;
string xa_line;

if(total_symbol_bars >= bars_check)
     {

      for(int i = z ; i < bars_check - z; i++)
        {

         if(IsSwingHigh(high, i, z))
           {

            X = high[i];
            X_time = time[i];
            X_letter = StringFormat("X  %d",i);

            ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
            ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

            for(int j = i; j < bars_check - z; j++)
              {

               if(IsSwingLow(low, j, z) && low[j] < X)
                 {

                  A = low[j];
                  A_time = time[j];
                  A_letter = StringFormat("A %d",j);

                  ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
                  ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");
                  
                  xa_line = StringFormat("XA Line  %d",i);
                  ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);
                  
                  break;

                 }
              }
           }
        }
     }

Вывод:

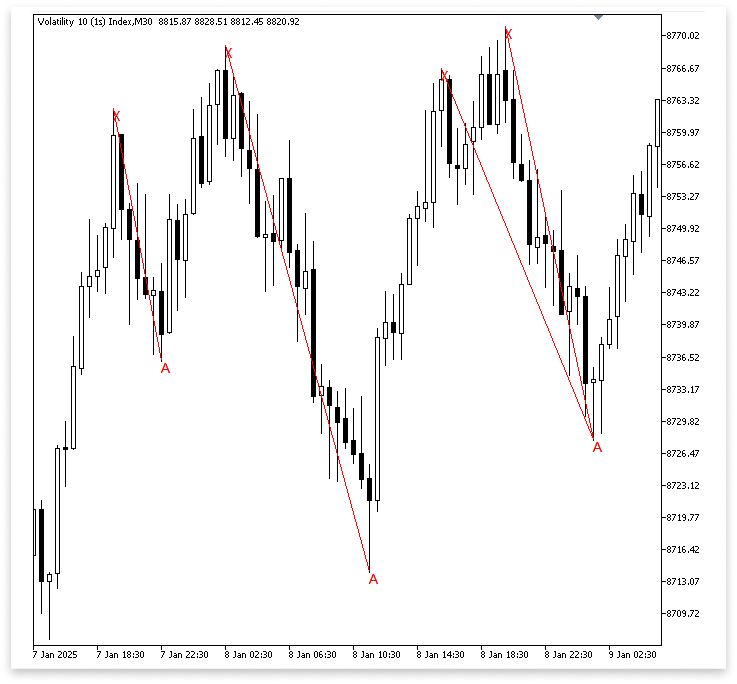
Пояснение:

Советник быстро начинает искать точку A, следующую ключевую точку паттерна, после того как определяет, что точка X является действительным максимумом свинга. Он начинает с позиции точки X и просматривает каждую свечу, которая идет после нее, чтобы определить минимум, соответствующий критериям минимума свинга. Чтобы убедиться, что структура соответствует медвежьему гармоническому паттерну, в ходе этого поиска программа проверяет, действительно ли новый минимум находится ниже ранее обозначенного максимума. Когда бар удовлетворяет этим требованиям, программа отмечает этот ключевой уровень на графике текстовой меткой и сохраняет цену и время точки A.

Советник размещает текстовую метку "A" в выбранной точке с помощью ObjectCreate, чтобы сделать идентификацию на графике ясной. Затем он использует объект OBJ_TREND для построения трендовой линии от X до A. Эта линия соединяет первый максимум свинга с последующим минимумом свинга и графически представляет собой отрезок XA гармонического паттерна. Чтобы гарантировать, что компьютер зацепится за ближайшую и наиболее актуальную точку A после точки X и не будет продолжать искать, поиск завершается с помощью оператора break; при нахождении первого действительного минимума свинга.

Внешний цикл (for(int i = z; i < bars_check - z; i++)) предназначен для перебора каждой свечи в диапазоне, когда советник ищет X (максимум свинга). Чтобы выявлять возможные начальные точки гармонического паттерна, советник должен исследовать каждый из возможных максимумов свинга в данных. Если здесь поставить оператор break, советник будет игнорировать другие действительные X точки, которые могут впоследствии дать развитие паттернам на графике, потому что цикл остановится после выявления первого максимума свинга.

С другой стороны, советник мгновенно будет искать сопоставимую точку A (минимум свинга, который следует за X) после нахождения точки X. В этом случае, поскольку он выявляет отрезок XA, программе просто потребуется первый действительный минимум свинга после точки X. Такой оператор прерывания цикла гарантирует, что советник не продолжит искать минимумы после первого действительного A, потенциально вызывая путаницу или наложение отрезков XA друг на друга. Решением здесь является нахождение точки X, которая ближе всего к точке A, при этом необходимо обеспечивать, чтобы каждая точка A была связана с ближайшей действительной точкой X. Таким образом, отрезок XA остается постоянным и исключает наложение формаций друг на друга.

Пример:

if(total_symbol_bars >= bars_check)
  {

   for(int i = z ; i < bars_check - z; i++)
     {

      if(IsSwingHigh(high, i, z))
        {

         for(int j = i; j < bars_check - z; j++)
           {

            if(IsSwingLow(low, j, z) && low[j] < high[i])
              {

               A = low[j];
               A_time = time[j];
               A_letter = StringFormat("A %d",j);

               for(int a = j; a >= i; a--)
                 {

                  if(IsSwingHigh(high, a, z) && high[a] > A)
                    {

                     X = high[a];
                     X_time = time[a];
                     X_letter = StringFormat("X  %d",a);

                     ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
                     ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

                     ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
                     ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

                     xa_line = StringFormat("XA Line  %d",i);
                     ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);

                     break;

                    }
                 }

               break;

              }
           }
        }
     }
  }
  }
  }

  }

Вывод: 

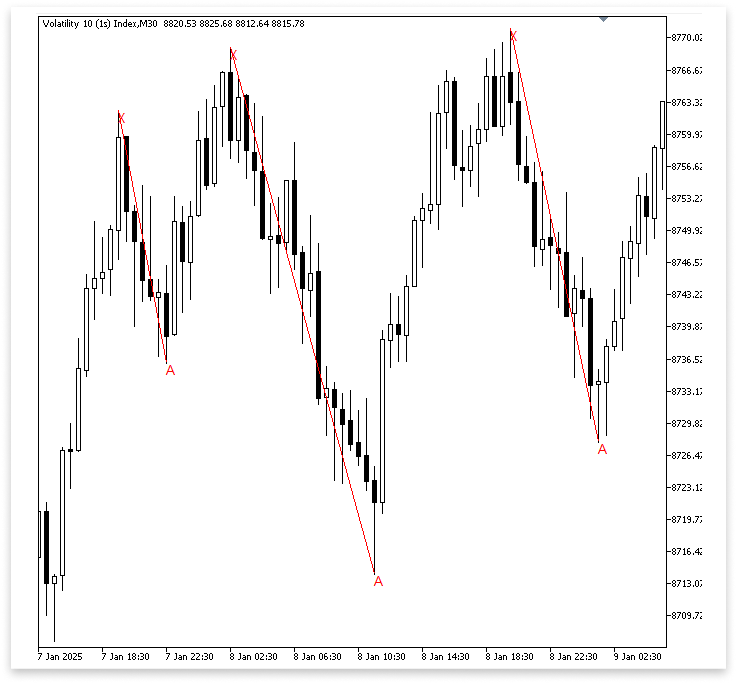
Пояснение:

Когда впервые используем условие low[j] < high[i] для проверки минимума свинга, мы используем high[i] исключительно как временный эталон. Все еще остается неясным, какой максимум свинга следует формально выбрать в качестве точки X. Структура все еще может рассматриваться как начало отрезка XA, поскольку использование high[i] лишь гарантирует, что точка A (минимум свинга) находится ниже, чем хотя бы один предшествующий ей максимум свинга. Иными словами, high[i] служит плейсхолдером для проверки, который исключает минимумы, не соответствующие точке A.

Поскольку этот максимум свинга может не быть наибольшим или ближайшим претендентом перед A, мы не можем просто выбрать high[i] в качестве точки X, как только будет определена действительная точка A. Чтобы улучшить этот процесс, введен обратный цикл for(int a = j; a >= i; a--). Этот цикл движется назад от позиции точки A к начальному максимуму. Это самый разумный вариант для точки X, так как цикл стремится выявить максимум свинга, который ближе всего к точке A и превышает A. Это гарантирует, что наш отрезок XA будет надежно и корректно сформирован и не будет основан на произвольном предыдущем максимуме.

Поскольку мы хотим отрисовывать эти элементы только после проверки, что точка X является действительной, мы в конечном итоге переносим процесс создания объекта (отметку точки X, отметку точки A и рисование линии XA) внутрь этого обратного цикла. Создание объектов за его пределами может привести к тому, что точки X и A будут отмечены на графике слишком рано и, возможно, с неправильным максимумом свинга. Делая это внутри цикла, мы обеспечиваем, чтобы отрезок XA отображался на графике только после того, как будет подтвержден действительный ближайший максимум свинга.

Выявление отрезка BC

Следующим шагом после завершения отрезка XA является нахождение отрезка BC. В медвежьем паттерне Гартли этот участок структуры представлен двумя точками – B и C. Точка C должна формировать минимум свинга, который следует за точкой B, а точка B должна являться максимумом свинга, который следует за точкой A. Устанавливая эти две точки, мы начинаем очерчивать вторую часть гармонического паттерна.

На данном этапе условия для коррекции или расширения Фибоначчи не вводятся. Основное внимание уделяется определению естественных точек свинга в движении цены.

Пример:

double B;
datetime B_time;
string B_letter;

double C;
datetime C_time;
string C_letter;
string ab_line;
string bc_line;

for(int k = j; k < bars_check - z; k++)
  {

   if(IsSwingHigh(high, k, z) && high[k] > A)
     {

      B = high[k];
      B_time = time[k];
      B_letter =  StringFormat("B %d",k);


      for(int l = k; l < bars_check - z; l++)
        {

         if(IsSwingLow(low, l, z) && low[l] < B)
           {

            C = low[l];
            C_time = time[l];
            C_letter = StringFormat("C  %d",l);

            ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B);
            ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

            ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C);
            ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

            ab_line = StringFormat("AB Line  %d",i);
            ObjectCreate(chart_id,ab_line,OBJ_TREND,0,A_time,A,B_time,B);

            bc_line = StringFormat("BC Line  %d", i);
            ObjectCreate(chart_id,bc_line,OBJ_TREND,0,B_time,B,C_time,C);

            ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
            ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

            ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
            ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

            xa_line = StringFormat("XA Line  %d",i);
            ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);

            i = l+1;

            break;
           }
        }

      break;
     }
  }

Вывод:

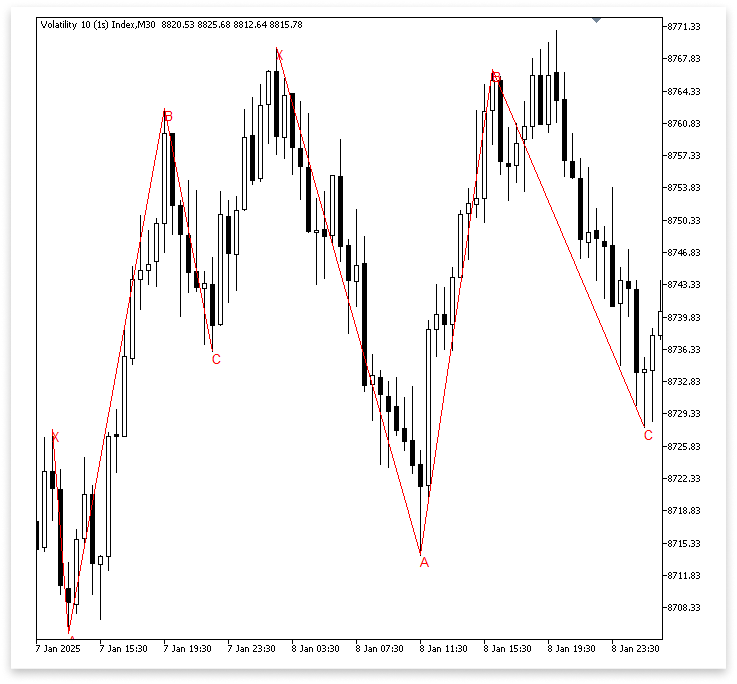
Пояснение:

Начинаясь с точки A, первый цикл, for(int k = j; k < bars_check - z; k++), осуществляет поиск точки B. Внутри этого цикла программа использует функцию IsSwingHigh для поиска максимума свинга. Программа также проверяет, что high[k] > A, что указывает на то, что максимум свинга выше точки A, чтобы убедиться, что точка B подходит под требования структуры. После выполнения этого условия программа записывает значение, время и метку для точки B.

Затем используется второй цикл, for(int l = k; l < bars_check - z; l++), чтобы определить точку C, которая должна быть минимумом свинга, возникающим после B. Корректность медвежьей структура Гартли поддерживается критерием low[l] < B, который гарантирует, что точка C действительно находится ниже максимума свинга B. Подробные данные (цена, время и метка) сохраняются, как только обнаруживается действительная точка C. После выявления точек B и C и их маркировки на графике программа перерисовывает точки X и A, чтобы поддерживать ясность паттерна. 

Алгоритм перескакивает вперед и избегает постоянного обнаружения одних и тех же мест, используя выражение i = l+1; для пропуска итераций внешнего цикла. Алгоритм может пропустить много действительных сигналов Гартли, если после выявления точки C используется i = l+1. Он пропускает возможные точки свинга, потому что прыгает слишком далеко вперед. Этой стратегии следует избегать; вместо этого стоит позволить циклам функционировать нормально или уточнять сигналы с помощью техник фильтрации для сохранения потенциальных возможностей.

Выявление точки D

Следующим этапом является нахождение точки D для завершения паттерна Гартли после того, как точки X, A, B и C будут успешно определены. Поскольку точка D является потенциальной зоной входа, это последний отрезок структуры, и он имеет решающее значение. Чтобы выявить точку D, мы ищем максимум свинга, возникающий после точки C. Чтобы завершить отрезок CD, этот свинг должен быть направлен в противоположную сторону по сравнению с BC.

Пример:

double D;
datetime D_time;
string D_letter;
string cd_line;

for(int m = l; m < bars_check - z; m++)
  {

   if(IsSwingHigh(high, m, z) && high[m] > B)
     {

      D = high[m];
      D_time = time[m];
      D_letter = StringFormat("D  %d",m);

      ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
      ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

      cd_line = StringFormat("CD Line  %d",i);
      ObjectCreate(chart_id,cd_line,OBJ_TREND,0,C_time,C,D_time,D);

      ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,B_time,B);
      ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

      ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,C_time,C);
      ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

      ab_line = StringFormat("AB Line  %d",i);
      ObjectCreate(chart_id,ab_line,OBJ_TREND,0,A_time,A,B_time,B);

      bc_line = StringFormat("BC Line  %d", i);
      ObjectCreate(chart_id,bc_line,OBJ_TREND,0,B_time,B,C_time,C);

      ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,X_time,X);
      ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

      ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,A_time,A);
      ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

      xa_line = StringFormat("XA Line  %d",i);
      ObjectCreate(chart_id,xa_line,OBJ_TREND,0,X_time,X,A_time,A);

      i = m+1;
      break;
     }
  }

Вывод:

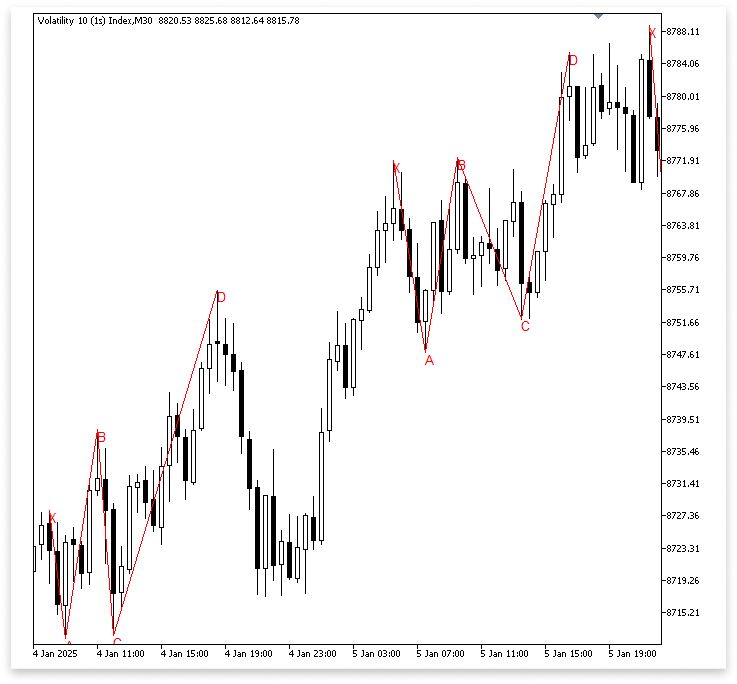
Пояснение:

Цикл начинает сканировать график вперед, начиная с индекса точки C (l), ищет возможные максимумы свинга, которые могут быть точкой D. Условие IsSwingHigh(high, m, z) && high[m] > B гарантирует, что выбранная точка D будет выше точки B и не будет неким произвольным максимумом свинга. Поскольку точка D должна превысить уровень точки B в медвежьем паттерне Гартли, чтобы соблюдалась корректная структура, это правило имеет решающее значение.

После выявления такого максимума свинга код создает линию CD, чтобы соединить этот максимум свинга с точкой C, обозначает его меткой "D" на графике и вводит данные о цене и времени в переменные точки D. Одновременно с этим код перерисовывает линии, которые соответствуют другим значимым точкам.

Когда свинги корректно идентифицированы, следующий шаг заключается в подтверждении того, что каждая точка корректно отображает доминирующий свинг внутри каждого отрезка. Недостаточно отметить максимумы и минимумы, поскольку даже небольшие изменения могут привести к тому, что система станет запутанной. Чтобы предотвратить ложные сигналы, необходимы строгие указания для проверки легитимности каждой точки свинга.

Сначала, в диапазоне между двумя точками C и D, точка C должна быть наименьшим минимумом. Таким образом, отрезок CD гарантированно начнется от настоящего минимума свинга, а не от кратковременного падения. Чтобы гарантировать, что отрезок BC чертит коррекцию от действительного доминирующего пика, точка B также должна быть наибольшим максимумом между B и C.

Аналогичным образом, следует проверить, что точка A является минимумом между точками A и B. Это условие подтверждает, что отрезок AB начинается с правильного минимума вместо произвольной флуктуации. Наконец, между X и A, точка X должна быть наибольшим максимумом. Отрезок XA начинается от наибольшего максимума свинга в этой области благодаря этой проверке.

Пример:

int x_a_bars;
int x_highest_index;
double x_a_hh;
datetime x_a_hh_t;

int a_b_bars;
int a_lowest_index;
double a_b_ll;
datetime a_b_ll_t;

int b_c_bars;
int b_highest_index;
double b_c_hh;
datetime b_c_hh_t;

int c_d_bars;
int c_lowest_index;
double c_d_ll;
datetime c_d_ll_t;

for(int m = l; m < bars_check - z; m++)
  {

   if(IsSwingHigh(high, m, z) && high[m] > B)
     {

      D = high[m];
      D_time = time[m];
      D_letter = StringFormat("D  %d",m);

      c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time);
      c_lowest_index = ArrayMinimum(low,l,c_d_bars);
      c_d_ll = low[c_lowest_index];
      c_d_ll_t = time[c_lowest_index];

      b_c_bars = Bars(_Symbol, PERIOD_CURRENT, B_time, c_d_ll_t);
      b_highest_index = ArrayMaximum(high, k, b_c_bars);
      b_c_hh = high[b_highest_index];
      b_c_hh_t = time[b_highest_index];

      a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_hh_t);
      a_lowest_index = ArrayMinimum(low,j,a_b_bars);
      a_b_ll = low[a_lowest_index];
      a_b_ll_t = time[a_lowest_index];

      x_a_bars = Bars(_Symbol, PERIOD_CURRENT, X_time, a_b_ll_t);
      x_highest_index = ArrayMaximum(high, a, x_a_bars);
      x_a_hh = high[x_highest_index];
      x_a_hh_t = time[x_highest_index];

      ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
      ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

      cd_line = StringFormat("CD Line  %d",i);
      ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D);

      ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh);
      ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

      ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll);
      ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

      ab_line = StringFormat("AB Line  %d",i);
      ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);

      bc_line = StringFormat("BC Line  %d", i);
      ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll);

      ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh);
      ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

      ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll);
      ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

      xa_line = StringFormat("XA Line  %d",i);
      ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll);

      i = m+1;
      break;
     }
  }

Пояснение:

Основными целями этого фрагмента кода являются проверка точности найденных точек свинга и обеспечение того, чтобы структура Гартли была основана на самых экстремальных максимумах и минимумах в рамках каждого отрезка. Процесс начинается когда после точки C обнаруживается новый максимум свинга, который выше точки B. Хотя точка D привязана к этому максимуму свинга, код сначала проверяет все предшествующие ей точки, прежде чем сделать вывод о наличии паттерна.

Проверка начинается с диапазона C-D. Код ищет наименьший минимум в этом диапазоне, чтобы убедиться, что точка C является фактическим дном между этими двумя точками, а не просто временным падением. Затем исследуется диапазон между B и C, чтобы определить наибольший максимум. Это гарантирует, что точка B является наивысшей точкой в этом диапазоне, а не просто небольшим пиком, который мог исказить паттерн.

Затем, чтобы убедиться, что точка A действительно является самым заметным минимумом на этом отрезке, осуществляется поиск наименьшего минимума в диапазоне между точками A и B. Наконец, чтобы подтвердить, что точка X является наивысшим пиком перед снижением к точке A, осуществляется поиск наивысшего максимума в диапазоне от X до A. Благодаря этим проверкам код гарантирует, что все точки X, A, B и C являются правильными структурными свингами для создания гармонического паттерна.

Коррекция Фибоначчи

Следующим шагом после выявления и валидации точек свинга является выяснение, соответствует ли структура критериям паттерна Гартли. Поскольку не каждый набор свингов создает действительный гармонический паттерн, самого по себе указания на графике точек X, A, B, C и D недостаточно. Чтобы отличить паттерн, мы должны использовать критерии коррекции и расширения Фибоначчи на различных структурных отрезках.

"Фильтрами", которые проверяют, соответствуют ли движения цены соотношениям, необходимым для паттерна Гартли, являются измерения Фибоначчи. Например, должны соблюдаться определенные диапазоны Фибоначчи для расширения точки D относительно других свингов, коррекции точки B относительно отрезка XA и коррекции точки C относительно отрезка AB. Если эти требования выполнены, структура может быть классифицирована как действительный паттерн Гартли.

Пример:

input double b_xa_max = 78.6; // MAX B RETRACEMENT LEVEL FOR XA
input double b_xa_min = 61.8; // MIN B RETRACEMENT LEVEL FOR XA

input double c_ab_max = 88.6; // MAX C RETRACEMENT LEVEL FOR AB
input double c_ab_min = 38.2; // MIN C RETRACEMENT LEVEL FOR AB

input double d_xa_max = 76.0; // MAX D RETRACEMENT LEVEL FOR XA
input double d_xa_min = 80.0; // MIN D RETRACEMENT LEVEL FOR XA

double lvl_max_b;
double lvl_min_b;

double lvl_max_c;
double lvl_min_c;

double lvl_max_d;
double lvl_min_d;

if(IsSwingHigh(high, m, z) && high[m] > B)
  {

   D = high[m];
   D_time = time[m];
   D_letter = StringFormat("D  %d",m);

   c_d_bars = Bars(_Symbol,PERIOD_CURRENT,C_time,D_time);
   c_lowest_index = ArrayMinimum(low,l,c_d_bars);
   c_d_ll = low[c_lowest_index];
   c_d_ll_t = time[c_lowest_index];

   b_c_bars = Bars(_Symbol, PERIOD_CURRENT, B_time, c_d_ll_t);
   b_highest_index = ArrayMaximum(high, k, b_c_bars);
   b_c_hh = high[b_highest_index];
   b_c_hh_t = time[b_highest_index];

   a_b_bars = Bars(_Symbol,PERIOD_CURRENT,A_time,b_c_hh_t);
   a_lowest_index = ArrayMinimum(low,j,a_b_bars);
   a_b_ll = low[a_lowest_index];
   a_b_ll_t = time[a_lowest_index];

   x_a_bars = Bars(_Symbol, PERIOD_CURRENT, X_time, a_b_ll_t);
   x_highest_index = ArrayMaximum(high, a, x_a_bars);
   x_a_hh = high[x_highest_index];
   x_a_hh_t = time[x_highest_index];

   lvl_min_b = a_b_ll + ((b_xa_min / 100) * (x_a_hh - a_b_ll));
   lvl_max_b = a_b_ll + ((b_xa_max / 100) * (x_a_hh - a_b_ll));

   lvl_min_c = b_c_hh - ((c_ab_min / 100) * (b_c_hh - a_b_ll));
   lvl_max_c = b_c_hh - ((c_ab_max / 100) * (b_c_hh - a_b_ll));

   lvl_min_d = a_b_ll + ((d_xa_min / 100) * (x_a_hh - a_b_ll));
   lvl_max_d = a_b_ll + ((d_xa_max / 100) * (x_a_hh - a_b_ll));

   if(b_c_hh >= lvl_min_b && b_c_hh <= lvl_max_b && c_d_ll <= lvl_min_c && c_d_ll >= lvl_max_c
      && D >= lvl_min_d && D <= lvl_max_d)
     {

      ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
      ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

      cd_line = StringFormat("CD Line  %d",i);
      ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D);

      ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh);
      ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

      ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll);
      ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

      ab_line = StringFormat("AB Line  %d",i);
      ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);

      bc_line = StringFormat("BC Line  %d", i);
      ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll);

      ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh);
      ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

      ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll);
      ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

      xa_line = StringFormat("XA Line  %d",i);
      ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll);

     }

// i = m+1;
   break;
  }

  }

Пояснение:

Мы начинаем со входных параметров. Чтобы определить, является ли структура из точек X, A, B, C и D действительным паттерном Гартли, советник будет использовать определяемые пользователем уровни коррекции Фибоначчи. Например, в зависимости от входных данных, точка B должна находиться в указанном диапазоне коррекции относительно отрезка XA, точка C – в заданном диапазоне коррекции относительно отрезка AB, а точка D указанном уровне коррекции Фибоначчи относительно отрезка XA.

Фактические ценовые уровни, на которых должна формироваться каждая точка свинга, представлены вычисляемыми переменными. На основе принципов Фибоначчи, заложенных во входных данных, эти переменные рассчитываются относительно максимумов и минимумов для отрезков XA и AB. Например, коррекция для отрезка XA устанавливает корректный диапазон для точки B, и при расчете диапазонов для точек C и D относительно отрезков AB и XA используется тот же метод.

Последнее условие проверяет принадлежность каждой из точек паттерна требуемому диапазону Фибоначчи. Оно подтверждает выполнение условий коррекции для точек B, C и D. Когда все эти требования выполнены, программа генерирует графические объекты для визуального представления распознанного паттерна Гартли, обозначая точки X, A, B, C и D и рисуя соединяющие линии.

Исполнение сделок

За успешной идентификацией действительного паттерна Гартли следует исполнение сделки. Чтобы проверять, что структура соответствует указаниям для формации Гартли, советник до сих пор был сосредоточен на анализе ценовых данных, выявлении максимумов и минимумов свинга и проверке соотношений Фибоначчи. Однако само выявление паттерна дает трейдеру лишь потенциальную торговую возможность; оно не приносит прибыль само по себе. Самое интересное начинается, когда советник приступает к совершению рыночных сделок на основе этих знаний.

Фактически это означает, что советник теперь должен выбрать где входить в сделку, где установить тейк-профит и где установить стоп-лосс. Например, в медвежьем паттерне Гартли советник обычно открывает в точке D ордер на продажу. Чтобы защититься от инвалидации паттерна, стоп-лосс будет установлен немного выше максимума свинга D. Тейк-профит может быть определен с помощью целей по расширению Фибоначчи или на основе соотношения риска к вознаграждению, например, 1:3. Автоматизируя этот процесс, советник обеспечивает стабильную эффективность без замешательства или эмоциональной предвзятости.

Пример:

#include <Trade/Trade.mqh>
CTrade trade;
input int MagicNumber = 61626;
input double lot_size = 0.1;

double ask_price;
datetime time_price[];
double take_p;

string XAB;
string BCD;
datetime lastTradeBarTime = 0;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   trade.SetExpertMagicNumber(MagicNumber);
   ArraySetAsSeries(time_price,true);

//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

   ObjectsDeleteAll(chart_id);

  }

CopyTime(_Symbol, timeframe, 0, 2, time_price);
ask_price = SymbolInfoDouble(_Symbol,SYMBOL_ASK);
datetime currentBarTime = iTime(_Symbol,timeframe,0);

if(b_c_hh >= lvl_min_b && b_c_hh <= lvl_max_b && c_d_ll <= lvl_min_c && c_d_ll >= lvl_max_c
   && D >= lvl_min_d && D <= lvl_max_d)
  {

   ObjectCreate(chart_id,D_letter,OBJ_TEXT,0,D_time,D);
   ObjectSetString(chart_id,D_letter,OBJPROP_TEXT,"D");

   cd_line = StringFormat("CD Line  %d",i);
   ObjectCreate(chart_id,cd_line,OBJ_TREND,0,c_d_ll_t,c_d_ll,D_time,D);

   ObjectCreate(chart_id,B_letter,OBJ_TEXT,0,b_c_hh_t,b_c_hh);
   ObjectSetString(chart_id,B_letter,OBJPROP_TEXT,"B");

   ObjectCreate(chart_id,C_letter,OBJ_TEXT,0,c_d_ll_t,c_d_ll);
   ObjectSetString(chart_id,C_letter,OBJPROP_TEXT,"C");

   ab_line = StringFormat("AB Line  %d",i);
   ObjectCreate(chart_id,ab_line,OBJ_TREND,0,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);

   bc_line = StringFormat("BC Line  %d", i);
   ObjectCreate(chart_id,bc_line,OBJ_TREND,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll);

   ObjectCreate(chart_id,X_letter,OBJ_TEXT,0,x_a_hh_t,x_a_hh);
   ObjectSetString(chart_id,X_letter,OBJPROP_TEXT,"X");

   ObjectCreate(chart_id,A_letter,OBJ_TEXT,0,a_b_ll_t,a_b_ll);
   ObjectSetString(chart_id,A_letter,OBJPROP_TEXT,"A");

   xa_line = StringFormat("XA Line  %d",i);
   ObjectCreate(chart_id,xa_line,OBJ_TREND,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll);

   XAB = StringFormat("XAB TRIANGLE %d", i);
   BCD = StringFormat("BCD TRIANGLE %d", i);

   ObjectCreate(chart_id,XAB,OBJ_TRIANGLE,0,x_a_hh_t,x_a_hh,a_b_ll_t,a_b_ll,b_c_hh_t,b_c_hh);
   ObjectSetInteger(chart_id,XAB,OBJPROP_FILL,true);
   ObjectSetInteger(chart_id,XAB,OBJPROP_COLOR,clrPink);
   ObjectSetInteger(chart_id,XAB,OBJPROP_BACK,true);

   ObjectCreate(chart_id,BCD,OBJ_TRIANGLE,0,b_c_hh_t,b_c_hh,c_d_ll_t,c_d_ll,D_time,D);
   ObjectSetInteger(chart_id,BCD,OBJPROP_FILL,true);
   ObjectSetInteger(chart_id,BCD,OBJPROP_COLOR,clrPink);
   ObjectSetInteger(chart_id,BCD,OBJPROP_BACK,true);

   if(time[m+z] == time_price[1] && currentBarTime != lastTradeBarTime)
     {

      take_p = ask_price - (MathAbs(D - ask_price) * 3);
      trade.Sell(lot_size,_Symbol,ask_price,D,take_p);

      lastTradeBarTime = currentBarTime;

     }

  }

Вывод:

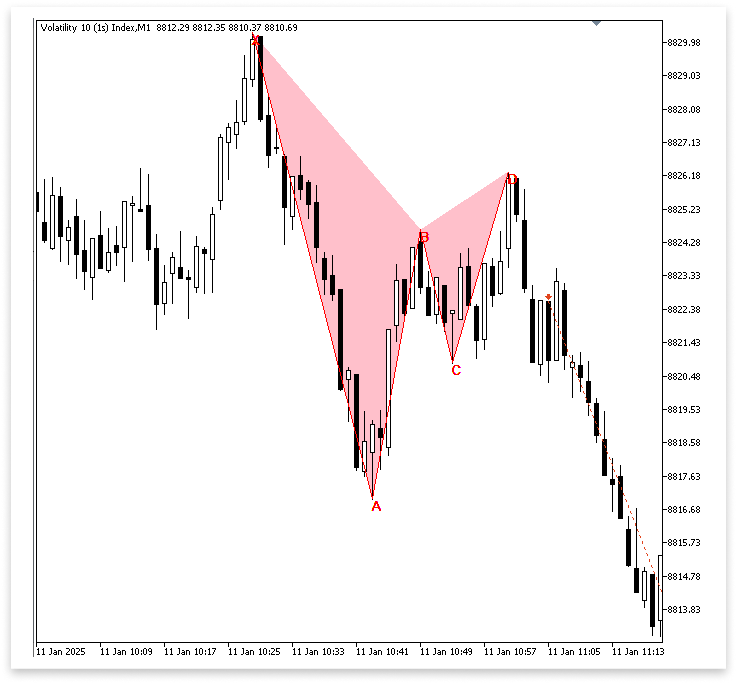
Пояснение:

Этот раздел программы управляет визуальным представлением паттерна Гартли на графике, а также торговой логикой. Сначала подключается стандартная торговая библиотека MQL5 с помощью директивы #include <Trade/Trade.mqh>. Из этой библиотеки создается объект CTrade с именем trade для управления всеми задачами, связанными с торговлей, включая открытие и закрытие позиций. В строке others.MagicNumber; SetExpertMagicNumber; объявляется входной параметр под названием MagicNumber, который используется в транзакциях для различения сделок, выполненных этим советником.

Объем, который будет обменен, определяется другими важными факторами, такими как lot_size. Для хранения рыночной цены, временных данных и вычисленных уровней тейк-профита объявлены такие вспомогательные переменные, как ask_price, time_price[] и take_p. В качестве меры предосторожности, переменная lastTradeBarTime используется для обеспечения того, чтобы на одном и том же баре сделка не открывалась более одного раза.

Благодаря строке ArraySetAsSeries(time_price, true); самый последний элемент хранится по индексу 0, чтобы гарантировать корректную обработку ценовых данных. Время открытия последних двух баров затем копируется в массив time_price с помощью метода CopyTime(_Symbol, таймфрейм, 0, 2, time_price). Строка Ask_price = SymbolInfoDouble(_Symbol, SYMBOL_ASK); возвращает текущую цену Ask, а строка currentBarTime = iTime(_Symbol, таймфрейм, 0); сохраняет временную метку самой последней свечи.

Компьютер может использовать эти указания, чтобы точно определить момент, когда торговые требования будут удовлетворены. Сравнивая время баров, проверка по условию гарантирует, что программа будет реагировать только один раз за каждый бар. Если условия удовлетворены, исполняется ордер на продажу, при этом уровень тейк-профита определяется с помощью строк take_p = ask_price - (MathAbs(D - ask_price) * 3); и Sell(lot_size, D, take_p, ask_price, _Symbol);. Затем, чтобы предотвратить повторные сделки на одном и том же баре, изменяется lastTradeBarTime.

Программа не только исполняет сделки, но и отображает паттерн Гартли прямо на графике. Например, XAB = StringFormat("XAB TRIANGLE %d", i); и BCD = StringFormat("BCD TRIANGLE %d", i); – это строки, которые создаются с помощью StringFormat для уникального именования графических объектов. Затем используется ObjectCreate для рисования двух треугольных фигур с использованием этих идентификаторов. XAB-часть паттерна представлена первым треугольником, а BCD-часть – вторым. Их координаты устанавливаются согласно координатам соответствующих точек свинга, которые программа нашла ранее.

Свойства треугольников задаются с помощью ObjectSetInteger, где они заливаются, окрашиваются в розовый цвет и переносятся на фон, чтобы найденные паттерны выделялись. Программа не только реагирует на распознанные паттерны Гартли, но и делает их доступными трейдеру для проверки благодаря сочетанию автоматического исполнения сделок и понятной графической визуализации.

Заключение

В этой статье мы рассмотрели, как строить паттерн Гартли и торговать по нему с помощью языка MQL5. Мы начали с выявления точек свинга (X, A, B, C и D), применили уровни коррекции и расширения Фибоначчи для подтверждения структуры, а затем автоматизировали выполнение сделок, как только паттерн оказался действительным. Наконец, мы добавили графические объекты для четкой визуализации, что облегчает восприятие паттерна по мере его формирования. Этот проект демонстрирует, как можно оформить сложные гармонические паттерны в виде кода и автоматически торговать по ним. На этой основе вы сможете уточнять правила, добавлять критерии подтверждения или применить предложенную логику к другим гармоническим паттернам.