
Возможности Мастера MQL5, которые вам нужно знать (Часть 37): Регрессия гауссовских процессов с линейными ядрами и ядрами Матерна
Введение
Мы продолжаем серию статей о различных способах реализации ключевых классов компонентов советников, собранных в Мастере. Здесь мы рассмотрим два ядра гауссовского процесса. Линейное ядро и ядро Матерна. Первое ядро довольно простое, у него даже нет своей страницы в Википедии, у ядра Матерна имеется здесь.
Если подвести итог тому, что мы рассмотрели ранее, говоря о ядрах гауссовых процессов (GP), то это непараметрические модели, которые способны отображать сложные взаимосвязи между наборами данных (обычно в векторной форме) без каких-либо функциональных или предварительных знаний о паре задействованных наборов данных. Это делает их идеальными для обработки ситуаций, когда используемые наборы данных нелинейны или даже зашумлены. Кроме того, эта гибкость делает их идеальными для финансовых временных рядов, которые часто могут быть нестабильными, поскольку гауссовы процессы, как правило, дают неоднозначные результаты. Они предоставляют прогнозную оценку и доверительный интервал. Гауссовы процессы помогают определить сходство между двумя наборами данных, и поскольку в регрессии гауссовского процесса можно использовать несколько типов ядер, всегда важно определить подходящее ядро или учитывать недостатки выбранного ядра, особенно в случаях, когда ядра используются для экстраполяции прогноза.
Ниже приведена сводная таблица, охватывающая ядра, представленные на данный момент в этих сериях, и некоторые их характеристики:
| Тип ядра | Лучше всего отслеживает | Пояснение |
|---|---|---|
| Линейное ядро | Тренды | Отслеживает линейные тренды с течением времени. Идеально подходит для активов, которые демонстрируют долгосрочные восходящие или нисходящие ценовые движения. Простой и эффективный с точки зрения вычислений, но предполагает линейную зависимость. |
| Ядро радиальной базисной функции (RBF) | Тренды и волатильность | Лучше всего подходит для отслеживания плавных долгосрочных трендов с постепенными изменениями цен. Обеспечивает плавные оценки и хорош для непрерывных моделей. Испытывает трудности с резкими переходами и сильной волатильностью. |
| Ядро Матерна | Тенденции, волатильность, циклы | Может улавливать более резкие, менее плавные тренды и резкие изменения волатильности. Параметр ν контролирует сглаженность, поэтому более низкое значение ν отражает грубую волатильность, тогда как более высокое значение ν сглаживает тренды. |
В зависимости от экстраполируемого временного ряда необходимо выбрать подходящее ядро на основе его сильных сторон. Финансовые временные ряды часто могут демонстрировать периодическое или циклическое поведение, и такие ядра, как Matérn, которые мы представляем ниже, могут помочь в отображении этих отношений. Более того, количественная оценка неопределенности, как мы видели в случае с радиальной базисной функцией в статье может оказаться огромным благом, когда трейдеры сталкиваются с вялыми или резкими колебаниями рынка. Такие ядра, как RBF, не просто предоставляют точечные оценки, но и определяют доверительные интервалы, что может быть полезно в таких ситуациях. Это связано с тем, что доверительный интервал может помочь отсеять слабые сигналы, а также выделить важные поворотные моменты в неопределенной обстановке.
Наборы данных, возвращающиеся к среднему значению, также могут обрабатываться специальными ядрами, такими как ядро Орнштейна-Уленбека, о котором мы, возможно, поговорим в будущей статье. Еще один интересный аспект, который мы могли бы рассмотреть в будущем, заключается в том, что гауссовы процессы допускают композицию ядер. В частности, стекинг линейного ядра и ядра RBF, могут быть выполнены для моделирования более сложных взаимосвязей между наборами данных. Композиция может включать в себя пары из краткосрочных ценовых действий и долгосрочных трендов, где модель, таким образом, способна размещать выходы из открытых позиций в оптимальных точках, а также извлекать выгоду из любого базового долгосрочного действия, которое может иметь ценная бумага.
У гауссовых процессов есть несколько дополнительных преимуществ и применений, таких как управление и снижение шума, а также адаптация к смене режима и многое другое. Однако, как трейдеры, мы хотим извлечь выгоду из этих преимуществ, поэтому давайте рассмотрим очень простое линейное ядро.
Линейные ядра
Основное применение линейных ядер — отображение простых линейных связей между наборами данных в гауссовском процессе. Рассмотрим очень простую пару наборов данных: стоимость доставки контейнера в США из Китая и стоимость доставки ETF BOAT. При нормальных обстоятельствах мы бы ожидали, что высокие расходы на доставку будут отражать ценовую мощь судоходных компаний, их доходы и выручку, что приведет к росту стоимости их акций. В этом сценарии трейдер, трейдер, желающий со временем приобрести судоходные компании или ETF, будет заинтересован в моделировании своих ожидаемых цен на акции и текущих расходов на доставку с помощью линейного ядра.
Расчет прост и требует наименьшего количества вычислительных ресурсов среди всех ядер. В формуле также требуется только один постоянный параметр c. Формула представлена ниже:
![]()
где:
- x и x′ - входные векторы
- x⊤x′ - скалярное произведение транспонированного вектора x и x′
- c - константа
Требование только одного параметра c делает его быстрым и очень эффективным при работе с большими наборами данных. Роль константы многогранна. Во-первых, это помогает в корректировке смещения, то есть в случае, если набор данных или график не проходит через начало координат, константа обеспечивает смещение, которое сдвигает гиперплоскость и позволяет ядру лучше представлять базовую модель. Без этой константы ядро предполагало бы, что все точки данных центрированы вокруг начала координат. Эту константу невозможно оптимизировать как таковую, но ее можно настроить на предустановленных этапах перекрестной проверки.
Во-вторых, константа позволяет более гибко настраивать разделение между двумя классами наборов данных, контролируя этот зазор. Это особенно важно, когда ядро используется с машинами опорных векторов, а также в ситуациях, когда имеются большие наборы данных, которые нелегко линейно разделить. В-третьих, константа обеспечивает нелинейную однородность, которая может присутствовать в определенных наборах данных. Без этой константы, если все входные данные масштабируются с коэффициентом, выходные данные ядра будут масштабироваться с тем же коэффициентом. Некоторые наборы данных демонстрируют такие черты, но не все. Вот почему добавление константы c вносит некоторую внутреннюю погрешность и гарантирует, что модель автоматически не предполагает линейность.
Наконец, утверждается, что константа обеспечивает численную устойчивость скалярных произведений, которые могут привести к очень малым значениям, что может исказить матрицу ядра. В случае, если входные векторы имеют очень малые значения, скалярное произведение без константы также будет очень малым, что повлияет на процесс оптимизации. Таким образом, константа обеспечивает некоторую стабильность для лучшей оптимизации.
Линейное ядро нашло применение в экстраполяции и прогнозировании трендов, поскольку, как мы увидим ниже, оно экстраполирует тренды за пределы наблюдаемых данных. Поэтому линейное ядро может оказаться полезным особенно при рассмотрении скорости линейного роста цены актива с течением времени. Кроме того, взвешивание признаков из скалярного произведения делает модель линейного ядра более интерпретируемой. Интерпретируемость полезна, когда имеется вектор входных данных и необходимо знать относительную важность или значимость каждой из точек входных данных в этом векторе. Представьте, что у вас есть ядро, которое вы используете для прогнозирования цен на дома. Ядро имеет входной вектор данных размером 4, который включает: площадь дома (в квадратных футах), количество спален в доме, средний доход в этом районе и год постройки. Прогнозируемая цена от нашего ядра будет рассчитана по следующей формуле:
где
- b - константа, которую мы добавляем к векторному скалярному произведению, роль которого уже была подчеркнута выше (обозначается как c)
- w 1 – w 4 – это веса, которые оптимизируются посредством тренировок
- x 1 - x 4 - это входные данные, о которых мы упоминали выше.
После обучения вы получите значения для w1 – w4, и при такой простой настройке линейного ядра чем больше вес, тем важнее характеристика или точка данных для следующей цены недвижимости. То же самое верно, если вес w4, скажем, наименьший, так как это будет означать, что x4 (год покупки недвижимости) наименее важен для следующей цены. Однако здесь мы не будем рассматривать использование линейного ядра в данной ситуации, а рассмотрим использование линейных ядер с регрессией гауссовского процесса. Это означает, что если кому-то нужно вывести важность признаков, он не сможет сделать это так просто, как мы показали выше, поскольку вывод нашего скалярного произведения выше является скаляром, а в нашем приложении это матрица. Альтернативы, позволяющие оценить относительную важность входных данных, включают автоматическое определение релевантности, анализ чувствительности (где корректируются выбранные входные данные и наблюдается их влияние на прогноз), а также предельное правдоподобие и гиперпараметры (где величина гиперпараметров, как при пакетной нормализации, может вывести относительную важность входных данных).
Мы реализуем линейное ядро для использования в регрессии гауссовых процессов на языке MQL5 следующим образом:
//+------------------------------------------------------------------+ // Linear Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Linear_Kernel(vector &Rows, vector &Cols) { matrix _linear, _c; _linear.Init(Rows.Size(), Cols.Size()); _c.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _linear[i][ii] = Rows[i] * Cols[ii]; } } _c.Fill(m_constant); _linear += _c; return(_linear); }
Входными данными здесь являются 2 вектора, как уже указано в формуле, один из которых обозначен как Rows (строки), что подразумевает транспонирование этого вектора перед его применением в скалярном произведении. Таким образом, линейные ядра, несмотря на свою простоту, в дополнение к тем положительным качествам, о которых мы упомянули выше, служат базой для сравнения моделей с другими, более сложными ядрами, поскольку их проще всего настраивать и тестировать. Начав с них, можно постепенно масштабировать, в зависимости от того, оправдана ли дополнительная сложность других ядер. Это особенно важно, поскольку по мере усложнения ядер растут и затраты на вычисления, что имеет решающее значение при работе с очень большими наборами данных и ядрами. Линейные ядра, однако, охватывают долгосрочные зависимости, их можно комбинировать с другими ядрами для определения более сложных отношений, и они могут выступать в качестве формы регуляризации в случаях, когда сравниваемые наборы данных имеют сильную линейную связь.
Ядра Матерна
Ядро Матерна также является распространенной ковариационной функцией, используемой в гауссовых процессах, благодаря своей регулируемой гладкости и способности улавливать зависимости данных. Его гладкость контролируется входным параметром ν (ню). Этот параметр способен регулировать свою гладкость таким образом, что ядро Матерна может быть отображено как зубчатое экспоненциальное ядро, когда ν равно ½, или вплоть до ядра радиальной базисной функции, когда этот параметр стремится к ∞. Его формула, исходя из начальных принципов, имеет вид:
где:
- ∥x−x′∥ - евклидово расстояние между двумя точками
- ν - параметр, контролирующий гладкость
- l — параметр масштаба длины (аналогичный параметру в ядре RBF)
- Γ(ν) - гамма-функция
- K ν - модифицированная функция Бесселя второго рода
Гамма-функция и функция Бесселя несколько нестандартны, и мы не будем вдаваться в подробности, однако для наших целей значение ν составляет 3/2, что делает наше ядро почти промежуточным между экспоненциальным ядром и ядром радиальной базисной функции. После этого наша формула для ядра Матерна упрощается до:
где
- Представления аналогичны первой формуле, приведенной выше.
Особые случаи:
- При ν=1/2 ядро Матерна становится экспоненциальным.
- При ν→∞ оно становится ядром RBF.
Гладкость этого ядра очень чувствительна к параметру ν, и обычно ему присваивается одно из следующих значений: 1/2 или 3/2 или 5/2 . Каждое из значений этих параметров подразумевает различную степень гладкости, причем большее значение приводит к большей гладкости.
При v равном 1/2 ядро эквивалентно экспоненциальному ядру, как уже упоминалось, и это делает его пригодным для моделирования наборов данных, где резкие изменения или разрывы являются обычным явлением. С точки зрения трейдера это обычно указывает на очень волатильные ценные бумаги или валютные пары. Такая настройка ядра предполагает неровный процесс и, следовательно, приводит к менее плавным результатам, которые, как утверждается, более восприимчивы к немедленным изменениям. При v равном 3/ 2 (это настройка, которую мы используем в статье при тестировании советника, собранного в Мастере) его плавность часто оценивается как средняя. Это компромисс, поскольку он может обрабатывать как умеренно изменчивые данные, так и наборы данных со слабо выраженными трендами. Можно утверждать, что такая настройка делает ядро подходящим для определения поворотных моментов во временном ряду или точек колебания на рынке. Настройка 5/2 и выше делает ядро более подходящим для трендовых сред, особенно при рассмотрении скорости.
Таким образом, для зашумленных данных или наборов данных, имеющих скачки или разрывы, лучше подходят меньшие значения ν, в то время как для наборов данных, которые являются более постепенными и имеют плавные изменения, лучше подойдут более высокие значения v. В качестве примечания: дифференцируемость, или количество раз, которое может быть дифференцирована функция ядра, увеличивается с параметром v. Это, в свою очередь, коррелирует с более высокими значениями параметра ν, использующими больше вычислительных ресурсов. Реализуем ядро Матерна на MQL5 следующим образом:
//+------------------------------------------------------------------+ // Matern Kernel Function //+------------------------------------------------------------------+ matrix CSignalGauss::Matern_Kernel(vector &Rows,vector &Cols) { matrix _matern; _matern.Init(Rows.Size(), Cols.Size()); for(int i = 0; i < int(Rows.Size()); i++) { for(int ii = 0; ii < int(Cols.Size()); ii++) { _matern[i][ii] = (1.0 + (sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next)) * exp(-1.0 * sqrt(3.0) * fabs(Rows[i] - Cols[ii]) / m_next); } } return(_matern); }
Таким образом, по сравнению с линейными ядрами ядра Матерна более гибкие и лучше подходят для фиксации сложных нелинейных взаимосвязей данных. При моделировании большого количества реальных явлений и данных они явно имеют преимущество перед линейными ядрами, поскольку, как мы видели выше, небольшая настройка/корректировка параметра v позволяет им обрабатывать не только трендовые наборы данных, но также изменчивые и прерывистые данные.
Класс сигналов
Мы создаем пользовательский класс сигнала, который объединяет два ядра как два варианта реализации в классе сигналов. Наша функция получения выходных данных также перекодирована для обеспечения возможности выбора ядра из входных данных советника. Новая функция будет выглядеть так, как показано ниже:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalGauss::GetOutput(double BasisMean, vector &Output) { ... matrix _k_s; matrix _k_ss; _k_s.Init(_next_time.Size(), _past_time.Size()); _k_ss.Init(_next_time.Size(), _next_time.Size()); if(m_kernel == KERNEL_LINEAR) { _k_s = Linear_Kernel(_next_time, _past_time); _k_ss = Linear_Kernel(_next_time, _next_time); } else if(m_kernel == KERNEL_MATERN) { _k_s = Matern_Kernel(_next_time, _past_time); _k_ss = Matern_Kernel(_next_time, _next_time); } ... }
Шаги, необходимые для интерполяции следующих изменений цен, после выбора соответствующего ядра, идентичны тем, что мы рассмотрели в одной из предыдущих статей. Обработка условий на покупку и на продажу также не сильно различается, и их код приводится здесь для полноты картины:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalGauss::LongCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] > _o[0]) { result = int(round(100.0 * ((_o[_o.Size()-1] - _o[0])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalGauss::ShortCondition(void) { int result = 0; vector _o; GetOutput(0.0, _o); if(_o[_o.Size()-1] < _o[0]) { result = int(round(100.0 * ((_o[0] - _o[_o.Size()-1])/(_o.Max() - _o.Min())))); } //printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0); return(result); }
Условия, указанные в связанной статье, основаны на том, будет ли прогнозируемое изменение цены положительным или отрицательным. Затем эти изменения нормализуются и находятся в диапазоне целых чисел от 0 до 100, как и ожидается от всех экземпляров пользовательских классов сигналов. Сборка файла сигнала в виде советника с помощью Мастера MQL5 рассматривается здесь и здесь.
Отчеты тестера стратегий
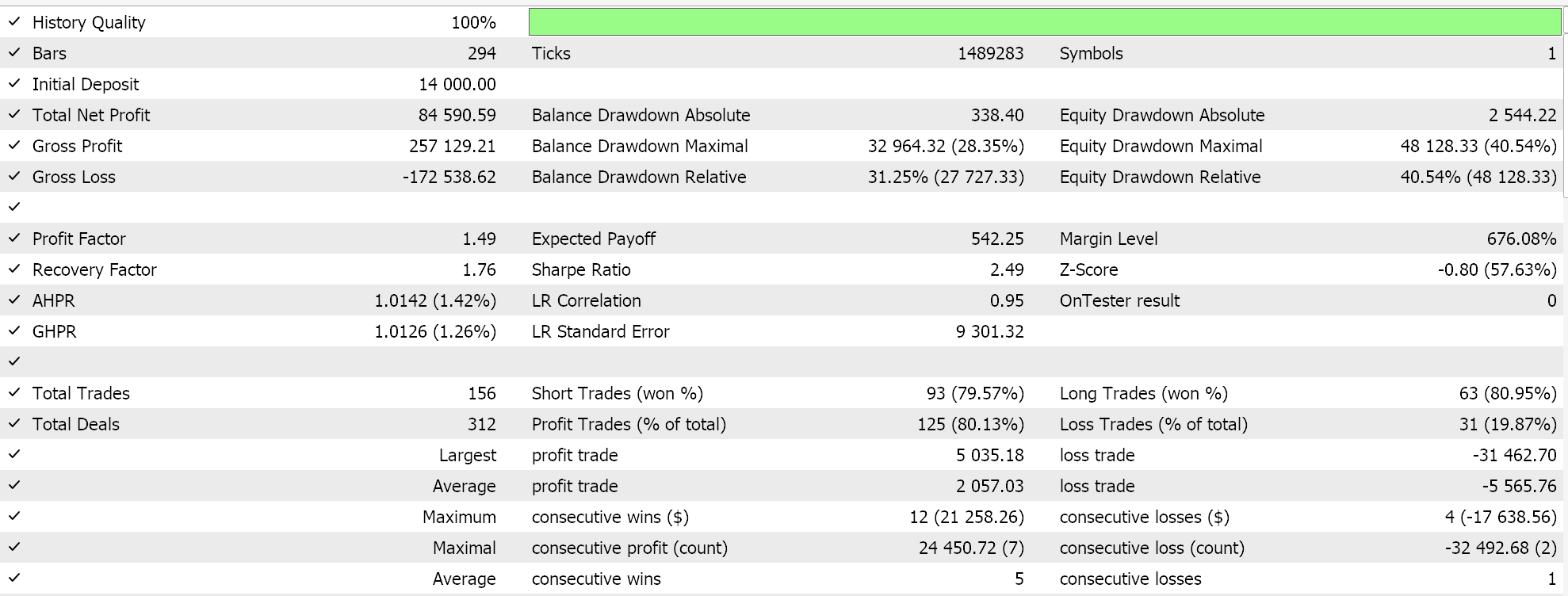
Проведем оптимизацию на паре GBPJPY на дневном временном интервале для 2023 года с использованием линейного ядра и ядра Матерн. Ниже приведены результаты, которые просто демонстрируют удобство использования советника, но никоим образом не указывают на будущую производительность:

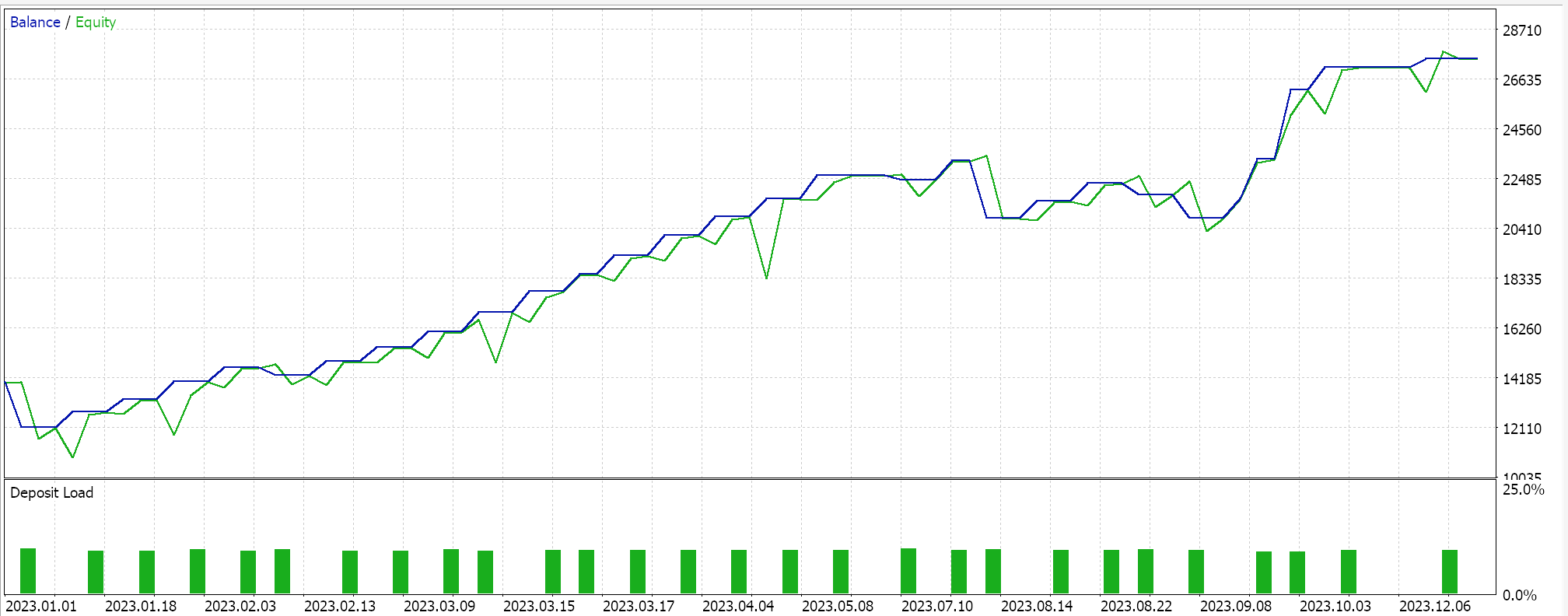
Результаты для ядра Матерн следующие:

Альтернативной реализацией обоих ядер может быть также использование специального класса управления капиталом. Как и сигнал, его можно собрать в Мастере MQL5 с той разницей, что выбирается только один пользовательский экземпляр управления капиталом. Чтобы использовать регрессию гауссовского процесса, как мы это делали с классом сигналов, в идеале нам нужен общий якорный класс, на который ссылались бы как пользовательский класс сигнала, так и пользовательский класс управления капиталом. Это позволит свести к минимуму дублирование в кодировании одних и тех же функций, которые выполняют очень похожие задачи в двух пользовательских классах.
Однако в классе управления капиталом у нас есть некоторые небольшие изменения в типе данных, которые подаются в ядра гауссовского процесса. В то время как в качестве входных данных для класса пользовательских сигналов у нас были близкие изменения цен, для этого класса управления капиталом в качестве входных данных для нашего ядра у нас есть изменения в индикаторе ATR. Выходные данные для нашего ядра обучаются быть следующим изменением в ATR. Этот пользовательский класс также является адаптацией общего класса, оптимизированного по размеру капитала, который создан для уменьшения размера позиции, если советник терпит серию убытков. Пропорция сокращения размеров лотов пропорциональна понесенным убыткам. Мы принимаем этот класс и вносим некоторые изменения, регулирующие момент сокращения лотов.
Благодаря нашим модификациям мы уменьшаем лоты только в том случае, если советник терпит убытки и существует прогноз роста ATR в пределах прогнозируемых значений. Число этих прогнозируемых значений задается параметром m_next, как обсуждалось в уже указанной статье, в которой была представлена регрессия гауссовского процесса. Ниже представлены эти изменения вместе с большей частью исходного кода для оптимизации размера позиции:
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneyGAUSS::Optimize(int Type, double lots) { double lot = lots; //--- calculate number of losses orders without a break if(m_decrease_factor > 0) { //--- select history for access HistorySelect(0, TimeCurrent()); //--- int orders = HistoryDealsTotal(); // total history deals int losses = 0; // number of consequent losing orders //-- int size = 0; matrix series; series.Init(fmin(m_series_size, orders), 2); series.Fill(0.0); //-- CDealInfo deal; //--- for(int i = orders - 1; i >= 0; i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket() == 0) { Print("CMoneySizeOptimized::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol() != m_symbol.Name()) continue; //--- check profit double profit = deal.Profit(); //-- series[size][0] = profit; size++; //-- if(size >= m_series_size) break; if(profit < 0.0) losses++; } //-- double _cond = 0.0; //-- vector _o; GetOutput(0.0, _o); //--- //decrease lots on rising ATR if(_o[_o.Size()-1] > _o[0]) lot = NormalizeDouble(lot - lot * losses / m_decrease_factor, 2); } //--- normalize and check limits double stepvol = m_symbol.LotsStep(); lot = stepvol * NormalizeDouble(lot / stepvol, 0); //--- double minvol = m_symbol.LotsMin(); if(lot < minvol) lot = minvol; //--- double maxvol = m_symbol.LotsMax(); if(lot > maxvol) lot = maxvol; //--- return(lot); }
Аналогичный подход можно использовать и при создании пользовательского класса трейлинга, использующего ядра гауссовского процесса, как мы продемонстрировали выше. Помимо простого доступа к ценам, который обеспечивается векторными и матричными типами данных, существует множество индикаторов на выбор.
Заключение
Мы продолжили изучение регрессии гауссовского процесса, рассмотрев другой набор ядер, которые можно использовать с этой формой регрессии при составлении прогнозов с использованием финансовых временных рядов. Линейное ядро и ядро Матерна практически противоположны не только по типам наборов данных, для которых они подходят, но и по своей гибкости. Хотя линейное ядро может обрабатывать только определенный тип набора данных, часто бывает целесообразно начать моделирование с него, особенно в случаях, когда выборки набора данных могут быть небольшими по размеру в начале исследования. Со временем, когда выборка набора данных увеличивается и данные становятся более сложными или даже зашумленными, можно использовать более надежное ядро, такое как ядро Матерн, для обработки не только зашумленных данных, пробелов или разрывов, но и наборов данных, которые могут быть очень гладкими. Это связано с тем, что настраиваемость его ключевого входного параметра v позволяет ему играть разные роли в зависимости от проблем, возникающих при работе с набором данных, и именно поэтому он, пожалуй, лучше подходит для большинства сред обработки данных.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15767
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Адаптивное обнаружение рыночных аномалий (Окончание)
Нейросети в трейдинге: Адаптивное обнаружение рыночных аномалий (Окончание)
 Реализация торговой стратегии Rapid-Fire с использованием индикаторов Parabolic SAR и простой скользящей средней (SMA) на MQL5
Реализация торговой стратегии Rapid-Fire с использованием индикаторов Parabolic SAR и простой скользящей средней (SMA) на MQL5
 Алгоритм оптимизации центральной силы — Central Force Optimization (CFO)
Алгоритм оптимизации центральной силы — Central Force Optimization (CFO)
 Разработка системы репликации (Часть 72): Неожиданный способ оповещений (I)
Разработка системы репликации (Часть 72): Неожиданный способ оповещений (I)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
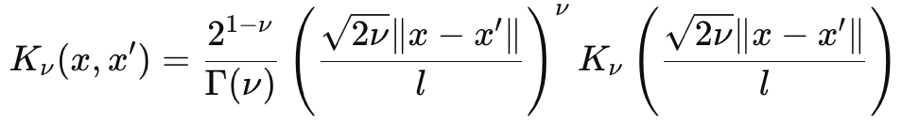
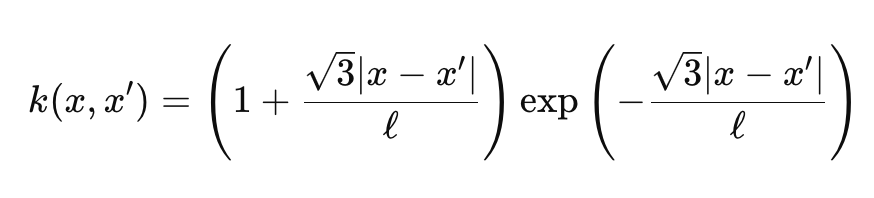
Я получаю критическую ошибку.
index out of range in 'MoneyWZ_37.mqh' (197,17)
относящаяся к строке
series[size][0] = profit;
индекс вне диапазона в 'MoneyWZ_37.mqh' (197,17)
относящаяся к строке
series[size][0] = profit;
Здравствуйте,
Только что внес изменения в приложенный код и повторно отправил на публикацию.