Нейросети в трейдинге: Адаптивное обнаружение рыночных аномалий (Окончание)

Введение

В предыдущей статье мы познакомились с теоретическими аспектами фреймворка DADA (Adaptive Bottlenecks and Dual Adversarial Decoders), который предназначен для выявления аномалий во временных рядах с помощью методов глубокого обучения. Этот инструмент помогает анализировать данные и выделять аномальные рыночные состояния, что особенно важно в условиях высокой волатильности. Использование адаптивных методов обработки информации позволяет модели гибко подстраиваться под изменяющуюся рыночную среду, что делает её универсальным средством для анализа различных временных рядов.

Архитектура фреймворка DADA простроена на трёх ключевых компонентах, каждый из которых выполняет свою специфическую задачу. Первый — это модуль адаптивных узких мест (Adaptive Bottlenecks), способный динамически изменять степень сжатия анализируемых данных. Такой подход помогает сохранить наиболее значимые характеристики рыночных данных и минимизировать потери информации, которые могли бы повлиять на качество анализа. В отличие от традиционных моделей, где параметры сжатия фиксированы, здесь всё настраивается в реальном времени, в зависимости от ситуации на рынке.

Второй важный элемент — это система из двух состязательных декодеров. Первый декодер восстанавливает нормальные рыночные состояния, что позволяет модели лучше понимать типичные паттерны поведения рынка. Второй декодер фокусируется на аномальных данных, помогая чётко различать стандартные и отклоняющиеся ситуации. Такой подход снижает вероятность ложных срабатываний и делает модель более надёжной.

Третий ключевой компонент — механизм патчинга и маскирования, который играет важную роль в обработке временных рядов. Этот механизм позволяет динамически выделять критические участки данных, скрывать шумовые компоненты и улучшать качество представления информации. Патчинг используется для разбиения данных на небольшие сегменты, что позволяет модели анализировать локальные особенности временного ряда. Случайное маскирование способствует лучшему обучению модели. Восстанавливая замаскированные участки, модель вынуждена учитывать скрытые зависимости в данных, что улучшает её способность выявлять сложные паттерны и закономерности. В сочетании, эти методы повышают точность детектирования аномалий и делают модель более устойчивой к рыночным колебаниям. Маскирование также позволяет повысить обобщающую способность модели, предотвращая её переобучение на конкретных участках рыночных данных.

Одно из главных преимуществ фреймворка DADA — его адаптивность. В отличие от традиционных алгоритмов, которые требуют повторного обучения при изменении рыночных условий, DADA может автоматически корректировать свои параметры. Это особенно важно в высокочастотной торговле, где решения принимаются в доли секунды. Возможность динамической настройки позволяет модели эффективно работать в самых разных рыночных ситуациях — от устойчивых трендов до резких всплесков волатильности.

Авторская визуализация фреймворка DADA представлена ниже.

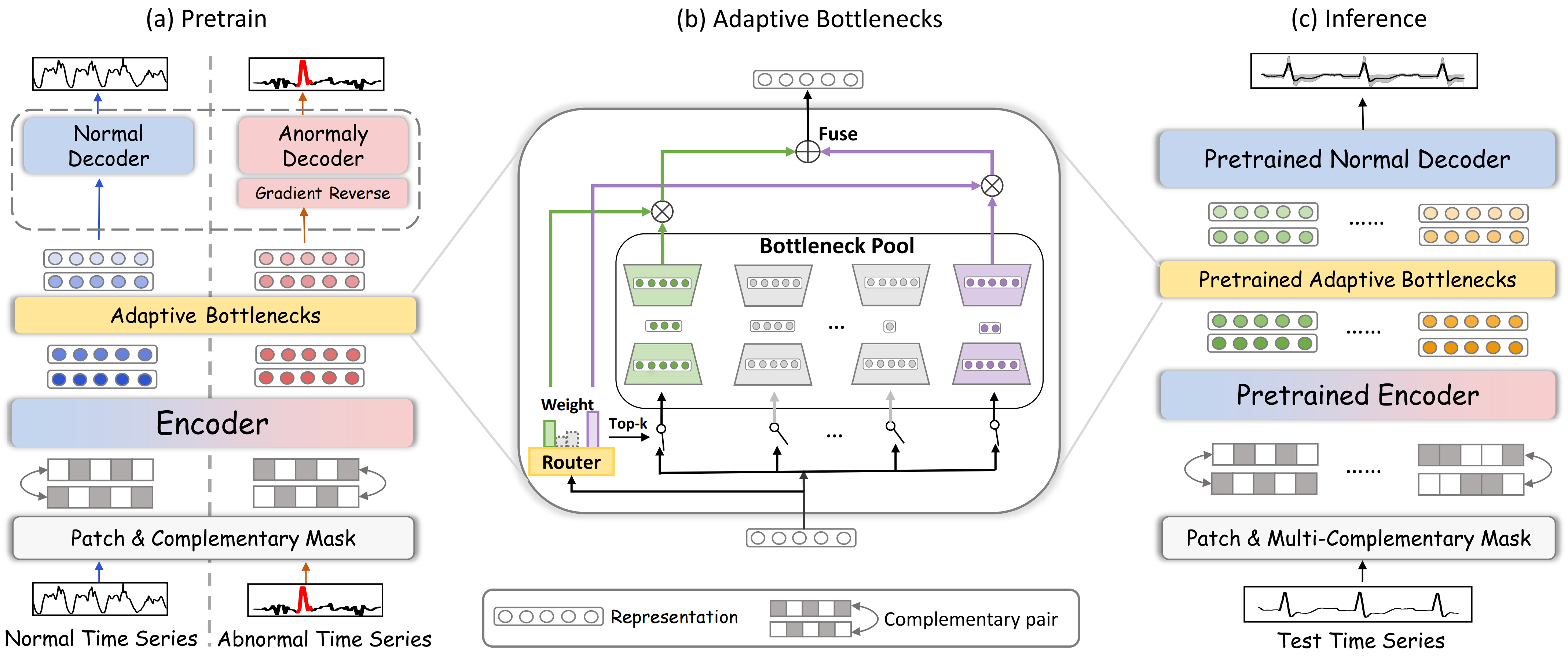
В практической части предыдущей статьи был построен объект мультиоконного сверточного слоя CNeuronMultiWindowsConvOCL. Надо сказать, что создание такого объекта напрямую не следует из авторского описания архитектуры фреймворка DADA. Однако, в нашей реализации он будет выполнять одну из ключевых ролей в модуле Adaptive Bottlenecks. Именно его использование позволит нам динамически изменять степень сжатия анализируемых данных.

Модуль Adaptive Bottlenecks

Следующим важным этапом нашей работы будет непосредственное построение модуля адаптивных узких мест (Adaptive Bottlenecks). Этот модуль представляет собой мощный инструмент для динамической обработки исходных данных, позволяющий эффективно анализировать сложные временные ряды и выявлять аномалии в их поведении.

Мы уже упоминали о его концептуальном сходстве с модулем Mixture of Experts (MoE), который ранее был реализован в рамках объекта CNeuronMoE. Оба модуля эксплуатируют подход параллельной работы нескольких минимоделей, которые выполняют анализ исходных данных. Модуль динамически выбирает k наиболее подходящих минимоделей для обработки анализируемого сегмента, на основе анализа его контекста. Такой подход повышает адаптивность и точность работы общей модели, позволяя ей концентрироваться на наиболее релевантных паттернах.

Ключевая особенность Adaptive Bottlenecks заключается в использовании набора автоэнкодеров в качестве минимоделей, каждый из которых обладает разной степенью сжатия анализируемой информации в латентном пространстве. Это позволяет моделе более гибко адаптироваться к изменчивым условиям и корректировать уровень детализации представления исходных данных в зависимости от выявленных особенностей временного ряда. Благодаря такой архитектуре, Adaptive Bottlenecks эффективно снижает избыточность данных, минимизирует влияние шумов и улучшает выявление аномальных паттернов.

Свое видение модуля Adaptive Bottlenecks мы построим в рамках объекта CNeuronAdaBN. Как можно догадаться, в качестве родительского класса используется CNeuronMoE. Такое решение обусловлено желанием повторного использования ключевых механизмов Mixture of Experts, таких, как динамическое распределение нагрузки между минимоделями и адаптивный выбор наиболее релевантных экспертов. Ведь они полностью соответствуют концепции Adaptive Bottlenecks. Это отражается и в структуре нового объекта, которая представлена ниже.

class CNeuronAdaBN   :  public CNeuronMoE
  {
public:
                     CNeuronAdaBN(void) {};
                    ~CNeuronAdaBN(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint &bottlenecks[], uint top_k, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronAdaBN; }
  };

Как можно заметить, мы планируем переопределить лишь метод инициализации объекта, без создания дополнительных внутренних объектов.

Здесь следует напомнить, что родительский класс CNeuronMoE включает в себя объект выбора k наиболее релевантных экспертов (cGates) и динамический массив (cExperts), содержащий указатели на последовательные объекты внутренней модели. На первый взгляд, концепция параллельных экспертов может показаться не совсем совместимой с традиционным представлением о последовательных моделях. Однако, мы использовали последовательность сверточных слоев, способных анализировать унитарные последовательности независимо друг от друга. Это позволило создать специализированные мини-MLP, которые функционируют параллельно. При этом, каждая минимодель обладает своими собственными обучаемыми параметрами.

Такое архитектурное решение существенно повышает адаптивность системы, поскольку каждый эксперт обучается на своей специфической подзадаче, что позволяет лучше выявлять сложные закономерности во временных рядах. Более того, динамическая система выбора оптимальных экспертов гарантирует, что в процессе анализа задействуются только наиболее релевантные модели, что повышает точность прогнозирования.

class CNeuronMoE  :  public CNeuronBaseOCL
  {
protected:
   CNeuronTopKGates     cGates;
   CLayer               cExperts;
   //---
   ..........
   ..........
   ..........
  };

Унаследованный от родительского класса механизм выбора k наиболее релевантных экспертов полностью удовлетворяет требованиям модуля CNeuronAdaBN. Поэтому мы просто воспользуемся унаследованным функционалом. Кроме того, нам достаточно наполнить унаследованный динамический массив новой последовательностью объектов в соответствии с решаемой задачей, а его обслуживание можно осуществлять существующими средствами родительского класса. Это также относится к организации процессов прямого и обратного проходов.

Последовательность внутренних объектов задается в методе Init, который мы и переопределим.

bool CNeuronAdaBN::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                        uint window, uint window_out, uint units_count,
                        uint &bottlenecks[], uint top_k, uint variables,
                        ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables,
                                                                 optimization_type, batch))
      return false;

В параметрах метода, как обычно, получаем ряд констант, которые позволяют однозначно интерпретировать архитектуру класса. Среди прочих параметров, известных нам по родительскому классу, выделяется массив bottlenecks, который содержит размеры латентных состояний создаваемых автоэнкодеров.

В теле метода сразу вызываем одноименный метод базового класса полносвязного нейронного слоя. Напомню, что именно этот объект является общим прародителем всех объектов нейронных слоев в нашей библиотеке. В данном случае, мы намеренно не используем метод инициализации прямого родительского класса, так как не хотим инициализировать пул экспертов родительского объекта. Однако, такое решение приводит нас к необходимости построения процесса инициализации всех унаследованных объектов.

После успешной инициализации базовых интерфейсов, переходим к инициализации объектов, унаследованных от родительского класса. Первым инициализируем модуль адаптивного выбора k наиболее релевантных экспертов. Здесь общее количество экспертов определяем по размеру массива bottlenecks. В качестве остальных параметров используем константы, полученные от внешней программы.

   int index = 0;
   if(!cGates.Init(0, index, OpenCL, window, units_count * variables, bottlenecks.Size(), top_k, optimization, iBatch))
      return false;

Затем, подготовим динамический массив и локальные переменные для временного хранения указателей на внутренние объекты создаваемого модуля Adaptive Bottlenecks.

   cExperts.Clear();
   cExperts.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronMultiWindowsConvOCL *mwconv = NULL;
   CNeuronTransposeRCDOCL *transp = NULL;

Тут же организуем цикл и посчитаем общий размер всех латентных состояний создаваемых автоэнкодеров.

   uint bn_size = 0;
   for(uint i = 0; i < bottlenecks.Size(); i++)
      bn_size += bottlenecks[i];

На этом подготовительный этап завершен, и мы переходим к созданию последовательности объектов наших автоэнкодеров.

Как это ни удивительно, но первым мы создаем стандартный сверточный слой. На первый взгляд, это может показаться неочевидным выбором, особенно учитывая сложность архитектуры модуля Adaptive Bottlenecks. Однако, этот шаг играет важную роль в дальнейшей обработке данных.

Ключевой момент заключается в том, что при создании сверточного слоя, мы указываем количество фильтров, равное сумме всех латентных состояний автоэнкодеров. Это решение обусловлено тем, что каждый автоэнкодер работает с одним и тем же набором исходных данных. А уровень детализации сжатых данных зависит от размера латентного состояния. При этом каждый фильтр сверточного слоя работает независимо от других и формирует значение своего собственного элемента в буфере результатов. По-существу, это можно сравнить с большим количеством минимоделей сжимающих анализируемые данные до одного элемента. И теперь мы можем объединить их в нужное нам количество групп с необходимым нам количеством элементов в каждой. При этом количество элементов в отдельных группах может быть разное. Необходимо лишь чтобы сохранялось общее количество элементов.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, bn_size, units_count, variables, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

Этим свойством мы и воспользуемся. Следующим объявим мультиоконный сверточный слой. Каждое окно свертки возьмет свою группу элементов, которые и составят латентное состояние отдельного автоэнкодера. А потом восстановит данные до заданного размера.

   index++;
   mwconv = new CNeuronMultiWindowsConvOCL();
   if(!mwconv ||
      !mwconv.Init(0, index, OpenCL, bottlenecks, window_out, units_count, variables, optimization, iBatch) ||
      !cExperts.Add(mwconv))
     {
      delete conv;
      return false;
     }
   mwconv.SetActivationFunction(SoftPlus);

Далее мы планируем добавить ещё один слой в декодер создаваемых автоэнкодеров. При этом, каждый автоэнкрдер должен получить свой слой с уникальными обучаемыми параметры. Но здесь следует обратить внимание, что результат работы мультиоконного сверточного слоя, который был инициализирован последним, можно представить в виде 4-мерного тензора [Variable, Units, Autoencoder, Dimension]. При простом использовании сверточного слоя, мы не сможем обеспечить уникальность параметров автоэнкодерам. Однако, это легко реализовать, если вынести размерность автоэнкодера на первое место. Поэтому следующим объявим слой транспонирования данных.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_count * variables, bottlenecks.Size(), window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

За ним добавляем сверточный слой, указав в параметре переменных количество автоэнкодеров, что укажет инициализируемому объекту на необходимость создания уникальных весовых матриц.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_out, window_out, window, units_count * variables, bottlenecks.Size(),
                                                                                       optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

А затем, добавим объект транспонирования данных, который вернет результаты операций в исходное представление.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, bottlenecks.Size(), units_count * variables, window, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

На этом мы завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.

Вместе с тем завершаем рассмотрение алгоритмов построения методов нашего видения организации работы модуля Adaptive Bottlenecks. Как уже было сказано выше, операции прямого и обратного проходов осуществляются унаследованными от родительского класса средствами. А с полным кодом данного объекта и всех его методов можно ознакомиться во вложении.

Архитектура моделей

Сегодня мы решили отказаться от объединения всего фреймворка DADA в единый объект. Вместо этого, возьмем уже проверенные решения из нашей библиотеки, добавим к ним созданный выше модуль Adaptive Bottlenecks и выстроим из всего этого гибкую линейную архитектуру обучаемой модели.

Такой подход дает нам гораздо больше свободы. Во-первых, он делает систему более гибкой — можно без труда заменить или оптимизировать отдельные модули, не переписывая код целиком. Во-вторых, это "развязывает нам руки" в выборе архитектуры энкодера и декодера. Теперь у нас нет жестких ограничений и можно экспериментировать, адаптировать модель под конкретные задачи и искать оптимальные конфигурации.

Да, такая модульность немного усложняет процесс описания модели, но это разумная цена за гибкость и адаптивность модели.

В рамках данного эксперимента мы будем обучать сразу три модели, каждая из которых играет ключевую роль в общей системе анализа и принятия решений. Такой подход позволяет создать многоуровневую интеллектуальную систему, которая способна анализировать данные, адаптироваться к изменениям рыночной динамики, прогнозировать дальнейшее движение цены и корректировать стратегию на основе комплексного анализа данных.

Первая модель — Энкодер состояния окружающей среды, построенный на архитектуре фреймворка DADA с декодером нормального состояния. Его обучение будет построено на принципах классического автоэнкодера, главная задача которого — восстанавливать исходные данные из латентного пространства с минимальными потерями. Это позволяет нам обучить систему находить наиболее информативное сжатие данных, при котором сохраняются все значимые характеристики окружающей среды. Данный механизм позволяет не просто уменьшать объём информации, но и выявлять скрытые зависимости в анализируемых данных, что крайне важно для построения высокоточной аналитической модели.

Второй ключевой компонент системы — Актер, который заменяет собой декодер аномальных элементов, присутствующий в оригинальной архитектуре фреймворка DADA. Данный модуль выполняет функционал активного взаимодействия с рыночной средой, поскольку его главная цель — выявление устойчивых трендов, распознавание точек возможного разворота тенденции и принятие решений, направленных на оптимизацию торговой стратегии.

Актер анализирует многомерные исходные данные, распознаёт повторяющиеся паттерны и динамику изменения рыночных состояний, а затем генерирует торговые сигналы, основываясь на выявленных закономерностях. Это делает систему не просто аналитической, а адаптивной, способной анализировать данные и адаптироваться к изменениям, находить оптимальные моменты для входа или выхода из рынка.

Однако, даже при наличии мощного механизма анализа и генерации сигналов, важным остаётся вопрос точности прогнозов. Именно здесь вступает в действие третья модель, основная задача которой заключается в оценке наиболее вероятного направления дальнейшего движения цены. Этот компонент системы дополняет работу Актера и выступает в качестве дополнительного фильтра для торговых решений.

Архитектура всех моделей описана в методе CreateDescriptions. В параметрах данного метода передается 3 указателя на динамические буфера данных, в которых нам предстоит сформировать описание архитектурного решения обучаемых моделей.

bool CreateDescriptions(CArrayObj *&encoder, CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

В теле метода сразу проверяем актуальность полученных указателей и, при необходимости создаем новые экземпляры объектов.

На первом этапе мы формируем описание архитектуры Энкодера состояния окружающей среды. Как не сложно догадаться, данная модель получает на вход тензор описания анализируемого состояния окружающей среды. Для записи исходных данных, создаем полносвязный слой достаточного размера.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

На вход модели мы планируем передавать "сырые" исходные данные, получаемые от терминала. Очевидно, что различные переменные мультимодального описания состояния окружающей среды относятся к различным распределениям. И это в значительной степени затрудняет их анализ. Поэтому следующим идет слой пакетной нормализации данных, который приводит их в сопоставимый вид.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Далее авторы фреймворка DADA предлагают использовать модуль патчинга и маскирования. Для случайного маскирования 20% анализируемых данных мы воспользуемся слоем Dropout.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDropoutOCL;
   descr.count = prev_count;
   descr.probability = 0.2f;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Патчинг данных авторы фреймворка DADA осуществляют в рамках унитарных последовательностей. В нашем случае, для создания оптимальных условий обработки унитарных последовательностей, необходимо транспонировать данные.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.window = BarDescr;
   prev_count = descr.count = HistoryBars;
   descr.activation = SoftPlus;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И теперь нам достаточно воспользоваться сверточным слоем, чтобы осуществить независимую обработку сегментов заданного размера. В данном случае мы используем 2 последовательных сверточных слоя, которые осуществляют параллельное кодирование непересекающихся сегментов и одновременно выполняют роль энкодера нашей модели кодирования состояния окружающей среды.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.window = HistoryBars / Segments;
   prev_count = descr.count = (HistoryBars + descr.window - 1) / descr.window;
   descr.step = descr.window;
   descr.layers = BarDescr;
   descr.activation = SoftPlus;
   int prev_wout = descr.window_out = EmbeddingSize;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize;
   descr.layers = BarDescr;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Далее следует модуль Adaptive Bottlenecks, в рамках которого мы создаем 15 малых автоэнкодеров с латентным состоянием кратным 8. Для кодирования данных каждого сегмента, будем использовать 3 наиболее подходящих автоэнкодера.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronAdaBN;
   descr.window = prev_wout;
   descr.count = prev_count;
   descr.window_out = 256;
   descr.step = 3; // Top K
   descr.layers = BarDescr; // Variables
     {
      int temp[15];
      for(uint i = 0; i < temp.Size(); i++)
         temp[i] = int(i + 1) * 8;
      if(ArrayCopy(descr.windows, temp) < (int)temp.Size())
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Для восстановления данных анализируемых сегментов воспользуемся декодером, роль которого выполняю 2 последовательных сверточных слоя, аналогично энкодеру модели.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = EmbeddingSize / 2;
   descr.activation = SoftPlus;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = prev_count * BarDescr;
   descr.window = prev_wout;
   descr.step = prev_wout;
   prev_wout = descr.window_out = HistoryBars / Segments;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Обратите внимание, что на выходе декодера мы используем гиперболический тангенс в качестве функции активации. И это не случайно. Ведь модель, после слоя пакетной нормализации, работает с нормализованными данными, дисперсия которых приближена к "1" с нулевым средним. По правилу "3-сигм" чуть более 68% нормально распределенных данных попадает в диапазон ± одно стандартное отклонение от среднего. При стандартном отклонении равном "1", получаем диапазон [-1, 1]. Именно в этом диапазоне находится область значений гиперболического тангенса. Таким образом, на выходе декодера получаем значения в наиболее вероятном диапазоне, исключая выбросы.

Далее, для проверки качества восстановления анализируемых данных, нам необходимо сравнить результаты работы декодера с анализируемыми данными. Однако следует вспомнить, что с целью удобства обработки унитарных последовательностей, мы транспонировали данные. Вернем их в исходное представление путем обратного транспонирования.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

И вернем полученные значения в распределение исходных данных.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = HistoryBars * BarDescr;
   descr.layers = 1;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Работа двух других моделей построена на анализе латентного состояния нашего Энкодера состояния окружающей среды, генерируемого на выходе модуля Adaptive Bottlenecks. Поэтому мы сохраним параметры данного модуля в локальную переменную.

//--- Latent
   CLayerDescription *latent = encoder.At(LatentLayer);
   if(!latent)
      return false;

Следующим этапом создаем описание архитектуры Актера. Предполагается, что Актер анализирует состояние окружающей среды в контексте текущего баланса и открытых позиций, а затем генерирует наиболее оптимальную торговую операцию. С целью организации подобного процесса, на вход модели мы планируем подавать вектор описания состояния счета. Для записи данных создадим полносвязный слой достаточного размера.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Полученные данные мы также подвергаем нормализации.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Далее, применяется слой конкатенации, который объединяет две группы данных: информацию о состоянии счета и сжатое представление окружающей среды, полученное из латентного состояния Энкодера. Это позволяет модели учитывать как финансовые показатели, так и обобщенные характеристики среды при принятии решений.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConcatenate;
   descr.count = LatentCount;
   descr.window = prev_count;
   descr.step = latent.count * latent.window * latent.layers;
   descr.batch = 1e4;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

За ним следует модуль принятия решений, состоящий из 3 полносвязных слоев. Этот модуль обрабатывает объединенные данные, извлекая ключевые закономерности и формируя итоговое решение модели.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SIGMOID;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Последняя модель прогнозирования вероятностей предстоящего ценового движения получила наиболее простую архитектуру. В рамках данной модели планируется анализировать только сжатое представление состояния окружающей среды. Для получения исходных данных, создаем полносвязный слой по данным латентного состояния Энкодера.

   probability.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = latent.count * latent.window * latent.layers;
   descr.activation = latent.activation;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

Далее идет модуль принятия решений из 3 полносвязных слоев.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions / 3;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }

Результаты анализа переводятся в область вероятностных значений с помощью функции SoftMax.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSoftMaxOCL;
   prev_count = descr.count = prev_count;
   descr.step = 1;
   descr.activation = None;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!probability.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Полное описание архитектуры моделей представлено во вложении к статье.

Обучение моделей

После описания архитектуры моделей, мы переходим к следующему этапу — их обучения, алгоритм которого реализован в советнике "...\DADA\Study.mq5". Нам предстоит осуществить параллельное обучение сразу 3 моделей, что потребовало внесение некоторых правок в алгоритм указанного советника. В рамках данной статьи мы не будем останавливаться на детальном рассмотрении кода всего советника. Разберем лишь метод непосредственного обучения моделей Train.

В теле метода мы сначала проводим небольшую подготовительную работу — объявим несколько локальных переменных.

void Train(void)
  {
//---
   vector<float> probability = vector<float>::Full(Buffer.Size(), 1.0f / Buffer.Size());
//---
   vector<float> result, target, state;
   matrix<float> fstate = matrix<float>::Zeros(1, NForecast * BarDescr);
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Непосредственно обучение моделей осуществляется внутри системы циклов. Внешней цикл перебирает пакеты обучения. Здесь для каждого пакета случайным образом сэмплируется траектория из буфера воспроизведения опыта и состояние начала обучения на выбранной траектории.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch)
     {
      int tr = SampleTrajectory(probability);
      int start = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast - Batch));
      if(start <= 0)
        {
         iter -= Batch;
         continue;
        }
      if(!Encoder.Clear() ||
         !Actor.Clear())
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }
      result = vector<float>::Zeros(NActions);

А в рамках вложенного цикла, осуществляется обучение моделей на последовательных состояниях одного пакета.

Здесь следует обратить внимание, что разработанные в рамках данной статьи модели не содержат рекуррентных блоков. Обычно такие модели обучаются на полностью случайных состояниях, извлекаемых из буфера воспроизведения опыта. Однако, в данном случае, обучение будет происходить на "почти идеальных" траекториях, действия которых генерируются непосредственно алгоритмом данного советника на основе доступной информации о последующих состояниях окружающей среды. Ведь в отличие от обучения моделей в реальном времени, при работе с буфером воспроизведения опыта у нас есть данные о последующих состояниях окружающей среды для всех сохраненных записей, за исключением последней. Это позволяет более точно направлять процесс обучения.

Но есть и другая "сторона медали". В таком случае у нас нет информации об открытых позициях. А нам важно обучить модель не только открывать позиции, но и сопровождать их с поиском оптимальной точки выхода из неё. Поэтому, в процессе обучения мы будем формировать небольшие пакеты обучения с формированием "оптимальных" позиций.

      for(int i = start; i < MathMin(Buffer[tr].Total, start + Batch); i++)
        {
         if(!state.Assign(Buffer[tr].States[i].state) ||
            MathAbs(state).Sum() == 0 ||
            !bState.AssignArray(state))
           {
            iter -= Batch + start - i;
            break;
           }
         //---
         bTime.Clear();
         double time = (double)Buffer[tr].States[i].account[7];
         double x = time / (double)(D'2024.01.01' - D'2023.01.01');
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_MN1);
         bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_W1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         x = time / (double)PeriodSeconds(PERIOD_D1);
         bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
         if(bTime.GetIndex() >= 0)
            bTime.BufferWrite();
         //--- Account
         float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
         float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
         float profit = float(bState[0] / _Point * (result[0] - result[3]));
         bAccount.Clear();
         bAccount.Add(1);
         bAccount.Add((PrevEquity + profit) / PrevEquity);
         bAccount.Add(profit / PrevEquity);
         bAccount.Add(MathMax(result[0] - result[3], 0));
         bAccount.Add(MathMax(result[3] - result[0], 0));
         bAccount.Add((bAccount[3] > 0 ? profit / PrevEquity : 0));
         bAccount.Add((bAccount[4] > 0 ? profit / PrevEquity : 0));
         bAccount.Add(0);
         bAccount.AddArray(GetPointer(bTime));
         if(bAccount.GetIndex() >= 0)
            bAccount.BufferWrite();

В теле цикла мы сначала извлекаем информацию из буфера воспроизведения данных и формируем объекты исходных данных для обучаемых моделей. После чего, вызываем методы прямого прохода Энкодера состояния окружающей среды.

         //--- Feed Forward
         if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

А затем, вызываем аналогичные методы двух других моделей, передав им в качестве исходных данных указатель на объект Энкодера состояния окружающей среды.

         if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }
         if(!Probability.feedForward(GetPointer(Encoder), LatentLayer, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Далее идет процесс формирования "оптимальной торговой операции". Данный процесс был полностью перенесен из статьи, посвященной мультизадачному обучению. С его подробным описанием можно ознакомиться по ссылке, а здесь мы его опустим.

После подготовки целевых значений, переходим к оптимизации параметров моделей с целью минимизации отклонений от целевых значений. Первым обучаем Энкодер состояния окружающей среды. В качестве тензора целевых значений, ему мы передаем вектор описания анализируемого состояния окружающей среды, который использовали и при прямом проходе.

         //--- State Encoder
         if(!Encoder.backProp(GetPointer(bState), (CBufferFloat*)NULL, NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Вторым обучаем Актера, минимизируя отклонение от "оптимальной торговой операции".

         //--- Actor Policy
         if(!Actor.backProp(GetPointer(bActions), (CNet*)GetPointer(Encoder), LatentLayer)
            || !Encoder.backPropGradient((CBufferFloat*)NULL, (CBufferFloat*)NULL, LatentLayer, true)
            )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Для обучения третьей модели мы определяем направление предстоящего ценового движения по цвету следующего бара.

         target = vector<float>::Zeros(NActions / 3);
         if(fstate[0, 0] > 0)
            target[0] = 1;
         else
            if(fstate[0, 0] < 0)
               target[1] = 1;
         if(!Result.AssignArray(target) ||
            !Probability.backProp(Result, (CBufferFloat*)NULL)
            || !Encoder.backPropGradient((CBufferFloat*)NULL, (CBufferFloat*)NULL, LatentLayer)
           )
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

И теперь остается лишь проинформировать пользователя о ходе процесса обучения и перейти к следующей итерации системы циклов.

         //---
         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + i - start) * 100.0 / (Iterations);
            string str = StringFormat("%-13s %6.2f%% -> Error %15.8f\n", "Encoder",
                                         percent, Encoder.getRecentAverageError());
            str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent,
                                                     Actor.getRecentAverageError());
            str += StringFormat("%-13s %6.2f%% -> Error %15.8f\n", "Probability", 
                                      percent, Probability.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

После успешного выполнения всех итераций обучения моделей, мы выводим в журнал полученные результаты и инициализируем процесс завершения работы советника.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Probability", Probability.getRecentAverageError());
   ExpertRemove();
//---
  }

Полный код данного советника представлен во вложении и доступен для самостоятельного изучения. Кроме того, во вложении представлены программы взаимодействия с окружающей средой и тестирования обученных моделей.

Тестирование

После проведения масштабной работы по реализации подходов, предложенных авторами фреймворке DADA, средствами MQL5 и интеграции их в обучаемые модели наступает ключевой этап — проверка эффективности реализованных решений на реальных исторических данных. Это позволит нам оценить возможность их использования в реальных рыночных условиях.

Для обучения модели была сформирована выборка случайных проходов в тестере стратегий MetaTrader 5 на исторических данных валютной пары EURUSD таймфрейма M1 за весь 2024 год. Исторические данные собираются с использованием стандартных параметров индикаторов, что обеспечивает чистоту эксперимента и исключает влияние сторонних факторов.

Тестирование обученных моделей проводится на исторических данных за Январь-Февраль 2025 года. При этом, все параметры эксперимента сохраняются без изменений, что позволяет получить объективную оценку политики поведения обученного Актера. Проверка эффективности работы модели на данных, которые не использовались в процессе обучения, является важным шагом её валидации. Поскольку демонстрирует качество работы модели в условиях, близких к реальным.

Результаты тестирования представлены ниже.

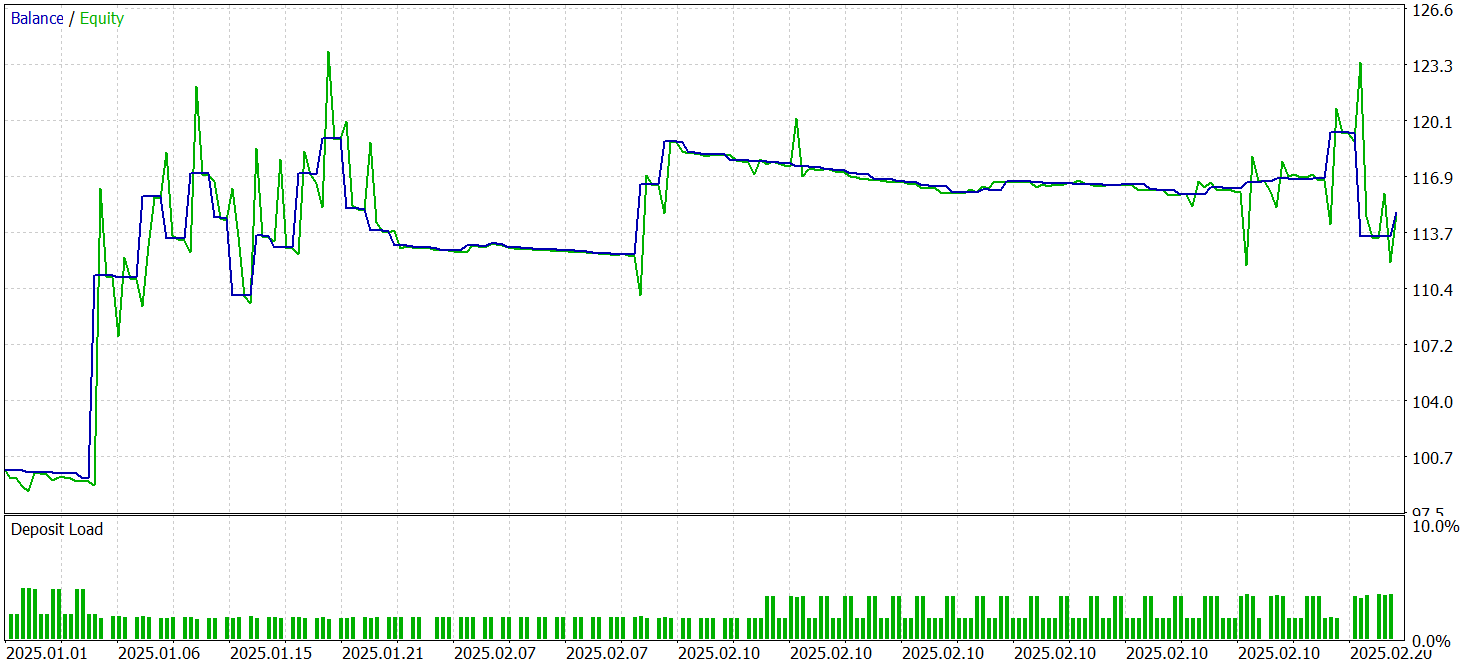
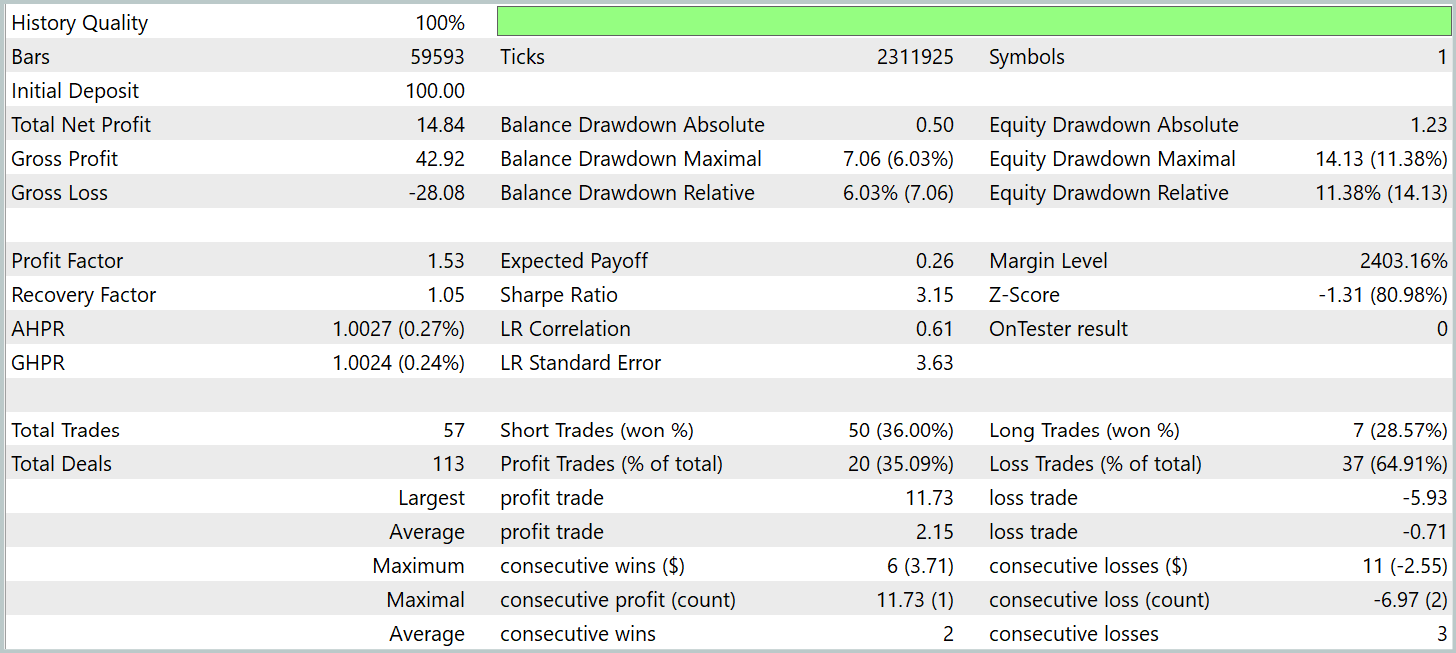
За период тестирования модель совершила 57 торговых операций, более 35% из которых были закрыты с прибылью. Тем не менее, трехкратное превышение средней прибыльной позиции над аналогичным показателем убыточных операций позволило модели получить прибыль за период тестирования и зафиксировать профит-фактор на уровне 1.53.

Однако, следует обратить внимание, что прибыль получена в первой половине Января. В остальной период график баланса колебался в узком диапазоне. Это может свидетельствовать о необходимости изучения вариантов оптимизации работы модели.

Здесь следует обратить внимание, что в процессе реализации мы внесли ряд конструктивных изменений в архитектуру фреймворка DADA. Поэтому полученные результаты релевантны только для данной реализации.

Заключение

В данной работе мы познакомились с фреймворком DADA, который предлагает инновационный подход сочетания механизма адаптивных узких мест и двух параллельных декодеров для более точного анализа временных рядов. Ключевое преимущество этого метода заключается в его способности динамически подстраиваться под различные структуры данных без необходимости предварительной адаптации.

Была проведена большая работа по имплементации средствами MQL5 собственного видения предложенных авторами фреймворка подходов. Реализованные решения были интегрированы в модели, после чего они прошли обучение на реальных исторических данных. В ходе тестирования обученные модели смогли показать прибыльность. Однако, график баланса не продемонстрировал устойчивой тенденции к росту, что указывает на необходимость дальнейшей оптимизации стратегии.

Ссылки

• Towards a General Time Series Anomaly Detector with Adaptive Bottlenecks and Dual Adversarial Decoders
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы