MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
Популяционные алгоритмы оптимизации: Светлячковый алгоритм (Firefly Algorithm - FA)

Популяционные алгоритмы оптимизации: Светлячковый алгоритм (Firefly Algorithm - FA)

MetaTrader 5 — Примеры | 20 декабря 2022, 16:55
1 688 0
Andrey Dik
Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов


1. Введение

Природа была, есть и будет источником вдохновения для создания многих метаэвристических алгоритмов. Ей удалось найти решение проблем без подсказок, на основе индивидуального опыта. Естественный отбор и выживание наиболее приспособленных особей было основой мотивации создания ранних метаэвристических алгоритмов. В природе животные общаются друг с другом разными способами. Светлячки используют свою способность мигать для общения. Существует около 2000 видов светлячков со своими особыми паттернами вспышек. Обычно они производят короткую вспышку с определенным рисунком. При этом свет и его интенсивность становятся результатом биохимических процессов, называемых биолюминесценцией. Считается, что основной функцией таких вспышек является привлечение особей противоположного пола и потенциальных жертв. Некоторые тропические светлячки могут синхронизировать свои мерцания, демонстрируя тем самым пример биологической самоорганизации. Интенсивность света, как функция расстояния от его источника, подчиняется закону обратных квадратов, следовательно мерцающий свет, исходящий от светлячка, вызывает реакцию светлячков вокруг него в пределах видимости вспышки.

Известны два варианта популяционных алгоритмов оптимизации, инспирированных поведением светлячков: алгоритм светлячков (Firefly algorithm) и алгоритм оптимизации роем светлячков (Glowworm Swarm Optimization, GSO). Основное различие между firefly и glоwwоrm светлячками состоит в том, что вторые являются бескрылыми. В данной статье мы рассмотрим первый тип алгоритма оптимизации.

2. Описание алгоритма

Алгоритм светлячков (F-алгоритм) был предложен в Кембриджском университете (Великобритания) в 2007 г. Янгом (X-Sh. Yang) и сразу привлек  к себе внимание исследователей в области оптимизации. Алгоритм светлячка является частью семейства алгоритмов роевого интеллекта, которые в последнее время показывают впечатляющие результаты при решении задач оптимизации. Светлячковый алгоритм, в частности, применяется для решения задач непрерывной и дискретной оптимизации.

Алгоритм светлячка имеет три правила, которые основаны на характеристиках мерцания реальных светлячков. Вот они:

  1. Все светлячки будут двигаться к более привлекательным и ярким.
  2. Степень притяжения светлячка пропорциональна его яркости, которая снижается по мере увеличения расстояния от другого светлячка из-за того, что воздух поглощает свет. Следовательно, между любыми двумя мигающими светлячками менее яркий будет двигаться к более яркому. Если нет более яркого или более привлекательного светлячка, чем конкретный, он будет двигаться случайным образом.
  3. Яркость или интенсивность света светлячка определяется значением целевой функции задачи.


Изначально в начале алгоритма все светлячки случайным образом рассредоточены по всему пространству поиска. Затем алгоритм определяет оптимальные разбиения на основе двух фаз:

  1. Изменение интенсивности света - яркость светлячка в текущем положении отражается на значении его приспособленности, движение к привлекательному светлячку.
  2. Светлячок меняет свое положение, наблюдая интенсивность света соседних светлячков.


Теперь можно более подробно окунуться в тонкости светлячковой оптимизации. Суть алгоритма наглядно представлена на рисунке 1.

Fas

Рисунок 1. Светлячки в пространстве поиска. Снижение видимости с увеличением расстояния.

Основной идеей, заложенной в принцип поиска, является нелинейное снижение видимости с увеличением расстояния между светлячками. Если бы не было этой нелинейной зависимости, каждый светлячок двигался бы детерминировано к более яркому источнику света. Однако, как мы видим на рисунке 1, светлячок выбирает не самого яркого своего сородича, так как его свет менее заметен в связи с поглощением света средой, а менее яркого, но самого яркого в его окружении. Эта особенность объясняет хорошие способности алгоритма к разделению на более мелкие рои, причем это происходит естественным образом только лишь за счет нелинейной функции поглощения света от расстояния. На рисунке 2 ниже можно увидеть функцию зависимости видимости от расстояния для алгоритма с разными значениями коэффициента поглощения среды gamma, который является одним из параметров алгоритма.


visibility

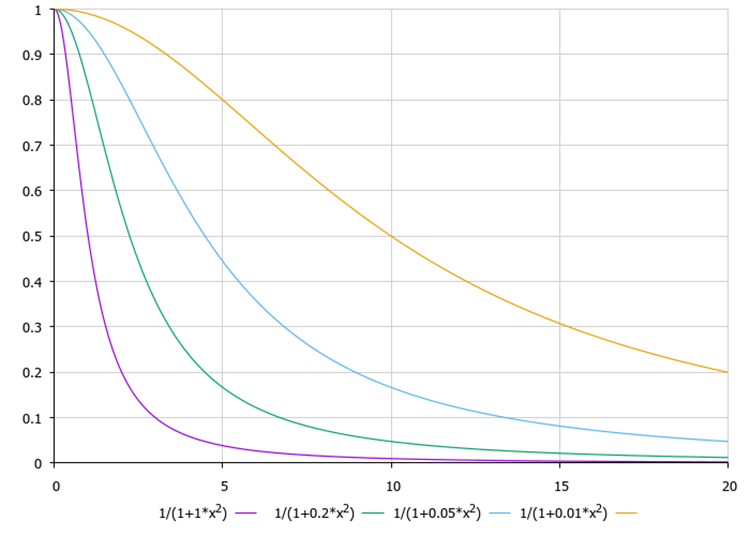
Рисунок 2. Функция прозрачности среды от расстояния f(x), где коэффициент прозрачности gamma равен 1.0, 0.2, 0.05, 0.01 соответственно.

При gamma стремящемся к бесконечности среда становится непрозрачной, а при gamma равным нулю среда полностью прозрачна, и каждый светлячок видит другого на любом удалении в пространстве поиска. Что будет, если gamma = 0.0 ? Ответ: все светлячки будут лететь к самому яркому сородичу, они сойдутся в какую-то одну не оптимальную точку и алгоритм не сойдется, застряв в одном из локальных экстремумов. Что будет если среда совершенно непрозрачная? Это означает, что светлячки не будут видеть никого привлекательнее себя, но согласно концепции, предложенной автором алгоритма, не видя никого лучше себя, светлячок будет двигаться случайным образом. Алгоритм будет вырождаться в случайный поиск. В нашей рейтинговой таблице классификации алгоритмов алгоритм случайного поиска занимает последнее место.  

Углубимся в дальнейший разбор алгоритма, рассмотрим формулы, описывающие движения светлячков. Функция зависимости видимости от расстояния лежит в основе расчета так называемого показателя привлекательности:

attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

где:
attractiveness - привлекательность
gamma - коэффициент непрозрачности среды
distance - евклидово расстояние между светлячками
fireflies [k].f - яркость света k-того светлячка

Из формулы можно заметить, что функция привлекательности будет зависеть напрямую от размерности задачи и зависеть от пределов значения distance, поэтому автор алгоритма рекомендует подбирать коэффициент прозрачности под конкретную задачу оптимизации. Думаю, что это неудобно и трудоемко - подбирать параметры, не зная заранее как поведет себя алгоритм, поэтому считаю необходимо нормализовать значения distance в диапазон от 0 до 20. Применим для этого функцию Scale (), которую мы неоднократно применяли в других алгоритмах. Преобразование distance перед тем, как рассчитать привлекательность, будет выглядеть таким образом:

distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);

где:

maxDist - максимальное евклидово расстояние между парой светлячков среди всех

В таком случае привлекательность светлячков не будет зависима от размерности задачи и отпадает необходимость подбирать коэффициент gamma под конкретную задачу оптимизации. Функция привлекательности определяет какой выбор своей пары сделает каждый светлячок. Этот выбор строго детерминирован. Влияние привлекательности светлячков друг к другу определяет коэффициент beta (второй параметр алгоритма). Каким же образом обеспечиваются поисковые способности алгоритма, если выбор светлячков уже определен заранее на каждой соответствующей итерации? Для этого введен случайный векторный компонент и третий параметр алгоритма alpha. Сложные поведенческие отношения светлячков будут выглядеть так:

fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];

где:
fireflies [i].c [c] - c-тая координата i-того светлячка
beta - коэффициент влияния притяжения светлячков друг к другу
alpha - коэффициент, влияющий на случайную компоненту при движении светлячков, дающий отклонения от цели перемещения
r - случайное число в диапазоне [-1.0;1.0]
v[c] - векторный компонент, характеризующий расстояние между крайними точками диапазона поиска по c-той координате
Хj - соответствующая координата светлячка в паре, к которому будет движение
Xi - соответствующая координата светлячка, для которого рассчитывается движение

Переходим к описанию кода алгоритма. Код не отличается особенной сложностью, достаточно прост. Рассмотрим подробнее.

Чудесное создание природы - светлячок, опишем простой структурой S_Firefly, в котором есть всего лишь две компоненты с [] - координаты, f - значение светимости светлячка, оно же и значение фитнесс - функции. Поскольку для каждого светлячка есть только одна особь на соответствующей итерации, к которой он будет двигаться, образуя пару, мы не рискуем перезаписать координаты при расчете следующего движения поскольку для этих целей введем специальную структуру, которую рассмотрим ниже.
//——————————————————————————————————————————————————————————————————————————————
struct S_Firefly
{
  double c  []; //coordinates
  double f;     //the value of the fitness function
};
//——————————————————————————————————————————————————————————————————————————————

Структура S_Attractiveness предназначена для хранения значения привлекательности и номер соответствующего светлячка в качестве пары. Каждый светлячок двигается не в сторону координат самого привлекательного, а в сторону координат, куда его пассия уже переместилась, в этом есть некоторое несоответствие с вариантом алгоритма, описанным автором, но именно так он работает лучше.

//——————————————————————————————————————————————————————————————————————————————
struct S_Attractiveness
{
  double a; //attractiveness
  int    i; //index of the most attractive firefly
};
//——————————————————————————————————————————————————————————————————————————————

Светлячковый алгоритм опишем классом C_AO_FA. Здесь три открытых метода, один из которых Init() для первоначальной инициализации и два открытых метода, необходимых для вызова на каждой итерации, Flight() и  Luminosity(), закрытые вспомогательные методы и члены для хранения констант параметров.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_FA
{
  //----------------------------------------------------------------------------
  public: S_Firefly fireflies []; //fireflies
  public: double    rangeMax  []; //maximum search range
  public: double    rangeMin  []; //minimum search range
  public: double    rangeStep []; //step search
  public: double    cB        []; //best coordinates
  public: double    fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,  //number of opt. parameters
                     const int    sizeP,    //swarm size
                     const double alphaP,   //alpha, randomness in motion
                     const double betaP,    //beta, effect of attractiveness
                     const double gammaP);  //gamma, transparency of the environment

  public: void Flight ();
  public: void Luminosity ();

  //----------------------------------------------------------------------------
  private: S_Attractiveness att [];
  private: int    swarmSize;
  private: int    params;
  private: double maxDist;
  private: double v [];

  private: double alpha;      //randomness in motion
  private: double beta;       //effect of attractiveness
  private: double gamma;      //transparency of the environment
  private: bool   luminosity;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  protected: double Scale   (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Открытый метод Init(), служит для инициализации, параметры которого есть надстроечные параметры для алгоритма, необходимо вызвать перед началом каждой оптимизации. Метод распределит память под массивы и сбросит значение светимости глобального и каждого светлячка по отдельности. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Init (const int    paramsP, //number of opt. parameters
                    const int    sizeP,   //swarm size
                    const double alphaP,  //alpha, randomness in motion
                    const double betaP,   //beta, effect of attractiveness
                    const double gammaP)  //gamma, transparency of the environment
{
  fB = -DBL_MAX;

  params    = paramsP;
  swarmSize = sizeP;
  alpha     = alphaP;
  beta      = betaP;
  gamma     = gammaP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);
  ArrayResize (v,         params);
  ArrayResize (att,       swarmSize);

  luminosity = false;

  ArrayResize (fireflies, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (fireflies [i].c,  params);
    fireflies [i].f = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

Рассмотрим первый открытый метод, вызываемый на каждой итерации - Flight (). В этом одном методе сосредоточена вся основная логика алгоритма, поэтому необходимо его рассмотреть более подробно частями. Для определения того, запущен ли алгоритм на первой итерации или на последующих, служит переменная luminosity, являясь флагом. Если флаг не взведен, необходимо распределить светлячков случайным образом в пространстве координат в соответствии с равномерным распределением. Вместе с этим действием задаем вектор смещений по каждой координате и сразу посчитаем максимально возможное евклидово расстояние, которое может быть между светлячками (это необходимо для нормализации расстояний между светлячками чтобы избежать зависимости коэффициента прозрачности среды от размерности задачи, о чем мы говорили ранее). После этих операций взводим флаг luminosity.

if (!luminosity)
{
  fB = -DBL_MAX;

  //--------------------------------------------------------------------------
  double summCoordinates = 0.0;
  for (int c = 0; c < params; c++)
  {
    v [c] = rangeMax [c] - rangeMin [c];
    summCoordinates += pow (v [c], 2.0);
  }
  maxDist = pow (summCoordinates, 0.5);

  //--------------------------------------------------------------------------
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < params; k++)
    {
      fireflies [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      fireflies [s].c  [k] = SeInDiSp (fireflies [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }

  luminosity = true;
}

Со второй и далее итерации после того, как на первой итерации светлячки были распределены случайным образом и начали светиться, т.е. для них была рассчитана фитнесс - функция, можно рассчитать степень привлекательности для каждого светлячка. Для этого нам понадобится рассчитать евклидово расстояние между всеми возможными парами светлячков. Сделать это просто сложив квадраты разностей координат, а из их суммы извлечь корень. Рассчитанное расстояние будет участвовать в формуле расчета привлекательности. Так мы получим для каждого светлячка единственно возможную пару. Тут же определим максимальную светимость среди всех светлячков, это потребуется для того, чтобы определить самого яркого светлячка, для которого найти пару будет не суждено и который будет блуждать в пространстве в одиночестве. Ну ничего, на следующей итерации, возможно, ему повезет больше.

//measure the distance between all------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  att [i].a = -DBL_MAX;

  for (int k = 0; k < swarmSize; k++)
  {
    if (i == k) continue;

    summCoordinates = 0.0;
    for (int c = 0; c < params; c++) summCoordinates += pow (fireflies [i].c [c] - fireflies [k].c [c], 2.0);

    distance = pow (summCoordinates, 0.5);
    distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);
    attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

    if (attractiveness > att [i].a)
    {
      att [i].a = attractiveness;
      att [i].i = k;
    }

    if (fireflies [i].f > maxF) maxF = fireflies [i].f;
  }
}

Эта часть кода метода Flight() отвечает за полеты светлячков. Для того самого несчастливого светлячка, светимость у которого больше всех остальных, расчет производится несколько иначе. К его текущему положению прибавляем вектор перемещения через коэффициент alpha помноженный на случайное число [-1.0;1.0]. Теоретически в алгоритме это выполняет роль дополнительного исследования наилучшего решения с расчетом, что оно будет еще лучше, впрочем, как мы увидим это дальше данный прием окажется бесполезным. На данном этапе мы рассматриваем классический вариант алгоритма.

Для всех остальных светлячков, для которых уже найдена пара, расчет движения будет заключаться в перемещении в точку соответствующей ему пары с добавлением случайной компоненты (о ней мы говорили ранее).

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      fireflies [i].c [c] = fireflies [i].c [c] + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); 
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];
      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Простой открытый метод, вызываемый на каждой итерации. Здесь мы обновим наилучшее решение. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Luminosity ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    if (fireflies [i].f > fB)
    {
      fB = fireflies [i].f;
      ArrayCopy (cB, fireflies [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Переходим к обсуждению тестов. Посмотрим на распечатку результатов работы алгоритма на тестовых функциях:

2022.12.16 13:39:00.102    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.901742065217812
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    Score: 0.99603
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    20 Skin's; Func runs 10000 result: 3.2208359936020665
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    Score: 0.59468
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    500 Skin's; Func runs 10000 result: 0.98491319842575
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    Score: 0.06082
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.578196881663454
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    Score: 0.89271
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.3101994341994826
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    Score: 0.17546
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.06829102669136165
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    Score: 0.03863
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 8.2
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    Score: 0.68333
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.5900000000000003
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    Score: 0.13250
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.2892
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    Score: 0.02410
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    All score for C_AO_FA: 0.39980648892951776

Результаты, мягко говоря, не впечатлили. Алгоритм лишь немногим лучше таких алгоритмов как PSO, FSS, GWO в отдельных тестах, однако в суммарном показателе рейтинга он находится на второй позиции снизу, оказавшись лучше только алгоритма со случайным поиском. Исходя из сказанного, возникла идея пересмотреть расчет оценочных показателей в тестах и в следующих статьях мы перейдем на более удобную схему подсчета рейтинга, а в этой статье добавим гистограмму итоговых результатов, в ней наглядно будет видно соотношение производительности между отдельными алгоритмами.

Классический алгоритм Firefly прост в реализации. Однако исследования показывают, что он медленно сходится и легко попадает в ловушку локального экстремума для мультимодальных задач. Кроме того, в нем отсутствуют коэффициенты, параметрически зависимые от текущей итерации. Следовательно, модификация стандартного алгоритма Firefly для повышения его производительности была одной из задач исследования.

Сама идея алгоритма восхищает своей оригинальностью и было бы жаль оставить все как есть и не попробовать улучшить его характеристики. Поэтому я предпринял попытку модифицировать алгоритм, заменив случайную компоненту полетом Леви. Надо отметить, что не для каждого алгоритма полет Леви может улучшить поисковые способности, после рассмотрения алгоритма поиска с кукушкой, я предпринимал попытки улучшения других алгоритмов с помощью этого метода, однако это не принесло ожидаемых результатов. По-видимому, это должно согласовываться каким-то образом с внутренней стратегией поиска внутри алгоритма дополняя его. В данном конкретном случае применение Полета Леви дало поразительный эффект, возможности алгоритма возросли кардинально. Об этом поговорим в части статьи о результатах тестирования.

Вот, собственно, та часть кода, где было внесено изменение. Во-первых, в классическом варианте светлячок с наилучшей светимостью перемещается в случайном направлении от своего текущего положения, тогда наш лучший светлячок будет двигаться от лучшего глобального положения, пытаясь улучшить не свое текущее положение, а решение в целом. К координатам лучшего решения прибавляем случайное число распределения полета Леви (распределение с тяжелыми хвостами) с тем же коэффициентом alpha с учетом вектора перемещений. Это действительно позволило улучшить координаты глобального решения, уточняя окрестности.

Как видим, поведение остальных светлячков теперь подчиняется тем же классическим правилам, но с поправкой на случайный компонент полета Леви. Вот и вся модификация, которая была внесена в алгоритм. 

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      fireflies [i].c [c] = cB [c] + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];

      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

График функции Полет Леви на рисунке 3. Как может влиять показатель степени в формуле функции на поведение алгоритма? Согласно моим исследованиям, при повышении степени количество длинных (тяжелых хвостов) прыжков уменьшается по отношению к коротким, при этом улучшается способность алгоритма уточнять координаты в окрестностях лучшего решения, но за счет того, что длинных прыжков становится мало, растет вероятность застревания в локальных экстремумах. Данный эффект будет больше проявляться при исследовании дискретных функций, тогда как на гладких это не будет настолько явно выражено. Наоборот, при уменьшении показателя степени, количество длинных прыжков растет, поисковые способности алгоритма улучшаются, но ухудшается точность схождения, поэтому необходима золотая середина между точностью и поиском, к тому же она может быть разная в зависимости от поставленной задачи оптимизации.


Levi

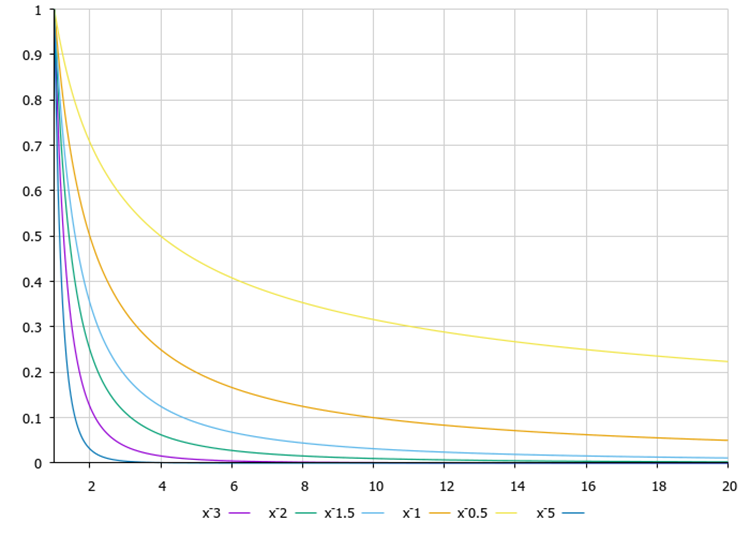
Рисунок 3. Функция Полёт Леви, степени 0.5...3.0. 


Итак, перейдем к результатам модифицированной версии алгоритма на тестовом стенде. Ниже представлена распечатка, где можно увидеть, насколько улучшились показатели оригинальной версии по сравнению с классической.

2022.12.16 13:07:15.925    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.854437214435259
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    Score: 0.98473
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    20 Skin's; Func runs 10000 result: 4.588539001298423
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    Score: 0.92124
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.981278990090829
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    Score: 0.29872
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.7665409595127233
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    Score: 0.99924
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.6261364994589462
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    Score: 0.35417
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.14269062630878
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    Score: 0.08071
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 10.0
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    Score: 0.83333
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.7899999999999998
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    Score: 0.14917
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.5076
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    Score: 0.04230
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    All score for C_AO_FAm: 0.5181804234713119

Как можно увидеть, модифицированный алгоритм показал результаты не только лучше, но и смог занять лидирующую позицию в рейтинговой таблице. Немного подробнее рассмотрим результаты в следующем разделе. Ниже представлена анимация работы модифицированной версии алгоритма на тестовом стенде.

Skin

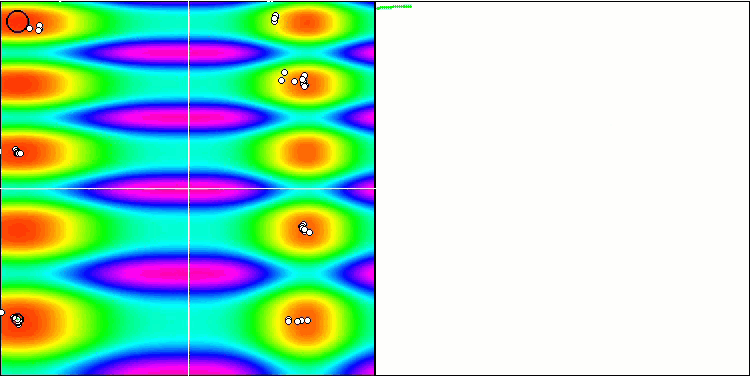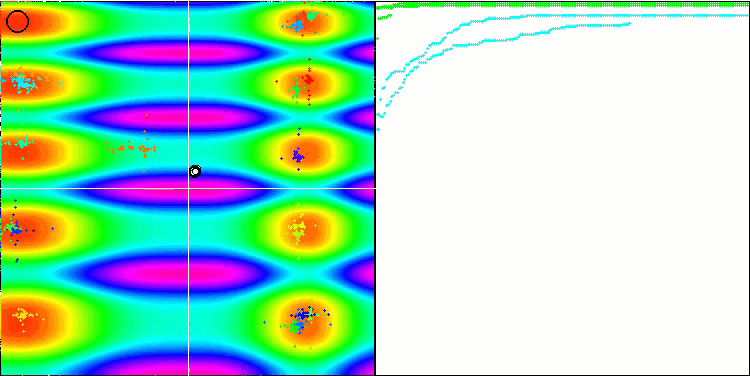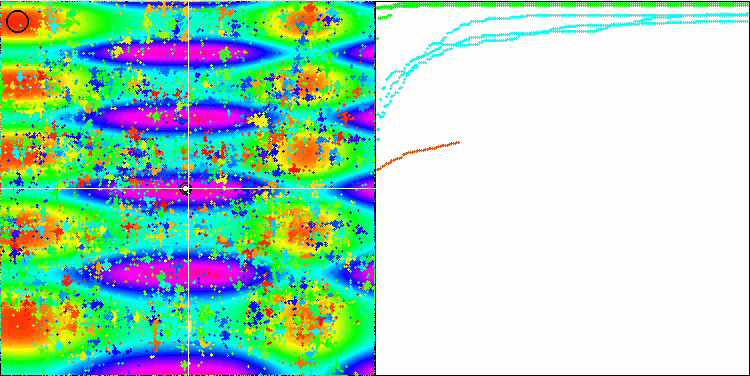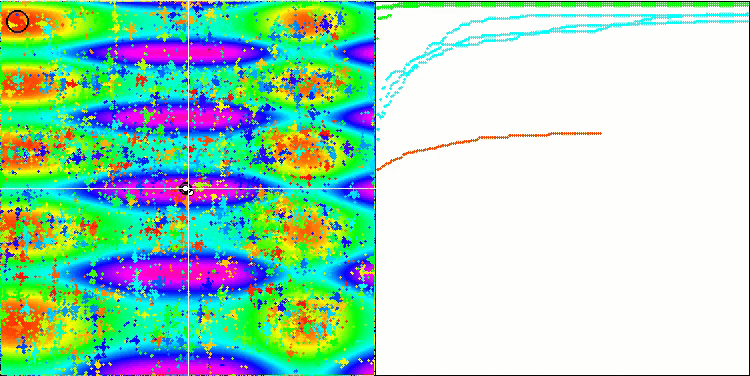
  FAm на тестовой функции Skin.

Forest

  FAm на тестовой функции Forest.

Megacity

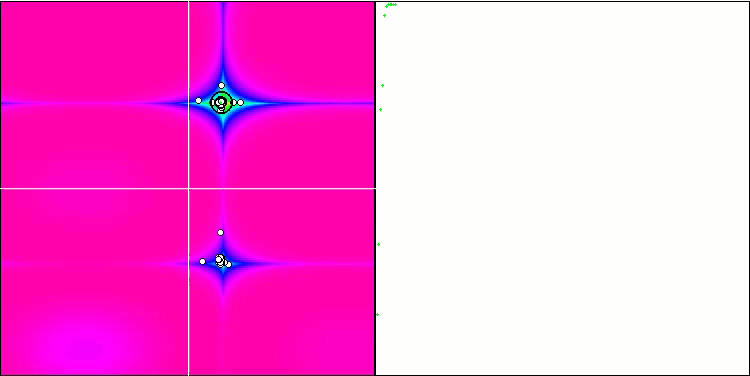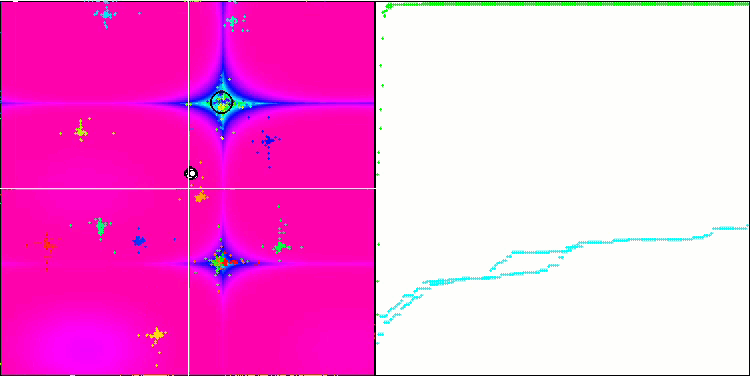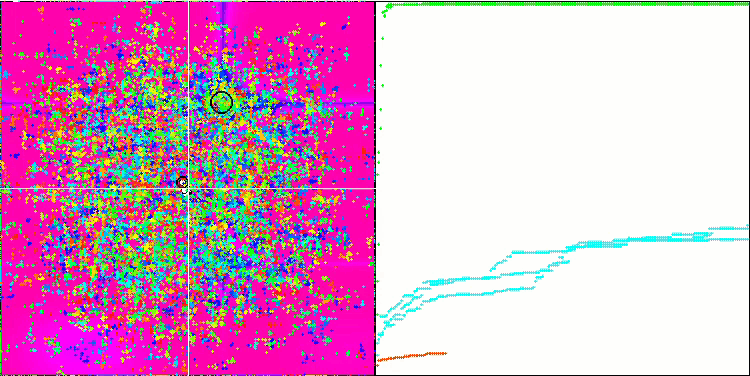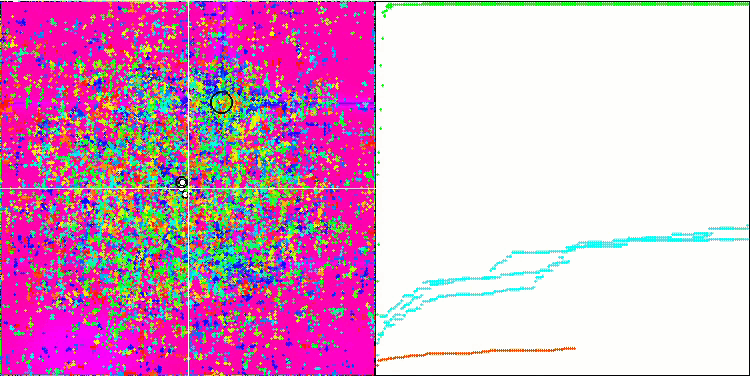
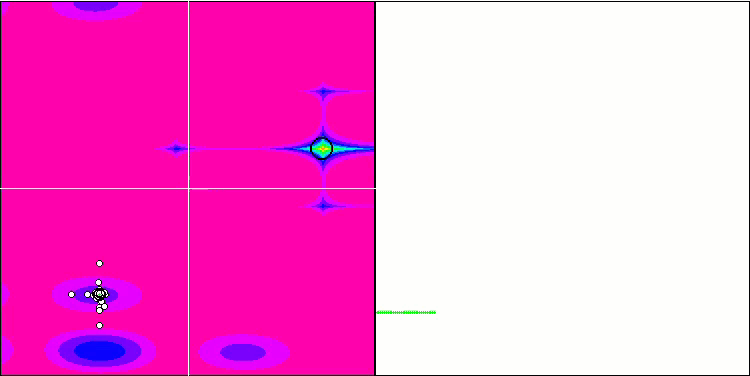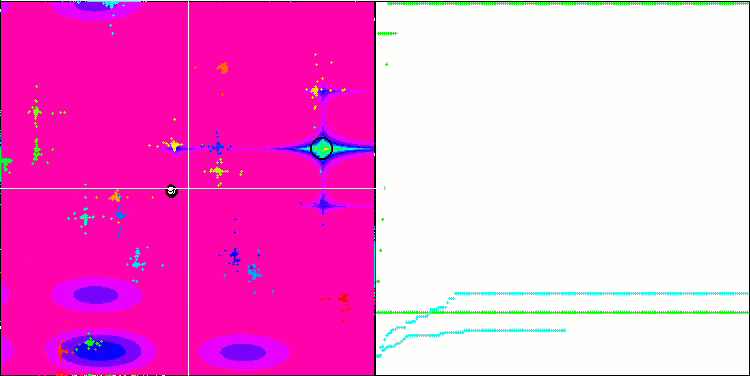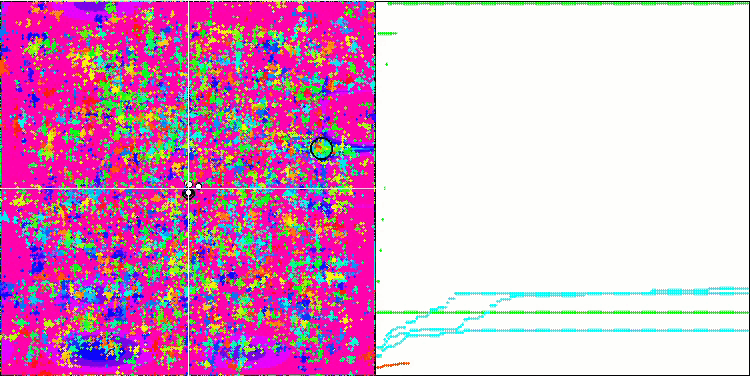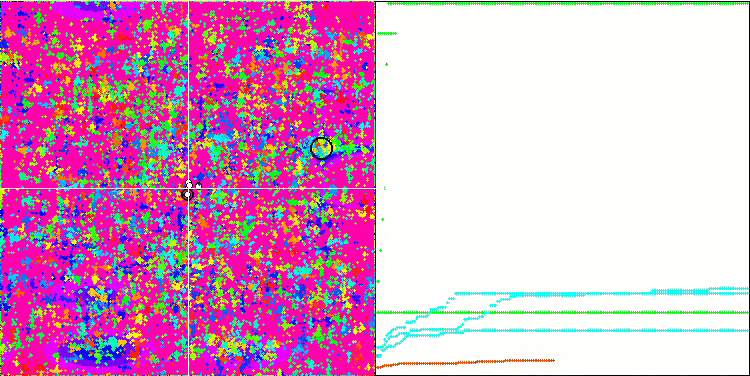
  FAm на тестовой функции Megacity.


3. Результаты тестов

Модифицированный светлячковый алгоритм (FAm) показал себя превосходно на всех тестах, в целом, результаты зависят от настроек алгоритма, при некоторых настройках была достигнута 100% сходимость на всех трех функциях с двумя переменными. Высокая масштабируемость алгоритма обеспечивает лидерство в тестах с 40 и 1000 параметров. Сильное влияние оказывают параметры beta  и gamma, которые позволяют получить как высокую сходимость, так и устойчивость к застреванию в локальных экстремумах. Результаты варьируются в широких пределах, что в целом можно отнести к недостаткам алгоритма. При прочих равных условиях, факт остается фактом, что на данный момент алгоритм является сильнейшим среди рассмотренных ранее, может быть рекомендован для применения в очень широком спектре задач, в том числе в задачах машинного обучения и искусственного интеллекта, в частности при обучении нейронных сетей.

Ниже представлена итоговая рейтинговая таблица, в которой модифицированный светлячковый алгоритм является лидером. Классический алгоритм, несмотря на свою оригинальность, к сожалению, не смог достичь хороших результатов, также подбор настроечных параметров не принес успеха.

AO

Description

Skin

Skin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

2 params (1 F)

40 params (20 F)

1000 params (500 F)

2 params (1 F)

40 params (20 F)

1000 params (500 F)

2 params (1 F)

40 params (20 F)

1000 params (500 F)

FAm

firefly algorithm M

0,98473

0,92124

0,29872

0,73490

0,99924

0,35417

0,08071

0,47804

0,83333

0,14917

0,04230

0,34160

0,51817889

COAm

cuckoo optimization algorithm M

1,00000

0,85911

0,14316

0,66742

0,99283

0,28787

0,04551

0,44207

1,00000

0,24917

0,03537

0,42818

0,51255778

ACOm

ant colony optimization M

0,98229

0,79108

0,12602

0,63313

1,00000

0,62077

0,11521

0,57866

0,38333

0,44000

0,02377

0,28237

0,49805222

ABCm

artificial bee colony M

1,00000

0,63922

0,08076

0,57333

0,99908

0,20112

0,03785

0,41268

1,00000

0,16333

0,02823

0,39719

0,46106556

ABC

artificial bee colony

0,99339

0,73381

0,11118

0,61279

0,99934

0,21437

0,04215

0,41862

0,85000

0,16833

0,03130

0,34988

0,46043000

GWO

grey wolf optimizer

0,99900

0,48033

0,18924

0,55619

0,83844

0,08755

0,02555

0,31718

1,00000

0,10000

0,02187

0,37396

0,41577556

FSS

fish school search

0,99391

0,5692

0,11341

0,55884

0,85172

0,12143

0,03223

0,33513

0,91667

0,08583

0,02583

0,34278

0,41224778

PSO

particle swarm optimisation

0,99627

0,38080

0,05089

0,47599

0,93772

0,14540

0,04856

0,37723

1,00000

0,09333

0,02233

0,37189

0,40836667

FA

firefly algorithm

0,99603

0,59468

0,06082

0,55051

0,89271

0,17546

0,03863

0,36893

0,68333

0,13250

0,02410

0,27998

0,39980649

RND

random

0,99932

0,44276

0,06827

0,50345

0,83126

0,11524

0,03048

0,32566

0,83333

0,09000

0,02403

0,31579

0,38163222


Начиная с этой статьи буду публиковать гистограмму, на которой лучший на момент тестирования алгоритм будет иметь 100 условных баллов, а худший - 1 балл. Мне представляется это наиболее удобным для визуального восприятия, где наглядно видно масштаб итоговых результатов алгоритмов рейтинговой таблицы. Теперь видно, насколько рандомный алгоритм отстает от лидера.

rating

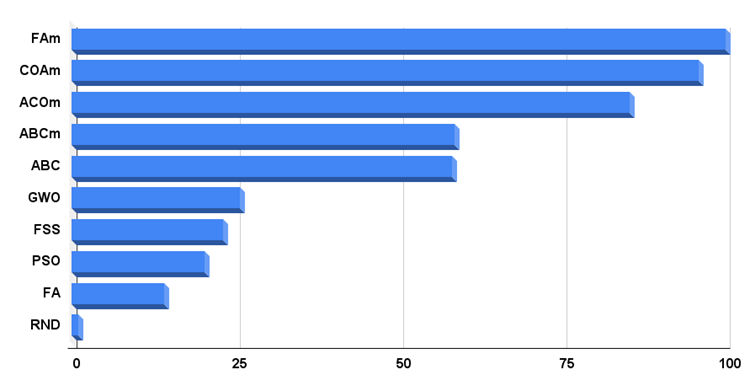
Рисунок 4. Гистограмма итоговых результатов тестирования алгоритмов.


Напомню, что метаэвристические алгоритмы — это приближенные методы решения задач оптимизации, которые используют свойство случайности с обоснованным предположением в своем механизме поиска и пытаются улучшить качество имеющихся решений посредством итераций из случайно сгенерированного набора допустимых решений путем изучения и использования пространства решений. Несмотря на то, что эти алгоритмы не гарантируют оптимальности, они тестируются, чтобы дать разумное и приемлемое решение. Кроме того, у них есть то преимущество, что поведение проблемы не сильно влияет на них и именно это делает их полезными во многих задачах. Наличие множества доступных алгоритмов дает возможность выбрать подходящий для решения проблемы в зависимости от его поведения.

С момента появления эволюционных алгоритмов было проведено множество исследований эвристических алгоритмов. Внедрение новых алгоритмов было одной из ведущих областей исследований. В настоящее время существует более 40 метаэвристических алгоритмов, большинство из которых созданы путем имитации сценария из природы.

Плюсы и минусы относятся к модифицированной версии Светлячкового алгоритма (FAm).

Плюсы:
  • Простая реализация. Прост для модификации.
  • Высокая масштабируемость.
  • Высокая сходимость (варьируется от настроек алгоритма).
  • Свойство кластеризировать область пространства поиска на отдельные группы вокруг локальных экстремумов.

Минусы:
  • Сильное влияние настроек на результаты оптимизации.
  • Необходимо учитывать, что при некоторых настройках алгоритм склонен к застреванию в локальных экстремумах.

К каждой статье я прикрепляю архив, который содержит обновленные актуальные версии кодов алгоритмов ко всем предыдущим статьям. Каждая новая статья является накопленным личным опытом автора и выводы, и суждения основываются на проведенных экспериментах на разработанном для этого специальном тестовом стенде.



Прикрепленные файлы |
Загрузить ZIP
8_The_world_of_AO_vFA2.ZIP (78.22 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Машинное обучение и Data Science (Часть 8): Кластеризация методом k-средних в MQL5 Машинное обучение и Data Science (Часть 8): Кластеризация методом k-средних в MQL5
Для всех, кто работает с данными, включая трейдеров, data mining может открыть совершенно новые возможности, ведь зачастую данные не такие простые, какими кажутся. Человеческому глазу сложно увидеть глубинные закономерности и отношения в наборе данных. Одно из решений — алгоритм К-средних. Давайте посмотрим, полезен ли он.
Разработка торговой системы по индикатору фракталов Fractals Разработка торговой системы по индикатору фракталов Fractals
Перед вами новая статья из серии, в которой мы учимся создавать торговые системы на основе популярных технических индикаторов. Мы изучим еще один технический инструмент — индикатор Fractals, а также разработаем на его основе торговые системы для работы в терминале MetaTrader 5.
DoEasy. Элементы управления (Часть 31): Прокрутка содержимого элемента управления "ScrollBar" DoEasy. Элементы управления (Часть 31): Прокрутка содержимого элемента управления "ScrollBar"
В статье создадим функционал прокрутки содержимого контейнера кнопками горизонтальной полосы прокрутки.
DoEasy. Элементы управления (Часть 30): Оживляем элемент управления "ScrollBar" DoEasy. Элементы управления (Часть 30): Оживляем элемент управления "ScrollBar"
В статье продолжим разрабатывать элемент управления ScrollBar и начнём делать функционал взаимодействия с мышкой. Помимо этого расширим списки флагов состояния и событий мышки.