Полиномиальные модели в трейдинге

Введение

Эффективность трейдинга во многом зависит от методов анализа рыночных данных. Одним из таких методов являются ортогональные многочлены. Эти многочлены представляют собой математические функции, с помощью которых можно решать ряд задач связанных с трейдингом.

Наиболее известными ортогональными многочленами являются полиномы Лежандра, Чебышева, Лагерра и Эрмита. Каждый из этих полиномов обладает уникальными свойствами, которые позволяют использовать их для решения разных задач. Вот несколько основных способов их использования:

• Моделирование временных рядов. Ортогональные многочлены можно использовать для описания временных рядов. Их применение может помочь в выявлении трендов и других паттернов.
• Регрессия. Ортогональные многочлены могут быть применены в регрессионном анализе. Их использование позволяет улучшить качество модели и сделать ее более интерпретируемой.
• Прогнозирование. Ортогональные многочлены могут использоваться для построения прогнозов — какой будет цена, если текущие тенденции сохранятся.

Давайте посмотрим, как можно применять ортогональные многочлены на практике.

Ортогональные полиномы и индикаторы

Вся суть технического анализа сводится к выявлению закономерностей в движении цены. Но финансовые временные ряды, как правило, содержат шумы, которые скрывают эти закономерности. Давайте посмотрим, как можно применять ортогональные многочлены в условиях рынка.

Основная идея заключается в том, что эти многочлены могут быть использованы для разложения сложных сигналов на более простые компоненты. Это разложение позволяет фильтровать шумы и выявлять тренды.

Для примера я возьму многочлены Лежандра, и сделаю на их основе сглаживающий индикатор. Общая формула этих многочленов и область их определения заданы следующими выражениями:

Я буду использовать многочлены до 9-ой степени. Для сглаживания этого вполне достаточно, а использование многочленов более высоких степеней может добавить шумов и скрыть основные тенденции в движении цены. Формулы полиномов, которые я буду использовать приведены в таблице.

n	полиномы Лежандра
0	1
1	x
2	(3*x^2-1)/2
3	(5*x^3-3*x)/2
4	(35*x^4-30*x^2+3)/8
5	(63*x^5-70*x^3+15*x)/8
6	(231*x^6-315*x^4+105*x^2-5)/16
7	(429*x^7-693*x^5+315*x^3-35*x)/16
8	(6435*x^8-12012*x^6+6930*x^4-1260*x^2+35)/128
9	(12155*x^9-25740*x^7+18018*x^5-4620*x^3+315*x)/128

В первую очередь мне нужно перевести индексы цен в область определения этих полиномов. Для этого, для каждого индекса i я применяю сдвигающую функцию:

После этого, я рассчитываю значения всех интересующих меня полиномов для каждого значения x[i]. Для примера, я рассчитаю значение полинома 2-ой степени с периодом равным 3:

Теперь мне нужно ввести поправку на дискретность. Сумма значений полинома степеней от 1-ой и выше должна быть равна нулю. Чтобы выполнить это условие мне нужно рассчитать поправку:

С помощью этой поправки я корректирую значения полинома:

Дальше начинается самое интересное. Любой временной ряд можно разложить на сумму многочленов, взятых с определенным весом:

Сами веса можно рассчитать следующим образом:

Выглядит непонятно и немного пугающе. На самом деле — все просто. Возьмем полином 0-ой степени с периодом N. Его значения во всех точках равны 1. А его вес будет:

Это формула SMA. Веса полиномов старших степеней равносильны неким осцилляторам со специально подобранными коэффициентами. То есть, можно сказать, что ортогональные полиномы — это SMA с какими-то хитро рассчитанными добавками. Полиномы Лежандра очень устойчивы к шумам и превосходно справляются с задачами фильтрации. Например, полином Лежандра 1-ой степени выглядит так.

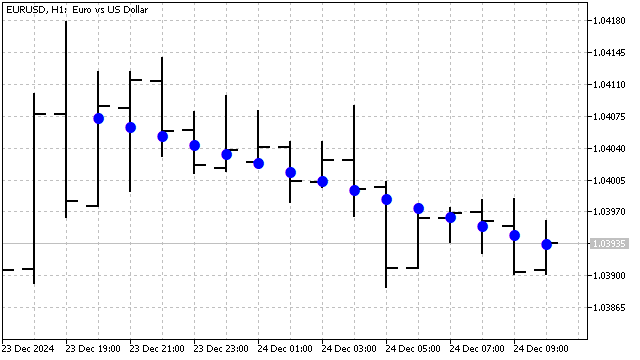
Кроме полиномов Лежандра, для выделения трендов и сглаживания можно использовать полиномы Чебышева. Существуют два типа таких полиномов. Они отличаются друг от друга поведением на краях. Главное достоинство этих полиномов — чувствительность к резким изменениям цены. Формула этих многочленов очень проста:

n	полиномы I рода	полиномы II рода
0	1	1
1	x	2*x
2	2*x^2-1	4*x^2-1
3	4*x^3-3*x	8*x^3-4*x
4	8*x^4-8*x^2+1	16*x^4-12*x^2+1
5	16*x^5-20*x^3+5*x	32*x^5-32*x^3+6*x
6	32*x^6-48*x^4+18*x^2-1	64*x^6-80*x^4+24*x^2-1
7	64*x^7-112*x^5+56*x^3-7*x	128*x^7-192*x^5+80*x^3-8*x
8	128*x^8-256*x^6+160*x^4-32*x^2+1	256*x^8-448*x^6+240*x^4-40*x^2+1
9	256*x^9-576*x^7+432*x^5-120*x^3+9*x	512*x^9-1024*x^7+672*x^5-160*x^3+10*x

А так выглядит сглаживание полиномом Чебышева 3-ей степени.

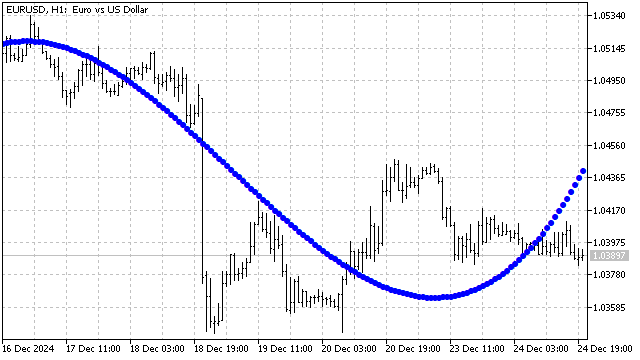
До сих пор мы рассматривали полиномы с областью определения +/-1, но существуют многочлены с другими областями определения. Например, полином Лагерра определен для всех неотрицательных значений аргумента. Его формула выглядит так:

n	полиномы Лагерра
0	1
1	-x+1
2	(x^2-4*x+2)/2
3	(-x^3+9*x^2-18*x+6)/6
4	(x^4-16*x^3+72*x^2-96*x+24)/24
5	(-x^5+25*x^4-200*x^3+600*x^2-600*x+120)/120
6	(x^6-36*x^5+450*x^4-2400*x^3+5400*x^2-4320*x+720)/720
7	(-x^7+49*x^6-882*x^5+7350*x^4-29400*x^3+52920*x^2-35280*x+5040)/5040
8	(x^8-64*x^7+1568*x^6-18816*x^5+117600*x^4-376320*x^3+564480*x^2-322560*x+40320)/40320
9	(-x^9+81*x^8-2592*x^7+42336*x^6-381024*x^5+1905120*x^4-5080320*x^3+6531840*x^2-3265920*x+362880)/362880

А сдвигающая функция для его аргумента выглядит так:

Такое изменение ведет к тому, что поведение полинома Лагерра зависит не только от степени, но и от его периода. Этот полином чувствителен к последним изменениям цены. Например, так выглядит полином Лагерра 5-ой степени на графике:

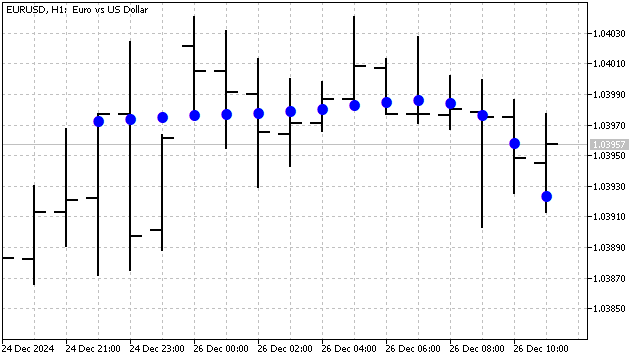
Еще одним интересным примером ортогональности являются многочлены Эрмита. Эти полиномы применяются во многих областях математики и физики. Эти полиномы определены для любых значений аргумента, а их формула выглядит так:

n	полиномы Эрмита
0	1
1	x
2	x^2-1
3	x^3-3*x
4	x^4-6*x^2+3
5	x^5-10*x^3+15*x
6	x^6-15*x^4+45*x^2-15
7	x^7-21*x^5+105*x^3-105*x
8	x^8-28*x^6+210*x^4-420*x^2+105
9	x^9-36*x^7+378*x^5-1260*x^3+945*x

Сдвигающая функция центрирует значения цены:

В результате мы получили сглаживающий фильтр, эффективность которого зависит от степени полинома и его периода.

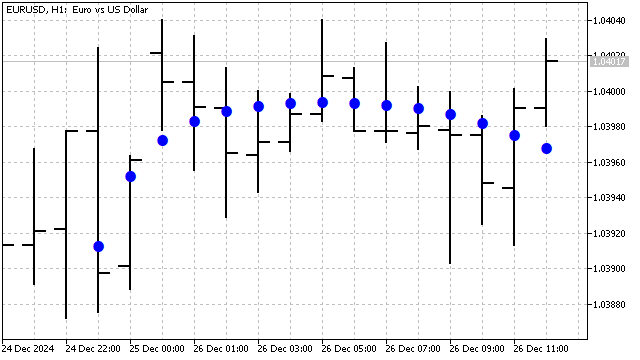
Мы рассмотрели основные классические ортогональные полиномы. Но вполне возможно создать и свой вариант таких полиномов. Например, полином, объединяющий достоинства полиномов Чебышева и Эрмита, задается формулой:

n	полиномы Чебышева - Эрмита
0	1
1	2*x
2	4*x^2-2
3	8*x^3-12*x
4	16*x^4-48*x^2+12
5	32*x^5-160*x^3+120*x
6	64*x^6-480*x^4+720*x^2-120
7	128*x^7-1344*x^5+3360*x^3-1680*x
8	256*x^8-3584*x^6+13440*x^4-13440*x^2+1680
9	512*x^9-9216*x^7+48384*x^5-80640*x^3+30240*x

Этот полином чувствителен к нелинейным трендам — квадратичным, кубическим и т.д. Так выглядит полином Чебышева – Эрмита 9-ой степени на графике:

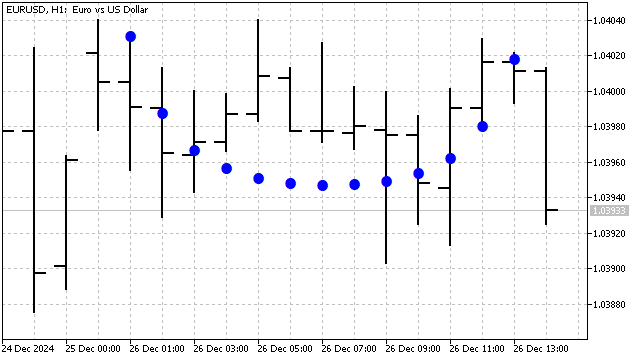
Применение ортогональных полиномов дает ряд преимуществ.

• Стабильность и устранение корреляции. Ортогональность полиномов обеспечивает их устойчивость к изменениям параметров модели. Каждый многочлен не зависит от других, что позволяет моделировать и изучать каждый компонент временного ряда отдельно.
• Интерпретируемость. Каждый ортогональный многочлен соответствует своей модели поведения цены. Весовые коэффициенты многочленов позволяют выделить наиболее важные модели и сосредоточиться именно на них.
• Адаптивность и эффективность. Ортогональные многочлены подстраиваются под конкретные значения временного ряда. Появление новых цен приводит к изменению весовых коэффициентов, благодаря чему, полиномиальная модель адаптируется к текущему состоянию рынка. А использование нелинейных полиномов делают эту адаптацию эффективной.

Единственная особенность ортогональных полиномов, которую можно считать недостатком, заключается в том, что эти полиномы обрабатывают все цены внутри полинома. Говоря иначе, индикатор, построенный на таких полиномах, «рисует». С моей точки зрения, эта особенность недостатком не является — просто индикатор находит наилучшее приближение при поступлении новых данных.

Применение ортогональных многочленов накладывает некоторые ограничения. Период индикатора должен быть больше степени полинома. Для практических целей можно ограничиться 3-ей степенью полинома. Такой индикатор совмещает SMA, линейный тренд и две параболы —квадратичную и кубическую. Этого хватит для сглаживания довольно сложных ситуаций. Но, при увеличении периода индикатора, можно увеличивать и степень полинома.

Теперь, давайте рассмотрим несколько примеров применения ортогональных полиномов в трейдинге.

Торговые стратегии

На основе ортогональных многочленов трейдеры могут создавать различные торговые стратегии. Например, с помощью полиномиальной регрессии на основе ортогональных многочленов трейдер может не только проанализировать прошлые движения цены, но и создать модель, способную адаптироваться к текущим изменениям на рынке.

Для примера давайте рассмотрим несколько торговых стратегий, основанных на отклонениях от среднего.

Возьмем простейшую стратегию — открытие позиций происходит при пересечении ценой SMA. Скользящую среднюю заменим на ортогональный полином, а правила открытия и закрытия позиций оставим прежними:

• Цена пересекает полином снизу вверх — открыть позицию buy, закрыть позицию sell.
• Цена пересекает полином сверху вниз — открыть позицию sell, закрыть позицию buy.

Несмотря на простоту, эта стратегия вполне работоспособна.

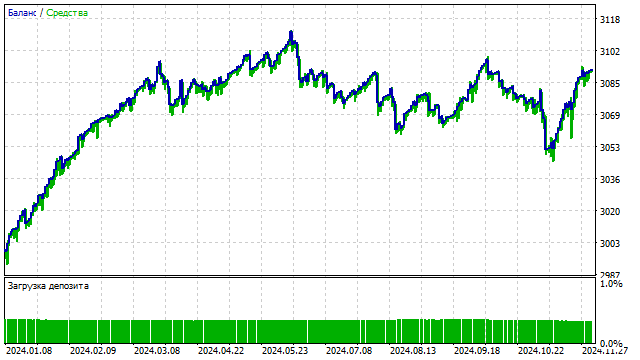
Давайте немного усложним эту стратегию и заменим цену на значение какого-либо полинома. То есть, у нас получится аналог стратегии с пересечением двух SMA. Результат немного предсказуем: из всех возможных вариантов оптимизатор стратегий предпочел ортогональные полиномы.

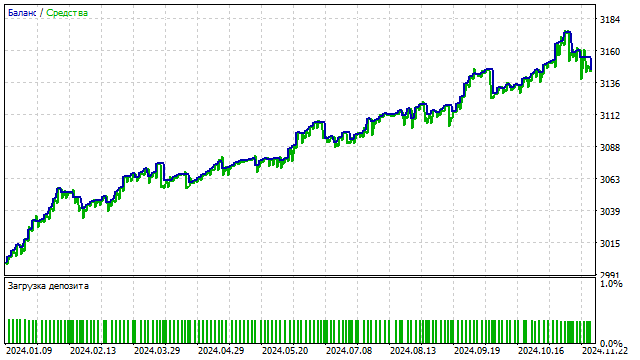
Полиномиальные модели можно использовать и в более сложных стратегиях. Если в стратегии используются какие-либо индикаторы, то можно попытаться заменить их на ортогональные полиномы. Такая замена может улучшить стратегию.

Для примера я возьму индикатор Commodity channel index (CCI). Классическая формула этого индикатора выглядит так:

Я внесу в этот индикатор небольшие изменения. Как я уже говорил: SMA это полином 0-ой степени. Вместо SMA я буду использовать ортогональный полином любой степени. Соответственно, среднее абсолютное отклонение я буду рассчитывать относительно этого полинома. Индикатор получился таким:

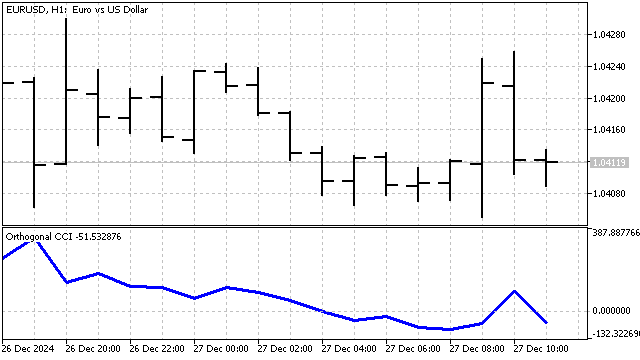
Торговая стратегия будет похожа на классическую:

• открыть позицию buy, если индикатор ниже заданного уровня и продолжает снижаться;
• открыть позицию sell, если индикатор выше заданного уровня и продолжает расти;
• закрытие позиций по противоположному сигналу.

Результат тестирования такой стратегии с полиномом 3-ей степени:

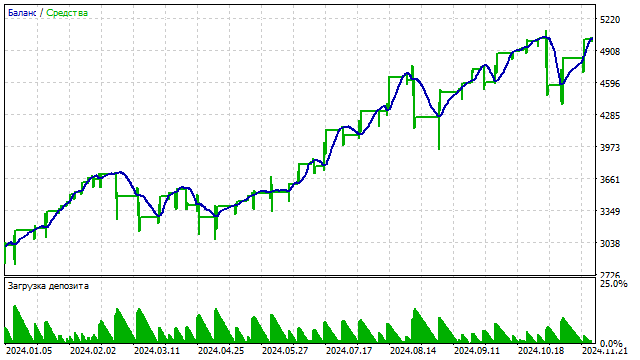
На основе ортогональных многочленов можно построить и другие индикаторы. Например, я решил построить аналог RSI. Суть проста —сначала я строю полином, а потом считаю сколько цен располагалось выше этого полинома. На основании этого числа я делаю вывод о перекупленности/перепроданности.

На основе этого индикатора я создаю простую стратегию:

• открыть позицию, если индикатор достиг уровня перекупленности или перепроданности;
• закрыть позиции, если индикатор находится в центре.

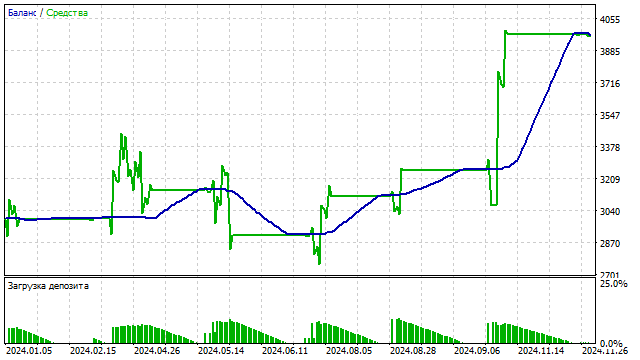
Кроме того, ортогональные многочлены могут быть интегрированы в различные алгоритмы машинного обучения. Гибкость полиномиальных функций дает возможность машинным алгоритмам выявлять сложные зависимости в данных. 

Например, многочлены можно использовать для генерации новых признаков из исходных данных. Ортогональные многочлены обеспечивают независимые оценки различных компонентов временного ряда. Благодаря этому свойству, они могут уменьшить переобучение. Это может повысить качество обучающих данных и улучшить работу моделей.

Возьмите любую нейронную сеть и подайте на вход значения весовых коэффициентов ортогональных полиномов. Но в этом случае нужно будет строить полную систему полиномов: начиная с полинома 1-ой степени, и заканчивая N-1, где N – количество обрабатываемых цен.

Заключение

Ортогональные многочлены являются мощным инструментом для анализа финансовых временных рядов. Они обеспечивают ряд преимуществ и позволяют оценивать изменения на рынке. Использование ортогональных полиномов в торговых стратегиях может повысить их эффективность и улучшить результаты трейдинга.

При написании статьи были использованы следующие программы.

Название	Тип	Описание
Orthogonal polynomials	индикатор	моделирует ортогональные полиномы на графике Type - тип полинома iPeriod - период полинома (не меньше 2) N - степень полинома, допустимые значения 0 - 9 Shift - сдвиг индикатора
EA Orthogonal polynomials	советник	реализует торговую стратегию, построенную на пересечении цены и полинома
EA Orthogonal polynomials 2	советник	реализует стратегию на пересечении двух полиномов
Orthogonal CCI	индикатор	CCI в котором вместо SMA можно использовать ортогональные полиномы
EA Orthogonal CCI	советник	реализует стратегию на основе ортогонального варианта CCI
Orthogonal RSI	индикатор	определяет перекупленность/перепроданность с помощью ортогональных полиномов
EA Orthogonal RSI	советник	реализует стратегию на основе ортогонального варианта RSI