MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
Популяционные алгоритмы оптимизации: Алгоритм летучих мышей (Bat algorithm - BA)

Популяционные алгоритмы оптимизации: Алгоритм летучих мышей (Bat algorithm - BA)

MetaTrader 5 — Примеры | 12 января 2023, 13:47
1 746 0
Andrey Dik
Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов


1. Введение

Летучие мыши — удивительные животные, ученые считают, что первые летучие мыши появились 65-100 миллионов лет назад, в то же время, что и динозавры. Среди всех млекопитающих только летучие мыши имеют крылья. Насчитывается более 1300 видов этих рукокрылых. Их можно встретить почти везде, кроме полярных регионов. Днем они прячутся в укрытиях. Чтобы перемещаться по темным пещерам и охотиться после наступления темноты, летучие мыши полагаются на эхолокацию – систему, которая позволяет им обнаруживать объекты с помощью звуковых волн. Они эхолоцируют, издавая высокой частоты звук, который распространяется, пока не ударяется о предмет и не отражается обратно. Эхолокация — это своего рода сонар: летучая мышь (основная маленькая летучая мышь) издает громкий и короткий импульсный звук. Когда звук достигает объекта, эхо возвращается к их ушам через короткий промежуток времени, таким способом летучие мыши ориентируются в пространстве и определяют положение добычи. 

Алгоритм летучих мышей (BA) — это эвристический алгоритм, представленный Янгом в 2010 год, который имитирует эхолокационное поведение летучих мышей для выполнения глобальной оптимизации. Метаэвристика, обычно вдохновленная природой и физическими процессами, теперь используется как один из самых мощных методов для решения многих сложных задач оптимизации. Оптимизация - это выбор лучших элементов для определенного набора критериев из ряда эффективных вариантов, который показывает множество различных преимуществ и недостатков с точки зрения вычислительной эффективности и вероятности глобальной оптимизации.

Оптимизация функций предлагает формальную основу для моделирования и решения ряда конкретных проблем, предоставляя «целевую» функцию, которая принимает параметр в качестве входных данных, и цель состоит в том, чтобы найти значение комбинированного параметра, чтобы вернуть наилучшее значение. Эта структура достаточно абстрактна, чтобы различные проблемы можно было интерпретировать как проблемы «оптимизации функций».


Однако традиционная оптимизация функций используется только для решения некоторых небольших задач, которые часто не применимы на практике. Поэтому ученые обращают внимание на природу, которая предоставляет богатые модели для решения этих проблем. Путем моделирования естественных биологических систем предлагается множество интеллектуальных алгоритмов оптимизации роя для решения прикладных задач нетрадиционными методами. Они широко используются в различных задачах оптимизации из-за отличной производительности. BA —это новый и современный алгоритм, близкий к роевым типам, который выполняет процесс поиска с использованием искусственных летучих мышей в качестве поисковых агентов, имитирующих естественную громкость звукового импульса и частоту излучения настоящих летучих мышей.


2. Описание алгоритма

В базовом алгоритме летучих мышей каждая летучая мышь рассматривается как частица "без массы и размера", представляющая допустимое решение в пространстве решений. Для различных функций приспособленности каждая летучая мышь имеет соответствующее значение функции и определяет текущего оптимального индивидуума путем сравнения значений функции. Затем обновляются частота акустической волны, скорость, скорость испускания импульсов и громкость каждой летучей мыши в популяции, продолжается итеративная эволюция, приближается и генерируется текущее оптимальное решение, и, наконец, находится глобальное оптимальное решение. Алгоритм обновляет частоту, скорость и положение каждой летучей мыши.

Для стандартного алгоритма требуются пять основных параметров: частота, громкость, пульсация и коэффициенты громкости и пульсации. Частота используется для балансировки влияния исторической оптимальной позиции на текущую позицию. Особь летучей мыши будет искать далеко от исторического положения группы, когда диапазон частот поиска велик, и наоборот.

Параметров алгоритма достаточно много по сравнению с другими рассмотренными ранее:

input double MIN_FREQ_P          = 0.0;
input double MAX_FREQ_P         = 1.0;
input double MIN_LOUDNESS_P  = 0.0;
input double MAX_LOUDNESS_P = 1.5;
input double MIN_PULSE_P        = 0.0;
input double MAX_PULSE_P        = 1.0;
input double ALPHA_P               = 0.3;
input double GAMMA_P              = 0.3;

При написании алгоритма BA я столкнулся с тем, что во многих источниках авторы статей описывают алгоритм совершенно по-разному, отличия заключались как в применении терминов в описании ключевых моментов так и в принципиальных алгоритмических особенностях, поэтому опишу как понял сам. Основные физические принципы, лежащие в основе эхолокации, могут быть применены в алгоритме со значительными оговорками и условностями. Предполагаем, что мыши используют звуковые импульсы с частотой в диапазоне от MinFreq до MaxFreq. Частота влияет на скорость перемещения мыши в пространстве. Так же используется условное понятие громкости, которое влияет на переход из состояния локального поиска по месту текущего положения летучей мыши к глобальному в окрестностях наилучшего решения. Частота пульсаций увеличивается на протяжении всей оптимизации, в то время как громкость звуков понижается.

Псевдокод алгоритма BA (рисунок 1):

1. Инициализация популяции летучих мышей.
2. Генерация частоты, скорости и новых решений.
3. Поиск локального решения.
4. Обновление глобального решения.
5. Понижение громкости и увеличение частоты пульсаций.
6. Повторить п.2 до выполнения критерия останова.

scheme

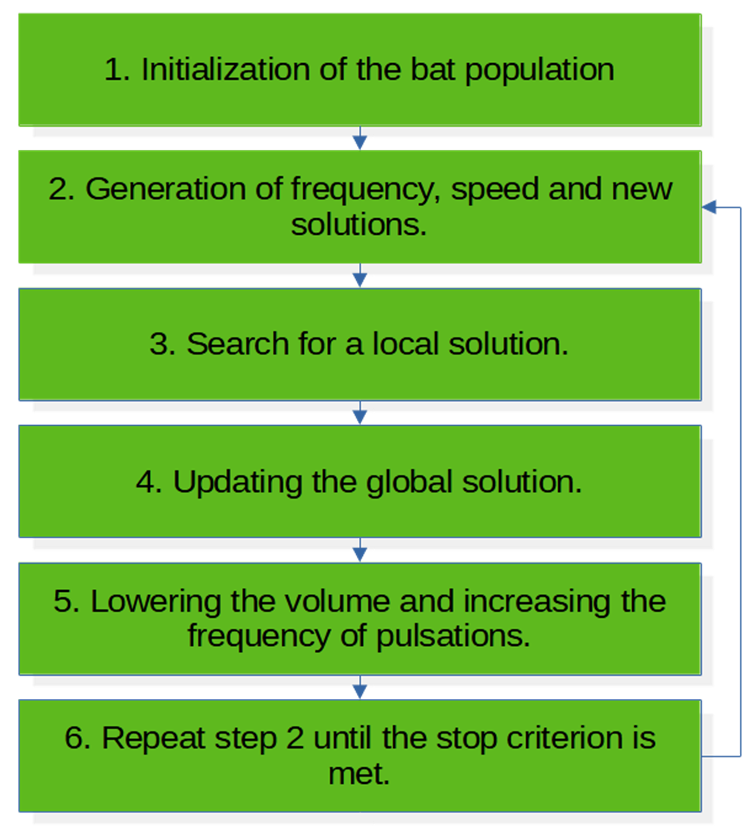
Рисунок 1. Блок-схема алгоритма BA.

Приступим к описанию кода. Для описания поискового агента "летучая мышь" нам понадобится структура, в которой опишем все характеристики, необходимые для полного описания состояния на момент каждой итерации. Массив position [] служит для хранения лучших координат положения в пространстве, а массив auxPosition [] для текущих "операционных" координат. Ещё один массив speed [] нужен в расчетах вектора скоростей по координатам. frequency - частота звуковых импульсов, initPulseRate - начальная частота пульсации (индивидуальная для каждой летучей мыши с самого начала оптимизации), pulseRate - частота пульсации на текущей итерации, loudness - громкость звуковых импульсов, fitness - значение фитнес функции после последнего перемещения, fitnessBest - лучшее значение фитнес функции агента за все итерации.  

//——————————————————————————————————————————————————————————————————————————————
struct S_Bat
{
  double position    [];
  double auxPosition [];
  double speed       [];
  double frequency;
  double initPulseRate;
  double pulseRate;
  double loudness;
  double fitness;
  double fitnessBest;
};
//——————————————————————————————————————————————————————————————————————————————

Класс алгоритма летучих мышей включает в себя массив структур поисковых агентов, границы и шаг исследуемого пространства, лучшие, найденные алгоритмом, координаты, лучшее значение фитнес функции и константы для хранения параметров алгоритма, а так же открытый метод инициализации, два открытых метода, необходимых для работы с алгоритмом, и специфичные для алгоритма приватные методы. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BA
{
  //============================================================================
  public: S_Bat  bats      []; //bats
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,
                     const int    batsNumberP,
                     const double min_FREQ_P,
                     const double max_FREQ_P,
                     const double min_LOUDNESS_P,
                     const double max_LOUDNESS_P,
                     const double min_PULSE_P,
                     const double max_PULSE_P,
                     const double alpha_P,
                     const double gamma_P,
                     const int    maxIterP);

  public: void Flight (int epoch);
  public: void Preparation ();

  //============================================================================
  private: void Walk               (S_Bat &bat);
  private: void AproxBest          (S_Bat &bat, double averageLoudness);
  private: void AcceptNewSolutions (S_Bat &bat);
  private: int  currentIteration;
  private: int  maxIter;

  private: double MIN_FREQ;
  private: double MAX_FREQ;

  private: double MIN_LOUDNESS;
  private: double MAX_LOUDNESS;

  private: double MIN_PULSE;
  private: double MAX_PULSE;

  private: double ALPHA;
  private: double GAMMA;

  private: int    params;
  private: int    batsNumber;

  private: bool   firstFlight;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

В открытом методе Init () назначен внутренним константам значения надстроечных параметров алгоритма распределим память под массивы, сбросим до минимального значения переменную для хранения лучшей приспособленности, сбросим флаг начальной итерации. В целом этот метод не является сложным и чем-то особенным.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Init (const int    paramsP,
                    const int    batsNumberP,
                    const double min_FREQ_P,
                    const double max_FREQ_P,
                    const double min_LOUDNESS_P,
                    const double max_LOUDNESS_P,
                    const double min_PULSE_P,
                    const double max_PULSE_P,
                    const double alpha_P,
                    const double gamma_P,
                    const int    maxIterP)
{
  MathSrand (GetTickCount ());

  fB = -DBL_MAX;

  params       = paramsP;
  batsNumber   = batsNumberP;
  MIN_FREQ     = min_FREQ_P;
  MAX_FREQ     = max_FREQ_P;
  MIN_LOUDNESS = min_LOUDNESS_P;
  MAX_LOUDNESS = max_LOUDNESS_P;
  MIN_PULSE    = min_PULSE_P;
  MAX_PULSE    = max_PULSE_P;
  ALPHA        = alpha_P;
  GAMMA        = gamma_P;
  maxIter      = maxIterP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);

  firstFlight = false;

  ArrayResize (bats, batsNumber);

  for (int i = 0; i < batsNumber; i++)
  {
    ArrayResize (bats [i].position,    params);
    ArrayResize (bats [i].auxPosition, params);
    ArrayResize (bats [i].speed,       params);

    bats [i].fitness  = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

Первый метод, вызываемый на каждой итерации - Flight (). В нем сосредоточен основной каркас поисковой логики, а остальная детализация вынесена во вспомогательные приватные методы, специфичные для этого алгоритма оптимизации. На самой первой итерации флаг firstFlight сброшен (сброс происходит при инициализации в методе Init ()).  Это означает, что необходимо назначить первоначальное состояние каждой летучей мыши, заключающееся в случайном положении пространства поиска:

  • нулевое значение скорости,
  • индивидуальная частота звуковых импульсов, назначенная случайным числом в диапазоне, заданным параметрами,
  • начальная индивидуальная частота пульсации, также заданная случайным числом в диапазоне параметров,
  • и громкость звуковых импульсов в диапазоне параметров.

Как видим, все искусственные летучие мыши отличаются индивидуальностью, каждой соответствует индивидуальный набор характеристик звуковых сигналов, что делает их более похожими на настоящих летучих мышей в природе. Во всей популяции, которая может состоять из нескольких сотен тысяч особей мать, может найти одного единственного детеныша по уникальной звуковой сигнатуре, которую издает малыш.

Если флаг firstFlight взведен, значит необходимо проводить основные операции по перемещению летучих мышей. Одна из интересных особенностей алгоритма заключается в том, что используется понятие средней громкости звука всей популяции, в целом громкость звука на протяжении всех итераций снижается через коэффициент alpha. Здесь происходит два вида перемещения летучих мышей: Walk () - индивидуальное перемещение с расчетом вектора скорости для каждого компонента координат и локальное перемещение в окрестностях наилучшего решения.

С каждой следующей итерацией интенсивность пульсаций снижается, это влияет на интенсивность исследования окрестностей. Таким образом исследование и эксплуатация динамически изменяются на протяжении всей оптимизации. Далее мы увидим каким образом текущая итерация влияет на поведение летучих мышей.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Flight (int epoch)
{
  currentIteration = epoch;

  //============================================================================
  if (!firstFlight)
  {
    fB = -DBL_MAX;

    //--------------------------------------------------------------------------
    for (int b = 0; b < batsNumber; b++)
    {
      for (int p = 0; p < params; p++)
      {
        bats [b].position    [p] = RNDfromCI (rangeMin [p], rangeMax [p]);
        bats [b].position    [p] = SeInDiSp (bats [b].position [p], rangeMin [p], rangeMax [p], rangeStep [p]);
        bats [b].auxPosition [p] = bats [b].position    [p];
        bats [b].speed       [p] = 0.0;
        bats [b].frequency       = RNDfromCI (MIN_FREQ, MAX_FREQ);
        bats [b].initPulseRate   = RNDfromCI (MIN_PULSE, MAX_PULSE / 2);
        bats [b].pulseRate       = bats [b].initPulseRate;
        bats [b].loudness        = RNDfromCI (MAX_LOUDNESS / 2, MAX_LOUDNESS);
        bats [b].fitness         = -DBL_MAX;
        bats [b].fitnessBest     = -DBL_MAX;
      }
    }

    firstFlight = true;
  }
  //============================================================================
  else
  {
    double avgLoudness = 0;

    for (int b = 0; b < batsNumber; b++)
    {
      avgLoudness += bats [b].loudness;
    }

    avgLoudness /= batsNumber;

    for (int b = 0; b < batsNumber; b++)
    {
      Walk (bats [b]);

      if (RNDfromCI (MIN_PULSE, MAX_PULSE) > bats [b].pulseRate)
      {
        AproxBest (bats [b], avgLoudness);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Второй обязательный открытый метод, вызываемый на каждой итерации - Preparation () необходим для обновления глобального лучшего решения. Здесь мы можем видеть каким образом используется понятие "громкость". Так как с каждой итерацией громкость каждой мыши снижается через коэффициент (настроечный параметр алгоритма alpha), то снижается вероятность локального исследования но одновременно с этим интенсивность исследования глобального решения. То есть вероятность обновления лучшего положения каждой летучей мыши снижается с каждой итерацией. Это один из тех моментов в алгоритме, который наименее понятен по крайней мере для меня, однако, автор алгоритма это реализовал, значит это необходимо.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Preparation ()
{
  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (bats [b].fitness > fB)
    {
      fB = bats [b].fitness;
      ArrayCopy (cB, bats [b].auxPosition, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (RNDfromCI (MIN_LOUDNESS, MAX_LOUDNESS) < bats [b].loudness && bats [b].fitness >= bats [b].fitnessBest)
    {
      AcceptNewSolutions (bats [b]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Приватный метод Walk () обеспечивает индивидуальное перемещение каждой летучей мыши относительно своего текущего наилучшего положения достигнутого на данный момент с учетом глобального лучшего решения. В этом методе применяется частота звуковых импульсов, которая мееняется случайным образом в диапазоне [MIN_FREQ;MAX_FREQ]. Частота нужна для расчета скорости перемещения поискового агента которая заключается в произведении частоты на разность лучшего положения мыши и лучшего глобального решения. После этого значение скорости повекторно прибавляем к текущему лучшему решению летучей мыши. Таким образом мы оперируем несоразмерными физическими величинами, но что мы можем: это лишь приближение к настоящим физическим объектам. Правдоподобием в данном случае приходится принебречь. После расчетов нового положения координаты необходимо проверить на выход за допустимый диапазон с помощью метода SeInDiSp ().

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Walk (S_Bat &bat)
{
  for (int j = 0; j < params; ++j)
  {
    bat.frequency       = MIN_FREQ + (MAX_FREQ - MIN_FREQ) * RNDfromCI (0.0, 1.0);
    bat.speed       [j] = bat.speed [j] + (bat.position [j] - cB [j]) * bat.frequency;
    bat.auxPosition [j] = bat.position [j] + bat.speed [j];

    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Второй приватный метод AproxBest () отвечает за перемещение летучих мышей относительно глобального лучшего решения, обеспечивая дополнительное уточнение координат. Физический смысл понять в этом действии для меня не представляется возможным, которое заключается в повекторном прибавлении к координатам приращения в виде усреднённой громкости среди всей популяции летучих мышей помноженную на случайное число в диапазоне [-1.0;1.0]. Я предпринимал попытку свести величины в размерность оптимизируемой функции через вектор допустимых значений области определения, но результаты тестирования оказались хуже, чем в авторском варианте алгоритма, поэтому я оставил всё как есть, но уверен, что эффективность алгоритма BA может быть улучшена, но на это потребуются дополнительные исследования, что не ставилось целью в данном случае. После расчетов координат значения проверяются на выход за допустимый диапазон методом SeInDiSp (). 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AproxBest (S_Bat &bat, double averageLoudness)
{
  for (int j = 0; j < params; ++j)
  {
    bat.auxPosition [j] = cB [j] + averageLoudness * RNDfromCI (-1.0, 1.0);
    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Еще один специфичный приватный метод AcceptNewSolutions (), который вызывается при выполнении условия проверки по частоте пульсации звуковых импульсов для каждой летучей мыши. Здесь акцептируется новое лучшее индивидуальное решение, пересчитывается индивидуальная громкость и индивидуальная частота пульсаций. Тут как раз можем видеть, каким образом порядковый номер итераций участвует в расчетах частоты пульсаций.

В данном месте логики алгоритма я позволил себе некотоую вольность и изменил логику, сделав независимым результат от размерности общего количества итераций, что в конечном итоге немного повысило эффективность алгоритма. В оригинальной авторской версии номер итерации напрямую участвовал в нелинейной формуле расчета частоты инмульсов, в BA и так очень много условностей, а в данном случае я не смог закрыть глаза на ещё одну. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AcceptNewSolutions (S_Bat &bat)
{
  ArrayCopy(bat.position, bat.auxPosition, 0, 0, WHOLE_ARRAY);
  bat.fitnessBest = bat.fitness;
  bat.loudness    = ALPHA * bat.loudness;
  double iter     = Scale (currentIteration, 1, maxIter, 0.0, 10.0, false);
  bat.pulseRate   = bat.initPulseRate *(1.0 - exp(-GAMMA * iter));
}
//——————————————————————————————————————————————————————————————————————————————

Зависимость частоты пульсации от номера текущей итерации (на графике - х) и настроечного параметра GAMMA представлена на рисунке 2.

gamma

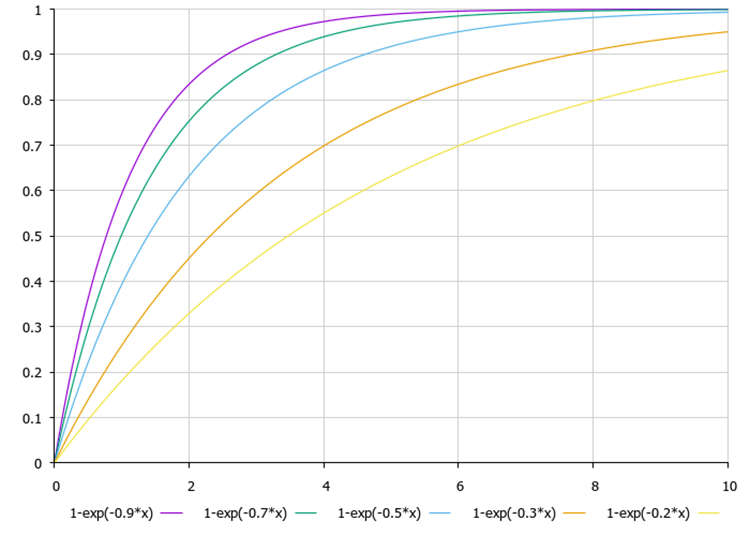
Рисунок 2. Зависимость частоты пульсации от номера текущей итерации и настроечного параметра GAMMA со значениями 0.9, 0.7, 0.5, 0.3, 0.2.

3. Результаты тестов

В прошлой статье я упомянул о планах пересмотреть методику подсчета рейтинга тестируемых алгоритмов. Во-первых, так как большинство алгоритмов с легкостью справляется с тестовыми функциями двух переменных и разница между результатами практически неразличима, то я решил увеличить количество переменных для первых двух тестов на всех тестовых функциях. Теперь количество переменных будет 10, 50 и 1000.

Во-вторых, тестовая функция Skin заменена на широко используемую функцию Растригина (рисунок 3). Эта функция гладкая так же как и Skin, имеет сложную поверхность со множеством локальных экстремумов, глобальный максимум в четырёх точках, один глобальный минимум в центре осей координат.

В третьих, результаты тестов я решил нормализовать в диапазон значений среди всех алгоритмов в таблице, где самый лучший результат равен 1.0, а самый худший 0.0, это позволяет равномерно оценивать результаты тестов, при том, что сложность функций учтена соответственно результатам каждого из алгоритмов оптимизации в тестировании.

После этого результаты тестирования алгоритмов суммируются, максимальному результату присваивается значение - 100 (эталонный максимальный результат), а минимальному значение - 1. Это позволяет напрямую сравнивать алгоритмы между собой равномерно учитывая сложность тестовых функций. Теперь результаты, распечатанные в Print (), сохраняем в исходных файлах тестовых скриптов для каждого алгоритма соответственно, а скрипт, подсчитывающий баллы в тестах прилагается в архиве к статье и в последующих статьях будет обновляться с добавлением в него результатов новых рассматриваемых алгоритмов.



rastrigin

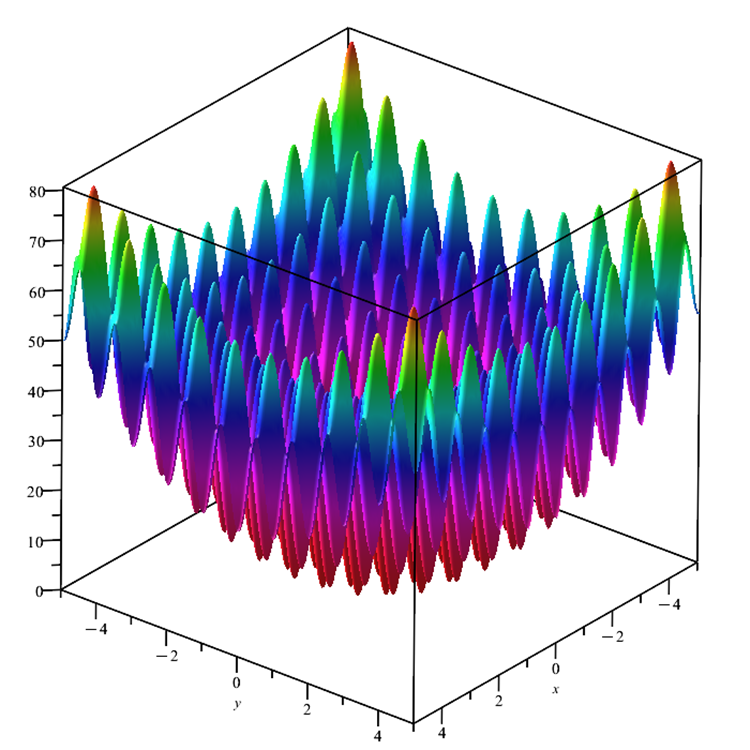
Рисунок 3. Тестовая функция Rastrigin.

Распечатка работы тестового стенда: 

2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    C_AO_BA:50;0.0;1.0;0.0;1.5;0.0;1.0;0.3;0.3
2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 66.63334336098077
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    Score: 0.82562
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 65.51391114042588
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    Score: 0.81175
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 59.84512760590815
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    Score: 0.74151
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.5861602092218606
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    Score: 0.33156
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.2895682720055589
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    Score: 0.16379
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.09867854051596259
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    Score: 0.05582
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 3.3199999999999994
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    Score: 0.27667
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 1.2079999999999997
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    Score: 0.10067
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.40759999999999996
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    Score: 0.03397

Алгоритм летучих мышей показал впечатляющие результаты на гладкой функции Растригина, причем, что интересно, с увеличением количества переменных в функции стабильность (повторяемость) результатов растет, что говорит о великолепной масштабируемости BA на гладких функциях. Так BA оказался лучшим на функции Растригина с 50 и 1000 переменными среди всех участников тестирования, что позволяет рекомендовать алгоритм летучих мышей для работы со сложными гладкими функциями, для работы с нейронными сетями. На функциях Forest и Megacity алгоритм летучих мышей показал средние результаты, продемонстрировав склонность к застреванию в локальных экстремумах, координаты локализуются в группы и не показывают динамики изменения и перемещения в сторону глобального оптимума. Предполагаю, что подобное поведение алгоритма обусловлено тем, что алгоритм чувствителен к наличию градиента на поверхности исследуемой функции, при отсутствии градиента алгоритм быстро останавливается в окрестностях локальных участков не имеющих значительного приращения в значениях фитнес функции, к тому же в алгоритме BA отсутствуют механизмы, позволяющие "перепрыгивать" на новые неизвестные участки, подобные механизму, реализованному в COA - с помощью полётов Леви.

Необходимо остановиться на таком важном аспекте, как наличие большого количества настроечных параметров у BA. Мало того, что параметров (степеней свободы) много самих по себе, но и каждый из параметров очень сильно влияет как на характер поисковых свойств, так и на общие показатели сходимости. Некоторые параметры могут давать отличные результаты на гладких функциях, а некоторые на дискретных и функциях с изломами, причем найти какие-то универсальные параметры, позволяющие одинаково хорошо справляться с различными типами тестовых функций представляется не тривиальной задачей. К статье приложен исходный код алгоритма летучих мышей с параметрами, которые мне представляются наиболее оптимальными. В целом, BA я бы не рекомендовал использовать пользователям, имеющих мало опыта в работе с алгоритмами оптимизации, поскольку результаты оптимизации могут сильно разниться.  

rastrigin

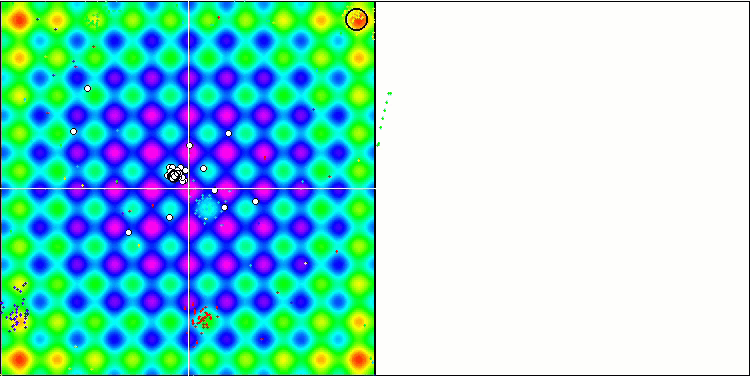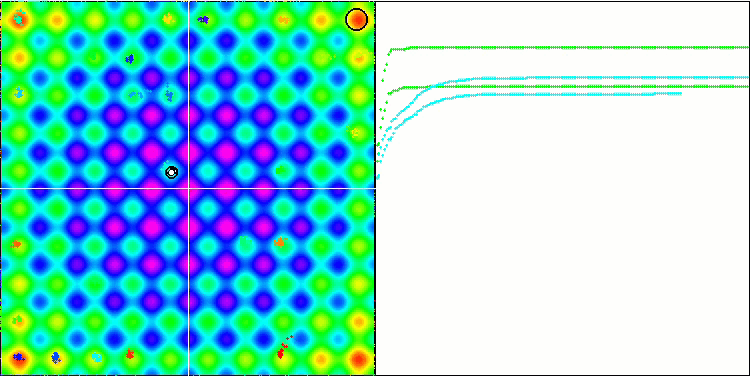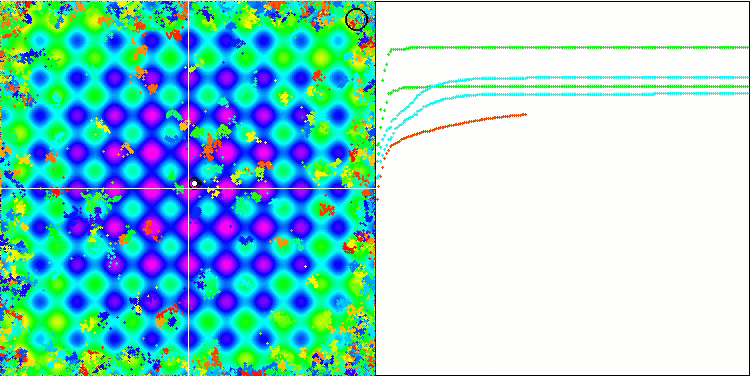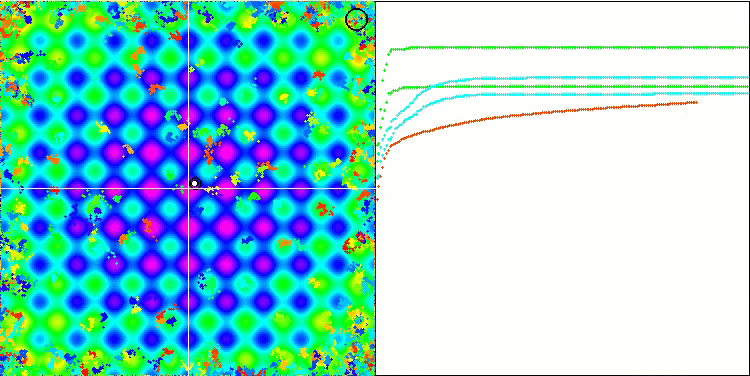
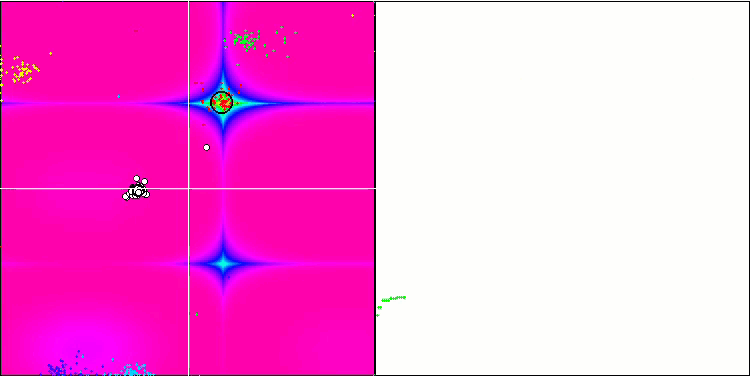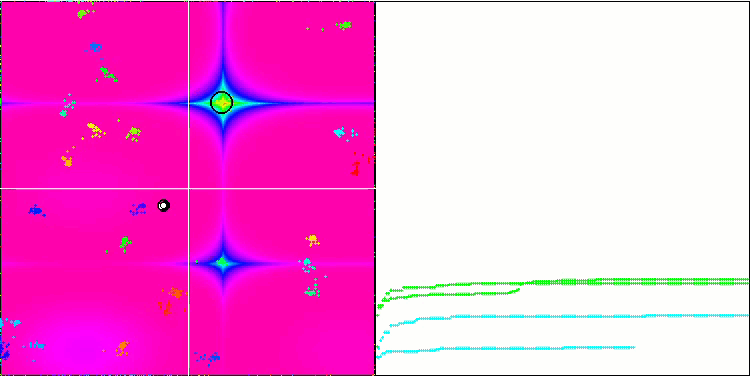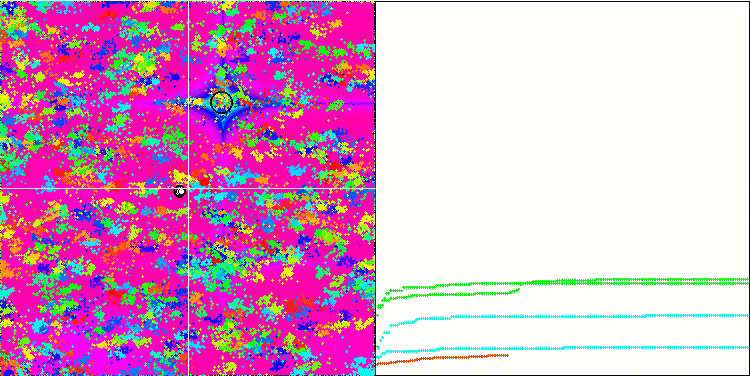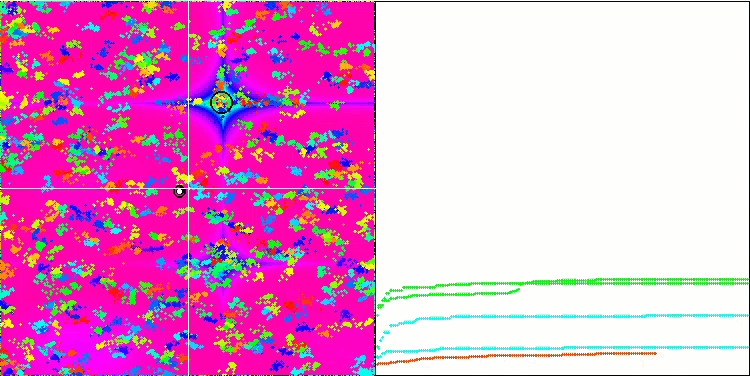
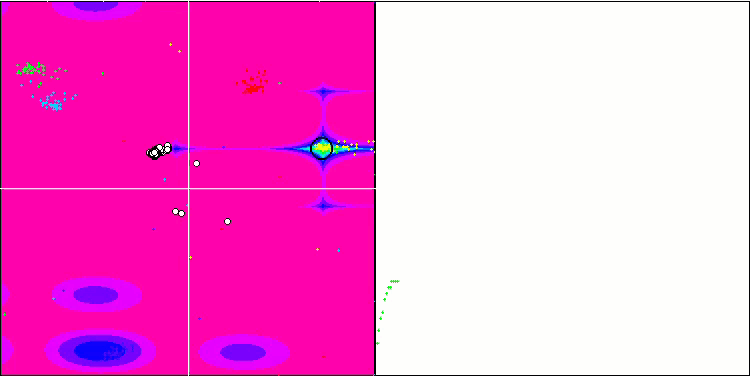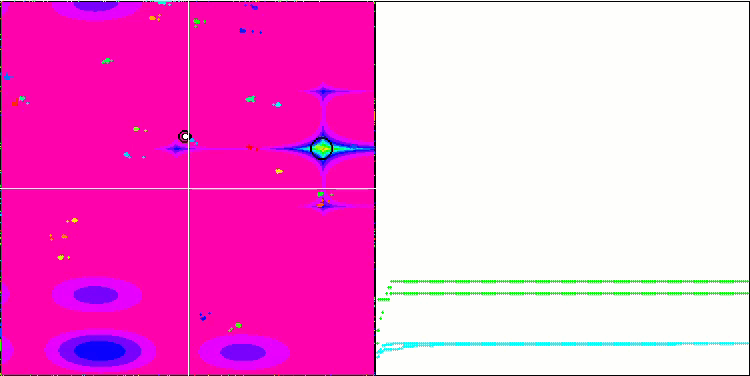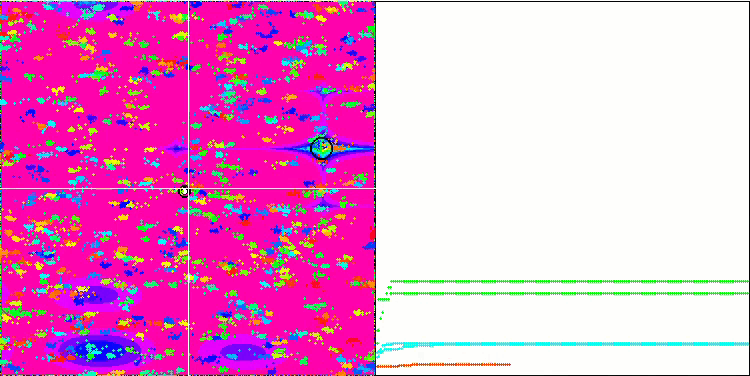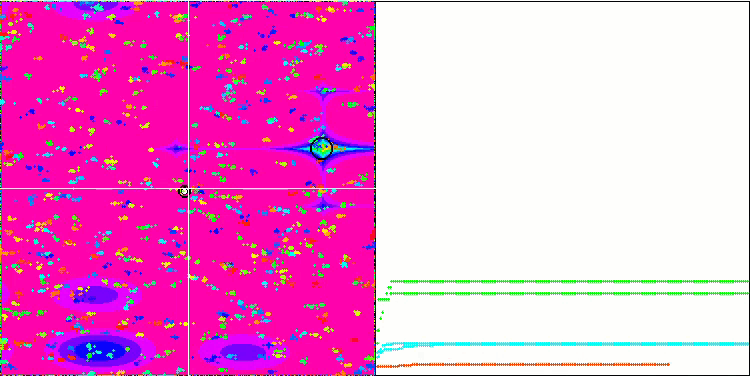
  BA на тестовой функции Rastrigin.

forest

BA на тестовой функции Forest.

megacity

BA на тестовой функции Megacity.

Обращая внимание на визуализацию тестовых функций можно получить представление о характерных особенностях алгоритма летучих мышей. В частности при работе на всех тестовых функциях для алгоритма характерно группирование координат на очень небольших локальных участках, но если для гладкой функции эта особенность даёт возможность двигаться даже там, где градиент фитнес функции изменяется слабо, то на дискретной функции эта особенность как раз и является проявлением недостатка, алгоритм застревает на плоских плато.

Распечатка результатов скриптом подсчета баллов алгоритмов оптимизации:

2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_RND=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18210 | 0.15281 | 0.07011 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08623 | 0.04810 | 0.06094 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.08904 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.6893397068905002
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_PSO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.22131 | 0.12861 | 0.05966 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15345 | 0.10486 | 0.28099 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08028 | 0.02385 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.053004072893302
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ACOm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.37458 | 0.28208 | 0.17991 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 0.10959 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ABC=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.84599 | 0.51308 | 0.22588 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.58850 | 0.21455 | 0.17249 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.47444 | 0.26681 | 0.35941 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.661160435265267
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_GWO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18977 | 0.04119 | 0.01802 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_COAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 0.73390 | 0.28892 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64504 | 0.34034 | 0.21362 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.67153 | 0.34273 | 0.45422 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.690306586791184
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FSS=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.50663 | 0.39737 | 0.11006 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.07806 | 0.05013 | 0.08423 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.01084 | 0.18998 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.4272897567648186
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64746 | 0.53292 | 0.18102 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.55408 | 0.42299 | 0.64360 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.21167 | 0.28416 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.477897116029613
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_BA=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.43859 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.17768 | 0.17477 | 0.33595 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15329 | 0.07158 | 0.46287 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.8147314003892507
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956 | 5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_RND: 8.652
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_PSO: 14.971
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ACOm: 100.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ABC: 60.294
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_GWO: 1.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_COAm: 78.177
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FSS: 21.475
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FAm: 74.486
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_BA: 62.962

Итак, переходим к рассмотрению итоговой рейтинговой таблицы. Как говорилось выше, методика подсчета оценочных характеристик алгоритмов изменилась, поэтому алгоритмы заняли новое положение. Из таблицы убраны некоторые классические алгоритмы и оставлены только их модифицированные версии, демонстрирующие более высокие показатели в тестировании. Теперь результаты тестирования не абсолютные как было раньше (абсолютные нормированные результаты значений тестовых функций), а относительные по результатам сравнения алгоритмов между собой.

Из таблицы видно, что абсолютным лидером на момент этой статьи является ACOm (оптимизация колонией муравьёв), алгоритм показал лучшие результаты в пяти тестах из девяти, поэтому итоговый результат у него 100 баллов. На второй строке рейтинга расположился COAm, модифицированная версия алгоритма оптимизации кукушкой. Этот алгоритм оказался лучшим на гладкой функции Растригина, а так же показал неплохие результаты на остальных тестах по сравнению с другими участниками тестирования. Третье место занял модифицированный светлячковый алгоритм FAm, он показал лучшие результаты на дискретной функции Megacity, такой же результат на этом тесте показал ещё только FSS.

AO

Description

Rastrigin

Rastrigin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

ACOm

ant colony optimization M

0,37458

0,28208

0,17991

0,83657

1,00000

1,00000

1,00000

3,00000

1,00000

1,00000

0,10959

2,10959

100,000

COAm

cuckoo optimization algorithm M

1,00000

0,73390

0,28892

2,02282

0,64504

0,34034

0,21362

1,19900

0,67153

0,34273

0,45422

1,46848

78,177

FAm

firefly algorithm M

0,64746

0,53292

0,18102

1,36140

0,55408

0,42299

0,64360

1,62067

0,21167

0,28416

1,00000

1,49583

74,486

BA

bat algorithm

0,43859

1,00000

1,00000

2,43859

0,17768

0,17477

0,33595

0,68840

0,15329

0,07158

0,46287

0,68774

62,962

ABC

artificial bee colony

0,84599

0,51308

0,22588

1,58495

0,58850

0,21455

0,17249

0,97554

0,47444

0,26681

0,35941

1,10066

60,294

FSS

fish school search

0,64746

0,53292

0,18102

1,36140

0,55408

0,42299

0,64360

1,62067

0,21167

0,28416

1,00000

1,49583

21,475

PSO

particle swarm optimisation

0,22131

0,12861

0,05966

0,40958

0,15345

0,10486

0,28099

0,53930

0,08028

0,02385

0,00000

0,10413

14,971

RND

random

0,18210

0,15281

0,07011

0,40502

0,08623

0,04810

0,06094

0,19527

0,00000

0,00000

0,08904

0,08904

8,652

GWO

grey wolf optimizer

0,00000

0,00000

0,00000

0,00000

0,00000

0,00000

0,00000

0,00000

0,18977

0,04119

0,01802

0,24898

1,000


Гистограмма результатов тестирования алгоритмов на рисунке 4.

rating

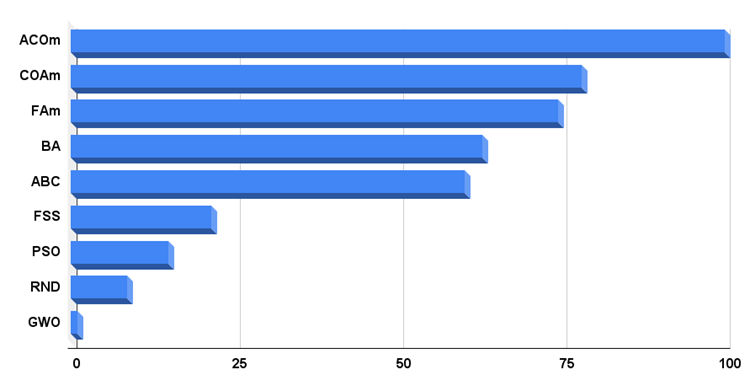
Рисунок 4. Гистограмма итоговых результатов тестирования алгоритмов.

Выводы по свойствам алгоритма летучих мышей (BA):

Плюсы:
1. Быстрый.
2. Хорошо работает с гладкими функциями.
3. Масштабируемость.

Минусы:
1. Очень много настроечных параметров.
2. Посредственные результаты на дискретных функциях.


Прикрепленные файлы |
Загрузить ZIP
9_The_world_of_AO_gBAs.ZIP (69.48 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Бегущая строка котировок: базовая версия Бегущая строка котировок: базовая версия
Здесь я покажу, как создать в терминале бегущую строку, которая обычно используется для отображения котировок на бирже. Создавать такую строку мы будем только при помощи MQL5, не используя никакое другое внешнее программирование.
Возможности Мастера MQL5, которые вам нужно знать (Часть 04): Линейный дискриминантный анализ Возможности Мастера MQL5, которые вам нужно знать (Часть 04): Линейный дискриминантный анализ
Современный трейдер почти всегда находится в поиске новых идей. Он постоянно пробует новые стратегии, модифицирует их и отбрасывает те, что не оправдали себя. В этой серии статей я постараюсь доказать, что Мастер MQL5 является настоящей опорой трейдера в его поисках.
Как работать с линиями средствами MQL5 Как работать с линиями средствами MQL5
В этой статье мы поговорим о том, как работать с наиболее важными линиями, такими как линии тренда, поддержка и сопротивление, используя средства языка MQL5.
Машинное обучение и Data Science (Часть 9): Алгоритм k-ближайших соседей (KNN) Машинное обучение и Data Science (Часть 9): Алгоритм k-ближайших соседей (KNN)
Это ленивый алгоритм, который не учится на обучающей выборке, а хранит все доступные наблюдения и классифицирует данные сразу же, как только получает новую выборку. Несмотря на простоту, этот метод используется во множестве реальных приложений.