Популяционные алгоритмы оптимизации: Алгоритм имитации отжига (Simulated Annealing, SA). Часть I

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Алгоритм оптимизации имитации отжига (Simulated Annealing) был разработан Скоттом Киркпатриком (Scott Kirkpatrick), Джорджем Гелатти (George Gelatt) и Марио Веччи (Mario Vecchi) в 1983 году. При исследовании свойств жидкостей и твердых тел при высокой температуре установлено, что металл переходит в жидкое состояние и частицы распределяются случайным образом, а состояние с минимальной энергией достигается при условии достаточно высокой начальной температуры и достаточно длительного времени охлаждения. Если это не выполняется, то материал окажется в метастабильном состоянии с неминимальной энергией - это называется закаливанием, которое заключается в резком охлаждении материала. В этом случае структура атомов не имеет симметрии (анизотропное состояние, или неравномерность свойств материала внутри кристаллической решетки).

Во время же медленного процесса отжига материал также переходит в твердое состояние, но с организованными атомами и с симметрией, поэтому было предложено использовать этот процесс для разработки алгоритма оптимизации, который бы мог найти глобальный оптимум в сложных задачах. Алгоритм также был предложен как метод решения задач комбинаторной оптимизации.

Таким образом, основная идея алгоритма основана на математическом аналоге процесса отжига металла. В процессе отжига, чтобы равномерно распределить его внутреннюю энергию, металл нагревается до высокой температуры, а затем медленно охлаждается, позволяя молекулам металла перемещаться и упорядочиваться в более стабильные состояния, при этом снимаются внутренние напряжения в металле и удаляются межкристалические дефекты. Термин "отжиг" также связан с термодинамической свободной энергией, которая является атрибутом материала и зависит от его состояния.

В алгоритме оптимизации имитации отжига используется аналогичный процесс. Алгоритм применяет операции, аналогичные нагреву и охлаждению материала. Алгоритм начинает свою работу с исходного решения, которое может быть случайным или полученным из предыдущих итераций. Затем применяет операции изменения состояния решения, которые могут быть случайными или управляемыми, чтобы получить новое состояние, даже если оно хуже текущего. Вероятность принятия худшего решения определяется функцией "охлаждения", которая со временем уменьшает вероятность принятия худшего решения, что позволяет алгоритму временно "выскочить" из локальных оптимумов и искать лучшие решения в других местах пространства поиска.

Алгоритм имитации отжига основан на трёх основных концепциях:

• Применение случайности: Алгоритм использует случайные операции для изменения состояния решения и выбора следующего состояния. Это позволяет исследовать различные области пространства поиска и избегать застревания в локальных оптимумах.

• Принятие худших решений: SA один из очень немногих алгоритмов, который предпочитает худшие решения с некоторой вероятностью лучшим решениям.

• Постепенное уменьшение вероятности принятия худших решений: Алгоритм использует процесс "охлаждение", который со временем уменьшает вероятность принятия худших решений. Это позволяет сначала исследовать пространство поиска более широко, а затем сосредоточиться на улучшении решения, что позволяет балансировать исследование и эксплуатацию пространства поиска.

Алгоритм оптимизации имитации отжига является одним из методов, применяемых в метаэвристике, который описывает класс алгоритмов для решения сложных оптимизационных задач. Они основаны на эвристических методах, которые позволяют искать приближенные решения в пространстве поиска, не требуя полного перебора всех возможных вариантов. Случайность является одним из ключевых элементов метаэвристик, которые позволяют им обнаруживать новые и перспективные регионы решений. Алгоритм относится к группе алгоритмов, называемых "методами стохастической оптимизации".

Алгоритм SA имеет недостатки, о которых мы поговорим ниже. На базе SA были разработаны другие алгоритмы, такие как "Адаптивный моделируемый отжиг, ASA", "Квантовая нормализация, QN" (также называют "Квантовый отжиг, QA").

2. Описание алгоритма

Базовая версия алгоритма имитации отжига авторов чрезвычайна проста, но представить себе, как работает алгоритм без визуального отображения графиков процесса изменения температуры и графика вероятности принятия худших решений, непросто.

Давайте разбираться по шагам. Алгоритм начинает работу с некоторой начальной высокой температуры (внешний параметр), что соответствует нагреву материала в металлургии. Высокая температура означает высокую энергию молекул, переходящих из разного энергетического состояния (то в меньшую, то в большую сторону). Аналогично этому процессу высокоэнергичного движения в металле, система может принимать худшие решения с некоторой вероятностью.

Если представить себе движение лыжника с вершины горы, то попадая в некоторую локальную низменность лыжник может решить, что достиг подножия горы. А что бы убедиться в верности решения, нужно немного ухудшить своё положение и приподняться на некоторую возвышенность, что бы с ещё большей скоростью устремится вниз. В этом и заключается смысл принятия худших решений с некоторой вероятностью. Чтобы выпрыгнуть из локальной "ловушки", был, кстати, разработан алгоритм квантового отжига, имитирующий квантовые эффекты присутствия в двух местах одновременно, где предполагается с помощью туннелирования перескакивать через "стенки", но пытаясь избавиться от одних недостатков квантовый отжиг получил другие, в частности проблему выбора силы квантового перехода.

Для описания процесса имитации отжига применяют несколько простых формул. Формула для вычисления энергии:

E = f (x)

То есть, E представляет собой значение фитнес-функции для текущего состояния агента.

Формула для вычисления изменения энергии:

ΔE = E_new - E_old

где:

• ΔE - изменение энергии при переходе от текущего состояния к новому состоянию (разница значений фитнес-функции на двух последовательных итерациях)
  
• E_new - значение энергии для нового состояния
• E_old - значение энергии для предыдущего состояния

Формула для вычисления вероятности принятия худшего решения:

P = exp (-ΔE / T)

где:

• P - вероятность принятия худшего решения
• T - текущая температура

Из графика ниже, на котором показана зависимость вероятности P, видно, что более высокой ΔE соответствует более низкая вероятность. Это означает, что с уменьшением температуры вероятность высокоэнергичных переходов в худшую сторону падает быстрее, чем переходов с меньшей разницей в энергии. Т.е., алгоритм всё меньше и меньше "рискует" в попытке выбраться из "ловушки", предпочитая только улучшение решения. График зависимости вероятностей показан на рисунке 1, причем используется линейное уменьшение температуры для наглядности, хотя в алгоритме используется нелинейное изменение температуры.

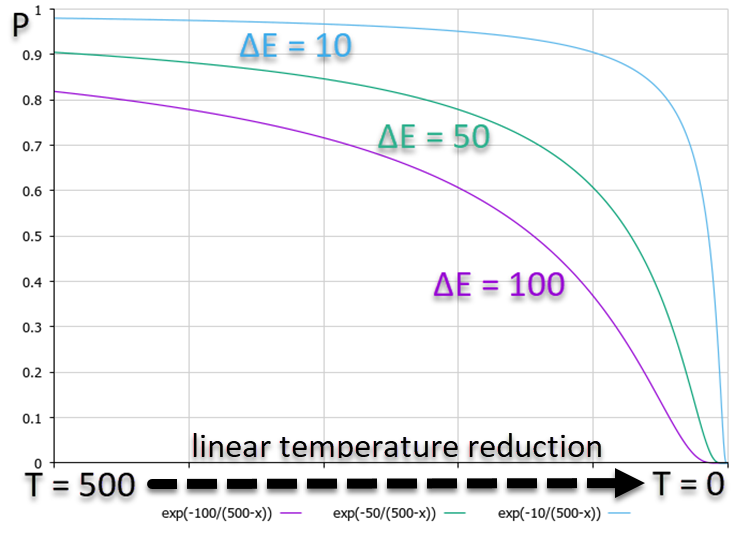
Рисунок 1. График вероятностей принятия решений в зависимости от изменения энергии в худшую сторону с линейным уменьшением температуры.

Формула для обновления температуры:

Tnew = α * Tprev

где:

• α - коэффициент охлаждения, обычно α находится в интервале от 0.8 до 0.99
• Tnew - новая температура
• Tprev - предыдущая температура
  

График изменения температуры на каждой итерации с коэффициентом α = 0.99, 0.8, 0.5 и 0.1 при стартовой температуре T = 500 показан на рисунке 2. Температура постепенно уменьшается, что соответствует охлаждению материала. Уменьшение температуры на каждой итерации приводит к уменьшению вероятности принятия худших решений, что соответствует уменьшению возможности молекулам изменять своё энергетическое состояние при снижении температуры.

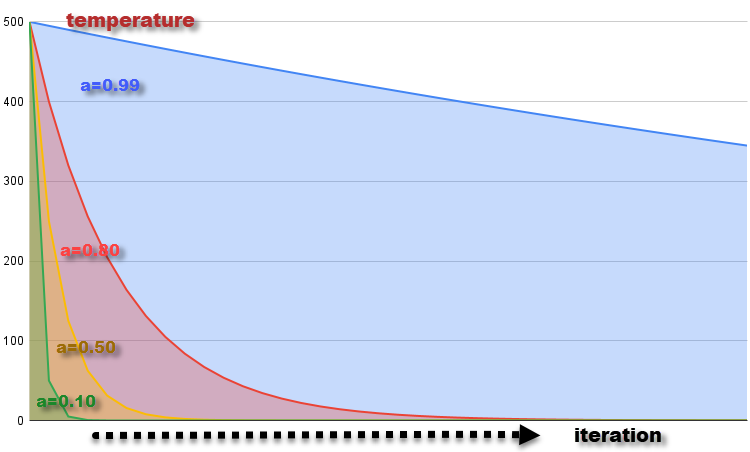
Рисунок 2. График измнения температуры с коэффициентами α = 0.99, 0.8, 0.5 и 0.1.

Формула для генерации нового состояния системы:

x_new = GenerateNeighbor (x)

где:

• x_new - новое состояние, сгенерированное на основе текущего состояния x
  
• GenerateNeighbor (x) - функция генерирующая новое состояние путем внесения случайных изменений с равномерным распределением в текущее состояние
  

Теперь, зная все теоретические основы алгоритма имитации отжига, нам не составит труда написать код SA. Движение молекул, которые изменяют своё энергетическое состояние и которые являются агентами, мы можем представить в виде структуры, S_Agent, которая содержит информацию об агенте в оптимизационной задаче. Описание полей и методов структуры:

• Init (int coords): метод инициализирует агента и выделяет память для массивов "c" и "cPrev" размером "coords". Он также устанавливает начальные значения "f" и "fPrev" равными "-DBL_MAX" (отрицательная бесконечность)
• c []: массив "c" представляет координаты агента в оптимизационном пространстве
  
• cPrev []: массив "cPrev" представляет предыдущие координаты агента
  
• f: представляет значение функции приспособленности для текущих координат агента
  
• fPrev: представляет собой предыдущее значение функции приспособленности агента
  

//————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c,     coords);
    ArrayResize (cPrev, coords);
    f     = -DBL_MAX;
    fPrev = -DBL_MAX;
  }

  double c     []; //coordinates
  double cPrev []; //previous coordinates
  double f;        //fitness
  double fPrev;    //previous fitness
};
//————————————————————————————————————————

Опишем класс алгоритма SA и назовём его C_AO_SA. Он получится очень простым, поскольку не содержит ничего необычного, чего бы мы не использовали ранее, кроме специфических тепловых переменных и констант.

Поля и методы класса:

• cB []: массив лучших координат, найденных алгоритмом оптимизации на момент текущей итерации
  
• fB: значение функции приспособленности для лучших координат
  
• a []: массив представляет агентов, он используется для хранения информации о каждом агенте в оптимизационной задаче, каждый элемент массива является экземпляром структуры S_Agent
• rangeMax []: массив максимальных значений диапазона поиска для каждой координаты и используется для определения верхней границы поиска для каждой координаты агента
• rangeMin []: массив минимальных значений диапазона поиска для каждой координаты и используется для определения нижней границы поиска для каждой координаты агента
• rangeStep []: массив представляет шаги поиска для каждой координаты
• Init (const int coordsP, const int popSizeP, const double tP, const double aP, const double dP): метод инициализирует алгоритм оптимизации, принимает параметры: количество координат "coordsP", размер популяции "popSizeP", начальную температуру "tP", коэффициент снижения температуры "aP" и коэффициент диффузии "dP", метод выполняет инициализацию полей класса и агентов
• Moving (): метод выполняет перемещение агентов в процессе оптимизации и используется алгоритм для определения новых координат агентов
• Revision (): метод выполняет ревизию и обновление лучших координат и функции приспособленности на основе текущих значений агентов
• SeInDiSp (double In, double InMin, double InMax, double Step): приватный метод используется для нормализации значения "In" в диапазоне от "InMin" до "InMax" с шагом "Step"
• RNDfromCI (double min, double max): приватный метод используется для генерации случайного числа в заданном диапазоне от "min" до "max"

Необходимо отметить, что коэффициент диффузии dP отсутствует в оригинальной версии SA. Дело в том, что идея авторов заключалась в генерации нового состояния системы и соответственно новой координаты агентов на всём диапазоне от "min" до "max" по каждой координате, это соответствовало бы хаотичному движению молекул во всём "объёме" металла, подвергаемому отжигу. Мои эксперименты показали, что результаты улучшаются, если ограничивать диапазон колебаний молекул только некоторым интервалом, выраженном в частях от всего допустимого интервала. В этом и есть смысл этого параметра коэффициента диффузии - ограничить область возможного перемешивания молекул.

Для получения результатов работы, эквивалентных оригинальному SA, достаточно просто выставить этот параметр равным 1 (по умолчанию 0.2).

//————————————————————————————————————————
class C_AO_SA
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,      //coordinates number
                     const int    popSizeP,     //population size
                     const double tP,           //temperature
                     const double aP,           //temperature reduction coefficient
                     const double dP);          //diffusion coefficient


  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;       //coordinates number
  private: int    popSize;      //population size

  private: double T;
  private: double α;
  private: double d;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//————————————————————————————————————————

Методом инициализации послужит функция "Init", выполняющая инициализацию всех полей класса и распределяющая размеры необходимых массивов для работы алгоритма оптимизации.

//————————————————————————————————————————
void C_AO_SA::Init (const int    coordsP,      //coordinates number
                    const int    popSizeP,     //population size
                    const double tP,           //temperature
                    const double aP,           //temperature reduction coefficient
                    const double dP)           //diffusion coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords     = coordsP;
  popSize    = popSizeP;
  T          = tP;
  α          = aP;
  d          = dP;

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//————————————————————————————————————————

Для перемещения агентов в пространстве поиска напишем метод "Moving". 
На первой итерации, когда алгоритм только что запущен, переменная - флаг "revision" равна "false", необходимо инициализировать агентов популяции начальными значениями, лежащими в диапазоне [min;max] координат с равномерным распределением. Полученные значения координат агентов нормализуем функцией SeInDiS, чтобы соблюсти требуемый шаг перемещения. Далее флаг "revision" устанавливается в значение "true", чтобы указать, что на следующей итерации будет необходимо применять операторы алгоритма имитации отжига.

На второй и последующих итерациях, если бы это был оригинальный SA, то мы бы выполняли то, что сделали на первой итерации, т.е. продолжали бы генерировать случайные числа в заданном диапазоне с равномерным распределением. В нашем слегка исправленном варианте мы поступим также, но с регулированием диапазона значений, ограничив тем самым область диффузионного взаимодействия молекул в металле, при этом перемещение осуществляется с того места, где молекула находилась на предыдущей итерации. Полученные значения координат агентов нормализуем функцией SeInDiS, чтобы соблюсти требуемый шаг перемещения.

//————————————————————————————————————————
void C_AO_SA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      rnd = RNDfromCI (-0.1, 0.1);
      a [i].c [c] = a [i].cPrev [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
      a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//————————————————————————————————————————

Если в методе "Moving" мы выполняли генерацию новых состояний системы, т.е. перемещали молекулы в расплавленном металле, то в методе "Revision" будем выполнять расчет "теплового баланса" и вероятность перехода молекул в новое состояние.

В начале метода мы проверим значения всех фитнес-функций агентов, если обнаружим значения лучше глобального, тогда обновим его.

Далее в цикле "for" выполняем для каждого агента в популяции следующие действия:

• вычисляется значение "ΔE" как абсолютное значение разницы между "a[i].f" и "a[i].fPrev", т.е. разницы между значениями фитнес-функции на текущей и предыдущей итерации

Если значение "a[i].f" больше значения "a[i].fPrev" (т.е., текущая приспособленность лучше, чем предыдущая), то выполняется следующий блок кода:

• значение "a[i].fPrev" заменяется значением "a[i].f"
• значения массива "a[i].cPrev" копируется из массива "a[i].c"

Иначе, выполняется следующий блок кода (текущее значение фитнес-функции хуже предыдущего):

• значение вероятности "P" вычисляется как экспонента от отрицательного отношения "ΔE" к "T"
• генерируем случайное число из диапазона [0.0;1.0] для "rnd" моделируя вероятность перехода в новое состояние, которое хуже предыдущего

Если значение "rnd" меньше значения "P" (т.е., вероятность исполнена), то:

• значение "a[i].fPrev" заменяется значением "a[i].f"
• значения массива "a[i].cPrev" копируется из массива "a[i].c"

Значение температуры "T" умножается на тепловой коэффициент "α", что даёт понижение температуры с каждой новой итерацией.

//————————————————————————————————————————
void C_AO_SA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double ΔE;
  double P;

  for (int i = 0; i < popSize; i++)
  {
    ΔE = fabs (a [i].f - a [i].fPrev);

    if (a [i].f > a [i].fPrev)
    {
      a [i].fPrev = a [i].f;
      ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
    else
    {
      P = exp (-ΔE / T);
      rnd = RNDfromCI (0, 1.0);

      if (rnd < P)
      {
        a [i].fPrev = a [i].f;
        ArrayCopy (a [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
      }

    }
  }

  T = α * T;
}
//————————————————————————————————————————

3. Результаты тестов

Распечатка работы оригинального алгоритма на тестовом стенде с генерацией случайных чисел во всем допустимом диапазоне значений:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 61.3646399742684
Score: 0.76034
25 Rastrigin's; Func runs 10000 result: 47.454223750487884
Score: 0.58798
500 Rastrigin's; Func runs 10000 result: 39.06494648961887
Score: 0.48404
=============================
5 Forest's; Func runs 10000 result: 0.4708272303190655
Score: 0.26632
25 Forest's; Func runs 10000 result: 0.17553657864203864
Score: 0.09929
500 Forest's; Func runs 10000 result: 0.0538869772164491
Score: 0.03048
=============================
5 Megacity's; Func runs 10000 result: 2.6
Score: 0.21667
25 Megacity's; Func runs 10000 result: 1.0
Score: 0.08333
500 Megacity's; Func runs 10000 result: 0.3044
Score: 0.02537
=============================
All score: 2.55383

А это распечатка работы алгоритма на тестовом стенде с добавлением коэффициента диффузии:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 65.78409729002105
Score: 0.81510
25 Rastrigin's; Func runs 10000 result: 52.25447043222567
Score: 0.64746
500 Rastrigin's; Func runs 10000 result: 40.40159931988021
Score: 0.50060
=============================
5 Forest's; Func runs 10000 result: 0.5814827554067439
Score: 0.32892
25 Forest's; Func runs 10000 result: 0.23156336186841173
Score: 0.13098
500 Forest's; Func runs 10000 result: 0.06760002887601002
Score: 0.03824
=============================
5 Megacity's; Func runs 10000 result: 2.92
Score: 0.24333
25 Megacity's; Func runs 10000 result: 1.256
Score: 0.10467
500 Megacity's; Func runs 10000 result: 0.33840000000000003
Score: 0.02820
=============================
All score: 2.83750

По результатам этих двух тестов мы можем видеть, что результаты работы алгоритма заметно улучшились с применением коэффициента диффузии. Оригинальный алгоритм потребовал улучшений, чтобы попасть в нашу таблицу. Неожиданно для такого известного и популярного метода оптимизации иметь столь слабые результаты, тем более что применение его очень обширное, в том числе использования для обучения нейронных сетей.

Визуализация работы SA не обнаружила сколь-нибудь заметных отличительных черт в поведении агентов в пространстве поиска, точки ведут себя хаотично без формирования структур, подобно тепловому броуновскому движению. К вышесказанному можно добавить, что наблюдается застревание в локальных экстремумах и сходимость оставляет желать лучшего, хотя в разнообразии популяции недостатка не ощущается, т.е. популяция не истощается к завершению итераций.

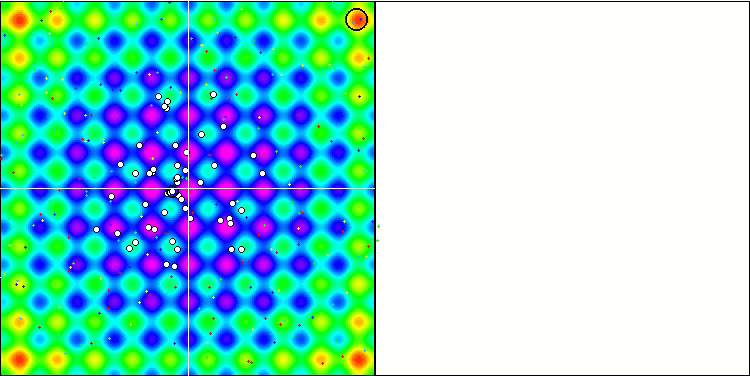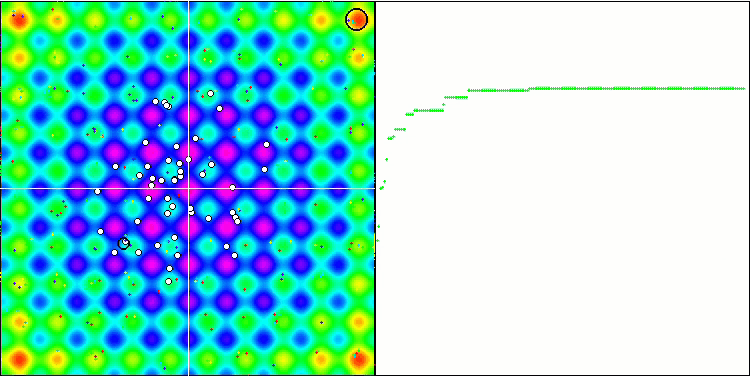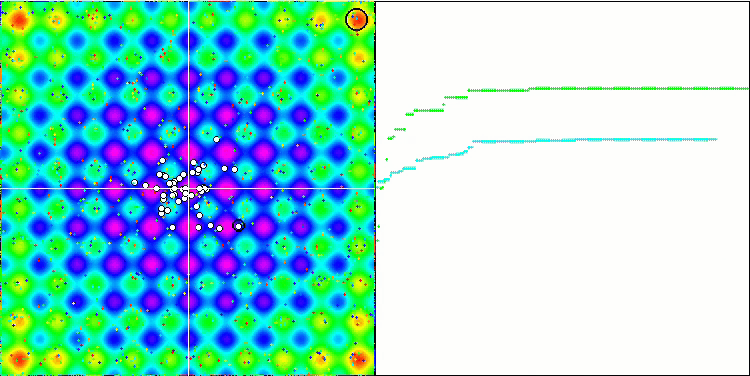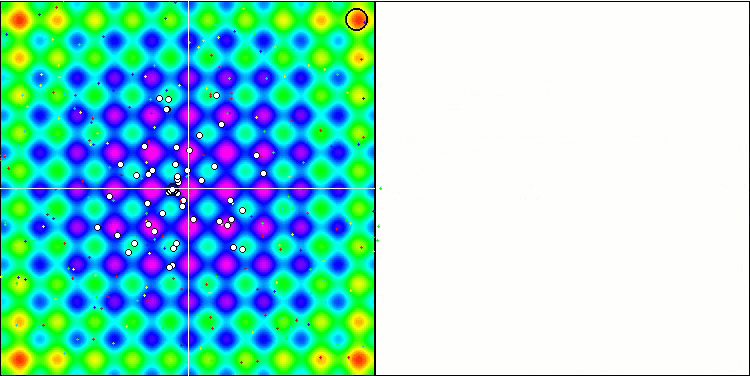
  SA на тестовой функции Rastrigin.

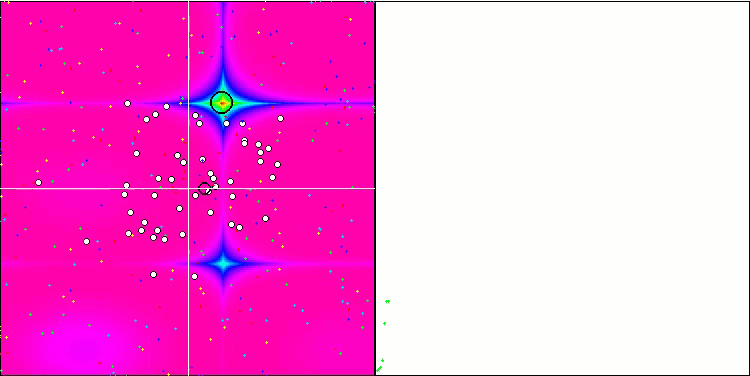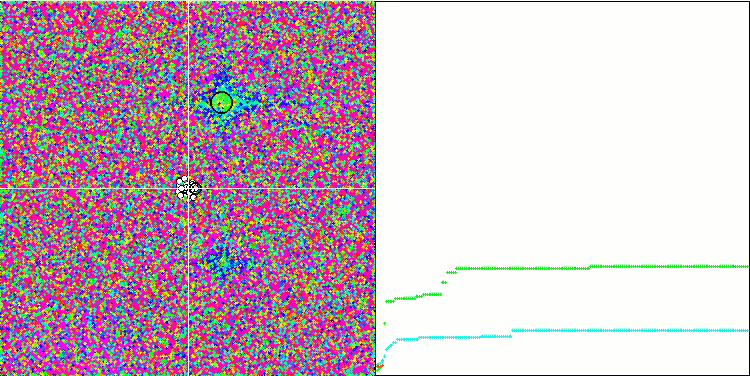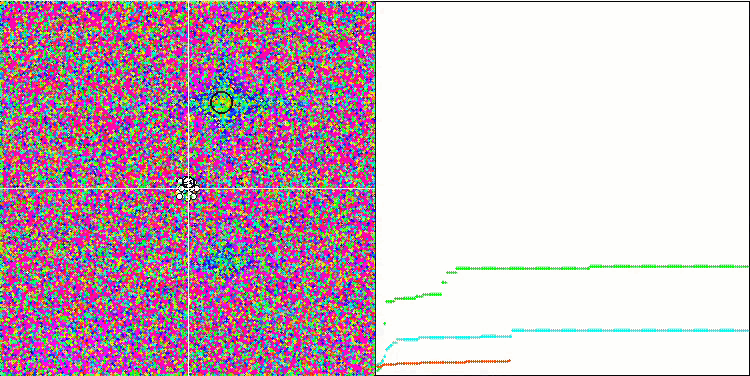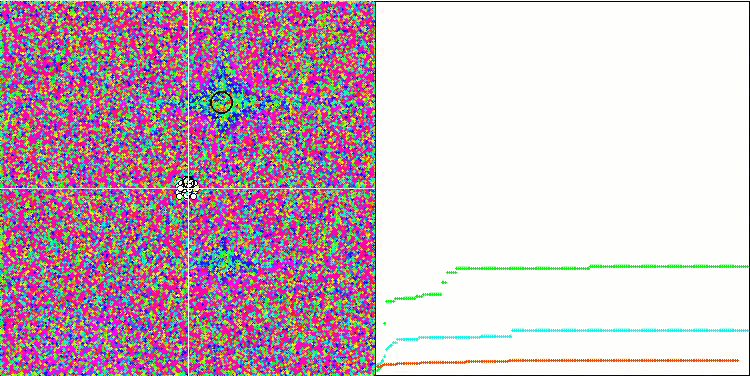
  SA на тестовой функции Forest.

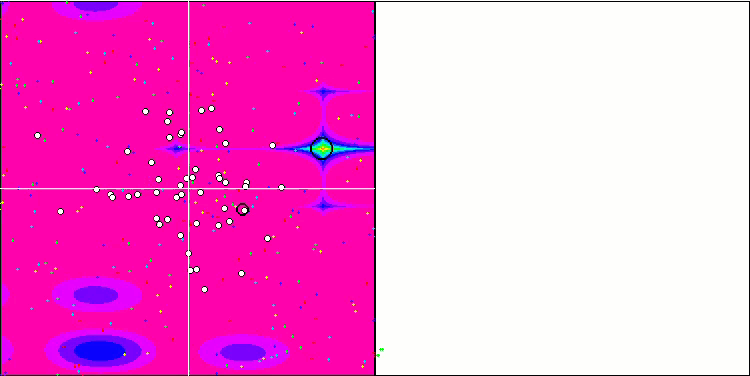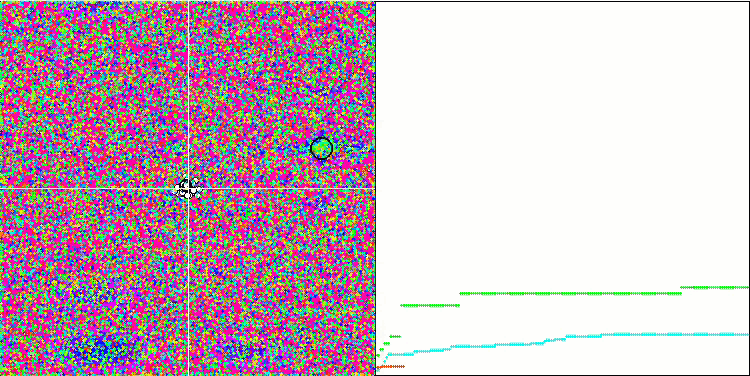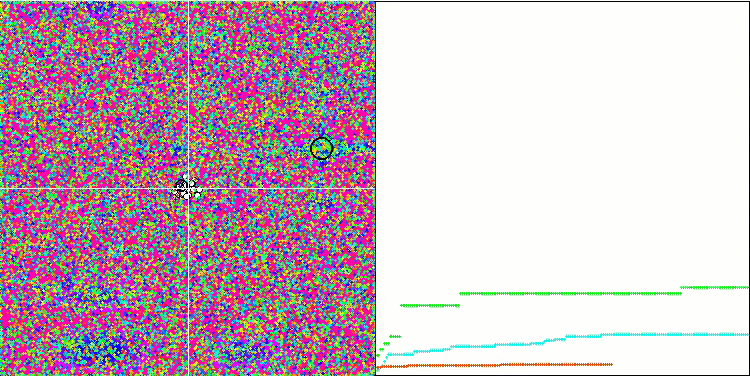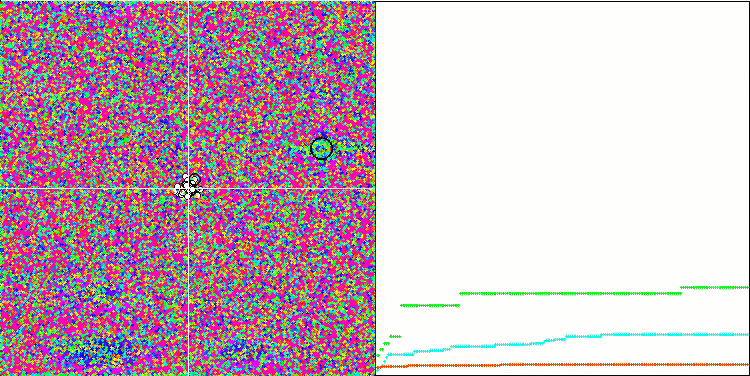
   SA на тестовой функции Megacity.

Алгоритм имитации отжига занял место в нижней части таблицы. Сравнительная таблица показывает, что в алгоритме не присутствует никаких отличительных особенностей в отдельных тестах, все результаты ниже среднего. В таблице присутствуют алгоритмы, такие как CSS, которые демонстрируют великолепные результаты в отдельных тестах, хотя и находятся в нижней части таблицы, к сожалению, алгоритм SA к таким не относится.

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastic diffusion search M	0,99809	1,00000	0,69149	2,68958	0,99265	1,00000	1,00000	2,99265	1,00000	1,00000	1,00000	3,00000	100,000
2	SSG	saplings sowing and growing	1,00000	0,92761	0,51630	2,44391	0,72120	0,65201	0,83760	2,21081	0,54782	0,61841	0,99522	2,16146	77,683
3	DE	differential evolution	0,98295	0,89236	0,51375	2,38906	1,00000	0,84602	0,65510	2,50112	0,90000	0,52237	0,12031	1,54268	73,099
4	HS	harmony search	0,99676	0,88385	0,44686	2,32747	0,99148	0,68242	0,37529	2,04919	0,71739	0,71842	0,41338	1,84919	70,623
5	IWO	invasive weed optimization	0,95828	0,62227	0,27647	1,85703	0,70170	0,31972	0,26613	1,28755	0,57391	0,30527	0,33130	1,21048	48,250
6	ACOm	ant colony optimization M	0,34611	0,16683	0,15808	0,67103	0,86147	0,68980	0,64798	2,19925	0,71739	0,63947	0,05579	1,41265	47,387
7	MEC	mind evolutionary computation	0,99270	0,47345	0,21148	1,67763	0,60244	0,28046	0,21324	1,09615	0,66957	0,30000	0,26045	1,23002	44,049
8	SDOm	spiral dynamics optimization M	0,69840	0,52988	0,33168	1,55996	0,59818	0,38766	0,37600	1,36183	0,35653	0,15262	0,25842	0,76758	40,289
9	NMm	Nelder-Mead method M	0,88433	0,48306	0,45945	1,82685	0,46155	0,24379	0,21903	0,92437	0,46088	0,25658	0,16810	0,88555	39,660
10	COAm	cuckoo optimization algorithm M	0,92400	0,43407	0,24120	1,59927	0,57881	0,23477	0,13842	0,95200	0,52174	0,24079	0,17001	0,93254	37,830
11	FAm	firefly algorithm M	0,59825	0,31520	0,15893	1,07239	0,50637	0,29178	0,41704	1,21519	0,24783	0,20526	0,35090	0,80398	33,139
12	ABC	artificial bee colony	0,78170	0,30347	0,19313	1,27829	0,53379	0,14799	0,11177	0,79355	0,40435	0,19474	0,13859	0,73768	29,766
13	BA	bat algorithm	0,40526	0,59145	0,78330	1,78002	0,20664	0,12056	0,21769	0,54488	0,21305	0,07632	0,17288	0,46225	29,499
14	CSS	charged system search	0,56605	0,68683	1,00000	2,25289	0,13961	0,01853	0,13638	0,29452	0,07392	0,00000	0,03465	0,10856	27,930
15	GSA	gravitational search algorithm	0,70167	0,41944	0,00000	1,12111	0,31390	0,25120	0,27812	0,84322	0,42609	0,25525	0,00000	0,68134	27,807
16	BFO	bacterial foraging optimization	0,67203	0,28721	0,10957	1,06881	0,39364	0,18364	0,17298	0,75026	0,37392	0,24211	0,18841	0,80444	27,542
17	EM	electroMagnetism-like algorithm	0,12235	0,42928	0,92752	1,47915	0,00000	0,02413	0,29215	0,31628	0,00000	0,00527	0,10872	0,11399	19,002
18	SFL	shuffled frog-leaping	0,40072	0,22021	0,24624	0,86717	0,19981	0,02861	0,02221	0,25063	0,19565	0,04474	0,06607	0,30646	13,200
19	SA	simulated annealing	0,36938	0,21640	0,10018	0,68595	0,20341	0,07832	0,09372	0,37545	0,16956	0,08422	0,10394	0,35772	13,138
20	MA	monkey algorithm	0,33192	0,31029	0,13582	0,77804	0,09927	0,05443	0,07482	0,22852	0,15652	0,03553	0,10669	0,29874	11,777
21	FSS	fish school search	0,46812	0,23502	0,10483	0,80798	0,12730	0,03458	0,05458	0,21647	0,12175	0,03947	0,08244	0,24366	11,332
22	IWDm	intelligent water drops M	0,26459	0,13013	0,07500	0,46972	0,28358	0,05445	0,05112	0,38916	0,22609	0,05659	0,05054	0,33322	10,423
23	PSO	particle swarm optimisation	0,20449	0,07607	0,06641	0,34696	0,18734	0,07233	0,18207	0,44175	0,16956	0,04737	0,01947	0,23641	8,426
24	RND	random	0,16826	0,09038	0,07438	0,33302	0,13381	0,03318	0,03949	0,20648	0,12175	0,03290	0,04898	0,20363	5,054
25	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06514	0,00000	0,00000	0,06514	0,23478	0,05789	0,02545	0,31812	1,000

Выводы

Алгоритм имитации отжига имеет несколько слабых сторон, которые могут ограничивать его эффективность при решении некоторых задач оптимизации. Некоторые из этих слабых сторон включают в себя:

• Зависимость от начального решения: как и многие другие методы оптимизации, алгоритм имитации отжига может зависеть от начального решения, которое выбирается случайным образом. Если начальное решение плохое, то алгоритм может застрять в локальном оптимуме и не сможет найти глобальный.
  
  Важно отметить, что алгоритм требует настройки таких параметров, как начальная "температура", шаг изменения температуры, влияющих на вероятность принятия худшего решения. Эти параметры влияют на производительность и качество решений, поэтому выбор и настройка параметров являются важными аспектами при применении алгоритма имитации отжига к конкретной задаче оптимизации. Настройка этих параметров может быть сложной задачей, и неправильная настройка может привести к плохим результатам. Настройки по умолчанию выбраны мной для получения наилучших результатов в тестовом наборе функций.
  
  
• Еще одной слабой стороной алгоритма имитации отжига является возможность застревания в локальных экстремумах. Это происходит, когда алгоритм находит оптимальное решение, которое является локальным экстремумом, но не является глобальным экстремумом. В этом случае алгоритм не сможет продвинуться дальше и остановится на локальном оптимуме. Очень хорошо это заметно на визуализации выше.
  
  
• Низкая скорость сходимости: SA может быть медленным в сходимости к оптимальному решению, особенно для сложных задач оптимизации. Это связано с тем, что алгоритм использует случайность и может принимать худшие решения, что может замедлить процесс оптимизации.
  
  
• Необходимость большого количества итераций: Для достижения оптимального решения, алгоритм имитации отжига может требовать большого количества итераций. Это может быть проблемой для задач, где время выполнения является критическим фактором.
  
  
• Неэффективность при решении задач с большим количеством переменных: SA может быть неэффективным при решении задач с большим количеством переменных, так как пространство поиска может быть слишком велико. В этом случае, другие методы оптимизации, такие как генетические алгоритмы или методы оптимизации на основе градиента, могут быть более эффективны. С малым количеством переменных (1-2) алгоритм справляется хорошо, как, впрочем, и любой алгоритм, даже простой случайный RND.

Существует несколько улучшений, которые могут быть применены к алгоритму имитации отжига для улучшения его производительности и эффективности:

1. Модификация функции охлаждения: функция охлаждения является важным параметром алгоритма, который регулирует скорость охлаждения и температуру системы.

2. Использование более эффективных методов выбора следующего состояния: SA использует случайный выбор следующего состояния. Однако, существуют более эффективные методы выбора следующего состояния, такие как методы мутирования и кроссинговера.

3. Использование адаптивных параметров: параметры алгоритма, такие как начальная температура и коэффициент охлаждения, могут быть адаптивно настраиваемыми в зависимости от характеристик задачи оптимизации.

4. Использование комбинации алгоритмов: SA может быть комбинирован с другими алгоритмами оптимизации, такими как генетические алгоритмы или методы градиентного спуска, чтобы улучшить производительность и эффективность оптимизации.

Применение различных распределений случайной величины при генерации нового состояния системы, вместо равномерного, не помогло улучшить результаты. Однако, существует способ кардинально преобразить этот очень известный и популярный алгоритм до такой степени, что он способен потягаться с лидерами таблицы за призовые места. Как это возможно? - Этим способом я готов поделиться во второй части статьи и рассказать о всех проделанных этапах модификации. Но, как мы знаем, не существует универсального способа улучшить любой алгоритм оптимизации и это зависит исключительно только от стратегии поиска в самом алгоритме. Поэтому улучшение будет касаться только старого доброго, но практически бесполезного, алгоритма имитации отжига.

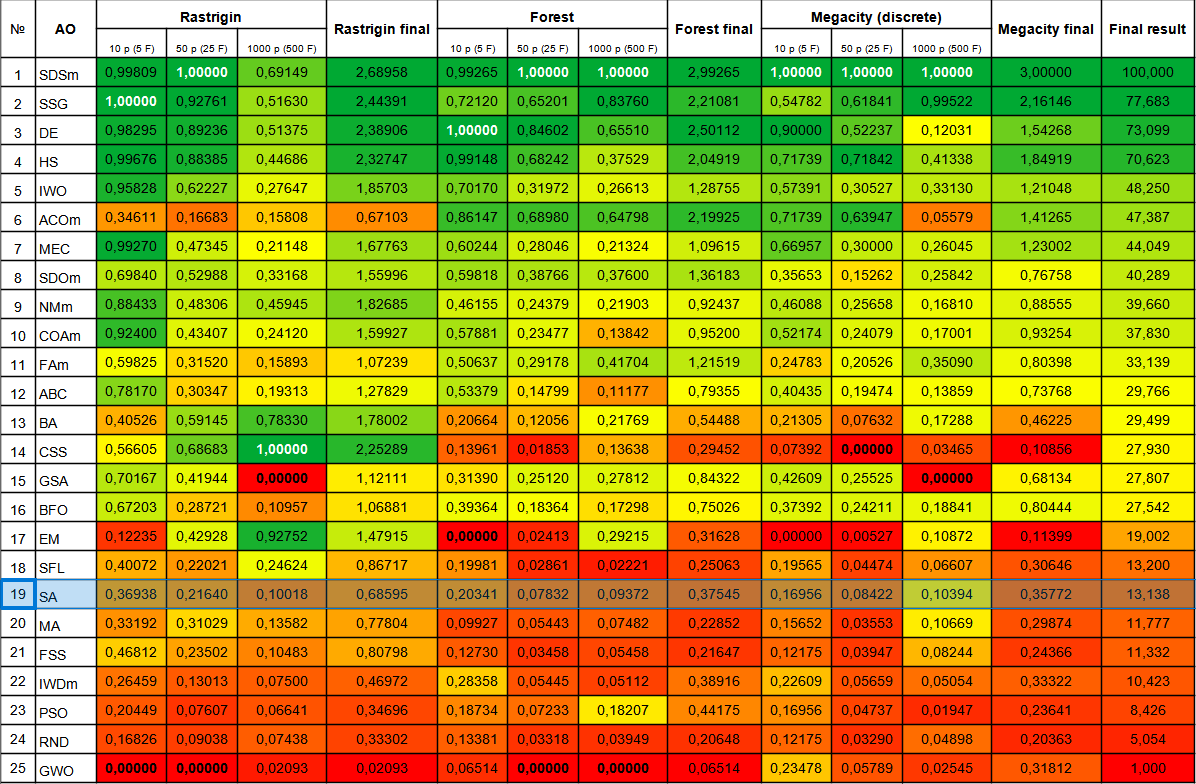
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам.

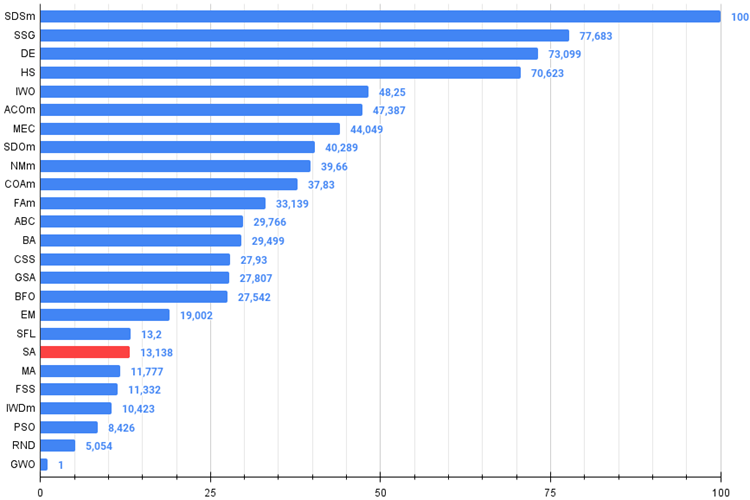
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье).

Плюсы и минусы алгоритма имитации отжига (SA):

Плюсы:

1. Небольшое количество внешних параметров.
2. Высокая скорость работы.
3. Очень простая реализация.
   

Минусы:

1. Неочевидные настройки (непонятно, как и на что влияет температура).
   
2. Очень плохая масштабируемость.
3. Высокий разброс результатов.
4. Склонность к застреванию в локальных экстремумах.
5. Плохая сходимость.

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.