Нейронная сеть на практике: Псевдообратная (I)

Введение

Рад приветствовать всех в новой статье о нейронных сетях.

В предыдущей статье "Нейронная сеть на практике: Функция прямой линии", мы говорили о том, как с помощью алгебраических уравнений можно определить часть искомой информации. Это нужно для того, чтобы составить уравнение, которое в нашем конкретном случае является уравнением прямой линии, поскольку наш небольшой набор данных фактически можно выразить в виде прямой линии. Весь материал, связанный с объяснением работы нейронных сетей, не так просто изложить без понимания уровня знания математики каждого читателя.

Хотя многие могут подумать, что данный процесс будет намного проще и понятнее, особенно с учетом того, что в Интернете появилось множество библиотек, обещающих, что можно разработать собственную нейронную сеть, реальность такова, что всё не так просто.

Я не хочу давать ложных ожиданий, я не буду говорить вам, что, не имея практически никаких знаний или опыта, вы сможете создать нечто действительно практичное, что можно использовать для заработка денег, используя нейронные сети или искусственный интеллект для торговли на рынке. Если кто-то скажет вам это, то он однозначно обманывает.

Создание даже самой простой нейронной сети во многих случаях является сложной задачей. Здесь я хочу показать, как можно создать нечто, что вдохновит вас на более глубокое изучение этой темы. Данный вопрос о нейронных сетях изучается как минимум несколько десятилетий. Как уже упоминалось в трех статьях об искусственном интеллекте, которые предшествовали этой, данная тема гораздо сложнее, чем многие пытаются ее представить.

Использование той или иной функции не означает, что наша нейронная сеть будет лучше или хуже, это просто означает, что мы будем выполнять вычисления с помощью той или иной функции. Это относится к тому, что мы сегодня увидим в этой статье.

По сравнению с первыми тремя статьями из цикла о нейронных сетях, после сегодняшней статьи вы можете задуматься об отказе от изучения этой темы. Но также это может подтолкнуть вас и к более глубокому погружению в тему. Здесь мы рассмотрим, как можно реализовать псевдообратные вычисления с помощью чистого MQL5. Хотя всё выглядит не так страшно, сегодняшний код будет значительно сложнее для новичков, чем хотелось бы, так что не пугайтесь. Изучайте код тщательно и спокойно, без спешки. Я, в свою очередь, постарался сделать код максимально простым. Как таковой, он не рассчитан на эффективное и быстрое выполнение. Наоборот, он стремится быть как можно более обучающим. Однако, поскольку мы будем использовать матричную факторизацию, сам код немного сложнее того, что многие привыкли видеть или программировать.

И да, пока никто не упомянул об этом, я знаю, что в MQL5 есть функция PInv, которая реализует именно то, что мы увидим в данной статье. Я также знаю, что в MQL5 есть операции для работы с матрицами. Но здесь мы не будем выполнять вычисления с использованием матриц, как это определено в MQL5, здесь мы будем использовать массивы, которые хотя и похожи, но имеют несколько иную логику доступа к элементам, находящимся в памяти.

Псевдообратная

Реализация этого расчета не является одной из самых сложных задач, пока всё понятно разработчику. По сути, нам нужно выполнить несколько умножений и другие несложные действия, с использованием всего лишь одной матрицы. В результате будет получена матрица, являющаяся результатом всех внутренних факторизаций псевдообратной.

На данном этапе нам нужно кое-что прояснить. Псевдообратную можно разложить на множители двумя способами: в одном случае значения внутри матрицы не игнорируются, а в другом - для элементов, присутствующих в матрице, используется минимальное лимитное значение. Если этот минимальный предел не достигнут, значение данного элемента в матрице будет равно нулю. Это условие накладываю не я, а правила, заложенные в расчетную модель, используемую всеми программами, которые вычисляют псевдообратную. Каждый из этих случаев преследует вполне конкретную цель. Поэтому то, что мы увидим здесь, - это НЕ окончательный расчет для псевдообратной. Мы проведем расчет, целью которого является получение результатов, аналогичных тем, которые получают такие программы, как MatLab, SciLab и другие, которые также реализуют псевдообратную.

Поскольку MQL5 также может вычислять псевдообратную величину, можно сравнить результаты, полученные с помощью приложения, которое мы реализуем, с теми же результатами, полученными с помощью функции псевдообратной величины библиотеки MQL5. Это необходимо для того, чтобы проверить, всё ли правильно. Таким образом, цель данной статьи - не просто реализовать псевдообратное исчисление, а понять, что стоит за этим исчислением. Это важно, так как знание о том, как работают вычисления, позволит вам понимать, почему и когда следует использовать тот или иной метод в нашей нейронной сети.

Начнем с реализации наиболее простого кода для использования псевдообратной от библиотеки MQL5. Это первый шаг, чтобы убедиться, что расчет, который мы создадим позже, действительно работает. Пожалуйста, не изменяйте код без его предварительной проверки. Если вы измените что-либо перед этим, вы можете получить результаты, отличающиеся от тех, что показаны здесь. Итак, сначала попробуйте код, который я вам покажу. Затем, и только после этого (при желании) измените его, чтобы лучше понять происходящее, но, пожалуйста, не вносите никаких изменений в код до тестирования оригинальной версии.

Оригинальные коды доступны в приложении к этой статье. Давайте рассмотрим первый из них. Ниже приводится полная его версия:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart()
05. {
06.     matrix M_A {{1, -100}, {1, -80}, {1, 30}, {1, 100}};
07. 
08.     Print("Moore–Penrose inverse of :");
09.     Print(M_A);
10.     Print("is :");
11.     Print(M_A.PInv());
12. }
13. //+------------------------------------------------------------------+

Результат его выполнения показан на изображении ниже:

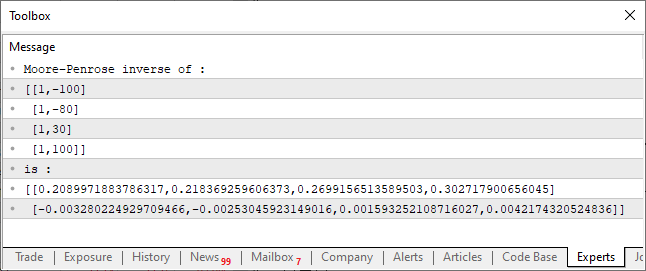
Этот очень простой код, который вы можете видеть выше, способен вычислить псевдообратную матрицу. Результат отображается на консоли, как видно на рисунке. Всё предельно просто. Однако обратите внимание на построение кода, это очень специфический момент в плане создания кода. Используя матрицу и вектор, мы получаем целый ряд возможных и вполне функциональных операций. Однако данные операции включены в стандартную библиотеку MQL5, а также могут быть включены в стандартные библиотеки других языков, в зависимости, конечно, от того, о каком языке программирования идет речь.

Но, несмотря на то, что это очень полезно, бывают случаи, когда нам нужно или хочется, чтобы код выполнялся определенным образом. Либо потому что мы хотим как-то оптимизировать его, либо просто потому что мы не хотим генерировать код, который можно выполнить другим способом. В конце концов, причина не имеет такого большого значения. Хотя многие говорят, что программисты на C / C++ любят изобретать колесо, это не наш с вами случай. В этой статье мы вместе рассмотрим, что скрывается за этими сложными расчетами, которые вы видите. Результат виден вам, но при этом вы совершенно не понимаете, как он получился. И любое исследование без понимания того, откуда взялся именно такой результат, а не какой-либо другой, - это не настоящее исследование, это всего лишь вера. Иными словами, вы видите это и просто верите, но вы не знаете, правда это или ложь, вы просто верите. А настоящие программисты не могут слепо доверять, им нужно потрогать, увидеть, попробовать и испытать, чтобы по-настоящему поверить в то, что они создают. Давайте теперь посмотрим, как был достигнут результат, показанный на рисунке. Для этого перейдем к новой теме.

Понимание вычислений, лежащих в основе псевдообратной

Если для вас достаточно просто увидеть результаты, не зная того, как они были достигнуты, то это прекрасно. Это значит, что данная тема больше не будет вам полезна, и не стоит тратить время на ее прочтение. Но если вы хотите понять, как выполняются расчеты, будьте готовы. Хотя я постараюсь максимально упростить процесс, вам всё равно придется быть внимательными. Я буду по возможности избегать использование сложных формул, но всё же ваше внимание здесь важно, так как код, который мы будем создавать, может выглядеть гораздо более запутанным, чем то, какой он на самом деле. Начнем со следующего: псевдообратная в основном вычисляется с помощью умножения и обратной матрицы.

Это умножение выполняется довольно просто. Многие используют для этого некоторые ресурсы, которые лично мне кажутся ненужными. В статьях, где мы рассказывали о матрицах, был рассмотрен метод выполнения умножения, но этот метод был предназначен для довольно специфического сценария. Здесь нам нужен немного более общий метод, потому что мы должны будем сделать несколько вещей, отличающихся от того, что мы видели в статье о матрицах.

Чтобы было проще, мы будем рассматривать код небольшими фрагментами, каждый из которых объясняет что-то конкретное. Начнем с умножения, которое можно увидеть в приведенном ниже отрывке:

01. //+------------------------------------------------------------------+
02. void Generic_Matrix_A_x_B(const double &A[], const uint A_Row, const double &B[], const uint B_Line, double &R[], uint &R_Row)
03. {
04.     uint A_Line = (uint)(A.Size() / A_Row),
05.          B_Row  = (uint)(B.Size() / B_Line);
06. 
07.     if (A_Row != B_Line)
08.     {
09.         Print("Operation cannot be performed because the number of rows is different from that of columns...");
10.         B_Row = (uint)(1 / MathAbs(0));
11.     }
12.     if (!ArrayIsDynamic(R))
13.     {
14.         Print("Response array must be of the dynamic type...");
15.         B_Row = (uint)(1 / MathAbs(0));
16.     }
17.     ArrayResize(R, A_Line * (R_Row = B_Row));
18.     ZeroMemory(R);
19.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == B_Row ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
20.         for (uint c = 0; c < A_Row; c++)
21.             R[cp] += (A[Ai + c] * B[Bi + (c * B_Row)]);
22. }
23. //+------------------------------------------------------------------+

Глядя на этот фрагмент кода, возможно, вы уже почувствуете себя дезориентированными. Или будете в ужасе от приближающегося конца света. А некоторые могут захотеть попросить прощения у Бога за все свои грехи. Но если отбросить шутки, данный код очень прост, даже если он кажется чем-то необычным или чрезвычайно сложным.

Возможно, он кажется вам сложным, потому что он очень сжатый, и, казалось бы, многие вещи в нем происходят одновременно. Я прошу прощения у начинающих, но те из вас, кто следил за моими статьями, уже знают мою манеру написания кода, и вы увидите, что этот стиль для меня вполне привычен. Давайте теперь разберемся, что здесь происходит. В отличие от кода, показанного выше, этот код является общим, в нем даже есть тест, который проверяет, можем ли мы перемножить две матрицы. Это довольно полезно, хотя и не очень удобно для нас.

Во второй строке мы имеем объявление процедуры. Мы должны быть внимательны, чтобы объявлять и передавать параметры в правильных местах. Затем матрица A будет умножена на матрицу B, и результат помещен в матрицу R. Нам нужно указать, сколько столбцов у матрицы A и сколько строк у матрицы B. Последний аргумент вернет количество столбцов в матрице R. Причина возврата количества столбцов в матрице R будет объяснена позже, поэтому пока не беспокойтесь об этом.

Хорошо. В четвертой и пятой строках мы рассчитаем оставшиеся значения, чтобы нам не пришлось указывать их вручную. Затем, в седьмой строке, мы проводим небольшой тест, чтобы проверить, можно ли перемножать матрицы, поэтому порядок передачи матриц имеет значение. Это не похоже на код для скалярных вычислений; в матричных вычислениях мы должны быть очень осторожны.

Если умножение не удастся выполнить, то в девятой строке мы выведем сообщение на консоль MetaTrader 5. И сразу после этого, в десятой строке, будет выдана ошибка RUN-TIME, что приведет к закрытию приложения, которое пытается выполнить умножение матрицы. Если такая ошибка появляется на консоли, надо будет проверять, не появилось ли также сообщение в девятой строке. Если это произойдет, то ошибка будет не в рассмотренном фрагменте кода, а в месте вызова этого кода. Я знаю, что принудительно закрывать приложение при ошибке RUN-TIME не очень красиво, не говоря уже об элегантности данного подхода, но таким образом мы не дадим приложению показать нам неверные результаты.

Теперь идет часть, которая начинает пугать многих людей: в строке 17 мы выделяем память для хранения всего выведенного результата. Таким образом, матрица R должна иметь динамический вид в программе, который выполняет вызов. Не используйте статический массив, потому что в таком случае строка 12 обнаружит это, и код закроется с ошибкой RUN-TIME с сообщением в строке 14, указывающим на причину закрытия.

Одна из деталей данного способа генерации ошибки заключается в том, что при выполнении приложение попытается выполнить деление на ноль, что заставит процессор запустить внутреннее прерывание. Это прерывание заставит операционную систему принять меры против приложения, которое вызвало прерывание, и заставит его закрыться. Даже если операционная система ничего не предпримет, процессор перейдет в режим прерывания, что приведет к его остановке, даже во встроенной системе, предназначенной для выполнения приложения.

Теперь надо обратить внимание на следующее: здесь я использую трюк, чтобы компилятор не обнаружил, что будет сгенерирована ошибка RUN-TIME. Если бы я делал это не так, как показано в коде, компилятор не смог бы скомпилировать код, даже если строка, вызывающая ошибку RUN-TIME, редко будет выполняться в обычных ситуациях. Если нужно принудительно завершить выполнение программы, можно воспользоваться аналогичным приемом, это всегда срабатывает. Хотя это не очень элегантно, ведь пользователь может злиться на ваше приложение или на вас, написавшего его. Поэтому используйте данный подход с умом.

В строке 18 мы полностью очищаем всё, что находится в выделенной памяти. Обычно некоторые компиляторы выполняют очистку сами, но спустя некоторое время программирования на MQL5 я заметил, что он, естественно, не очищает динамически выделенную память. Я полагаю, что это связано с тем, что динамически выделяемая память в MetaTrader 5 предназначена для использования в индикаторных буферах. А поскольку данные буферы обновляются по мере поступления и вычисления данных, очищать память не имеет смысла. Кроме того, такая чистка отнимает много времени, которое можно потратить на другие задачи. Поэтому именно нам предстоит провести эту очистку и убедиться, что мы не используем ненужные значения в расчетах. Обратите на это внимание в своих программах, если вы пользуетесь динамически выделяемой памятью и она не используется в качестве пользовательских индикаторных буферов.

Идем дальше. Теперь будет самая интересная часть процедуры: умножим матрицу A на матрицу B и поместим результат в матрицу R. Это делается в двух строках. На первый взгляд строка 19 может показаться очень сложной, но давайте разберем ее по порядку. Идея заключается в том, чтобы сделать умножение двух матриц полностью динамичным и универсальным. То есть не имеет значения, больше или меньше строк или столбцов, если процедура дошла до этого момента, матрицы будут перемножены.

Точно так же, как порядок матриц влияет на результат, здесь, в строке 19, порядок выполнения операций также влияет. Но чтобы не продолжать слишком долго, мы упростим объяснение. Чтобы понять, что происходит, давайте прочитаем код так, как он написан, то есть слева направо, термин за термином. Именно так компилятор обрабатывает его для создания исполняемого файла, так что, хотя это может показаться запутанным, это не так. Код очень сжатый, и отличается от того, что использует большинство людей. В любом случае, идея заключается в том, чтобы считать столбец за столбцом из матрицы A и умножить значение, читая строку за строкой из матрицы B. По этой причине порядок следования коэффициентов будет влиять на результат. Вам не нужно беспокоиться о том, как организована матрица B (по строкам или по столбцам), она может быть организована так же, как и матрица A, и эта процедура умножения всё равно будет успешной.

Первая из операций, необходимых для получения значения псевдообратной, готова. Теперь давайте посмотрим на вид вычислений, которые нам нужно выполнить, чтобы знать, что еще нам нужно реализовать. Возможно, нам нужно будет не общее решение, как в случае с умножением, а что-то более конкретное, чтобы помочь определить значение псевдообратной.

Формула для вычисления псевдообратной приведена ниже.

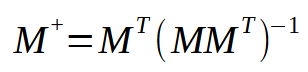
В этой формуле M представляет собой используемую матрицу. Обратите внимание, что она всегда одна и та же. Однако, анализируя данную формулу, мы замечаем, что нам нужно выполнить умножение между исходной матрицей и ее транспонированием. Затем берем результат и находим значение обратной матрицы. И, наконец, мы умножаем транспонированную матрицу на результат инверсии. Звучит просто, не правда ли? Здесь мы можем создать несколько «ярлыков». Разумеется, чтобы создать идеальное сокращение, нам придется смоделировать процедуру, способную вычислять только псевдообратную. Но создание такой процедуры, хотя и несложно, но значительно усложняет объяснение того, как она работает. Чтобы лучше понимать, о чем я говорю, давайте сделаем следующее: я помещу умножение транспонированной и исходной матрицы в одну процедуру. Обычно, когда мы изучаем этот вопрос в университете, нас просят сделать это в два блока. То есть сначала мы создаем транспонированную матрицу, а затем используем процедуру умножения для получения конечного результата. Однако можно создать процедуру, которая не будет включать в себя эти два этапа и выполнит их за один шаг. И хотя реализовать это очень просто, вы увидите, что код может показаться сложным для понимания.

Давайте посмотрим в приведенном ниже отрывке, как выполнить операцию, показанную в скобках на изображении выше.

01. //+------------------------------------------------------------------+
02. void Matrix_A_x_Transposed(const double &A[], const uint A_Row, double &R[], uint &R_Row)
03. {
04.     uint BL = (uint)(A.Size() / A_Row);
05.     if (!ArrayIsDynamic(R))
06.     {
07.         Print("Response array must be of the dynamic type...");
08.         BL = (uint)(1 / MathAbs(0));
09.     }
10.     ArrayResize(R, (uint) MathPow(R_Row = (uint)(A.Size() / A_Row), 2));
11.     ZeroMemory(R);
12.     for (uint cp = 0, Ai = 0, Bi = 0; cp < R.Size(); cp++, Bi = ((++Bi) == BL ? 0 : Bi), Ai += (Bi == 0 ? A_Row : 0))
13.         for (uint c = 0; c < A_Row; c++)
14.             R[cp] += (A[c + Ai] * A[c + (Bi * A_Row)]);
15. }
16. //+------------------------------------------------------------------+

Обратите внимание, что данный фрагмент очень похож на предыдущий, за исключением того, что строка, в которой получается результат, в этих двух фрагментах немного отличается. Тем не менее, этот фрагмент способен выполнить необходимые вычисления для умножения исходной матрицы на ее транспонирование, избавляя нас от создания транспонированной матрицы. Мы можем реализовать данный вид оптимизации. Разумеется, в этой же процедуре можно было бы накопить еще больше функций, например, сгенерировать обратную матрицу или даже выполнить умножение обратной матрицы на транспонирование исходной матрицы. Но, как вы уже представляете, каждый из этих шагов усложняет процедуру, не глобально, но локально. Именно поэтому я предпочитаю знакомить вас с ней понемногу, чтобы вы могли понять, что происходит, и даже опробовать концепции, если захотите.

Но поскольку я не хочу изобретать колесо (и это не является целью данной статьи), мы не будем сваливать всё в одну функцию. Я показал данный отрывок только для того, чтобы вы поняли, что не всё, что мы изучаем в школе, применяется на практике. Часто процессы оптимизируются для решения конкретной задачи. А оптимизация чего-либо позволяет выполнить работу намного быстрее, чем при более обобщенном процессе.

Далее сделаем следующее: у нас уже есть вычисление умножения, теперь нам нужен расчет, который генерирует обратную от полученной матрицы. Существует несколько способов запрограммировать эту обратную. Несмотря на то, что математических способов его выражения немного, методы программирования могут значительно отличаться, делая один алгоритм быстрее другого. Однако то, что нас действительно интересует, - это получение правильного результата, а как мы его генерируем, не так уж и важно.

Для вычисления обратной матрицы я предпочитаю использовать особый метод, предполагающий использование определителя матрицы. На этом этапе можно использовать другой метод для нахождения определителя, но по привычке я предпочитаю использовать метод Саррюса. Я считаю, что так легче программировать. Расскажу для тех, кто с ним не знаком: метод Саррюса вычисляет определитель на основе значений диагоналей. Программировать это довольно интересно. В приведенном ниже фрагменте вы увидите одно предложение о том, как это сделать. Оно работает для любой матрицы, точнее, массива, если он квадратный.

01. //+------------------------------------------------------------------+
02. double Determinant(const double &A[])
03. {
04. #define def_Diagonal(a, b)  {                                                                                                                       \
05.                 Tmp = 1;                                                                                                                            \
06.                 for (uint cp = a, cc = (a == 0 ? 0 : cp - 1), ct = 0; (a ? cp > 0 : cp < A_Row); cc = (a ? (--cp) - 1 : ++cp), ct = 0, Tmp = 1)     \
07.                 {                                                                                                                                   \
08.                     do {                                                                                                                            \
09.                         for (; (ct < A_Row); cc += b, ct++)                                                                                         \
10.                             if ((cc / A_Row) != ct) break; else Tmp *= A[cc];                                                                       \
11.                         cc = (a ? cc + A_Row : cc - A_Row);                                                                                         \
12.                     }while (ct < A_Row);                                                                                                            \
13.                     Result +=  (Tmp * (a ? -1 : 1));                                                                                                \
14.                 }                                                                                                                                   \
15.                             }
16. 
17.     uint A_Row, A_Size = A.Size();
18.     double Result, Tmp;
19. 
20.     if (A_Size == 1)
21.         return A[0];
22.     Tmp = MathSqrt(A_Size);
23.     A_Row = (uint)MathFloor(Tmp);
24.     if ((A_Row != (uint)MathCeil(Tmp)) || (!A_Size))
25.     {
26.         Print("The matrix needs to be square");
27.         A_Row = (uint)(1 / MathAbs(0));
28.     }
29.     if (A_Row == 2)
30.         return (A[0] * A[3]) - (A[1] * A[2]);
31.     Result = 0;
32. 
33.     def_Diagonal(0, A_Row + 1);
34.     def_Diagonal(A_Row, A_Row - 1);
35. 
36.     return Result;
37. 
38. #undef def_Diagonal
39. }
40. //+------------------------------------------------------------------+

Этот прекрасный фрагмент, который можно видеть здесь, способен установить значение определителя матрицы. Здесь мы делаем нечто настолько замечательное, что код даже не требует пояснений.

Итак, в четвертой строке у нас определен макрос. Данный макрос способен обойти массив, или, в нашем случае, массив внутри массива, по диагонали. Всё именно так. Математика, заложенная в этом коде, позволяет вычислять значение диагоналей одну за другой, как в направлении главной диагонали, так и в направлении вторичной диагонали, и все это элегантно и эффективно. Обратите внимание, что всё, что нам нужно указать в коде, - это массив, содержащий нашу матрицу, а возвращаемое значение будет определителем этой матрицы. Однако метод Саррюса, реализованный в этом коде, имеет ограничение: если у матрицы размерность 1x1, определителем является сама матрица, и она возвращается сразу, что можно увидеть в строке 21. Если массив пуст или не является квадратным, мы выдадим ошибку RUN-TIME в строке 27, не позволяя коду выполняться дальше. Если у матрицы размер 2x2, то вычисление диагоналей не проходит через макрос, а выполняется перед ним в строке 30. Для любого другого случая вычисление определителя идет через макрос: сначала в строке 33 вычисляется главная диагональ, а в строке 34 - второстепенная диагональ. Если вы не поняли, что происходит, посмотрите на рисунок ниже, где я наглядно всё показываю. Это для тех, кто не знаком с методом Саррюса.

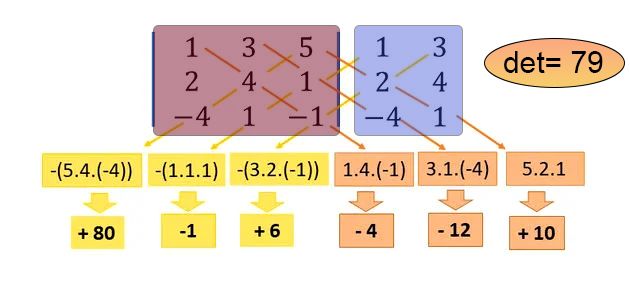
На этом изображении область, выделенная красным цветом, представляет собой матрицу, для которой мы хотим вычислить определитель, а область, выделенная синим цветом, является виртуальной копией некоторых элементов матрицы. Код макроса выполняет именно такое вычисление, показанное на рисунке, возвращая определитель, который в данном примере равен 79.

Заключительные идеи

Ну что ж, дорогой читатель, мы подошли к концу очередной статьи. Однако мы еще не реализовали все необходимые процедуры для вычисления значения псевдообратной. Об этом мы расскажем в следующей статье, где мы увидим приложение, которое будет выполнять эту задачу. Хотя можно сказать, что мы можем использовать код, приведенный в приложении к данной статье, проблема в том, что он не дает нам свободы в использовании любого вида структуры. Чтобы использовать псевдообратную (PInv), нам действительно нужно работать с одним видом матрицы. В той, что я показываю в качестве объяснения вычислений, мы можем использовать любой вид моделирования данных. Нужно лишь внести необходимые изменения, чтобы иметь возможность использовать всё, что хочется.  Так что до встречи в следующей статье.