Популяционные алгоритмы оптимизации: Алгоритм интеллектуальных капель воды (Intelligent Water Drops, IWD)

MetaTrader 5 — Примеры | 21 ноября 2023, 14:49

656

Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Модифицированная версия SDSm
4. Результаты тестов

1. Введение

Русло реки — это одно из самых изящных творений природы, в котором каждая капля воды играет свою роль в уникальном танце жизни. С каждым километром пути река формирует свои новые границы, величественно излучая свою энергию и мудрость. Подобно этому природному явлению, алгоритм оптимизации "интеллектуальные капли воды" стремится обрести гармонию и совершенство в своем функционировании, используя принципы самоорганизации и взаимодействия между частицами. Этот алгоритм отражает величие природы и ее умение создавать и сохранять баланс, что делает его важным инструментом в области оптимизации процессов и решения сложных задач.

Любая река имеет собственную долину, образованную эрозионными процессами под действием поверхностных и подземных вод. Самая низкая часть этой долины, пробитая в грунте речным потоком, и называется руслом. Именно по нему осуществляется перемещение основной части речного потока и донных наносов.

Рельеф русла пребывает в постоянном изменении. Захватываемые водой камни и песок формируют гряды и перекаты, пересекающие русло под острым углом. На изгибах реки могут промывать новый путь и образовывать старицы – участки старого русла, которые постепенно превращаются в озеро со своей экосистемой, а позже высыхают или сохраняются в виде болота.

Наблюдая за реками в природе, мы замечаем множество изгибов и поворотов на их пути. Возникает вопрос, почему были созданы эти повороты и есть ли за ними какая-либо логика или разум? И если это так, можем ли мы использовать механизмы, которые происходят в реках, и, как следствие, можем ли мы проектировать и разрабатывать интеллектуальные алгоритмы на их основе? Алгоритм IWD - это попытка моделирования некоторых процессов, которые происходят в естественных реках, и затем реализации их в виде алгоритма.

Алгоритм интеллектуальных капель воды - один из относительно недавно разработанных алгоритмов в области роевого интеллекта: этот алгоритм имитирует динамику речных систем. IWD - это популяционный алгоритм, в котором каждая капля представляет собой решение, а совместное использование капель во время поиска приводит к лучшим решениям.

В 2007 году иранский ученый Хамед Шах-Хоссейни (Hamed Shah-Hosseini) разработал алгоритм поведения интеллектуальных капель. В IWD алгоритме, несколько искусственных капель воды, которые в результате взаимодействия способны менять свое окружение таким образом, что находят оптимальный путь по пути наименьшего сопротивления. IWD алгоритм – это конструктивный популяционно - ориентированный алгоритм оптимизации.

2. Описание алгоритма

IWD - это модель, в которой водяные капли находят оптимальный путь к месту назначения, изменяя русло реки. Этому способствуют три важных параметра. За счет собственной скорости капли способны захватывать почву со дна реки, и чем выше скорость, тем большее количество почвы каждая капля способна унести с собой, соответственно, тем свободнее станет путь для последующих агентов. Скорость потока растет там, где нет почвы, которую необходимо расчищать. Оптимальным можно назвать такой путь, на котором встречается меньше всего почвы и где можно развить наибольшую скорость. С помощью IWD можно реализовать стратегию оптимизации, когда случайные агенты интеллектуально взаимодействуют друг с другом таким образом, что совместными усилиями меняют русло реки и создают оптимальный путь, на котором почва вообще не встречается и скорость потока агентов становится наивысшей из возможных.

Основные принципы:

капля воды предпочитает путь с меньшим количеством почвы, чем пути с большим количеством почвы
капля воды предпочитает более короткий путь, когда приходится выбирать между несколькими маршрутами на пути от источника к месту назначения
лёгкость или твёрдость пути определяется количеством почвы на этом пути, путь с большим уровнем почвы считается трудным путем, тогда как путь с меньшим уровнем почвы считается лёгкий путем.

В природе множество капель воды наблюдаются в реках, где они образуют огромные массы (рои капель воды). Пути, которыми текут природные реки, были созданы роями из капель воды. Рои капель воды (реки) являются частью окружающей среды, которая была значительно изменена роем, а также подвержена изменениям в будущем. Более того, сама среда оказывает существенное влияние на пути следования капель воды. Им оказывают сопротивление берега реки. Например, рою капель воды сопротивляются больше те части окружающей среды, из которых состоит жесткий грунт, чем части из мягкого грунта. Естественное русло реки является результатом конкуренции между каплями воды и окружающей средой, которая оказывает сопротивление движению капель воды.

Одной из характеристик капли воды, текущей в реку, является её скорость. Другая характеристика - почва, определённое количество которой может каждая река нести. Таким образом, капля воды способна переносить некоторое количество почвы с одного места на другое место. Эта почва передается от быстрых частиц к медленным частицам. Т.е. почва, захваченная рекой вместе с быстрым течением, осядет в месте с медленным течением.

Три очевидных изменения произойдет в течение этого переходного периода:

скорость капли воды увеличивается
насыщенность грунтом капли воды увеличивается
между этими двумя точками, количество грунта в русле уменьшается (точками графа)

Выше было отмечено, что каждая капля воды имеет свою скорость. Эта скорость играет непосредственную роль в сборе почвы в русле реки. Капля воды с высокой скоростью собирает больше грунта, чем капля с меньшей скоростью. Таким образом, капли воды с большей скоростью удаляют больше грунта со дна реки, чем капли воды с меньшей скоростью. Удаление грунта, таким образом, связано со скоростью капли воды.

Скорость капли воды возрастает на пути с низким уровнем почвы больше, чем на пути с высоким уровнем грунта. Таким образом, путь с небольшим количеством грунта позволяет текущей капле воды собрать больше почвы и получить большую скорость, в то время как путь с большими уровнями грунта приводит к уменьшению скорости.

Итак, в алгоритме IWD капли характеризуются двумя основными свойствами:

скорость
почва

Оба этих свойства могут изменяться в течение работы алгоритма. Капли в IWD двигаются от источника к месту назначения и начинает свой путь с начальной скоростью и нулевым грунтом. Во время своего путешествия капли перемещаются в окружающей среде, из которой удаляют некоторое количество почвы, и могут набирать некоторую скорость. Предполагается, что IWD выполняется итерационно. От текущего местоположения до следующего скорость капли увеличивается на величину, нелинейно пропорциональную обратной величине грунта между двумя местоположениями:

vel = vel (t-1) + Av / [Bv + Cv * soil^2(i,j)]

где: Av, Bv, Cv - коэффициенты скорости (входные параметры), а soil (i,j) - количество грунта между вершинами графа.

Следовательно, путь с меньшим грунтом позволяет капле IWD двигаться быстрее, чем путь с большим количеством грунта.

Капля IWD собирает грунт во время своего путешествия по окружающей среде. Этот грунт удаляется с дорожки, соединяющей два места. Количество грунта, добавляемого в каплю IWD, нелинейно пропорционально времени, необходимому для перемещения IWD от его текущего местоположения к следующему местоположению. Этот временной интервал вычисляется по простым законам физики для линейного движения:

time(i,j,vel) = R / vel

где: R - расстояние между двумя точками.

Количество грунта, добавляемого в каплю:

dSoil(i,j) = As / [Bs + Cs * time(i,j,vel)]

где: As, Bs, Cs - коэффициенты намыва грунта.

А новое количество грунта на пути между точками будет выглядеть так:

soil (i+1,j+1) = Po * soil(i,j) + Pn * dSoil(i,j)

где: Po и Pn - коэффициенты процесса изменения количества грунта.

Таким образом, время, затрачиваемое на движение, обратно пропорционально скорости движения и прямо пропорционально расстоянию между двумя точками. Можно сказать, что грунт является количественным показателем информации об окружающей среде. Эти формулы определяют предпочтение капель выбирать пути с низким уровнем грунтования вместо путей с высоким уровнем грунтования. Такой выбор пути осуществляется путем применения равномерного случайного распределения к доступным путям. Вероятность выбора следующего пути обратно пропорциональна уровню грунтования доступных путей. Поэтому пути с более низким уровнем грунтования имеют больше шансов быть выбранными каплями IWD.

Исходный алгоритм IWD был разработан автором с целью решения задач поиска оптимальных путей, таких как задачи поиска на графах и задачи коммивояжера. Однако, данный алгоритм не является подходящим для решения задач, которые мы рассматриваем в наших тестах. Поэтому необходимо адаптировать алгоритм IWD для решения наших задач оптимизации. В отличие от этого, алгоритмы, описанные в статьях "Популяционные алгоритмы оптимизации", способны решать задачи любого типа, включая задачи поиска на графах. В предыдущих статьях уже был представлен аналогичный узкоспециализированный алгоритм, который требовал переделки, а именно "Муравьиная колония (ACO)".

Для адаптации IWD к способности решать любые задачи оптимизации, а также для участия IWD в соревнованиях популяционных алгоритмов, необходимо сначала определить, как применять процесс наноса и перемещения грунта. Мы не можем следовать подходу, использованному в алгоритме ACO, где феромоны эквивалентны значению функции приспособленности. В случае IWD грунт является динамическим показателем и не соответствует пропорционально приспособленности.

Возникла идея разделить координаты на секторы, аналогично разбиению долины реки на участки с одинаковой площадью. Идея заключается в том, что если положение капли (агента) улучшается, то количество грунта на соответствующих секторах по всем координатам уменьшается. Количественное изменение грунта будет определяться разницей в изменении функции приспособленности за две последние итерации, нормированной по всем каплям на разницу между максимальным и минимальным изменением приспособленности.

Поведение движения капель будет основываться на случайном выборе секторов, которые имеют наименьшее количество грунта, т.е., где вероятность будет пропорциональна количеству грунта на соотвествующем секторе. Лучшие координаты на всех участках будем хранить в глобальном хранилище "русло". После того как капля выберет сектор будет предпринята пыпытка улучшить координату, сохраненную в хранилище таким образом, что вероятность новой координаты будет подчиняться квадратичному закону, по которому новая координата будет лежать ближе к прежней координате с большей вероятностью, чем дальше. Ширина участка в пределах которого будет лежать новая координата определеяется внешним параметром и выражается в частях от размера сектора. Иллюстрация разбивки координаты на секторы и распределение вероятности новой координаты показана на рисунке 1.

iwd

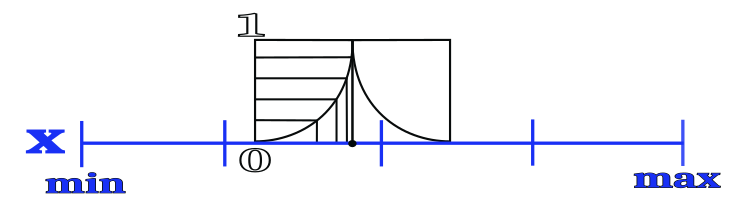
Рисунок 1. Разбивка координаты на секторы и распределение вероятности выбора новой координаты в окрестностях лучшей известной.

На основании вышеизложенных положений и понятий алгоритма IWD мы можем составить псевдокод с разбивкой по шагам:

Случайная генерация капель (первая итерация)
Вычислить ФФ
Обновить лучший глобальный результат
Случайная генерация капель (вторая итерация)
Вычислить ФФ
Обновить лучший глобальный результат
Вычислить изменение высоты каждой капли (текущая высота и предыдущая)
Обновить высоты по секторам
Новые капли (вероятностно выбрать сектор, капля в окрестностях известной ямы)
Вычислить ФФ
Обновить лучший глобальный результат
Повторить с п. 7

Переходим к разбору кода.

Поискового агента "капля" представим в виде структуры S_Drop, содержащая следующие поля:

Init (int coords): функция инициализирует объект структуры, принимая в качестве аргумента количество координат "coords". Внутри функции происходит изменение размеров массивов "c" и "rSection" до указанного количества координат, а также инициализация переменных "f", "fPrev" и "altChange"
c: массив для хранения координат
rSection: массив для хранения секций реки
f: показатель пригодности (fitness) для данной капли (drop)
fPrev: предыдущее значение показателя пригодности
altChange: изменение высоты

struct S_Drop
{
  void Init (int coords)
  {
    ArrayResize (c,            coords);
    ArrayResize (rSection,     coords);
    f         = -DBL_MAX;
    fPrev     = -DBL_MAX;
    altChange = 0.0;
  }
  double c            []; //coordinates
  int    rSection     []; //river section          (количество ячеек: количество координат, значение ячеек: индекс сектора на координате)
  double f;               //fitness
  double fPrev;           //previous fitness
  double altChange;       //change in altitude
};

Нам понадобится хранилище, где будет описание реки (лучшие координаты глубин и, собственно, сами глубины), так и назовём структуру, S_Riverbed:

riverbedDepth: массив для хранения глубин русла реки, количество ячеек в массиве соответствует количеству секторов на координате, а значение каждой ячейки - глубина русла на соответствующем секторе
coordOnSector: массив для хранения конкретной координаты самого глубокого места на секторе, количество ячеек в массиве соответствует количеству секторов на координате, а значение каждой ячейки - координата на соответствующем секторе.

//——————————————————————————————————————————————————————————————————————————————
struct S_Riverbed //русло реки
{
  double riverbedDepth []; //riverbed depth 
  double coordOnSector []; //coordinate on the sector
};
//——————————————————————————————————————————————————————————————————————————————

Объявим класс C_AO_IWDm (m - модифицированный), который реализует алгоритм искусственной оптимизации на основе водных капель. Вот описание каждого элемента класса:

Свойства класса:

cB: массив для хранения лучших координат
fB: хранит значение целевой функции для лучших координат
p: массив для частиц (водных капель)
массивы "rangeMax", "rangeMin" и "rangeStep" используются для определения диапазона поиска

Методы класса:

Init: инициализирует объект класса C_AO_IWDm с заданными параметрами: "coordsP" - количество координат, "popSizeP" - размер популяции, "sectorsNumberP" - количество секторов, "waterViscosityP" - вязкость воды.
Moving: выполняет перемещение водных капель
Revision: выполняет ревизию состояния водных капель

Приватные свойства класса:

coords: количество координат
popSize: количество капель
sectorsNumbe: количество секторов
waterViscosity: коэффициент вязкости воды, в частях от размера сектора
sectorSpace : размер сектора
rb: массив по координатам, для описания русла реки
iterationCounter
revision: флаг, указывающий на необходимость ревизии

Приватные методы класса:

SeInDiSp: вычисляет новое значение координаты в заданном диапазоне с заданным шагом
RNDfromCI: генерирует случайное число в заданном интервале
Scale: масштабирование числа в указанный диапазон

//——————————————————————————————————————————————————————————————————————————————
class C_AO_IWDm
{
  //----------------------------------------------------------------------------
  public: double cB  [];       //best coordinates
  public: double fB;           //FF of the best coordinates
  public: S_Drop p   [];       //particles (drops)

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,          //coordinates number
                     const int    popSizeP,         //population size
                     const int    sectorsNumberP,   //sectors number
                     const double waterViscosityP); //water viscosity (>= 1)

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;           //coordinates number
  private: int    popSize;          //population size

  private: int    sectorsNumber;    //sectors number
  private: double waterViscosity;   //water viscosity
  private: double sectorSpace [];   //sector space
  private: S_Riverbed      rb [];   //riverbed

  private: int    iterationCounter;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Метод Init инициализирует объект класса C_AO_IWDm с заданными параметрами: количество координат, количество капель, количество секторов, вязкость воды.

Этот метод выполняет следующие действия:

1. Сбрасывает генератор случайных чисел.
2. Инициализирует значение целевой функции "fB" значением "-DBL_MAX"
3. Устанавливает счетчик итераций в ноль
4. Устанавливает количество координат "coords" и размер популяции "popSize" на заданные значения
5. Устанавливает количество секторов "sectorsNumber" и вязкость воды "waterViscosity" на заданные значения
6. Изменяет размер массива "sectorSpace" на "coord"
7. Изменяет размер массива "p" на "popSize" и инициализирует каждую водную каплю в массиве "p"
8. Изменяет размеры массивов "rangeMax", "rangeMin", "rangeStep" и "cB" на "coords"
9. Изменяет размер массива "rb" на "coords" и инициализирует каждый элемент массива "rb", включая массивы "riverbedDepth" и "coordOnSector", устанавливая их значения по умолчанию

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWDm::Init (const int    coordsP,          //coordinates number
                      const int    popSizeP,         //population size
                      const int    sectorsNumberP,   //sectors number
                      const double waterViscosityP)  //water viscosity (>= 1)
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB               = -DBL_MAX;
  iterationCounter = 0;

  coords  = coordsP;
  popSize = popSizeP;

  sectorsNumber  = sectorsNumberP;
  waterViscosity = waterViscosityP;
  ArrayResize (sectorSpace, coords);

  ArrayResize (p, popSize);
  for (int i = 0; i < popSize; i++) p [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (rb,        coords);
  for (int i = 0; i < coords; i++)
  {
    ArrayResize     (rb [i].riverbedDepth, sectorsNumber);
    ArrayResize     (rb [i].coordOnSector, sectorsNumber);
    ArrayInitialize (rb [i].riverbedDepth, 0.0);
    ArrayInitialize (rb [i].coordOnSector, -DBL_MAX);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Рассмотрим по частям метод Moving ().

Этот блок кода выполняется только на первой и второй итерациях. Он вычисляет и устанавливает размер каждого сектора "sectorSpace" для каждой координаты. Размер сектора определяется путем разделения диапазона значений "rangeMax - rangeMin" на количество секторов "sectorsNumber".

Далее выполняется инициализация капель начальными значениями на основе случайных значений в заданных диапазонах с равномерным распределением.

//----------------------------------------------------------------------------
  if (iterationCounter == 0)
  {
    for (int i = 0; i < coords; i++) sectorSpace [i] = (rangeMax [i] - rangeMin [i]) / sectorsNumber;
  }

  //1,4-------------------------------------------------------------------------
  if (iterationCounter == 0 || iterationCounter == 1)
  {
    double min = 0.0;
    double max = 0.0;
    int    s   = 0;

    for (int i = 0; i < popSize; i++)
    {
      p [i].fPrev = p [i].f;

      for (int c = 0; c < coords; c++)
      {
        s = (int)(RNDfromCI (0, sectorsNumber));
        if (s >= sectorsNumber) s = sectorsNumber - 1;

        p [i].rSection [c] = s;

        min = rangeMin [c] + sectorSpace [c] * s;
        max = min + sectorSpace [c];

        p [i].c [c] =  SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < popSize; i++) p [i].fPrev = p [i].f;

    return;
  }

Далее фрагмент кода выполняет вычисление и нормализацию изменений высоты "altChange" для каждой капли в популяции. Единственная тонкость в этом коде заключается в проверке равенства максимального и минимального изменения высоты, чтобы избежать деления на "0", в этом случае принимаем, что никаких изменений в высотах капель не было.

Значение "altChange" для каждой капли вычисляется как нормализованное значение, которое приведено к диапазону от 0 до 1. Нормализация выполняется путем вычитания "minAltChange" из "altChange" и деления результата на разницу между "maxAltChange" и "minAltChange".

//7---------------------------------------------------------------------------
double maxAltChange = -DBL_MAX;
double minAltChange =  DBL_MAX;
double altChange    = 0.0;
double randSC       = 0.0; //random selection component
double maxRC        = 0.0;
double nowRC        = 0.0;
int    indSector    = 0;

for (int i = 0; i < popSize; i++)
{
  altChange = fabs (p [i].f - p [i].fPrev);
  p [i].altChange = altChange;
  if (altChange < minAltChange) minAltChange = altChange;
  if (altChange > maxAltChange) maxAltChange = altChange;
}

if (minAltChange == maxAltChange)
{
  for (int i = 0; i < popSize; i++)
  {
    p [i].altChange = 0.0;
  }
}
else
{
  for (int i = 0; i < popSize; i++)
  {
    altChange = p [i].altChange;
    p [i].altChange = (altChange - minAltChange) / (maxAltChange - minAltChange);
  }
}

Следующий фрагмент кода обновляет глубину русла реки для каждой координаты, если текущее значение фитнес функции больше предыдущего значения для соответствующей капли. Это позволяет учесть изменения высоты и влиять на форму русла реки. Таким образом, каждый раз, когда капля улучшила свое положение мы считаем, что русло реки изменилось.

//8---------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > p [i].fPrev)
    {
      for (int c = 0; c < coords; c++)
      {
        rb [c].riverbedDepth [p [i].rSection [c]] += p [i].altChange;
      }
    }
  }

В следующем фрагменте кода выполняется два основных действия по изменению координат агентов, обеспечивающих стратегию поиска:

капля выбирает другую каплю случайным образом по популяции и заимствует у нее номер сектора, обеспечивается комбинаторные свойства алгоритма
капля выбирает случайным образом сектор реки пропорционально известной глубины в каждом секторе

Как только сектор выбран производим генерацию новой координаты для капли с равномерным распределением в случае если сектор был взят у другой капли, и с распределением квадратичной функции, если сектор был выбран из информации, хранящейся в русле реки. Полученное значение по каждой координате приводим в допустимый диапазон.

//9---------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, popSize));
      if (n >= popSize) n = popSize - 1;

      if (p [n].f > p [i].f)
      {
        p [i].rSection [c] = p [n].rSection [c];

        min = rangeMin [c] + sectorSpace [c] * p [i].rSection [c];
        max = min + sectorSpace [c];

        p [i].c [c] = SeInDiSp (RNDfromCI (min, max), rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        randSC = RNDfromCI (0.0, 1.0);

        nowRC = rb [c].riverbedDepth [0] * randSC;
        maxRC = nowRC;
        indSector = 0;

        for (int r = 1; r < sectorsNumber; r++)
        {
          nowRC = rb [c].riverbedDepth [r] * randSC;
          if (nowRC > maxRC)
          {
            maxRC     = nowRC;
            indSector = r;
          }
        }

        if (rb [c].coordOnSector [indSector] == -DBL_MAX)
        {
          min = rangeMin [c] + sectorSpace [c] * indSector;
          max = min + sectorSpace [c];

          p [i].c [c] = RNDfromCI (min, max);
        }
        else
        {
          double x = RNDfromCI (-1.0, 1.0);
          double y = x * x;
          double pit = 0.0;

          double dif = Scale (y, 0.0, 1.0, 0.0, sectorSpace [c] * waterViscosity, false);

          pit = rb [c].coordOnSector [indSector];
          pit += x > 0.0 ? dif : -dif;

          p [i].c [c] = pit;
        }

        min = rangeMin [c] + sectorSpace [c] * indSector;
        max = min + sectorSpace [c];

        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        p [i].rSection [c] = indSector;
      }
    }
  }

Далее обновляем предыдущее значение приспособленности "fPrev" для каждой водной капли, если текущее значение целевой функции `f` больше предыдущего значения. Это позволяет отслеживать изменение целевой функции и использовать эту информацию в алгоритме для принятия решений о выборе следующего шага.

for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > p [i].fPrev)
    p [i].fPrev = p [i].f;
  }

И в завершение - метод Revision. Он предназначен для обновления наилучшего решения "cB" и соответсвующего ему значения фитнес функции. Если на текущей итерации найдено решение лучше, то сохраняем координату соответсвующего сектора. Таким образом русло реки помнит самые глубокие места в каждом секторе по каждой координате. В этом методе увеличиваем счетчик итераций "iterationCounter" на единицу, что бы в методе Moving мы могли ориентироваться и выполнять соответсвующие итерациям действия.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWDm::Revision ()
{
  //3,6,11----------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > fB)
    {
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);

      for (int c = 0; c < coords; c++)
      {
        rb [c].coordOnSector [p [i].rSection [c]] = p [i].c [c];
      }
    }
    else
    {
      for (int c = 0; c < coords; c++)
      {
        if (rb [c].coordOnSector [p [i].rSection [c]] == -DBL_MAX)
        {
          rb [c].coordOnSector [p [i].rSection [c]] = p [i].c [c];
        }
      }
    }
  }

  iterationCounter++;
}
//——————————————————————————————————————————————————————————————————————————————

3. Модифицированная версия SDSm

Результаты работы алгоритма IWDm мы рассмотрим позднее, но они натолкнули на мысль попробовать улучшить другой алгоритм, лучший в рейтинге - SDS, благо и в IWDm и в SDS используются похожие сущности (сектора и рестораны соответсвенно). Метод, который использовался в IWD, а именно - использование уточнения координаты с момощью распределения вероятности по кватратичной функции, помог сделать SDS еще лучше: методика уточнения лучшего положения оказала большое влияние на итоговые результаты тестирования. Единственное отличие - в SDSm распределение усекается, если оно выходит на соседний ресторан.

Изменения были внесены в метод Revision алгоритма SDS, и из-за существенных изменений в распределении новых координат в пределах ресторана (ранее оно было равномерным) и результатов тестирования алгоритму присвоен индекс "m".

В коде видим, что теперь за распределение случайной величины отвечает функция Research, которая принимает в качестве аргументов коэффициент ширины распределения, адрес ресторана, размер ресторана, минимально возможное значение по координате, шаг по координате, приспособленность на предыдущем шаге и координату, которую пытаемся улучшить.

В алгоритме SDSm мы пытаемся улучшить три вида координат (блюд в ресторанах):

координату кандидата-собеседника
лучшую координату в случайно выбранном ресторане (так же как и в IWDm для русла реки в SDSm мы храним лучшие координаты для всех ресторанов - это как хранение в списке лучших блюд во всех ресторанах города)
свою собственную координату для соответсвующего ресторана

Коэффициенты ширины распределения вероятности можно было бы вынести во внешние параметры, но я не стал это делать, установил лучшие, на мой взгляд, значения.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDSm::Revision ()
{
  /*
  тут код старый, без изменений
  */

  for (int i = 0; i < populationSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      n = (int)(RNDfromCI (0, populationSize));
      if (n >= populationSize) n = populationSize - 1;

      if (cands [n].fPrev > cands [i].fPrev)
      {
        cands [i].raddr [c] = cands [n].raddrPrev [c];

        Research (0.25,
                  cands     [i].raddr [c],
                  restSpace [c],
                  rangeMin  [c],
                  rangeStep [c],
                  cands     [n].cPrev [c],
                  cands     [i].c     [c]);
      }
      else
      {
        rnd = RNDfromCI (0.0, 1.0);

        if (rnd < probabRest)
        {
          n = (int)(RNDfromCI (0, restNumb));
          if (n >= restNumb) n = restNumb - 1;
          cands [i].raddr [c] = n;

          Research (1.0,
                    cands     [i].raddr         [c],
                    restSpace [c],
                    rangeMin  [c],
                    rangeStep [c],
                    rb        [c].coordOnSector [n],
                    cands     [i].c             [c]);
        }
        else
        {
          cands [i].raddr [c] = cands [i].raddrPrev [c];

          Research (0.25,
                    cands     [i].raddr [c],
                    restSpace [c],
                    rangeMin  [c],
                    rangeStep [c],
                    cands     [i].cPrev [c],
                    cands     [i].c     [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

А вот та самая "волшебная" функция Research, которая позволила улучшить прежнего лидера тестирования на более чем 12%.

Функция делает следующее:

генерируется случайное число в диапазоне [-1.0;1.0],
полученное значение масштабируется в приращение соответсвующее размеру ресторана с коэффициентом масштаба распределения
прибавляется к текущей улучшаемой координате
определяются границы ресторана
число переводится в допустимые значения в соответствии с шагом оптимизируемого параметра с обрезкой по границам ресторана

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDSm::Research (const double  ko,
                          const int     raddr,
                          const double  restSpaceI,
                          const double  rangeMinI,
                          const double  rangeStepI,
                          const double  pitOld,
                          double       &pitNew)
{
  double x = RNDfromCI(-1.0, 1.0);
  double y = x * x;
  double pit = pitOld;
  double min = 0.0;
  double max = 0.0;

  double dif = Scale(y, 0.0, 1.0, 0.0, restSpaceI * ko, false);

  pit += x > 0.0 ? dif : -dif;

  min = rangeMinI + restSpaceI * raddr;
  max = min + restSpaceI;

  pitNew = SeInDiSp (pit, min, max, rangeStepI);
}
//——————————————————————————————————————————————————————————————————————————————

4. Результаты тестов

Распечатка работы алгоритма IWD на тестовом стенде:

C_AO_IWDm:50;10;3.0
=============================
5 Rastrigin's; Func runs 10000 result: 63.304838882364926
Score: 0.78438
25 Rastrigin's; Func runs 10000 result: 49.20424466627239
Score: 0.60967
500 Rastrigin's; Func runs 10000 result: 39.68464591598694
Score: 0.49172
=============================
5 Forest's; Func runs 10000 result: 0.6975685023058024
Score: 0.39458
25 Forest's; Func runs 10000 result: 0.19878497533879688
Score: 0.11244
500 Forest's; Func runs 10000 result: 0.0569274044494088
Score: 0.03220
=============================
5 Megacity's; Func runs 10000 result: 3.44
Score: 0.28667
25 Megacity's; Func runs 10000 result: 1.088
Score: 0.09067
500 Megacity's; Func runs 10000 result: 0.28480000000000005
Score: 0.02373
=============================
All score: 2.82606

Результаты, мягко говоря, ниже средних по сравнительной таблице.

Распечатка работы алгоритма SDSm на тестовом стенде:

C_AO_SDSm:100;100;0.05
=============================
5 Rastrigin's; Func runs 10000 result: 80.65976429448276
Score: 0.99942
25 Rastrigin's; Func runs 10000 result: 79.95659847225565
Score: 0.99071
500 Rastrigin's; Func runs 10000 result: 57.23107170601535
Score: 0.70913
=============================
5 Forest's; Func runs 10000 result: 1.7241883676504082
Score: 0.97529
25 Forest's; Func runs 10000 result: 1.497160007591401
Score: 0.84687
500 Forest's; Func runs 10000 result: 0.29481739063639945
Score: 0.16676
=============================
5 Megacity's; Func runs 10000 result: 10.559999999999999
Score: 0.88000
25 Megacity's; Func runs 10000 result: 6.824000000000001
Score: 0.56867
500 Megacity's; Func runs 10000 result: 1.2384
Score: 0.10320
=============================
All score: 6.24004

А вот результаты SDSm действительно впечатляют.

По анимированной визуализации алгоритма IWDm заметна некоторая степень способности кластеризовать потенциально хорошие области поиска, особенно это заметно по функции Rastrigin. Но по продолжительным пологим участкам графика сходимости заметно так же и застревание алгоритма.

rastrigin

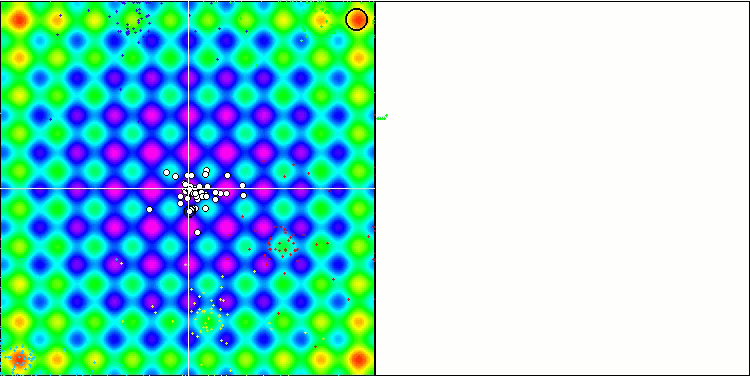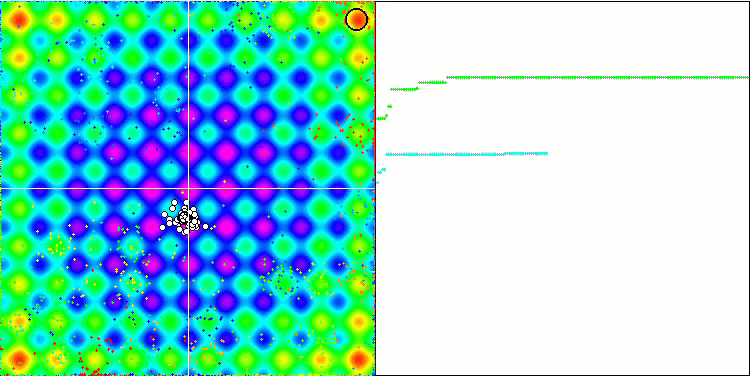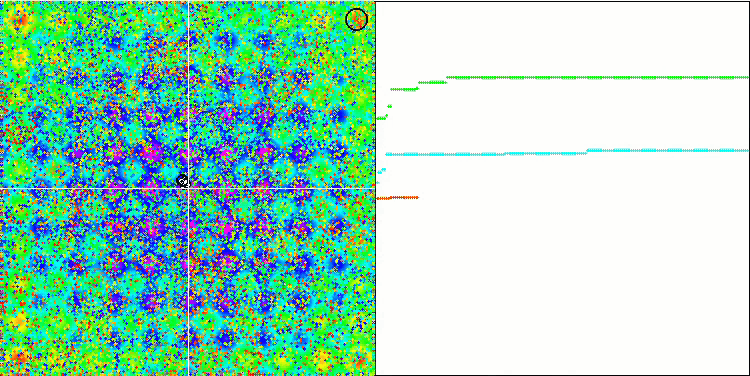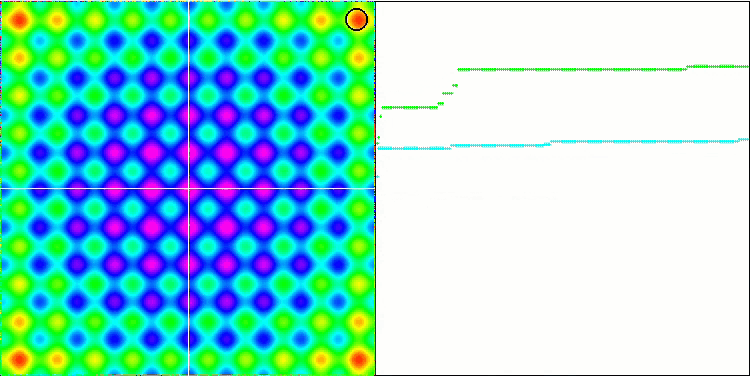
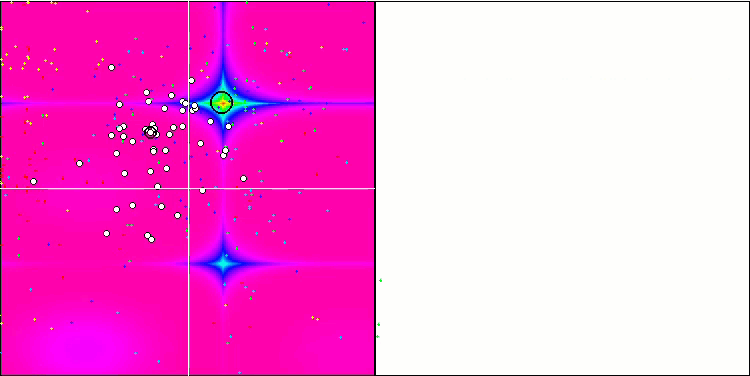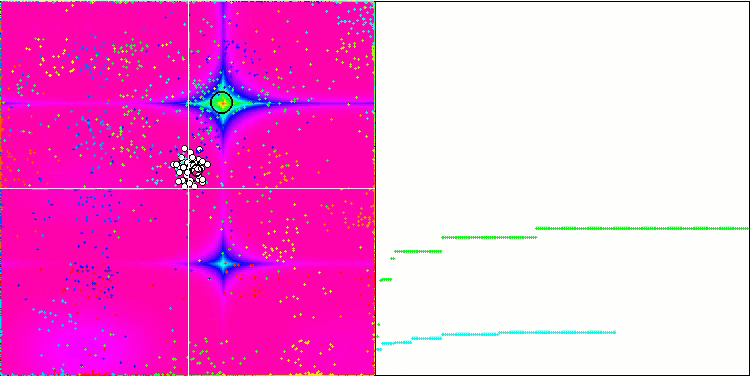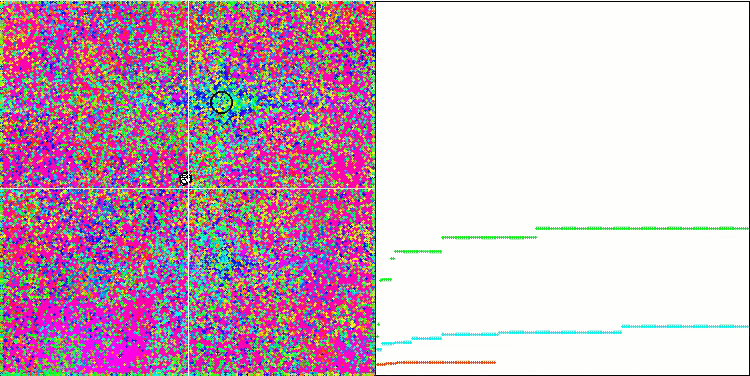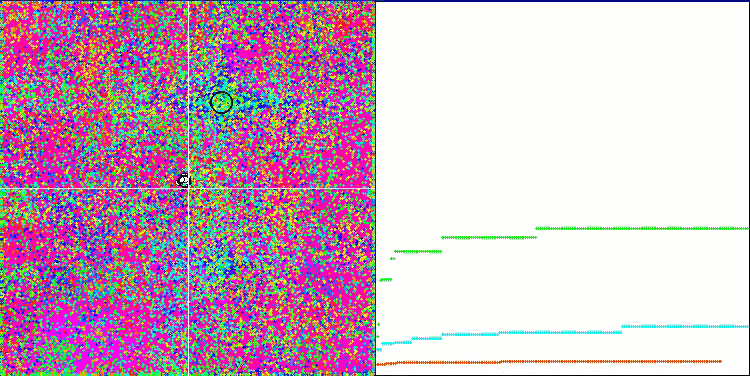
IWDm на тестовой функции Rastrigin.

forest

IWDm на тестовой функции Forest.

megacity

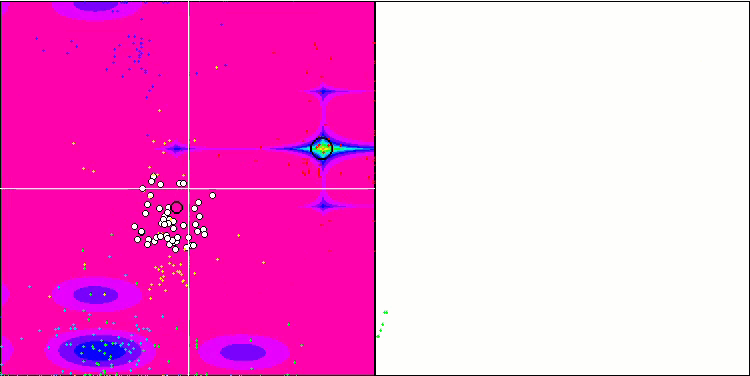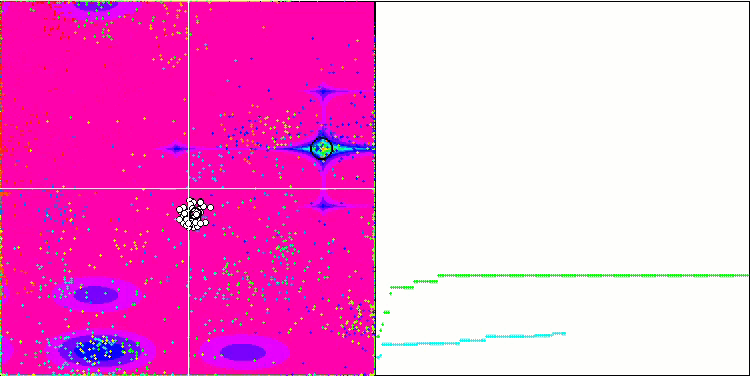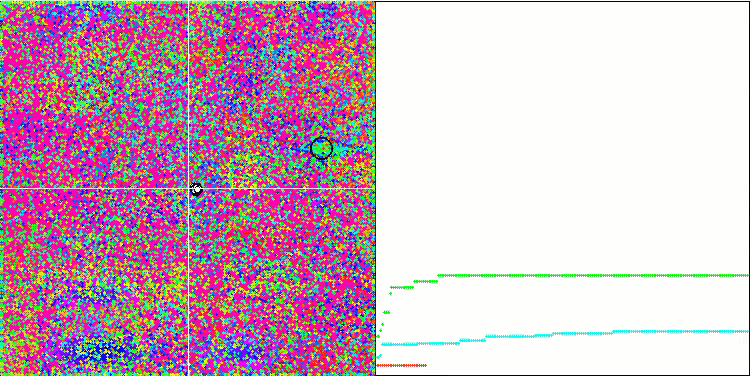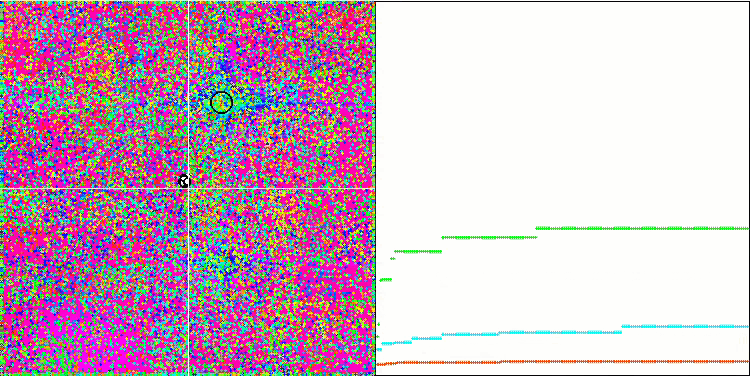
IWDm на тестовой функции Megacity.

В данной статье был рассмотрен алгоритм IWDm, который занял 19-е место среди 22-х алгоритмов, или 4-е место снизу, обогнав известный и популярный алгоритм PSO. IWDm показывает лучшие результаты на гладких функциях. Последовательное улучшение графика сходимости на всех трех тестовых функциях дает надежду, что при увеличении числа итераций алгоритм будет продолжать сходиться, но тогда пропадает практический смысл и целесообразность его применении, условие тестовых испытаний жёсткое, 10000 итераций, не больше и не меньше.

Кроме того, следует отметить модифицированный алгоритм SDSm, который занял 7 из 9 возможных первых мест. Этот алгоритм является настоящим "многоборцем" среди алгоритмов оптимизации. Особенно заметно улучшение результатов SDSm по сравнению с обычным SDS на функциях "острой" Forest и сложной дискретной Megacity (на последней функции улучшение почти 30% при 1000 параметрах). Таким образом, помимо основного героя статьи - IWD, мы видим нового и великолепного гостя таблицы - SDSm. Анимацию работы SDS можно посмотреть здесь, а для просмотра работы SDSm необходимо запустить тестовый скрипт из архива, который находится в папке с SDS.

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
№	AO	Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Rastrigin final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity final	Final result
1	SDSm	stochastic diffusion search M	0,99809	1,00000	0,69149	2,68958	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	1,00000	3,00000	100,000
2	SDS	stochastic Diffusion Search	0,99737	0,97322	0,58904	2,55963	0,96778	0,93572	0,79649	2,69999	0,78696	0,93815	0,71804	2,44315	88,208
3	SSG	saplings sowing and growing	1,00000	0,92761	0,51630	2,44391	0,72654	0,65201	0,83760	2,21615	0,54782	0,61841	0,99522	2,16146	77,678
4	HS	harmony search	0,99676	0,88385	0,44686	2,32747	0,99882	0,68242	0,37529	2,05653	0,71739	0,71842	0,41338	1,84919	70,647
5	IWO	invasive weed optimization	0,95828	0,62227	0,27647	1,85703	0,70690	0,31972	0,26613	1,29275	0,57391	0,30527	0,33130	1,21048	48,267
6	ACOm	ant colony optimization M	0,34611	0,16683	0,15808	0,67103	0,86785	0,68980	0,64798	2,20563	0,71739	0,63947	0,05579	1,41265	47,419
7	MEC	mind evolutionary computation	0,99270	0,47345	0,21148	1,67763	0,60691	0,28046	0,21324	1,10061	0,66957	0,30000	0,26045	1,23002	44,061
8	COAm	cuckoo optimization algorithm M	0,92400	0,43407	0,24120	1,59927	0,58309	0,23477	0,13842	0,95629	0,52174	0,24079	0,17001	0,93254	37,845
9	FAm	firefly algorithm M	0,59825	0,31520	0,15893	1,07239	0,51012	0,29178	0,41704	1,21894	0,24783	0,20526	0,35090	0,80398	33,152
10	ABC	artificial bee colony	0,78170	0,30347	0,19313	1,27829	0,53774	0,14799	0,11177	0,79750	0,40435	0,19474	0,13859	0,73768	29,784
11	BA	bat algorithm	0,40526	0,59145	0,78330	1,78002	0,20817	0,12056	0,21769	0,54641	0,21305	0,07632	0,17288	0,46225	29,488
12	CSS	charged system search	0,56605	0,68683	1,00000	2,25289	0,14065	0,01853	0,13638	0,29555	0,07392	0,00000	0,03465	0,10856	27,914
13	GSA	gravitational search algorithm	0,70167	0,41944	0,00000	1,12111	0,31623	0,25120	0,27812	0,84554	0,42609	0,25525	0,00000	0,68134	27,807
14	BFO	bacterial foraging optimization	0,67203	0,28721	0,10957	1,06881	0,39655	0,18364	0,17298	0,75317	0,37392	0,24211	0,18841	0,80444	27,549
15	EM	electroMagnetism-like algorithm	0,12235	0,42928	0,92752	1,47915	0,00000	0,02413	0,29215	0,31628	0,00000	0,00527	0,10872	0,11399	18,981
16	SFL	shuffled frog-leaping	0,40072	0,22021	0,24624	0,86717	0,20129	0,02861	0,02221	0,25211	0,19565	0,04474	0,06607	0,30646	13,201
17	MA	monkey algorithm	0,33192	0,31029	0,13582	0,77804	0,10000	0,05443	0,07482	0,22926	0,15652	0,03553	0,10669	0,29874	11,771
18	FSS	fish school search	0,46812	0,23502	0,10483	0,80798	0,12825	0,03458	0,05458	0,21741	0,12175	0,03947	0,08244	0,24366	11,329
19	IWDm	intelligent water drops M	0,26459	0,13013	0,07500	0,46972	0,28568	0,05445	0,05112	0,39126	0,22609	0,05659	0,05054	0,33322	10,434
20	PSO	particle swarm optimisation	0,20449	0,07607	0,06641	0,34696	0,18873	0,07233	0,18207	0,44313	0,16956	0,04737	0,01947	0,23641	8,431
21	RND	random	0,16826	0,09038	0,07438	0,33302	0,13480	0,03318	0,03949	0,20747	0,12175	0,03290	0,04898	0,20363	5,056
22	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06562	0,00000	0,00000	0,06562	0,23478	0,05789	0,02545	0,31812	1,000

Выводы

Оригинальный алгоритм IWD был разработан автором с целью решения задач поиска кратчайших путей, таких как транспортная логистика, маршрутизация сетей и поиск оптимальных путей в географических информационных системах. В данной статье не рассматривались его возможности и результативность в этих специфических задачах, а новый модифицированный алгоритм IWDm, представленный как универсальный, не смог показать впечатляющих результатов. Повышение количества секторов, к сожалению, не привело к повышению эффективности алгоритма.

Однако работа над алгоритмом IWDm оставила ощущение, что потенциал этого элегантного алгоритма еще не полностью раскрыт. Идея разделения пространства поиска на секторы и учет их рейтинга, основанного на моделировании перемещения грунта в русле реки, представляется очень интересной. Как показали результаты, подобный подход, например, сохранение лучших блюд в каждом ресторане, и, возможно, использование смещения вероятности новой точки в окрестностях предыдущей, значительно улучшило характеристики алгоритма SDS.

Что важно, если увеличивать количество ресторанов в новом SDSm (по умолчанию параметр 100) и разбивать координаты на более мелкие участки (в SDS используется параметр 1000), то результаты ухудшаются. Это означает, что при таком подходе более важным становится выбор отдельного ресторана, а конкретная точка в его окрестностях перестает быть значимой (алгоритм превращается в обычный SDS). Из этого следует, что квадратичное распределение вероятности оказывает максимальное влияние при определенном размере секторов на координатах. Это является своего рода балансом между различными по своим целям методами, присутствующими в алгоритме.

Самый важный вывод из этой статьи заключается в том, что нельзя однозначно утверждать, какой прием или метод, применяемые в отдельных стратегиях поиска, являются лучшими или худшими. Применение различных методов может как ухудшить одни алгоритмы, так и значительно улучшить другие. Важна именно комбинация применяемых методов в алгоритмах оптимизации, а не сами методы в отдельности.

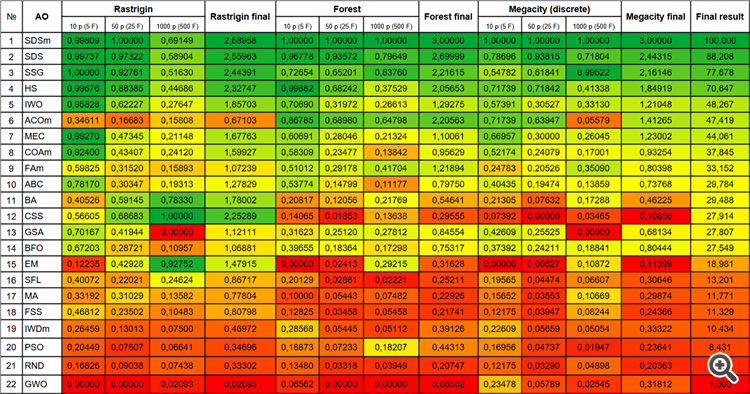
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам.

Гистограмма результатов тестирования алгоритмов на рисунке 3 (по шкале от 0 до 100, чем больше тем лучше, в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье):

chart

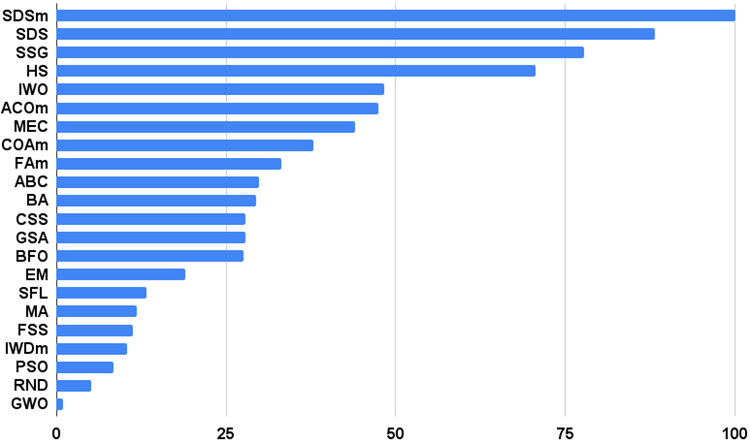
Рисунок 3. Гистограмма итоговых результатов тестирования алгоритмов.

Плюсы и минусы модифицированного алгоритма интеллектуальных капель воды (IWDm):

Плюсы:
1. Небольшое количество внешних параметров.

Минусы:
1. Невысокие результаты на гладких и дискретных функциях.
2. Низкая сходимость.
3. Склонность к застреванию в локальных экстремумах.

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

Прикрепленные файлы |

Загрузить ZIP

21_The_world_of_AO_IWD.ZIP (778.83 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (4)

fxsaber | 21 нояб. 2023 в 15:45

Все внимание на SDSm, спасибо!

Andrey Dik | 21 нояб. 2023 в 16:13

fxsaber #:
Все внимание на SDSm, спасибо!

Спасибо за интерес к работе.

Интрига только-только начинается.))

Vladislav Vidiukov | 21 нояб. 2023 в 16:15

MetaQuotes:

Опубликована статья Популяционные алгоритмы оптимизации: Алгоритм интеллектуальных капель воды (Intelligent Water Drops, IWD):

Автор: Andrey Dik

Это не имеет отношения к трейдингу.

Andrey Dik | 21 нояб. 2023 в 16:27

Vladislav Vidiukov #:
Это не имеет отношения к трейдингу.

Ну, тогда никакого отношения к трейдингу не имеет и оптимизатор в МТ5.)))

Кросс-валидация и основы причинно-следственного вывода в моделях CatBoost, экспорт в ONNX формат

В данной статье предложен авторский способ создания ботов с использованием машинного обучения.

Торговая техника RSI Deep Three Move

В статье представлена техника торговли RSI Deep Three Move в MetaTrader 5. Статья основана на новой серии исследований, демонстрирующих несколько торговых методов, основанных на RSI - техническом индикаторе для измерения силы и импульса ценных бумаг, включая акции, валюты и товары.

Разработка системы репликации - Моделирование рынка (Часть 21): ФОРЕКС (II)

Мы продолжим строить систему для работы на рынке ФОРЕКС. Поэтому для того, чтобы решить эту проблему необходимо сначала объявить загрузку тиков до загрузки предыдущих баров. Это решает проблему, но в то же время заставляет пользователя следовать некой структуре в конфигурационном файле, которая, лично для меня, не имеет особого смысла. Причина в том, что, разработав программу, которая отвечает за анализ и выполнение того, что находится в конфигурационном файле, мы можем позволить пользователю объявлять нужные ему элементы в любом порядке.

Разработка системы репликации - Моделирование рынка (Часть 20): ФОРЕКС (I)

Первоначальная цель данной статьи заключается не в охвате всех возможностей ФОРЕКС, а скорее в адаптации системы таким образом, чтобы вы могли совершить хотя бы одну репликацию рынка. Моделирование оставим для другого момента. Однако, если у нас нет тиков, а есть только бары, приложив немного усилий, мы можем смоделировать возможные сделки, которые могли произойти на рынке ФОРЕКС. Так будет до тех пор, пока мы не рассмотрим, как адаптировать тестер. Попытка работать с данными ФОРЕКС внутри системы без их модификации приводит к ошибкам диапазона.