Нейронная сеть на практике: Функция прямой линии

Введение

Очень рад приветствовать всех и приглашаю вас к прочтению новой статьи о нейронных сетях.

В предыдущей статье " Нейронная сеть на практике: Наименьшие квадраты", мы рассмотрели, как в очень простых случаях можно найти уравнение, которое лучше всего описывает набор данных, используемый нами. Уравнение, которое составляется в этой системе, было очень простым, в нем использовалась только одна переменная. Мы уже показывали, как можно выполнить расчет, так что здесь мы сразу приступим к делу. Это связано с тем, что математика, используемая для создания уравнения на основе значений, имеющихся в базе данных, требует значительных знаний в области аналитической математики и алгебраического вычисления. Помимо этого, конечно, необходимо знать, какой тип данных есть в используемой нами базе данных.

Поскольку эта статья призвана быть максимально обучающей, я не хочу усложнять жизнь своим читателям. Если вам действительно интересно углубиться в расчеты, я предлагаю вам изучить материалы на эту тему. Как уже говорилось, в основном вам придется изучать аналитическую математику и алгебраическое исчисление. Чтобы сделать данный процесс менее теоретическим и утомительным, я предлагаю вам начать с изучения теории игр. Там можно познакомиться с расчетами и анализом в более увлекательной форме, без монотонного просмотра бесконечных счетов.

В Интернете есть множество материалов на эту тему с хорошим объяснением и простые для понимания. Но если ваша цель - просто посмотреть на код, то добро пожаловать, поскольку в этой статье я не буду углубляться в математическую часть. Математический вопрос довольно глубокий и требует понимания каждой детали и много времени, а большинству читателей эти аспекты могут быть неинтересны.

Поэтому в данной статье мы бегло рассмотрим некоторые методы получения функции, которая могла бы представлять наши данные в базе данных. Я не буду подробно останавливаться на том, как использовать статистику и исследования вероятностей для интерпретации результатов. Оставим это для тех, кто действительно хочет углубиться в математическую сторону вопроса. Тем не менее, изучение этих вопросов будет иметь решающее значение для понимания того, что связано с изучением нейронных сетей. Здесь мы довольно спокойно рассмотрим этот вопрос.

Создаем уравнение в общем виде

Для начала проведем некоторые расчеты. (О Боже, опять начинается!). Не волнуйтесь, вам не нужно беспокоиться о том, что мы будем делать. На этот раз я обещаю быть добрее. Сегодня мы будем действовать иначе. Наша цель - создать систему, способную генерировать более общие уравнения прямой линии. И чтобы не оставить вас в полном недоумении от разработки формул, которые мы будем использовать, мы не будем углубляться в математическую разработку используемых уравнений. В этом нет необходимости, так как в предыдущей статье мы показали, как выглядит разработка математического уравнения, основываясь на некоторых фундаментальных идеях и принципах. Здесь мы просто попытаемся понять, что на самом деле означают эти уравнения. Конечно, мы постараемся, насколько это возможно, сделать всё максимально доступным. Хотя поначалу они могут показаться запутанными, я не позволю вам растеряться. Прочитайте статью без спешки. Смотрите, как всё это разворачивается, ведь здесь я обобщу различные исследования в области математики, чтобы показать вам, как мы можем заставить нейронную сеть усваивать знания, основанные на информации, содержащейся в базе данных.

Но прежде чем мы начнем, я хочу прояснить один момент: то, что мы увидим здесь, относится к нейронной сети, которая не будет получать никакой новой информации в свою базу данных. То есть база данных уже полностью создана, и мы просто хотим, чтобы она генерировала уравнение, которое наилучшим образом представляет то, что уже находится в базе данных. Только позже, используя другие механизмы, мы сможем отфильтровать вероятность того, что новая информация связана или не связана с тем, что уже есть в базе данных. Такие механизмы обычно относятся к области искусственного интеллекта. Но об этом в другой раз.

Давайте теперь вернемся к нашему примеру кода. В нем у нас уже есть два набора данных, которые можно построить на двумерной плоскости. Используя только координаты X и Y. После спокойного анализа ситуации, мы можем заметить, что искомое уравнение построить относительно просто, поскольку наши данные можно выразить с некоторой приближенностью к вероятной прямой линии. Бывают случаи, когда это не так, поскольку уравнение может быть кривой или тригонометрической функцией. Но давайте делать по одному шагу за раз. Сначала нужно разобраться с более простыми случаями. Начнем с понимая следующего: уравнение, которое мы хотим получить, имеет следующий формат, показанный на рисунке ниже.

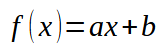
Здесь значение константы < a > представляет собой угловой коэффициент. Постоянная < b > является точкой пересечения. Когда < b > равен нулю, корень функции также равен нулю. В предыдущей статье мы рассмотрели, как вычислить этот коэффициент, если < b > равен нулю. Кроме того, в конце той же статьи мы увидели, как поправить оба значения, чтобы попытаться приблизить константы уравнения, построив таким образом линейную функцию, показанную выше. Давайте еще раз вспомним, что если мы изменим значение константы < b >, то изменится и корень функции. Понимание этого важно для того, чтобы решать систему с помощью полиномов. Однако здесь мы будем использовать метод, адаптированный к предыдущей статье.

Думаю, стало ясно, что пытаться найти данные значения методом проб и ошибок - это то, что в программировании известно как грубая сила, когда проверяются все возможные значения (и это далеко не лучший способ). Хотя это можно сделать, в большинстве случаев время обработки будет очень большим. В таких случаях, как наш, это просто потребует много времени и усилий, но вполне осуществимо. Однако при значительном увеличении числа переменных этот процесс становится нецелесообразным - либо вручную, либо методом грубой силы.

Тем не менее, даже если мы решили применить грубую силу, в предыдущей статье я продемонстрировал способ вычисления углового коэффициента, когда константа < b > равна нулю. Данный метод позволил найти коэффициент относительно просто и быстро, независимо от объема данных в базе. Единственным ограничением было то, что полученное уравнение должно быть прямой линией. Однако если константа < b > не равна нулю, то данное вычисление уже не сработает. Это даст нам лишь приблизительное представление о том, в каком направлении двигаться. Мы рассмотрим это попозже. Пока что мы будем опираться на известные функции, такие как функция, которую мы рассматривали в начале этой темы.

Давайте теперь вспомним общий случай решения. Помните, что необходимо знать вид используемого полинома. Без этого знания поиск уравнения, которое наилучшим образом представит данные, может занять очень много времени даже в самых простых случаях. Поэтому запомните: всё, что мы увидим в дальнейшем, основано на этих предварительных знаниях.

Давайте обобщим метод наименьших квадратов для любых случаев. Для этого необходимо знать вид используемого полинома. Начнем с простого, который генерирует прямую линию. Этот полином можно обобщить с помощью выражения, показанного ниже.

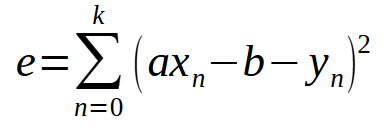
Постойте, разве это не та же самая формула, которую мы видели в предыдущей статье? Так и есть! В принципе, это одно и то же, но теперь в формулу включена переменная < b >, поскольку теперь мы не предполагаем, что она равна нулю. Если мы разовьем эту сумму, то придем к чему-то похожему на то, что мы делали в предыдущей статье. Однако, для лучшего понимания, при обобщении этого расчета мы должны рассматривать производную как по переменной < a >, так и по < b >. Это нам даст определение, показанное ниже.

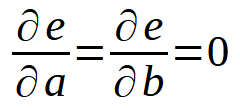
Другими словами, всё то же самое, что мы делали в предыдущей статье. Однако данный принцип не ограничивается только уравнением прямой линии. Мы можем использовать один и тот же подход в любом случае. Например, предположим, что набор данных можно лучше всего выражать или представлять в виде параболы. В данном случае мы должны подумать, как найти квадратное уравнение, используя данные, которые есть в нашей базе. Последние два определения преобразуются в следующие.

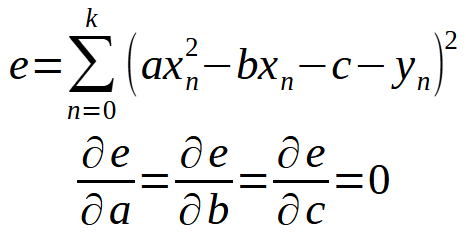
Таким образом, нам нужно будет разработать новое слагаемое, чтобы найти способ составления уравнения, которое в данном случае будет квадратным уравнением. То есть надо найти константы, необходимые для того, чтобы такое квадратное уравнение отображало всё, что есть в базе данных. Но, возвращаясь к нашему случаю, где мы используем уравнение прямой линии, если мы теперь будем развивать расчет, считая < b > отличным от нуля, мы сначала получим следующее уравнение, показанное ниже.

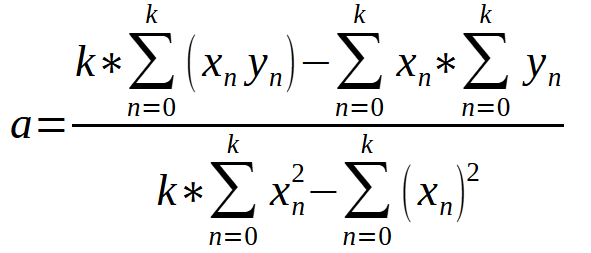
Это уравнение позволяет рассчитать значение < a > на основе данных, содержащихся в нашей базе.

Получив значение константы < a >, мы можем использовать приведенное ниже уравнение для нахождения константы < b >.

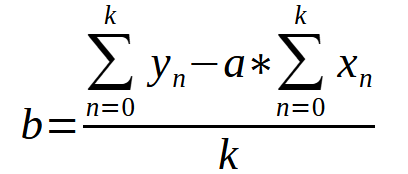
В обоих случаях значение < k > - это количество точек на графике. Возможно, глядя на одни только уравнения, вы растеряетесь и подумаете, что это нечто сложное, или не будете знать, как преобразовать эти выражения в код с помощью какого-либо языка программирования. Таким образом, вы сможете получить значения констант, не делая этого вручную. Однако, как и в предыдущей статье, здесь мы собираемся перевести этот математический формат в формат языка программирования, в данном случае MQL5, но вы могли бы использовать любой другой язык, и результаты были бы такими же. Ниже видно, как эти уравнения будут выглядеть в нашем MQL5-коде. Об этом можно судить по приведенному ниже фрагменту.

28. //+------------------------------------------------------------------+
29. void Func_01(void)
30. {
31.     int A[]={
32.                   -100, -150,
33.                    -80,  -50,
34.                     30,   80,
35.                    100,  120
36.             };
37. 
38.     int vx, vy;
39.     uint k;
40.     double ly, err, dx, dy, dxy, dx2, a, b;
41.     string s0 = "";
42. 
43.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
44.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
45. 
46.     err = dx = dy = dxy = dx2 = 0;
47.     k = 0;    
48.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++, k++)
49.     {
50.         vx = A[c1++];
51.         vy = A[c1++];
52.         dx += vx;
53.         dy += vy;
54.         dxy += (vx * vy);
55.         dx2 += MathPow(vx, 2);
56.         canvas.FillCircle(global.x + vx, global.y - vy, 5, ColorToARGB(clrRed, 255));
57.         ly = vy - (vx * -MathTan(_ToRadians(global.Angle))) - global.Const_B;
58.         s0 += StringFormat("%.4f || ", MathAbs(ly));
59.         canvas.LineVertical(global.x + vx, global.y - vy, global.y + (int)(ly - vy), ColorToARGB(clrPurple));
60.         err += MathPow(ly, 2);
61.     }
62.     a = ((k * dxy) - (dx * dy)) / ((k * dx2) - MathPow(dx, 2));
63.     b = (dy - (a * dx)) / k;
64.     PlotText(3, StringFormat("Error: %.8f", err));
65.     PlotText(4, s0);
66.     PlotText(5, StringFormat("f(x) = %.4fx %c %.4f", a, (b < 0 ? '-' : '+'), MathAbs(b)));
67. }
68. //+------------------------------------------------------------------+

Давайте разберемся, что происходит в этом фрагменте. В строках 46 и 47 мы инициализируем все переменные значением ноль. Это связано с тем, что мы хотим явно показать, что они начинаются с нуля, хотя мы могли бы пропустить это объявление, поскольку обычно компилятор инициализирует переменные нулем неявно. В строке 52 мы вычисляем сумму всех значений X, а в строке 53 - сумму значений Y. В строке 54 мы вычисляем сумму произведения значений X и Y. И в конце, в строке 55 мы вычисляем сумму квадратов значений X.

Все эти расчеты используются в формулах, которые мы уже рассматривали ранее. Другими словами, сделать расчеты гораздо проще, чем кажется. Все приведенные выше расчеты используются в ранее рассмотренных нами формулах. Так что расчеты гораздо проще.

Теперь, по сути, нам предстоит вычислить значения констант, используемых в уравнении прямой линии. Для этого мы используем строку 62, где вычисляем значение коэффициента наклона, а в строке 63 - значение пересечения. Вы заметили, как легко превратить математическую формулу в расчет, который может выполнить наша программа? Есть люди, которые утверждают, что понимают математику, но не могут переводить ее на термины программирования. На мой взгляд, эти люди сами себя обманывают, ведь написать математическую формулу в коде так же просто, как и прочитать ее. Конечно, если мы не понимаем формулу, мы не сможем объяснить компьютеру, который является просто гигантским калькулятором, как произвести расчет.

Однако мы не строим линию на графике, а только показываем полученное уравнение. Это делается в строке 66, чтобы мы могли вручную визуализировать, являются ли рассчитанные значения наиболее подходящими для данного набора данных. В анимации ниже мы показываем результат выполнения нашей программы со значениями, указанными в матрице A, присутствующей в строке 31.

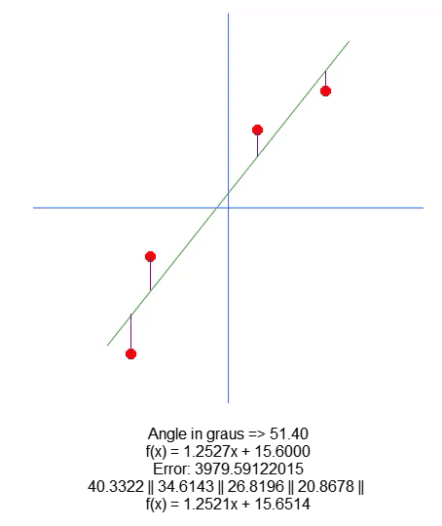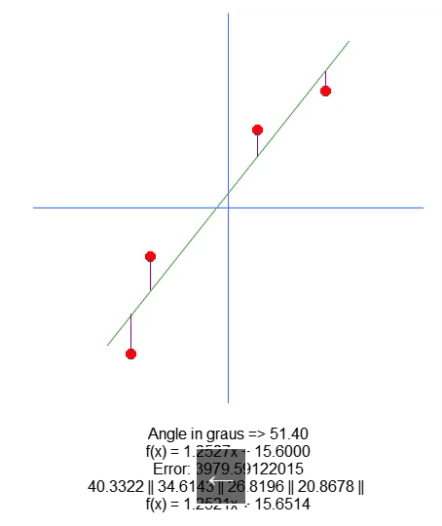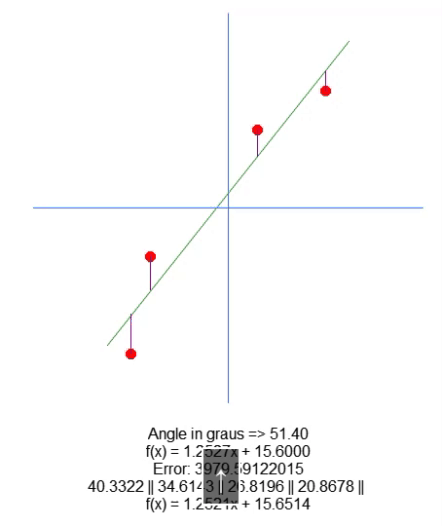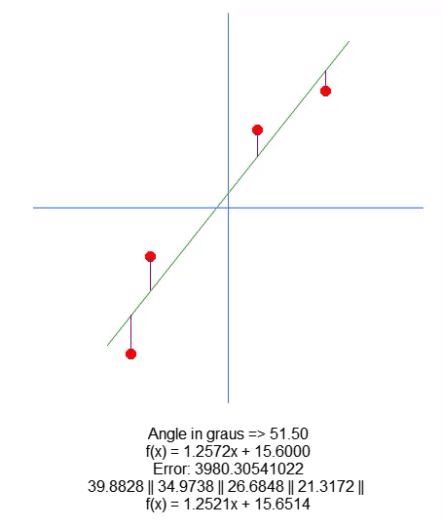
Посмотрите как меняются значения ошибок по мере того, как мы пытаемся найти идеальную точку. Сравните уравнение идеальной прямой линии с уравнением линии, которую мы пытаемся построить, используя стрелки направления. Из-за отсутствия идеальной настройки мы получаем значение, близкое к идеальному. Понимание этого важно, так как вскоре мы будем изучать это же свойство, но в другом ключе.

Теперь вы, наверное, зададитесь вопросом: есть ли способ приблизиться к расчетному значению? Да, уважаемый читатель. Для этого просто нужно изменить в программе значение, которое показано в приведенном ниже коде.

void NewAngle(const char direct, const char updow, const double step = 0.1)

Изменяемое значение является аргументом step. Здесь мы используем шаг 0,1, как можно видеть в коде, но вы можете использовать меньшее или большее значение. Если использовать меньшее значение, программе потребуется больше времени для достижения расчетных значений, но точность ошибки будет выше из-за меньшего разброса. Помните, что одно перевешивает другое: не существует 100% идеального решения, а есть идеальная точка равновесия.

Получив код, способный вычислить уравнение линии, мы можем свободно изменять значения, находящиеся в матрице A, создавая любые условия или базу знаний. Возможно, вам всего лишь нужно изменить вид используемых переменных. Здесь мы используем целые числа, но если хотите использовать плавающие типы данных, такие как double или float, просто измените тип, расчет не изменится. Это нужно для того, чтобы получить уравнение линии. Однако если данные в базе лучше всего представлены, например, квадратным уравнением, нам придется изменить расчеты, чтобы найти наилучшую систему констант для представления нашей базы данных, как уже говорилось выше. Всё зависит от контекста; не существует 100% эффективного решения для всех возможных и мыслимых случаев.

Но вы можете подумать, что существует только такой способ вычисления уравнения прямой линии. Если вы подумали именно так, значит, ваше знания еще недостаточны. Чтобы показать другой способ получения тех же значений, которые мы рассматривали в данной теме, мы изучим новый раздел, разделив понятия соответствующим образом. Однако данный раздел будет лишь введением к тому, что мы увидим в следующей статье.

Псевдообратная

До сих пор всё казалось очень сложным и трудно реализуемым в коде. Это связано с тем, что каждое необходимое изменение должно быть соответствующим образом реализовано в сгенерированном коде. Однако есть и более приятный способ написания кода данной ситуации, в котором переменные постоянно меняются. По крайней мере, так думаю я, хотя не знаю вашего мнения на этот счет. Когда речь идет о написании какого-то кода, где количество переменных часто меняется, я предпочитаю переходить от скалярных вычислений к матричным. Работа с матрицами позволяет нам учитывать любые факторы без необходимости создавать множество временных переменных. Я знаю, что многие из вас считают создание кода для факторизации матриц очень сложным и часто используют библиотеки, которые выполняют данную факторизацию, не понимая, как она работает. Это может сделать вас зависимым от этих библиотек, потому что вы не понимаете, как выполняются вычисления.

Некоторое время назад я написал две статьи для ознакомления с матричной факторизацией. Там мы посмотрели самые основные элементы, которые необходимо изучить, чтобы создать код, выполняющий операции факторизации с матрицами. Многие задачи решаются проще и быстрее, если использовать матрицы для вычислений.

Статьи: "Матричная факторизация: основы" и "Матричная факторизация: моделирование, которое более практично". Если вы хотите узнать больше про эту тему, я вам рекомендую прочитать и применить на практике то, что изложено в этих статьях. Конечно, они охватывают только основы, но если разбираться в их содержании, то можно понять, что мы будем делать в этом разделе.

Здесь мы будем использовать матрицы, чтобы найти значения, полученные в предыдущей теме. Чтобы понять, что мы собираемся делать, необходимо знать, как складываются матрицы. Мы не имеем в виду программирование, так как программирование этих вычислений - самая простая часть, а то, что вы должны иметь хотя бы базовые знания о том, как выполнять вычисления с использованием матриц. Я не буду подробно рассказывать о том, как проводить данные расчеты, поскольку предполагаю, что вы обладаете минимальными знаниями в этой области, вам не нужно быть экспертом. Знания азов будет достаточно для того, что мы собираемся делать.

Давайте теперь вернемся к тому, как найти уравнение прямой линии, учитывая, что у нас есть база данных, содержимое которой мы хотим сохранить в виде математического уравнения. На первый взгляд, это кажется очень сложно, как будто только гений мог совершить такой подвиг, но нет, мы поступим так же, как и в предыдущей теме. Только немного по-другому.

Давайте начнем с основ. Уравнение ошибки показано на рисунке ниже.

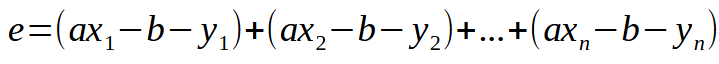
Это скалярная форма написания уравнения. Однако мы можем написать то же самое уравнение в матричной форме, как показано ниже.

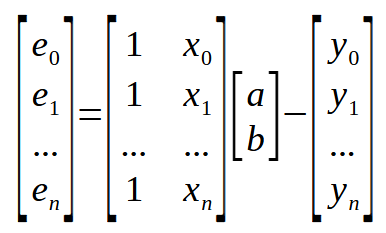
Данное матричное представление показано выше, это именно то, что показано на предыдущее картинке, без каких-то добавлений. Но мы можем еще больше упростить данное матричное представление. Создается оно следующим образом:

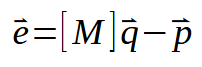
Я знаю, что это представление может показаться очень сложным, но мы по-прежнему представляем именно то, что должно было бы делать скалярное вычисление. Однако эта более компактная форма матричной факторизации позволит нам лучше понять, как будут проводиться вычисления, так как в формуле нам придется написать меньше элементов. Здесь мы утверждаем, что вектор < e > равен матрице < M >, которая содержит значения x, умножен на вектор < q >, который содержит искомые константы. К ним относятся: угловой коэффициент и точка пересечения. Затем мы вычитаем вектор < p >, который представляет собой значения матрицы, содержащей значения y.

Теперь я хочу напомнить вам следующее: мы ищем производную констант < a > и < b > по отношению к погрешности, которую мы можем легко вычислить. Теперь у нас есть расположение точек, которые будем использовать в расчете. Поэтому, представив его в матричной форме, можно увидеть то, что показано ниже.

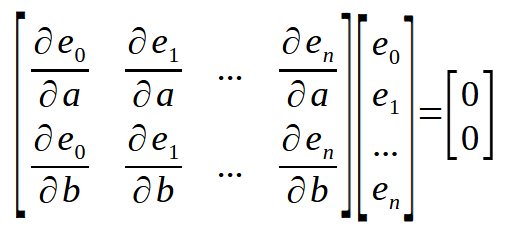
Вот небольшая деталь, которую можем увидеть сразу под ним.

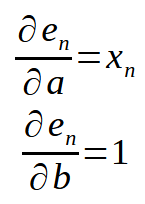
Если помнить, что < n > представляет собой индекс массива в нашем коде, приведенное выше уравнение можно переписать, как показано ниже.

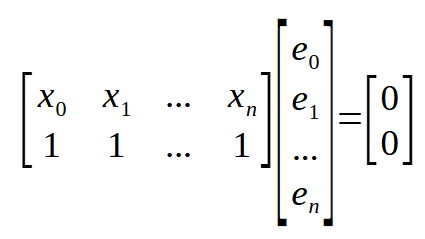
Идеально. Теперь у нас есть кое-что действительно интересное. Если посмотреть на матрицы выше, то можно заметить, что этот же результат мы показываем здесь. Он также встречается в других местах, только эта матрица, что называется, транспонирована, и это делает формулу еще более компактной. Посмотрите на изображение ниже.

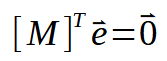
Следующий шаг - сделать некоторые замены в уже имеющихся данных. Таким образом, мы получим следующую формулировку, приведенную ниже.

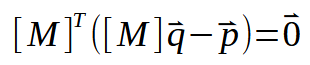
Давайте теперь разработаем этот расчет или формулу (можете называть ее так, как хотите), показанную выше. Это приводит нас к следующему:

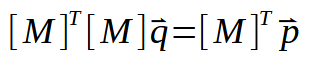
Если транспонированную матрицу можно инвертировать, то мы получим что-то такое:

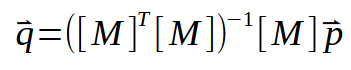
Данный результат на самом деле является очень приятной и интересной факторизацией, настолько, что человек, создавший его, фактически заслужил Нобелевскую премию по математике в 2020 году. Эта формулировка известна как псевдообратная, или псевдообращение Мура-Пенроуза, в честь ее создателей. Она дает нам именно то, что мы ищем, то есть значения углового коэффициента и пересечения. И оба будут находиться внутри вектора < q >. Данный вид вычислений может быть реализован во множестве различных программ, многие из которых предназначены исключительно для работы с вычислениями. Например, используя SCILab, можно воспользоваться программой, показанной ниже. Она рассчитает значения углового коэффициента и точки пересечения.

clc;
clear;
clf;

x=[-100; -80; 30; 100];
y=[-150; -50; 80; 120];

A = [ones(x), x];

plot(x, y, 'ro');
zoom_rect([-150, -180, 180, 180]);
xgrid;

x = pinv(A) * y;
b = x(1);
a = x(2);

x =[-120:1:120];
y = a * x + b;

plot(x, y, 'b-');

Результат выполнения можно увидеть чуть ниже:

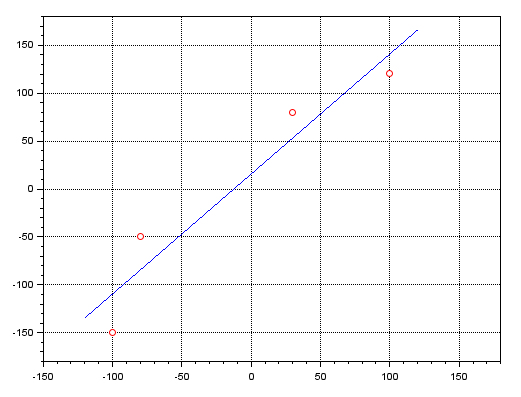
Красные точки указывают на расположение тех же точек, что и в программе на MQL5. Синяя линия показывает результат уравнения линии, полученной с помощью псевдообратной. То же самое можно сделать с помощью MATLAB, а также других программ, например, Excel. Это объясняется большой полезностью данной псевдообратной в различных областях знаний.

Чтобы дать вам представление о том, насколько интересна эта псевдообратная, достаточно слегка изменить используемые векторы, а также матрицы уравнения. Можно решать полиномы любого вида, причем довольно эффективно.

Заключительные идеи

Поскольку псевдообратная - это факторизация, которую надо выполнить с помощью матриц, я не буду показывать в этой статье, как будет выглядеть программа для поиска констант < a > и < b >. Это связано с объяснениями, необходимыми для того, чтобы вы действительно поняли, что происходит. Дело не только в представлении самого кода. Работа с матрицами требует гораздо большего внимания из-за особенностей их обработки. При ручном выполнении операции относительно просты. Однако делать это в виде кода - совсем другая история. Даже в тех статьях, где мы рассказываем о том, как использовать факторизацию в матрицах, то, что там делается, не является общим, они очень специфичны. А для нашей с вами цели нам нужен более общий код. В противном случае псевдообратная не может быть вычислена корректно в любом случае, когда мы пытаемся это сделать.