Популяционные алгоритмы оптимизации: Алгоритм оптимизации бактериального поиска пищи (Bacterial Foraging Optimization — BFO)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Алгоритм оптимизации бактериального поиска пищи (BFO) — это увлекательная техника оптимизации, которую можно использовать для поиска приблизительных решений чрезвычайно сложных или невозможных числовых задач максимизации или минимизации функций. Алгоритм получил широкое признание в качестве алгоритма глобальной оптимизации, представляющего текущий интерес для распределенной оптимизации и управления. BFO вдохновлен социальным поведением Escherichia coli при поиске пищи. BFO уже привлек внимание исследователей своей эффективностью в решении реальных задач оптимизации, возникающих в нескольких областях применения. Биология, лежащая в основе стратегии поиска пищи E.coli эмулируется оригинальным образом и используется как простой алгоритм оптимизации.

Бактерии, такие как кишечная палочка или сальмонелла (лат. Salmonella), являются одними из самых успешных организмов на планете. Эти подвижные бактерии имеют полужесткие придатки, называемые жгутиками, с помощью которых они продвигают себя при помощи вращательных движений. Когда все жгутики вращаются против часовой стрелки, создается эффект пропеллера, и бактерия будет двигаться в более или менее прямолинейном направлении. При этом бактерия совершает движение, которое называют плавание (swims), все жгутики вращаются в одном и том же направлении.

Жгутики помогают бактерии E.coli кувыркаться или плавать, что является двумя основными операциями, выполняемыми бактерией во время поиска пищи. Когда они вращают жгутики по часовой стрелке, каждый жгутик толкает клетку. При вращении жгутиков в разные стороны бактерия разворачивается - совершает движение кувырок (tumble). В итоге бактерия кувыркается с меньшим числом кувырков в благоприятной среде, тогда как во вредном месте она часто кувыркается, чтобы найти градиент питательных веществ. Движение жгутиков против часовой стрелки помогает бактериям плавать с очень высокой скоростью.

В вышеупомянутом алгоритме поведение бактерий обусловлено механизмом, который называется бактериальным хемотаксисом (bacterial chemotaxis) и представляет собой двигательную реакцию этих микроорганизмов на химический раздражитель среды. Данный механизм позволяет бактерии двигаться по направлениям к аттрактантам (чаще всего, питательным веществам) и от репеллентов (потенциально вредных для бактерии веществ). Рецепторы, детектирующие аттрактанты и репелленты, расположены на полюсах бактерии.

В силу малого размера бактерии она не способна уловить разницу концентраций полезных и вредных веществ между полюсами. Градиенты указанных веществ бактерии определяют путем измерения изменений их концентраций при движении. Скорость этого движения может достигать нескольких десятков длин бактерии в секунду. Так, бактерия кишечной палочки обычно перемещается со скоростью 10-20 своих длин в секунду.

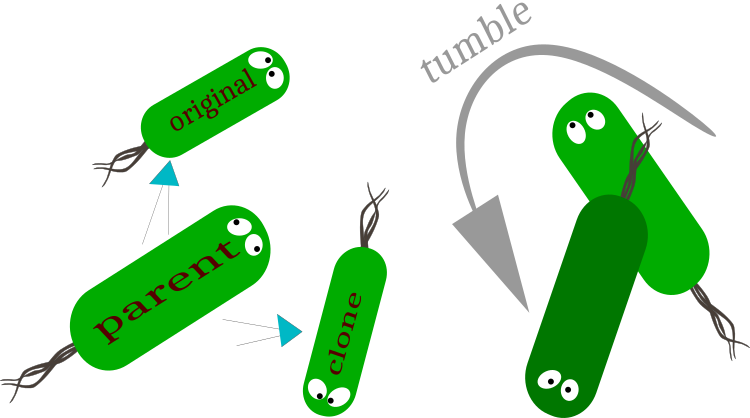
Рисунок 1. Репликация: деление на оригинальную (сохранение вектора движения) и клонированную (изменение вектора движения ) бактерии.
Кувырок - изменение вектора движения бактерии.

Если выбранное бактерией направление движения соответствует увеличению концентрации аттрактанта (снижению концентрации репеллента), то время до следующего кувырка увеличивается. В силу малого размера бактерии сильное влияние на её перемещения оказывает броуновское движение. В результате бактерия только в среднем движется в направлениях к полезным веществам и от вредных веществ.

Рассмотренный механизм движения бактерии не является единственным. Так, у некоторых бактерий имеется один жгутик. Варианты движения бактерии в этом случае обеспечивают различные режимы его вращения и остановки. Однако во всех случаях, если бактерия движется в нужном направлении, то продолжительность такого движения увеличивается. Таким образом, в целом бактериальный хемотаксис можно определить как сложное сочетание плавания и кувырков, позволяющее бактерии удерживаться в местах высокой концентрации питательных веществ и избегать неприемлемой концентрации вредных веществ.

В контексте задачи поисковой оптимизации, бактериальный хемотаксис можно также интерпретировать как механизм оптимизации использования бактерией известных пищевых ресурсов и поиска новых, потенциально более ценных областей.  Популяция бактерий достаточной численности может формировать сложные пространственно-временные структуры - эффект структурообразования в популяциях бактерий. Этот эффект может быть вызван как хемотаксисом, так и многими другими причинами.

Для некоторых бактерий образование таких структур объясняется регулирующими свойствами их продуктов метаболизма. Аналогичный эффект возможен на основе явлений магнитотаксиса (чувствительности к магнитному полю), биоконвекции, отрицательного геотаксиса (предпочтительное движение микроорганизмов против направления силы тяжести) и других явлений. Как правило, бактерии перемещаются на большее расстояние в дружественной среде. Когда они получают достаточно пищи, они увеличиваются в длину и при наличии подходящей температуры ломаются посередине, превращаясь в точную копию себя.

Это явление вдохновило Пассино на введение в BFO события воспроизведения. Из-за возникновения внезапных изменений окружающей среды, или нападения, хемотаксический процесс может быть нарушен, и группа бактерий может переместиться в какие-то другие места. Это представляет собой событие элиминации - рассеяния (elimination and dispersal) в реальной бактериальной популяции, когда все бактерии в регионе погибают или группа рассеивается в новую часть окружающей среды. Кроме того, рассмотренных процедур хемотаксиса и репродукции в общем случае недостаточно для отыскания глобального максимума многоэкстремальной целевой функции, поскольку эти процедуры не позволяют бактериям покидать найденные ими локальные максимумы этой функции. Процедура ликвидации и рассеивания призвана преодолеть этот недостаток. В соответствии с естественным отбором (выживание наиболее приспособленных) бактерии с плохой приспособленностью будут уничтожены, а бактерии с более высокой приспособленностью будут воспроизводить себя.

2. Описание алгоритма

Каноническая версия BFO включает в себя следующие основные этапы:

1. Инициализировать колонию бактерий.
2. Хемотаксис.
3. Роение.
4. Воспроизведение.
5. Ликвидация и устранение.

      
1. Инициализировать параметр.
Бактерии могут образовывать сложные устойчивые пространственно - временные паттерны в некоторых полутвердых питательных веществах, и они могут выжить в среде, если изначально поместить их вместе в ее центр. Более того, при определенных условиях они будут секретировать межклеточные аттрактантные сигналы, так что они будут группироваться и защищать друг друга.
2. Хемотаксис.
Характеристики движения бактерий в поисках пищи можно определить двумя способами, т.е. совместное плавание и кувыркание известно как хемотаксис. Говорят, что бактерия "плавает", если она движется в нужном направлении, и "кувыркается", если движется в сторону ухудшения среды.

3. Роение.
Для того чтобы бактерии могли добраться до наиболее богатого пищей места, желательно, чтобы оптимальная бактерия до момента времени в периоде поиска пыталась привлечь другие бактерии, чтобы вместе они быстрее сходились в желаемом месте. Для этого к исходной функции стоимости добавляется штрафная функция, основанная на относительном расстоянии каждой бактерии от наиболее приспособленной бактерии до этой продолжительности поиска. Наконец, когда все бактерии сливаются в точку решения, эта штрафная функция становится равной нулю. Эффект роения заключается в том, что бактерии собираются в группы и двигаются концентрическими паттернами с высокой плотностью бактерий.

4. Воспроизведение.
Исходный набор бактерий, пройдя несколько хемотаксических стадий, достигает стадии размножения. Здесь лучший набор бактерий делится на две группы. Более здоровая половина заменяется другой половиной бактерий, которые уничтожаются из-за их меньшей способности к поиску пищи. Это делает популяцию бактерий постоянной в процессе эволюции.

5. Устранение и рассеивание.
В процессе эволюции может произойти внезапное непредвиденное событие, которое может резко изменить плавный процесс эволюции и вызвать элиминацию множества бактерий и/или рассеять их в новую среду. По иронии судьбы, вместо того, чтобы нарушать обычный хемотаксический рост набора бактерий, это неизвестное событие может поместить более новый набор бактерий ближе к месту нахождения пищи. С широкой точки зрения, элиминация и рассредоточение являются частями поведения популяции на больших расстояниях. Применительно к оптимизации это помогает уменьшить стагнацию, часто наблюдаемую в таких алгоритмах параллельного поиска.

Моя реализация BFO несколько отличается от канонической версии, при рассмотрении конкретных участков кода мы будем останавливаться на различиях дополнительно с обоснованием необходимости этих изменений. В целом изменения в реализации нельзя считать значительными, поэтому не буду присваивать маркер "m" (модифицированная версия) к названию алгоритма. Замечу только, что результаты после внесения изменений в алгоритм улучшились.

Далее рассмотрим алгоритм и код моей реализации.

Шаги алгоритма:

1. Инициализация колонии бактерий.
2. Измерить здоровье бактерий (приспособленность).
3. Репликация?
3.1. Да. Производим репликацию.
3.2. Нет. п4.
4. Старый (достигнут лимит жизней)?
4.1. Да. Совершаем кувырок (изменение вектора движения).
4.2. Нет. п.5.
5. Движение в нужном направлении?
5.1. Да. Продолжение движения с тем же вектором.
5.2. Нет. Совершаем кувырок (изменение вектора движения).
6. Измерить здоровье бактерий (приспособленность).
7. Продолжить с п.3 до выполнения критерия останова.

Логическая схема алгоритма представлена на рис.1.

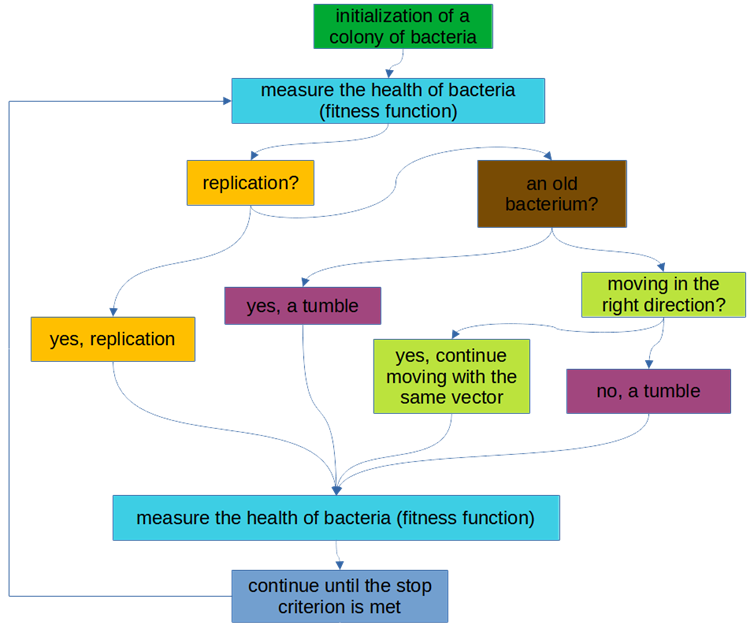
Рисунок 2. Блок-схема логики алгоритма BFO.

Приступим к рассмотрению кода.

Для описания бактерии лучше всего подходит структура, содержащая массивы координат и векторы движения. Значения текущего и предыдущего здоровья бактерии и счетчик жизней. По сути своей счетчик жизней необходим для ограничения количества последовательного движения в одном направлении, в отличии от оригинальной версии, в которой по достижению лимита жизней бактерия будет уничтожена и создана новая в случайном месте пространства поиска, но так как мы уже затрагивали эту тему в предыдущих статьях, создание нового агента в случайном месте не имеет практического смысла и только ухудшает поисковые способности. В этом случае целесообразнее либо создать нового агента в месте наилучшего решения, либо продолжить движение с текущего места, но изменить вектор направления. Второй вариант показал результат лучше.

В канонической версии используется постоянный вектор движения и при большом количестве жизней это приводило бы к движению бактерий вдоль прямой линии по пространству поиска, если бы эта линия не проходила через какой либо экстремум лучше, то этот процесс прямолинейного движения происходил бесконечно, но здесь счетчик выполняет роль принудительного кувырка, что позволяет бактерии избегать прямолинейного движения на протяжении всей своей жизни и на функциях с участками не имеющими градиента в конечном итоге все равно приведет к месту, где она может начать улучшать свою приспособленность.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c  [];   //coordinates
  double v  [];   //vector
  double f;       //current health
  double fLast;   //previous health
  double lifeCNT; //life counter
};
//——————————————————————————————————————————————————————————————————————————————

Обьявим класс алгоритма BFO как C_AO_BFO. Класс содержит обьявления колонии бактерий, границы поиского пространства, значение наилучшего решения и массив координат наилучшего решения. Также обьявим константные значения параметров алгоритма.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP);   //life counter

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];
  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: bool   evaluation;

  private: void   Sorting ();
  private: double SeInDiSp             (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Открытый метод Init () предназначен для инициализации константных переменных, распределения размеров массивов, сброса флагов и значения наилучшего решения.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP)    //life counter
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,  parameters);
    ArrayResize (b [i].v,  parameters);
    b [i].f  = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,  parameters);
    ArrayResize (bT [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

Первый обязательный для вызова на каждой итерации открытый метод - Swimming (), или плавание бактерий, включает в себя всю основную логику алгоритма.

void C_AO_BFO::Swimming ()
{}

Рассмотрим подробно метод частями. На первой итерации, когда флаг evalution равен false, разбросаем бактерии по всему пространству поиска случайно с равномерным распределением. На этом этапе текущее здоровье (приспособленность) и предыдущее не известны, присвоим соответствующим переменным значение - DBL_MAX. Полученные случайным образом координаты проверяем на выход за границы и применяем шаг изменения оптимизируемых параметров. На этой итерации необходимо задать индивидуальный вектор перемещения для каждой бактерии приватным методом NewVector () (рассмотрим его ниже). Все бактерии плавают равномерно поступательно и прямолинейно с одним и тем же своим индивидуальным вектором пока не будут выполнены условия для его изменения.

//----------------------------------------------------------------------------
if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f  = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
}

На второй и последующих итерациях выполняются операции плавания, кувыркания, репликации и уничтожения бактерий при достижении лимита жизней. Первой в логике является операция репродукции (с заданной в параметрах вероятностью), она подразумевает, что колония бактерий отсортирована на предыдущей итерации по убыванию значения здоровья.

Репродукция в алгоритме выполняет важную функцию: ускорение сходимости алгоритма за счет улучшения "генофонда" колонии бактерий. Операция представляет собой воображаемое деление бактерий на две части, причем делиться позволено только первой, лучшей половине колонии. Первая половина колонии делится на двое, оригинальная родительская версия помещается во вторую часть колонии. Родительская бактерия продолжит движение с тем же своим вектором в отличие от его клона. Клон остается на своем месте в колонии и ему назначается новый вектор движения. Родитель и его клон продолжат движение из точки пространства, где произошло деление.

r = RNDfromCI (0.0, 1.0);

//==========================================================================
if (r < reproduction)
{
  int st = populationSize / 2;
  for (int s = 0; s < st; s++)
  {
    //bacterium original--------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [st + s].v [k] = b [s].v [k];
      b [st + s].c [k] = b [s].c [k] + b [s].v [k];
      b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [st + s].fLast = b [s].f;
      b [st + s].lifeCNT++;
    }

    //bacterium clone-------------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT = 0;
    }
  }
}

Далее, если вероятность репликации не реализована, то выполняется проверка на достижение лимита жизней бактерии. В каноническом варианте алгоритма "старая" бактерия должна быть уничтожена, а на её месте, в списке бактерий, необходимо создать новую в случайном месте пространства поиска. В общем случае операций репродукции и хемотаксиса недостаточно для нахождения глобального максимума многоэкстремальной фитнес-функции, поскольку
эти процедуры не позволяют бактериям покидать найденные ими локальные минимумы. Процедура ликвидации как раз призвана преодолеть этот недостаток. Однако, как показала практика экспериментов с этим и с другими алгоритмами, эффективнее в таком случае просто изменить вектор движения. Счетчик жизней при этом сбрасывается. Счетчик - триггер изменения направления движения через заданное количество шагов (жизней). Общее количество бактерий в результате репликации и ликвидации остаётся постоянным.

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);
    b [s].c [k] = b [s].c [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    b [s].fLast = b [s].f;
    b [s].lifeCNT = 0;
  }
}

Если лимит жизней не исчерпан, то реализуем проверку, движется ли бактерия в сторону улучшения градиента фитнесс функции. То есть, проверяем два значения здоровья, на текущей итерации и на предыдущей. Если здоровье улучшилось, то вектор движения сохраняется, в противном случае бактерия должна совершить кувырок (изменить вектор движения).

В канонической версии осуществляется строгая проверка "больше" текущего и предыдущего здоровья, тогда как в моей версии "больше либо равно", что позволяет бактерии продолжать движение даже на совершенно "горизонтальном" участке исследуемой поверхности, где нет градиента фитнес функции, в противном случае бактерия бы кувыркалась бесконечно на одном месте (нет изменения здоровья, а значит и нет направления куда нужно плыть). На этом этапе также нужно сделать проверку на выход полученных новых координат за границы пространства поиска.

else
{
  if (b [s].f >= b [s].fLast)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
  else
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
}

NewVecror () - приватный метод изменения вектора движения (кувырок). Метод применяется для каждой координаты. Смысл тут простой: разницу между границами поиска по соответствующей координате v умножаем на случайное число r из диапазона [-1.0;1.0] и умножаем на масштабный коэффициент lambda (один из параметров алгоритма). Вектор движения бактерия использует без изменений до момента исчерпания лимита жизней (создается новая бактерия на том же месте, но с новым вектором движения), при репликации (клон имеет новый вектор), при ухудшении состояния здоровья (попытка найти новую более благоприятную среду).  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

Второй открытый обязательный к исполнению на каждой итерации метод Evaluation () выполняет вызов метода сортировки, проверяет обновления глобального решения, сравнивая здоровье лучшей в отсортированной колонии бактерии с лучшим найденным решением.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Evaluation ()
{
  Sorting ();

  if (b [0].f > fB)
  {
    fB = b [0].f;
    ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Результаты работы тестового стенда для BFO:

2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash,M1)    C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash,M1)    5 Rastrigin's; Func runs 10000 result: 72.94540549092933
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash,M1)    Score: 0.90383
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash,M1)    25 Rastrigin's; Func runs 10000 result: 54.75744312933767
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash,M1)    Score: 0.67848
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    500 Rastrigin's; Func runs 10000 result: 40.668487609790404
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    Score: 0.50391
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash,M1)    5 Forest's; Func runs 10000 result: 0.8569098398505888
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash,M1)    Score: 0.48471
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash,M1)    25 Forest's; Func runs 10000 result: 0.37618151461180294
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash,M1)    Score: 0.21279
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    500 Forest's; Func runs 10000 result: 0.08748190028975696
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    Score: 0.04948
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash,M1)    5 Megacity's; Func runs 10000 result: 4.8
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash,M1)    Score: 0.40000
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash,M1)    25 Megacity's; Func runs 10000 result: 2.216
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash,M1)    Score: 0.18467
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash,M1)    500 Megacity's; Func runs 10000 result: 0.4232
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash,M1)    Score: 0.03527

Глядя на распечатку результатов тестового стенда, однозначные выводы пока делать рано, необходимо разобрать результаты по отношению к другим участникам тестирования.

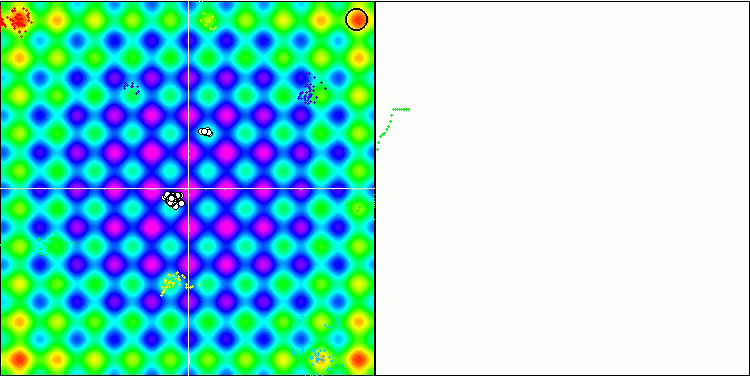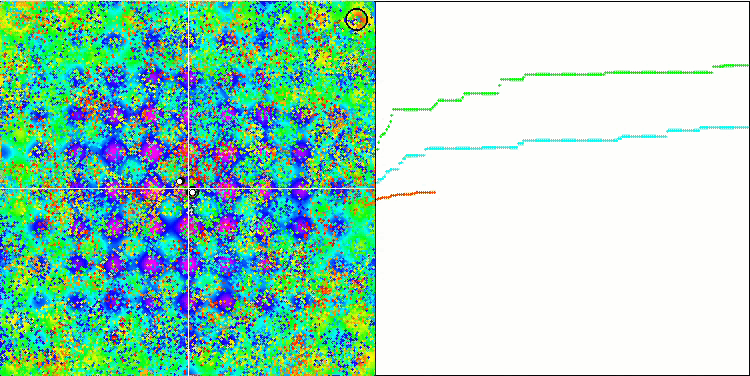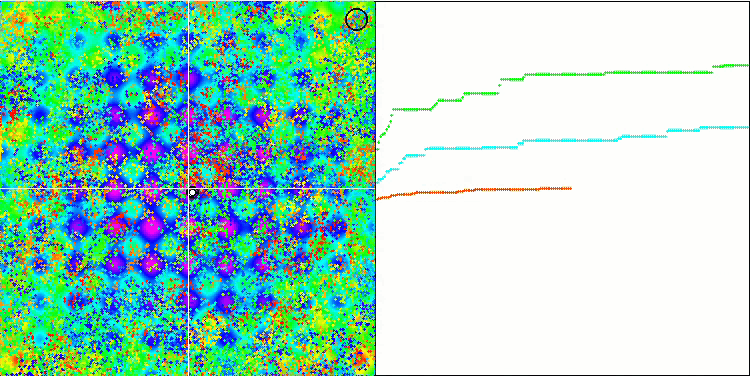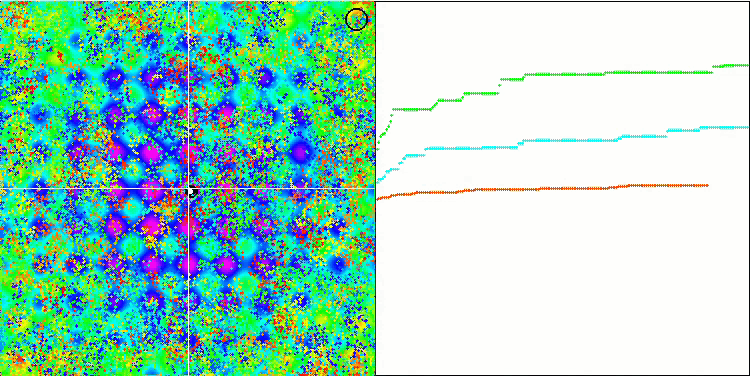
  BFO на тестовой функции Rastrigin.

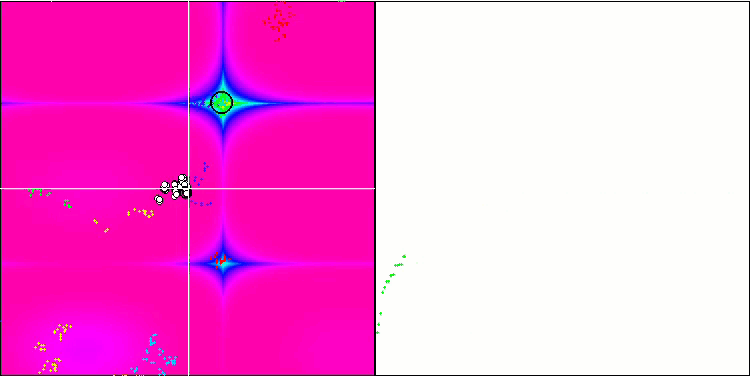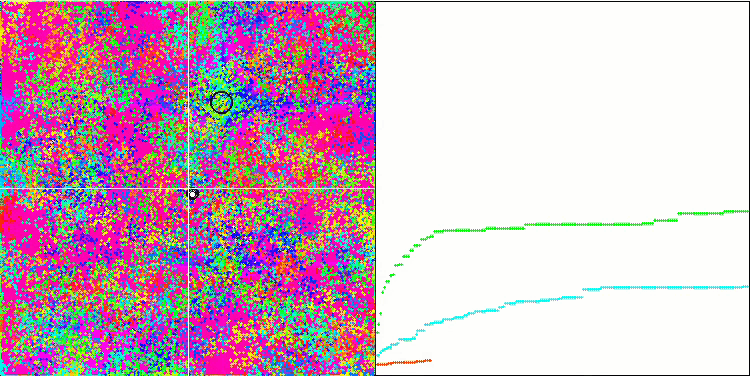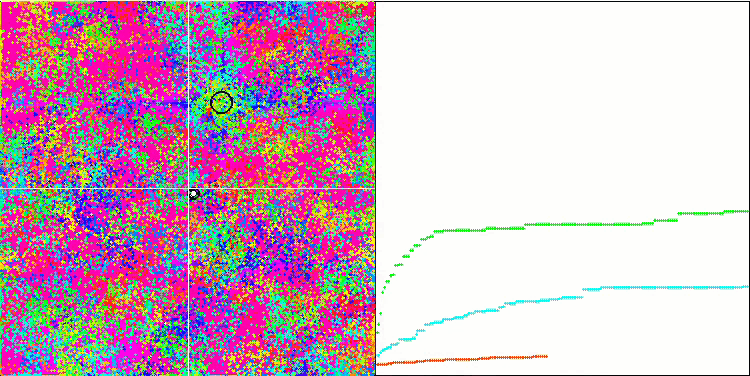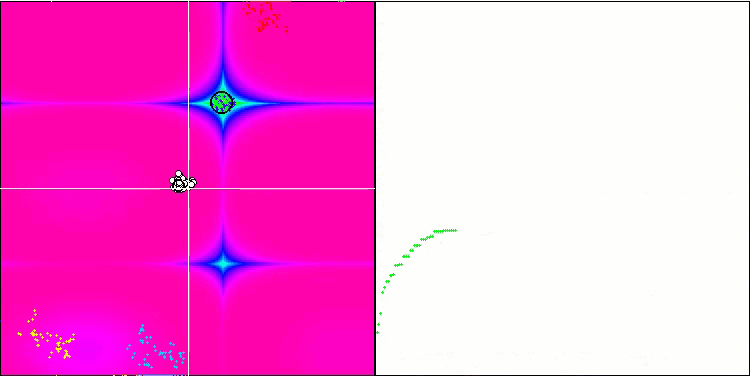
BFO на тестовой функции Forest.

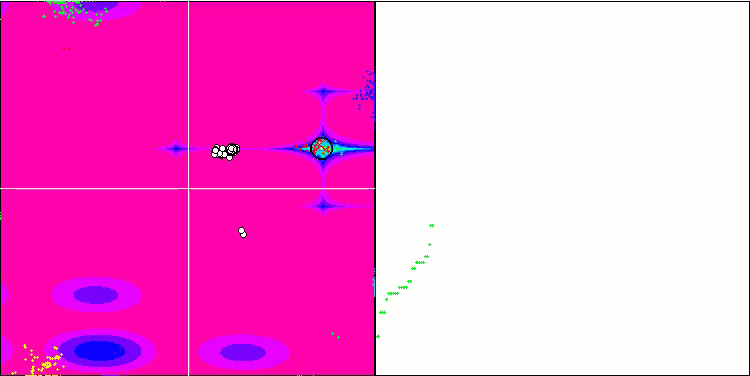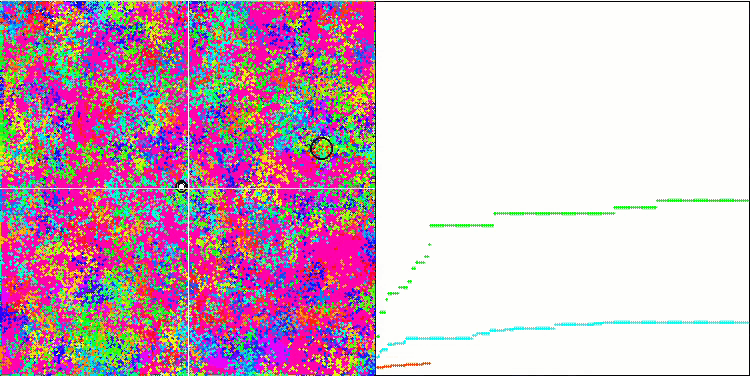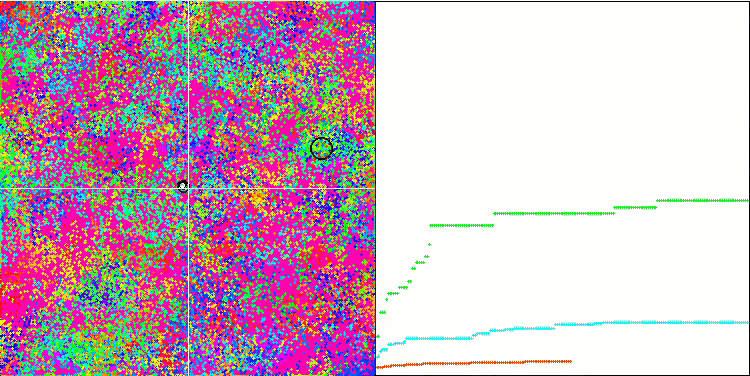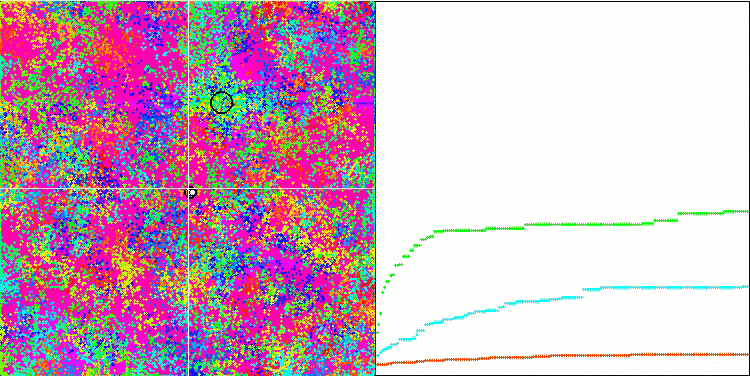
BFO на тестовой функции Megacity.

Обратим внимание на визуализацию тестирования. Анимация подтвердила правильность решения заменить знак "больше" на "больше или равно" в нашем алгоритме, это позволило бактериям продолжать движение на горизонтальных участках тестовых функций, особенно это заметно на функциях Forest и Megacity, бактерии пытаются двигаться дальше даже там, где градиента функции нет совсем. Так же необходимо отметить способность колонии бактерий разделяться на несколько отдельных колоний, визуально разделенных территориально на отдельные локальные экстремумы, что можно однозначно считать положительным свойством, хотя в алгоритме и нет никаких логических приемов для образования субколоний. В целом заметно равномерное перемещение бактерий по пространству поиска без попыток резкого скачка в каком-либо из направлений, что объясняется равномерным поступательным движением - хемотаксисом.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
IWO	invasive weed optimization	1,00000	1,00000	0,33519	2,33519	0,79937	0,46349	0,41071	1,67357	0,75912	0,44903	0,94088	2,14903	100,000
ACOm	ant colony optimization M	0,36118	0,26810	0,17991	0,80919	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	0,10959	2,10959	95,996
COAm	cuckoo optimization algorithm M	0,96423	0,69756	0,28892	1,95071	0,64504	0,34034	0,21362	1,19900	0,67153	0,34273	0,45422	1,46848	74,204
FAm	firefly algorithm M	0,62430	0,50653	0,18102	1,31185	0,55408	0,42299	0,64360	1,62067	0,21167	0,28416	1,00000	1,49583	71,024
BA	bat algorithm	0,42290	0,95047	1,00000	2,37337	0,17768	0,17477	0,33595	0,68840	0,15329	0,07158	0,46287	0,68774	59,650
ABC	artificial bee colony	0,81573	0,48767	0,22588	1,52928	0,58850	0,21455	0,17249	0,97554	0,47444	0,26681	0,35941	1,10066	57,237
BFO	bacterial foraging optimization	0,70129	0,46155	0,11627	1,27911	0,41251	0,26623	0,26695	0,94569	0,42336	0,34491	0,50973	1,27800	55,516
FSS	fish school search	0,48850	0,37769	0,11006	0,97625	0,07806	0,05013	0,08423	0,21242	0,00000	0,01084	0,18998	0,20082	20,109
PSO	particle swarm optimisation	0,21339	0,12224	0,05966	0,39529	0,15345	0,10486	0,28099	0,53930	0,08028	0,02385	0,00000	0,10413	14,232
RND	random	0,17559	0,14524	0,07011	0,39094	0,08623	0,04810	0,06094	0,19527	0,00000	0,00000	0,08904	0,08904	8,142
GWO	grey wolf optimizer	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,18977	0,04119	0,01802	0,24898	1,000

Настало время разобрать результаты тестирования. BFO разместился в середине рейтинговой таблице, получив в составе текущего списка участвующих алгоритмов общий балл чуть более 55. Результаты нельзя назвать впечатляющими, но и плохими тоже. В частности, хорошие результаты оказались на функции Rastrigin с 10 переменными, с 50 и 1000 переменными результаты заметно хуже. Так же алгоритм не особо хорошо показал себя на функции Forest. Вызывает удивление относительно неплохое поведение на дискретной функции Megacity, хотя каких-либо механизмов для работы на подобного вида функциях в алгоритме не предусмотрено, а также неплохую относительно других алгоритмов масштабируемость (тест с 1000 параметров Megacity).

BFO представляет собой научную область с широким диапазоном возможностей. Существует ряд аспектов бактериального поиска пищи и поиска пищи у животных в целом, которые могут быть смоделированы для повышения улучшенной результативности оптимизации. Для алгоритма BFO автоматическая адаптация регулировочных параметров, возможно, имеет особое значение, поскольку параметров достаточно много, и она может дать улучшенную результативность, что является поводом для дополнительных экспериментов.

BFO обладает рядом преимуществ, включая не высокую чувствительность к начальным значениям координат при инициализации и выбору параметров, неплохую надежность, простоту логики, простоту реализации, возможность распараллеливания и глобальный поиск. Таким образом, алгоритм BFO применяется для решения широкого круга задач оптимизации. Однако BFO имеет и некоторое количество недостатков, в том числе медленную скорость сходимости, невозможность в некоторых случаях выйти за пределы локальных оптимумов и фиксированную длину шага. BFO — это метаэвристика, то есть это просто концептуальная структура, которую можно использовать для разработки модификаций алгоритма. Версия BFO, которую я представил здесь, является лишь одной из многих возможностей, и ее следует рассматривать как отправную точку для экспериментов, а не как последнее слово по теме.

Гистограмма результатов тестирования алгоритмов на рисунке 3.

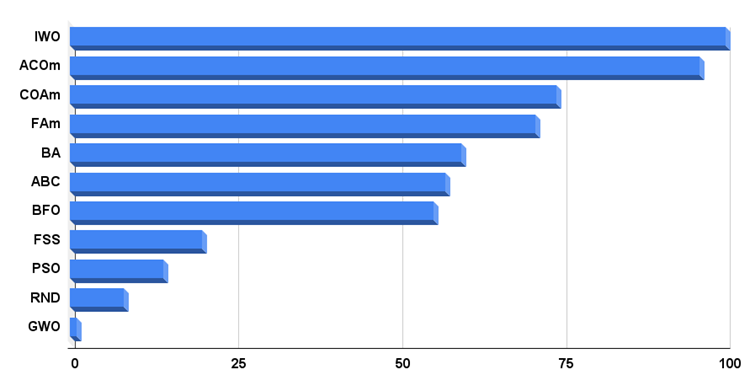
Рисунок 3. Гистограмма итоговых результатов тестирования алгоритмов.

Выводы по свойствам алгоритма оптимизации бактериального поиска пищи (BFO):

Плюсы:
1. Быстрый.
2. Простая логика.
3. Хотя и медленно, но продолжает сходиться на протяжении всех итераций.

Минусы:
1. Медленная сходимость.
2. Не предусмотрены методы выхода из локальных экстремумов.