Criação de uma estratégia de retorno à média com base em aprendizado de máquina

Introdução

Neste artigo, é proposto um novo método para criar sistemas de trading com base em aprendizado de máquina. No artigo anterior, já foram apresentadas formas de aplicar a clusterização à tarefa de inferência causal. Aqui, a clusterização será utilizada para dividir séries temporais financeiras em vários regimes com propriedades únicas, e depois serão construídos e verificados sistemas de trading em cada um deles.

Além disso, veremos alguns métodos de rotulação de exemplos para estratégias de retorno à média e os testaremos no par de moedas EUR/GBP, considerado lateral, de modo que tais estratégias devem ser aplicáveis a ele por completo.

No final do artigo será possível treinar diferentes modelos de aprendizado de máquina em Python e convertê-los em sistemas de trading para o terminal MetaTrader 5.

Preparação dos pacotes necessários

O treinamento dos modelos será feito em Python, portanto é necessário garantir a instalação dos seguintes pacotes:

import math
import pandas as pd
import pickle
from datetime import datetime
from catboost import CatBoostClassifier

from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans

from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import tester
from bots.botlibs.export_lib import export_model_to_ONNX

Os três últimos módulos foram escritos por mim e estarão anexados ao final do artigo. Em cada um deles, é possível importar outros pacotes, como Scipy, Numpy, Sklearn e Numba, que também devem ser instalados. Eles são amplamente conhecidos e de acesso aberto, portanto não deve haver problemas com a instalação.

Se você estiver usando uma versão limpa do Python, abaixo está a lista de pacotes que será necessário instalar:

pip install numpy
pip install pandas
pip install scipy
pip install scikit-learn
pip install catboost
pip install numba

Também pode ser necessário usar caminhos absolutos de importação das bibliotecas anexadas no final do artigo, dependendo do ambiente de desenvolvimento e da localização delas.

O código foi projetado de forma que não dependa muito da versão do interpretador Python ou de pacotes específicos, mas é melhor usar versões estáveis e atualizadas.

Como é possível fazer a anotação de exemplos para estratégias de retorno à média

Vamos relembrar como rotulamos os exemplos nos artigos anteriores. Era criado um laço no qual a duração de cada trade individual era definida aleatoriamente, por exemplo, de 1 a 15 barras. Depois, dependendo de se o mercado subiu ou caiu nesse número de barras desde a abertura da operação virtual, era atribuída uma marca de compra ou venda. A função retornava um dataframe com características e rótulos já anotados e, assim, o conjunto de dados estava totalmente pronto para o treinamento de um modelo de aprendizado de máquina.

def get_labels(dataset, markup, min = 1, max = 15) -> pd.DataFrame:
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'].iloc[i]
        future_pr = dataset['close'].iloc[i + rand]

        if (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
        
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2.0].index)
    return dataset

No entanto, esse tipo de anotação tem uma desvantagem significativa: é aleatória. Ao rotular os dados dessa maneira, não estamos incorporando nenhuma ideia sobre quais padrões o modelo de aprendizado de máquina deve aproximar. Por isso, o resultado dessa anotação e do treinamento também será, em grande parte, aleatório. Tentamos corrigir isso com múltiplos treinamentos, usando força bruta e complicando as próprias arquiteturas dos algoritmos, porém, a anotação em si continuava sem sentido. Devido ao sampling aleatório, apenas alguns modelos conseguiam passar no OOS (teste em novos dados).

Neste artigo eu proponho uma nova abordagem para a anotação de trades, baseada na filtragem da série temporal original. Vamos analisar essa anotação diretamente em um exemplo.

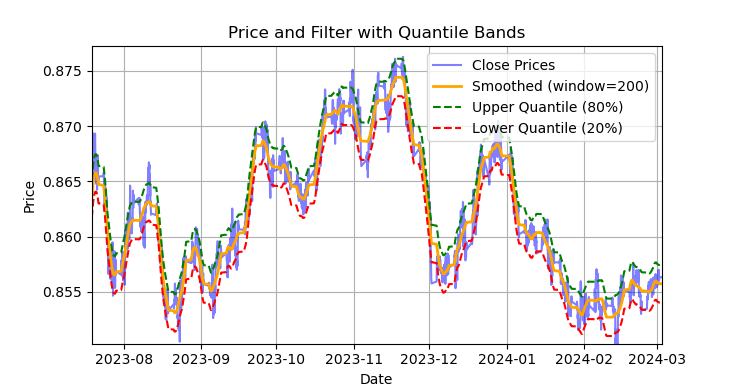
Fig. 1 Mostra a linha suavizada pelo filtro de Savitzky-Golay e as faixas dos quantis 20 e 80

A fig. 1 mostra a linha suavizada pelo filtro de Savitzky-Golay e as faixas dos quantis 20 e 80, que se assemelham, de certa forma, às bandas de Bollinger. A principal diferença entre o filtro de Savitzky-Golay e uma média móvel comum é que o primeiro não apresenta atraso em relação aos preços. Graças a essa propriedade, o filtro suaviza bem os preços e o "ruído" residual aparece como desvios em relação aos valores médios (os próprios valores do filtro), o que pode ser usado para desenvolver uma estratégia de retorno à média. Quando o preço cruza as faixas superior ou inferior, forma-se um sinal de venda ou compra. Se o preço cruzar a linha superior, será um sinal de venda. Se o preço cruzar a linha inferior, será um sinal de compra.

O filtro de Savitzky-Golay é um filtro digital usado para suavizar dados e reduzir ruído, preservando ao mesmo tempo características importantes do sinal, como picos e tendências. Ele foi proposto por Abraham Savitzky e Marcel J. E. Golay em 1964. Esse filtro é amplamente aplicado em processamento de sinais e análise de dados.

O filtro de Savitzky-Golay aproxima os dados localmente por meio de um polinômio de baixo grau (geralmente de segundo a quarto grau) pelo método dos mínimos quadrados.  Para cada ponto de dados, é escolhida uma vizinhança (janela) e, dentro dela, os dados são aproximados por um polinômio. Após a aproximação, o valor no ponto central da janela é substituído pelo valor calculado do polinômio. Isso permite suavizar o ruído, preservando a forma do sinal.

A seguir está o código para construir e avaliar visualmente o filtro.

def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8], polyorder=3):
    # Calculate smoothed prices
    smoothed = savgol_filter(dataset['close'], 
                            window_length=rolling, 
                            polyorder=polyorder)
    
    # Calculate difference between prices and filter
    lvl = dataset['close'] - smoothed
    
    # Get quantile values
    q_low, q_high = lvl.quantile(quantiles).tolist()
    
    # Calculate bands based on quantiles
    upper_band = smoothed + q_high  # Upper band
    lower_band = smoothed + q_low   # Lower band
    
    # Create plot
    plt.figure(figsize=(14, 7))
    plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5)
    plt.plot(dataset.index, smoothed, label=f'Smoothed (window={rolling})', color='orange', linewidth=2)
    plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', 
             color='green', linestyle='--')
    plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', 
             color='red', linestyle='--')
    
    # Configure display
    plt.title('Price and Filter with Quantile Bands')
    plt.xlabel('Date')
    plt.ylabel('Price')
    plt.legend()
    plt.grid(True)
    plt.show()

Portanto, é incorreto aplicar esse filtro em tempo real em séries temporais não estacionárias, pois os últimos valores podem ser redesenhados, mas para a anotação de trades em dados já existentes ele é perfeitamente adequado.

Vamos escrever o código que vai implementar a anotação dos exemplos de treinamento usando o filtro de Savitzky-Golay. A função de anotação, junto com outras funções semelhantes, está no módulo Python labeling_lib.py, que depois será importado em nosso projeto.

@njit
def calculate_labels_filter(close, lvl, q):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        curr_lvl = lvl[i]

        if curr_lvl > q[1]:
            labels[i] = 1.0
        elif curr_lvl < q[0]:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:
    """
    Generates labels for a financial dataset based on price deviation from a Savitzky-Golay filter.

    This function applies a Savitzky-Golay filter to the closing prices to generate a smoothed
    price trend. It then calculates trading signals (buy/sell) based on the deviation of the 
    actual price from this smoothed trend. Buy signals are generated when the price is 
    significantly below the smoothed trend, anticipating a potential price reversal. 

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling (int, optional): Window size for the Savitzky-Golay filter. Defaults to 200.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - The temporary 'lvl' column is removed. 
    """

    # Calculate smoothed prices using the Savitzky-Golay filter
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder)
    
    # Calculate the difference between the actual closing prices and the smoothed prices
    diff = dataset['close'] - smoothed_prices
    dataset['lvl'] = diff  # Add the difference as a new column 'lvl' to the DataFrame
    
    # Remove any rows with NaN values 
    dataset = dataset.dropna()
    
    # Calculate the quantiles of the 'lvl' column (price deviation)
    q = dataset['lvl'].quantile(quantiles).to_list() 

    # Extract the closing prices and the calculated 'lvl' values as NumPy arrays
    close = dataset['close'].values
    lvl = dataset['lvl'].values
    
    # Calculate buy/sell labels using the 'calculate_labels_filter' function 
    labels = calculate_labels_filter(close, lvl, q) 

    # Trim the dataset to match the length of the calculated labels
    dataset = dataset.iloc[:len(labels)].copy()
    
    # Add the calculated labels as a new 'labels' column to the DataFrame
    dataset['labels'] = labels
    
    # Remove any rows with NaN values
    dataset = dataset.dropna()
    
    # Remove rows where the 'labels' column has a value of 2.0 (no signals)
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)
    
    # Return the modified DataFrame with the 'lvl' column removed
    return dataset.drop(columns=['lvl']) 

Para acelerar o processo de anotação é usado o pacote Numba, que já foi apresentado no artigo anterior.

A função get_labels_filter() recebe o dataset original com os preços e as features construídas a partir deles, o tamanho da janela de aproximação para o filtro, os limites do quantil inferior e superior e o grau do polinômio. Na saída, essa função adiciona os rótulos de compra ou venda ao dataset original, que então pode ser usado como conjunto de treinamento.

O laço de passagem pelo histórico está implementado em uma função separada chamada calc_labels_filter, que executa os cálculos pesados usando o pacote Numba.

Esse tipo de anotação tem suas particularidades:

• nem todos os trades anotados dão lucro, já que a mudança de preço após o cruzamento com as bandas nem sempre segue na direção oposta. Por isso, podem surgir exemplos falsamente marcados como compra ou venda.
• essa limitação, em teoria, é compensada pelo fato de que a anotação é homogênea e não aleatória, e por isso exemplos falsamente marcados podem ser tratados como erros de aprendizado ou da própria estratégia de trading no geral, o que pode resultar em menor sobreajuste no final.

A descrição completa da lógica de anotação de trades é apresentada abaixo:

Função calculate_labels_filter

Dados de entrada:

• close: array de preços de fechamento
• lvl: array de desvios do preço em relação à tendência suavizada
• q: array de quantis que definem as zonas de sinais

Lógica:

1. Inicialização: Criamos um array vazio labels do mesmo tamanho que close, para armazenar os sinais.

2. Laço pelos preços: Para cada preço close[i] e o desvio correspondente lvl[i]:

• Sinal "Sell": Se o desvio lvl[i] for maior que o quantil superior q[1], então o preço está bem acima da tendência suavizada, indicando um sinal de "Sell" (labels[i] = 1.0).
• Sinal "Buy": Se o desvio lvl[i] for menor que o quantil inferior q[0], então o preço está bem abaixo da tendência suavizada, indicando um sinal de "Buy" (labels[i] = 0.0).
• Sem sinal: Nos outros casos (quando o desvio está entre os quantis), nenhum sinal é gerado (labels[i] = 2.0).

3. Retorno do resultado: A função retorna o array labels com os sinais.

Função get_labels_filter

Dados de entrada:

• dataset: DataFrame com dados financeiros contendo a coluna 'close' (preços de fechamento)
• rolling: tamanho da janela para suavização do filtro de Savitzky-Golay
• quantiles: quantis para definir as zonas de sinais
• polyorder: ordem do polinômio para a suavização de Savitzky-Golay

Lógica:

1. Suavização do preço:

• Calculamos os preços suavizados smoothed_prices com o filtro de Savitzky-Golay, aplicado aos preços de fechamento (dataset['close']).

2. Cálculo do desvio:

• Calculamos a diferença (diff) entre os preços de fechamento reais e os preços suavizados.
• Adicionamos essa diferença como uma nova coluna 'lvl' no DataFrame.

3. Remoção de valores ausentes:

• Removemos as linhas com valores ausentes (NaN) do DataFrame.

4. Cálculo dos quantis:

• Calculamos os quantis para a coluna 'lvl', que serão usados para definir as zonas de sinais.

5. Cálculo dos sinais:

• Chamamos a função calculate_labels_filter, passando os preços de fechamento, os desvios e os quantis. 
• Obtemos o array labels com os sinais.

6. Processamento do DataFrame:

• Cortamos o DataFrame para o mesmo tamanho do array labels.
• Adicionamos o array labels como uma nova coluna 'labels' no DataFrame.
• Removemos as linhas em que 'labels' é igual a 2.0 (sem sinal).
• Removemos a coluna temporária 'lvl'.

7. Retorno do resultado: A função retorna o DataFrame modificado com os sinais "Buy" e "Sell" na coluna 'labels'.

O método de anotação descrito acima servirá de referência, pois demonstra os princípios básicos de anotação para uma estratégia de retorno à média. Trata-se de um método funcional que pode ser utilizado. Podemos generalizá-lo e modificá-lo para o caso de múltiplos filtros e para considerar a variância variável dos desvios em relação ao valor médio. A seguir, está a função get_labels_multiple_filters, que implementa essas modificações.

@njit
def calc_labels_multiple_filters(close, lvls, qs):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        label_found = False
        
        for j in range(len(lvls)):
            curr_lvl = lvls[j][i]
            curr_q_low = qs[j][0][i]
            curr_q_high = qs[j][1][i]
            
            if curr_lvl > curr_q_high:
                labels[i] = 1.0
                label_found = True
                break
            elif curr_lvl < curr_q_low:
                labels[i] = 0.0
                label_found = True
                break
                
        if not label_found:
            labels[i] = 2.0
            
    return labels

def get_labels_multiple_filters(dataset, 
                              rolling_periods=[200, 400, 600], 
                              quantiles=[.45, .55], 
                              window=100,
                              polyorder=3) -> pd.DataFrame:
    """
    Generates trading signals (buy/sell) based on price deviation from multiple 
    smoothed price trends calculated using a Savitzky-Golay filter with different
    rolling periods and rolling quantiles. 

    This function applies a Savitzky-Golay filter to the closing prices for each 
    specified 'rolling_period'. It then calculates the price deviation from these
    smoothed trends and determines dynamic "reversion zones" using rolling quantiles.
    Buy signals are generated when the price is within these reversion zones 
    across multiple timeframes.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling_periods (list, optional): List of rolling window sizes for the Savitzky-Golay filter. 
                                           Defaults to [200, 400, 600].
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.05, .95].
        window (int, optional): Window size for calculating rolling quantiles. Defaults to 100.
        polyorder (int, optional): Polynomial order for the Savitzky-Golay filter. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed. 
    """
    
    # Create a copy of the dataset to avoid modifying the original
    dataset = dataset.copy()
    
    # Lists to store price deviation levels and quantiles for each rolling period
    all_levels = []
    all_quantiles = []
    
    # Calculate smoothed price trends and rolling quantiles for each rolling period
    for rolling in rolling_periods:
        # Calculate smoothed prices using the Savitzky-Golay filter
        smoothed_prices = savgol_filter(dataset['close'].values, 
                                      window_length=rolling, 
                                      polyorder=polyorder)
        # Calculate the price deviation from the smoothed prices
        diff = dataset['close'] - smoothed_prices
        
        # Create a temporary DataFrame to calculate rolling quantiles
        temp_df = pd.DataFrame({'diff': diff})
        
        # Calculate rolling quantiles for the price deviation
        q_low = temp_df['diff'].rolling(window=window).quantile(quantiles[0])
        q_high = temp_df['diff'].rolling(window=window).quantile(quantiles[1])
        
        # Store the price deviation and quantiles for the current rolling period
        all_levels.append(diff)
        all_quantiles.append([q_low.values, q_high.values])
    
    # Convert lists to NumPy arrays for faster calculations (potentially using Numba)
    lvls_array = np.array(all_levels)
    qs_array = np.array(all_quantiles)
    
    # Calculate buy/sell labels using the 'calc_labels_multiple_filters' function 
    labels = calc_labels_multiple_filters(dataset['close'].values, lvls_array, qs_array)
    
    # Add the calculated labels to the DataFrame
    dataset['labels'] = labels
    
    # Remove rows with NaN values and no signals (labels == 2.0)
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)
    
    # Return the DataFrame with the new 'labels' column
    return dataset

Essa função pode receber uma quantidade ilimitada de parâmetros de suavização para o filtro de Savitzky-Golay. Isso pode trazer uma vantagem extra, pois a anotação contará com vários filtros de diferentes períodos simultaneamente. Para a formação de um sinal, basta que o desvio em relação à média, na distância definida pelos limites dos quantis, seja atingido em pelo menos um dos filtros.

Isso permite construir uma estrutura hierárquica de anotação de trades. Por exemplo, primeiro, é verificada a condição para o filtro de alta frequência; depois, para o de média frequência; e, por fim, para o de baixa frequência. Como os sinais do filtro de baixa frequência são mais confiáveis, os sinais anteriores serão sobrescritos por um sinal desse filtro, caso ele surja. Mas, se o filtro de baixa frequência não gerar sinal, os trades ainda serão anotados com base nos sinais dos filtros anteriores. Isso contribui para aumentar o número de exemplos anotados e elevar os limiares de entrada (quantis), já que aumenta a chance de surgimento de pelo menos um sinal no conjunto de filtros.

O cálculo dos quantis agora é feito em uma janela deslizante com período ajustável, o que permite levar em conta a variância variável dos desvios em relação à média, resultando em sinais mais precisos.

Por fim, pode-se considerar o caso de trades assimétricos, partindo da hipótese de que, para a anotação de compras e vendas, devido ao viés da média das cotações, podem ser necessários filtros com diferentes períodos de suavização. Essa abordagem está implementada na função get_labels_filter_bidirectional.

@njit
def calc_labels_bidirectional(close, lvl1, lvl2, q1, q2):
    labels = np.empty(len(close), dtype=np.float64)
    for i in range(len(close)):
        curr_lvl1 = lvl1[i]
        curr_lvl2 = lvl2[i]

        if curr_lvl1 > q1[1]:
            labels[i] = 1.0
        elif curr_lvl2 < q2[0]:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:
    """
    Generates trading labels based on price deviation from two Savitzky-Golay filters applied
    in opposite directions (forward and reversed) to the closing price data.

    This function calculates trading signals (buy/sell) based on the price's 
    position relative to smoothed price trends generated by two Savitzky-Golay filters 
    with potentially different window sizes (`rolling1`, `rolling2`). 

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        rolling1 (int, optional): Window size for the first Savitzky-Golay filter. Defaults to 200.
        rolling2 (int, optional): Window size for the second Savitzky-Golay filter. Defaults to 200.
        quantiles (list, optional): Quantiles to define the "reversion zones". Defaults to [.45, .55].
        polyorder (int, optional): Polynomial order for both Savitzky-Golay filters. Defaults to 3.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - Temporary 'lvl1' and 'lvl2' columns are removed.
    """

    # Apply the first Savitzky-Golay filter (forward direction)
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling1, polyorder=polyorder)
    
    # Apply the second Savitzky-Golay filter (could be in reverse direction if rolling2 is negative)
    smoothed_prices2 = savgol_filter(dataset['close'].values, window_length=rolling2, polyorder=polyorder)

    # Calculate price deviations from both smoothed price series
    diff1 = dataset['close'] - smoothed_prices
    diff2 = dataset['close'] - smoothed_prices2

    # Add price deviations as new columns to the DataFrame
    dataset['lvl1'] = diff1
    dataset['lvl2'] = diff2
    
    # Remove rows with NaN values 
    dataset = dataset.dropna()

    # Calculate quantiles for the "reversion zones" for both price deviation series
    q1 = dataset['lvl1'].quantile(quantiles).to_list()
    q2 = dataset['lvl2'].quantile(quantiles).to_list()

    # Extract relevant data for label calculation
    close = dataset['close'].values
    lvl1 = dataset['lvl1'].values
    lvl2 = dataset['lvl2'].values
    
    # Calculate buy/sell labels using the 'calc_labels_bidirectional' function
    labels = calc_labels_bidirectional(close, lvl1, lvl2, q1, q2)

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove bad signals (if any)
    
    # Return the DataFrame with temporary columns removed
    return dataset.drop(columns=['lvl1', 'lvl2']) 

Essa função recebe os períodos de suavização rolling1 e rolling2, que correspondem, respectivamente, às operações de venda e de compra. Ao variar esses parâmetros, é possível tentar obter uma anotação mais precisa e uma maior capacidade de generalização em novos dados. Se o par de moedas apresentar uma tendência de alta e for mais vantajoso abrir operações de compra, por exemplo, o tamanho da janela rolling1 pode ser aumentado para que as operações de venda sejam anotadas com menos frequência ou só apareçam em momentos de fortes reversões de tendência. Para operações de compra, é possível reduzir o tamanho da janela rolling2, fazendo com que as operações de compra se tornem mais numerosas do que as de venda.

Anotação com restrição a trades estritamente lucrativos e com escolha de filtro

Foi mencionado acima que os anotadores de trades propostos permitem a presença de operações anotadas que são sabidamente perdedoras. Isso não é um bug, mas sim uma característica.

É possível adicionar verificações que garantam a anotação apenas de operações lucrativas. Isso pode ser útil nos casos em que se deseja aproximar o gráfico de balanço de uma linha reta ideal, sem grandes rebaixamentos.

Até aqui foi utilizado apenas o filtro de Savitzky-Golay, mas é interessante aumentar a variedade incluindo como filtros a média móvel simples e o spline.

Vamos analisar as opções desses samplers de trades. Tomaremos como base a função get_labels_mean_reversion, que prevê restrições de lucratividade e a escolha do filtro.

@njit
def calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q):
    labels = np.empty(len(close) - max_l, dtype=np.float64)
    for i in range(len(close) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close[i]
        curr_lvl = lvl[i]
        future_pr = close[i + rand]

        if curr_lvl > q[1] and (future_pr + markup) < curr_pr:
            labels[i] = 1.0
        elif curr_lvl < q[0] and (future_pr - markup) > curr_pr:
            labels[i] = 0.0
        else:
            labels[i] = 2.0
    return labels

def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame:
    """
    Generates labels for a financial dataset based on mean reversion principles.

    This function calculates trading signals (buy/sell) based on the deviation of
    the price from a chosen moving average or smoothing method. It identifies
    potential buy opportunities when the price deviates significantly below its 
    smoothed trend, anticipating a reversion to the mean.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        rolling (float, optional): Rolling window size for smoothing/averaging. 
                                     If method='spline', this controls the spline smoothing factor.
                                     Defaults to 0.5.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        method (str, optional): Method for calculating the price deviation:
                                 - 'mean': Deviation from the rolling mean.
                                 - 'spline': Deviation from a smoothed spline.
                                 - 'savgol': Deviation from a Savitzky-Golay filter.
                                 Defaults to 'spline'.
        shift (int, optional): Shift the smoothed price data forward (positive) or backward (negative).
                                 Useful for creating a lag/lead effect. Defaults to 0.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - The temporary 'lvl' column is removed. 
    """

    # Calculate the price deviation ('lvl') based on the chosen method
    if method == 'mean':
        dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean())
    elif method == 'spline':
        x = np.array(range(dataset.shape[0]))
        y = dataset['close'].values
        spl = UnivariateSpline(x, y, k=3, s=rolling) 
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))
        yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift
        dataset['lvl'] = dataset['close'] - yHat_shifted
        dataset = dataset.dropna()  # Remove NaN values potentially introduced by spline/shift
    elif method == 'savgol':
        smoothed_prices = savgol_filter(dataset['close'].values, window_length=int(rolling), polyorder=3)
        dataset['lvl'] = dataset['close'] - smoothed_prices

    dataset = dataset.dropna()  # Remove NaN values before proceeding
    q = dataset['lvl'].quantile(quantiles).to_list()  # Calculate quantiles for the 'reversion zone'

    # Prepare data for label calculation
    close = dataset['close'].values
    lvl = dataset['lvl'].values
    
    # Calculate buy/sell labels 
    labels = calculate_labels_mean_reversion(close, lvl, markup, min_l, max_l, q) 

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)  # Remove sell signals (if any)
    return dataset.drop(columns=['lvl'])  # Remove the temporary 'lvl' column 

Para verificar a lucratividade das operações, foi utilizado o código da função get_labels, apresentada no início da seção e utilizada em artigos anteriores. Nesse princípio, são selecionadas as operações que passaram pela anotação por meio de um filtro. Apenas as que, em um número definido de passos à frente, resultam em lucro são mantidas; as demais são anotadas como 2.0 e depois removidas do dataset. Além disso, foram adicionados dois novos filtros: a média móvel simples e o spline.

Se a média móvel simples é amplamente conhecida entre traders, o método de construção do spline não é familiar para todos e precisa ser detalhado.

Splines são uma ferramenta flexível para aproximação de funções. Em vez de construir um único polinômio complexo para toda a função, os splines dividem o domínio em intervalos e constroem polinômios separados em cada intervalo. Esses polinômios são conectados suavemente nas fronteiras dos intervalos, criando uma curva contínua e suave.

Existem diferentes tipos de splines, mas todos são construídos de forma semelhante:

1. Divisão do domínio: o intervalo original, no qual a função está definida, é dividido em subintervalos por pontos chamados nós.
2. Escolha do grau do polinômio: é definido o grau do polinômio que será usado em cada subintervalo. 
3. Construção dos polinômios: em cada subintervalo é construído um polinômio do grau escolhido, que passa pelos pontos de dados daquele intervalo.
4. Garantia de suavidade: os coeficientes dos polinômios são ajustados de forma que o spline seja suave nas fronteiras dos intervalos. Normalmente isso significa que os valores dos polinômios vizinhos e suas derivadas devem coincidir nos nós.

Os splines podem ser úteis na análise de séries temporais financeiras para:

• Interpolação e suavização de dados: os splines permitem reduzir o ruído nos dados e estimar valores da série temporal em pontos onde não há medições. 
• Modelagem de tendências: os splines podem ser usados para modelar tendências de longo prazo nos dados, separando-as das flutuações de curto prazo.
• Previsão: alguns tipos de splines podem ser utilizados para prever valores futuros da série temporal.
• Estimativa de derivadas: os splines permitem calcular derivadas da série temporal, o que pode ser útil para analisar a velocidade de mudança dos preços.

No nosso caso, vamos suavizar a série temporal com spline e média móvel da mesma forma como foi feito com o filtro de Savitzky-Golay. É possível realizar a anotação usando cada filtro separadamente e depois comparar os resultados para escolher o melhor em cada situação específica.

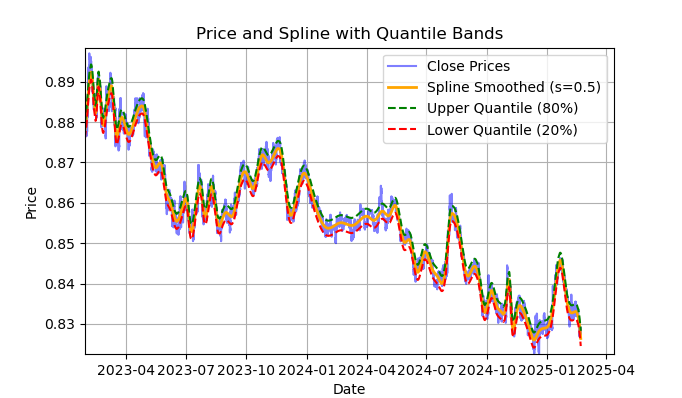
Fig. 2 Mostra a linha suavizada pelo filtro spline e as faixas de 20 e 80 quantis

A fig. 2 mostra a linha suavizada pelo filtro spline e as faixas de 20 e 80 quantis. A principal diferença entre o filtro spline e o filtro de Savitzky-Golay é que o primeiro suaviza a série por meio de funções lineares ou não lineares, dependendo do fator de suavização s (mais adequado quando definido entre 0,1 e 1) e do grau do polinômio (geralmente escolhido entre 1 e 3). Ao variar esses parâmetros, é possível avaliar visualmente as diferenças no suavizamento obtido. No código, o grau do polinômio k=3 está fixado, mas também pode ser alterado.

O código para construção e avaliação visual do spline é o seguinte:

import pandas as pd
from scipy.interpolate import UnivariateSpline
import matplotlib.pyplot as plt

def plot_close_filter_quantiles(dataset, rolling=200, quantiles=[0.2, 0.8]):
    """
    Plots close prices with spline smoothing and quantile bands.

    Args:
        dataset (pd.DataFrame): DataFrame with 'close' column and datetime index.
        rolling (int, optional): Rolling window size for spline smoothing. 
                                  Defaults to 200.
        quantiles (list, optional): Quantiles for band calculation. 
                                     Defaults to [0.2, 0.8].
        s (float, optional): Smoothing factor for UnivariateSpline. 
                             Adjusts the spline stiffness. Defaults to 1000.
    """
    
    # Create spline smoothing
    # Convert datetime index to numerical values (Unix timestamps)
    numerical_index = pd.to_numeric(dataset.index)
    
    # Create spline smoothing using the numerical index
    spline = UnivariateSpline(numerical_index, dataset['close'], k=3, s=rolling)  
    smoothed = spline(numerical_index)
    
    # Calculate difference between prices and filter
    lvl = dataset['close'] - smoothed
    
    # Get quantile values
    q_low, q_high = lvl.quantile(quantiles).tolist()
    
    # Calculate bands based on quantiles
    upper_band = smoothed + q_high
    lower_band = smoothed + q_low
    
    # Create plot
    plt.figure(figsize=(14, 7))
    plt.plot(dataset.index, dataset['close'], label='Close Prices', color='blue', alpha=0.5)
    plt.plot(dataset.index, smoothed, label=f'Spline Smoothed (s={rolling})', color='orange', linewidth=2)
    plt.plot(dataset.index, upper_band, label=f'Upper Quantile ({quantiles[1]*100:.0f}%)', 
             color='green', linestyle='--')
    plt.plot(dataset.index, lower_band, label=f'Lower Quantile ({quantiles[0]*100:.0f}%)', 
             color='red', linestyle='--')
    
    # Configure display
    plt.title('Price and Spline with Quantile Bands')
    plt.xlabel('Date')
    plt.ylabel('Price')
    plt.legend()
    plt.grid(True)
    plt.show()

Abaixo está a descrição detalhada da função calculate_labels_mean_reversion, para compreensão completa do código de anotação de trades.

Função calculate_labels_mean_reversion:

Dados de entrada:

• close: array de preços de fechamento
• lvl: array de desvios dos preços em relação à série suavizada
• markup: margem (em porcentagem)
• min_l: número mínimo de candles para a verificação da condição
• max_l: número máximo de candles para a verificação da condição
• array de quantis que definem as zonas de sinais

Lógica:

1. Inicialização: Criamos um array vazio labels com comprimento len(close) — max_l para armazenar os sinais. O comprimento é reduzido para levar em conta os valores futuros dos preços. 

2. Laço pelos preços: Para cada preço close[i], com índice i de 0 até len(close) — max_l - 1:

• Definimos um número rand aleatório entre min_l e max_l.
• Obtemos o preço atual curr_pr, o desvio atual curr_lvl e o preço futuro future_pr em rand candles à frente. 
• Sinal "Sell": Se curr_lvl for maior que o quantil superior (q[1]) e o preço futuro future_pr, considerando a margem markup, for menor que o preço atual, então labels[i] = 1.0.
• Sinal "Buy": Se curr_lvl for menor que o quantil inferior (q[0]) e o preço futuro future_pr, considerando o desconto da margem markup, for maior que o preço atual, então labels[i] = 0.0.
• Sem sinal: Nos outros casos, labels[i] = 2.0.

3. Retorno do resultado: A função retorna o array labels com os sinais.

Função get_labels_mean_reversion:

Dados de entrada:

• dataset: DataFrame com dados financeiros contendo a coluna 'close'
• markup: margem (em porcentagem)
• min_l: número mínimo de candles para a verificação da condição
• max_l: número máximo de candles para a verificação da condição
• rolling: parâmetro de suavização (tamanho da janela ou coeficiente)
• quantiles: quantis para definir as zonas de sinais
• method: método de suavização ('mean', 'spline', 'savgol')
• shift: deslocamento da série suavizada

Lógica:

1. Cálculo dos desvios: Calculamos os desvios lvl em relação à série suavizada dos preços (close), dependendo do método escolhido method:

• mean: desvio em relação à média móvel 
• spline: desvio em relação à curva suavizada por spline
• savgol: desvio em relação ao filtro suavizado de Savitzky-Golay

2. Remoção de valores ausentes: removemos as linhas com valores ausentes (NaN) do dataset.

3. Cálculo dos quantis: calculamos os quantis q para os desvios lvl.

4. Preparação dos dados: extraímos os arrays de preços close e de desvios lvl do dataset.

5. Cálculo dos sinais:

• Chamamos a função calculate_labels_mean_reversion com os dados preparados para obter o array labels com os sinais.

6. Processamento do DataFrame:

• Cortamos o dataset para o comprimento de labels.
• Adicionamos labels como uma nova coluna 'labels' no dataset.
• Removemos as linhas com valores ausentes (NaN) do dataset.
• Removemos as linhas em que labels é igual a 2.0 (sem sinal).
• Removemos a coluna lvl.

7. Retorno do resultado: A função retorna o dataset modificado com os sinais "Buy" e "Sell" na coluna 'labels'.

Dessa vez para variar, implementaremos uma versão do sampler que verificará as condições em vários filtros com diferentes períodos, e não apenas em um. Se todas as condições em todos os filtros forem atendidas e apontarem para a mesma direção (compra ou venda) e se a operação for lucrativa no intervalo de n barras à frente, ela satisfaz as condições de anotação; caso contrário, é ignorada e removida do conjunto de treinamento.

@njit
def calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows):
    labels = []
    for i in range(len(close_data) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close_data[i]
        future_pr = close_data[i + rand]

        buy_condition = True
        sell_condition = True
        qq = 0
        for rolling in windows:
            curr_lvl = lvl_data[i, qq]            
            if not (curr_lvl >= q[qq][1]):
                sell_condition = False
            if not (curr_lvl <= q[qq][0]):
                buy_condition = False
            qq+=1
    
        if sell_condition and (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif buy_condition and (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    return labels

def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]):
    """
    Generates labels for a financial dataset based on mean reversion 
    principles using multiple smoothing windows.

    This function calculates trading signals (buy/sell) based on the deviation 
    of the price from smoothed price trends calculated using multiple spline 
    smoothing factors (windows). It identifies potential buy opportunities when 
    the price deviates significantly below its smoothed trends across multiple
    timeframes.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        windows (list, optional): List of smoothing factors (rolling window equivalents) 
                                   for spline calculations. Defaults to [0.2, 0.3, 0.5].
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (sell signal) are removed.
                       - Rows with missing values (NaN) are removed. 
    """

    q = []  # Initialize an empty list to store quantiles for each window
    lvl_data = np.empty((dataset.shape[0], len(windows)))  # Initialize a 2D array to store price deviation data

    # Calculate price deviation from smoothed trends for each window
    for i, rolling in enumerate(windows):
        x = np.array(range(dataset.shape[0]))  # Create an array of x-values (time index)
        y = dataset['close'].values  # Extract closing prices
        spl = UnivariateSpline(x, y, k=3, s=rolling)  # Create a spline smoothing function
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))  # Generate smoothed price data
        lvl_data[:, i] = dataset['close'] - yHat  # Calculate price deviation from smoothed prices
        q.append(np.quantile(lvl_data[:, i], quantiles).tolist())  # Calculate and store quantiles

    dataset = dataset.dropna()  # Remove NaN values before proceeding

    close_data = dataset['close'].values  # Extract closing prices 

    # Calculate buy/hold labels using multiple price deviation series
    labels = calculate_labels_mean_reversion_multi(close_data, lvl_data, q, markup, min_l, max_l, windows)

    # Process the dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()  # Trim the dataset to match label length
    dataset['labels'] = labels  # Add the calculated labels as a new column
    dataset = dataset.dropna()  # Remove rows with NaN values
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index)  # Remove sell signals (if any)
    
    return dataset

Por fim, vamos escrever mais uma função de anotação de trades para retorno à média, que calcula os quantis em uma janela deslizante com período definido, e não em toda a série histórica. Isso ajuda a suavizar o impacto da volatilidade variável nos desvios de preço em relação ao valor médio.

@njit
def calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l):
    labels = []
    for i in range(len(close_data) - max_l):
        rand = random.randint(min_l, max_l)
        curr_pr = close_data[i]
        curr_lvl = lvl_data[i]
        curr_vol_group = volatility_group[i]
        future_pr = close_data[i + rand]

        q = quantile_groups[curr_vol_group]

        if curr_lvl > q[1] and (future_pr + markup) < curr_pr:
            labels.append(1.0)
        elif curr_lvl < q[0] and (future_pr - markup) > curr_pr:
            labels.append(0.0)
        else:
            labels.append(2.0)
    return labels

def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:
    """
    Generates trading labels based on mean reversion principles, incorporating
    volatility-based adjustments to identify buy opportunities.

    This function calculates trading signals (buy/sell), taking into account the 
    volatility of the asset. It groups the data into volatility bands and calculates 
    quantiles for each band. This allows for more dynamic "reversion zones" that 
    adjust to changing market conditions.

    Args:
        dataset (pd.DataFrame): DataFrame containing financial data with a 'close' column.
        markup (float): The percentage markup used to determine buy signals.
        min_l (int, optional): Minimum number of consecutive days the markup must hold. Defaults to 1.
        max_l (int, optional): Maximum number of consecutive days the markup is considered. Defaults to 15.
        rolling (float, optional): Rolling window size or spline smoothing factor (see 'method'). 
                                     Defaults to 0.5.
        quantiles (list, optional): Quantiles to define the "reversion zone". Defaults to [.45, .55].
        method (str, optional): Method for calculating the price deviation:
                                 - 'mean': Deviation from the rolling mean.
                                 - 'spline': Deviation from a smoothed spline.
                                 - 'savgol': Deviation from a Savitzky-Golay filter.
                                 Defaults to 'spline'.
        shift (int, optional): Shift the smoothed price data (lag/lead effect). Defaults to 1.
        volatility_window (int, optional): Window size for calculating volatility. Defaults to 20.

    Returns:
        pd.DataFrame: The original DataFrame with a new 'labels' column and filtered rows:
                       - 'labels' column: 
                            - 0: Buy
                            - 1: Sell
                       - Rows where 'labels' is 2 (no signal) are removed.
                       - Rows with missing values (NaN) are removed.
                       - Temporary 'lvl', 'volatility', 'volatility_group' columns are removed.
    """

    # Calculate Volatility
    dataset['volatility'] = dataset['close'].pct_change().rolling(window=volatility_window).std()
    
    # Divide into 20 groups by volatility 
    dataset['volatility_group'] = pd.qcut(dataset['volatility'], q=20, labels=False)
    
    # Calculate price deviation ('lvl') based on the chosen method
    if method == 'mean':
        dataset['lvl'] = (dataset['close'] - dataset['close'].rolling(rolling).mean())
    elif method == 'spline':
        x = np.array(range(dataset.shape[0]))
        y = dataset['close'].values
        spl = UnivariateSpline(x, y, k=3, s=rolling)
        yHat = spl(np.linspace(min(x), max(x), num=x.shape[0]))
        yHat_shifted = np.roll(yHat, shift=shift) # Apply the shift 
        dataset['lvl'] = dataset['close'] - yHat_shifted
        dataset = dataset.dropna() 
    elif method == 'savgol':
        smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=5)
        dataset['lvl'] = dataset['close'] - smoothed_prices

    dataset = dataset.dropna()
    
    # Calculate quantiles for each volatility group
    quantile_groups = {}
    for group in range(20):
        group_data = dataset[dataset['volatility_group'] == group]['lvl']
        quantile_groups[group] = group_data.quantile(quantiles).to_list()
    
    # Prepare data for label calculation (potentially using Numba)
    close_data = dataset['close'].values
    lvl_data = dataset['lvl'].values
    volatility_group = dataset['volatility_group'].values

    # Calculate buy/sell labels 
    labels = calculate_labels_mean_reversion_v(close_data, lvl_data, volatility_group, quantile_groups, markup, min_l, max_l)
    
    # Process dataset and labels
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2.0].index) # Remove sell signals
    
    # Remove temporary columns and return
    return dataset.drop(columns=['lvl', 'volatility', 'volatility_group'])

Assim, já temos uma quantidade de anotadores de trades com os quais é possível experimentar. Os métodos podem ser combinados e novos podem ser criados.

A lista completa dos samplers de trades descritos acima, que fazem parte da biblioteca labeling_lib.py, está apresentada a seguir. A partir deles, é possível modificar os antigos e criar novos, dependendo do seu nível de entendimento das regularidades do mercado e da estratégia desejada. O módulo também contém outros samplers de trades personalizados que não se relacionam com estratégias de retorno à média e, por isso, não foram descritos neste artigo.

# FILTERING BASED LABELING W/O RESTRICTIONS
def get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame
def get_labels_multiple_filters(dataset, rolling_periods=[200, 400, 600], quantiles=[.45, .55], window=100, polyorder=3) -> pd.DataFrame
def get_labels_filter_bidirectional(dataset, rolling1=200, rolling2=200, quantiles=[.45, .55], polyorder=3) -> pd.DataFrame:

# MEAN REVERSION WITH RESTRICTIONS BASED LABELING
def get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0) -> pd.DataFrame
def get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55]) -> pd.DataFrame
def get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=1, volatility_window=20) -> pd.DataFrame:

Agora é hora de passar para a segunda parte do artigo, que trata da clusterização dos regimes de mercado, e depois unir ambas as abordagens para criar sistemas de trading que operem segundo o princípio do retorno à média.

O que clusterizar e por que isso é necessário

Antes de clusterizar qualquer coisa, é preciso entender por que isso é necessário. Imagine um gráfico de cotações que contenha tendência, lateralidade, períodos de alta e baixa volatilidade, diferentes padrões e outras características. Ou seja, o gráfico de cotações não é algo homogêneo, com as mesmas regularidades o tempo todo. Pode-se até dizer que, em diferentes períodos de tempo, existem ou podem existir diferentes regularidades que desaparecem em outros intervalos temporais.

A clusterização permite dividir a série temporal original em vários estados com base em determinados atributos, de modo que cada estado descreva observações semelhantes. Isso pode facilitar a construção de um sistema de trading, já que o treinamento ocorrerá com dados mais homogêneos e consistentes. Pelo menos é o que se pode imaginar. Naturalmente, o sistema de trading não funcionará em todo o período histórico, mas em uma parte selecionada, composta por diferentes momentos cujos valores de atributos pertencem a um determinado cluster.

Após a clusterização, é possível anotar apenas os exemplos selecionados, ou seja, atribuir a eles rótulos de classes únicos para a construção do modelo final. Se um cluster contiver dados homogêneos com observações semelhantes, sua anotação também tende a se tornar mais uniforme e, consequentemente, mais previsível. Podemos pegar vários clusters de dados, anotar cada um separadamente, treinar modelos de aprendizado de máquina com os dados de cada cluster e testá-los tanto nos dados de treinamento quanto nos de teste. Se um cluster permitir que o modelo aprenda bem, ou seja, generalize e faça previsões em novos dados, a tarefa de construir o sistema de trading pode ser considerada praticamente concluída.

Clusterização de séries temporais financeiras para identificação de regimes de mercado

Antes de prosseguir com esta seção, é útil revisar os diferentes tipos de algoritmos de clusterização que foram descritos no artigo anterior. Também foi apresentada uma tabela comparativa de diversos algoritmos de clusterização e os resultados de seus testes. Para este artigo, foi escolhido o algoritmo clássico k-means, por ser o mais rápido e suficientemente eficaz.

Na etapa de criação de atributos com a função get_features, é necessário prever a inclusão, no dataset, especificamente daqueles que serão utilizados para a clusterização. Proponho considerar três opções básicas a partir das quais podemos evoluir. Se você tiver outros atributos que, em sua opinião, descrevam bem os regimes de mercado, poderá utilizá-los. Para isso, é necessário adicionar o cálculo desses atributos à função de formação de características e incluirmos o termo "meta_feature" em seus nomes, para que eles sejam distinguidos dos atributos principais.

def get_features(data: pd.DataFrame) -> pd.DataFrame:
    pFixed = data.copy()
    pFixedC = data.copy()
    count = 0

    for i in hyper_params['periods']:
        pFixed[str(count)] = pFixedC.rolling(i).mean()
        count += 1
    
    for i in hyper_params['periods_meta']:
        pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).skew()
        count += 1

    # for i in hyper_params['periods_meta']:
    #     pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std()
    #     count += 1

    # for i in hyper_params['periods_meta']:
    #     pFixed[str(count)+'meta_feature'] = pFixedC - pFixedC.rolling(i).mean()
    #     count += 1

    return pFixed.dropna()

No primeiro laço é feito o cálculo de todos os atributos definidos na lista 'periods'. Esses são os atributos principais, que serão usados para treinar o modelo de aprendizado de máquina principal, aquele que prevê trades de compra ou venda. Neste caso, tratam-se de médias móveis simples com diferentes períodos.

No segundo laço são calculados os atributos definidos na lista 'periods_meta'. Esses são justamente os atributos que participarão do processo de clusterização dos regimes de mercado. Por padrão, a clusterização será feita com base no viés (skewness) das cotações em uma janela deslizante. Os campos comentados correspondem ao cálculo de atributos pelo desvio padrão em janela deslizante ou pelas variações de preço. A escolha dos atributos é feita de maneira empírica, por meio da experimentação de diferentes opções. Os experimentos mostraram que a clusterização pelo viés (assimetria) separa bem os dados, por isso ela será utilizada no artigo.

O viés (ou assimetria) em distribuições é uma característica que descreve o grau de assimetria da distribuição dos dados em relação ao seu valor médio. O viés mostra o quanto uma distribuição se desvia de uma simétrica (como a normal).  O coeficiente de assimetria (skewness) é usado para medi-lo. A clusterização pelo viés permite separar grupos de dados com características de distribuição semelhantes, o que ajuda a identificar esses regimes. Por exemplo, um viés positivo pode indicar períodos com saltos de preço raros, mas fortes (como durante crises), enquanto um viés negativo pode indicar períodos de mudanças mais suaves.

Depois da formação dos atributos, o dataset final é passado para a função que executa a clusterização. E adiciona uma nova coluna "clusters", que contém os números dos clusters.

def clustering(dataset, n_clusters: int) -> pd.DataFrame:
    data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy()
    meta_X = data.loc[:, data.columns.str.contains('meta_feature')]
    data['clusters'] = KMeans(n_clusters=n_clusters).fit(meta_X).labels_
    return data

Para evitar vazamento de informação, os dados são cortados antes e depois das datas configuradas no algoritmo, de forma que a clusterização seja feita apenas nos dados que participarão do treinamento do modelo. No código também existe a seleção dos atributos usados na clusterização, que são identificados pela palavra-chave 'meta_feature' no nome da coluna.

Todos os hiperparâmetros do algoritmo são reunidos em um dicionário, cujos valores serão usados na geração dos atributos, na definição do período de treinamento e em outros parâmetros.

hyper_params = {
    'symbol': 'EURGBP_H1',
    'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files/MetaTrader 5/MQL5/Include/Mean reversion/',
    # 'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files (x86)/RoboForex MT4 Terminal/MQL4/Include/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.02000,
    'take_profit': 0.00200,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [10],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2021, 1, 1),
    'n_clusters': 10,
    'rolling': 200,
}

• Nome do arquivo no disco que contém as cotações do símbolo
• Caminho de exportação para enviar os modelos treinados ao diretório #include do terminal MetaTrader5
• Identificador do modelo, para diferenciá-los após a exportação, caso seja necessário exportar vários modelos
• Markup, que deve considerar o spread médio e a comissão, em pontos. Para uma anotação mais correta dos trades e para o teste posterior no histórico.
• Stop-loss, suportado pelo testador customizado rápido
• Take-profit
• Lista de períodos para o cálculo dos atributos principais. Cada elemento da lista representa o período de um atributo específico. Quanto mais elementos, mais atributos são gerados
• Lista de períodos para os atributos usados na clusterização
• Data inicial para o treinamento do modelo
• Data final para o treinamento do modelo
• Número de clusters (regimes) em que os dados serão divididos
• Parâmetro da janela deslizante para suavização pelo filtro

Agora vamos juntar tudo, observar o ciclo principal de treinamento dos modelos e analisar todas as etapas, tanto do pré-processamento quanto do próprio treinamento.

# LEARNING LOOP
dataset = get_features(get_prices())
models = []
for i in range(1):
    data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_filter(clustered_data, 
                                           rolling=hyper_params['rolling'],
                                           quantiles=[0.45, 0.55],
                                           polyorder=3
                                            )

        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

Primeiro é criado o dataset, que contém preços e atributos. O processo de criação dos atributos foi descrito anteriormente. Em seguida, é criado o objeto models, que armazenará os modelos já treinados. Depois temos a opção de definir quantas iterações de treinamento serão realizadas no laço. Por padrão, é feita apenas uma iteração. Se for necessário treinar vários modelos, basta indicar a quantidade no iterador range(). 

Após isso, ocorre a clusterização do dataset original, e a cada exemplo é atribuído o número de um cluster. Se nos hiperparâmetros estiver definido n_clusters = 10, esse parâmetro é passado para a função, e a clusterização é feita em 10 clusters. Os experimentos mostraram que 10 clusters é uma quantidade ótima de regimes de mercado, mas, claro, é possível experimentar com esse parâmetro. 

Depois é definido o número final de clusters, seus índices são ordenados em ordem crescente e, para cada número de cluster, são selecionadas apenas as linhas do dataset que pertencem a ele. Não nos interessam clusters com poucos exemplos, então é feita uma verificação para garantir que haja pelo menos 500 observações.

Na etapa seguinte, é chamada a função de anotação de trades para o cluster atualmente selecionado. Neste caso, usei a primeira função de anotação apresentada, a get_labels_filter, que foi o ponto de partida deste artigo. Após a anotação dos trades, os dados são divididos em dois datasets. O primeiro conterá os atributos principais e os rótulos, enquanto o segundo conterá os meta-atributos usados na clusterização, além das marcas 0 e 1. O valor 1 indica que os dados pertencem ao cluster selecionado, enquanto o valor 0 indica que pertencem a qualquer outro cluster diferente do escolhido. Pois queremos que o sistema de trading opere apenas em um regime de mercado específico.

Assim, o primeiro modelo aprenderá a prever a direção do trade, enquanto o segundo modelo aprenderá a prever quando abrir as operações e quando não abrir.

Vamos então analisar a função fit_final_models, que recebe dois datasets para os dois modelos finais e realiza o treinamento neles usando o algoritmo CatBoost.

def fit_final_models(clustered, meta) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = clustered[clustered.columns[:-1]], meta[meta.columns[:-1]]
    X = X.loc[:, ~X.columns.str.contains('meta_feature')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('meta_feature')]
    
    # labels for model\meta models
    y = clustered['labels']
    y_meta = meta['clusters']
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.7, test_size=0.3, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.7, test_size=0.3, shuffle=True)


    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=1000,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=False,
                               task_type='CPU',
                               thread_count=-1)
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=30, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=500,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU',
                                    thread_count=-1)
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=25, plot=False)

    
    R2 = test_model([model, meta_model], hyper_params['stop_loss'], hyper_params['take_profit'])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))

    return [R2, model, meta_model]

Descrição das etapas de treinamento:

1. Preparação dos dados:

• Dos dataframes de entrada clustered e meta são extraídos os atributos (X, X_meta) e os rótulos (y, y_meta).
• Os tipos de dados dos rótulos são convertidos para int16. Isso é necessário para a conversão transparente do modelo para o formato ONNX.
• Os dados são divididos em conjuntos de treinamento e teste com a ajuda do train_test_split.

2. Treinamento do modelo principal:

• É criado um objeto CatBoostClassifier com os hiperparâmetros definidos.
• O modelo é treinado nos dados de treinamento (train_X, train_y) usando o conjunto de validação (test_X, test_y) para early stopping.

3. Treinamento da meta-modelo:

• É criado um objeto CatBoostClassifier para a meta-modelo com os hiperparâmetros definidos.
• A meta-modelo é treinada de forma semelhante ao modelo principal, usando seus respectivos dados de treinamento e validação.

4. Avaliação dos modelos:

• Os modelos treinados (model, meta_model) são passados para a função test_model junto com os parâmetros stop_loss e take_profit para avaliar sua performance.
• O valor retornado R2 representa a métrica de desempenho do modelo.

5. Tratamento do R2 e retorno do resultado:

• Se R2 for igual a NaN, ele é substituído por -1.0.
• O valor de R2 é exibido na tela.
• A função retorna uma lista contendo R2 e os modelos treinados (model, meta_model). 

Para cada cluster, no resultado final são obtidos dois modelos classificadores treinados, prontos para o teste visual final e exportação para o terminal MetaTrader 5. Deve-se lembrar que, para cada iteração de treinamento, é criada uma quantidade de pares de modelos igual ao número de clusters definidos nos hiperparâmetros. Esse número deve ser multiplicado pelo número de iterações para estimar quantos pares de modelos serão gerados. Por exemplo, se forem definidos 10 clusters e 10 iterações, o resultado será 100 pares de modelos, excluindo aqueles que não passaram no filtro de quantidade mínima de exemplos.

Treinamento e teste dos modelos. Realizamos os testes do nosso algoritmo

Para facilitar o uso do algoritmo, é recomendável executá-lo em um ambiente interativo do Python linha a linha. Assim é possível alterar hiperparâmetros e experimentar com diferentes samplers. Outra opção é transferir todo o código para o formato .ipynb e rodá-lo no IPython Notebook. Caso você pretenda executar o script por completo, ainda assim será necessário editá-lo para ajustar os parâmetros.

Sugiro testar cada uma das funções de anotação, rodando 10 iterações para cada uma. Os demais parâmetros serão os mesmos definidos no script anexado.

Após a execução do ciclo de treinamento, os resultados de cada iteração serão exibidos para cada cluster de dados.

R2: 0.9815970951474068
Iteration: 9, Cluster: 5
R2: 0.9914890771969395
Iteration: 9, Cluster: 6
R2: 0.9450681335265942
Iteration: 9, Cluster: 7
R2: 0.9631330369697314
Iteration: 9, Cluster: 8
R2: 0.9680380185183347
Iteration: 9, Cluster: 9
R2: 0.8203651933893291

Em seguida, é possível ordenar todos os resultados em ordem crescente de R² para escolher o melhor entre eles. E então avaliar visualmente a curva de balanço no testador.

models.sort(key=lambda x: x[0])
test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)

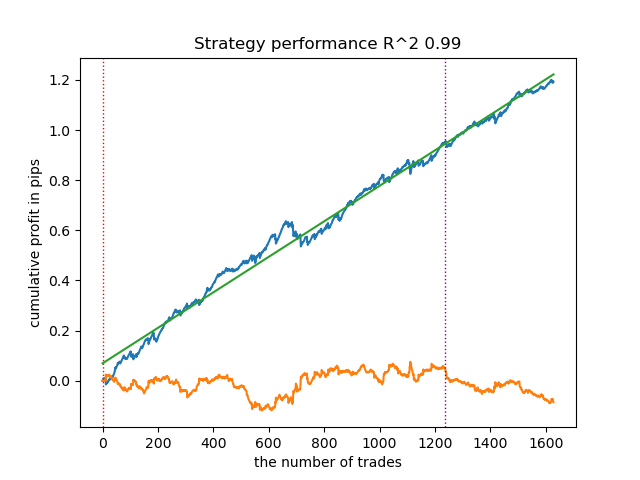
O destaque indica que será testado o primeiro modelo a partir do final. Ou seja, o que possui o maior R². Para testar o segundo modelo a partir do final, é necessário definir -2 e assim por diante. O testador exibirá o gráfico do balanço (azul) e o gráfico do par de moedas (laranja), além de uma linha vertical que separa o período de treinamento dos novos dados. Todos os modelos são treinados do início de 2010 até o início de 2021, conforme definido nos hiperparâmetros. Você pode alterar os intervalos de treinamento e teste conforme sua preferência. O período de teste para todos os modelos deste artigo vai do início de 2021 até o início de 2025.

Testando diferentes samplers de trades

• get_labels_filter(dataset, rolling=200, quantiles=[.45, .55], polyorder=3)

Abaixo está o melhor resultado para o anotador get_labels_filter.

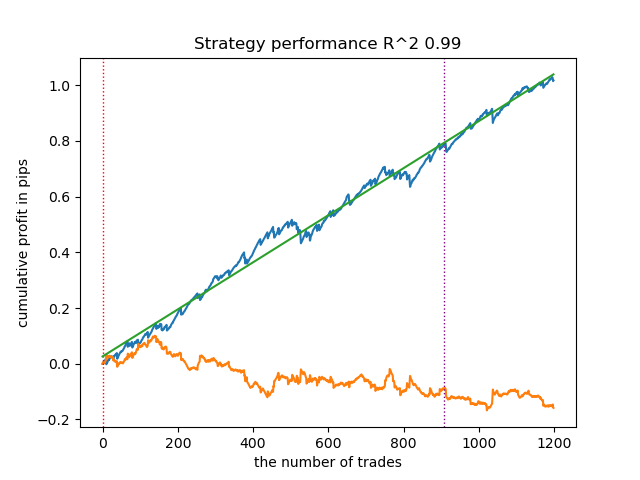
O anotador básico fez uma boa anotação das operações, e todos os modelos mostraram-se lucrativos em novos dados. Vamos repetir o mesmo processo para os demais anotadores e observar os resultados.

• get_labels_multiple_filters(dataset, rolling_periods=[50,100,200], quantiles=[.45,.55], window=100, polyorder=3)

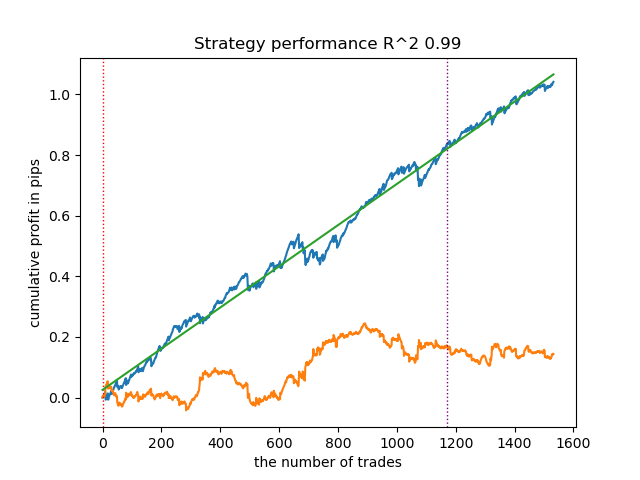
Os modelos treinados com os dados desse anotador frequentemente apresentam um aumento no número de operações em comparação com o anotador básico. Aqui não experimentei ajustes de parâmetros, pois o artigo ficaria longo demais.

• get_labels_filter_bidirectional(dataset, rolling1=50, rolling2=200, quantiles=[.45, .55], polyorder=3)

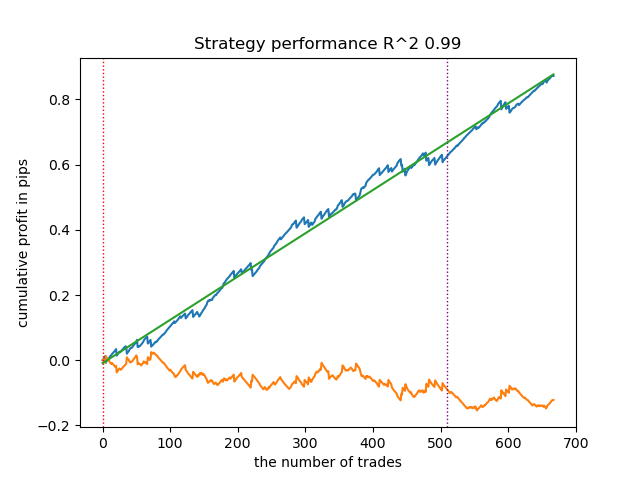
Esse anotador assimétrico também demonstrou sua eficácia em novos dados. Ajustando separadamente os parâmetros de suavização para operações de compra e venda, é possível alcançar resultados otimizados.

Agora passamos aos anotadores com restrição a trades estritamente lucrativos. É possível observar claramente que os anotadores anteriores não geram uma curva de balanço suave nem mesmo no período de treinamento, mas conseguem capturar bem as regularidades gerais. Vamos ver o que muda ao remover trades perdedores do dataset de treinamento.

• get_labels_mean_reversion(dataset, markup, min_l=1, max_l=15, rolling=0.5, quantiles=[.45, .55], method='spline', shift=0)

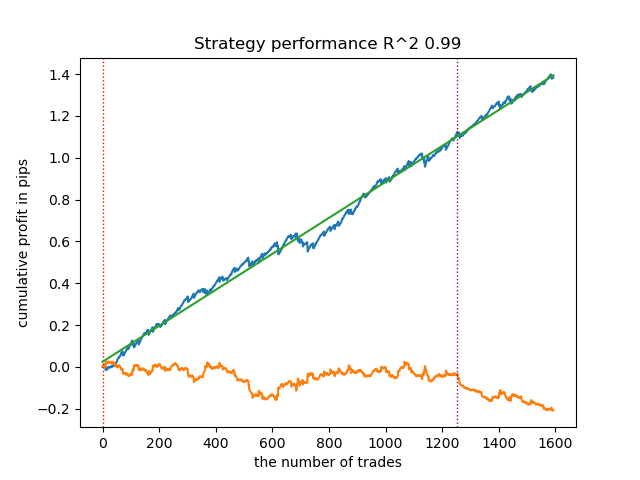
Testei esse anotador utilizando spline como filtro, com fator de suavização fixo em 0.5. No artigo não foram incluídos testes com o filtro de Savitzky-Golay nem com a média móvel simples. No entanto, fica evidente que é possível obter curvas mais suaves ao aplicar a restrição de lucratividade nos trades.

• get_labels_mean_reversion_multi(dataset, markup, min_l=1, max_l=15, windows=[0.2, 0.3, 0.5], quantiles=[.45, .55])

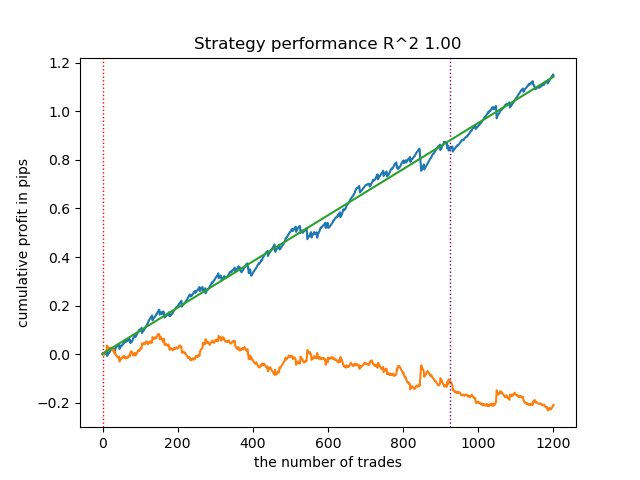
Esse sampler também é capaz de fornecer amostras de qualidade, graças às quais o modelo continua operando de forma lucrativa em novos dados.

• get_labels_mean_reversion_v(dataset, markup, min_l=1, max_l=15, rolling=0.2, quantiles=[.45, .55], method='spline', shift=0, volatility_window=20)

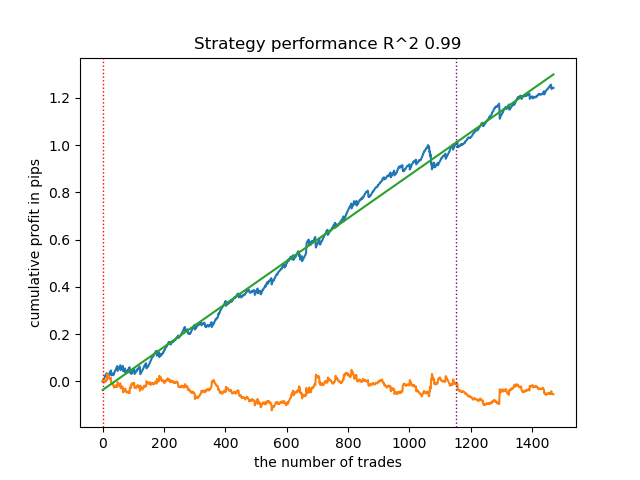
Esse algoritmo também é capaz de demonstrar uma anotação aceitável e bons modelos na saída.

Conclusões sobre os anotadores de trades:

• Quando você não souber por onde começar e tudo isso parecer muito complexo, use o sampler mais básico, que pode fornecer um resultado aceitável.
• Se as figuras bonitas não saírem de primeira, lembre-se de que na anotação de trades e no treinamento de modelos há componentes aleatórios. Basta reiniciar o algoritmo algumas vezes.
• Todos os samplers com configurações básicas podem fornecer um resultado aceitável. Para um ajuste fino, é preciso focar em um deles e fazer o ajuste de parâmetros.

Conclusões sobre a clusterização:

• Nos bastidores foram realizados múltiplos testes de samplers sem usar clusterização, assim como de clusterização sem usar samplers. Comprovei na prática que, isoladamente, esses algoritmos não funcionam tão bem quanto em conjunto.
• Não vale a pena criar atributos demais para realizar a clusterização. Isso complica o modelo e o torna menos robusto em dados novos.
• A quantidade ótima de clusters está no intervalo de 5-10. Um número menor de clusters leva a baixa capacidade de generalização e a maus resultados em dados novos, enquanto um número muito grande implica uma forte redução na quantidade de operações.

Para conveniência de uso, no código descomente o anotador de trades necessário.

# LEARNING LOOP
dataset = get_features(get_prices())
models = []
for i in range(10):
    data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
    sorted_clusters = data['clusters'].unique()
    sorted_clusters.sort()
    for clust in sorted_clusters:
        clustered_data = data[data['clusters'] == clust].copy()
        if len(clustered_data) < 500:
            print('too few samples: {}'.format(len(clustered_data)))
            continue
    
        clustered_data = get_labels_filter(clustered_data, 
                                           rolling=hyper_params['rolling'],
                                           quantiles=[0.45, 0.55],
                                           polyorder=3
                                            )
        # clustered_data = get_labels_multiple_filters(clustered_data, 
        #                                              rolling_periods=[50, 100, 200], 
        #                                              quantiles=[.45, .55], 
        #                                              window=100, 
        #                                              polyorder=3)
        # clustered_data = get_labels_filter_bidirectional(clustered_data, 
        #                                                  rolling1=50, 
        #                                                  rolling2=200, 
        #                                                  quantiles=[.45, .55], 
        #                                                  polyorder=3)
        # clustered_data = get_labels_mean_reversion(clustered_data,
        #                                             markup = hyper_params['markup'],
        #                                             min_l=1, max_l=15, 
        #                                             rolling=0.5, 
        #                                             quantiles=[.45, .55], 
        #                                             method='spline', shift=0)
        # clustered_data = get_labels_mean_reversion_multi(clustered_data, 
        #                                                  markup = hyper_params['markup'], 
        #                                                  min_l=1, max_l=15, 
        #                                                  windows=[0.2, 0.3, 0.5], 
        #                                                  quantiles=[.45, .55])
        # clustered_data = get_labels_mean_reversion_v(clustered_data,
        #                                             markup = hyper_params['markup'],
        #                                             min_l=1, max_l=15, 
        #                                             rolling=0.2, 
        #                                             quantiles=[.45, .55], 
        #                                             method='spline', 
        #                                             shift=0, 
        #                                             volatility_window=100)

        print(f'Iteration: {i}, Cluster: {clust}')
        clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)

        meta_data = data.copy()
        meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
        models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))

# TESTING & EXPORT
models.sort(key=lambda x: x[0])
test_model(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], plt=True)

Exportação de modelos treinados para MetaTrader 5 

Resta a etapa penúltima — exportar os modelos treinados e o arquivo de cabeçalho para o formato ONNX. O módulo export_lib.py, anexado ao final do artigo, contém a função export_model_to_ONNX(kwargs). Vamos analisá-la em detalhes.

def export_model_to_ONNX(**kwargs):
    model = kwargs.get('model')
    symbol = kwargs.get('symbol')
    periods = kwargs.get('periods')
    periods_meta = kwargs.get('periods_meta')
    model_number = kwargs.get('model_number')
    export_path = kwargs.get('export_path')

    model[1].save_model(
    export_path +'catmodel ' + symbol + ' ' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'main model',
        'onnx_graph_name': 'CatBoostModel_main'
    },
    pool=None)

    model[2].save_model(
    export_path + 'catmodel_m ' + symbol + ' ' + str(model_number) +'.onnx',
    format="onnx",
    export_parameters={
        'onnx_domain': 'ai.catboost',
        'onnx_model_version': 1,
        'onnx_doc_string': 'meta model',
        'onnx_graph_name': 'CatBoostModel_meta'
    },
    pool=None)
    
    code = '#include <Math\Stat\Math.mqh>'
    code += '\n'
    code += '#resource "catmodel '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel_' + symbol + '_' + str(model_number) + '[]'
    code += '\n'
    code += '#resource "catmodel_m '+ symbol + ' '+str(model_number)+'.onnx" as uchar ExtModel2_' + symbol + '_' + str(model_number) + '[]'
    code += '\n\n'
    code += 'int Periods' + symbol + '_' + str(model_number) + '[' + str(len(periods)) + \
        '] = {' + ','.join(map(str, periods)) + '};'
    code += '\n'
    code += 'int Periods_m' + symbol + '_' + str(model_number) + '[' + str(len(periods_meta)) + \
        '] = {' + ','.join(map(str, periods_meta)) + '};'
    code += '\n\n'

    # get features
    code += 'void fill_arays' + symbol + '_' + str(model_number) + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods'+ symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods' + symbol + '_' + str(model_number) + '[i],pr);\n'
    code += '       ret[0] = MathMean(pr);\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays_m' + symbol + '_' + str(model_number) + '( double &features[]) {\n'
    code += '   double pr[], ret[];\n'
    code += '   ArrayResize(ret, 1);\n'
    code += '   for(int i=ArraySize(Periods_m' + symbol + '_' + str(model_number) + ')-1; i>=0; i--) {\n'
    code += '       CopyClose(NULL,PERIOD_H1,1,Periods_m' + symbol + '_' + str(model_number) + '[i],pr);\n'
    code += '       ret[0] = MathSkewness(pr);\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

    file = open(export_path + str(symbol) + ' ONNX include' + ' ' + str(model_number) + '.mqh', "w")
    file.write(code)

    file.close()
    print('The file ' + 'ONNX include' + '.mqh ' + 'has been written to disk')

É necessário passar para a função uma lista de argumentos, tais como:

• model = models[-1]— lista de dois modelos treinados, que foi previamente preenchida com modelos de diferentes iterações de treinamento. Por analogia com o testador, o índice -1 corresponderá ao modelo com o R^2 mais alto, o índice -2 será o segundo melhor por score e assim por diante. Se você gostou de algum modelo específico no teste visual, então na exportação use o mesmo índice.
• symbol = hyper_params['symbol'] — nome do símbolo, por exemplo "EURGBP_H1", definido nos hiperparâmetros. Esse nome será acrescentado ao exportar os modelos, para distinguir modelos de símbolos diferentes.
• periods = hyper_params['periods']— lista de períodos dos atributos do modelo principal.
• periods_meta = hyper_params['periods_meta'] — lista de períodos dos atributos do modelo adicional, que determina o regime atual do mercado.
• model_number = hyper_params['model_number']— número do modelo, caso você exporte muitos modelos e não queira que sejam sobrescritos. É acrescentado aos nomes dos modelos.

• export_path = hyper_params['export_path']— caminho até a pasta include do terminal ou seu subdiretório para salvar os arquivos em disco.

A função salva ambos os modelos no formato .onnx e gera um arquivo de cabeçalho, através do qual ocorre a chamada desses modelos e o cálculo dos atributos para eles. É importante observar que o cálculo dos atributos é feito diretamente no terminal, portanto, é necessário garantir que ele seja idêntico ao cálculo realizado no script Python. Pelo código, é possível ver que a função fill_arrays calcula as médias móveis para o primeiro modelo, enquanto a função fill_arrays_m calcula o viés (skewness) dos preços para o segundo modelo. Se você alterar os atributos no script Python, será preciso modificar o cálculo deles nessa função ou diretamente no próprio arquivo de cabeçalho.

Um exemplo de chamada da função, para salvar os modelos no disco, é mostrado abaixo.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods_meta'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Criação de um robô de trading que utiliza modelos ONNX para executar operações

Suponhamos que tenhamos treinado e escolhido visualmente um modelo que nos agradou por meio do testador customizado, por exemplo, o seguinte:

Agora é necessário chamar a função de exportação para o terminal.

Após a exportação do modelo, na pasta include/mean reversion/ do terminal MetaTrader 5 (no meu caso, utilizei um subdiretório para evitar confusão com outros modelos) aparecerão 3 arquivos:

• catmodel EURGBP_H1 0.onnx — modelo principal, que fornece sinais de compra e venda
• catmodel_m EURGBP_H1 0.onnx — modelo adicional, que permite ou proíbe a operação
• EURGBP_H1 ONNX include 0.mqh — arquivo de cabeçalho, no qual é feito o import desses modelos e o cálculo dos atributos.

Os nomes dos modelos ONNX sempre começam com a palavra "catmodel", que significa catboost model, seguida pelo nome do símbolo e pelo time frame. O modelo adicional recebe o sufixo _m, que vem de meta model. O nome do arquivo de cabeçalho sempre começa com o símbolo de trading e termina com o número do modelo, que é definido no momento da exportação, para evitar que novos modelos exportados sobrescrevam os anteriores, caso isso não seja desejado.

Vejamos agora o conteúdo do arquivo .mqh.

#include <Math\Stat\Math.mqh>
#resource "catmodel EURGBP_H1 0.onnx" as uchar ExtModel_EURGBP_H1_0[]
#resource "catmodel_m EURGBP_H1 0.onnx" as uchar ExtModel2_EURGBP_H1_0[]

int PeriodsEURGBP_H1_0[10] = {5,35,65,95,125,155,185,215,245,275};
int Periods_mEURGBP_H1_0[1] = {10};

void fill_araysEURGBP_H1_0( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(PeriodsEURGBP_H1_0)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,PeriodsEURGBP_H1_0[i],pr);
       ret[0] = MathMean(pr);
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

void fill_arays_mEURGBP_H1_0( double &features[]) {
   double pr[], ret[];
   ArrayResize(ret, 1);
   for(int i=ArraySize(Periods_mEURGBP_H1_0)-1; i>=0; i--) {
       CopyClose(NULL,PERIOD_H1,1,Periods_mEURGBP_H1_0[i],pr);
       ret[0] = MathSkewness(pr);
       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }
   ArraySetAsSeries(features, true);
}

Primeiro, é conectada a biblioteca de cálculos matemáticos, necessária para o cálculo da média e do viés, além de, potencialmente, outros momentos de distribuição e demais operações matemáticas, caso seja preciso alterar o cálculo dos atributos. Em seguida, são carregados nossos dois modelos ONNX como recursos, que serão usados para gerar os sinais de trading. Depois disso, são declarados os arrays com os períodos para o cálculo dos atributos, que servirão como dados de entrada para o modelo principal e para o meta-modelo.

As duas funções restantes preenchem os arrays com os valores dos atributos. Lembro que esses arquivos são gerados durante a exportação dos modelos a partir do script em Python e não precisam ser escritos manualmente toda vez. Basta conectá-los ao EA (Expert Advisor). Isso é extremamente prático nos casos em que você deseja re-treinar o modelo após algum tempo: basta exportar novamente para o terminal, sobrescrevendo o modelo com a versão mais atualizada, e recompilar o bot, sem alterar nada no código. A quantidade de código pode assustar no início, mas na prática o treinamento se resume a rodar o script e depois compilar o bot, o que pode levar apenas alguns minutos.

Agora é preciso criar o EA, ao qual será conectado esse arquivo de cabeçalho e onde serão inicializados os modelos ONNX.

#include <Mean reversion/EURGBP_H1 ONNX include 0.mqh>
#include <Trade\Trade.mqh>
#include <Trade\AccountInfo.mqh>
#property strict
#property copyright "Copyright 2025, Dmitrievsky max."
#property link      "https://www.mql5.com/ru/users/dmitrievsky"
#property version   "1.0"

CTrade mytrade;
CPositionInfo myposition;

input bool Allow_Buy = true;           //Allow BUY
input bool Allow_Sell = true;          //Allow SELL
double main_threshold = 0.5;
double meta_threshold = 0.5;
sinput double   MaximumRisk=0.001;     //Progressive lot coefficient
sinput double   ManualLot=0.01;        //Fixed lot, set 0 if progressive
sinput ulong    OrderMagic = 57633493; //Orders magic
input int max_orders = 3;              //Max positions number
input int orders_time_delay = 5;       //Time delay between positions
input int max_spread = 20;             //Max spread
input int stoploss = 2000;             //Stop loss
input int takeprofit = 200;            //Take profit
input string comment = "mean reversion bot";

static datetime last_time = 0;
#define Ask SymbolInfoDouble(_Symbol, SYMBOL_ASK)
#define Bid SymbolInfoDouble(_Symbol, SYMBOL_BID)


const long  ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)};
const long  ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};
long     ExtHandle = INVALID_HANDLE, ExtHandle2 = INVALID_HANDLE;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   mytrade.SetExpertMagicNumber(OrderMagic);

   ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT);
   ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);

   if(ExtHandle == INVALID_HANDLE || ExtHandle2 == INVALID_HANDLE)
     {
      Print("OnnxCreateFromBuffer error ", GetLastError());
      return(INIT_FAILED);
     }

   if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape))
     {
      Print("OnnxSetInputShape 1 failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
     }

   if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2))
     {
      Print("OnnxSetInputShape 2 failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
     }

   const long output_shape[] = {1};
   if(!OnnxSetOutputShape(ExtHandle, 0, output_shape))
     {
      Print("OnnxSetOutputShape 1 error ", GetLastError());
      return(INIT_FAILED);
     }
   if(!OnnxSetOutputShape(ExtHandle2, 0, output_shape))
     {
      Print("OnnxSetOutputShape 2 error ", GetLastError());
      return(INIT_FAILED);
     }

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(ExtHandle);
   OnnxRelease(ExtHandle2);
  }

O mais importante é inicializar corretamente a dimensionalidade dos arrays de entrada de cada modelo. Ela é igual ao tamanho do array presente no arquivo de cabeçalho, que contém os valores dos períodos para o cálculo dos atributos. Ou seja, quantos períodos existirem, tantos serão os atributos.

A dimensionalidade de saída para ambos os modelos é igual a um.

const long  ExtInputShape [] = {1, ArraySize(PeriodsEURGBP_H1_0)};
const long  ExtInputShape2 [] = {1, ArraySize(Periods_mEURGBP_H1_0)};

Em seguida, são atribuídos os handles aos modelos.

ExtHandle = OnnxCreateFromBuffer(ExtModel_EURGBP_H1_0, ONNX_DEFAULT);
ExtHandle2 = OnnxCreateFromBuffer(ExtModel2_EURGBP_H1_0, ONNX_DEFAULT);

E são definidas as dimensões corretas de entradas e saídas dentro da função de inicialização do bot.

if(!OnnxSetInputShape(ExtHandle, 0, ExtInputShape))
     {
      Print("OnnxSetInputShape 1 failed, error ", GetLastError());
      OnnxRelease(ExtHandle);
      return(-1);
     }

if(!OnnxSetInputShape(ExtHandle2, 0, ExtInputShape2))
     {
      Print("OnnxSetInputShape 2 failed, error ", GetLastError());
      OnnxRelease(ExtHandle2);
      return(-1);
     }

Após a remoção do bot do gráfico, os modelos também são excluídos.

O bot realiza operações a cada nova barra, para acelerar os cálculos. Agora é necessário analisar a forma de obtenção dos sinais a partir dos modelos.

void OnTick()
  {
   if(!isNewBar())
      return;

   double features[], features_m[];
   fill_araysEURGBP_H1_0(features);
   fill_arays_mEURGBP_H1_0(features_m);

   double f[ArraySize(PeriodsEURGBP_H1_0)], f_m[ArraySize(Periods_mEURGBP_H1_0)];

   for(int i = 0; i < ArraySize(PeriodsEURGBP_H1_0); i++)
     {
      f[i] = features[i];
     }

   for(int i = 0; i < ArraySize(Periods_mEURGBP_H1_0); i++)
     {
      f_m[i] = features_m[i];
     }

   static vector out(1), out_meta(1);

   struct output
     {
      long           label[];
      float          proba[];
     };

   output out2[], out2_meta[];
   
   OnnxRun(ExtHandle, ONNX_DEBUG_LOGS, f, out, out2);
   OnnxRun(ExtHandle2, ONNX_DEBUG_LOGS, f_m, out_meta, out2_meta);

   double sig = out2[0].proba[1];
   double meta_sig = out2_meta[0].proba[1];

Ordem de obtenção dos sinais dos modelos ONNX:

• São criados dois arrays features e features_m
• Eles são preenchidos com os valores dos atributos pelas funções correspondentes fill_arrays.
• A ordem dos elementos nesses arrays é invertida em relação à ordem esperada pelo modelo. Por isso, são criados os arrays f e f_m e os dados são reescritos na sequência correta.
• São criados dois vetores out e out_meta, que informam aos modelos a dimensionalidade dos vetores de saída.
• É criada a estrutura output, que recebe os rótulos previstos 0;1 e as probabilidades. No cálculo dos sinais, são usadas as probabilidades. 
• São criadas duas instâncias da estrutura output out2 e out2_meta para receber os sinais.
• Os modelos são executados, recebendo os atributos e as dimensões dos vetores de saída, e retornam as previsões.
• Das instâncias das estruturas são extraídas as previsões (probabilidades).

Por fim, resta analisar a lógica de abertura de posições com base nos sinais recebidos. Os sinais de fechamento funcionam pela lógica inversa.

// OPEN POSITIONS BY SIGNALS
   if((Ask-Bid < max_spread*_Point) && meta_sig > meta_threshold &&
      AllowTrade(OrderMagic))
      if(countOrders(OrderMagic) < max_orders &&
         CheckMoneyForTrade(_Symbol, LotsOptimized(), ORDER_TYPE_BUY))
        {
         double l = LotsOptimized();
         if(sig < 1-main_threshold && Allow_Buy)
           {
            int res = -1;
            do
              {
               double stop = Bid - stoploss * _Point;
               double take = Ask + takeprofit * _Point;
               res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_BUY, l, Ask, stop, take, comment);
               Sleep(50);
              }
            while(res == -1);
           }
         else
           {
            if(sig > main_threshold && Allow_Sell)
              {
               int res = -1;
               do
                 {
                  double stop = Ask + stoploss * _Point;
                  double take = Bid - takeprofit * _Point;
                  res = mytrade.PositionOpen(_Symbol, ORDER_TYPE_SELL, l, Bid, stop, take, comment);
                  Sleep(50);
                 }
               while(res == -1);
              }
           }
        }

Primeiro é feita a verificação do sinal da segunda modelo. Se a probabilidade for maior que 0.5, então a abertura de trades é permitida (o mercado está no regime adequado). Em seguida, são verificadas as condições modelo principal, que prevê a probabilidade de compra ou venda. Probabilidade < 0.5 indica compra, enquanto probabilidade > 0.5 indica venda. Dependendo da condição, as operações são abertas.

Agora já é possível compilar o bot e testá-lo no testador de estratégias.

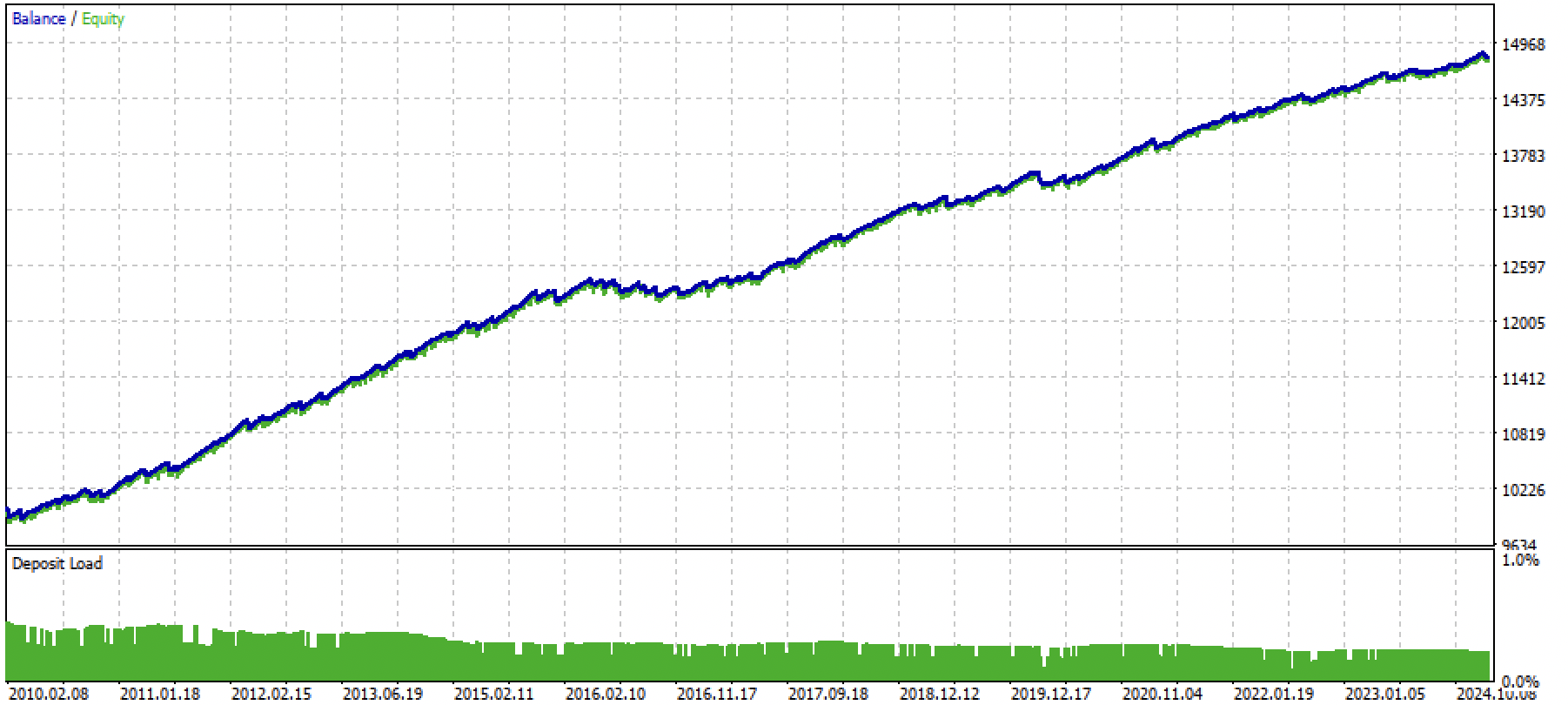
Fig. 3 teste do modelo treinado pela estratégia de retorno à média

Considerações finais

Neste artigo foram demonstradas todas as etapas de desenvolvimento de uma estratégia de retorno à média com aplicação de aprendizado de máquina. Foi exposta uma abordagem completa: desde a anotação de trades e a identificação dos regimes de mercado, até o treinamento de modelos e a criação de um bot de trading totalmente funcional.

Junto ao artigo estão anexados todos os códigos necessários para experimentos independentes.

O arquivo Python files.zip contém os seguintes arquivos para desenvolvimento em ambiente Python:

Nome do arquivo	Descrição
mean reversion.py	Script principal para o treinamento dos modelos
labeling_lib.py	Módulo com os anotadores de trades
tester_lib.py	Testador customizado de estratégias baseadas em aprendizado de máquina
export_lib.py	Biblioteca para exportação dos modelos para o terminal MetaTrader 5 em formato ONNX
EURGBP_H1.csv	Arquivo com as cotações, exportado do terminal MetaTrader 5

O arquivo MQL5 files.zip contém os arquivos para o terminal MetaTrader 5:

Nome do arquivo	Descrição
mean reversion.ex5	Bot compilado deste artigo
mean reversion.mq5	Código-fonte do bot do artigo
pasta Include//Mean reversion	Contém os modelos ONNX e o arquivo de cabeçalho para conexão com o bot