Algoritmo de otimização caótica — Chaos optimization algorithm (COA)

Conteúdo

1. Introdução
2. Implementação do algoritmo

Introdução

Nas tarefas computacionais modernas, especialmente na área dos mercados financeiros e da negociação algorítmica, métodos de otimização eficientes desempenham um papel decisivo. Entre a grande variedade de algoritmos de otimização global, destacam-se as abordagens inspiradas em fenômenos naturais. O algoritmo de otimização caótica (Chaos Optimization Algorithm, COA) representa uma dessas soluções inovadoras, combinando a teoria do caos com métodos de otimização global.

Neste artigo, apresento um algoritmo de otimização caótica aprimorado, que se baseia nas propriedades fundamentais dos sistemas caóticos, isto é, ergodicidade, sensibilidade às condições iniciais e comportamento quase estocástico. O algoritmo utiliza diferentes mapeamentos caóticos para explorar de forma eficiente o espaço de busca e tentar escapar de ótimos locais, um problema que ocorre com frequência nos métodos de otimização.

A particularidade do algoritmo apresentado está na combinação da busca caótica com o método da direção de gradiente ponderado e com mecanismos adaptativos, que permitem ajustar dinamicamente os parâmetros de busca. Graças ao uso de vários tipos de mapeamentos caóticos, logístico, senoidal e tenda, o algoritmo demonstra uma boa resistência à estagnação e a capacidade de encontrar ótimos globais em funções complexas com múltiplos extremos.  De modo geral, como de costume, vamos analisar todo o algoritmo e, em seguida, testar suas capacidades em nossas funções de teste, que já se tornaram padrão. 

Implementação do algoritmo

O algoritmo consiste em três fases principais:

• busca caótica com a primeira onda portadora, na qual as variáveis iniciais do caos são inicializadas, em seguida são gerados valores sequenciais das variáveis caóticas por meio do mapeamento logístico, e as variáveis caóticas são mapeadas para o intervalo das variáveis a serem otimizadas, sendo armazenada a melhor solução encontrada;
• busca ao longo da direção do gradiente ponderado;
• busca caótica com a segunda onda portadora, na qual é realizada uma busca local ao redor da melhor solução, com uma abordagem fractal para a implementação do tamanho do passo. 

Na imagem abaixo procurei representar a essência do funcionamento do algoritmo de otimização caótica, cuja ideia principal é o uso do caos como uma ferramenta útil de otimização, e não como um processo aleatório. O ótimo global, um brilho amarelo intenso no centro, é o objetivo que queremos encontrar. As partículas luminosas azuis são os agentes de busca, que se movem por trajetórias caóticas; essas trajetórias são mostradas como linhas brilhantes, demonstrando o caráter não linear do movimento.

Demonstração das propriedades-chave do comportamento caótico: determinismo, isto é, trajetórias suaves e não aleatórias; ergodicidade, pois as partículas exploram todo o espaço; sensibilidade às condições iniciais, já que partículas diferentes se movem por trajetórias distintas. Ao mesmo tempo, a dinâmica da busca é representada por brilhos de diferentes intensidades, mostrando a "energia" da busca em diferentes regiões, onde círculos concêntricos ao redor do ótimo simbolizam zonas de atração, e o desfoque e os gradientes transmitem a continuidade do espaço de busca. As etapas principais do algoritmo:

• busca ampla longe do centro, partículas distantes;
• aproximação gradual das zonas promissoras, trajetórias intermediárias;
• busca local nas proximidades do ótimo, partículas próximas ao centro.

Como resultado, obteve-se uma espécie de "retrato" da otimização caótica, no qual o caos não é apresentado como desordem, mas como um processo controlado de exploração do espaço de soluções.

Figura 1. Visualização da otimização caótica

O esquema visual do algoritmo, apresentado abaixo, reflete três etapas principais:

1. First Carrier Wave Search, bloco azul, utiliza um mapeamento caótico para a busca global e transforma as variáveis caóticas no espaço de busca;
2. Weighted Gradient Search, bloco laranja, método de gradiente ponderado, inclui o tratamento de restrições por meio de coeficientes de peso;
3. Second Carrier Wave Search, bloco violeta, busca local ao redor da melhor solução e ajuste adaptativo do parâmetro alpha.           

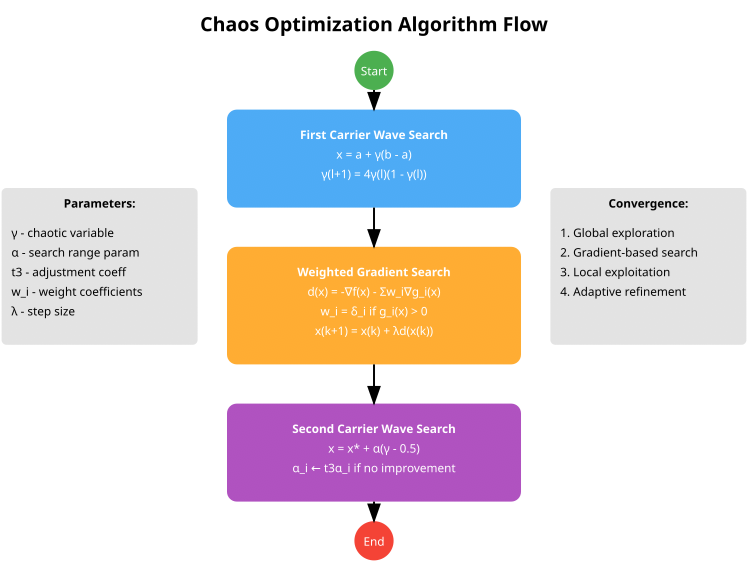
Figura 2. Esquema do algoritmo de otimização caótica

O esquema representa a estrutura básica de três etapas do algoritmo COA (CHAOS). Na minha implementação, e houve várias, decidi me concentrar em uma versão mais avançada e prática do algoritmo, ampliei a estrutura do agente, adicionei um contador de deslocamento, um contador de estagnação e variáveis caóticas para cada dimensão. Também foi importante adicionar diversidade aos mapeamentos caóticos; os autores se basearam apenas no logístico, enquanto na minha versão foram adicionados o mapeamento senoidal e o mapeamento tenda. Esta implementação inclui adaptação automática dos parâmetros de penalidade, adaptação dos parâmetros de busca dependendo do sucesso, com ajuste de inércia. Além disso, foi adicionada uma inicialização mais complexa utilizando o hipercubo latino.

Vamos começar a escrever o pseudocódigo do algoritmo:

Inicialização do algoritmo

1. Configuração dos parâmetros do algoritmo:
   • tamanho da população (popSize)
   • número de iterações da primeira fase (S1)
   • número de iterações da segunda fase (S2)
   • parâmetro de penalidade (sigma)
   • coeficiente de ajuste (t3)
   • pequena constante para os coeficientes de peso (eps)
   • parâmetro de inércia (inertia)
   • parâmetro de influência social (socialFactor)
   • probabilidade de mutação (mutationRate)
2. Inicialização dos agentes:
   • Para cada agente na população:
     • inicializar as variáveis caóticas (gamma) com diferentes valores iniciais
     • zerar os vetores de velocidade (velocity)
     • definir o contador de estagnação como 0
3. Inicialização dos parâmetros de busca (alpha):
   • adaptar os parâmetros de acordo com o tamanho do espaço de busca
   • alpha[c] = 0.1 * (rangeMax[c] - rangeMin[c]) / sqrt(coords)

Fase 1: População inicial com distribuição caótica

1. Criação da população inicial utilizando o hipercubo latino:
   • gerar valores para cada dimensão
   • embaralhar os valores para garantir uma distribuição uniforme
   • mapear os valores para o intervalo das variáveis
2. Aplicação de estratégias diversificadas de inicialização dos agentes:
   • para o primeiro quarto dos agentes: distribuição uniforme
   • para o segundo quarto: clusterização ao redor de vários pontos
   • para o terceiro quarto: posições aleatórias com deslocamento em direção aos limites
   • para o último quarto: posições caóticas com diferentes mapeamentos

Fase 2: Busca caótica com a primeira onda portadora

1. Para cada iteração até S1:
   • Para cada agente na população:
     • se a probabilidade de mutação for acionada, aplicar mutação
     • caso contrário, para cada coordenada:
       • atualizar a variável caótica por meio do mapeamento selecionado (logístico, senoidal ou tenda)
       • determinar a estratégia, busca global ou local, com base na fase da otimização
       • para a busca global: utilizar valores caóticos para definir a nova posição
       • para a busca local: combinar a atração às melhores soluções com perturbação caótica
       • atualizar a velocidade considerando a inércia
       • aplicar restrições de velocidade e de posição
       • verificar violações de restrições e aplicar correção
   • Avaliação e atualização:
     • calcular a função de penalidade para cada agente
     • atualizar as melhores soluções pessoais e a solução global
     • atualizar dinamicamente o parâmetro de penalidade
     • adaptar o parâmetro de busca (alpha) com base no sucesso

Fase 3: Busca caótica com a segunda onda portadora

1. Para cada iteração de S1 até S1+S2:
   • verificar a presença de convergência
   • para cada agente na população:
     • se a convergência for detectada, aplicar mutação aleatória a alguns agentes
     • caso contrário, para cada coordenada:
       • atualizar a variável caótica
       • estreitar de forma adaptativa o raio de busca
       • selecionar o ponto base com prioridade para as melhores soluções
       • adicionar perturbação caótica e ruído de Lévy para saltos longos aleatórios
       • atualizar velocidade e posição com inércia
       • aplicar restrições de posição
   • Avaliação e atualização:
     • calcular a função de penalidade para cada agente
     • atualizar as melhores soluções pessoais e a solução global
     • atualizar o histórico da melhor solução global para determinação da convergência
     • reinicializar agentes estagnados quando necessário

Funções auxiliares

1. Mapeamentos caóticos:
   • LogisticMap(x): x[n+1] = rx[n](1-x[n]) com verificação de validade
   • SineMap(x): x[n+1] = sin(π*x[n]) com normalização
   • TentMap(x): x[n+1] = μ*min(x[n], 1-x[n]) com verificação de validade
   • SelectChaosMap(x, type): seleção do mapeamento com base no tipo
2. Tratamento de restrições e penalidades:
   • CalculateConstraintValue(agent, coord): cálculo da violação das restrições
   • CalculateConstraintGradient(agent, coord): cálculo do gradiente das restrições
   • CalculateWeightedGradient(agent, coord): cálculo do gradiente ponderado
   • CalculatePenaltyFunction(agent): cálculo do valor da função de penalidade
3. Tratamento de estagnação e convergência:
   • IsConverged(): verificação da convergência com base no histórico das melhores soluções
   • ResetStagnatingAgents(): reinicialização de agentes em estagnação
   • ApplyMutation(agent): aplicação de diferentes tipos de mutação
   • UpdateSigma(): atualização dinâmica do parâmetro de penalidade
   • UpdateBestHistory(newBest): atualização do histórico dos melhores valores

Agora podemos avançar para a descrição da implementação do algoritmo COA (CHAOS). Neste artigo analisaremos todos os métodos-chave de implementação e, no próximo, passaremos diretamente aos testes e aos resultados do funcionamento do algoritmo. Vamos escrever a estrutura "S_COA_Agent", campos da estrutura:

• gamma [] — conjunto de variáveis caóticas do tipo pseudoaleatório, utilizado para introduzir elementos de aleatoriedade e diversidade no comportamento do agente,
• velocity [] — array de velocidades, permite que o agente se mova de forma mais dinâmica pelo espaço, levando em conta a inércia,
• stagnationCounter — contador que aumenta se o agente não apresentar melhorias na solução, ajuda a implementar mecanismos de reinicialização de estratégias em situações de estagnação.

No método "Init ()" são criados e definidos os valores iniciais dos arrays. Para "gamma []" é utilizada uma distribuição uniforme de 0.1 a 0.9, a fim de introduzir diversidade nas condições iniciais das variáveis caóticas. As velocidades "velocity []" começam com valores nulos e o contador de estagnação é definido como zero.

//——————————————————————————————————————————————————————————————————————————————
// Улучшенная структура агента с дополнительными полями
struct S_COA_Agent
{
    double gamma    [];       // хаотические переменные
    double velocity [];       // скорость перемещения (для усиления инерции)
    int    stagnationCounter; // счётчик стагнации

    void Init (int coords)
    {
      ArrayResize (gamma,    coords);
      ArrayResize (velocity, coords);

      // Равномерное распределение значений для gamma
      for (int i = 0; i < coords; i++)
      {
        // Используем различные начальные значения для лучшего разнообразия
        gamma [i] = 0.1 + 0.8 * (i % coords) / (double)MathMax (1, coords - 1);

        // Инициализация скорости нулями
        velocity [i] = 0.0;
      }

      stagnationCounter = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

A classe "C_AO_COA_chaos" é derivada da classe base "C_AO" e representa uma implementação do algoritmo COA (CHAOS). Ela inclui métodos e parâmetros necessários para o funcionamento, bem como funções adicionais para gerenciar o comportamento dos agentes, com base nos conceitos de busca caótica. Componentes da classe:

• SetParams () — método para configurar os parâmetros do algoritmo,
• Init () — método de inicialização, recebe os intervalos e parâmetros para o funcionamento do algoritmo,
• Moving () — método responsável pelo deslocamento dos agentes no espaço de soluções,
• Revision () — método para revisar as posições dos agentes.

Parâmetros do algoritmo:

• S1, S2 — número de iterações nas duas fases do algoritmo.
• sigma, t3, eps, inertia, socialFactor, mutationRate — parâmetros que influenciam o comportamento dos agentes e o algoritmo como um todo.
• alpha [] — array de parâmetros utilizados na busca.
• agent [] — array de agentes que compõem a população do algoritmo.

Métodos protegidos:

• métodos para cálculo de gradientes, valores de restrições e funções de penalidade, bem como verificação da viabilidade das soluções (IsFeasible),
• métodos para mapeamentos caóticos (LogisticMap, SineMap, TentMap, SelectChaosMap).

Campos privados do método:

• variáveis que armazenam informações sobre a época atual (epochs, epochNow) e o valor dinâmico da penalidade (currentSigma),
• globalBestHistory [] — array para armazenamento dos melhores valores globais ao longo de várias iterações,
• índice do histórico (historyIndex) para rastrear a posição no array dos melhores valores,
• métodos para gerenciar a população de agentes (InitialPopulation), executar diferentes fases da busca (FirstCarrierWaveSearch, SecondCarrierWaveSearch), realizar mutação dos agentes (ApplyMutation), atualizar a penalidade (UpdateSigma) e verificar a convergência (IsConverged), bem como reinicializar agentes estagnados (ResetStagnatingAgents).

Assim, a classe "C_AO_COA_chaos" representa um componente complexo do sistema de otimização, que utiliza agentes para a busca de soluções. Ela integra parâmetros, métodos e a lógica necessária para o gerenciamento dos agentes dentro do algoritmo, incluindo tanto estratégias determinísticas quanto caóticas. 

//——————————————————————————————————————————————————————————————————————————————
class C_AO_COA_chaos : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_COA_chaos () { }
  C_AO_COA_chaos ()
  {
    ao_name = "COA(CHAOS)";
    ao_desc = "Chaos Optimization Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/16729";

    // Внутренние параметры (не настраиваются извне)
    inertia      = 0.7;
    socialFactor = 1.5;
    mutationRate = 0.05;

    // Параметры по умолчанию
    popSize = 50;
    S1      = 30;
    S2      = 20;
    sigma   = 2.0;
    t3      = 1.2;
    eps     = 0.0001;

    // Инициализация массива параметров для интерфейса C_AO
    ArrayResize (params, 6);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "S1";      params [1].val = S1;
    params [2].name = "S2";      params [2].val = S2;
    params [3].name = "sigma";   params [3].val = sigma;
    params [4].name = "t3";      params [4].val = t3;
    params [5].name = "eps";     params [5].val = eps;
  }

  void SetParams ()
  {
    // Обновление внутренних параметров из массива params
    popSize = (int)params [0].val;
    S1      = (int)params [1].val;
    S2      = (int)params [2].val;
    sigma   = params      [3].val;
    t3      = params      [4].val;
    eps     = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], // минимальный диапазон поиска
             const double &rangeMaxP  [], // максимальный диапазон поиска
             const double &rangeStepP [], // шаг поиска
             const int     epochsP = 0);  // количество эпох

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  // Внешние параметры алгоритма
  int    S1;             // итерации первой фазы
  int    S2;             // итерации второй фазы
  double sigma;          // параметр штрафа
  double t3;             // коэффициент корректировки alpha
  double eps;            // малое число для весовых коэффициентов

  // Внутренние параметры алгоритма
  double inertia;        // параметр инерции для движения (внутренний)
  double socialFactor;   // параметр социального влияния (внутренний)
  double mutationRate;   // вероятность мутации (внутренний)

  S_COA_Agent agent [];  // массив агентов

  private: //-------------------------------------------------------------------
  int    epochNow;
  double currentSigma;           // Динамический параметр штрафа
  double alpha             [];   // параметры поиска
  double globalBestHistory [10]; // История значений глобального лучшего решения
  int    historyIndex;

  // Вспомогательные методы
  double CalculateWeightedGradient   (int agentIdx, int coordIdx);
  double CalculateConstraintValue    (int agentIdx, int coordIdx);
  double CalculateConstraintGradient (int agentIdx, int coordIdx);
  double CalculatePenaltyFunction    (int agentIdx);

  // Метод для проверки допустимости решения
  bool IsFeasible              (int agentIdx);

  // Хаотические отображения
  double LogisticMap           (double x);
  double SineMap               (double x);
  double TentMap               (double x);
  double SelectChaosMap        (double x, int type);

  void InitialPopulation       ();
  void FirstCarrierWaveSearch  ();
  void SecondCarrierWaveSearch ();
  void ApplyMutation           (int agentIdx);
  void UpdateSigma             ();
  void UpdateBestHistory       (double newBest);
  bool IsConverged             ();
  void ResetStagnatingAgents   ();
};
//——————————————————————————————————————————————————————————————————————————————

O método "Init" da classe "C_AO_COA" é responsável pela configuração inicial e pela preparação do algoritmo para a execução. Ele realiza várias tarefas importantes: em primeiro lugar, é executada a inicialização básica por meio do método "StandardInit ()", que define os intervalos, os passos e outros parâmetros. Caso essa etapa não seja concluída com sucesso, o método é finalizado com erro.

Em seguida, são definidos os parâmetros relacionados ao número de épocas (epochs), à época atual (epochNow) e ao coeficiente de penalidade (currentSigma). A história das melhores soluções é inicializada, o que ajuda a acompanhar o progresso. Verifica-se o tamanho dos arrays dos intervalos de valores mínimos e máximos para a busca. Caso os tamanhos não coincidam ou não estejam definidos, a inicialização é interrompida.

Na sequência, são inicializados os arrays que armazenam os agentes, os coeficientes "alpha", bem como as melhores soluções encontradas. Cada agente recebe uma posição inicial levando em conta diferentes estratégias:

• uma parte dos agentes é distribuída de forma uniforme por todo o intervalo,
• outros realizam "clustering", isto é, concentram-se ao redor de alguns pontos dentro do intervalo,
• uma parcela adicional é posicionada de maneira aleatória considerando os limites,
• os demais utilizam funções de mapeamento caótico para obter soluções iniciais.

O método de inicialização "Init" da classe "C_AO_COA_chaos" define os parâmetros iniciais e os arrays necessários para a busca da solução ótima. O processo inclui a verificação da correção dos dados de entrada, a configuração dos intervalos de busca, a inicialização do array de agentes com estratégias diversificadas de posições iniciais, bem como a definição de valores de variáveis globais, como a melhor solução encontrada. Durante a execução do método, são criadas as estruturas de dados necessárias para o processo iterativo posterior de otimização, e são definidos os parâmetros que regulam o comportamento dos agentes e do algoritmo como um todo.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_COA_chaos::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochNow     = 0;
  currentSigma = sigma;
  historyIndex = 0;

  // Инициализация истории лучших значений
  for (int i = 0; i < 10; i++) globalBestHistory [i] = -DBL_MAX;

  // Проверка и инициализация основных массивов
  int arraySize = ArraySize (rangeMinP);
  if (arraySize <= 0 || arraySize != ArraySize (rangeMaxP) || arraySize != ArraySize (rangeStepP))
  {
    return false;
  }

  ArrayResize (agent, popSize);
  ArrayResize (alpha, coords);

  // Адаптивная инициализация alpha в зависимости от диапазона поиска
  for (int c = 0; c < coords; c++)
  {
    // alpha зависит от размера пространства поиска
    double range = rangeMax [c] - rangeMin [c];
    alpha [c] = 0.1 * range / MathSqrt (MathMax (1.0, (double)coords));
  }

  // Инициализация агентов с разнообразными стратегиями
  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init (coords);

    for (int c = 0; c < coords; c++)
    {
      double position;

      // Различные стратегии инициализации
      if (i < popSize / 4)
      {
        // Равномерное распределение по пространству
        position = rangeMin [c] + (i * (rangeMax [c] - rangeMin [c])) / MathMax (1, popSize / 4);
      }
      else
        if (i < popSize / 2)
        {
          // Кластеризация вокруг нескольких точек
          int cluster = (i - popSize / 4) % 3;
          double clusterCenter = rangeMin [c] + (cluster + 1) * (rangeMax [c] - rangeMin [c]) / 4.0;
          position = clusterCenter + u.RNDfromCI (-0.1, 0.1) * (rangeMax [c] - rangeMin [c]);
        }
        else
          if (i < 3 * popSize / 4)
          {
            // Случайные позиции с смещением в сторону границ
            double r = u.RNDprobab ();
            if (r < 0.5) position = rangeMin [c] + 0.2 * r * (rangeMax [c] - rangeMin [c]);
            else position = rangeMax [c] - 0.2 * (1.0 - r) * (rangeMax [c] - rangeMin [c]);
          }
          else
          {
            // Хаотические позиции с использованием разных отображений
            int mapType = i % 3;
            double chaosValue = SelectChaosMap (agent [i].gamma [c], mapType);
            position = rangeMin [c] + chaosValue * (rangeMax [c] - rangeMin [c]);
          }

      a [i].cB [c] = u.SeInDiSp (position, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "LogisticMap" implementa o mapeamento logístico, que é utilizado para gerar sequências caóticas. Essa função é aplicada no algoritmo para introduzir aleatoriedade e diversidade na busca por soluções. A ideia principal do método é calcular um novo valor de estado com base no valor atual, utilizando a fórmula do mapeamento logístico com um parâmetro que varia levemente para aumentar a caoticidade extraída.

Antes do cálculo, o valor de entrada é verificado quanto à correção e ao intervalo; em caso de não conformidade, ele é substituído por um número aleatório dentro do intervalo especificado. Após o cálculo do novo valor, também é realizada uma verificação do intervalo permitido e, se necessário, o valor é substituído por um número aleatório para manter a estabilidade da função. Como resultado, a lógica interna garante a geração do próximo estado permanecendo dentro dos limites admissíveis.

//——————————————————————————————————————————————————————————————————————————————
// Улучшенные хаотические отображения
double C_AO_COA_chaos::LogisticMap (double x)
{
  // Защита от некорректных входных значений
  if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false)
  {
    x = 0.2 + 0.6 * u.RNDprobab ();
  }

  // x(n+1) = r*x(n)*(1-x(n))
  double r = 3.9 + 0.1 * u.RNDprobab (); // Слегка рандомизированный параметр для избежания циклов
  double result = r * x * (1.0 - x);

  // Дополнительная проверка корректности
  if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false)
  {
    result = 0.2 + 0.6 * u.RNDprobab ();
  }

  return result;
}
//——————————————————————————————————————————————————————————————————————————————

O método "SineMap" implementa um mapeamento caótico baseado na função seno. Ele recebe o estado atual, verifica sua correção e, se estiver incorreto ou fora do intervalo [0, 1], substitui-o por um valor aleatório dentro desse intervalo. Em seguida, calcula o novo valor usando a função seno, normaliza-o para que volte a estar no intervalo [0, 1] e realiza uma verificação adicional.

Se o valor final sair dos limites ou for considerado inválido, ele é novamente substituído por um número aleatório no intervalo [0.2, 0.8]. Como resultado, o método retorna um novo estado, obtido a partir do estado atual por meio do mapeamento caótico.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_COA_chaos::SineMap (double x)
{
  // Защита от некорректных входных значений
  if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false)
  {
    x = 0.2 + 0.6 * u.RNDprobab ();
  }

  // x(n+1) = sin(π*x(n))
  double result = MathSin (M_PI * x);

  // Нормализация результата к диапазону [0, 1]
  result = (result + 1.0) / 2.0;

  // Дополнительная проверка корректности
  if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false)
  {
    result = 0.2 + 0.6 * u.RNDprobab ();
  }

  return result;
}
//——————————————————————————————————————————————————————————————————————————————

O método "TentMap" implementa o mapeamento "tenda" (tent map) para a geração de uma sequência caótica. O método recebe o valor de entrada "x", que deve estar entre 0 e 1, verifica a correção de "x" e, se necessário, o substitui por um valor aleatório dentro do intervalo admissível. Em seguida, utilizando o parâmetro "mu", próximo de 2, é calculado um novo valor com base na função linear por partes característica do mapeamento "tenda".

Após o cálculo, é realizada mais uma verificação da validade do valor e, se necessário, ele é normalizado por meio de um número aleatório. Em seguida, o método retorna o novo valor gerado de forma caótica.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_COA_chaos::TentMap (double x)
{
  // Защита от некорректных входных значений
  if (x < 0.0 || x > 1.0 || MathIsValidNumber (x) == false)
  {
    x = 0.2 + 0.6 * u.RNDprobab ();
  }

  // Tent map: x(n+1) = μ*min(x(n), 1-x(n))
  double mu = 1.99; // Параметр близкий к 2 для хаотического поведения
  double result;

  if (x <= 0.5) result = mu * x;
  else result = mu * (1.0 - x);

  // Дополнительная проверка корректности
  if (result < 0.0 || result > 1.0 || MathIsValidNumber (result) == false)
  {
    result = 0.2 + 0.6 * u.RNDprobab ();
  }

  return result;
}
//——————————————————————————————————————————————————————————————————————————————

O método "SelectChaosMap" é destinado à seleção e aplicação da função de mapeamento caótico de acordo com o tipo especificado. Ele recebe o valor "x" e o parâmetro "type", que indica o tipo específico de mapeamento caótico. A ideia principal do método é utilizar o resto da divisão do tipo por 3 para determinar a variante do mapeamento, garantindo uma escolha cíclica entre três mapas caóticos diferentes: logístico, senoidal e tenda. Dependendo do resultado, a função correspondente é chamada, transformando o valor de entrada "x" em um novo valor por meio da dinâmica caótica selecionada.

Se, por algum motivo, o tipo não cair no intervalo esperado (0, 1, 2), por padrão é aplicado o mapeamento logístico. Cada um desses mapas modela um comportamento caótico e é utilizado para gerar números diversos e imprevisíveis dentro do processo de otimização.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_COA_chaos::SelectChaosMap (double x, int type)
{
  // Выбор хаотического отображения на основе типа
  switch (type % 3)
  {
    case 0:
      return LogisticMap (x);
    case 1:
      return SineMap (x);
    case 2:
      return TentMap (x);
    default:
      return LogisticMap (x);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "InitialPopulation" é destinado à inicialização da população inicial do algoritmo de otimização utilizando a técnica "Latin Hypercube Sampling (LHS)". O LHS é um método de amostragem estratificada que garante uma cobertura mais uniforme do espaço de busca multidimensional em comparação com a amostragem aleatória, aumentando assim a qualidade da população inicial.

O método começa com a declaração dos arrays para os valores do hipercubo latino e dos valores temporários que auxiliam na geração. O método tenta alocar memória para os arrays necessários e, caso a alocação falhe, é acionado um cenário de contingência que cria a população inicial de forma aleatória. Isso garante que o programa não seja encerrado com erro devido à falta de memória.

Em seguida, o método gera os valores para o hipercubo latino. Para cada coordenada é criado um array ordenado de valores, que depois é embaralhado aleatoriamente. Os valores embaralhados são atribuídos ao array do hipercubo. Os valores do hipercubo latino são transformados em coordenadas dos indivíduos no espaço de busca. O cálculo é realizado utilizando os intervalos definidos, e os valores obtidos são limitados ao intervalo e ao passo necessários.

Ao final, o método define um sinalizador indicando que a população inicial foi modificada ou criada. A vantagem dessa abordagem está na criação de uma população inicial mais diversificada.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA_chaos::InitialPopulation ()
{
  // Создаем Latin Hypercube для начальной популяции
  double latinCube []; // Одномерный массив для хранения значений гиперкуба
  double tempValues []; // Временный массив для хранения и перемешивания значений

  ArrayResize (latinCube, popSize * coords);
  ArrayResize (tempValues, popSize);

  // Генерируем Латинский гиперкуб
  for (int c = 0; c < coords; c++)
  {
    // Создаем упорядоченные значения
    for (int i = 0; i < popSize; i++)
    {
      tempValues [i] = (double)i / popSize;
    }

    // Перемешиваем значения
    for (int i = popSize - 1; i > 0; i--)
    {
      int j = (int)(u.RNDprobab () * (i + 1));
      if (j < popSize)
      {
        double temp = tempValues [i];
        tempValues [i] = tempValues [j];
        tempValues [j] = temp;
      }
    }

    // Присваиваем перемешанные значения
    for (int i = 0; i < popSize; i++)
    {
      latinCube [i * coords + c] = tempValues [i];
    }
  }

  // Преобразуем значения Латинского гиперкуба в координаты
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double x = rangeMin [c] + latinCube [i * coords + c] * (rangeMax [c] - rangeMin [c]);
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "FirstCarrierWaveSearch" implementa a fase de busca do algoritmo, voltada ao balanceamento entre a diversificação global do espaço e a intensificação local de soluções boas já conhecidas. Sua principal tarefa é atualizar as posições e velocidades dos agentes, continuando a encontrar e aprimorar soluções potenciais. No início do método, é determinado um coeficiente que controla o grau de diversificação na época atual da busca. Esse coeficiente diminui de forma quadrática à medida que as épocas avançam, o que garante um deslocamento gradual do foco das operações de busca global para o aprimoramento local. Em seguida, para cada agente da população, é realizada uma verificação de mutação, com uma certa probabilidade a mutação é aplicada para aumentar a diversidade das soluções. Depois disso, para cada direção de busca, isto é, cada coordenada:

• é selecionado o tipo de mapeamento caótico utilizado para o surgimento de novas soluções potenciais,
• é determinada a estratégia de busca, global ou local.

No caso da busca global, o agente atualiza sua posição utilizando um componente caótico, enquanto a velocidade é ajustada levando em conta a inércia e a direção do movimento. No caso da busca local, o agente se orienta pelas melhores soluções encontradas, realizando uma atração ponderada em direção a elas, com uma pequena variação aleatória para evitar o aprisionamento em ciclos. Em ambos os casos, a velocidade é limitada para evitar saltos excessivamente grandes para fora do espaço de busca. As posições dos agentes são atualizadas considerando as restrições do espaço de busca e, quando necessário, é aplicada uma correção caso sejam detectadas violações das restrições. Nessa situação, as posições são ajustadas e as velocidades reduzidas para suavizar os passos subsequentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA_chaos::FirstCarrierWaveSearch ()
{
  // Адаптивный баланс между исследованием и эксплуатацией
  double globalPhase = (double)epochNow / S1;
  double explorationRate = 1.0 - globalPhase * globalPhase; // Квадратичное снижение

  // Для каждого агента
  for (int i = 0; i < popSize; i++)
  {
    // Применяем мутации с некоторой вероятностью для усиления разнообразия
    if (u.RNDprobab () < mutationRate * (1.0 + explorationRate))
    {
      ApplyMutation (i);
      continue;
    }

    for (int c = 0; c < coords; c++)
    {
      // Выбор хаотического отображения с равномерным распределением
      int mapType = ((i + c + epochNow) % 3);

      // Безопасная проверка доступа к массиву gamma
      if (c < ArraySize (agent [i].gamma))
      {
        agent [i].gamma [c] = SelectChaosMap (agent [i].gamma [c], mapType);
      }
      else
      {
        continue; // Пропускаем, если индекс некорректен
      }

      // Определяем соотношение между глобальным и локальным поиском
      double strategy = u.RNDprobab ();
      double x;

      if (strategy < explorationRate)
      {
        // Глобальный поиск с хаотическим компонентом
        x = rangeMin [c] + agent [i].gamma [c] * (rangeMax [c] - rangeMin [c]);

        // Добавляем компонент скорости для сохранения направления движения
        agent [i].velocity [c] = inertia * agent [i].velocity [c] +
                                 (1.0 - inertia) * (x - a [i].c [c]);
      }
      else
      {
        // Локальный поиск вокруг лучших решений
        double personalAttraction = u.RNDprobab ();
        double globalAttraction = u.RNDprobab ();

        // Взвешенное притяжение к лучшим решениям
        double attractionTerm = //personalAttraction * (agent [i].cPrev [c] - a [i].c [c]) +
                                personalAttraction * (a [i].cB [c] - a [i].c [c]) +
                                socialFactor * globalAttraction * (cB [c] - a [i].c [c]);

        // Хаотическое возмущение для предотвращения застревания
        double chaosRange = alpha [c] * explorationRate;
        double chaosTerm = chaosRange * (2.0 * agent [i].gamma [c] - 1.0);

        // Обновление скорости с инерцией
        agent [i].velocity [c] = inertia * agent [i].velocity [c] +
                                 (1.0 - inertia) * (attractionTerm + chaosTerm);
      }

      // Ограничиваем скорость для предотвращения слишком больших шагов
      double maxVelocity = 0.1 * (rangeMax [c] - rangeMin [c]);
      if (MathAbs (agent [i].velocity [c]) > maxVelocity)
      {
        agent [i].velocity [c] = maxVelocity * (agent [i].velocity [c] > 0 ? 1.0 : -1.0);
      }

      // Применяем скорость к позиции
      x = a [i].c [c] + agent [i].velocity [c];

      // Применяем ограничения поискового пространства
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

      // Проверяем ограничения и применяем плавную коррекцию
      double violation = CalculateConstraintValue (i, c);
      if (violation > eps)
      {
        double gradient = CalculateWeightedGradient (i, c);
        double correction = -gradient * violation * (1.0 - globalPhase);
        a [i].c [c] = u.SeInDiSp (a [i].c [c] + correction, rangeMin [c], rangeMax [c], rangeStep [c]);

        // Сбрасываем скорость при коррекции нарушений
        agent [i].velocity [c] *= 0.5;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "SecondCarrierWaveSearch" representa uma etapa de otimização que se desenvolve após a busca inicial e é orientada ao aprofundamento e ao refinamento das soluções encontradas. O objetivo principal desse método é melhorar os resultados obtidos na etapa anterior, por meio da aplicação de estratégias de busca mais sutis e da adaptação de parâmetros.

O método inicia seu funcionamento com o cálculo de um parâmetro que reflete a fase da busca local, o qual se intensifica ao longo do tempo. Isso permite que o algoritmo faça uma transição gradual de uma busca ampla para uma investigação mais detalhada e precisa da região das soluções já conhecidas. No início do método, é realizada uma verificação quanto ao alcance da convergência. Caso o algoritmo tenha atingido um estado estável, alguns agentes são submetidos à mutação, com o objetivo de aumentar a diversidade das soluções e evitar ótimos locais.

Para cada agente, é realizada uma busca sequencial por novas soluções em seu espaço. São definidos os mapeamentos caóticos, que auxiliam na introdução de elementos de aleatoriedade. O parâmetro de busca é reduzido à medida que se aproxima da solução ótima. Isso garante um foco mais estreito ao buscar nas proximidades das melhores soluções atuais. Ao atualizar cada posição, os resultados anteriores dos agentes são levados em consideração. Define-se um ponto base, que pode ser tanto o ótimo global absoluto quanto conquistas pessoais anteriores do agente, o que permite considerar simultaneamente os resultados individuais e os resultados globais de toda a população.

Durante o processo de atualização das posições, são utilizados tanto deslocamentos caóticos quanto ruído aleatório, por exemplo, ruído de Lévy, o que adiciona um elemento de aleatoriedade e contribui para a busca de novas soluções potencialmente melhores. O método leva em conta a inércia ao atualizar as velocidades dos agentes, o que ajuda a suavizar as mudanças e a evitar movimentos excessivamente agressivos. Como resultado, as posições atualizadas são limitadas dentro das fronteiras especificadas, garantindo o cumprimento das condições do problema.

O método "SecondCarrierWaveSearch" é voltado para uma otimização mais precisa e profunda das soluções já existentes.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_COA_chaos::SecondCarrierWaveSearch ()
{
  // Уточняющий локальный поиск с адаптивными параметрами
  double localPhase = (double)(epochNow - S1) / S2;
  double intensificationRate = localPhase * localPhase; // Квадратичное увеличение интенсификации

  // Проверка на сходимость алгоритма
  bool isConverged = IsConverged ();

  // Для каждого агента
  for (int i = 0; i < popSize; i++)
  {
    // Если обнаружена сходимость, добавляем случайную мутацию к некоторым агентам
    if (isConverged && i % 3 == 0)
    {
      ApplyMutation (i);
      continue;
    }

    for (int c = 0; c < coords; c++)
    {
      // Выбор хаотического отображения с равномерным распределением
      int mapType = ((i * c + epochNow) % 3);
      agent [i].gamma [c] = SelectChaosMap (agent [i].gamma [c], mapType);

      // Адаптивный радиус поиска с сужением к концу оптимизации
      double adaptiveAlpha = alpha [c] * (1.0 - 0.8 * intensificationRate);

      // Выбор базовой точки с приоритетом лучших решений
      double basePoint;
      if (a [i].f > a [i].fB)
      {
        basePoint = a [i].c [c];  // Текущее положение лучше
      }
      else
      {
        double r = u.RNDprobab ();

        if (r < 0.7 * (1.0 + intensificationRate)) // Увеличиваем притяжение к глобальному лучшему
        {
          basePoint = cB [c];  // Глобальное лучшее
        }
        else
        {
          basePoint = a [i].cB [c];  // Личное лучшее
        }
      }

      // Локальный поиск с хаотическим компонентом
      double chaosOffset = adaptiveAlpha * (2.0 * agent [i].gamma [c] - 1.0);

      // Добавляем шум Леви для случайных дальних прыжков (тяжелый хвост распределения)
      double levyNoise = 0.0;
      if (u.RNDprobab () < 0.1 * (1.0 - intensificationRate))
      {
        // Упрощенное приближение шума Леви
        double u1 = u.RNDprobab ();
        double u2 = u.RNDprobab ();

        if (u2 > 0.01) // Защита от деления на очень малые числа
        {
          levyNoise = 0.01 * u1 / MathPow (u2, 0.5) * adaptiveAlpha * (rangeMax [c] - rangeMin [c]);
        }
      }

      // Обновляем скорость с инерцией
      agent [i].velocity [c] = inertia * (1.0 - 0.5 * intensificationRate) * agent [i].velocity [c] +
                               (1.0 - inertia) * (chaosOffset + levyNoise);

      // Применяем скорость к позиции
      double x = basePoint + agent [i].velocity [c];

      // Ограничиваем позицию
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

No próximo artigo, continuaremos a análise dos métodos restantes de funcionamento do algoritmo, realizaremos os testes e apresentaremos as considerações finais.