Redes neurais em trading: Integração da teoria do caos na previsão de séries temporais (Attraos)

Introdução

As séries temporais nos mercados financeiros consistem em sequências de dados de preços, volumes negociados e outros indicadores econômicos que variam ao longo do tempo sob a influência de múltiplos fatores. Elas refletem processos dinâmicos complexos, incluindo tendências de mercado, ciclos e flutuações de curto prazo causadas por notícias econômicas, pelo comportamento dos participantes do mercado e por condições macroeconômicas. A previsão precisa das séries temporais no âmbito das finanças é importante para a gestão de riscos, a construção de estratégias de trading, a otimização de portfólios e a negociação algorítmica. Erros nessas previsões podem resultar em perdas financeiras significativas, portanto o desenvolvimento de métodos mais precisos para a análise de séries temporais é uma tarefa prioritária para analistas, traders e instituições financeiras.

Os métodos modernos de previsão de séries temporais financeiras utilizam amplamente o aprendizado de máquina, incluindo redes neurais e modelos de aprendizado profundo. No entanto, a maioria das abordagens tradicionais baseia-se em métodos estatísticos e modelos lineares que enfrentam dificuldades para analisar dados altamente voláteis e caóticos, característicos dos mercados financeiros. Os processos de mercado frequentemente apresentam dependências não lineares, sensibilidade às condições iniciais e dinâmica complexa. Tudo isso torna a previsão uma tarefa bastante desafiadora. Os modelos tradicionais têm dificuldade em lidar com eventos repentinos de mercado, como crises, mudanças bruscas de liquidez ou vendas massivas de ativos causadas pelo pânico dos investidores. Por isso, a busca por novas abordagens capazes de se adaptarem à dinâmica complexa dos mercados financeiros é uma linha de pesquisa extremamente importante.

Para resolver essas questões, os autores do framework Attraos, proposto no trabalho "Attractor Memory for Long-Term Time Series Forecasting: A Chaos Perspective", integram os princípios da teoria do caos, tratando as séries temporais como projeções de baixa dimensionalidade de sistemas dinâmicos caóticos multidimensionais. Essa abordagem permite considerar dependências não lineares ocultas entre os dados de mercado, aumentando a precisão das previsões. A aplicação de métodos da dinâmica caótica na análise de séries temporais possibilita identificar estruturas estáveis nos dados de mercado e incorporá-las à construção de modelos preditivos.

O Attraos é um framework que resolve duas tarefas-chave. Primeiramente, ele modela processos dinâmicos ocultos por meio de métodos de reconstrução do espaço de fases. Isso possibilita a identificação de padrões ocultos e a consideração de interações não lineares entre diferentes variáveis de mercado, como correlações entre ativos, indicadores macroeconômicos e a liquidez do mercado. Em segundo lugar, Attraos utiliza uma estratégia de evolução local no domínio da frequência, adaptando-se às condições de mercado em mudança e acentuando as diferenças entre atratores. Diferentemente dos modelos tradicionais, baseados em suposições fixas sobre a distribuição dos dados, Attraos se adapta dinamicamente à estrutura mutável dos mercados financeiros, fornecendo previsões mais precisas em diferentes horizontes temporais.

Adicionalmente, o modelo inclui um bloco de memória dinâmica com múltiplas resoluções, permitindo-lhe memorizar e considerar padrões históricos de movimento de preços e adaptar-se às condições variáveis do mercado. Isso é especialmente relevante para os mercados financeiros, nos quais os mesmos padrões podem se repetir em diferentes intervalos de tempo, mas com amplitudes e intensidades distintas. A capacidade do modelo de aprender com dados em diferentes níveis de detalhamento lhe confere uma vantagem significativa sobre as abordagens tradicionais, que frequentemente ignoram a natureza multiescalar dos processos de mercado.

Os experimentos realizados pelos autores do framework mostram que Attraos supera os métodos tradicionais de previsão de séries temporais, oferecendo previsões mais precisas com um número menor de parâmetros ajustáveis. É importante destacar que a utilização da dinâmica caótica permite que o modelo capture melhor as dependências de longo prazo e reduza o impacto dos erros acumulados, o que é fundamental para estratégias de investimento de médio e longo prazos.

Algoritmo Attraos

De acordo com a teoria do caos, sistemas dinâmicos multidimensionais que evoluem ao longo do tempo podem apresentar um comportamento complexo e aparentemente aleatório. No entanto, uma análise detalhada desses sistemas mostra que há padrões ocultos que determinam sua dinâmica.

De acordo com o teorema de Takens, se o sistema for determinístico, seu espaço de fases pode ser reconstruído com base na observação de uma de suas variáveis. Essa afirmação se baseia na ideia de que, com uma série temporal suficientemente longa, é possível reconstruir a trajetória multidimensional do sistema, mesmo que apenas dados unidimensionais estejam disponíveis. Tal abordagem permite identificar atratores ocultos, que representam regiões no espaço de fases para as quais as trajetórias do sistema tendem a convergir após um tempo suficiente de evolução.

No contexto dos mercados financeiros, séries temporais, como cotações de ações, pares de moedas e outros ativos, contêm informações sobre a dinâmica interna do sistema de mercado. Apesar da aparência caótica, o comportamento do mercado pode obedecer a leis determinísticas, reveladas por métodos de reconstrução do espaço de fases. A aplicação desses métodos permite que analistas identifiquem atratores característicos, com base nos quais é possível fazer previsões sobre os movimentos futuros dos preços.

O Attraos é baseado nos princípios da teoria do caos e da reconstrução do espaço de fases, permitindo a criação de modelos topologicamente equivalentes de sistemas dinâmicos, sem a necessidade de conhecimento prévio sobre sua natureza. A ideia central é representar a série temporal em um espaço de fases multidimensional para identificar padrões ocultos. Isso é alcançado por meio da escolha de parâmetros-chave — a dimensionalidade da inserção d e o atraso temporal τ, que formam uma representação multidimensional da série temporal:

Essa abordagem permite reduzir a influência do ruído, destacar elementos estruturais do processo e aumentar a precisão da previsão. A metodologia de reconstrução do espaço de fases garante a construção de um retrato de fase estável, refletindo a dinâmica do sistema ao longo do tempo, o que permite sua análise e modelagem.

No Attraos, o processamento de dados começa no módulo de reconstrução do espaço de fases (Phase Space Reconstruction — PSR), responsável por escolher os valores ideais de d e de τ para representar corretamente a dinâmica do sistema. Essa etapa é de extrema importância, pois parâmetros escolhidos de maneira inadequada podem causar distorções significativas na imagem de fase reconstruída. Em seguida, o módulo MDMU (unidade de gerenciamento de dados multidimensionais) divide os dados em fragmentos não sobrepostos, utilizando tensores multidimensionais. Esse processo reduz a complexidade computacional, acelera a convergência do modelo e forma a memória dinâmica do sistema, registrando padrões evolutivos-chave. Com essa abordagem, as previsões se tornam mais estáveis e resistentes à possível degradação dos dados. Adicionalmente, o MDMU utiliza um método de seleção adaptativa de elementos significativos da série temporal, permitindo excluir dinamicamente componentes não informativos e focar nos fatores-chave que exercem maior impacto sobre a evolução do sistema.

Um dos elementos mais importantes de sua arquitetura é o módulo LMA (Linear Matrix Approximation), que implementa o método de aproximação matricial linear. Ele aplica uma projeção polinomial para destacar as principais características da dinâmica do sistema, utilizando matrizes parametrizadas com estruturas diagonais, que definem as "janelas de medição". Isso favorece a identificação precisa das particularidades locais da dinâmica e a adaptação do modelo conforme os dados de entrada mudam. O uso de matrizes diagonais reduz a complexidade computacional e permite trabalhar de maneira eficiente com estruturas de dados multidimensionais. A evolução do sistema nesse módulo é formalizada pela seguinte expressão:

onde M é a matriz diagonal parametrizada de estado, e ϵ representa o erro aleatório de modelagem. Dentro desse módulo, são utilizados diversos modos de evolução, incluindo projeções não lineares adaptativas, que permitem considerar transformações complexas na dinâmica do sistema e melhorar a precisão das previsões.

Para o processamento de processos dinâmicos, utiliza-se o módulo DP (Discrete Projection), que realiza a discretização do sistema por meio de métodos combinados. Em particular, é aplicada a representação exponencial de matrizes, o que garante alta precisão na análise de dados sequenciais. Esse método assegura uma aproximação correta da evolução do sistema e reduz o impacto do acúmulo de erros, o que é especialmente importante na análise de séries temporais longas. O módulo também implementa um mecanismo de quantização adaptativa dos dados, que otimiza a precisão da aproximação sem aumentar significativamente os custos computacionais.

Entre os mecanismos adaptativos adicionais incorporados ao Attraos, está uma estratégia de evolução local com reforço de frequência, que regula as características de frequência da série temporal e compensa distorções causadas por processos estocásticos. Isso é alcançado por meio da filtragem de componentes de alta frequência e do controle da densidade espectral dos dados. Também é implementada uma representação multinível da estrutura dinâmica, na qual o comprimento da janela de análise aumenta progressivamente, reduzindo erros de projeção e melhorando a precisão da aproximação. Essa abordagem permite considerar a complexa organização topológica dos atratores em diferentes escalas, o que é especialmente relevante para sistemas dinâmicos complexos. A arquitetura do framework também integra métodos híbridos de aprendizado, que combinam técnicas numéricas clássicas com algoritmos modernos de aprendizado de máquina, aumentando a adaptabilidade do modelo e sua capacidade de generalização.

A estabilidade do modelo Attraos é garantida por meio de métodos de minimização de erros e controle de desvios dos atratores. Para isso, calcula-se a distância entre os atratores, monitora-se sua variação e ajusta-se a trajetória do sistema ao detectar desvios significativos. Esse conjunto de medidas estabiliza as previsões e assegura a alta precisão do modelo, mesmo em condições de dinâmica instável. A utilização de métodos estatísticos de controle permite identificar automaticamente regiões de instabilidade e ajustar o modelo em tempo real. Além disso, foram implementados mecanismos de controle ativo dos parâmetros do modelo, que possibilitam a alteração dinâmica dos parâmetros de otimização de acordo com o estado atual do sistema, o que aumenta ainda mais a adaptabilidade e a precisão do modelo nas previsões.

A visualização desenvolvida pelos autores do framework Attraos é apresentada a seguir.

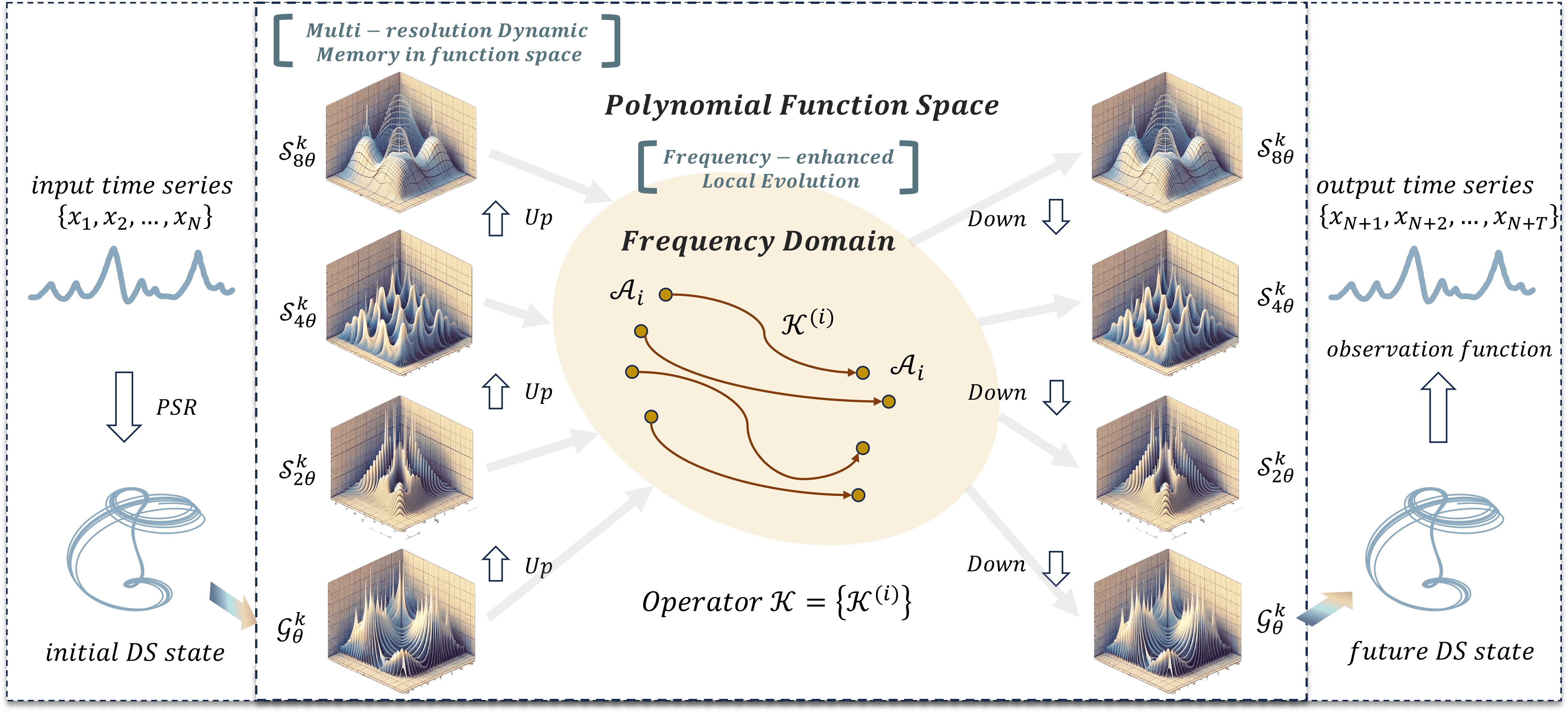
Implementação com MQL5

Após a análise dos aspectos teóricos do framework Attraos, passamos à parte prática do nosso trabalho, na qual implementamos nossa interpretação das abordagens propostas utilizando MQL5.

Iniciaremos preparando os processos essenciais para o funcionamento eficiente do algoritmo Attraos. Nele, são amplamente utilizadas matrizes diagonais, que desempenham um papel importante nos cálculos, pois simplificam o processamento de dados e reduzem o uso de memória.

Uma matriz diagonal é uma matriz quadrada em que todos os elementos fora da diagonal principal são iguais a zero. Na álgebra linear tradicional, essas matrizes são armazenadas como arrays bidimensionais de tamanho n x n. No entanto, esse método se mostra ineficiente, já que a grande maioria de seus elementos é zero. Uma solução mais otimizada é armazenar apenas os elementos não nulos da diagonal como um array unidimensional de comprimento n. Essa abordagem reduz consideravelmente o uso de memória e acelera os cálculos ao eliminar operações desnecessárias com elementos nulos.

Para realizar operações de álgebra linear, especialmente a multiplicação da matriz diagonal por uma matriz arbitrária, é necessário um algoritmo específico que use uma representação vetorial da matriz diagonal. Os algoritmos de multiplicação de matrizes desenvolvidos anteriormente pressupõem o armazenamento explícito de todos os elementos, o que resulta em cálculos redundantes. Neste caso, basta multiplicar cada elemento do vetor diagonal pela linha correspondente da outra matriz. Isso simplifica significativamente o algoritmo e o torna mais eficiente.

Para alcançar o máximo desempenho, implementamos esse processo no contexto do OpenCL, utilizando os recursos de computação paralela em unidades de processamento gráfico (GPUs). A ideia é que cada elemento da matriz resultante seja calculado de forma independente, utilizando apenas o elemento necessário do vetor diagonal. Isso reduz a complexidade computacional do algoritmo e acelera sua execução.

Multiplicação de matriz diagonal

O algoritmo da operação de multiplicação de uma matriz diagonal por outra foi implementado no kernel DiagMatMult. Sua execução é planejada em um espaço tridimensional de tarefas. As duas primeiras dimensões correspondem à dimensionalidade da segunda matriz. A terceira dimensão representa a quantidade de matrizes independentes utilizadas para processar as projeções das sequências unitárias da série temporal multidimensional analisada.

Como mencionado anteriormente, a operação de multiplicação da representação vetorial da matriz diagonal por uma matriz arbitrária consiste em multiplicar cada elemento do vetor diagonal pela linha correspondente da segunda matriz. Para otimizar sua execução na GPU, os fluxos de computação são agrupados em grupos de trabalho. Em cada grupo, apenas um fluxo acessa a memória global para buscar o elemento necessário do vetor diagonal e armazená-lo na memória local. Os demais fluxos utilizam esse valor da memória local para realizar os cálculos necessários, sem acessar novamente a memória global. Isso aumenta significativamente a velocidade de execução do algoritmo e reduz os custos de transferência de dados entre a memória global e os blocos computacionais do processador.

Nos parâmetros do kernel DiagMatMult, recebemos ponteiros para três buffers de dados. Dois deles contêm os dados de entrada e o terceiro é destinado ao armazenamento dos resultados das operações. Adicionamos também a possibilidade de aplicar uma função de ativação aos resultados da multiplicação das matrizes.

__kernel void DiagMatMult(__global const float * diag,
                          __global const float * matr,
                          __global float * result,
                          int activation)
  {
   size_t row = get_global_id(0);
   size_t col = get_local_id(1);
   size_t var = get_global_id(2);
   size_t rows = get_global_size(0);
   size_t cols = get_local_size(1);

No corpo do kernel, primeiro identificamos o fluxo de operações nas três dimensões do espaço de tarefas. Em seguida, o primeiro fluxo do grupo de trabalho armazena o valor do elemento diagonal na memória local, e então sincronizamos os fluxos de operação por meio de uma barreira.

   __local float local_diag[1];
   if(cols==0)
      local_diag[0] = diag[row + var * rows];
   barrier(CLK_LOCAL_MEM_FENCE);

Na etapa seguinte, determinamos o deslocamento no buffer da matriz arbitrária até o elemento necessário.

   int shift = (row  + var * rows) * cols + col;

Aqui é importante observar que os tamanhos da matriz arbitrária e da matriz resultante são iguais. Consequentemente, o deslocamento obtido é válido também para a matriz de resultados.

Extraímos o valor do elemento necessário do buffer da matriz arbitrária e o multiplicamos pelo elemento da diagonal previamente armazenado na memória local. O resultado da operação é ativado por meio da função especificada. O valor obtido é então salvo no buffer da matriz de resultados.

   float res = local_diag[0] * matr[shift];
//---
   result[shift] = Activation(res, activation);
  }

O kernel apresentado acima implementa o algoritmo de propagação para frente da multiplicação de uma matriz diagonal por uma matriz arbitrária. No entanto, isso é apenas metade do trabalho. Durante o treinamento do modelo, será necessário propagar o gradiente de erro por meio dessa operação. Para isso, criaremos outro kernel, chamado DiagMatMultGrad, cujo algoritmo será um pouco mais complexo.

Nos parâmetros do kernel, adicionam-se buffers para registrar os respectivos gradientes de erro. No entanto, o ponteiro para a função de ativação é removido. Assume-se que o gradiente dos resultados da operação já foi ajustado pela derivada da função de ativação correspondente.

__kernel void DiagMatMultGrad(__global const float *diag,
                              __global float *grad_diag,
                              __global const float *matr,
                              __global float * grad_matr,
                              __global const float * grad_result)
  {
   size_t row = get_global_id(0);
   size_t col = get_local_id(1);
   size_t var = get_global_id(2);
   size_t rows = get_global_size(0);
   size_t cols = get_local_size(1);
   size_t vars = get_global_size(2);

No corpo do kernel, identificamos o fluxo atual dentro do espaço tridimensional de tarefas, utilizando a mesma abordagem de definição do kernel de propagação para frente.

De forma análoga ao kernel de propagação para frente, apenas um fluxo do grupo de trabalho extrai o valor necessário do elemento da matriz diagonal para o array local.

   __local float local_diag[LOCAL_ARRAY_SIZE];
   if(cols==0)
      local_diag[0] = diag[row + var * rows];
   barrier(CLK_LOCAL_MEM_FENCE);

E sincronizamos a execução dos fluxos do grupo de trabalho.

Em seguida, definimos o deslocamento nos buffers da matriz arbitrária e da matriz de resultados.

   int shift = (row  + var * rows) * cols + col;
//---
   float grad = grad_result[shift];
   float inp = matr[shift];

Os valores dos elementos necessários dessas matrizes são armazenados em variáveis locais.

Com isso, a preparação está concluída. E podemos calcular o gradiente do erro no nível da matriz arbitrária. Para isso, basta multiplicar o valor do gradiente do erro do respectivo elemento da matriz de resultados pelo elemento da matriz diagonal previamente armazenado no array local.

   grad_matr[shift] = IsNaNOrInf(local_diag[0] * grad, 0);
   barrier(CLK_LOCAL_MEM_FENCE);

O resultado da operação é salvo no buffer correspondente da memória global, e os fluxos da operação são sincronizados dentro do grupo de trabalho.

Depois, precisamos calcular o gradiente do erro para os elementos da matriz diagonal. E aqui, será necessário reunir os valores de todos os elementos da linha correspondente da matriz de resultados. Como você pode imaginar, teremos que somar os valores de todos os fluxos do grupo de trabalho.

Para isso, organizamos um laço de soma paralela dos valores individuais nos elementos do array local.

   int loc = col % LOCAL_ARRAY_SIZE;
#pragma unroll
   for(int c = 0; c < cols; c += LOCAL_ARRAY_SIZE)
     {
      if(c <= col && (c + LOCAL_ARRAY_SIZE) > col)
        {
         if(c == 0)
            local_diag[loc] = IsNaNOrInf(grad * inp, 0);
         else
            local_diag[loc] += IsNaNOrInf(grad * inp, 0);
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

O número máximo de fluxos ativos em cada iteração do laço é limitado pelo número de elementos no array local. Por isso, após concluir as operações de uma iteração, é obrigatório sincronizar os fluxos do grupo de trabalho antes de passar para a próxima iteração do laço, para processar o próximo lote de fluxos ativos.

Em seguida, adicionamos o laço de soma paralela dos elementos do array local.

   int count = min(LOCAL_ARRAY_SIZE, (int)cols);
   int ls = count;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if((col + count) < ls)
        {
         local_diag[col] += local_diag[col + count];
         local_diag[col + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

A cada iteração do laço, o número de fluxos ativos diminui continuamente. Ainda assim, devemos manter a sincronização constante entre os fluxos paralelos de operação dentro do grupo de trabalho.

E para salvar o valor final no buffer global, é suficiente utilizar apenas um fluxo por grupo de trabalho.

   if(col == 0)
      grad_diag[row + var * rows] = IsNaNOrInf(local_diag[0], 0);
  }

Essa abordagem nos permite otimizar os acessos custosos à memória global e distribuir ao máximo a execução das operações entre fluxos paralelos, o que, por sua vez, reduz os custos de treinamento do modelo.

Algoritmo de varredura paralela

Continuamos nosso trabalho no lado do programa OpenCL, agora passando à implementação dos algoritmos do framework Attraos. Precisamos implementar o algoritmo de varredura paralela, utilizado para atualizar de forma eficiente os valores do array de dados brutos X, levando em conta as matrizes de coeficientes de interação A e os multiplicadores de normalização H. A ideia principal do algoritmo consiste no cálculo iterativo de somas prefixadas com divisão binária, o que reduz a complexidade computacional de O(L), típica dos métodos sequenciais, para O(log L).

O array X = {x0, x1, ..., xL-1} é atualizado com base nos elementos vizinhos conforme a seguinte relação recursiva:

onde θ1 e θ2 são definidos nos passos iterativos do algoritmo. O vetor A representa a matriz de coeficientes de interação entre elementos vizinhos, enquanto H é responsável pela normalização dos resultados dos cálculos. Esses parâmetros definem a distribuição adaptativa dos pesos, permitindo levar em consideração a estrutura dos dados processados e modelar de maneira eficiente dependências complexas.

Esse processo é implementado dentro do kernel PScan. Nos parâmetros do kernel, recebemos ponteiros para 4 buffers de dados. Três deles contêm os dados brutos, e um é utilizado para salvar os resultados.

__kernel void PScan(__global const float* A,
                    __global const float* X,
                    __global const float* H,
                    __global float* X_out)
  {
   const size_t idx = get_local_id(0);
   const size_t dim = get_global_id(1);
   const size_t L = get_local_size(0);
   const size_t D = get_global_size(1);

A execução deste kernel é planejada em um espaço de tarefas bidimensional, com agrupamento de fluxos em grupos de trabalho ao longo da primeira dimensão. No corpo do kernel, realiza-se a identificação dos fluxos dentro do espaço de tarefas especificado, bem como a definição de suas dimensões.

Em seguida, determina-se o número de iterações num_steps, que corresponde ao logaritmo binário do comprimento da sequência.

   const int num_steps = (int)log2((float)L);

O uso do logaritmo binário garante o número mínimo de iterações para realizar o processamento completo dos dados, assegurando uma distribuição ideal dos recursos do dispositivo de computação.

Com o objetivo de otimizar a quantidade de acessos à custosa memória global, são criados arrays locais que serão utilizados para armazenar temporariamente os valores.

   __local float local_A[1024];
   __local float local_X[1024];
   __local float local_H[1024];

Cada fluxo carrega os dados da memória global para a memória local. Isso reduz as latências de acesso aos dados durante as operações subsequentes e aumenta o desempenho geral dos cálculos.

//--- Load data to local memory
   int offset = dim + idx * D;
   local_A[idx] = A[offset];
   local_X[idx] = X[offset];
   local_H[idx] = H[offset];
   barrier(CLK_LOCAL_MEM_FENCE);

Após o carregamento dos dados, é essencial sincronizar os fluxos dentro do grupo de trabalho, garantindo a correção das leituras e gravações antes de continuar os cálculos.

Em seguida, inicia-se a etapa principal das operações, que consiste na soma paralela dos valores. A cada iteração do laço, o número de fluxos ativos é reduzido pela metade.

//--- Scan
#pragma unroll
   for(int step = 0; step < num_steps; step++)
     {
      int halfT = L >> (step + 1);
      if(idx < halfT)
        {
         int base = idx * 2;
         local_X[base + 1] += local_A[base + 1] * local_X[base];
         local_X[base + 1] *= local_H[base + 1];
         local_A[base + 1] *= local_A[base];
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

No corpo do laço, realiza-se a soma dos valores do array de dados brutos, seguida pela normalização com base no coeficiente H e a atualização dos coeficientes de interação A, o que mantém a coerência da sequência de cálculos durante o processo de atualização iterativa. A otimização com #pragma unroll permite ao compilador expandir antecipadamente o laço, reduzindo a sobrecarga com desvios de controle e proporcionando um processamento mais eficiente dos dados.

Após a conclusão das iterações do laço, os valores obtidos são transferidos da memória local para o buffer global de resultados.

//--- Save result
   X_out[offset] = local_X[idx];
  }

Essa abordagem permite acelerar significativamente o processamento dos dados, viabilizando uma varredura paralela com uso otimizado dos recursos computacionais.

A próxima etapa será a construção do algoritmo de propagação reversa do erro do processo de varredura paralela implementado acima. Para isso, criaremos um novo kernel chamado PScan_CalcHiddenGradient, cuja principal tarefa é realizar a diferenciação dos parâmetros por meio da varredura reversa.

Nos parâmetros do kernel, adicionam-se ponteiros para os buffers responsáveis pelo registro dos respectivos gradientes de erro.

__kernel void PScan_CalcHiddenGradient(__global const float* A,
                                       __global float*  grad_A,
                                       __global const float* X,
                                       __global float*  grad_X,
                                       __global const float* H,
                                       __global float*  grad_H,
                                       __global const float* grad_X_out)
  {
   const size_t idx = get_local_id(0);
   const size_t dim = get_global_id(1);
   const size_t L = get_local_size(0);
   const size_t D = get_global_size(1);
   const int num_steps = (int)log2((float)L);

O algoritmo começa com a identificação dos fluxos no espaço de tarefas, que é estruturado da mesma forma que no processo de propagação para frente. Como a varredura paralela é executada em várias iterações, o número de passos é calculado como o logaritmo binário do comprimento da sequência, o que permite dividir o processo em uma estrutura hierárquica com agregação sequencial de valores.

Um aspecto importante dessa implementação é a minimização dos acessos à memória global, o que é alcançado por meio do uso de arrays de memória local. Isso aumenta significativamente o desempenho, já que a memória local oferece acesso mais rápido aos dados em comparação à memória global. Para o armazenamento dos dados brutos e dos valores intermediários dos gradientes de erro, são declarados os buffers correspondentes.

   __local float local_A[1024];
   __local float local_X[1024];
   __local float local_H[1024];
   __local float local_grad_X[1024];
   __local float local_grad_A[1024];
   __local float local_grad_H[1024];

Após a declaração dos arrays locais, transferimos para eles os dados brutos a partir dos buffers globais. Isso permite que cada fluxo carregue o elemento correspondente. Em seguida, realizamos a sincronização dos fluxos dentro do grupo local, prevenindo conflitos de acesso.

//--- Load data to local memory
   int offset = idx * D + dim;
   local_A[idx] = A[offset];
   local_X[idx] = X[offset];
   local_H[idx] = H[offset];
   local_grad_X[idx] = grad_X_out[offset];
   local_grad_A[idx] = 0.0f;
   local_grad_H[idx] = 0.0f;
   barrier(CLK_LOCAL_MEM_FENCE);

A seguir, executamos a etapa chave do algoritmo — a varredura reversa. Essa etapa é organizada como um processo iterativo. A cada iteração, o tamanho do array processado é reduzido.

//--- Reverse Scan (Backward)
#pragma unroll
   for(int step = num_steps - 1; step >= 0; step--)
     {
      int halfT = L >> (step + 1);
      if(idx < halfT)
        {
         int base = idx * 2;
         // Compute gradients
         float grad_next = local_grad_X[base + 1] * local_H[base + 1];
         local_grad_H[base + 1] = local_grad_X[base + 1] * local_X[base];
         local_grad_A[base + 1] = local_grad_X[base + 1] * local_X[base];
         local_grad_X[base] += local_A[base + 1] * grad_next;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     } 

No corpo do laço, é calculado primeiro o número de fluxos ativos que participam da iteração atual (halfT). Depois, determina-se o gradiente do erro (grad_next), obtido pelo produto do valor atual com o coeficiente de normalização correspondente H. Em seguida, calculam-se as derivadas em relação aos coeficientes de normalização H e de interação A, utilizando o valor atual de X. Para propagar corretamente o erro para trás, o valor do gradiente de X é ajustado levando em conta o coeficiente de interação. E é obrigatória a sincronização dos fluxos dentro do grupo de trabalho em cada iteração do laço.

Ao final das operações do kernel, os gradientes de erro atualizados devem ser transferidos de volta para a memória global.

//--- Save gradients
   grad_A[offset] = local_grad_A[idx];
   grad_X[offset] = local_grad_X[idx];
   grad_H[offset] = local_grad_H[idx];
  }

Esse método de processamento de dados garante alta eficiência computacional, graças ao uso da memória local e ao número mínimo de acessos à memória global.

Com isso, encerramos o trabalho no contexto OpenCL para esta implementação. O código completo do programa OpenCL pode ser consultado no anexo.

A próxima etapa do nosso trabalho será a construção dos algoritmos no lado do programa principal. No entanto, estamos praticamente no limite do espaço disponível neste artigo. Portanto, faremos uma breve pausa e continuaremos a construção do framework Attraos no próximo artigo.

Considerações finais

Neste artigo, apresentamos o framework Attraos, que propõe um algoritmo de previsão de séries temporais baseado em métodos da teoria do caos. As séries temporais são interpretadas como projeções de sistemas dinâmicos caóticos multidimensionais, o que possibilita a identificação de padrões ocultos inacessíveis a modelos estatísticos e de regressão convencionais. O Attraos implementa a reconstrução do espaço de fases e mecanismos de memória dinâmica, favorecendo a identificação de dependências não lineares estáveis nos dados de mercado e aumentando a precisão das previsões.

Diferentemente dos modelos lineares tradicionais, que não consideram interações complexas e multidimensionais entre variáveis, o Attraos trabalha com a estrutura interna dos atratores caóticos, o que garante não apenas alta precisão na previsão dos valores futuros da série temporal, mas também adaptabilidade às condições de mercado em mudança. Essa abordagem permite detectar componentes determinísticos em processos que, à primeira vista, parecem aleatórios. Isso é especialmente relevante na análise de dados de alta frequência e na previsão de curto prazo de instrumentos financeiros.

Na parte prática do artigo, iniciamos a implementação da nossa interpretação das abordagens propostas utilizando MQL5 com a tecnologia OpenCL, o que permite acelerar significativamente os cálculos graças ao processamento paralelo de dados em GPUs. Essa solução torna viável o uso do método Attraos em sistemas de trading reais e em conjuntos analíticos automatizados, proporcionando alta velocidade de processamento de grandes volumes de informação e adaptação rápida às mudanças nas condições de mercado.

No próximo artigo, continuaremos a implementação iniciada das abordagens propostas e levaremos o processo à sua conclusão lógica, com verificação da eficácia em dados históricos reais.

Referências

• Attractor Memory for Long-Term Time Series Forecasting: A Chaos Perspective
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento dos modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para construção de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca com o código do programa OpenCL