
Redes neurais em trading: Modelos bidimensionais do espaço de conexões (Chimera)
Introdução
Modelar séries temporais é uma tarefa complexa com ampla aplicação em diversas áreas, incluindo medicina, mercados financeiros e setor de energia. As principais dificuldades na criação de modelos universais para séries temporais estão relacionadas a:
- Necessidade de considerar dependências multiescalares, como autocorrelações de curto prazo, sazonalidade e tendências de longo prazo. Isso exige o uso de arquiteturas flexíveis e robustas.
- Processamento adaptativo de séries temporais multidimensionais, nas quais a inter-relação entre as variáveis analisadas pode ser dinâmica e não linear. Para isso, é preciso desenvolver mecanismos que considerem interações dependentes do contexto.
- Minimização da necessidade de pré-processamento manual dos dados, permitindo a identificação automática de padrões estruturais sem exigir ajuste complexo de parâmetros.
- Eficiência computacional, especialmente ao lidar com sequências longas, o que requer otimização da arquitetura do modelo para usar os recursos computacionais de forma eficiente e reduzir o custo do treinamento.
Os métodos estatísticos clássicos exigem um pré-processamento significativo dos dados brutos e nem sempre capturam adequadamente as complexas dependências não lineares. Arquiteturas profundas de redes neurais demonstraram alta capacidade de representação, mas a complexidade computacional quadrática dos modelos baseados em arquitetura Transformer dificulta sua aplicação em séries temporais multidimensionais com grande número de características analisadas. Além disso, esses modelos frequentemente não distinguem entre componentes sazonais e de longo prazo, ou usam pressupostos rígidos prévios, o que reduz sua adaptabilidade em diferentes cenários aplicados.
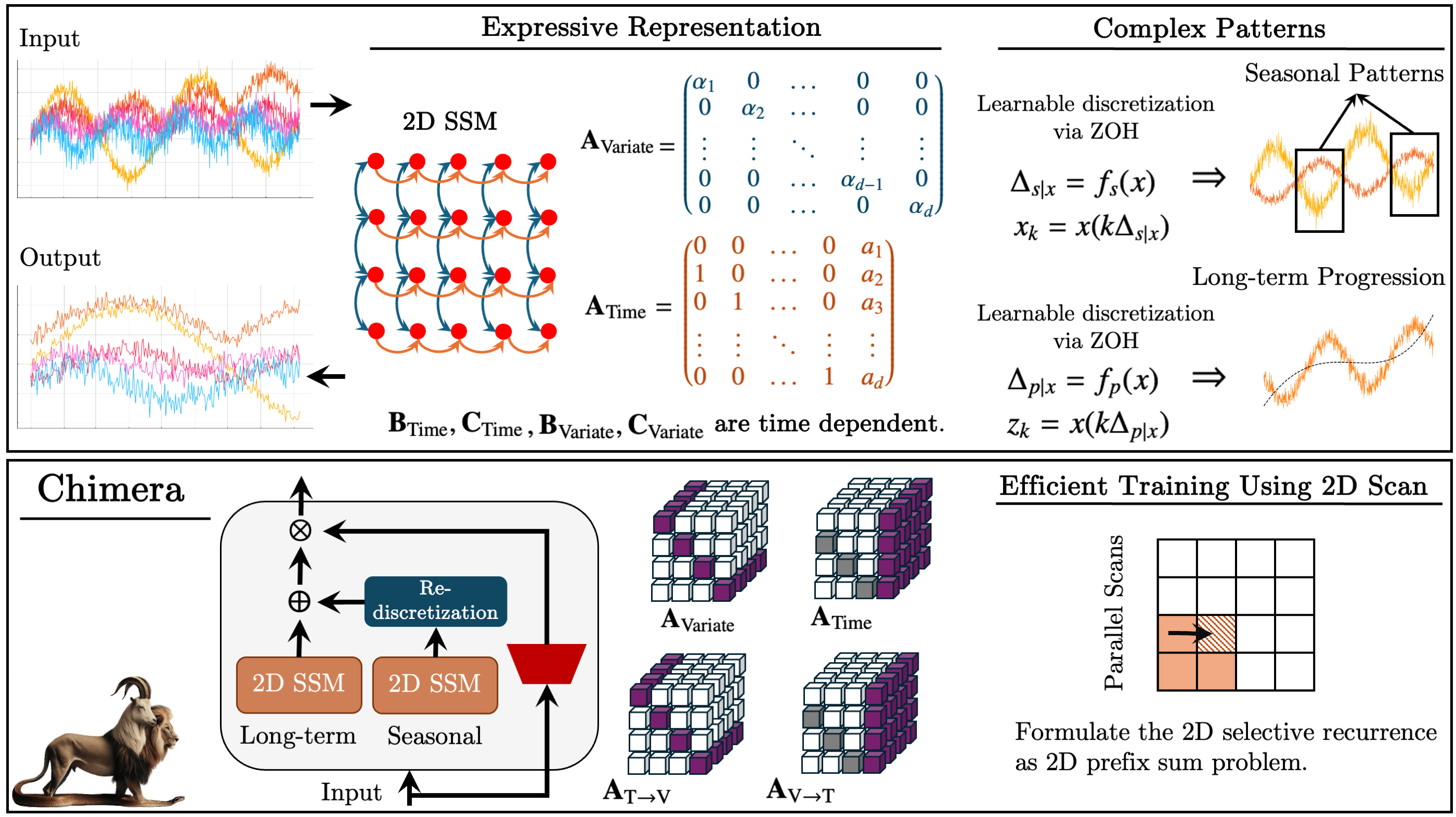
Uma das soluções propostas para esses problemas foi apresentada no trabalho "Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models". O framework Chimera é um modelo bidimensional do espaço de estados (2D-SSM), que utiliza transformações lineares tanto ao longo do eixo temporal quanto do eixo das variáveis. O framework Chimera inclui três componentes principais: modelos do espaço de estados ao longo da dimensão temporal, ao longo das variáveis analisadas e transições cruzadas entre essas dimensões. A parametrização do Chimera se baseia em matrizes diagonais compactas, o que o torna capaz de recuperar tanto métodos estatísticos clássicos quanto arquiteturas modernas de SSM.
Além disso, o Chimera utiliza uma discretização adaptativa para considerar padrões sazonais e particularidades de sistemas dinâmicos.
No trabalho original, os autores do Chimera analisaram o desempenho do framework proposto em diversas tarefas envolvendo séries temporais multidimensionais (classificação, previsão e detecção de anomalias). Os resultados experimentais apresentados mostram que o Chimera alcança uma precisão comparável ou superior aos métodos modernos, com uma redução geral nos custos computacionais.
Algoritmo Chimera
Modelos de espaço de estados (SSM) ocupam um papel importante entre os métodos de análise de séries temporais, graças à sua simplicidade e à capacidade expressiva para modelar dependências complexas, incluindo relações autorregressivas. Esses modelos são utilizados para representar sistemas nos quais o estado em um determinado momento depende do estado anterior do ambiente analisado. No entanto, tradicionalmente os SSM descrevem sistemas nos quais o estado depende de uma única variável (por exemplo, o tempo). Isso limita sua aplicação em casos que exigem modelagem de séries temporais multidimensionais, pois é necessário capturar dependências tanto no contexto temporal quanto no contexto das variáveis analisadas.
As séries temporais multidimensionais representam estruturas mais complexas, que exigem métodos capazes de considerar interdependências entre múltiplas variáveis simultaneamente. Os modelos clássicos bidimensionais de espaço de estados (2D-SSM), usados para descrever essas estruturas, enfrentam uma série de limitações que comprometem sua eficiência em comparação com os métodos modernos de redes neurais profundas. Destacam-se aqui as seguintes desvantagens:
- Restrição a dependências lineares. Os 2D-SSM clássicos conseguem modelar apenas relações lineares, o que se torna uma limitação relevante ao tentar descrever as dependências mais complexas e não lineares, características das séries temporais multidimensionais reais.
- Discretização fixa do modelo. Esses modelos frequentemente possuem uma resolução predefinida e não conseguem se ajustar automaticamente às mudanças nas características dos dados. Isso os torna ineficientes para modelar padrões sazonais ou outras regularidades com resolução variável.
- Dificuldade para lidar com grandes volumes de dados. Na prática, os 2D-SSM se mostram ineficientes quando aplicados a conjuntos de dados muito extensos, o que limita sua utilização em problemas do mundo real.
- Parâmetros de atualização estáticos. Os métodos clássicos de atualização dos parâmetros do modelo são fixos, o que impede uma consideração adequada da dinâmica das dependências, que pode variar ao longo do tempo. Isso representa uma limitação relevante em aplicações nas quais os dados evoluem e requerem abordagens adaptativas.
Por outro lado, os métodos de redes neurais profundas, que vêm sendo desenvolvidos ativamente nos últimos anos, oferecem potencial para superar diversas dessas limitações. Com eles, é possível modelar dependências mais complexas e não lineares, além de considerar a dinâmica das séries temporais, o que os torna promissores para aplicações em tarefas de análise de dados multidimensionais.
No framework Chimera, são utilizados 2D-SSM para modelar séries temporais multidimensionais, onde o primeiro eixo corresponde à dimensão temporal e o segundo eixo, às variáveis. Assim, cada estado é função tanto do tempo quanto das variáveis. A primeira etapa consiste em transformar a forma contínua do 2D-SSM em uma versão discreta, considerando o tamanho do passo Δ1 e Δ2, que representam a resolução do sinal original ao longo dos eixos. Utilizando o método Zero-Order Hold (ZOH), é possível discretizar os dados de entrada como:
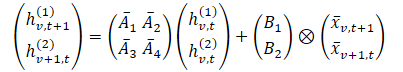
Onde t e v são usados para indicar o índice nas dimensões de tempo e das variáveis analisadas, respectivamente. Essa expressão pode ser representada de forma mais simples.
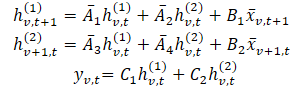
Nessa formulação, intuitivamente, hv,t(1) é o estado oculto que carrega informação ao longo do tempo (cada estado depende de sua marcação temporal anterior, mas dentro de uma mesma característica), onde A1 e A2 controlam o foco na informação passada cruzando o tempo e nas variações cruzadas, respectivamente. De forma análoga, hv,t(2) é o estado oculto que carrega informação sobre as variações cruzadas (cada estado depende de outras variáveis, mas com a mesma marcação temporal).
Os dados de séries temporais geralmente são extraídos de um processo contínuo subjacente. Nesses casos, a variável Δ1 na discretização do eixo do tempo pode ser interpretada como a resolução ou frequência de amostragem dos dados contínuos subjacentes. No entanto, a discretização no eixo das variáveis, que já é discreto por natureza, é um processo menos intuitivo, e levanta questões sobre sua relevância. O passo de discretização em 1D-SSM possui conexões profundas com os mecanismos de portas nas RNN, fornecendo automaticamente uma normalização do modelo e resultando em propriedades desejáveis, como a invariância à resolução.
O modelo SSM bidimensional discreto, representado pelos parâmetros ({Ai}, {Bi}, {Ci}, kΔ1, ℓΔ2), evolui k vezes mais rápido do que um 2D discreto SSM com parâmetros ({Ai}, {Bi}, {Ci}, Δ1ℓΔ2), e em ℓ vezes mais rápido do que ({Ai}, {Bi}, {Ci}, kΔ1, Δ2). Consequentemente, os parâmetros Δ1 podem ser interpretados como controladores do comprimento das dependências que o modelo é capaz de capturar. Ou seja, conforme descrito acima, a discretização ao longo do eixo do tempo pode ser entendida como uma definição da resolução ou frequência de amostragem. Um valor pequeno de Δ1 pode capturar progressões de longo prazo, enquanto um valor maior de Δ1 captura padrões sazonais.
A discretização ao longo do eixo das variáveis analisadas pode ser vista como um mecanismo análogo às portas das RNN, onde Δ2 controla o tamanho do contexto do modelo. Valores grandes de Δ2 indicam uma janela de contexto menor, ignorando outras variáveis, enquanto valores pequenos de Δ2 indicam uma ênfase maior nas dependências entre as variáveis analisadas.
Para aumentar a expressividade e a capacidade do modelo de recuperar processos autorregressivos, os estados ocultos hv,t(1) devem carregar informação de marcações temporais passadas. Para isso, na dimensão temporal, os autores do framework impõem restrições às matrizes A1 e A2, que devem possuir uma estrutura correspondente. Além disso, para A3 e A4 mesmo uma estrutura mais simples de matrizes diagonais é eficaz para combinar informação ao longo da dimensão das variáveis analisadas.
A natureza causal do 2D-SSM leva a um fluxo limitado de informação ao longo da dimensão das variáveis, uma vez que estas não possuem uma ordenação definida. Para resolver esse problema, são utilizados dois módulos distintos para a propagação para frente e a propagação reversa ao longo da dimensão das características.
Assim como nos 1D-SSM eficientes, a formulação independente de dados pode ser interpretada como uma convolução com kernel K. Essa formulação não apenas permite um treinamento mais rápido, com capacidade de processamento paralelo, como também conecta o Chimera às pesquisas mais recentes sobre arquitetura moderna baseada em convoluções para séries temporais.
Como discutido anteriormente, os parâmetros A1 e A2 controlam o foco na informação passada, tanto na dimensão temporal cruzada quanto nas variações cruzadas. De forma análoga, os parâmetros Δ1 e B1 controlam o foco sobre os dados de entrada atuais e históricos. Como esses parâmetros são independentes dos dados, podem ser interpretados como uma característica global do sistema. No entanto, em sistemas complexos, o foco depende do sinal de entrada atual. Portanto, é necessário que esses parâmetros sejam função dos dados de entrada. A dependência analisada dos parâmetros permite que o modelo selecione informações relevantes e filtre informações irrelevantes para cada conjunto de dados de entrada, oferecendo um mecanismo semelhante ao do Transformer. Além disso, dependendo dos dados, o modelo deve ser capaz de se ajustar de forma adaptativa para combinar utilmente as informações entre as variações. Tornar os parâmetros dependentes dos dados de entrada resolve ainda melhor essa questão e permite ao modelo misturar os parâmetros relevantes e filtrar os irrelevantes para modelar a variável de interesse. Uma das principais contribuições técnicas do Chimera é a construção de Bi, Ci e Δi como função dos dados de entrada 𝐱v,t.
O framework Chimera utiliza uma pilha de 2D-SSM com não linearidades entre eles. Para aumentar a expressividade e a capacidade dos 2D-SSM mencionados, assim como em modelos profundos de SSM, permite-se o treinamento de todos os parâmetros, e em cada camada são usados vários 2D-SSM, cada um com sua própria responsabilidade.
Chimera segue a decomposição amplamente adotada de séries temporais, separando-as em componentes de tendência e padrões sazonais. No entanto, ele utiliza características específicas dos 2D-SSM para capturar esses termos.
A visualização original do framework Chimera é apresentada a seguir.
Implementação com MQL5
Após a análise dos aspectos teóricos do framework Chimera, passamos para a implementação prática de nossa própria interpretação das abordagens propostas. Nesta seção, iremos abordar a interpretação do conceito apresentado, utilizando os recursos da linguagem de programação MQL5. Porém, antes de iniciar a implementação em código, é necessário projetar cuidadosamente a arquitetura do modelo, para garantir sua flexibilidade, eficiência e capacidade de adaptação a diferentes tipos de dados.
Decisões de arquitetura
Um dos componentes-chave do framework Chimera são as matrizes de foco do estado oculto A{1,…,4}. Os autores do framework propuseram o uso de matrizes diagonais com complemento, o que reduz o número de parâmetros a serem treinados e diminui a complexidade computacional. Essa abordagem permite reduzir significativamente o consumo de recursos e acelerar o processo de treinamento do modelo.
No entanto, essa solução também apresenta limitações. O uso de matrizes diagonais impõe restrições significativas ao modelo, já que ele só consegue analisar dependências locais entre os elementos subsequentes da sequência. Isso limita sua expressividade e sua capacidade de identificar padrões complexos. Por esse motivo, em nossa interpretação, utilizamos matrizes totalmente treináveis. Essa abordagem aumenta o número de parâmetros, mas amplia consideravelmente a adaptabilidade do modelo, permitindo considerar dependências mais complexas nos dados analisados.
Ao mesmo tempo, nossa versão das matrizes preserva o conceito central da solução original, pois elas não dependem diretamente dos dados de entrada e são treinadas. Isso permite que o modelo se torne mais universal, o que é especialmente importante para resolver diferentes tarefas de análise de sequências temporais multidimensionais.
Outro aspecto importante é a integração dessas matrizes no processo de cálculo. Como foi demonstrado na parte teórica, as matrizes de foco são multiplicadas pelos estados ocultos do modelo, o que está de acordo com os princípios de funcionamento das camadas neurais. Considerando isso, propomos implementá-las como uma camada convolucional de rede neural, na qual a matriz de foco será representada por um tensor de parâmetros treináveis. A integração com arquiteturas neurais padrão permite utilizar os algoritmos de otimização já existentes.
Além disso, para permitir o processo de cálculo paralelo de quatro matrizes de foco ao mesmo tempo, foi tomada a decisão de agrupá-las em um único tensor concatenado, o que, por sua vez, exigiu a junção de duas matrizes de estado oculto em um único tensor.
Apesar de todas as vantagens dessa abordagem, ela se mostra insuficientemente universal para lidar com outras matrizes paramétricas dentro do 2D-SSM. Uma das limitações está na estrutura fixa das matrizes, o que reduz a flexibilidade do modelo ao processar dados multidimensionais complexos. Diante disso, para aumentar a capacidade expressiva do modelo, utilizamos matrizes Bi, Ci e Δi, que são capazes de se adaptar dinamicamente aos dados de entrada, proporcionando uma análise mais profunda das dependências temporais.
As matrizes dependentes do contexto são formadas com base nas informações extraídas dos dados de entrada, o que permite considerar sua estrutura e variar os parâmetros do modelo conforme as características da sequência analisada. Esse abordagem permite ao modelo não apenas analisar inter-relações locais, mas também considerar tendências globais, o que é especialmente importante para tarefas de previsão e análise de séries temporais.
Seguindo as recomendações dos autores do framework, implementamos essas matrizes por meio de camadas neurais especializadas, responsáveis por adaptar os parâmetros de acordo com o contexto.
Na etapa seguinte, uma tarefa importante é organizar o processo de interação complexa dos dados dentro do 2D-SSM modelo. Isso exige uma gestão eficiente dos recursos computacionais, já que estruturas de dados multidimensionais complexas requerem uma abordagem otimizada para o processamento. Considerando os requisitos de eficiência computacional e desempenho do sistema, foi tomada a decisão de deslocar esse bloco de operações para um kernel separado, executado no lado do programa OpenCL.
Essa abordagem oferece várias vantagens significativas. Em primeiro lugar, permite reduzir substancialmente a latência no processamento de dados, por meio da execução paralela das operações no processador gráfico. Isso é crítico na análise de grandes volumes de informação, onde o processamento sequencial pode acarretar em custos de tempo elevados. Em segundo lugar, graças à aceleração por hardware do OpenCL, é possível paralelizar eficientemente os cálculos, o que possibilita a análise de séries temporais complexas em tempo real.
Extensão do programa OpenCL
Após o detalhado projeto da arquitetura das abordagens implementadas, o próximo passo é sua implementação em código. Em primeiro lugar, é necessário modificar o programa OpenCL para otimizar a execução das operações computacionais e garantir uma interação eficiente com os principais componentes do modelo. Vamos criar o algoritmo de interação complexa entre os parâmetros treináveis do 2D-SSM e os dados de entrada no kernel SSM2D_FeedForward.
Nos parâmetros do método, passamos ponteiros para os buffers de dados que contêm todos os parâmetros necessários do modelo e as projeções dos dados de entrada no contexto do tempo e das variáveis analisadas.
__kernel void SSM2D_FeedForward(__global const float *ah, __global const float *b_time, __global const float *b_var, __global const float *px_time, __global const float *px_var, __global const float *c_time, __global const float *c_var, __global const float *delta_time, __global const float *delta_var, __global float *hidden, __global float *y ) { const size_t n = get_local_id(0); const size_t d = get_global_id(1); const size_t n_total = get_local_size(0); const size_t d_total = get_global_size(1);
No corpo do kernel, como de costume, identificamos primeiro a thread atual no espaço bidimensional de tarefas. A primeira dimensão corresponde à quantidade de elementos da sequência, e a segunda, à dimensão das características. Nesse processo, agrupamos todos os elementos da sequência de uma mesma característica em grupos de trabalho.
Aqui vale destacar que as projeções dos parâmetros treináveis e dos dados de entrada, no contexto do tempo e dos indicadores analisados, devem estar convertidas para uma forma compatível na etapa de preparação dos dados, antes de serem enviados ao kernel.
Em seguida, definimos o estado oculto em ambos os contextos, considerando as informações atualizadas. Os valores obtidos são armazenados no buffer de dados correspondente.
//--- Hidden state for(int h = 0; h < 2; h++) { float new_h = ah[(2 * n + h) * d_total + d] + ah[(2 * n_total + 2 * n + h) * d_total + d]; if(h == 0) new_h += b_time[n] * px_time[n * d_total + d]; else new_h += b_var[n] * px_var[n * d_total + d]; hidden[(h * n_total + n)*d_total + d] = IsNaNOrInf(new_h, 0); } barrier(CLK_LOCAL_MEM_FENCE);
Após a execução das operações, é necessário sincronizar as threads do grupo de trabalho, já que os resultados de todo o grupo serão usados em operações subsequentes.
Na etapa seguinte, definimos o resultado do funcionamento do modelo. Para isso, precisamos multiplicar as matrizes de contexto e de discretização pelo estado oculto calculado anteriormente. Para realizar essa operação, organizamos um laço no qual realizamos a multiplicação dos elementos correspondentes das matrizes no contexto do tempo e das variáveis analisadas. Os resultados das operações em ambos os contextos são somados.
//--- Output uint shift_c = n; uint shift_h1 = d; uint shift_h2 = shift_h1 + n_total * d_total; float value = 0; for(int i = 0; i < n_total; i++) { value += IsNaNOrInf(c_time[shift_c] * delta_time[shift_c] * hidden[shift_h1], 0); value += IsNaNOrInf(c_var[shift_c] * delta_var[shift_c] * hidden[shift_h2], 0); shift_c += n_total; shift_h1 += d_total; shift_h2 += d_total; }
E agora, resta apenas transferir o valor obtido para o elemento correspondente do buffer global de resultados e finalizar a execução do kernel.
//--- y[n * d_total + d] = IsNaNOrInf(value, 0); }
Em seguida, devemos organizar os algoritmos de propagação reversa. A otimização dos parâmetros será realizada por meio das respectivas camadas neurais. Porém, para distribuir o gradiente do erro entre essas camadas, criaremos o kernel SSM2D_CalcHiddenGradient, no qual implementaremos um algoritmo inverso ao descrito acima.
Nos parâmetros do kernel, passamos ponteiros para o mesmo conjunto de matrizes, complementando com os buffers de gradientes de erro. Para evitar confusão com a grande quantidade de buffers, usamos o prefixo grad_ nos buffers correspondentes aos gradientes de erro.
__kernel void SSM2D_CalcHiddenGradient(__global const float *ah, __global float *grad_ah, __global const float *b_time, __global float *grad_b_time, __global const float *b_var, __global float *grad_b_var, __global const float *px_time, __global float *grad_px_time, __global const float *px_var, __global float *grad_px_var, __global const float *c_time, __global float *grad_c_time, __global const float *c_var, __global float *grad_c_var, __global const float *delta_time, __global float *grad_delta_time, __global const float *delta_var, __global float *grad_delta_var, __global const float *hidden, __global const float *grad_y ) { //--- const size_t n = get_global_id(0); const size_t d = get_local_id(1); const size_t n_total = get_global_size(0); const size_t d_total = get_local_size(1);
A execução deste kernel está prevista para o mesmo espaço de tarefas do kernel de propagação para frente. No entanto, neste caso, agrupamos as threads em grupos de trabalho segundo o espaço das características.
Antes de iniciar as operações, inicializamos várias variáveis locais, onde armazenaremos valores intermediários e os deslocamentos nos buffers de dados.
//--- Initialize indices for data access uint shift_c = n; uint shift_h1 = d; uint shift_h2 = shift_h1 + n_total * d_total; float grad_hidden1 = 0; float grad_hidden2 = 0;
Em seguida, organizamos o laço de distribuição do gradiente do erro desde o buffer de resultados até os estados ocultos, bem como às matrizes de contexto e de discretização, conforme sua contribuição para o resultado final do modelo. Ao mesmo tempo, distribuímos o gradiente do erro nos contextos temporal e das variáveis analisadas.
//--- Backpropagation: compute hidden gradients from y for(int i = 0; i < n_total; i++) { float grad = grad_y[i * d_total + d]; float c_t = c_time[shift_c]; float c_v = c_var[shift_c]; float delta_t = delta_time[shift_c]; float delta_v = delta_var[shift_c]; float h1 = hidden[shift_h1]; float h2 = hidden[shift_h2]; //-- Accumulate gradients for hidden states grad_hidden1 += IsNaNOrInf(grad * c_t * delta_t, 0); grad_hidden2 += IsNaNOrInf(grad * c_v * delta_v, 0); //--- Compute gradients for c_time, c_var, delta_time, delta_var grad_c_time[shift_c] += grad * delta_t * h1; grad_c_var[shift_c] += grad * delta_v * h2; grad_delta_time[shift_c] += grad * c_t * h1; grad_delta_var[shift_c] += grad * c_v * h2; //--- Update indices for the next element shift_c += n_total; shift_h1 += d_total; shift_h2 += d_total; }
Depois, distribuímos o gradiente do erro para as matrizes de foco.
//--- Backpropagate through hidden -> ah, b_time, px_time for(int h = 0; h < 2; h++) { float grad_h = (h == 0) ? grad_hidden1 : grad_hidden2; //--- Store gradients in ah (considering its influence on two elements) grad_ah[(2 * n + h) * d_total + d] = grad_h; grad_ah[(2 * (n_total + n) + h) * d_total + d] = grad_h; }
E também para as projeções dos dados de entrada.
//--- Backpropagate through px_time and px_var (influenced by b_time and b_var)
grad_px_time[n * d_total + d] = grad_hidden1 * b_time[n];
grad_px_var[n * d_total + d] = grad_hidden2 * b_var[n];
Já o gradiente do erro sobre a matriz Bi precisa ser reunido ao longo de todas as dimensões. Portanto, primeiro zeramos o valor do respectivo buffer de gradientes de erro e sincronizamos as threads do grupo de trabalho.
if(d == 0) { grad_b_time[n] = 0; grad_b_var[n] = 0; } barrier(CLK_LOCAL_MEM_FENCE);
Depois disso, somamos os valores de cada thread do grupo de trabalho.
//--- Sum gradients over all d for b_time and b_var
grad_b_time[n] += grad_hidden1 * px_time[n * d_total + d];
grad_b_var[n] += grad_hidden2 * px_var[n * d_total + d];
}
Os resultados das operações são enviados para os buffers globais de dados correspondentes e a execução do kernel é encerrada.
Com isso, concluímos o trabalho do lado do OpenCL. O código completo pode ser consultado por você mesmo no anexo.
Objeto 2D-SSM
Após finalizar a etapa de trabalho do lado do OpenCL, o próximo passo é construir a estrutura do 2D-SSM no lado do programa principal. Para isso, criaremos a classe CNeuron2DSSMOCL, dentro da qual implementaremos os algoritmos necessários. A estrutura da nova classe é apresentada a seguir.
class CNeuron2DSSMOCL : public CNeuronBaseOCL { protected: uint iWindowOut; uint iUnitsOut; CNeuronBaseOCL cHiddenStates; CLayer cProjectionX_Time; CLayer cProjectionX_Variable; CNeuronConvOCL cA; CNeuronConvOCL cB_Time; CNeuronConvOCL cB_Variable; CNeuronConvOCL cC_Time; CNeuronConvOCL cC_Variable; CNeuronConvOCL cDelta_Time; CNeuronConvOCL cDelta_Variable; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForwardSSM2D(void); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradientsSSM2D(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuron2DSSMOCL(void) {}; ~CNeuron2DSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuron2DSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
Na estrutura apresentada do objeto, vemos um conjunto já conhecido de métodos virtuais sobrescrevíveis e uma quantidade considerável de objetos internos. Creio que a quantidade de objetos não seja uma surpresa. Ela é ditada pela arquitetura do modelo. E em parte, a função de cada objeto pode ser deduzida com base em sua nomenclatura. Já uma descrição mais detalhada da funcionalidade de cada objeto será apresentada durante a implementação dos algoritmos de construção dos métodos da nossa classe.
Todos os objetos internos são declarados de forma estática, o que nos permite deixar o construtor e o destruidor da classe vazios. Já discutimos diversas vezes as vantagens dessa abordagem. A inicialização de todos os objetos declarados e herdados é feita no método Init.
bool CNeuron2DSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_out, optimization_type, batch)) return false; SetActivationFunction(None);
Nos parâmetros do método, recebemos várias constantes que permitem definir com clareza a arquitetura do objeto a ser criado. Entre elas, destacam-se as dimensões dos dados de entrada e do resultado esperado (units_in, window_in e units_out, window_out, respectivamente).
No corpo do método, como de costume, chamamos primeiro o método de mesmo nome da classe pai, ao qual passamos as dimensões do resultado esperado. Esse método da classe pai já contém o bloco de controles necessário e os algoritmos de inicialização dos objetos e interfaces herdados. Portanto, após a execução bem-sucedida das operações do método da classe pai, salvamos com segurança as dimensões do tensor de resultados em variáveis internas.
iWindowOut = window_out; iUnitsOut = units_out;
Como mencionado anteriormente, ao construir os kernels no lado do programa OpenCL, as projeções dos dados de entrada em ambos os contextos devem ter formato compatível. Em nossa implementação, ajustamos esses dados à dimensão do tensor de resultados. Começamos criando o modelo de projeção dos dados de entrada no contexto temporal.
Para preservar a informação das sequências unitárias da série temporal multidimensional, primeiro realizamos a projeção independente das sequências unidimensionais até o tamanho desejado. E aqui vale lembrar que os dados são recebidos na forma de uma matriz, cujas linhas correspondem aos passos de tempo. Sendo assim, para facilitar o trabalho com sequências unitárias, é necessário primeiro transpor a matriz de dados de entrada recebida.
//--- int index = 0; CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL; //--- Projection Time cProjectionX_Time.Clear(); cProjectionX_Time.SetOpenCL(OpenCL); transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) || !cProjectionX_Time.Add(transp)) { delete transp; return false; }
Somente depois disso podemos utilizar os recursos da camada convolucional para alterar a dimensão das sequências unitárias.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, iUnitsOut, window_in, 1, optimization, iBatch) || !cProjectionX_Time.Add(conv)) { delete conv; return false; }
Em seguida, devemos realizar a projeção dos dados ao longo da dimensão das características. Para isso, aplicamos uma transposição reversa dos dados.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, window_in, iUnitsOut, optimization, iBatch) || !cProjectionX_Time.Add(transp)) { delete transp; return false; }
E realizamos a projeção dos dados usando uma camada convolucional.
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, iWindowOut, iUnitsOut, 1, optimization, iBatch) || !cProjectionX_Time.Add(conv)) { delete conv; return false; }
De forma análoga, realizamos a projeção dos dados no contexto das características. Só que, desta vez, iniciamos com a projeção ao longo do eixo das variáveis, depois transpondo os dados e realizando a projeção ao longo do eixo do tempo.
//--- Projection Variables cProjectionX_Variable.Clear(); cProjectionX_Variable.SetOpenCL(OpenCL); index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, iUnitsOut, units_in, 1, optimization, iBatch) || !cProjectionX_Variable.Add(conv)) { delete conv; return false; }
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, iUnitsOut, optimization, iBatch) || !cProjectionX_Variable.Add(transp)) { delete transp; return false; }
index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, iWindowOut, iUnitsOut, 1, optimization, iBatch) || !cProjectionX_Variable.Add(conv)) { delete conv; return false; }
Após a inicialização dos modelos de projeção dos dados de entrada, passamos a trabalhar com os demais objetos internos. Aqui, começamos inicializando o objeto de estado oculto. Esse objeto é utilizado apenas para armazenar dados e não contém parâmetros treináveis. No entanto, ele deve ter volume suficiente para armazenar os dados de estado oculto de ambos os contextos.
//--- HiddenState index++; if(!cHiddenStates.Init(0, index, OpenCL, 2 * iUnitsOut * iWindowOut, optimization, iBatch)) return false;
Em seguida, passamos para as matrizes de foco do estado oculto. Como mencionado anteriormente, implementamos todas as 4 matrizes dentro de uma única camada convolucional. Isso nos permite executar o funcionamento paralelo dessas matrizes.
Vale destacar que, na saída dessa camada, esperamos obter o resultado da multiplicação do estado oculto por 4 matrizes independentes. Duas delas operam no contexto temporal, e as outras duas, no contexto das características. Para alcançar o efeito desejado, declaramos a camada convolucional com um número de filtros equivalente ao dobro da janela dos dados de entrada, o que corresponde a duas matrizes de foco. E indicamos que a camada convolucional deve operar com duas sequências independentes, correspondentes aos contextos de tempo e de características. Lembrando que, para sequências independentes, a camada convolucional utiliza diferentes matrizes de filtros. Dessa forma, obtemos 4 matrizes de foco, que atuam em pares com diferentes contextos.
//--- A*H index++; if(!cA.Init(0, index, OpenCL, iWindowOut, iWindowOut, 2 * iWindowOut, iUnitsOut, 2, optimization, iBatch)) return false;
É importante observar que valores altos nos parâmetros de foco podem causar o efeito de explosão do gradiente de erro. Por isso, reduzimos os parâmetros em 10 vezes após a inicialização aleatória.
if(!SumAndNormilize(cA.GetWeightsConv(), cA.GetWeightsConv(), cA.GetWeightsConv(), iWindowOut, false, 0, 0, 0, 0.05f)) return false;
Na etapa seguinte, passamos à geração das matrizes adaptativas e dependentes do contexto Bi, Ci e Δi, que, em nossa implementação, são funções dos dados de entrada. Para gerar essas matrizes, utilizamos camadas convolucionais, que recebem como entrada as projeções dos dados de entrada no respectivo contexto, e como saída geram a matriz desejada.
//--- B index++; if(!cB_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, optimization, iBatch)) return false; cB_Time.SetActivationFunction(TANH); index++; if(!cB_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, optimization, iBatch)) return false; cB_Variable.SetActivationFunction(TANH);
A abordagem proposta é semelhante ao funcionamento das portas nas RNN. Utilizamos a tangente hiperbólica como função de ativação para as matrizes Bi e Ci, ressaltando a possibilidade de dependência positiva e negativa.
//--- C index++; if(!cC_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cC_Time.SetActivationFunction(TANH); index++; if(!cC_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cC_Variable.SetActivationFunction(TANH);
A matriz Δi cumpre a função de discretização treinável e não pode conter valores negativos. Para ela, utilizamos a função de ativação SoftPlus, que é uma versão suavizada do ReLU.
//--- Delta index++; if(!cDelta_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cDelta_Time.SetActivationFunction(SoftPlus); index++; if(!cDelta_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1, optimization, iBatch)) return false; cDelta_Variable.SetActivationFunction(SoftPlus); //--- return true; }
Após a inicialização de todos os objetos internos, resta apenas retornar à aplicação chamadora o resultado lógico da execução das operações e encerrar o método.
Trabalhamos bastante hoje, mas nosso trabalho ainda não terminou. Proponho fazermos uma pequena pausa e continuarmos no próximo artigo. Nele, finalizaremos a construção dos objetos necessários, os integraremos ao modelo e verificaremos a eficácia das abordagens implementadas utilizando dados históricos reais.
Considerações finais
Neste artigo, conhecemos o framework da modelo bidimensional de espaço de estados Chimera, que propõe novas abordagens para modelar séries temporais multidimensionais considerando dependências nos contextos de tempo e características. O Chimera utiliza modelos bidimensionais de espaço de estados (2D-SSM), o que permite modelar de forma eficiente tanto progressões de longo prazo quanto padrões sazonais.
Na parte prática, iniciamos o trabalho de implementação de nossa própria interpretação das abordagens propostas, utilizando recursos do MQL5. No entanto, o trabalho iniciado ainda não está concluído. No próximo artigo, continuaremos a construção das abordagens propostas e certamente testaremos a eficácia das soluções implementadas com dados históricos reais.
Referências
- Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models
- Outros artigos da série
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos com o método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema e da arquitetura dos modelos |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17210
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Do básico ao intermediário: Eventos em Objetos (III)
Do básico ao intermediário: Eventos em Objetos (III)
 Desenvolvendo um EA multimoeda (Parte 22): Início da transição para substituição dinâmica de configurações
Desenvolvendo um EA multimoeda (Parte 22): Início da transição para substituição dinâmica de configurações
 Como funções de cem anos atrás podem atualizar suas estratégias de trading
Como funções de cem anos atrás podem atualizar suas estratégias de trading
 Algoritmo de busca circular — Circle Search Algorithm (CSA)
Algoritmo de busca circular — Circle Search Algorithm (CSA)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso