ブレインストーム最適化アルゴリズム(第2部）：マルチモーダリティ

MetaTrader 5 — 例 | 12 9月 2024, 09:36

130

Andrey Dik

内容

1. はじめに
2. アルゴリズムの実装
3. テスト結果

1. はじめに

第１部では、ブレインストーミングにヒントを得たこの革新的な手法の基本原理を明らかにするブレインストーム最適化(BSO)アルゴリズムで最適化の世界を掘り下げました。その論理構造を学ぶとともに、クラスタリング手法であるK-MeansとK-Means++の議論にも踏み込みました。ブレインストーム最適化(BSO: Brain Storm Optimization)は、グループ活動におけるアイデア創出と評価フェーズを組み込んだ最適化手法です。このアルゴリズムは、クラスタリング手法と組み合わせた最適化の分野に貢献しました。クラスタリングによって、似たようなデータ要素のグループを特定することができ、BSOが最適なソリューションを見つけるのに役立ちます。突然変異法を用いることで、アルゴリズムは解探索空間の障害物を迂回し、より効率的な最適解への経路を探索することができます。

今こそ実際の行動に移るときです。第2部では、アルゴリズムの実用的な実装に飛び込み、マルチモダリティについて話し、アルゴリズムをテストし、結果を要約します。

2. アルゴリズムの実装

BSOアルゴリズムロジックのキーポイントを簡単に概説しましょう。

クラスタリング
クラスタシフト
クラスタからアイデアを選択する：クラスタの重心またはクラスタからのアイデア
選択されたアイデアの融合
前の段階で得られたアイデアの変異
ステージ2、3、4のアイデアを選択する：新しいアイデアを親集団に入れ、分類する

BSOアルゴリズムコードの説明に移ります。

S_BSO_Agentエージェントアルゴリズムの構造体を実装してみましょう。この構造体は、BSOアルゴリズムの各エージェントを記述するために使用されます。

1. この構造体には以下のフィールドが含まれます。

c[]：エージェントの座標を格納する配列
f ：エージェントのスコア（適応度）を格納する変数
label：クラスタメンバーシップラベルを格納する変数

2. Init ：S_BSO_Agent構造体メソッドで、構造体フィールドを初期化します。これは、ArrayResize関数を使用してc座標配列のサイズを変更するために使用されるcoords整数引数を取ります。
3. f = -DBL_MAX：変数fの初期値をdoubleの可能な最小値に等しくします。
4. label = -1：label変数の初期値を-1に設定します。これは、エージェントがどのクラスタにも属さないことを意味します。

このコードは、BSO最適化アルゴリズムにおけるエージェントの基本的なデータ構造を表し、新しいエージェントが作成されたときにそのフィールドを初期化します。

//——————————————————————————————————————————————————————————————————————————————
struct S_BSO_Agent
{
    double c     []; //coordinates
    double f;        //fitness
    int    label;    //cluster membership label

    void Init (int coords)
    {
      ArrayResize (c,     coords);
      f     = -DBL_MAX;
      label = -1;
    }
};
//——————————————————————————————————————————————————————————————————————————————

K-MeansとK-Means++クラスタリングアルゴリズムについては、すでに前回の記事で詳しく説明したので、ここでは割愛します。

C_AO_BSOクラスコードの説明に移りましょう。C_AO_BSOクラスコードは、C_AO母集団アルゴリズムの基本クラスを継承したもので、以下のフィールドとメソッドを含んでいます。

1. publicフィールド

ao_name：最適化アルゴリズム名
ao_desc：最適化アルゴリズムの説明
ao_link：最適化アルゴリズムに関する記事へのリンク
popSize：母集団のサイズ
parentPopSize：親の母集団のサイズ
clustersNumb：クラスタの数
p_Replace：置換確率
p_One：一択の確率
p_One_center：選択されたクラスタ内の1つの中心または個体を選択する確率
p_Two_center：選択されたクラスタで2つの中心または2つの個体を選択する確率
k_Mutation：突然変異の比率
distribCoeff：分配比率
agent：エージェント配列
parents：親の配列
clusters：クラスタの配列
km：KMeansクラスオブジェクト

2. オプション

SetParams：アルゴリズムのパラメータを設定するメソッド
Init：アルゴリズムを初期化するメソッド（最小検索範囲と最大検索範囲、検索ステップ、エポック数を受ける）
Moving：エージェントを移動させるメソッド
Revision：エージェントの改訂メソッド

3. privateフィールド

parentsTemp：親の一時的な配列
epochs：最大エポック数
epochsNow：現在のエポック

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BSO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BSO () { }
  C_AO_BSO ()
  {
    ao_name = "BSO";
    ao_desc = "Brain Storm Optimization";
    ao_link = "https://www.mql5.com/ja/articles/14622";

    popSize        = 25;   //population size

    parentPopSize  = 50;   //parent population size;
    clustersNumb   = 5;    //number of clusters
    p_Replace      = 0.1;  //replace probability
    p_One          = 0.5;  //probability of choosing one
    p_One_center   = 0.3;  //probability of choosing one center
    p_Two_center   = 0.2;  //probability of choosing two centers
    k_Mutation     = 20.0; //mutation coefficient
    distribCoeff   = 1.0;  //distribution coefficient

    ArrayResize (params, 9);

    params [0].name = "popSize";       params [0].val  = popSize;

    params [1].name = "parentPopSize"; params [1].val  = parentPopSize;
    params [2].name = "clustersNumb";  params [2].val  = clustersNumb;
    params [3].name = "p_Replace";     params [3].val  = p_Replace;
    params [4].name = "p_One";         params [4].val  = p_One;
    params [5].name = "p_One_center";  params [5].val  = p_One_center;
    params [6].name = "p_Two_center";  params [6].val  = p_Two_center;
    params [7].name = "k_Mutation";    params [7].val  = k_Mutation;
    params [8].name = "distribCoeff";  params [8].val  = distribCoeff;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;

    parentPopSize = (int)params [1].val;
    clustersNumb  = (int)params [2].val;
    p_Replace     = params      [3].val;
    p_One         = params      [4].val;
    p_One_center  = params      [5].val;
    p_Two_center  = params      [6].val;
    k_Mutation    = params      [7].val;
    distribCoeff  = params      [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    parentPopSize; //parent population size;
  int    clustersNumb;  //number of clusters
  double p_Replace;     //replace probability
  double p_One;         //probability of choosing one
  double p_One_center;  //probability of choosing one center
  double p_Two_center;  //probability of choosing two centers
  double k_Mutation;    //mutation coefficient
  double distribCoeff;  //distribution coefficient

  S_BSO_Agent  agent   [];
  S_BSO_Agent  parents [];

  S_Clusters   clusters [];
  S_BSO_KMeans km;

  private: //-------------------------------------------------------------------
  S_BSO_Agent  parentsTemp [];
  int          epochs;
  int          epochsNow;
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSOクラスのInitメソッドは、最適化アルゴリズムを初期化するために以下のアクションを実行します。

初期化を確認する：まず、StandardInitメソッドが検索範囲とステップのパラメータで呼ばれます。StandardInitがfalseを返した場合、初期化は中止され、Initメソッドはfalseを返します。
エージェントの初期化：agent配列はpopSizeにリサイズされます。Initメソッドは、座標の数を定義するcoordsパラメータを持つ各エージェントに対して呼び出されます。
クラスタの初期化：clusters配列はclustersNumb（最大クラスタ数）にリサイズされ、各クラスタに対してInitメソッドが呼び出されます。
親の初期化：parents配列とparentsTemp配列はparentPopSize + popSizeにリサイズされ、それぞれの親に対してInitメソッドが呼び出されます。配列は、その後の並び替えのために、親と子の両方の集団を収容できるようなサイズでなければなりません。
エポックの設定：epochsとepochsNowの値は、それぞれ渡されたパラメータepochsPと0に従って設定されます。

このメソッドは、すべての初期化ステップが正常に完了した場合にtrueを返します。これは、与えられたエポック数の最適化を実行するためのアルゴリズムを準備します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BSO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (clusters, clustersNumb);
  for (int i = 0; i < clustersNumb; i++) clusters [i].Init (coords);

  ArrayResize (parents,     parentPopSize + popSize);
  ArrayResize (parentsTemp, parentPopSize + popSize);

  for (int i = 0; i < parentPopSize + popSize; i++)
  {
    parents     [i].Init (coords);
    parentsTemp [i].Init (coords);
  }

  epochs    = epochsP;
  epochsNow = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSOクラスのMovingメソッドは、最適化中にエージェントを移動させるために使用されます。このメソッドでは次がおこなわれます。

現在のエポックの値が増加される(epochsNow++)
revisionがfalseの場合、エージェントの座標が指定された範囲のランダムな値で初期化され、その後、メソッドが終了する
revisionがfalseでない場合、方程式と確率を用いて各エージェントの新しい座標が計算される
エージェントの新しい座標を決定するために、さまざまな数学的計算、乱数、確率が使用される
新しい座標が条件と確率に従って計算される
SeInDiSpメソッドを使用して新しい座標が設定され、検索範囲とステップに従って値が調整される
u.RNDprobab()<p_Replaceの条件を満たす場合、選択されたクラスタ中心（クラスタ中心オフセット）を置き換える新しいアイデアが生成される
u.RNDprobab()<p_Oneの条件を満たす場合、1つのクラスタからのアイデアが選択される
u.RNDprobab()<p_Oneの条件を満たさない場合、2つのクラスタからのアイデアが選択される
エージェント座標の変異が起こる
エージェントの新しい座標が保存される

このメソッドは、現在のエポックと確率に従って、BSO最適化アルゴリズムにおけるエージェントの座標を更新する役割を担っています。エージェントの動作の異なるモデルを記述するコードの対応する部分を色分けして強調してみましょう。

新しいアイデアを生み出す：新しいエポックごとに、エージェントはp_Replace比率に従って、発見された大域解の近傍をより徹底的に探索し、大域最適解に近づこうとし、重心を移動させます。
1つのクラスタの近傍を探索する：p_Oneの比率を考慮し、エージェントはランダムに選択された1つのクラスタの近傍を探索します。こうして、母集団の中でエージェントがいるすべての領域の探索が続けられます。
2つのクラスタからアイデアを選ぶ：u.RNDprobab()<p_Oneの条件を満たさない場合、ランダムに選択された2つのクラスタからアイデアが選択されます。
突然変異：エージェント座標は突然変異の対象となり、母集団の多様性を確保し、局所最適への早期収束を避けるのに役立ちます。
エージェントの保存：すべての操作の後、新しいエージェント座標は次の反復のために保存されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSO::Moving ()
{
  epochsNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  //----------------------------------------------------------------------------
  int    cIndx_1    = 0;  //index in the list of non-empty clusters
  int    iIndx_1    = 0;  //index in the list of ideas in the cluster
  int    cIndx_2    = 0;  //index in the list of non-empty clusters
  int    iIndx_2    = 0;  //index in the list of ideas in the cluster
  double min        = 0.0;
  double max        = 0.0;
  double dist       = 0.0;
  double val        = 0.0;
  double X1         = 0.0;
  double X2         = 0.0;
  int    clListSize = 0;
  int    clustList [];
  ArrayResize (clustList, 0, clustersNumb);

  //----------------------------------------------------------------------------
  //let's make a list of non-empty clusters
  for (int cl = 0; cl < clustersNumb; cl++)
  {
    if (clusters [cl].count > 0)
    {
      clListSize++;
      ArrayResize (clustList, clListSize);
      clustList [clListSize - 1] = cl;
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    //==========================================================================
    //generating a new idea that replaces the selected cluster center (cluster center offset)
    if (u.RNDprobab () < p_Replace)
    {
      cIndx_1 = u.RNDminusOne (clListSize);

      for (int c = 0; c < coords; c++)
      {
        val = clusters [clustList [cIndx_1]].centroid [c];

        dist = (rangeMax [c] - rangeMin [c]) * 0.8;

        min = val - dist; if (min < rangeMin [c]) min = rangeMin [c];
        max = val + dist; if (max > rangeMax [c]) max = rangeMax [c];

        val = u.GaussDistribution (val, min, max, 3);
        val = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        clusters [clustList [cIndx_1]].centroid [c] = val;
      }
    }

    //==========================================================================
    //an idea from one cluster is selected
    if (u.RNDprobab () < p_One)
    {
      cIndx_1 = u.RNDminusOne (clListSize);

      //------------------------------------------------------------------------
      if (u.RNDprobab () < p_One_center) //select cluster center
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = clusters [clustList [cIndx_1]].centroid [c];
        }
      }
      //------------------------------------------------------------------------
      else                               //random idea from the cluster
      {
        iIndx_1 = u.RNDminusOne (clusters [clustList [cIndx_1]].count);

        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = parents [clusters [clustList [cIndx_1]].ideasList [iIndx_1]].c [c];
        }
      }
    }
    //==========================================================================
    //select ideas from two clusters
    else
    {
      if (clListSize == 1)
      {
        cIndx_1 = 0;
        cIndx_2 = 0;
      }
      else
      {
        if (clListSize == 2)
        {
          cIndx_1 = 0;
          cIndx_2 = 1;
        }
        else
        {
          cIndx_1 = u.RNDminusOne (clListSize);

          do
          {
            cIndx_2 = u.RNDminusOne (clListSize);
          }
          while (cIndx_1 == cIndx_2);
        }
      }

      //------------------------------------------------------------------------
      if (u.RNDprobab () < p_Two_center) //two cluster centers selected
      {
        for (int c = 0; c < coords; c++)
        {
          X1 = clusters [clustList [cIndx_1]].centroid [c];
          X2 = clusters [clustList [cIndx_2]].centroid [c];

          a [i].c [c] = u.RNDfromCI (X1, X2);
        }
      }
      //------------------------------------------------------------------------
      else //two ideas from two selected clusters
      {
        iIndx_1 = u.RNDminusOne (clusters [clustList [cIndx_1]].count);
        iIndx_2 = u.RNDminusOne (clusters [clustList [cIndx_2]].count);

        for (int c = 0; c < coords; c++)
        {
          X1 = parents [clusters [clustList [cIndx_1]].ideasList [iIndx_1]].c [c];
          X2 = parents [clusters [clustList [cIndx_2]].ideasList [iIndx_2]].c [c];

          a [i].c [c] = u.RNDfromCI (X1, X2);
        }
      }
    }

    //==========================================================================
    //Mutation
    for (int c = 0; c < coords; c++)
    {
      int x = (int)u.Scale (epochsNow, 1, epochs, 1, 200);

      double ξ = (1.0 / (1.0 + exp (-((100 - x) / k_Mutation))));// * u.RNDprobab ();

      double dist = (rangeMax [c] - rangeMin [c]) * distribCoeff * ξ;
      double min = a [i].c [c] - dist; if (min < rangeMin [c]) min = rangeMin [c];
      double max = a [i].c [c] + dist; if (max > rangeMax [c]) max = rangeMax [c];

      val = a [i].c [c];

      a [i].c [c] = u.GaussDistribution (val, min, max, 8);
    }

    //Save the agent-----------------------------------------------------------
    for (int c = 0; c < coords; c++)
    {
      val = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a     [i].c [c] = val;
      agent [i].c [c] = val;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSOクラスのRevisionメソッドの主なタスクは、大域解を更新し、解クラスタを構築することです。このメソッドでは次がおこなわれます。

適応度を得る：集団内の各エージェントについて適応度値が抽出され、エージェント構造体の対応するフィールドに保存されます。
新しいアイデアを母集団に移転する：最適化の過程で生成された新しいアイデア（エージェント）が親集団に加えられます。
母集団を並び替える：親集団は適応度で並び替えられます。これによって、最良の解決策だけが、次のエポックにおける新しいアイデアの創造に参加することができます。
最良解を確認する：親集団における最良のエージェントの適合度が現在の最良解を上回った場合、最良解とその座標が更新されます。
クラスタリングをおこなう：これが最初の反復の場合、K-Meansアルゴリズムは親集団とクラスタで初期化されます。次にK-Meansアルゴリズムが親集団のクラスタリングのために起動されます。
クラスタの最良解をクラスタの中心として割り当てる：各クラスタについて、エージェントがあるかどうかが確認されます（クラスタは空の場合もある）。ある場合、親集団の各エージェントがクラスタに属しているかどうかが確認されます。エージェントの適応度が現在のクラスタ適応度を上回った場合、クラスタ適応度とその重心が更新されます（重心は新しいアイデアの作成に参加する）。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSO::Revision ()
{
  //get fitness--------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;
  }

  //pass new ideas to the population--------------------------------------------
  for (int i = parentPopSize; i < parentPopSize + popSize; i++)
  {
    parents [i] = agent [i - parentPopSize];
  }

  //sort out the parent population----------------------------------------
  u.Sorting (parents, parentsTemp, parentPopSize + popSize);

  if (parents [0].f > fB)
  {
    fB = parents [0].f;
    ArrayCopy (cB, parents [0].c, 0, 0, WHOLE_ARRAY);
  }

  //perform clustering-----------------------------------------------------
  if (!revision)
  {
    km.KMeansInit (parents, parentPopSize, clusters);
    revision = true;
  }

  km.KMeansInit (parents, parentPopSize, clusters);
  km.KMeans     (parents, parentPopSize, clusters);

  //Assign the best cluster solution as the cluster center--------------------------
  for (int cl = 0; cl < clustersNumb; cl++)
  {
    clusters [cl].f = -DBL_MAX;

    if (clusters [cl].count > 0)
    {
      for (int p = 0; p < parentPopSize; p++)
      {
        if (parents [p].label == cl)
        {
          if (parents [p].f > clusters [cl].f)
          {
            clusters [cl].f = parents [p].f;
            ArrayCopy (clusters [cl].centroid, parents [p].c, 0, 0, WHOLE_ARRAY);
          }
        }
      }
    }
  }
}//——————————————————————————————————————————————————————————————————————————————

マルチモーダルに関して：BSOアルゴリズムは、もともとマルチモーダル問題の解決を目指した最適化手法として導入されました。しかし、テスト結果から、このアルゴリズムは重要な極値を十分に探索できておらず、多くの有用な解が見逃されていることが明らかになりました。現在の実装は、最適とは言い難いため、エージェントの適応性により焦点を当てるべく、K-Meansクラスタリングの手法に注目し、いくつかの改良を加える必要が生じました。

覚えていらっしゃるかもしれませんが、最適化アルゴリズムにおいて、マルチモーダリティとは、最適化対象の関数が複数の最適点やピークを持つ状態を指します。こうした関数には、局所的最適解が多数存在する可能性があり、それらは適応度関数の観点から、大域的最適解に近いものや、問題を解く上で重要な解である場合があります。クラスタリング手法は、探索空間内で特徴量が異なるモダリティを持つ異なる領域を浮き彫りにするのに役立ちます。

そこで、エージェントの適応度がクラスタリングに与える影響を高めてみましょう。エージェント間の距離を計算する機能を、新しいFitnessDistance関数で包んでみましょう。この関数には追加のパラメータ「alpha」があり、これにより距離と適応度の重要性のバランスを調整できます。

FitnessDistance関数は、エージェントとクラスタの重心間の距離と適応度関数の差を同時に考慮して距離を計算します。これは、エージェントの適応度関数と重心間の差の絶対値と距離の加重和を使っておこなわれます。重み「alpha」は、適応度関数の差と比較した距離の相対的な重要度を決定します。

//——————————————————————————————————————————————————————————————————————————————
double FitnessDistance (S_BSO_Agent &data, S_Cluster &clust, double alpha)
{
  double distance = VectorDistance (data.c, clust.centroid);
  double fitness_diff = fabs (data.f - clust.f);
  return alpha * distance + (1 - alpha) * fitness_diff;
}
//——————————————————————————————————————————————————————————————————————————————

KMeans法は、alphaパラメータで補足されます。

void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [], double alpha)

重心の更新を担当するKMeansメソッドのコードセクションを変更して、各クラスタがクラスタの一部である個体の最大適応度値を持つようにしましょう。

// Update the centroids
double sum_c [];
ArrayResize (sum_c, ArraySize (data [0].c));
double sum_f = 0.0;

for (int cl = 0; cl < nClusters; cl++)
{
  ArrayInitialize (sum_c, 0.0);

  clust [cl].count = 0;
  ArrayResize (clust [cl].ideasList, 0);
  sum_f = -DBL_MAX;

  for (int d = 0; d < dataSizeClust; d++)
  {
    if (data [d].label == cl)
    {
      for (int k = 0; k < ArraySize (data [d].c); k++)
      {
        sum_c [k] += data [d].c [k];
      }

      if (data [d].f > sum_f) sum_f = data [d].f;

      clust [cl].count++;
      ArrayResize (clust [cl].ideasList, clust [cl].count);
      clust [cl].ideasList [clust [cl].count - 1] = d;
    }
  }

  if (clust [cl].count > 0)
  {
    for (int k = 0; k < ArraySize (sum_c); k++)
    {
      clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
    }
  }
}

この変更により、クラスタリング中に適応度関数を考慮できるようになりましたが、適応度関数における個々のモードの割り当てに顕著な改善は見られず、結果にも影響しませんでした。これは、少なくともこのBSOの実装では、クラスタリングプロセスで適応度関数を使用することが必ずしも効率的ではないという事実によるものでしょう。

K-MeansやK-Means++で望ましい結果が得られない場合は、他のクラスタリング手法を試すことができます。

1. Density-based spatial clustering for noisy applications (DBSCAN)：このクラスタリング手法は、データ点間の距離ではなく、密度に基づいてクラスタを形成します。特徴空間内で、互いに近接し、十分な数の近傍点を持つデータ点をグループ化するアプローチです。DBSCANは、最も広く使用されているクラスタリングアルゴリズムの1つです。

2.階層的クラスタリング(Hierarchical Clustering)：この手法では、クラスタの階層構造を構築し、クラスタ同士を近接性に基づいて結びつけていきます。階層的クラスタリングには、凝集型（ボトムアップ型）と分割型（トップダウン型）があります。

3. ガウス混合モデル(GMM)：この統計モデルは、すべての観測データが、パラメータが未知の複数のガウス分布の混合から生成されると仮定します。各クラスタは、これらの分布のいずれかに対応しています。

4. スペクトラルクラスタリング：この手法では、低次元空間にクラスタリングする前に、類似度行列の固有ベクトルを使用してデータの次元を削減します。

この分野でさらに研究を進めようとすると、かなり多くのクラスタリング手法があります。実験してみたい場合、添付のコードでK-Meansメソッドを他のものと置き換えてください。

3. テスト結果

以下は、BSOアルゴリズムの結果です。

BSO|Brain Storm Optimization|25.0|50.0|5.0|0.1|0.5|0.3|0.2|20.0|1.0|
=============================
5 Hilly's; Func runs:10000; result:0.9301770731803266
25 Hilly's; Func runs:10000; result:0.5801719580773876
500 Hilly's; Func runs:10000; result:0.30916005647304245
=============================
5 Forest's; Func runs:10000; result:0.929981802038364
25 Forest's; Func runs:10000; result:0.5907047167619348
500 Forest's; Func runs:10000; result:0.2477599978259004
=============================
5 Megacity's; Func runs:10000; result:0.5246153846153847
25 Megacity's; Func runs:10000; result:0.2784615384615384
500 Megacity's; Func runs:10000; result:0.1253384615384627
=============================
All score:4.51637 (50.18%)

テスト関数でアルゴリズムをテストした結果（全スコア4.51637は、可能な最大値の50.18%に相当する）、出力の最初の行で指定されたパラメータを使用すると、かなり良い結果が得られることが示されました。関数の結果は、最適化されたパラメータが1000個の場合はそれぞれ0.125、10個の場合は0.93の範囲にあり、このアルゴリズムが最適解を見つけるのにかなり成功していることを示しています。

解のクラスタリングが可視化されたときにどのように見えるかについては、別途記しておきたいです。このプロセスは、パラメータの数が最大となる関数で特に顕著であり、初期のカオス状態から、反復が完了するごとに、クラスタの特徴的な部分がよりはっきりと目立ち始めます。

Hilly

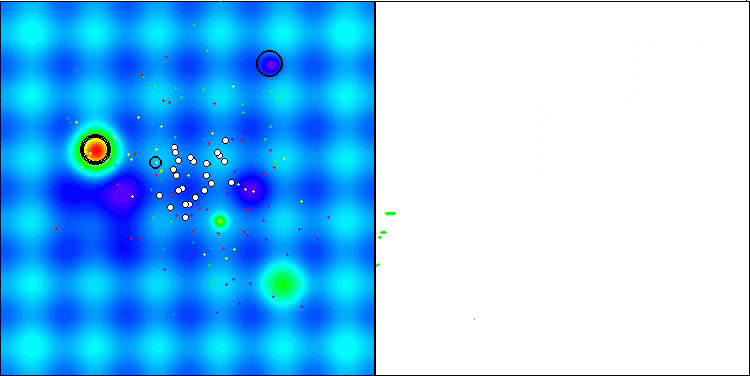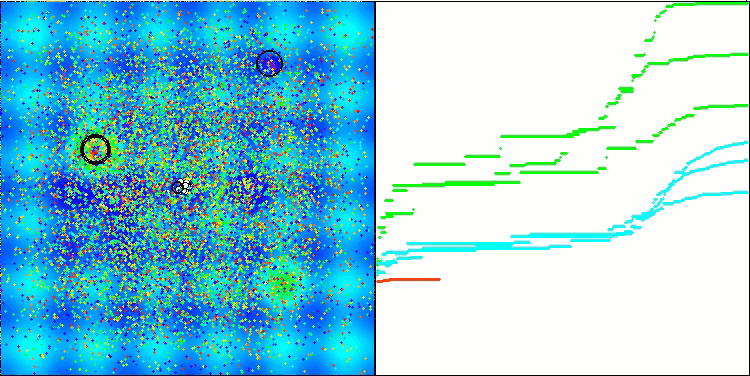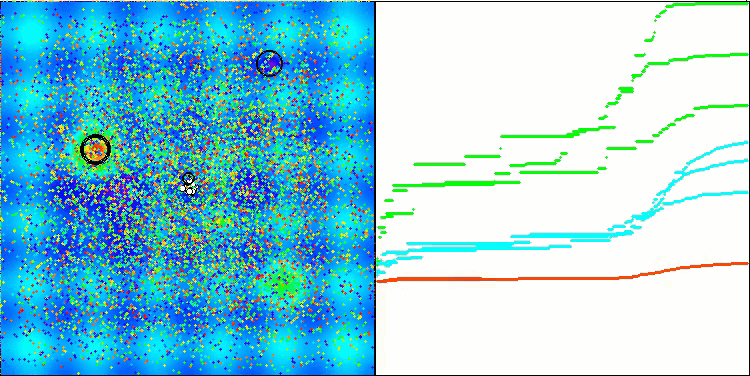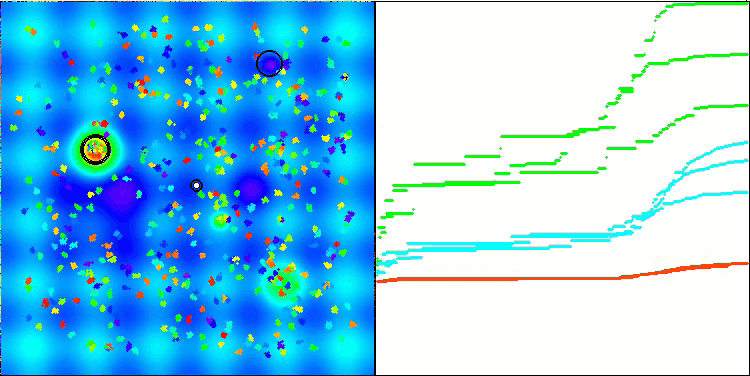
Hillyテスト関数のBSO

Forest

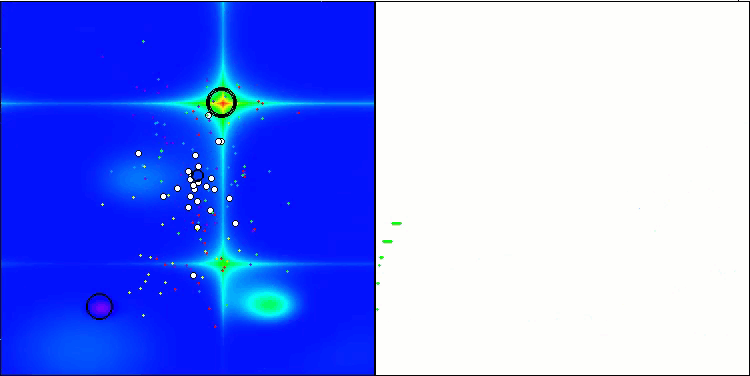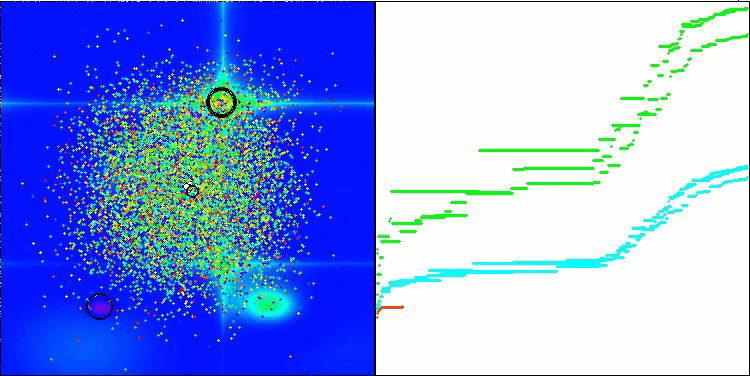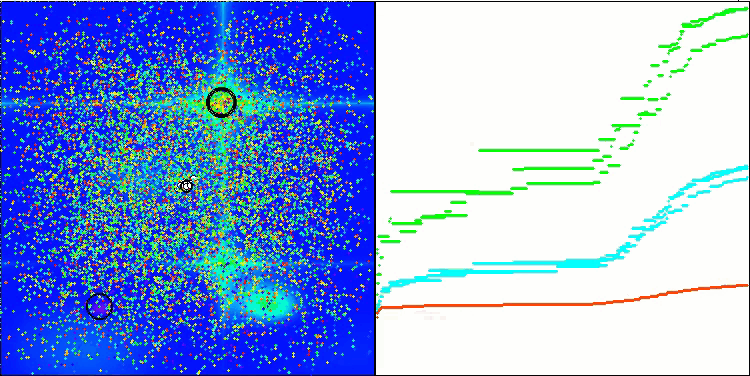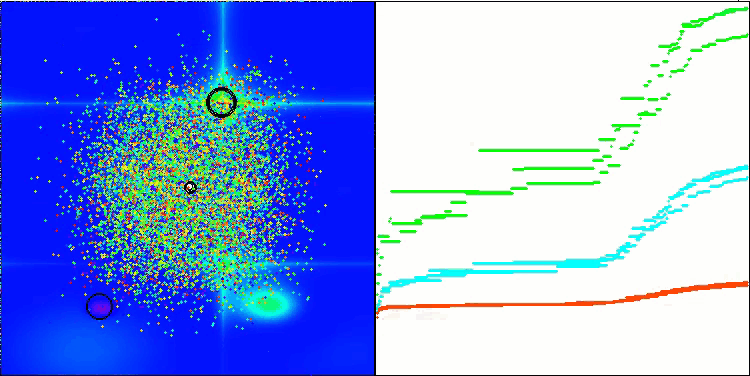
Forestテスト関数のBSO

Megacity

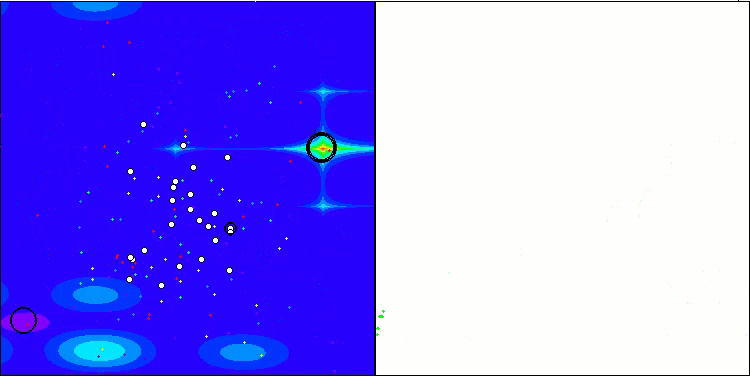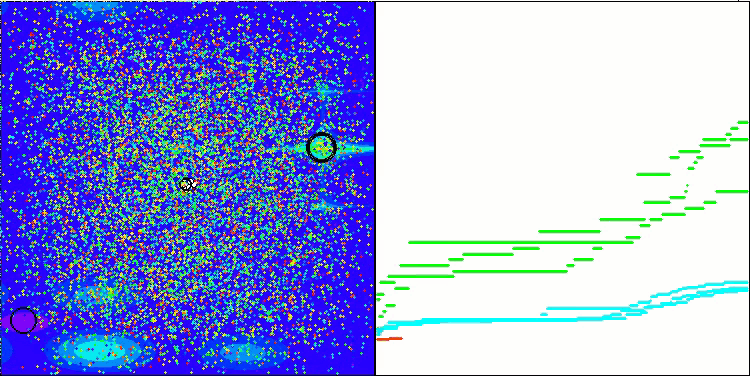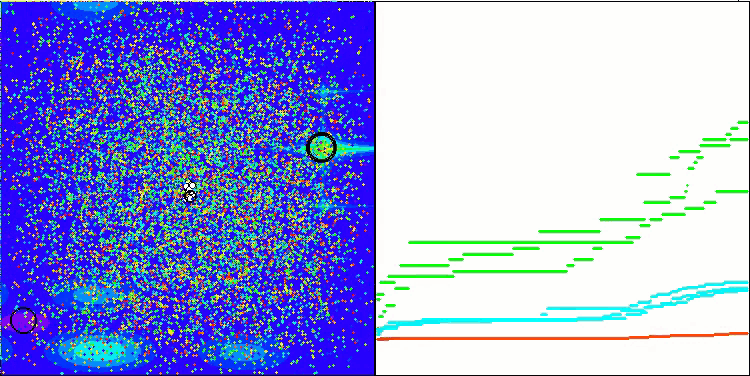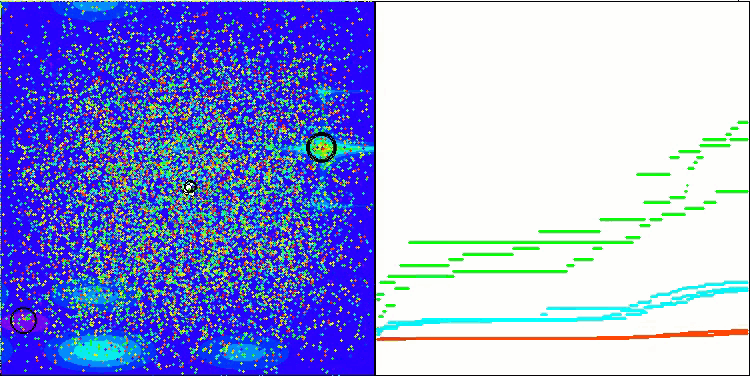
Megacityテスト関数のBSO

このアルゴリズムには大きな期待を寄せており、ランキング表のトップに立つことを期待していました。特に、クラスタリング手法と突然変異手法を組み合わせたのは初めてで、これによりユニークな結果が出ると確信していたためです。しかし、実際にはランキングの上位に位置するものの、トップには届かず、少し残念に思っています。BSOは、1000個のパラメータを持つForest関数やMegacity関数で優れた結果を示しており、テーブルリーダーに相応しいものです。

BSOは全体的に良好な結果を収め、ランキング上位に位置していますが、最大限の効率を引き出すためには、より慎重なパラメータチューニングが求められます。調整可能なパラメータには、収束率、母集団サイズ、突然変異の方法、アイデアの評価など多数あり、これらはアルゴリズムの性能に影響を与えます。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最終	最終結果	MAXの%
1	BGA	バイナリ遺伝的アルゴリズム	0.99992	0.99484	0.50483	2.49959	1.00000	0.99975	0.32054	2.32029	0.90667	0.96400	0.23035	2.10102	6.921	76.90
2	(P+O)ES	(P+O）進化戦略	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
3	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
4	ESG	社会集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
5	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
6	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
7	BSA	鳥群アルゴリズム	0.90857	0.73661	0.25767	1.90285	0.90437	0.81619	0.16401	1.88457	0.61692	0.54154	0.10951	1.26797	5.055	56.17
8	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
9	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
10	(PO)ES	(PO）進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
11	BSO	ブレインストーム最適化	0.91301	0.56222	0.30047	1.77570	0.97162	0.57162	0.23449	1,77772	0.60462	0.27138	0.12011	0.99611	4.550	50.55
12	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
13	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
14	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
15	MEC	Mind Evolutionary Computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
16	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
17	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
18	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
19	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
20	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
21	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
22	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
23	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
24	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
25	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
26	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
27	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
28	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
29	ボイド	ボイドアルゴリズム	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
30	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
31	SFL	Shuffled Frog-Leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
32	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
33	RND	ランダム	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
34	GWO	灰色オオカミオプティマイザ	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
35	CSS	荷電系探索	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
36	EM	電磁気学的アルゴリズム	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

まとめ

BSOアルゴリズムには、柔軟性、探索と搾取のバランス、様々な最適化問題への適応性など、いくつかの利点があります。

しかし、アルゴリズムの効率は外部パラメータの設定に大きく依存する（外部パラメータの数がBSOの主な欠点である）ため、特定のタスクごとに最適な設定を決定するための入念な調査と実験が必要です。

すべての最適化愛好家に対して、実験に参加し、実用的な問題解決に向けてアルゴリズムの能力を共に探求することを強く奨励します。もし、より興味深い結果や優れた外部パラメータ設定を見つけた方がいれば、ぜひ記事のコメント欄で共有していただければと思います。

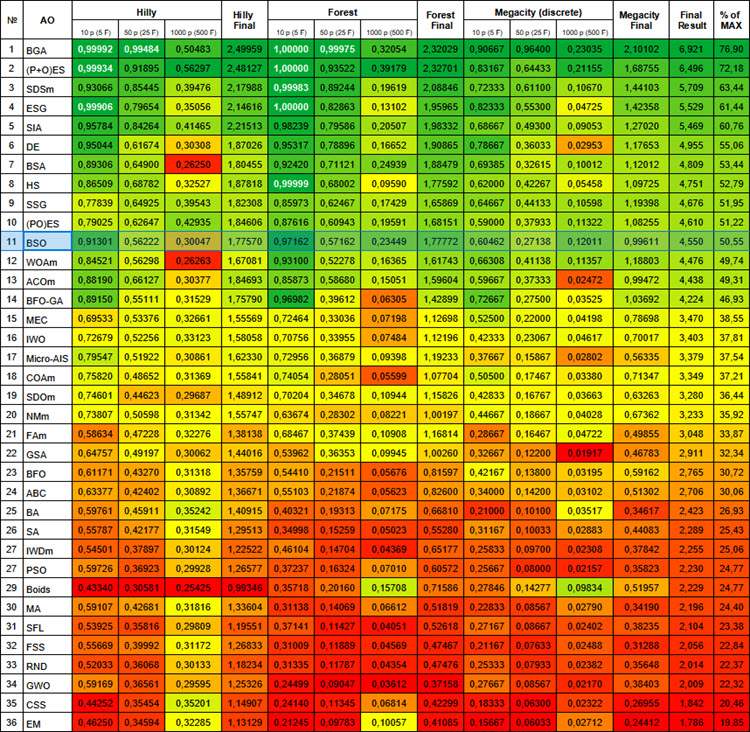
図1：関連テストに応じたアルゴリズムのカラー勾配0.99以上の結果は白で強調表示

チャート

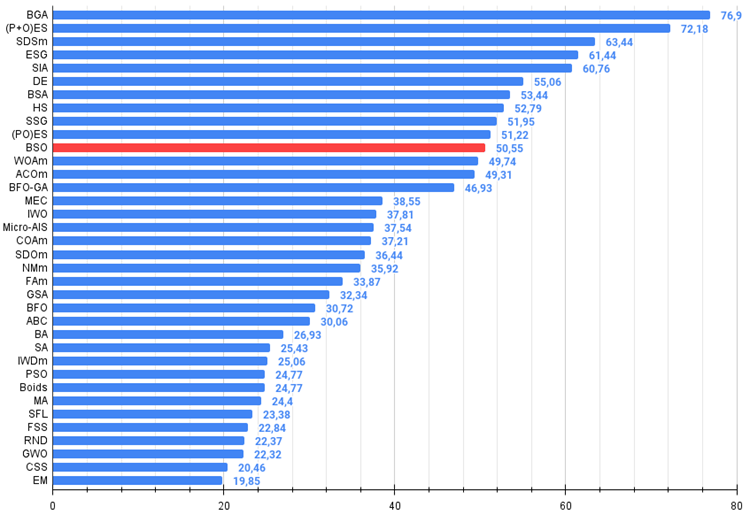
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）

BSOの長所と短所

長所

シャープなForest関数と高次元の離散Megacityでの良い結果

短所

非常に多くの外部パラメータ
複雑なアーキテクチャと実装
コンピューティングリソースへの負荷が高い

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14622

添付されたファイル |

ZIPをダウンロード

BSO.zip (28.18 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ニューラルネットワークが簡単に（第84回）：RevIN (Reversible Normalization)

入力データの前処理がモデル訓練の安定性に大きく寄与することは、すでに広く知られています。オンラインで「生」の入力データを処理するために、バッチ正規化層が頻繁に使用されますが、時には逆の手順が求められる場合もあります。この記事では、この問題を解決するための1つのアプローチについて解説します。

多通貨エキスパートアドバイザーの開発（第8回）：新しいバーの負荷テストと処理

進歩に伴い、1つのEAでより多くの取引戦略インスタンスを同時に実行するようになりました。リソースの限界に達する前に、どのくらいのインスタンスが利用可能かを検討することが重要です。

ニューラルネットワークが簡単に（第85回）：多変量時系列予測

この記事では、線形モデルとTransformerの長所を調和的に組み合わせた、新しい複雑な時系列予測手法を紹介します。

ブレインストーム最適化アルゴリズム(第1部）：クラスタリング

この記事では、「ブレインストーミング」と呼ばれる現象にヒントを得た、BSO (Brain Storm Optimization)と呼ばれる革新的な最適化手法を見ていきます。また、BSO法が適用するマルチモーダル最適化問題を解くための新しいアプローチについても説明します。これにより、部分集団の数を事前に決定することなく、複数の最適解を見つけることができるのです。K-MeansとK-Means++のクラスタリング法も検討します。