
ハースト指数の計算
イントロダクション
相場のダイナミクスの定義は、トレーダーのタスクの 1 つです。 標準的なテクニカル分析ツールでは、この問題はあまりに難しすぎます。 たとえば、МА や MACD はトレンドを示すこともありますが、その信頼性を評価するための追加のツールが必要です。 結局、すぐにトレンドが消えて短期スパイクになるかもしれません。
正常に外国為替をトレードするためには、他の相場参加者よりも多くを知っている必要があります。 一歩先に、最も有利なエントリポイントを選択すれば、トレードの収益性を確保することができます。 トレードの成功は、トレンドの反転かつ技術的なデータの巧みな使用と、無感情で正確に売買オーダーの組み合わせによるものです。 すべて、トレードの成功に重要な要素です。
フラクタル解析は、多くの相場評価の問題に包括的なソリューションを提供しています。 相場の動向とその信頼性評価の効率化がしばしばトレーダーや投資家によって無視されます。 ハースト指数は、フラクタル解析の基本的な値の 1 つです。
計算する前に、フラクタル解析の主な規定を考慮してハースト指数の要約を見ていきましょう。
1. フラクタル相場仮説 (FMH)。 フラクタル解析
フラクタルとは、自己相似性を持つ数学的な集合です。 自己相似オブジェクトは、同じような図形が繰り返されます。 (すなわち全体が 1 つまたは複数のパートと同じ形を持っている)。 フラクタル構造の最も鮮やかな例は、「フラクタル ツリー」です。

自己相似のオブジェクトが、別の次元で統計的に相似のままです。
相場に適用する場合、「フラクタル」は、"再発"または"循環"を意味します。
フラクタル次元は、オブジェクトまたはプロセスが、様々な次元でその構造がどのように変化するかを定義します。 金融相場にこの定義を適用するとき (または、外国為替) 、フラクタル次元が時系列の「ムラ」(ばらつき)の程度を定義することができます。 したがって、ある直線がd次元で1のとき、ランダムウォークになります。d = 1 フラクタル時系列の場合 1.5 < d < 1.5 または 1.5 < d < 1。
FMH の目的は、相場価格変動のモデルを提供することです。 すべての情報が、価格に反映されないかもしれません。E. Peters、フラクタル相場分析。
この読者がすでに分析法のアイデアを持っていると仮定して、フラクタルの概念にこだわるつもりはありません。 「相場の (誤) 動作への応用に関する包括的な情報を見つけることができます。 フラクタル金融"の観点 B ・ マンデル ブロー、r ・ ハドソン、「フラクタル相場分析」と"資本相場のオーダーと混沌: サイクル、価格、および相場のボラティリティの新しい観点"E. Peters 。
2. R/S 解析とハースト指数
2.1. R/S 解析
フラクタル解析の重要なパラメータは、時系列を研究するためにハースト指数を使用することです。 2つの時系列の間の遅延が大きければ大きいほど、ハースト指数は小さくなります。
この指数は、ハロルド ・ エドウィン ・ ハーストによって紹介されました。ナイル川のダムのプロジェクトに携わる優れたイギリスの学者です。 建設現場では、ハースト指数で水位の変動を評価する必要があります。 初期のころは、水の流入がランダムなプロセスであるとされていました。 しかし、9 世紀のナイル洪水の記録を経て、ハーストはパターンを検出しました。 これが、研究の出発点でした。 平均以上の洪水は、さらに強力な洪水に続いていたと判明しました。 その後、このプロセスはその方向を変え、平均以下の洪水後も弱い洪水が続きました。 これらは、明らかに非定期的なサイクルでした。
ハーストの統計モデルは、ブラウン運動の粒子のランダム ・ ウォークのモデルについてのアルベルト ・ アインシュタインの論文に基づいています。 この理論の背後にある考え方は、粒子による距離 (R) が (T)時間の平方根に比例して増加することです。
![]()
方程式を見てみましょう。テスト数が多くなる場合、変動範囲 (R) はテスト (T) の数の平方根に等しい。 この方程式は、ナイル川の洪水がランダムではないことを証明するときに、Hurst によって使用されました。
彼の方法論を形成するため、X1..Xnを洪水の時系列として使います。 次のアルゴリズムは、 再スケーリングしたメソッドまたはR/S 解析に適用されました。
- X1、Xmの平均値を計算する。
- Sシリーズに標準偏差を計算します。
- 各値から平均値、Zr を控除したシリーズの正規化 (ただし、r =1...n)
- 累積的なタイム シリーズを作成。 Y1=Z1+Zr, ただし r=2..n
- 累積的なタイム シリーズ R の大きさを計算 R= max (Y1..Yn)-min (Y1..Yn)
- 累積的なタイム シリーズの大きさを標準偏差 (S) で割る。
ハーストは拡張アインシュタインの方程式より一般的な形式に変換しました。
![]()
ただし、 с は定数。
一般に、R/S 値はハースト指数のHに等しい依存度にしたがって時間単位の増加スケールを変化させます。
ハーストによると、 もし洪水がランダムなら、Hは0.5と等しいはずです。 しかし、彼の観察により、H = 0.91であることが発見されました! つまり、正規化された変更時間の平方根よりも高速です。 言い換えれば、過去と現在と未来に大きな影響を与えるランダム プロセスよりも長い距離を渡します。
2.2. 相場への理論の適用
その後、ハースト指数の計算メソッドは、金融・株式相場に適用されました。 インフレ コンポーネントを補うために平均と標準偏差の正規化が含まれます。 言い換えると、R/S 解析を扱っています。
どうやって相場にハースト指数を使えばいいでしょうか。1. ハースト指数は 0.5 ~ 1、2 とより多くの標準偏差によって、予期される値とは異なり、長期的なメモリによって特徴付けられます。 言い換えると、永続性があります。
つまり、すべての結果が一定時間内で以前のものに強く依存します。 信頼性と影響力のある企業の株価チャートは、永続的な時系列を表しています。 米国企業、アップル GE、ボーイングと同様、ロシアのロスネフチ、アエロフロート、VTB のようなものは他にちなんで名づけることができます。 企業の株価チャートが表示されます。 すべての投資家がこのチャートを見ながら身近な写真を見分けることができると信じています。すべての新しい高値と安値が前のものより高い。
アエロフロート株価:
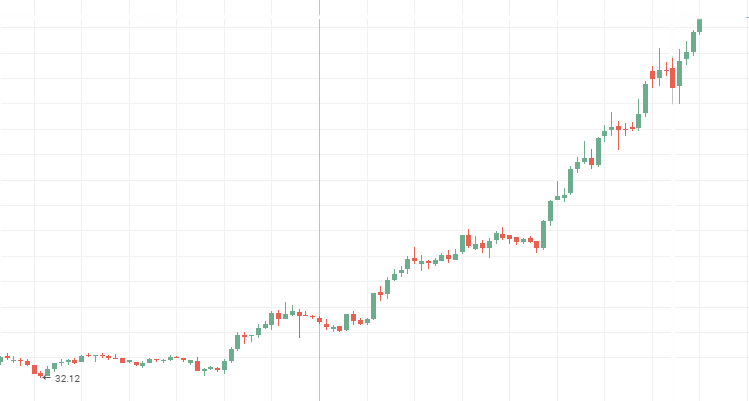
ロスネフチ株価:
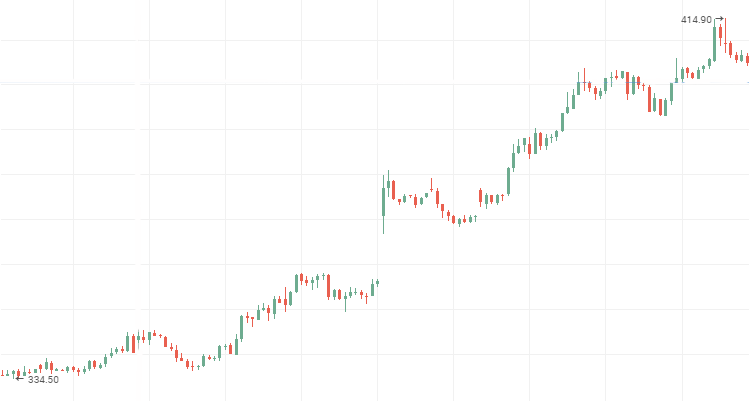
VTM 株価、ダウントレンドの永続的な時系列
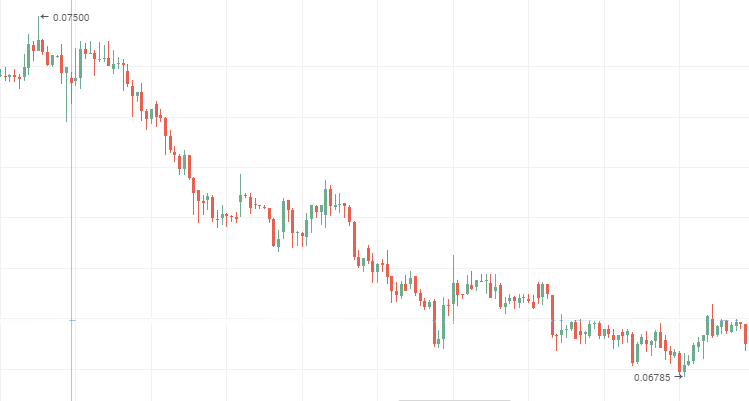
2. ハースト指数が絶対値で 2 以上の標準偏差で予期される値と異なり、また、0~0.5 の間の場合、反永続的な時系列です。
システム変更はランダムよりも速く小さいが、頻繁に変更する傾向があります。 反永続的なプロセスで明確に 2 層の株価チャートを見ることができます。 レンジの動きの中で、「ブルーチップ」価格チャートが反永続的なラインを示しています。 Mechel、AvtoVAZ、Lenenergo の株価チャートは、鮮やかな反永続的な時系列データの例です。
Mechel株式:
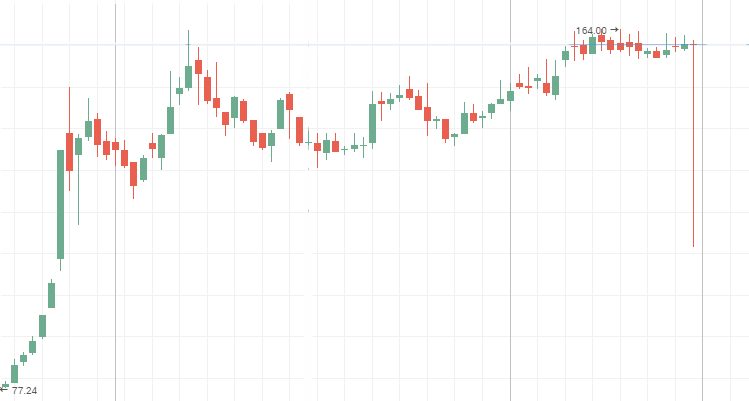
レンジ中のAvtoVAZ株
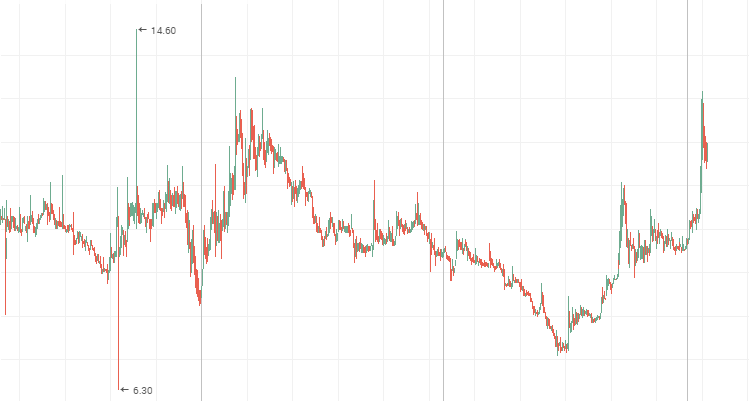
Lenenergo:
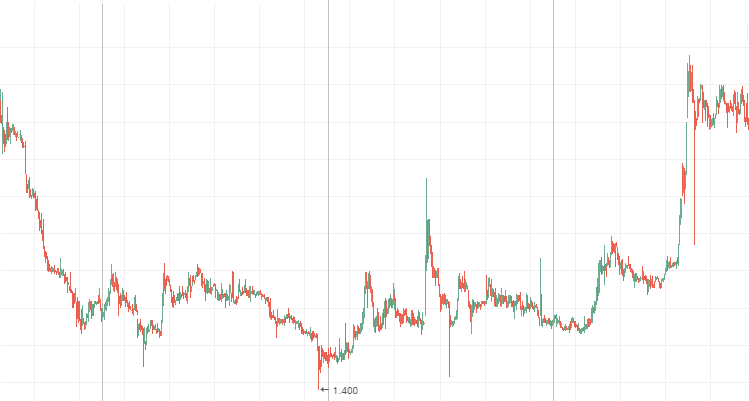
3. ハースト指数が0.5か、その値が想定値よりも標準偏差2つ分よりも離れている場合、ランダム ・ ウォークと見なされます。 短期または長期循環的な依存関係はありません。 トレードにおいては、現在の値が前の値に影響をほとんど受けないので、意味がないということになります。 よって、基本的な分析を使用することをお勧めします。
(工業、証券など様々な企業がある)株式相場の ハースト指数は、次の表のようになります。 過去 7 年間の計算です。 「優良」企業は金融危機の中でも低い指数を示しています。 多くの有価証券は永続危機に対する頑健性を示しています。
| 名前 | ハースト指数、H |
|---|---|
| Gazprom |
0.552 |
| VTB |
0.577 |
| Magnit |
0.554 |
| MTS |
0.543 |
| Rosneft |
0.648 |
| Aeroflot | 0.624 |
| Apple | 0.525 |
| GE | 0.533 |
| Boeing | 0.548 |
| Rosseti |
0.650 |
| Raspadskaya |
0.656 |
| TGC-1 |
0.641 |
| Tattelecom |
0.582 |
| Lenenergo |
0.642 |
| Mechel |
0.635 |
| AvtoVAZ |
0.574 |
| Petrol | 0.586 |
| Tin | 0.565 |
| Palladium | 0.564 |
| 天然ガス | 0.560 |
| ニッケル | 0.580 |
3. サイクルを定義します。 フラクタル解析
どうすれば結果がランダムではないことを確認できるでしょうか 。 この質問に答えるためには、まず分析されたシステムがランダムな性質であると仮定し、RS 解析を考察する必要があります。 言い換えると、その構造は独立して正規分布を示す仮説の有効性を確認する必要があります。
3.1. R/S 解析の予期される値を計算します。
R/S 解析の期待値の概念を紹介してみましょう。
1976年、アニスとロイドは必要な期待値を表現する方程式を導出しました。
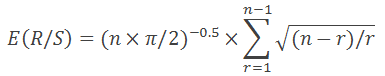
ただし、nは観測数、 rは1からn-1の整数を表します。
「フラクタル相場分析」で述べたように、式は n > 20 に対してのみ有効です。N < 20の場合、次の式を使用します。
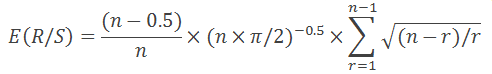
かなりシンプルです。
- 各観測数の期待値を計算して、Log (N)からLog(R/S) と (n) から得られた Log(E(R/S)) チャートを表示
- 統計理論でよく知られている方程式を用いた、ハースト指数の予想される分散計算
![]()
ただし、H はハースト指数;
N-観測サンプル数
3. H がE(H) を超過する標準偏差の数を評価することによって得られたハースト比率の妥当性を確認します。 絶対値で 2 を超えている場合、この結果は関連していると見なされます
3.2. サイクルの定義
次の例を考えてみましょう。 RS 統計と期待値 E(R/S) の 2 つのチャートをプロットし、相場の力学計算結果が引用の動きを一致するかどうかを比較します。
V統計を作成するサイクルの存在を定義する最良の方法は、サブグループ内の観測値の数の対数に基づく対数スケール、だとピーターは述べています。
得られた結果は、評価しやすいです。
- 対数スケールのチャートは水平線に独立したランダムなプロセスを扱っています。
- 上昇トレンドの場合、永続的なプロセスを扱っています。 すでに述べたように、 R/S スケール変更が時間の平方根より速く発生することを意味します。
- そして最後に、このチャートが下降トレンドを示す場合、反永続的なプロセスを扱います。
3.3. フラクタル解析とその深さを定義するメモリの概念
フラクタル解析の詳細について、メモリの概念を紹介してみよう。
長期および短期メモリについてはすでに言及しています。 フラクタル分析において、メモリは時間間隔、現在および将来のイベントへの影響を考慮します。 この時間間隔はメモリの深さ、フラクタル解析があります。 このデータは、過去の技術的なパターンの関連性を定義するときに不可欠です。
過剰な処理能力はメモリの深さを決定するには必要ありません。 V統計対数チャートの視覚的分析のみで十分です。
- 関連するすべてのチャート ポイントに沿ってトレンド ラインを描画します。
- 曲線が水平ではないことを確認してください。
- 関数が最大値に達したポイントを定義します。 最大値は、既存のサイクルの最初とします。
- 対数目盛でチャートの X 座標を定義し、理解しやすいように数字を変換します。 期間の長さ = exp ^ (期間対数スケール)。 したがって、GBPUSDの12000時間のデータを分析し、対数目盛で 8.2 を取得している場合は、サイクルが exp ^8.2 = 3772 時間または 157 日に等しい 。
- 真のサイクルは、基盤として同じ時間間隔ではなく別の時間枠が必要です。 たとえば、p . 4, GBPUSDの12000 時間のデータを調査し、157 日間のサイクルが存在することが示唆されました。 H4 に切り替え、12000/4 = 3000 データを分析します。 157 日間サイクルが実際に存在する場合、仮説はおそらく正しいでしょう。 異なる場合、メモリサイクルの短縮を見つけることができる可能性があります。
3.4. 実際の通貨ペアのハースト指数値
フラクタル解析理論の基本的な原則の導入が完了しました。 MQL5を用いた RS 解析の実施前に、より多くの例を考えてみましょう。
次の表は、様々な時間枠での11 通貨ペアの指数値を示しています。 比率を計算するには、最小自乗 (LS) 法を用いた回帰をします。 ほとんどの通貨ペアは永続的なプロセスをサポートする抗永続的なものです。 しかしこの結果は重要でしょうか。 この数字を信頼できますか。 これは後で議論します。
表1 2000本の足のハースト指数を分析
| Symbol | H (D1) | H. (H4) | H (H1) | H(15M) | H (5 M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.559 | 0.513 | 0.567 | 0.577 |
| EURCHF | 0.520 | 0.468 | 0.457 | 0.463 | 0.522 | 0.577 |
| EURJPY | 0.574 | 0.501 | 0.527 | 0.511 | 0.546 | 0.577 |
| EURGBP | 0.553 | 0.571 | 0.540 | 0.562 | 0.550 | 0.577 |
| EURRUB | 不十分な足 | 0.536 | 0.521 | 0.543 | 0.476 | 0.577 |
| USDJPY | 0.591 | 0.563 | 0.583 | 0.519 | 0.565 | 0.577 |
| USDCHF | 不十分な足 | 0.509 | 0.564 | 0.517 | 0.545 | 0.577 |
| USDCAD | 0.549 | 0.569 | 0.540 | 0.519 | 0.565 | 0.577 |
| USDRUB | 0.582 | 0.509 | 0.564 | 0.527 | 0.540 | 0.577 |
| AUDCHF | 0.522 | 0.478c | 0.504 | 0.506 | 0.509 | 0.577 |
| GBPCHF | 0.554 | 0.559 | 0.542 | 0.565 | 0.559 | 0.577 |
表2 400本の足のハースト指数を分析
| Symbol | H (D1) | H. (H4) | H (H1) | H(15M) | H (5 M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.513 | 0.604 | 0.617 | 0.578 |
| EURCHF | 0.471 | 0.460 | 0.522 | 0.603 | 0.533 | 0.578 |
| EURJPY | 0.545 | 0.494 | 0.562 | 0.556 | 0.570 | 0.578 |
| EURGBP | 0.620 | 0.589 | 0.601 | 0.597 | 0.635 | 0.578 |
| EURRUB | 0.580 | 0.551 | 0.478 | 0.526 | 0.542 | 0.578 |
| USDJPY | 0.601 | 0.610 | 0.568 | 0.583 | 0.593 | 0.578 |
| USDCHF | 0.505 | 0.555 | 0.501 | 0.585 | 0.650 | 0.578 |
| USDCAD | 0.590 | 0.537 | 0.590 | 0.587 | 0.631 | 0.578 |
| USDRUB | 0.563 | 0.483 | 0.465 | 0.531 | 0.502 | 0.578 |
| AUDCHF | 0.443 | 0.472 | 0.505 | 0.530 | 0.539 | 0.578 |
| GBPCHF | 0.568 | 0.582 | 0.616 | 0.615 | 0.636 | 0.578 |
表3 M15 と M5 の Hurst 指数の計算結果
| Symbol | H (15 M) | Significance | H (5 M) | Significance | E(H) |
|---|---|---|---|---|---|
| EURUSD | 0.543 | insignificant | 0.542 | insignificant | 0.544 |
| EURCHF | 0.484 | significant | 0.480 | significant | 0.544 |
| EURJPY | 0.513 | insignificant | 0.513 | insignificant | 0.544 |
| EURGBP | 0.542 | insignificant | 0.528 | insignificant | 0.544 |
| EURRUB | 0.469 | significant | 0.495 | significant | 0.544 |
| USDJPY | 0.550 | insignificant | 0.525 | insignificant | 0.544 |
| USDCHF | 0.551 | insignificant | 0.525 | insignificant | 0.544 |
| USDCAD | 0.519 | insignificant | 0.550 | insignificant | 0.544 |
| USDRUB | 0.436 | significant | 0.485 | significant | 0.544 |
| AUDCHF | 0.518 | insignificant | 0.499 | significant | 0.544 |
| GBPCHF | 0.533 | insignificant | 0.520 | insignificant | 0.544 |
E. ピーターは、基本的な期間を使って、循環依存関係を有する時系列の分析を推奨しています。 その後、解析の時間間隔は、ヒストリー深さに時間枠を変更して分かれています。 これは、以下のことを意味します。
サイクルがベースとなる時間枠に存在する場合、その有効性は、別の時間枠で同じサイクルが見つかった場合に証明されるでしょう。
利用可能な足のさまざまな組み合わせを使用して、非周期サイクルを見出すことができます。 その長さは、テクニカルインジケーターの過去のシグナルの有用性についての疑問を解消できます。
4. 理論から実践へ
フラクタル分析、ハースト指数とその値の解釈についての基本的な知識を得て、MQL5で実装してみましょう。
技術的な要件を定義してみましょう。指定された通貨ペア 1000ヒストリーデータのハースト指数を計算するプログラム。
ステップ1 新しいスクリプトを作成
データを格納する「stub」を得ます。 また、エントリで通貨ペアを選択するので、 #property script_show_inputs を追加します。
//+------------------------------------------------------------------+ //| New.mq5 | //| Copyright 2016, Piskarev D.M. | //| piskarev.dmitry25@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Piskarev D.M." #property link "piskarev.dmitry25@gmail.com" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- }
ステップ2 終値配列を設定して、1001のヒストリーバーが選択した通貨ペアにおいて利用可能かどうかを確認します。
1000が要件に設定されて場合 1001を使用する理由は何でしょう? 答え: 対数を返す配列を形成する以前の値が必要です。
double close[]; //終値の動的配列を宣言 int copied=CopyClose(symbol,timeframe,0,barscount1+1,close); //選択したペアの終値 //close[]配列 ArrayResize(close,1001); //配列のサイズを設定 ArraySetAsSeries(close,true); if(bars<1001) //1001 ヒストリーの存在の条件を作成 { Comment("Too few bars are available! Try another timeframe."); Sleep(10000); //10 秒間遅らせる Comment(""); return; }
ステップ 3。 対数を返す配列を作成します。
LogReturns 配列が既に宣言され、ArrayResize(LogReturns,1001) の文字列があります。
for(int i=1;i<=1000;i++) LogReturns[i]=MathLog(close[i-1]/close[i]);
ステップ 4。 ハースト指数を計算します。
ヒストリーバーの分析量の除算サブグループの要素の数が 10 未満ではない必要があります。 つまり、 10を超える値を持つ仕切りを検索する必要があります。 このような仕切りがあります。
//---各サブグループに含まれる要素の数を設定。 num1=10; num2=20; num3=25; num4=40; num5=50; num6=100; num7=125; num8=200; num9=250; num10=500; num11=1000;
11 回 RS 統計のデータのため、カスタム関数を開発するが妥当でしょう。 RSの統計情報の計算対象となる、サブグループの最終インデックスとして分析されたバーの数は、関数のパラメータとして使用されます。 このアルゴリズムは、記事の冒頭に記載されている1つに似ています。
//+----------------------------------------------------------------------+ // R/S 計算関数 | //+----------------------------------------------------------------------+ double RSculc(int bottom,int top,int barscount) { Sum=0.0; //初期の和はゼロ DevSum=0.0; //累積合計 //偏差ゼロ //---リターンの合計を計算。 for(int i=bottom; i<=top; i++) Sum=Sum+LogReturns[i]; //合計 //---平均を計算。 M=Sum/barscount; //---累積偏差を計算。 for(int i=bottom; i<=top; i++) { DevAccum[i]=LogReturns[i]-M+DevAccum[i-1]; StdDevMas[i]=MathPow((LogReturns[i]-M),2); DevSum=DevSum+StdDevMas[i]; //偏差の計算コンポーネント if(DevAccum[i]>MaxValue) //配列の値が小さい場合 MaxValue=DevAccum[i]; //最大よりも。DevAccum 配列の要素の値に割り当てられて //最大値 if(DevAccum[i]<MinValue) //ロジックが同一 MinValue=DevAccum[i]; } //---R の振幅との偏差を計算。 R=MaxValue-MinValue; //振幅が最大の違い MaxValue=0.0; MinValue=1000; //最小値 S1=MathSqrt(DevSum/barscount); //標準偏差を計算 //---R/S パラメータを計算。 if(S1!=0)RS=R/S1; //ゼロ除算エラーを排除 // else Alert("Zero divide!"); return(RS); //RS の統計値を返す }
スイッチ ケースを使用して計算。
//---複合 Log(R/S) を計算。 for(int A=1; A<=11; A++) //サイクルで、コードを短くすることができます { //その上、すべての可能な仕切りを考える switch(A) { case 1: //100 グループ含んでいる 10 要素 { ArrayResize(rs1,101); RSsum=0.0; for(int j=1; j<=100; j++) { rs1[j]=RSculc(10*j-9,10*j,10); //RScuclc のカスタム関数を呼び出す RSsum=RSsum+rs1[j]; } RS1=RSsum/100; LogRS1=MathLog(RS1); } break; case 2: //50 グループ含む 20 要素 { ArrayResize(rs2,51); RSsum=0.0; for(int j=1; j<=50; j++) { rs2[j]=RSculc(20*j-19,20*j,20); //RScuclc のカスタム関数を呼び出す RSsum=RSsum+rs2[j]; } RS2=RSsum/50; LogRS2=MathLog(RS2); } break; ... ... ... case 9: //125 と 16 のグループ { ArrayResize(rs9,5); RSsum=0.0; for(int j=1; j<=4; j++) { rs9[j]=RSculc(250*j-249,250*j,250); RSsum=RSsum+rs9[j]; } RS9=RSsum/4; LogRS9=MathLog(RS9); } break; case 10: //125 と 16 のグループ { ArrayResize(rs10,3); RSsum=0.0; for(int j=1; j<=2; j++) { rs10[j]=RSculc(500*j-499,500*j,500); RSsum=RSsum+rs10[j]; } RS10=RSsum/2; LogRS10=MathLog(RS10); } break; case 11: //200 と 10 のグループ { RS11=RSculc(1,1000,1000); LogRS11=MathLog(RS11); } break; } }
ステップ 5。 最小自乗 (LS) 法を用いた線形回帰を計算するカスタム関数。
エントリーパラメータは、計算された RS 統計コンポーネントの値です。
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6, double Y7,double Y8,double Y9,double Y10,double Y11) { double SumY=0.0; double SumX=0.0; double SumYX=0.0; double SumXX=0.0; double b=0.0; double N[]; //ディバイダーの対数を格納する配列 double n={10,20,25,40,50,100,125,200,250,500,1000} //ディバイダー配列 //---N 比を計算。 for (int i=0; i<=10; i++) { N[i]=MathLog(n[i]); SumX=SumX+N[i]; SumXX=SumXX+N[i]*N[i]; } SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11; SumYX=Y1*N1+Y2*N2+Y3*N3+Y4*N4+Y5*N5+Y6*N6+Y7*N7+Y8*N8+Y9*N9+Y10*N10+Y11*N11;
//---ベータ回帰率または必要なハースト指数を計算。
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX); return(b); }
ステップ 6.予想される RS 統計値を計算するカスタム関数。 計算ロジックは、理論パートで説明します。
//+----------------------------------------------------------------------+ // 計算する関数は、E(R/S) 値を予想 | //+----------------------------------------------------------------------+ double ERSculc(double m) //m-1000 ディバイダー { double e; double nSum=0.0; double part=0.0; for(int i=1; i<=m-1; i++) { part=MathPow(((m-i)/i), 0.5); nSum=nSum+part; } e=MathPow((m*pi/2),-0.5)*nSum; return(e); }
プログラム コードは、次のようになります。
//+------------------------------------------------------------------+ // hurst_exponent.mq5 | //| Copyright 2016, Piskarev D.M. | //| piskarev.dmitry25@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Piskarev D.M." #property link "piskarev.dmitry25@gmail.com" #property version "1.00" #property script_show_inputs #property strict input string symbol="EURUSD"; //シンボル input ENUM_TIMEFRAMES timeframe=PERIOD_D1; //期間 double LogReturns[],N[], R,S1,DevAccum[],StdDevMas[]; int num1,num2,num3,num4,num5,num6,num7,num8,num9,num10,num11; double pi=3.14159265358979323846264338; double MaxValue=0.0,MinValue=1000.0; double DevSum,Sum,M,RS,RSsum,Dconv; double RS1,RS2,RS3,RS4,RS5,RS6,RS7,RS8,RS9,RS10,RS11, LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,LogRS9, LogRS10,LogRS11; double rs1[],rs2[],rs3[],rs4[],rs5[],rs6[],rs7[],rs8[],rs9[],rs10[],rs11[]; double E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11; double H,betaE; int bars=Bars(symbol,timeframe); double D,StandDev; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { double close[]; //終値の動的配列を宣言 int copied=CopyClose(symbol,timeframe,0,1001,close); //コピーする選択したペアの終値 //close[]配列 ArrayResize(close,1001); //配列のサイズを設定 ArraySetAsSeries(close,true); if(bars<1001) //1001 ヒストリーバーの存在の条件を作成する { Comment("Too few bars are available! Try another timeframe."); Sleep(10000); //10 秒間遅らせる Comment(""); return; } //+------------------------------------------------------------------+ //配列の準備 | //+------------------------------------------------------------------+ ArrayResize(LogReturns,1001); ArrayResize(DevAccum,1001); ArrayResize(StdDevMas,1001); //+------------------------------------------------------------------+ //対数を返す配列 | //+------------------------------------------------------------------+ for(int i=1;i<=1000;i++) LogReturns[i]=MathLog(close[i-1]/close[i]); //+------------------------------------------------------------------+ // | // R/S 解析 | // | //+------------------------------------------------------------------+ //---各サブグループに含まれる要素の数を設定。 num1=10; num2=20; num3=25; num4=40; num5=50; num6=100; num7=125; num8=200; num9=250; num10=500; num11=1000; //---複合 Log(R/S) を計算。 for(int A=1; A<=11; A++) { switch(A) { case 1: { ArrayResize(rs1,101); RSsum=0.0; for(int j=1; j<=100; j++) { rs1[j]=RSculc(10*j-9,10*j,10); RSsum=RSsum+rs1[j]; } RS1=RSsum/100; LogRS1=MathLog(RS1); } break; case 2: { ArrayResize(rs2,51); RSsum=0.0; for(int j=1; j<=50; j++) { rs2[j]=RSculc(20*j-19,20*j,20); RSsum=RSsum+rs2[j]; } RS2=RSsum/50; LogRS2=MathLog(RS2); } break; case 3: { ArrayResize(rs3,41); RSsum=0.0; for(int j=1; j<=40; j++) { rs3[j]=RSculc(25*j-24,25*j,25); RSsum=RSsum+rs3[j]; } RS3=RSsum/40; LogRS3=MathLog(RS3); } break; case 4: { ArrayResize(rs4,26); RSsum=0.0; for(int j=1; j<=25; j++) { rs4[j]=RSculc(40*j-39,40*j,40); RSsum=RSsum+rs4[j]; } RS4=RSsum/25; LogRS4=MathLog(RS4); } break; case 5: { ArrayResize(rs5,21); RSsum=0.0; for(int j=1; j<=20; j++) { rs5[j]=RSculc(50*j-49,50*j,50); RSsum=RSsum+rs5[j]; } RS5=RSsum/20; LogRS5=MathLog(RS5); } break; case 6: { ArrayResize(rs6,11); RSsum=0.0; for(int j=1; j<=10; j++) { rs6[j]=RSculc(100*j-99,100*j,100); RSsum=RSsum+rs6[j]; } RS6=RSsum/10; LogRS6=MathLog(RS6); } break; case 7: { ArrayResize(rs7,9); RSsum=0.0; for(int j=1; j<=8; j++) { rs7[j]=RSculc(125*j-124,125*j,125); RSsum=RSsum+rs7[j]; } RS7=RSsum/8; LogRS7=MathLog(RS7); } break; case 8: { ArrayResize(rs8,6); RSsum=0.0; for(int j=1; j<=5; j++) { rs8[j]=RSculc(200*j-199,200*j,200); RSsum=RSsum+rs8[j]; } RS8=RSsum/5; LogRS8=MathLog(RS8); } break; case 9: { ArrayResize(rs9,5); RSsum=0.0; for(int j=1; j<=4; j++) { rs9[j]=RSculc(250*j-249,250*j,250); RSsum=RSsum+rs9[j]; } RS9=RSsum/4; LogRS9=MathLog(RS9); } break; case 10: { ArrayResize(rs10,3); RSsum=0.0; for(int j=1; j<=2; j++) { rs10[j]=RSculc(500*j-499,500*j,500); RSsum=RSsum+rs10[j]; } RS10=RSsum/2; LogRS10=MathLog(RS10); } break; case 11: { RS11=RSculc(1,1000,1000); LogRS11=MathLog(RS11); } break; } } //+----------------------------------------------------------------------+ // ハースト指数の計算 | //+----------------------------------------------------------------------+ H=RegCulc1000(LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8, LogRS9,LogRS10,LogRS11); //+----------------------------------------------------------------------+ // 期待の log(E(R/S)) 値を計算 | //+----------------------------------------------------------------------+ E1=MathLog(ERSculc(num1)); E2=MathLog(ERSculc(num2)); E3=MathLog(ERSculc(num3)); E4=MathLog(ERSculc(num4)); E5=MathLog(ERSculc(num5)); E6=MathLog(ERSculc(num6)); E7=MathLog(ERSculc(num7)); E8=MathLog(ERSculc(num8)); E9=MathLog(ERSculc(num9)); E10=MathLog(ERSculc(num10)); E11=MathLog(ERSculc(num11)); //+----------------------------------------------------------------------+ // 期待の E(R/S) 値のベータを計算 | //+----------------------------------------------------------------------+ betaE=RegCulc1000(E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11); Alert("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3)); Comment("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3)); } //+----------------------------------------------------------------------+ // R/S 計算関数 | //+----------------------------------------------------------------------+ double RSculc(int bottom,int top,int barscount) { Sum=0.0; //最初の合計値は 0 DevSum=0.0; //累積合計 //偏差ゼロ //---リターンの合計を計算。 for(int i=bottom; i<=top; i++) Sum=Sum+LogReturns[i]; //合計 //---平均を計算。 M=Sum/barscount; //---累積偏差を計算。 for(int i=bottom; i<=top; i++) { DevAccum[i]=LogReturns[i]-M+DevAccum[i-1]; StdDevMas[i]=MathPow((LogReturns[i]-M),2); DevSum=DevSum+StdDevMas[i]; //偏差の計算コンポーネント if(DevAccum[i]>MaxValue) //配列の値が小さい場合 MaxValue=DevAccum[i]; //最大よりも。DevAccum 配列の要素の値に割り当てられて //最大値 if(DevAccum[i]<MinValue) //ロジックが同一 MinValue=DevAccum[i]; } //---R の振幅との偏差を計算。 R=MaxValue-MinValue; //振幅が最大の違い MaxValue=0.0; MinValue=1000; //最小値 S1=MathSqrt(DevSum/barscount); //標準偏差を計算 //---R/S パラメータを計算。 if(S1!=0)RS=R/S1; //ゼロ除算エラーを排除 // else Alert("Zero divide!"); return(RS); //RS の統計値を返す } //+----------------------------------------------------------------------+ // 回帰計算機 | //+----------------------------------------------------------------------+ double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6, double Y7,double Y8,double Y9,double Y10,double Y11) { double SumY=0.0; double SumX=0.0; double SumYX=0.0; double SumXX=0.0; double b=0.0; //ディバイダーの対数を格納する配列 double n[]={10,20,25,40,50,100,125,200,250,500,1000}; //ディバイダー配列 //---N 比を計算。 ArrayResize(N,11); for (int i=0; i<=10; i++) { N[i]=MathLog(n[i]); SumX=SumX+N[i]; SumXX=SumXX+N[i]*N[i]; } SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11; SumYX=Y1*N[0]+Y2*N[1]+Y3*N[2]+Y4*N[3]+Y5*N[4]+Y6*N[5]+Y7*N[6]+Y8*N[7]+Y9*N[8]+Y10*N[9]+Y11*N[10]; //---ベータ回帰率または必要なハースト指数を計算。 b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX); return(b); } //+----------------------------------------------------------------------+ // 計算する関数は、E(R/S) 値を予想 | //+----------------------------------------------------------------------+ double ERSculc(double m) //m-1000 ディバイダー { double e; double nSum=0.0; double part=0.0; for(int i=1; i<=m-1; i++) { part=MathPow(((m-i)/i), 0.5); nSum=nSum+part; } e=MathPow((m*pi/2),-0.5)*nSum; return(e); }
ユーザーフレンドリーなグラフィカルインターフェイスを作成することによって、自分のコードをアップグレードできます。
最後のチャプターでは、既存のソフトウェア ・ ソリューションについて説明します。
5. ソフトウェア ソリューション
R/S 解析アルゴリズムを実装するソフトウェア リソースが複数あります。 しかし、このアルゴリズムの実装は、一般的にユーザーの分析タスクになります。 このようなリソースの 1 つに、Matlab のパッケージがあります。
金融相場のフラクタル解析と呼ばれる相場で利用可能なMT5のユーティリティもあります。 少し見てみましょう。
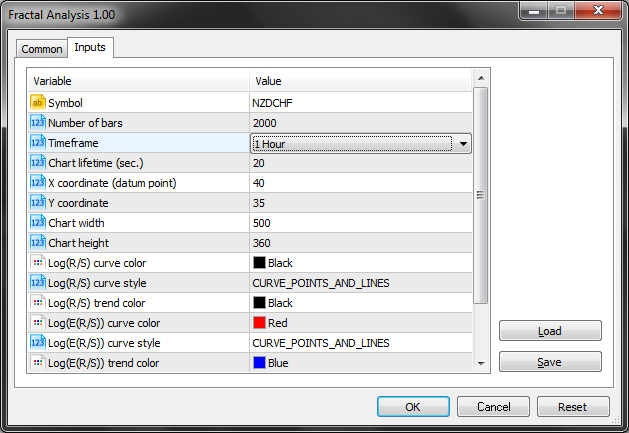
5.1. インプット
実際には、最初の 3 つエントリーパラメータのみ (シンボル、足の数、時間枠)必要があります。
下のスクリーンショットからもわかるように、フラクタル解析により、シンボルのウィンドウで通貨ペアを選択します。
以下のパラメータで指定された特定の時間枠を選択します。
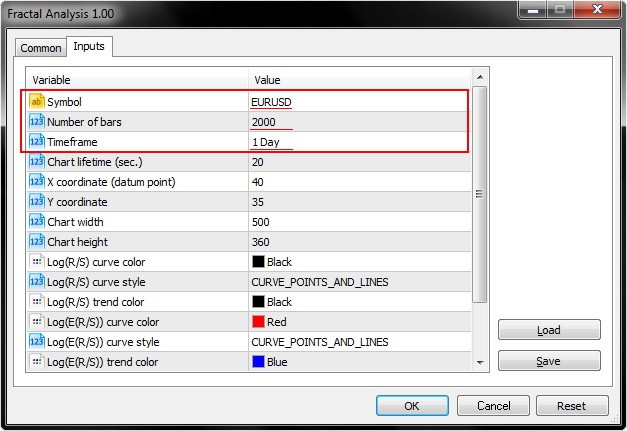
また、チャートライフタイムパラメータがユーティリティで動作することができる秒数の設定に注意を払います。 OKをクリックすると、MT5メインターミナルウィンドウの左上隅にアナライザが表示されます。 この例は以下のスクリーン ショットのようになります。
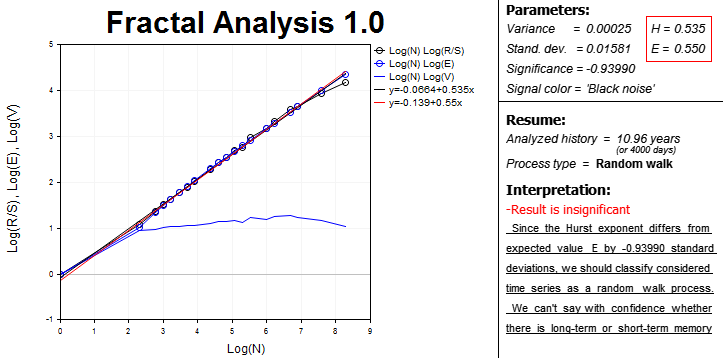
最終的には、すべてのデータとフラクタル解析に必要なブロックを組み合わせて画面に表示されます。
左部は、対数スケールです。
- R/S 統計サンプルの観測値の数
- 予想される R/S 統計値観測数の E(R/S)
- 観察数のV統計情報。
サイクルの長さを定義することは難があるので、MT5チャート分析ツールの使用を含むインタラクティブなエリアです。
曲線とトレンド ラインの方程式もあります。 トレンドラインの傾斜を使用して、数値のハースト指数 (H) を定義します。 予想されるハースト指数 (E)は、同様に計算されます。 これらの式は、右の隣接ブロックにあります。 シグナルのスペクトルの色は同様に計算されます。
便宜上、分析期間日数の長さが計算されます。 ヒストリーデータの意義を評価するときこれを覚えておいてください。
「プロセスタイプ」ラインは、時間系列パラメータを指定します。
- persistent;
- anti-persistent;
- ランダム ・ ウォーク。
最後に、フラクタル解析の分野で初心者の役に立つことができる簡単な要約をします。
5.2. 操作例
シンボルと分析に使用する時間枠を定義してください。NZDCHF とH1で見ていきましょう。
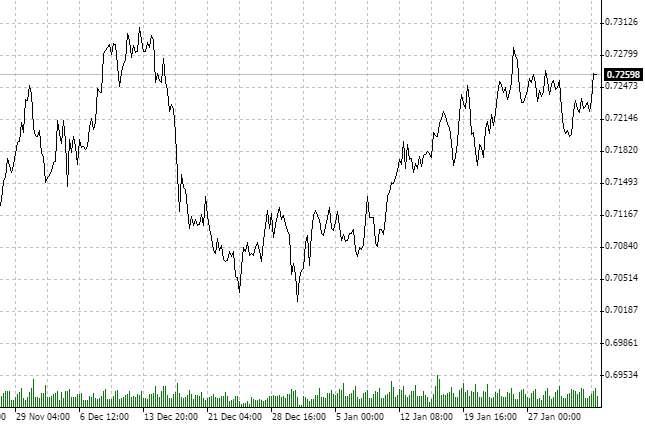
相場は最後の 2 ヶ月で統合されていることに注意してください。 また、 その他の投資の地平線に興味はありません。 D1 チャートが上昇トレンドもしいくは下降トレンドを示す可能性があります。 H1 とヒストリーデータを選択しました。
どうやら、このプロセスは反固定です。 フラクタル解析を用いたチェックしましょう。
3.02 に 21.11 から 75 日のヒストリーがあります。 75日を時間に変換すると、1800時間のデータになります。 多くの足が最も近い値を指定することがないので、2000 時間を分析しました。
結果は下の通りです。
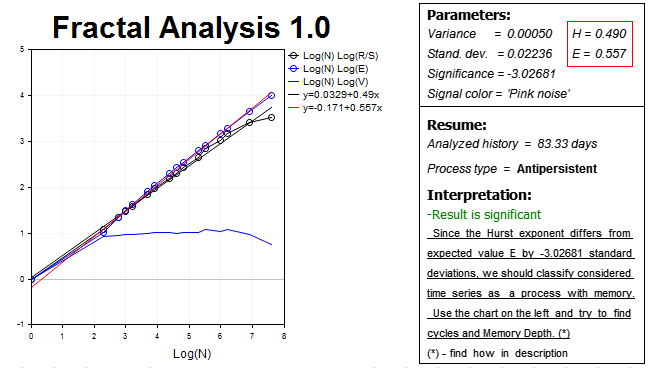
したがって、 ハースト指数 H = 0.490 期待値 E = 0.557 より低いほぼ 3 つの標準偏差です。
結果を修正し、ヒストリー (1000 の値) で (H2)よりわずかに高い時間枠および足に応じて 2 倍より小さい数を使用します。 結果は次のとおりです。
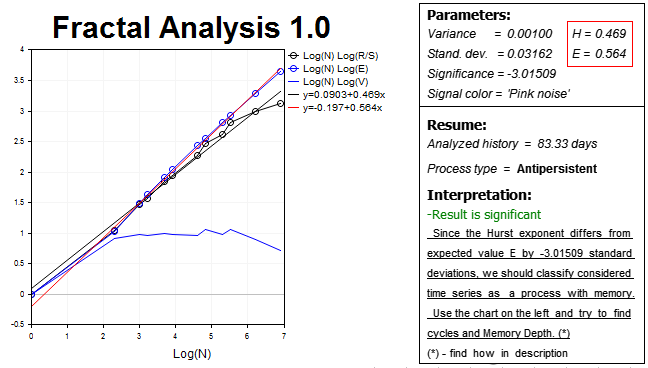
再び反永続的なプロセスを得ました。 ハースト指数 H = 0.469 は E = 0.564 予想指数値より低い 3 つ以上の標準偏差です。
サイクルを検索してみましょう。
H1のチャートに戻り、R/s 字カーブが E(R/S) からデタッチされるモーメントを定義する必要があります。 このモーメントは、V 統計チャート上の形成によって特徴付けられます。 したがって、おおよそのサイクルのサイズを定義することができます。
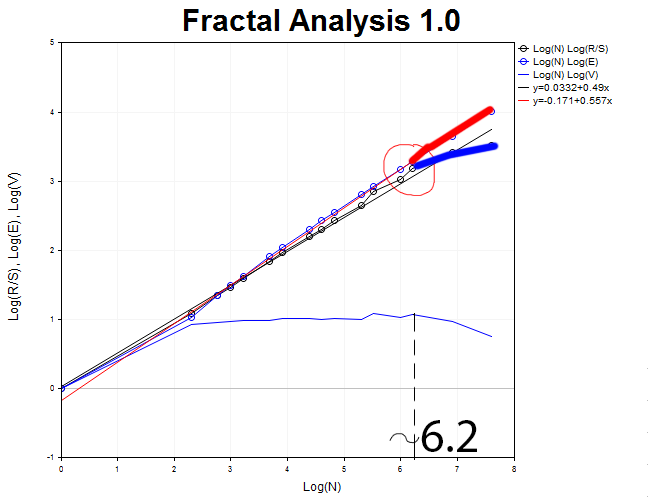
N1 = 2.71828 ^6.2 = 493 時間 21 日間に相当します。
もちろん、単一の実験では、この結果の信頼性は保証されません。 前述のように、異なる時間枠とすべきであり、"時間枠-足の数"組み合わせの結果が有効かどうかを確認します。
1000のH2期間足でグラフィカルな分析をしましょう。
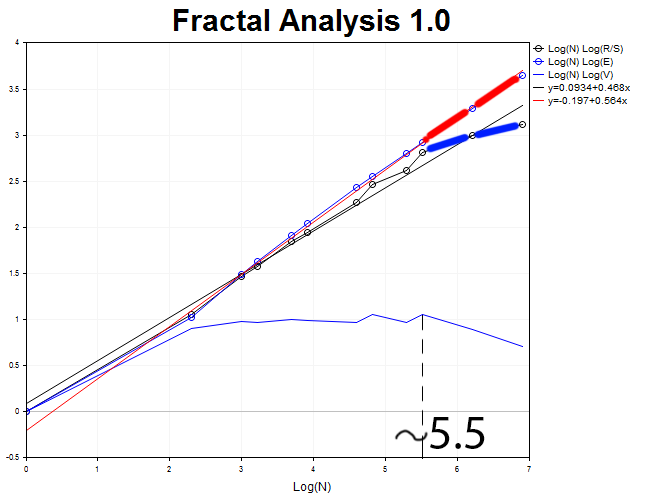
サイクルの長さは、N2 = 2.71828 ^5.5 = 245 2 時間 (約 20 日)です。
M30期間と 4000 の値を分析してみましょう。 ハースト指数 H = 0.492 と期待値 E = 0.55 標準偏差3.6 を得ます。
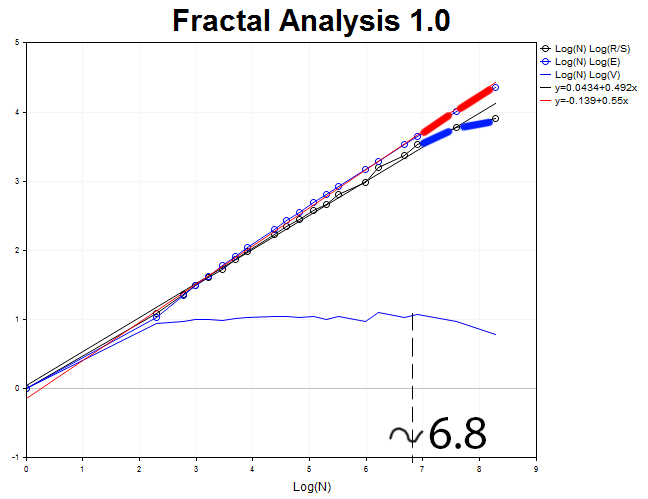
サイクル長 N3 = 2.71828 ^6.8 = 898 30 分セグメント (18.7 日)。
この3つのテストは、例として十分です。 得られた周期長の平均値を見つけてみましょう。 M= (N1 + N2 + N3)/3 = (21 + 20 + 18.7)/3 = 19.9 (20 days)。
その結果、技術的なデータとして十分な信頼性とトレード戦略を開発するための期間を取得しました。 すでに述べたように、計算、分析は 2 ヶ月間のものです。 おそらく、デイトレードの場合、その期間が短すぎるため、分析結果がはっきりしないということになるのでしょう。 サイクルが検出されない場合、テクニカル分析はその関連性と効率を失います。 その場合は、ニューストレードや相場感情によるトレードが最も合理的なソリューションです。
結論
フラクタル分析は、相場のダイナミクスを予測する技術的、統計的アプローチです。 汎用性の高いデータ処理メソッドであり、R/S 解析とハースト指数は地理学、生物学、物理学、経済学で使用されます。 フラクタル分析は、推定モデルの開発に適用できます。
冒頭で述べたように、外国為替のトレードで勝つには、その他の投資家より多くの情報を知っている必要があります。 誤解を招くことを恐れずに言うと、相場はアナリストを「欺く」傾向にあることを読者に警告しておきます。 したがって、いつでも非周期サイクルの存在を確認してください。 他の時間枠で検出されない場合、おそらくそれはノイズです。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/2930
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 可視化の可能性 Rのプロットに似たMQL5のグラフィックス ライブラリ
可視化の可能性 Rのプロットに似たMQL5のグラフィックス ライブラリ
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
実際の取引では、トレンド検出のためのハースト係数の使用は、古典的なダッシュの交差よりもさらに悪く機能する。理由は古典的なもので、ラグが大きいからだ。
しかし、その応用のアイデアはマットボットのアルゴコマンドの中でまだ時々生じている。ハースト・トレンド検知に基づく米ドル・トレードの失敗例は、エッジストーンのw-surf戦略である-最初の年はプラスで、残りはすべてマイナスである(実際のパフォーマンスを見るには、同社のウェブサイトの広告ではなく、w-surf + mfdでググってください)。
アレクセイ、建設的なコメントをどうもありがとう。これからも勉強と研究を続けます。ご指摘を参考にさせていただきます。
ドミトリー、
この映画を見て、この男について読むことを勧めるよ。
https://forecaster-movie.com/en/the-movie/
もしかしたら、次にこのプログラムを書くのはあなたかもしれない。もし書き始めたら連絡をくれ。ありがとう。
作者の皆さん!もちろん、インジケーターはとても重要です。コメント欄でコメントされた方々の中で、このインジケーターを使用したことがある方はいらっしゃらないと思います。
あなたのインジケータは、小さなタイムフレームでは動作せず、新しいバーの出現で動作しないことが判明したとき(それはロボットに接続し、テストすることができないことを意味します)、負の決定係数を計算し、私はそれを修正するために内部に入って、...あなたは簡単な方法を取らない。 実数型が 必要なところでは整数型を使い、不必要な変数や無駄な計算ステップを大量に導入し、理解を混乱させ複雑にするだけの古いメソッドや参照を大量に残し、データ配列を何度もダイレクト・インデックスからリバース・インデックスに変え、同じ変数セットを渡す不必要なオブジェクトを大量に作り、mqlの標準的な簡潔な過去の計算の勘定システムの代わりに、なぜか怖くて面倒な独自のシステムを考案する......。
mqlの標準的なインジケーターを使って、そのインジケーターを基に必要な計算をする方が簡単ではないか?信じてください、あなたのコードよりずっと理解しやすいと思います...。
ソースのアーカイブを添付しますが、そこで動作しなかったものはすべて動作し、不要なものはすべて(あるいはほとんどすべて)削除しました。問題は、この設計が実際のテストでどれだけ遅くなるかだ。まだテストはしていないが、修正し続けなければならないような気がする...。
作者の皆さん!もちろん、インジケーターはとても重要です。コメントにコメントされた方々の中で、このインジケーターを使ったことのある方はいらっしゃらないようですね :D
あなたのインジケータは、小さなタイムフレームでは動作せず、新しいバーの出現で動作しないことが判明したとき(それはロボットに接続し、テストすることができないことを意味します)、負の決定係数を計算し、私はそれを修正するために内部に入って、...あなたは簡単な方法を取らない。 実数型が 必要なところでは整数型を使い、不必要な変数や無駄な計算ステップを大量に導入し、理解を混乱させ複雑にするだけの古いメソッドや参照を大量に残し、データ配列をダイレクト・インデックスからリバース・インデックスに何度も変え、同じ変数セットを渡す不必要なオブジェクトを大量に作り、mqlの標準的な簡潔な計算システムの代わりに、なぜか怖くて面倒な独自の計算システムを考案している......。
mqlの標準的なインジケーターを使って、そのインジケーターに基づいて必要な計算をする方が簡単ではないか?信じてください、あなたのコードよりずっと理解しやすいと思います...。
ソースのアーカイブを添付しますが、そこで動作しなかったものはすべて動作し、不要なものはすべて(あるいはほとんどすべて)削除しました。問題は、この設計が実際のテストでどれだけ遅くなるかだ。まだテストはしていないが、修正し続けなければならないような気がする...。
コメントありがとう。ここで紹介したコードが最適だとは誰も言っていない。記事を書いた時点では、すべてがテストされ、機能した。目標は、ハースト係数の概念が存在し、それを適用できることを伝えることだった。あなたのコードに感謝し、その実装がさらに成功することを祈っています。
ドミトリー、こんにちは!
あなたの仕事に感謝するとともに、いくつか質問させてください。
私はかなり長い間フラクタルを研究しており、いくつかの結果を持っています。2017年にEXELでハーストパラメータを計算する最初のコードを書きました。
今、私はMT4でハーストパラメータを使用していくつかの年表を研究することに興味があります。
前のサイクルに続く次のサイクルの持続性を評価するために、サイクル間隔の境界に対応する一定の間隔(チャート上では日足、4時間足、時間足)を設定する必要があります。ローソク足の本数を選択する際、どのような設定が可能ですか?
つまり、フラクタル数列を形成する、あるサイクルから別のサイクルへの遷移の境界の一点でのみ、ハースト・パラメーターに興味を持つことになる。
実施した研究については、またお知らせします。
敬具