MetaTrader 5 / エキスパート
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
MetaTrader 5での自己組織化機能マップ(Kohonenマップ)の使用

MetaTrader 5での自己組織化機能マップ(Kohonenマップ)の使用

MetaTrader 5 — エキスパート | 17 11月 2015, 16:09
4 175 0
MetaQuotes
MetaQuotes

はじめに

自己組織化機能マップ (SOM)は、トレーニングのサンプルにおける、入力スペースを二次元離散化マップを作成できるようにする非監視型学習機能を用いる人工的なニューラルネットワークの一種です。

これらのマップは、多次元尺度に類似した高次元データの低次元での表示と分類において役に立ちます。このモデルは、フィンランド人教授Teuvo Kohoneによって人工的ニューラルネットワークとして紹介され、時々Kohonenマップと呼ばれます。

多くのアルゴリズムを使用することができ、こちらhttp://www.ai-junkie.comで示されているコードに従います。MetaTrader5のデータをビジュアル化するために、BMP画像の作成のためのライブラリであるcIntBMPを使用します。この記事では、いくつかのKohonenマップの使用を紹介します。


1. 自己組織化機能マップ

自己組織化マップは、Teuvo Kohonen に1982年初めて紹介されました。多くのニューラルネットワークと比較して、これは、入力データとターゲットの出力データが一つ一つ一致している必要がありません。このニューラルネットワークは、教師なし学習を行います。

SOMは、高次元の入力データの規則的な低次元の配列要素へ非線形でマッピングするものとして述べられているかもしれません。基本的な形式では、入力データの相似グラフを作成します。

SOMは、高次元データ間の非線形な統計的関連性を、二次元のノードグリッドの写真のシンプルな幾何学的な関係性へ変換します。SOMマップは、高次元のデータの分類とビジュアル化のために使用することができます。


1.1. ネットワークアーキテクチャ

16ノードのグリッドであるシンプルなKohonenマップは図１にて示されています。

図1. シンプルなKohonenマップ(16ノード)

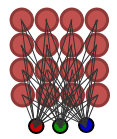
図1. シンプルなKohonenマップ (16 ノード)

各ノードは、 （x、y）は入力ベクトルを基準に定義されたコンポーネントと重みの格子ベクトルの座標です。


1.2. 学習アルゴリズム

ニューラルネットのその他多くとは異なり、SOMはターゲットアウトプットが明記される必要はありません。 そのかわり、ノードの重みが入力ベクトルと合う格子の場所が入力ベクターがメンバーであるクラスにおけるデータがより近く類似するように最適化されます。

ランダムな重みの初期配分から、SOMは最終的にマップの安定区域に落ち着きます。それぞれの区域は特徴の分類子であり、入力スペースの機能マップとしてグラフィカルアウトプットを捉えることができます。

学習のための訓練は、いくつかのステップ、数多くの反復のなかで起こります。

  1. それぞれのノードの重みはランダムな値で初期化されます。
  2. ベクトルは、トレーニング用データセットからランダムに選ばれます。
  3. それぞれのノードは、どの重みが入力ベクトルと類似するか計算します。勝利ノードは、ベストマッチングユニット（BMU）として知られています。
  4. BMUの近隣の半径が計算されます。まず、この値は、格子の半径にセットされますが、毎回スリープ状態に入るときに消滅します。
  5. BMUの半径内のノードに関しては、ノードの重みは入力ベクトルと類似するよう調節されます。BMUにノードが近いほど、重みはより警告されます。
  6. Nの反復のための繰り返しステップ２

詳しくはこちら http://www.ai-junkie.com.


2. ケーススタディ


2.1. 例１SOMで"Hello World!" を行う

Kohonenマップの古典亭な例は、カラークラスタリング問題です。

８つの色を持っていると想定し、それぞれが、RGBカラーモデルの３次元ベクトルとして表記されると考えます。

  1. clrRed Red: (255,0,0);
  2. clrGreen Green: (0,128,0);
  3. clrBlue Blue: (0,0,255);
  4. clrDarkGreen Dark Green: (0,100,0);
  5. clrDarkBlue Dark Blue: (0,0,139);
  6. clrYellow Yellow: (255,255,0);
  7. clrOrange Orange: (255,165,0);
  8. clrPurple Purple: (128,0,128).

MQL5 languageでKohonenマップを扱う際、オブジェクト指向に則ります。

ここでは、二つのクラスが必要です：レギュラーグリッドのノード用クラス、CSOMNode と、ニュラルネットワーククラスのCSOMです。 

//+------------------------------------------------------------------+
//| CSOMNode class                                                   |
//+------------------------------------------------------------------+
class CSOMNode
  {
protected:
   int               m_x1;
   int               m_y1;
   int               m_x2;
   int               m_y2;

   double            m_x;
   double            m_y;
   double            m_weights[];
public:
   //--- class constructor
                     CSOMNode();
   //--- class destructor
                    ~CSOMNode();
   //--- node initialization
   void              InitNode(int x1,int y1,int x2,int y2);
   //--- return coordinates of the node's center
   double            X()  const { return(m_x);}
   double            Y()  const { return(m_y);}
   //--- returns the node coordinates
   void              GetCoordinates(int &x1,int &y1,int &x2,int &y2);
   //--- returns the value of weight_index component of weight's vector
   double            GetWeight(int weight_index);
   //--- returns the squared distance between the node weights and specified vector
   double            CalculateDistance(double &vector[]);
   //--- adjust weights of the node
   void              AdjustWeights(double &vector[],double learning_rate,double influence);
  };

クラスのメソッドの実装はこちら（som_ex1.mq5）で見ることができますそのコードにはたくさんのコメントがあります。

CSOMクラスの記述は以下のようになります。

//+------------------------------------------------------------------+
//| CSOM class                                                       |
//+------------------------------------------------------------------+
class CSOM
  {
protected:
   //--- class for using of bmp images
   cIntBMP           m_bmp;
   //--- grid mode
   int               m_gridmode;
   //--- bmp image size
   int               m_xsize;
   int               m_ysize;
   //--- number of nodes
   int               m_xcells;
   int               m_ycells;
   //--- array with nodes
   CSOMNode          m_som_nodes[];
   //--- total items in training set
   int               m_total_training_sets;
   //--- training set array
   double            m_training_sets_array[];
protected:
   //--- radius of the neighbourhood (used for training)
   double            m_map_radius;
   //--- time constant (used for training)
   double            m_time_constant;
   //--- initial learning rate (used for training)
   double            m_initial_learning_rate;
   //--- iterations (used for training)
   int               m_iterations;

public:
   //--- class constructor
                     CSOM();
   //--- class destructor
                    ~CSOM();
   //--- net initialization
   void              InitParameters(int iterations,int xcells,int ycells,int bmpwidth,int bmpheight);
   //--- finds the best matching node, closest to the specified vector
   int               BestMatchingNode(double &vector[]);
   //--- train method
   void              Train();
   //--- render method
   void              Render();
   //--- shows the bmp image on the chart
   void              ShowBMP(bool back);
   //--- adds a vector to training set
   void              AddVectorToTrainingSet(double &vector[]);
   //--- shows the pattern title
   void              ShowPattern(double c1,double c2,double c3,string name);
   //--- adds a pattern to training set
   void              AddTrainPattern(double c1,double c2,double c3);
   //--- returns the RGB components of the color
   void              ColToRGB(int col,int &r,int &g,int &b);
   //--- returns the color by RGB components
   int               RGB256(int r,int g,int b) const {return(r+256*g+65536*b);      }
   //--- deletes image from the chart
   void              NetDeinit();
  };

CSOMクラスの使用は簡単です：

CSOM KohonenMap;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
void OnInit()
  {
  MathSrand(200);
//--- initialize net, 10000 iterations will be used for training
//--- the net contains 15x20 nodes, bmp image size 400x400
   KohonenMap.InitParameters(10000,15,20,400,400);
//-- add RGB-components of each color from training set
   KohonenMap.AddTrainPattern(255,  0,  0);   // Red
   KohonenMap.AddTrainPattern(  0,128,  0);   // Green
   KohonenMap.AddTrainPattern(  0,  0,255);   // Blue
   KohonenMap.AddTrainPattern(  0,100,  0);   // Dark green
   KohonenMap.AddTrainPattern(  0,  0,139);   // Dark blue
   KohonenMap.AddTrainPattern(255,255,  0);   // Yellow
   KohonenMap.AddTrainPattern(255,165,  0);   // Orange
   KohonenMap.AddTrainPattern(128,  0,128);   // Purple
//--- train net
   KohonenMap.Train();
//--- render map to bmp
   KohonenMap.Render();
//--- show patterns and titles for each color
   KohonenMap.ShowPattern(255,  0,  0,"Red");
   KohonenMap.ShowPattern(  0,128,  0,"Green");
   KohonenMap.ShowPattern(  0,  0,255,"Blue");
   KohonenMap.ShowPattern(  0,100,  0,"Dark green");
   KohonenMap.ShowPattern(  0,  0,139,"Dark blue");
   KohonenMap.ShowPattern(255,255,  0,"Yellow");
   KohonenMap.ShowPattern(255,165,  0,"Orange");
   KohonenMap.ShowPattern(128,  0,128,"Purple");
//--- show bmp image on the chart
   KohonenMap.ShowBMP(false);
//---
  }

結果は図２で示されています。

図２SOM_ex1.mq5エキスパートアドバイザーの結果

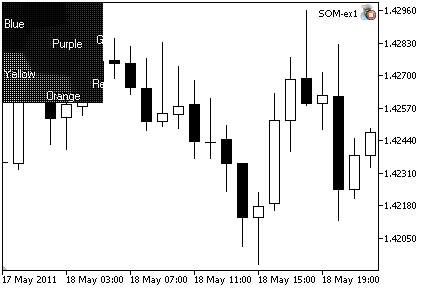
図２SOM_ex1.mq5エキスパートアドバイザーの結果

Kohoneマップ学習の原動力が図３で示されています（写真の下のステップをみてください。）

図３. Kohonenマップ学習のエネルギー

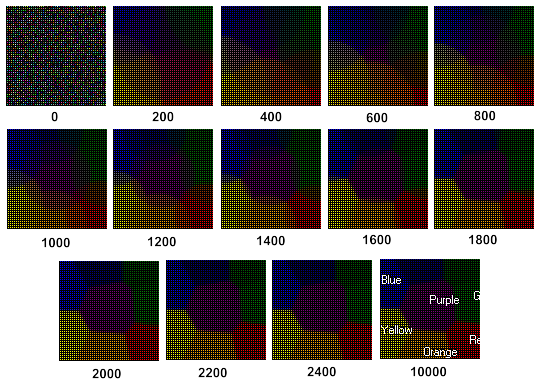
図3. Kohonenマップ 学習の原動力

図３からわかる通り、Kohonenマップは2400ステップののち形成されます。

もし300ノードの格子を作成し、400x400とイメージサイズを明記すると：

//--- lattice of 15x20 nodes, image size 400x400
   KohonenMap.InitParameters(10000,15,20,400,400);

図４のようなイメージを得ることができます：

図4. 400x400のイメージサイズでの300ノードのKohonenマップ

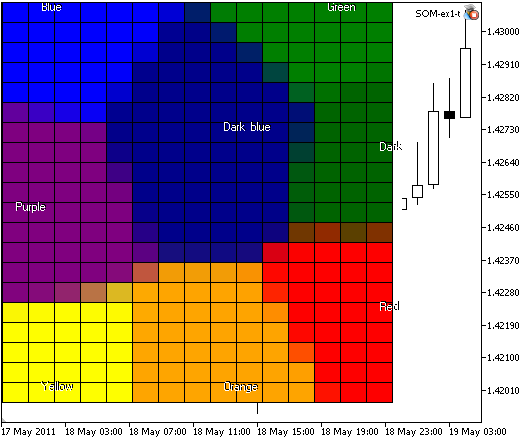
図4. 400x400のイメージサイズでの300ノードのKohonenマップ

Guido DeboeckとTeuvo Kohonenの著書Visual Explorations in Finance: with Self-Organizing Mapsを読めば、格子ノードは六角形のセルにもなることがわかります。エキスパートアドバイザーのコードを修正することで、他のビジュアル化を実装できます。

SOM-ex1-hex.mq5の結果は図５で示されています。

図5. イメージサイズ400x400、300ノードのKohonenマップが六角形のセルで示されています。

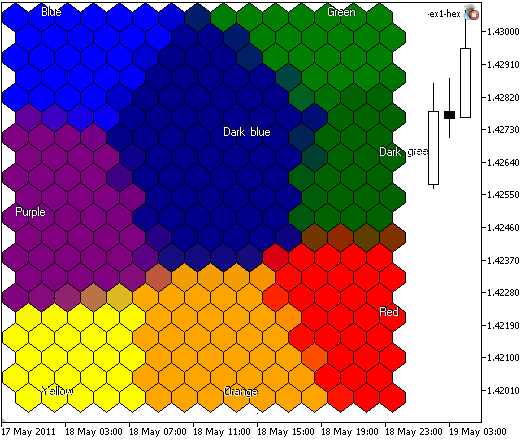
図5. イメージサイズ400x400、300ノードのKohonenマップが六角形のセルで示されています。

このバージョンでは、入力パラメーターを使用してセルの境界線の表示を定義することができます。

// input parameter, used to show hexagonal cells
input bool HexagonalCell=true;
// input parameter, used to show borders
input bool ShowBorders=true;

ある場合では、セルの境界線を示す必要はありません。もしShowBorders=falseと明記すれば、以下のイメージを得ることができます。（図６をご覧ください）

図6. イメージサイズ400x400、300ノードのKohonenマップが六角形のセルで描画され、セルの境界線が消されています。

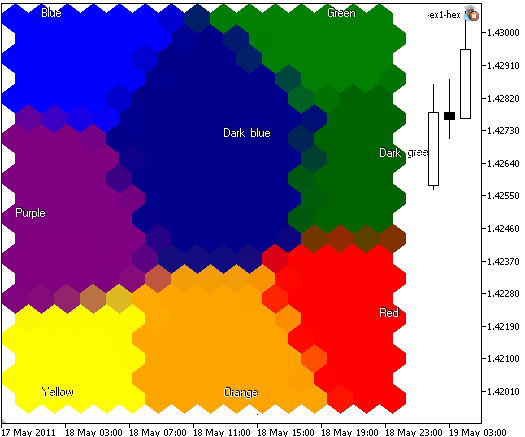
図6. イメージサイズ400x400、300ノードのKohonenマップが六角形のセルで描画され、セルの境界線が消されています。

始めの例では、トレーニングセットにて８色を使用し、カラーコンポーネントを設定しました。トレーニングセットを拡大し、二つのメソッドをCSOMクラスに追加し、カラーコンポーネントの明記を単純化できます。

この場合、Kohonenマップは、カラースペースに個別されたいくつかの色があるのみなのでとてもシンプルになっています。結果として、ローカル化されたクラスターを取得しました。

問題は、もしより近い色のコンポーネントでより多くの色を扱う場合に生じます。


2.2. 例２ウェブカラーをトレーニングサンプルとして使用する

MQL5言語では、Webカラーは事前に定義された定数です。

図７Webカラー

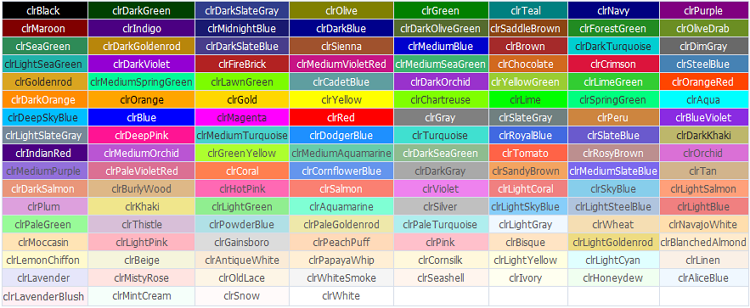
図７Webカラー

Kohonenアルゴリズムを類似したコンポーネントのベクター群に適用すればどうなるでしょうか？

CSOMクラスから派生したCSOMWebクラスを作成できます。

//+------------------------------------------------------------------+
//| CSOMWeb class                                                    |
//+------------------------------------------------------------------+
class CSOMWeb : public CSOM
  {
public:
//--- adds a color to training set (used for colors, instead of AddTrainPattern)
   void              AddTrainColor(int col);
//--- method of showing of title of the pattern (used for colors, instead of ShowPattern)
   void              ShowColor(int col,string name);
  };

ご覧の通り、色を扱うことについて単純化するために、二つの新しいメソッドを追加し、外部のカラーコンポーネントの明記は必要ではなくなりました。

クラスメソッドの実装は以下の通りです。

//+------------------------------------------------------------------+
//| Adds a color to training set                                     |
//| (used for colors, instead of AddTrainPattern)                    |
//+------------------------------------------------------------------+
void CSOMWeb::AddTrainColor(int col)
  {
   double vector[];
   ArrayResize(vector,3);
   int r=0;
   int g=0;
   int b=0;
   ColToRGB(col,r,g,b);
   vector[0]=r;
   vector[1]=g;
   vector[2]=b;
   AddVectorToTrainingSet(vector);
   ArrayResize(vector,0);
  }
//+------------------------------------------------------------------+
//| Method of showing of title of the pattern                        |
//| (used for colors, instead of ShowPattern)                        |
//+------------------------------------------------------------------+
void CSOMWeb::ShowColor(int col,string name)
  {
   int r=0;
   int g=0;
   int b=0;
   ColToRGB(col,r,g,b);
   ShowPattern(r,g,b,name);
  }

すべてのウェブカラーは、web_colors[]配列にて組み合わさります。

//--- web colors array
color web_colors[132]=
  {
   clrBlack, clrDarkGreen, clrDarkSlateGray, clrOlive, clrGreen, 
   clrTeal, clrNavy, clrPurple, clrMaroon, clrIndigo, clrMidnightBlue, 
   clrDarkBlue, clrDarkOliveGreen, clrSaddleBrown, clrForestGreen, clrOliveDrab, 
   clrSeaGreen, clrDarkGoldenrod, clrDarkSlateBlue, clrSienna, clrMediumBlue, 
   clrBrown, clrDarkTurquoise, clrDimGray, clrLightSeaGreen, clrDarkViolet, 
   clrFireBrick, clrMediumVioletRed, clrMediumSeaGreen, clrChocolate, clrCrimson, 
   clrSteelBlue, clrGoldenrod, clrMediumSpringGreen, clrLawnGreen, clrCadetBlue, 
   clrDarkOrchid, clrYellowGreen, clrLimeGreen, clrOrangeRed, clrDarkOrange, 
   clrOrange, clrGold, clrYellow, clrChartreuse, clrLime, clrSpringGreen, 
   clrAqua, clrDeepSkyBlue, clrBlue, clrMagenta, clrRed, clrGray, 
   clrSlateGray, clrPeru, clrBlueViolet, clrLightSlateGray, clrDeepPink, 
   clrMediumTurquoise, clrDodgerBlue, clrTurquoise, clrRoyalBlue, clrSlateBlue, 
   clrDarkKhaki, clrIndianRed, clrMediumOrchid, clrGreenYellow, clrMediumAquamarine, 
   clrDarkSeaGreen, clrTomato, clrRosyBrown, clrOrchid, clrMediumPurple, 
   clrPaleVioletRed, clrCoral, clrCornflowerBlue, clrDarkGray, clrSandyBrown, 
   clrMediumSlateBlue, clrTan, clrDarkSalmon, clrBurlyWood, clrHotPink, 
   clrSalmon, clrViolet, clrLightCoral, clrSkyBlue, clrLightSalmon, 
   clrPlum, clrKhaki, clrLightGreen, clrAquamarine, clrSilver, 
   clrLightSkyBlue, clrLightSteelBlue, clrLightBlue, clrPaleGreen, clrThistle, 
   clrPowderBlue, clrPaleGoldenrod, clrPaleTurquoise, clrLightGray, clrWheat, 
   clrNavajoWhite, clrMoccasin, clrLightPink, clrGainsboro, clrPeachPuff, 
   clrPink, clrBisque, clrLightGoldenrod, clrBlanchedAlmond, clrLemonChiffon, 
   clrBeige, clrAntiqueWhite, clrPapayaWhip, clrCornsilk, clrLightYellow, 
   clrLightCyan, clrLinen, clrLavender, clrMistyRose, clrOldLace, 
   clrWhiteSmoke, clrSeashell, clrIvory, clrHoneydew, clrAliceBlue, 
   clrLavenderBlush, clrMintCream, clrSnow, clrWhite
  };

OnInit()関数は以下のシンプルな形です：

CSOMWeb KohonenMap;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
void OnInit()
  {
   MathSrand(200);
   int total_web_colors=ArraySize(web_colors);
//--- initialize net, 10000 iterations will be used for training
//--- the net contains 15x20 nodes, bmp image size 400x400
   KohonenMap.InitParameters(10000,50,50,500,500);
//-- add all web colors to training set
   for(int i=0; i<total_web_colors; i++)
     {
      KohonenMap.AddTrainColor(web_colors[i]);
     }
//--- train net
   KohonenMap.Train();
//--- render map to bmp
   KohonenMap.Render();
//--- show patterns and titles for each color
   for(int i=0; i<total_web_colors; i++)
     {
      KohonenMap.ShowColor(web_colors[i],ColorToString(web_colors[i],true));
     }
//--- show bmp image on the chart
   KohonenMap.ShowBMP(false);
  }

もしsom-ex2-hex.mq5を起動すれば、図８で見られるようなイメージを得ることができます。

図８. ウェブカラーのためのKohonenマップ

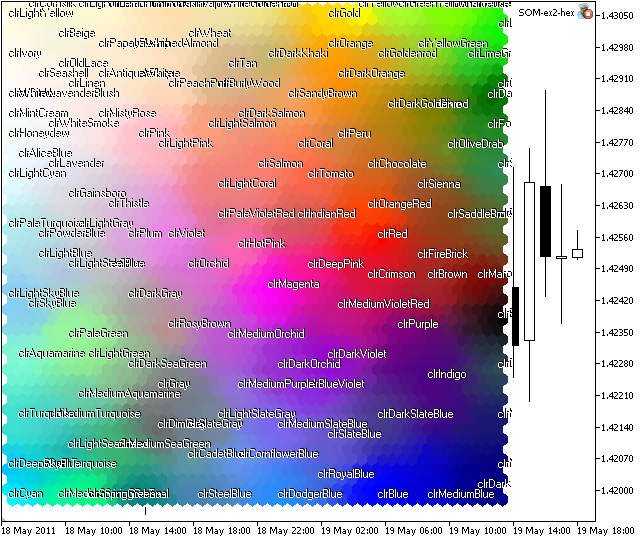
図８. ウェブカラーのためのKohonenマップ

ご覧の通り、いくつかのクラスターがありますが、いくつかの色は異なる区域に位置しています。

この理由は、トレーニングセットの構造にあり、クローズコンポーネントにたくさんのベクトルがあるためです。


2.3. 例3プロダクトクラスタリング

次に、25種類の食物を、３つの変数、プロテイン、炭水化物と脂肪に基づきグループ化する簡単な例を紹介します。

 食物
プロテイン 炭水化物 脂肪
  1 りんご
0.4
11.8
0.1
  2 アボカド
1.9
1.9
19.5
  3 バナナ
1.2
23.2
0.3
  4 ビーフステーキ
20.9
0
7.9
  5 ビッグマック
13
19
11
  6 ブラジルナッツ
15.5
2.9
68.3
  7 パン
10.5
37
3.2
  8 バター
1
0
81
  9 チーズ
25
0.1
34.4
 10 チーズケーキ
6.4
28.2
22.7
 11 クッキー
5.7
58.7
29.3
 12 コーンフレーク
7
84
0.9
 13 卵
12.5
0
10.8
 14 フライドチキン
17
7
20
 15 ポテトフライ
3
36
13
 16 ホットチョコレート
3.8
19.4
10.2
 17 ペペロニ
20.9
5.1
38.3
 18 ピザ
12.5
30
11
 19 ポークパイ
10.1
27.3
24.2
 20 ジャガイモ
1.7
16.1
0.3
 21 米
6.9
74
2.8
 22 ローストチキン
26.1
0.3
5.8
 23 砂糖
0
95.1
0
 24 ツナステーキ
25.6
0
0.5
 25 水
0
0
0

図表１25種類の食物におけるプロテイン、炭水化物、脂肪

この問題は、入力ベクトルが異なる値を持ち、それぞれのコンポーネントが独自の値を持っているため、興味深い問題です。0から255に渡るRGBカラーモデルを使用しているため、ビジュアル化が重要です。

幸運にも、この場合、入力ベクトルは、３次元であり、RGBカラーモデルをKohonenマップのビジュアル化に使用することができます。

//+------------------------------------------------------------------+
//| CSOMFood class                                                   |
//+------------------------------------------------------------------+
class CSOMFood : public CSOM
  {
protected:
   double            m_max_values[];
   double            m_min_values[];
public:
   void              Train();
   void              Render();
   void              ShowPattern(double c1,double c2,double c3,string name);
  };

ご覧の通り、トレーニングセットの最大・最小値の保存のためm_max_values[]と m_min_values[]配列を追加しました。RGBカラーモデルでのビジュアル化において、「拡張」は必要とされているため、高負荷なTrain()、Render()やShowPattern()メソッドを持ちます。

最大・最小値の検索は、Train()メソッドにて実行されます。

//--- find minimal and maximal values of the training set
   ArrayResize(m_max_values,3);
   ArrayResize(m_min_values,3);

   for(int j=0; j<3; j++)
     {
      double maxv=m_training_sets_array[3+j];
      double minv=m_training_sets_array[3+j];
      for(int i=1; i<m_total_training_sets; i++)
        {
         double v=m_training_sets_array[3*i+j];
         if(v>maxv) {maxv=v;}
         if(v<minv) {minv=v;}
        }
      m_max_values[j]=maxv;
      m_min_values[j]=minv;
      Print(j,"m_min_value=",m_min_values[j],"m_max_value=",m_max_values[j]);
     }

RGBカラーモデルにてコンポーネントを表示するために、Render()メソッドを修正する必要があります。

// int r = int(m_som_nodes[ind].GetWeight(0));
// int g = int(m_som_nodes[ind].GetWeight(1));
// int b = int(m_som_nodes[ind].GetWeight(2));

int r=int ((255*(m_som_nodes[ind].GetWeight(0)-m_min_values[0])/(m_max_values[0]-m_min_values[0])));
int g=int ((255*(m_som_nodes[ind].GetWeight(1)-m_min_values[1])/(m_max_values[1]-m_min_values[1])));
int b=int ((255*(m_som_nodes[ind].GetWeight(2)-m_min_values[2])/(m_max_values[2]-m_min_values[2])));

som_ex3.mq5の結果は図９にあります。

図９プロテイン、炭水化物、脂肪に基づく、グループ化された食物マップ

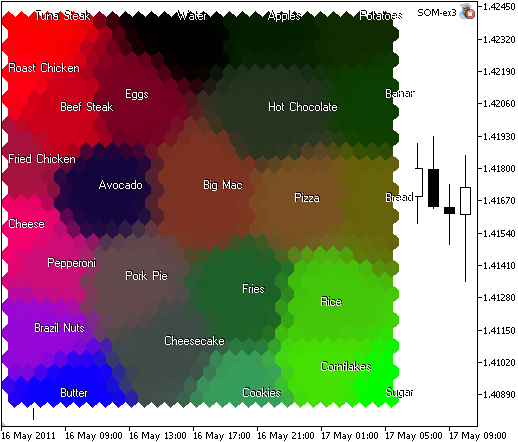
図９プロテイン、炭水化物、脂肪に基づく、グループ化された食物マップ

コンポーネント分析. 砂糖、米、コーンフレークは、炭水化物のため緑色で描画されていることがマップからわかります。バターは、多くの脂肪を含むため緑の区域にあります。たくさんのプロテインがビーフステーキ、ローストチキン、ツナステークに含まれています。

トレーニングセットを食物構成表 (代わりの表)から新しい食物を追加し、拡張することができます。

ご覧の通り、問題は、「純粋な」RGBの方向性において解決されました。複数の等しいコンポーネントを持つ他の食物はどうなのでしょうか？コンポーネントプレーンをさらに詳しく見ていきます。それは、入力ベクトルが３次元以上である場合に特に役に立ちます。


2.4. 例４四次元の場合Fisher' IrisのデータセットCMYK

３次元ベクトルにおいて、ビジュアル化の問題はありません。結果は、カラーコンポーネントのビジュアル化のために使用されるRGBカラーモデルのおかげで明確になっています。

高次元データを扱う際には、ビジュアル化する方法を見つける必要があります。簡単な方法は、ベクトルの長さに比例して、色付きの（例えば、白と黒の）グラデーションマップを描くことです。その他の方法としては、 カラースペースの使用です。この例では、Fisher's IrisデータセットのCMYKカラーモデル を見ていきます。より良いソリューションもあり、それについては後に紹介します。

Fisher's Irisにおけるアイリス花のデータは、R. Fisherにより導入された多変量のデータであり、判別式分析の例となります。そのデータセットはそれぞれのアイリス花の種から５０のサンプルを持っています。(Iris setosa, Iris virginicaやIris versicolorなど)

それぞれのサンプルから４つの特徴が導き出され、それらは、花弁と萼片の長さ、幅です。

図１０アイリス花

図１０アイリス 花

それぞれのサンプルは４つの特徴を持っています：

  1. 萼片の長さ；
  2. 萼片の幅；
  3. 花弁の長さ；
  4. 花弁の幅；

アイリス花のデータセット は、SOM_ex4.mq5にて見ることができます。

この例では、中間CMYKカラースペースを使用します。つまり、ノードの重みをCMYKスペースのベクトルとして考えていきます。結果をビジュアル化するため、CMYKからRGBへの変換が使用されます。CSOM::CMYK2Col(uchar c,uchar m,uchar y,uchar k)の新しいメソッドが、CSOM::Render()メソッドにて使用したCSOMクラスに追加されます。また、四次元のベクトルのサポートのためのクラスを修正する必要があります。

結果は図１１にて示されています。

図１１CMYKカラーモデルで描画されたアイリス花のデータセットにおけるKohonenマップ

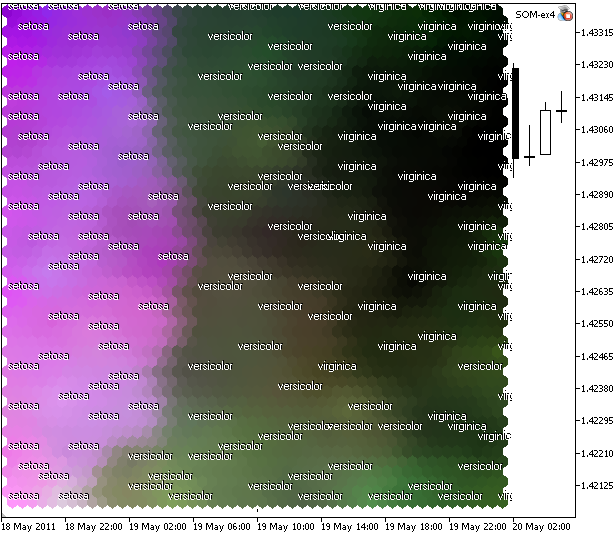
図１１CMYKカラーモデルで描画されたアイリス花のデータセットにおけるKohonenマップ

何が見えるでしょうか？（問題の機能のため）まだ完璧なクラスタリングは得られていません。しかし、 iris setosaの戦型分離を見ることができます。

setosaの分離の理由は、CMYKスペースの大きい「マジェンタ」コンポーネントにあります。


2.6. コンポーネントプレーン分析

（食物とアイリスデータのクラスタリングなど）以前の例からわかる通り、データのビジュアル化において問題があります。

例えば、食物の問題に関しては、特定の色（緑、赤、青）の情報を使用し、Kohonenマップを分析しました。基礎的なクラスターに加えて、いくつかのコンポーネントを持つ複数の食物がありました。さらに、分析はそのコンポーネントが互いに等しければ、より難しくなります。

コンポーネントプレーンは、それぞれの食物において相関的な強度を見ることができます。

CIntBMPクラスインスタンスをCSOMクラスに追加する必要があり、一致するrenderメソッドを修正する必要があります。また、（低い値が青色で、高い値が赤色の）それぞれのコンポーネントの強度をビジュアル化するグラデーションマップを必要とします。

図１２グラデーションパレット

図１２グラデーションパレット

Palette[768]配列、GetPalColor()とBlend()メソッドを追加しました。ノードの描画は、RenderCellメソッドに位置しています。

アイリス花のデータセット

som-ex4-cpr.mq5の結果は図１３にて示されています。

図１３アイリス花のデータセットのコンポーネントプレーンでの表現

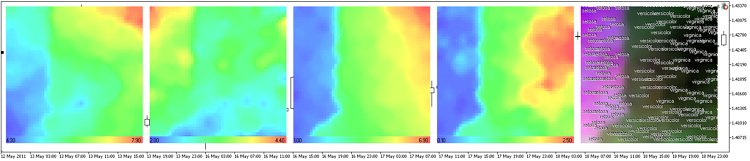
Figure 13. アイリス花のデータセットのコンポーネントプレーンでの表現

この場合、30x30ノードの300x300のイメージサイズのグリッドを使用します。

コンポーネントプレーンは、相関関係の発見において重要な役割を担います：これらのプレーンを比較し、相関する変数が発見されます。これは、もしコンポーネントプレーンが認識された際により簡単になり、相関するもの同士で近くに配置されます。このように、面白いコンポーネントの組み合わせをさらなる調査において簡単に選択することができます。

（図１４の）コンポーネントプレーンを考察してみましょう。 

最大・最小のコンポーネントの値は、グラデーション表にて表示されています。

図１４アイリス花のデータセットコンポーネントプレーン

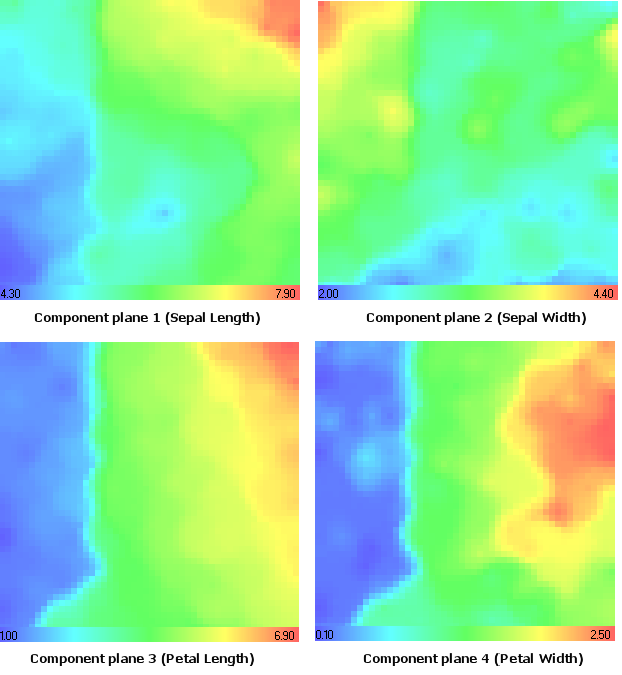
図１４アイリス花のデータセットコンポーネントプレーン

CMYKカラーモデルにて示されるこれら全てのコンポーネントプレーンは、図１５にて説明されています。

図１５アイリス花のデータセットCMYKカラーモデルでのKohonenマップ

図15. アイリス花のデータセットCMYKカラーモデルでのKohonenマップ

setosaアイリス種を思い出してみましょう。コンポーネントプレーン分析（図14）を使用し、１番目、３番目、４番目のコンポーネントプレーンに最小値があることがわかります。

２番目のコンポーネントプレーン（萼片の幅）に最大値、CMYKカラーモデル（マジェントコンポーネント、図１５）にて取得した同じ結果があります。

食物クラスタリング

それでは食物クラスタリング問題をコンポーネントプレーン分析を使用し、考えていきましょう。(som-ex3-cpr.mq5)

結果は、図１６でしめされています（30x30ノード、イメージサイズ300x300、境界線なしの六角形のセル）

図１６食物に関するKohonenマップ、コンポーネントプレーンの描写

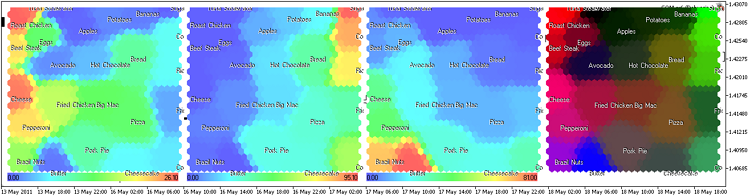
図１６食物に関するKohonenマップ、コンポーネントプレーンの描写

(入力パラメーター、ShowTitles=trueの).CSOMクラスのShowPattern() におけるタイトルのオブションの表示を追加しました。

（プロテイン、炭水化物、脂肪の）コンポーネントプレーンは以下のようになります：

図17食物におけるKohonenマップコンポーネントプレーンとRGBカラーモデル

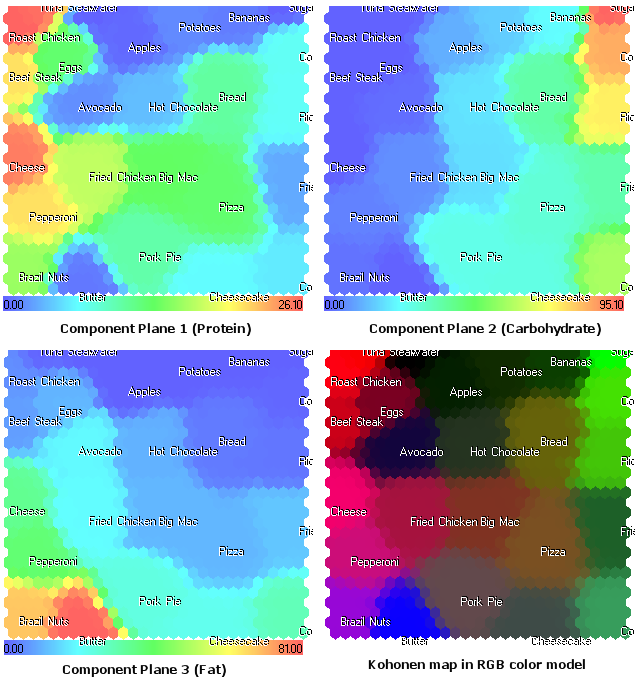
図17食物におけるKohonenマップコンポーネントプレーンとRGBカラーモデル

図17で見られるコンポーネントプレーンの表示は、食物コンポーネントの構造において新しい表示を行います。さらに、RGBカラーモデルでは見られない追加情報を提供します。

例えば、１番目のコンポーネントプレーン（プロテイン）のチーズが見えます。RGBカラーモデルでは、脂肪であるため、マジェンタに近い色で表示されます。


2.5. 任意次元の場合のコンポーネントプレーンの実行

考察したその例は、特定の機能を持っており、その任意次元は固定され、ビジュアル化のアルゴリズムは異なります。

任意次元のアルゴリズムを一般化することができましたが、この場合、コンポーネントプレーンのみをビジュアル化することになります。プログラムは、任意データをCSVファイルからロードする必要があります。

例えば、food.csvは以下のようになります；

Protein;Carbohydrate;Fat;Title
0.4;11.8;0.1;Apples
1.9;1.9;19.5;Avocado
1.2;23.2;0.3;Bananas
20.9;0.0;7.9;Beef Steak
13.0;19.0;11.0;Big Mac
15.5;2.9;68.3;Brazil Nuts
10.5;37.0;3.2;Bread
1.0;0.0;81.0;Butter
25.0;0.1;34.4;Cheese
6.4;28.2;22.7;Cheesecake
5.7;58.7;29.3;Cookies
7.0;84.0;0.9;Cornflakes
12.5;0.0;10.8;Eggs
17.0;7.0;20.0;Fried Chicken
3.0;36.0;13.0;Fries
3.8;19.4;10.2;Hot Chocolate
20.9;5.1;38.3;Pepperoni
12.5;30.0;11.0;Pizza
10.1;27.3;24.2;Pork Pie
1.7;16.1;0.3;Potatoes
6.9;74.0;2.8;Rice
26.1;0.3;5.8;Roast Chicken
0.0;95.1;0.0;Sugar
25.6;0.0;0.5;Tuna Steak
0.0;0.0;0.0;Water

そのファイルの最初の業は、入力データベクトルの名前（タイトル）があります。そのタイトルは、コンポーネントプレーンを区別するために必要であり、グラデーションパネルに名前が記入されます。

そのパターン名は、最後のカラムに位置しており、この場合、それは食物名です。

SOM.mq5 (OnInit function)のコードは単純化されます：

CSOM KohonenMap;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   MathSrand(200);
//--- load patterns from file
   if(!KohonenMap.LoadTrainDataFromFile(DataFileName))
     {
      Print("Error in loading data for training.");
      return(1);
     }
//--- train net
   KohonenMap.Train();
//--- render map
   KohonenMap.Render();
//--- show patterns from training set
   KohonenMap.ShowTrainPatterns();
//--- show bmp on the chart
   KohonenMap.ShowBMP(false);
   return(0);
  }

トレーニングパターンを持つファイル名は、「food.csv」のDataFileName入力パラメーターにて明記されます。

結果は図18にて示されています。

図18白/黒のグラデーションカラースキームでの食物Kohonenマップ

図18白/黒のグラデーションカラースキームでの食物Kohonenマップ

また、ColorScheme入力パラメーターをグラデーションスキーム選択のために追加します。

現在、４色のスキームが使用可能です (ColorScheme=0,1,2,4=Black-White, DarkBlue-Blue-Green-Yellow-Red, Red-Black-Green, Red-White-Green).


簡単に独自のスキームをCSOM::InitParameters()メソッド内にグラデーションを追加することで、付け足すことができます。

カラースキームは、エキスパートアドバイザーの入力パラメータから選択できます。


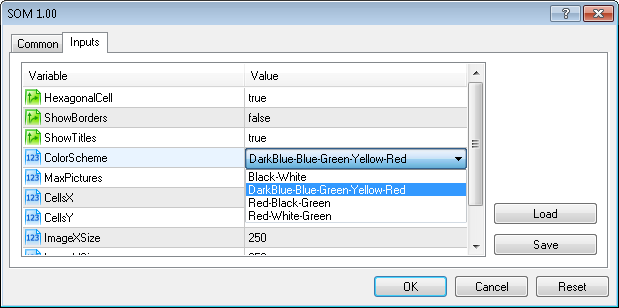
同様にアイリス花のデータを準備できます。(iris-fisher.csv):

Sepal length;Sepal width;Petal length;Petal width;Title
5.1;3.5;1.4;0.2;setosa
4.9;3.0;1.4;0.2;setosa
4.7;3.2;1.3;0.2;setosa
4.6;3.1;1.5;0.2;setosa
5.0;3.6;1.4;0.2;setosa
5.4;3.9;1.7;0.4;setosa
4.6;3.4;1.4;0.3;setosa
5.0;3.4;1.5;0.2;setosa
4.4;2.9;1.4;0.2;setosa
4.9;3.1;1.5;0.1;setosa
5.4;3.7;1.5;0.2;setosa
4.8;3.4;1.6;0.2;setosa
4.8;3.0;1.4;0.1;setosa
4.3;3.0;1.1;0.1;setosa
5.8;4.0;1.2;0.2;setosa
5.7;4.4;1.5;0.4;setosa
5.4;3.9;1.3;0.4;setosa
5.1;3.5;1.4;0.3;setosa
5.7;3.8;1.7;0.3;setosa
5.1;3.8;1.5;0.3;setosa
5.4;3.4;1.7;0.2;setosa
5.1;3.7;1.5;0.4;setosa
4.6;3.6;1.0;0.2;setosa
5.1;3.3;1.7;0.5;setosa
4.8;3.4;1.9;0.2;setosa
5.0;3.0;1.6;0.2;setosa
5.0;3.4;1.6;0.4;setosa
5.2;3.5;1.5;0.2;setosa
5.2;3.4;1.4;0.2;setosa
4.7;3.2;1.6;0.2;setosa
4.8;3.1;1.6;0.2;setosa
5.4;3.4;1.5;0.4;setosa
5.2;4.1;1.5;0.1;setosa
5.5;4.2;1.4;0.2;setosa
4.9;3.1;1.5;0.2;setosa
5.0;3.2;1.2;0.2;setosa
5.5;3.5;1.3;0.2;setosa
4.9;3.6;1.4;0.1;setosa
4.4;3.0;1.3;0.2;setosa
5.1;3.4;1.5;0.2;setosa
5.0;3.5;1.3;0.3;setosa
4.5;2.3;1.3;0.3;setosa
4.4;3.2;1.3;0.2;setosa
5.0;3.5;1.6;0.6;setosa
5.1;3.8;1.9;0.4;setosa
4.8;3.0;1.4;0.3;setosa
5.1;3.8;1.6;0.2;setosa
4.6;3.2;1.4;0.2;setosa
5.3;3.7;1.5;0.2;setosa
5.0;3.3;1.4;0.2;setosa
7.0;3.2;4.7;1.4;versicolor
6.4;3.2;4.5;1.5;versicolor
6.9;3.1;4.9;1.5;versicolor
5.5;2.3;4.0;1.3;versicolor
6.5;2.8;4.6;1.5;versicolor
5.7;2.8;4.5;1.3;versicolor
6.3;3.3;4.7;1.6;versicolor
4.9;2.4;3.3;1.0;versicolor
6.6;2.9;4.6;1.3;versicolor
5.2;2.7;3.9;1.4;versicolor
5.0;2.0;3.5;1.0;versicolor
5.9;3.0;4.2;1.5;versicolor
6.0;2.2;4.0;1.0;versicolor
6.1;2.9;4.7;1.4;versicolor
5.6;2.9;3.6;1.3;versicolor
6.7;3.1;4.4;1.4;versicolor
5.6;3.0;4.5;1.5;versicolor
5.8;2.7;4.1;1.0;versicolor
6.2;2.2;4.5;1.5;versicolor
5.6;2.5;3.9;1.1;versicolor
5.9;3.2;4.8;1.8;versicolor
6.1;2.8;4.0;1.3;versicolor
6.3;2.5;4.9;1.5;versicolor
6.1;2.8;4.7;1.2;versicolor
6.4;2.9;4.3;1.3;versicolor
6.6;3.0;4.4;1.4;versicolor
6.8;2.8;4.8;1.4;versicolor
6.7;3.0;5.0;1.7;versicolor
6.0;2.9;4.5;1.5;versicolor
5.7;2.6;3.5;1.0;versicolor
5.5;2.4;3.8;1.1;versicolor
5.5;2.4;3.7;1.0;versicolor
5.8;2.7;3.9;1.2;versicolor
6.0;2.7;5.1;1.6;versicolor
5.4;3.0;4.5;1.5;versicolor
6.0;3.4;4.5;1.6;versicolor
6.7;3.1;4.7;1.5;versicolor
6.3;2.3;4.4;1.3;versicolor
5.6;3.0;4.1;1.3;versicolor
5.5;2.5;4.0;1.3;versicolor
5.5;2.6;4.4;1.2;versicolor
6.1;3.0;4.6;1.4;versicolor
5.8;2.6;4.0;1.2;versicolor
5.0;2.3;3.3;1.0;versicolor
5.6;2.7;4.2;1.3;versicolor
5.7;3.0;4.2;1.2;versicolor
5.7;2.9;4.2;1.3;versicolor
6.2;2.9;4.3;1.3;versicolor
5.1;2.5;3.0;1.1;versicolor
5.7;2.8;4.1;1.3;versicolor
6.3;3.3;6.0;2.5;virginica
5.8;2.7;5.1;1.9;virginica
7.1;3.0;5.9;2.1;virginica
6.3;2.9;5.6;1.8;virginica
6.5;3.0;5.8;2.2;virginica
7.6;3.0;6.6;2.1;virginica
4.9;2.5;4.5;1.7;virginica
7.3;2.9;6.3;1.8;virginica
6.7;2.5;5.8;1.8;virginica
7.2;3.6;6.1;2.5;virginica
6.5;3.2;5.1;2.0;virginica
6.4;2.7;5.3;1.9;virginica
6.8;3.0;5.5;2.1;virginica
5.7;2.5;5.0;2.0;virginica
5.8;2.8;5.1;2.4;virginica
6.4;3.2;5.3;2.3;virginica
6.5;3.0;5.5;1.8;virginica
7.7;3.8;6.7;2.2;virginica
7.7;2.6;6.9;2.3;virginica
6.0;2.2;5.0;1.5;virginica
6.9;3.2;5.7;2.3;virginica
5.6;2.8;4.9;2.0;virginica
7.7;2.8;6.7;2.0;virginica
6.3;2.7;4.9;1.8;virginica
6.7;3.3;5.7;2.1;virginica
7.2;3.2;6.0;1.8;virginica
6.2;2.8;4.8;1.8;virginica
6.1;3.0;4.9;1.8;virginica
6.4;2.8;5.6;2.1;virginica
7.2;3.0;5.8;1.6;virginica
7.4;2.8;6.1;1.9;virginica
7.9;3.8;6.4;2.0;virginica
6.4;2.8;5.6;2.2;virginica
6.3;2.8;5.1;1.5;virginica
6.1;2.6;5.6;1.4;virginica
7.7;3.0;6.1;2.3;virginica
6.3;3.4;5.6;2.4;virginica
6.4;3.1;5.5;1.8;virginica
6.0;3.0;4.8;1.8;virginica
6.9;3.1;5.4;2.1;virginica
6.7;3.1;5.6;2.4;virginica
6.9;3.1;5.1;2.3;virginica
5.8;2.7;5.1;1.9;virginica
6.8;3.2;5.9;2.3;virginica
6.7;3.3;5.7;2.5;virginica
6.7;3.0;5.2;2.3;virginica
6.3;2.5;5.0;1.9;virginica
6.5;3.0;5.2;2.0;virginica
6.2;3.4;5.4;2.3;virginica
5.9;3.0;5.1;1.8;virginica

結果は図19にて示されています。

図19アイリス花のデータセット赤ー黒ー緑のカラースキームでのコンポーネントプレーン (ColorScheme=2, iris-fisher.csv)

図19アイリス花のデータセット赤ー黒ー緑のカラースキームでのコンポーネントプレーン (ColorScheme=2, iris-fisher.csv)

それでは、実際に適用するためのツールを紹介します。


2.6. 例５市場ヒートマップ

自己組織化機能マップは、マーケットの動きにおけるマップに使用できます。時々、マーケットのグローバルな図が必要とされ、 市場のヒートマップ はとても役に立ちます。株は、個々の経済セクターに依存し組み合わさっています。

株の現在の色は、現在の成長率（%）に基づきます。

図20S&P500からの株における市場ヒートマップ

図20S&P500からの株における市場ヒートマップ

S&P (http://finviz.com)の週間株市場ヒートマップは図20にて表示されています。色は、成長率に依存します。

株のチャートの大きさは、マーケットの資本化に依存します。Kohonenマップを使用し、同じ分析がMetaTrader5クライアントターミナルでも行われます。

アイディアとしては、いくつかのタイムフレームにおいての成長率を使用することです。Kohonenマップを扱うためのツールがあり、データをcsbファイルに保存するためのスクリプトのみが必要です。

アメリカのCFD株価に関する価格データ(#AA, #AIG, #AXP, #BA, #BAC, #C, #CAT, #CVX, #DD, #DIS, #EK, #GE, #HD, #HON, #HPQ, #IBM, #INTC, #IP, #JNJ, #JPM, #KFT, #KO, #MCD, #MMM, #MO, #MRK, #MSFT, #PFE, #PG, #T, #TRV, #UTX, #VZ, #WMT и #XOM)は、MetaQuotes Demoサーバーにて見ることができます。

dj.csvファイルを準備するそのスクリプトは、とてもシンプルです：

//+------------------------------------------------------------------+
//|                                                           DJ.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

string s_cfd[35]=
  {
   "#AA","#AIG","#AXP","#BA","#BAC","#C","#CAT","#CVX","#DD","#DIS","#EK","#GE",
   "#HD","#HON","#HPQ","#IBM","#INTC","#IP","#JNJ","#JPM","#KFT","#KO","#MCD","#MMM",
   "#MO","#MRK","#MSFT","#PFE","#PG","#T","#TRV","#UTX","#VZ","#WMT","#XOM"
  };
//+------------------------------------------------------------------+
//| Returns price change in percents                                 |
//+------------------------------------------------------------------+
double PercentChange(double Open,double Close)
  {
   return(100.0*(Close-Open)/Close);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {

   ResetLastError();
   int filehandle=FileOpen("dj.csv",FILE_WRITE|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error opening file");
      return;
     }
//---
   MqlRates MyRates[];
   ArraySetAsSeries(MyRates,true);

   string t="M30;M60;M90;M120;M150;M180;M210;M240;Title";
   FileWrite(filehandle,t);
   Print(t);

   int total_symbols=ArraySize(s_cfd);

   for(int i=0; i<total_symbols; i++)
     {
      string cursymbol=s_cfd[i];

      int copied1=CopyRates(cursymbol,PERIOD_M30,0,8,MyRates);
      if(copied1>0)
        {
         string s="";
         s=s+DoubleToString(PercentChange(MyRates[1].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[2].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[3].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[4].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[5].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[6].open,MyRates[0].close),3)+";";
         s=s+DoubleToString(PercentChange(MyRates[7].open,MyRates[0].close),3)+";";
         s=s+cursymbol;
         Print(s);
         FileWrite(filehandle,s);
         }
         else
           {
            Print("Error in request of historical data on symbol ",cursymbol);
            return;
           }
     }
   Alert("OK");
   FileClose(filehandle);

  }
//+------------------------------------------------------------------+

履歴データはダウンロードされる必要があり、DownloadHistoryスクリプトを使用し、自動的に行うことができます。

dj.mq5スクリプトの結果、dj.csvを以下のデータで得ることができます。

M30;M60;M90;M120;M150;M180;M210;M240;Title
0.063;-0.564;-0.188;0.376;0.251;0.313;0.627;0.439;#AA
-0.033;0.033;0.067;-0.033;0.067;-0.133;0.266;0.533;#AIG
-0.176;0.039;0.039;0.274;0.196;0.215;0.430;0.646;#AXP
-0.052;-0.328;-0.118;0.315;0.223;0.367;0.288;0.328;#BA
-0.263;-0.351;-0.263;0.000;-0.088;0.088;0.000;-0.088;#BAC
-0.224;-0.274;-0.374;-0.100;-0.274;-0.224;-0.324;-0.598;#C
-0.069;-0.550;-0.079;0.766;0.727;0.638;0.736;0.589;#CAT
-0.049;-0.168;0.099;0.247;0.187;0.049;0.355;0.266;#CVX
0.019;-0.058;0.058;0.446;0.174;0.349;0.136;-0.329;#DD
-0.073;-0.219;-0.146;0.267;0.170;0.292;0.170;0.267;#DIS
-1.099;-1.923;-1.099;0.275;0.275;0.275;-0.549;-1.374;#EK
-0.052;-0.310;-0.103;0.362;0.258;0.362;0.465;0.258;#GE
-0.081;-0.244;-0.326;-0.136;0.081;0.326;0.489;0.489;#HD
-0.137;-0.427;-0.171;0.427;0.445;0.342;0.325;0.359;#HON
-0.335;-0.363;-0.112;0.112;0.168;0.307;0.475;0.251;#HPQ
0.030;-0.095;0.065;0.190;0.071;0.214;0.279;0.327;#IBM
0.000;-0.131;-0.044;-0.088;-0.044;0.000;0.000;0.044;#INTC
-0.100;-0.200;-0.166;0.100;-0.067;0.033;-0.532;-0.798;#IP
-0.076;0.076;0.259;0.473;0.427;0.336;0.336;-0.076;#JNJ
-0.376;-0.353;-0.494;-0.259;-0.423;-0.329;-0.259;-0.541;#JPM
-0.057;-0.086;-0.029;0.086;0.114;0.057;0.257;-0.114;#KFT
0.059;-0.030;0.119;0.282;0.119;0.193;0.208;-0.119;#KO
-0.109;-0.182;0.206;0.352;0.279;0.473;0.521;0.194;#MCD
-0.043;-0.195;-0.151;0.216;0.270;0.227;0.411;0.206;#MMM
-0.036;-0.072;0.072;0.144;-0.072;-0.108;0.108;0.072;#MO
0.081;-0.081;0.027;0.081;-0.054;0.027;-0.027;-0.108;#MRK
0.083;0.083;0.041;0.331;0.083;0.248;0.166;0.041;#MSFT
0.049;0.000;0.243;0.680;0.194;0.243;0.340;0.097;#PFE
-0.045;0.060;0.104;0.015;-0.179;-0.149;-0.224;-0.224;#PG
0.097;-0.032;0.000;0.129;0.129;0.064;0.097;0.064;#T
-0.277;-0.440;-0.326;-0.358;-0.537;-0.619;-0.570;-0.733;#TRV
-0.081;-0.209;0.035;0.325;0.198;0.093;0.128;-0.035;#UTX
0.054;0.000;0.054;0.190;0.136;0.326;0.380;0.353;#VZ
-0.091;-0.091;-0.036;0.036;-0.072;0.000;0.145;-0.127;#WMT
-0.062;-0.211;0.087;0.198;0.186;0.050;0.347;0.508;#XOM

som.mq5(ColorScheme=3, CellsX=30,CellsY=30, ImageXSize=200, ImageXSize=200, DataFileName="dj.csv")を開始すると、８つの図を得ることができ、それらは、30、60、90、120、150、180、210、240分のタイムインターバルに一致します。

2011年5月23日最後４時間のマーケット成長率のKohonenマップデータは、図21にて示されています。

図21. （2011年5月23日最後４時間のトレードセッションの）アメリカの株に関するKohonenマップ

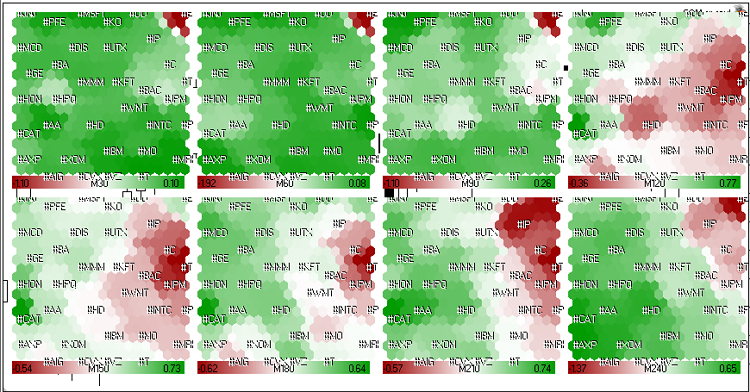
図21. （2011年5月23日最後４時間のトレードセッションの）アメリカの株に関するKohonenマップ

図21からわかるように、#C (Citigroup Inc.)、#T (AT&T Inc.)、#JPM (JPMorgan Chase & Co)、#BAC (Bank of America)の変動は類似しています。長期間赤色クラスターに分類されています。

最後1.5時間(M30、M60、M90)の間に、その変動率は、緑色になりましたが、一般的にその株は赤色区域にあります。

Kohonenマップを使用し、株の相関的な変動をビジュアル化でき、リーダーや敗者、その環境を発見できます。クラスターの類似データの要素

図21からわかる通り、Citigroup Incの株価は、降下のリーダーです。一般的に、全ての金融企業の株は赤色区域にあります。

図21a2011年5月2３日の市場ヒートマップ (http://finviz.com)

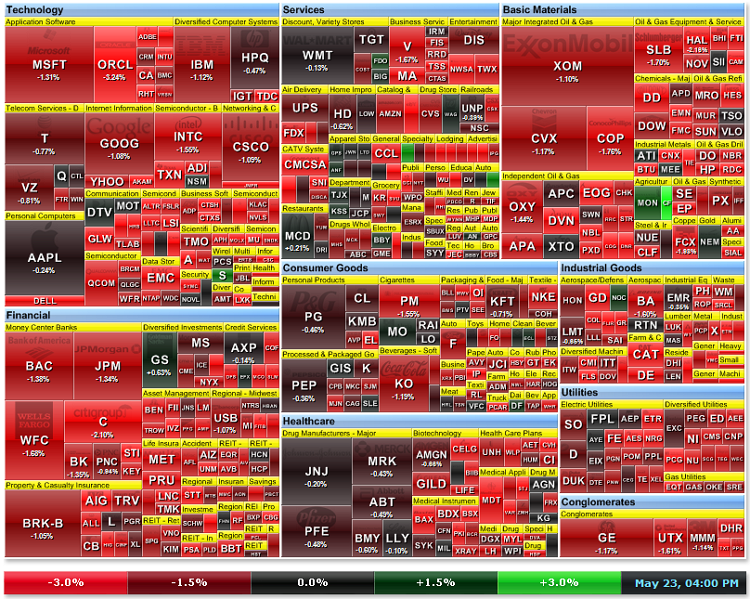
図21a2011年5月2３日の市場ヒートマップ (http://finviz.com)

同様に、FOREX市場のKohonenマップを計算することができます(図 22):

図22. FOREX市場のKohonenマップ(2011年5月24日ヨーロッパ期間)

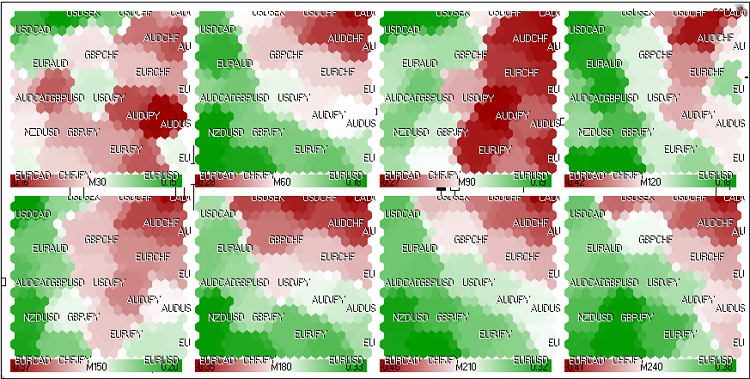
図22. FOREX市場のKohonenマップ(2011年5月24日ヨーロッパ期間)

以下のペアが使用されます： EURUSD, GBPUSD, USDCHF, USDJPY, USDCAD, AUDUSD, NZDUSD, USDSEK, AUDNZD, AUDCAD, AUDCHF, AUDJPY, CHFJPY, EURGBP, EURAUD, EURCHF, EURJPY, EURNZD, EURCAD, GBPCHF, GBPJPY, CADCHF. 

fx.mq5スクリプトを使用し、成長率はfx.csvに移行されます。

M30;M60;M90;M120;M150;M180;M210;M240;Title
0.058;-0.145;0.045;-0.113;-0.038;-0.063;0.180;0.067;EURUSD
0.046;-0.100;0.078;0.094;0.167;0.048;0.123;0.160;GBPUSD
-0.048;0.109;-0.142;-0.097;-0.219;-0.143;-0.277;-0.236;USDCHF
0.042;0.097;0.043;-0.024;-0.009;-0.067;0.024;0.103;USDJPY
-0.045;0.162;0.155;0.239;0.217;0.246;0.157;0.227;USDCAD
0.095;-0.126;-0.018;-0.141;-0.113;-0.062;0.081;-0.005;AUDUSD
0.131;-0.028;0.167;0.096;-0.013;0.147;0.314;0.279;NZDUSD
-0.047;0.189;-0.016;0.107;0.084;0.076;-0.213;-0.133;USDSEK
-0.034;-0.067;-0.188;-0.227;-0.102;-0.225;-0.234;-0.291;AUDNZD
0.046;0.039;0.117;0.102;0.097;0.170;0.234;0.216;AUDCAD
0.057;-0.016;-0.158;-0.226;-0.328;-0.215;-0.180;-0.237;AUDCHF
0.134;-0.020;0.024;-0.139;-0.124;-0.127;0.107;0.098;AUDJPY
0.083;-0.009;0.184;0.084;0.208;0.082;0.311;0.340;CHFJPY
0.025;-0.036;-0.030;-0.200;-0.185;-0.072;0.058;-0.096;EURGBP
-0.036;-0.028;0.061;0.010;0.074;-0.006;0.088;0.070;EURAUD
0.008;-0.049;-0.098;-0.219;-0.259;-0.217;-0.094;-0.169;EURCHF
0.096;-0.043;0.085;-0.124;-0.049;-0.128;0.206;0.157;EURJPY
-0.073;-0.086;-0.119;-0.211;-0.016;-0.213;-0.128;-0.213;EURNZD
0.002;0.009;0.181;0.119;0.182;0.171;0.327;0.284;EURCAD
-0.008;0.004;-0.077;-0.015;-0.054;-0.127;-0.164;-0.080;GBPCHF
0.079;-0.005;0.115;0.079;0.148;-0.008;0.144;0.253;GBPJPY
0.013;-0.060;-0.294;-0.335;-0.432;-0.376;-0.356;-0.465;CADCHF

価格に加えて、異なるタイムフレームでインジケーターの値を使用できます。


2.6. 例６最適化結果の分析

MetaTrader 5のストラテジーテスターは、パラメータースペースの構造を詳しく知り、最適な戦略パラメーターを見つける機会を提供します。また、「Export to XML (MS Office Excel)」オプションを「Optimization Results」タブのコンテキストメニューから選択し、最適化結果を見ることができます。

テスト統計は、最適化結果に含まれています。

  1. 結果
  2. 利益
  3. 総利益
  4. 総損失
  5. 引き出し
  6. 予定支払い
  7. 利益要因
  8. 再生要因
  9. シャープ・レシオ
  10. マージンレベル
  11. カスタム
  12. 最小収支
  13. 最大DD収支
  14. 最小DD収支(%)
  15. 相関DD収支
  16. 相関DD収支(%)
  17. 最小資産
  18. 最大DD資産
  19. 最大DD資産(%)
  20. 相関DD資産
  21. 相関DD資産(%)
  22. トレード
  23. 取引
  24. ショート・トレード
  25. プロフィット・ショート・トレード
  26. ロング・トレード
  27. プロフィット・ロング・トレード
  28. プロフィットトレード
  29. ロストレード
  30. 最大プロフィットトレード
  31. 最大ロストレード
  32. 最大連続勝ち
  33. 最大連続勝ち($)
  34. 最大連続利益
  35. 最大連続利益数    
  36. 最大連続損失
  37. 最大連続損失($)
  38. 最大連続損失
  39. 最大連続損失数
  40. 平均連続勝ち
  41. 平均連続損失

テスト統計の使用により、パラメータースペースの分析に役立ちます。統計の多くのパラメーターが、近く関連し、トレードパフォーマンスの結果に依存しています。

例えば、最適なトレード結果は、Profit、Profit Factor、Recovery Factor、Sharpe Ratioパラメーターの最大値を持っています。これにより、結果の分析にそれらを使用することができます。

MovingAverage.mq5エキスパートアドバイザーの最適化結果

この章では、MetaTrader5クライアントターミナルの標準パッケージ内のMovingAvereage.mq5エキスパートアドバイザーの最適化結果の分析を考察します。このエキスパートアドバイザーは、価格と移動平均指標のクロスオーバーに基づきます。二つのパラメーターを持っています: MovingPeriodとMovingShiftの二つです。つまり、43のカラムを持つXMLファイルを結果として持つようになります。

パラメーターの43次元スペースは考察しません。

  1. Profit;
  2. Profit Factor;
  3. Recovery Factor;
  4. Sharpe Ratio;
  5. Trades;
  6. ProfitTrades(%);
  7. MovingPeriod;
  8. MovingShift;

（結果には存在しない）ProfitTrades (%) パラメーターを追加しました。これは、利益の得られる取引の率を意味し、100で掛けられたTrades (22)によるProfitTrades (28)の割り算の結果として計算されます。

9カラムを持つ、optim.csvファイルをMetaTrader5の400の入力パラメーターのために準備しましょう。

Profit;Profit Factor;Recovery Factor;Sharpe Ratio;Trades;ProfitTrades(%);MovingPeriod;MovingShift;Title
-372.3;0.83;-0.51;-0.05;71;28.16901408;43;6;43
-345.79;0.84;-0.37;-0.05;66;27.27272727;50;6;50
...

MOvinPeriodをタイトルカラムとして使用しました。Kohonenマップにてパターンに「印を入れる」ために使用されます。

ストラテジーテスターにて、MovingPeriodとMovingShiftの値の最適化を以下のパラメーターで行いました。

  • シンボル - EURUSD,
  • 期間 - H1,
  • ティック生成モード - "1 Minute OHLC",
  • テストインターバル - 2011.01.01-2011.05.24,
  • 最適化 - Fast (遺伝アルゴリズム),
  • 最適化 - 最大収支

図23. MovingAverage EAの最適化結果におけるKohonenマップ（コンポーネントプレーンの表示）

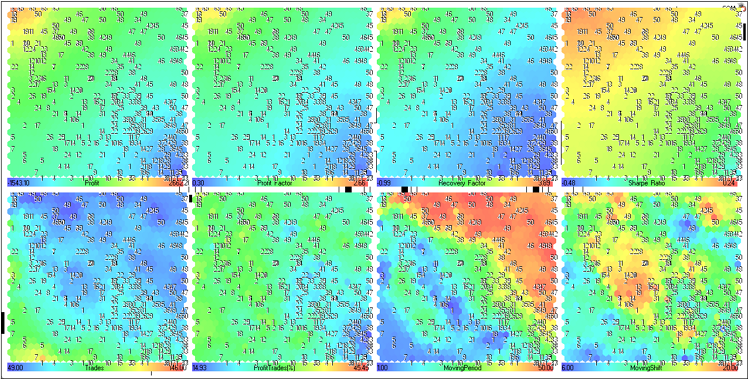
図23. MovingAverage EAの最適化結果におけるKohonenマップ（コンポーネントプレーンの表示） https://c.mql5.com/2/3/figure23_som_image__1.png

上列のコンポーネントプレーンを考察しましょう。(Profit、Profit Factor、Recovery Factor、 Sharpe Ratio).

図24にて組み合わさります。

図24. Profit、Profit Factor、Recovery Factor、Sharpe Ratio パラメーターのコンポーネントプレーン

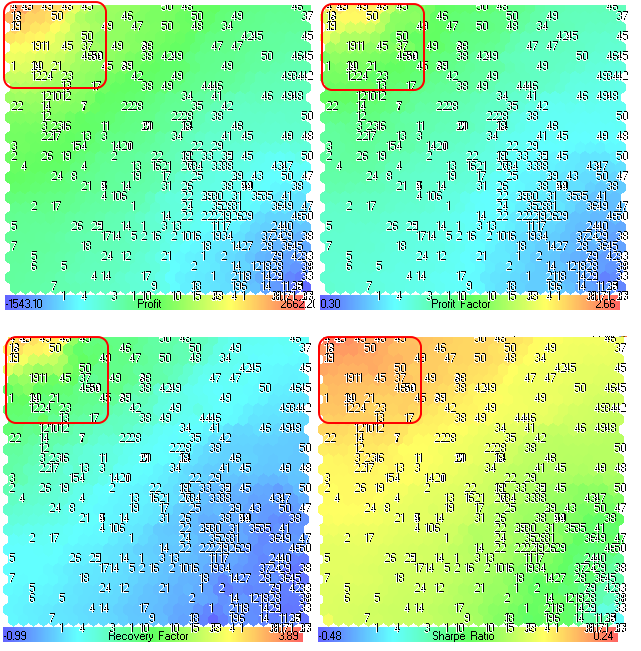
図24. Profit、Profit Factor、Recovery Factor、Sharpe Ratio パラメーターのコンポーネントプレーン

まず必要なこととしては、最適化結果の区域を見つけることです。

図24からわかる通り、最大値の区域は、上方左角に位置します。その数は、Moving Averageインジケーターの平均期間に一致します。（MovingPeriodパラメーター、タイトルとして使用しました）数字の位置は、全てのコンポーネントプレーンと同様です。個々のコンポーネントプレーンは、それぞれの値の範囲を持ち、その値は、グラデーションパネルに記載されています。

最適化結果は、Profit、Profit Factor、Recovery Factor、 Sharpe Ratioの最大値を持っており、マップのその区域の情報を持ちます。（図２４の通り）

Trades、ProfitTrades(%)、MovingPeriodとMovingShiftのコンポーネントプレーンは図25の通りです。

図25. Trades、ProfitTrades(%)、MovingPeriodとMovingShiftパラメーターのコンポーネントプレーン

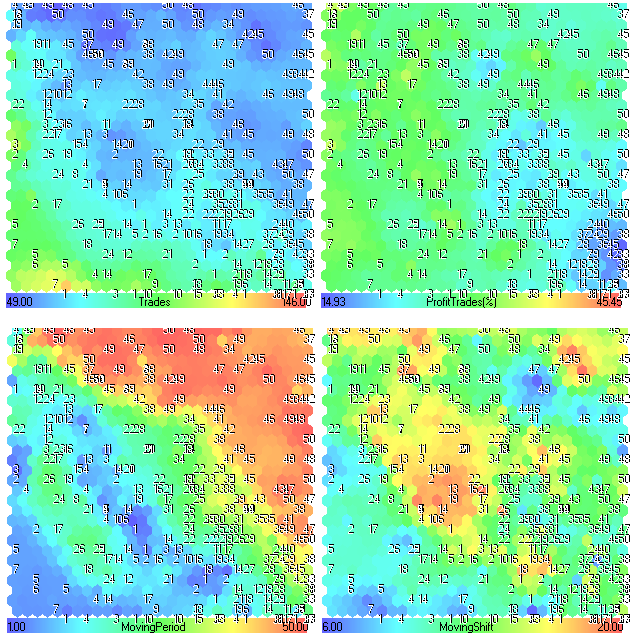
図25. Trades、ProfitTrades(%)、MovingPeriodとMovingShiftパラメーターのコンポーネントプレーン

コンポーネントプレーン分析

一見すると、何も興味深い情報がありません。最初４つのコンポーネントプレーン（Profit、Profit Factor、Recovery Factor、Sharpe Ratio）は、トレードシステムのぱフォーマンスに直接依存するため、類似して見えます。

図24から、上方左の区域は、とても興味深いとわかります。（例えば、最良の結果は、もしMovingPeriodwp45から50で設定すれば取得できます。）

エキスパートアドバイザーは、EURUSDの１時間ごとのタイムフレームにてテストされ、トレンドに基づく戦略などこれらの値を「マーケットトレンド」メモリーとして考えることができます。もし正しければ、2011年度前半のマーケットトレンドメモリーは2日に等しいです。

その他のコンポーネントプレーンを考えてみましょう。

図26. Trades-MovingPeriodのコンポーネントプレーン

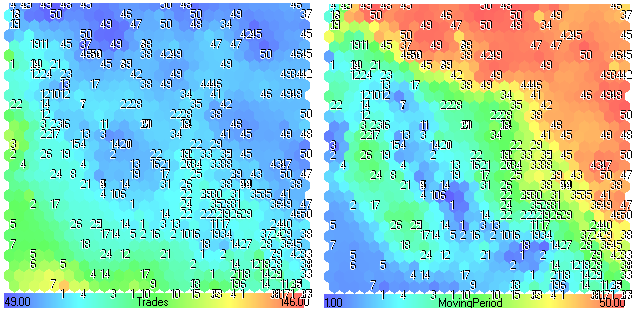
図26. Trades-MovingPeriodのコンポーネントプレーン

図26を見ると、MovingPeriodnoもし移動平均期間が低ければ、多くのクロスオーバーが存在します。

また、トレードコンポーネントプレーンにおいてのこの事実も見ることができます（20以下の数字での緑の区域）

図27Tredes-MovingShiftのコンポーネントプレーン

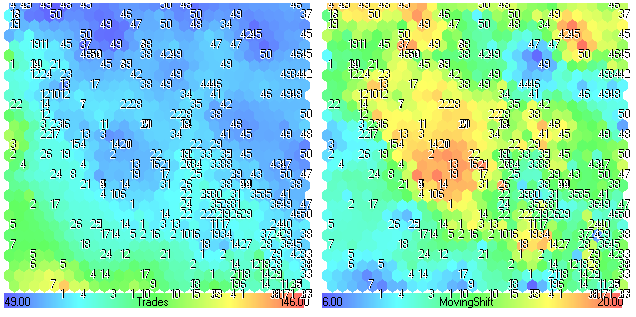
図27. Tredes-MovingShiftのコンポーネントプレーン

（青色区域の）トレード数は、MovingShiftの上昇に伴い、減少します。（yellow-red区域）MOvingShiftのコンポーネントプレーンと図24を比較すると、MovingShiftパラメーターは、このトレード戦略の実行においてそこまで重要ではありません。

利益を生むトレード、ProfitTrades(%)率はMovingPeriodやMovingShiftに直接依存せず、トレードシステムの必須の特徴です。言い換えれば、入力パラメーターの相関性の分析には何も意味がありません。

より複雑なトレード戦略は、同様に分析されます。あなたのトレードシステムの最重要なパラメーターを見つけ、タイトルとして使用する必要があります。


結論

自己組織機能マップの主な利点は、高次元データの二次元離散表示の作成です。類似した特徴を持つデータは、クラスターを形成し、相関関係分析を単純化します。

その詳細や他のアプリケーションについては、Guido DeboeckとTeuvo KohonenのVisual Explorations in Finance: with Self-Organizing Mapsに掲載されています。


アペンディクス

ロシア版の発行後、 SOM_Alex-Sergeev_en.zipのクラスのAlex Sergeevは改定版を提案しました。

変更点：

1. イメージの表示が変更しました: cIntBMP::Show(int aX, int aY, string aBMPFileName, string aObjectName, bool aFromImages=true)
2. イメージつきのフォルダーを開く機能が追加されました:

#import "shell32.dll"
   int ShellExecuteW(int hwnd, string oper, string prog, string param, string dir, int show);
#import

input bool OpenAfterAnaliz=true; // open folder with maps after finish

CSOM クラスの変更点:

  1. CSOM::HideChartメソッドを追加しました - チャートを隠します
  2. m_chart、m_wnd、m_x0、m_y0のクラスメンバーを追加しました。 - (イメージを表示するためのチャート、ウィンドウ、調整など)
    + m_sID - オブジェクト名の接頭辞を追加接頭辞は、ファイル名を使用し、標準として、「SOM」接頭辞が使用されます。
  3. 全てのマップは、 m_sIDの名前のあるフォルダーに保存されます。
  4. bmpファイルはパターンの カラム名がつけられます。
  5. CSOM::ShowBMPメソッドを修正しました。(\Imagesではなく、\Files フォルダーに保存されたマップは、より速く動きます)
  6. CSOM::NetDeinit はCSOM::HideBMPに変更されました。
  7. CSOM::ReadCSVDataメソッドを修正しました。最初の カラムがタイトルを保持します。
  8. CSOM::Train(bool bShowProgress).にて中間マップを示すフラッグを追加しました。
  9. CSOM::Trainの中間マップの表示は、（反復の代わりに）2秒毎に実行され、進行状態はコメントを使用し、チャートに表示されます。
  10. いくつかの変数名が最適され、クラスメソッドがカテゴリーにより呼ばれます。

bmpの描画は、とても遅いプロセスです。必要なければ、毎度描画する必要はありません。

最適化結果のSOMイメージの例はアーカイブにあります。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/283

添付されたファイル |
ZIPをダウンロード
som_alex-sergeev_en.zip (1162.74 KB)
kohonen_maps_mql5_en.zip (58.56 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
購入前に売買ロボットを検証する方法 購入前に売買ロボットを検証する方法
MQL5 マーケットで売買ロボットを買うことは似たような選択肢をしのぐ明らかなメリットがあります。提供される自動化されたシステムを MetaTrader 5 ターミナルで直接徹底的に検証することができるのです。購入前にシステムを完全に把握するため、内蔵ストラテジーテスタで Expert Advisor を不都合なモードで注意して実行することができる／する必要があるのです。
夜間の取引はどれ程信頼性があるか? 夜間の取引はどれ程信頼性があるか?
この記事では、クロスペアの夜間取引の特徴について明らかにしていきたいと思います。どこから利益は生まれ、なぜ深刻な損失が発生することがあるのかを説明していきます。夜間取引の為に開発されたエキスパートアドバイザの例を引用しています。この戦略に基づく取引経験についてお話していきます。
自動売買システム作成にたいする新手法としてのオートマタ準拠プログラミング 自動売買システム作成にたいする新手法としてのオートマタ準拠プログラミング
本稿は MQL4 および MQL5で EA、インディケータ、スクリプトを作成するまったく新しい方向にわれわれを導きます。将来、このプログラミングパラダイムが EAを実装するすべてのトレーダーにとってしだいに基本となり標準となることでしょう。オートマタ準拠プログラミングパラダイムを使用することで MQL5 および MetaTrader 5 の開発者は新しい言語MQL6、そして新しいプラットフォームMetaTrader 6を作成に近づくのです。
取引口座の分析 取引口座の分析
この記事は、MT4での取引履歴を元に取引の分析を行うためのツールについて説明しています。特に、その技術面を分析します。分析後に、取引要因の改善方法をまとめます。分析には、MQLab™ Graphic Reportスクリプトを使用します。