MQL5における行列とベクトル：活性化関数

はじめに

ニューラルネットワークの訓練については、すでに膨大な数の書籍や論文が発表されています。MQL5.comのメンバーも、いくつかの連載記事を含む多くの資料を発表しています。

この記事では、機械学習の一側面である活性化関数についてのみ説明します。その内幕に迫ります。

概要

人工ニューラルネットワークでは、ニューロンの活性化関数は、入力シグナルまたは入力シグナルのセットの値に基づいて出力シグナル値を計算します。活性化関数は、値の集合全体で微分可能でなければなりません。この条件によって、ニューラルネットワークを訓練する際に誤差逆伝播法が可能になります。誤差を逆伝播するには、活性化関数の勾配を計算しなければなりません。これは、入力信号ベクトルの各値に対する活性化関数の偏導関数のベクトルです。非線形活性化関数の方が訓練に適していると考えられています。完全な線形ReLU関数は、多くのモデルでその有効性を示してきました。

イラスト

活性化関数とその導関数のグラフは、-5から5まで単調に増加する順序で用意されています。価格チャート上に関数グラフを表示するスクリプトも開発しました。Page Downキーを押すと、保存画像名を指定するためのファイルオープンダイアログが表示されます。

ESCキーはスクリプトを終了させます。スクリプト自体は以下に添付されています。同様のスクリプトは、「MQL5行列を使用した誤差逆伝播法によるニューラルネットワーク」稿の著者によって書かれました。ここでは彼のアイデアを使って、対応する活性化関数の導関数の値のグラフを、活性化関数そのもののグラフと一緒に表示しています。

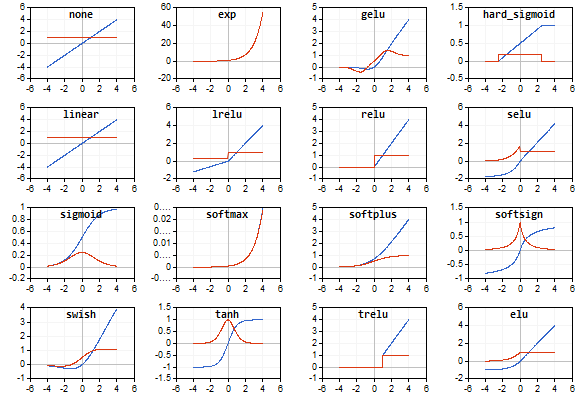
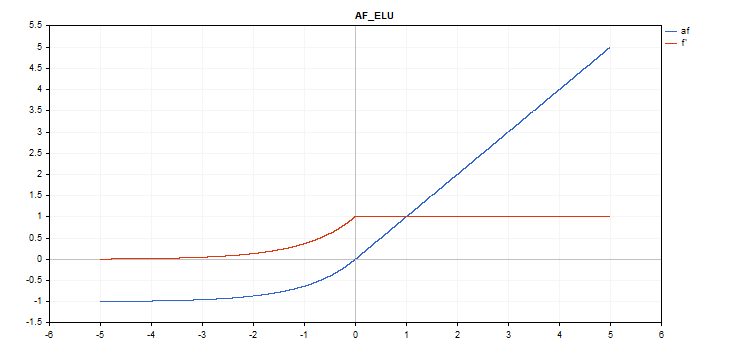
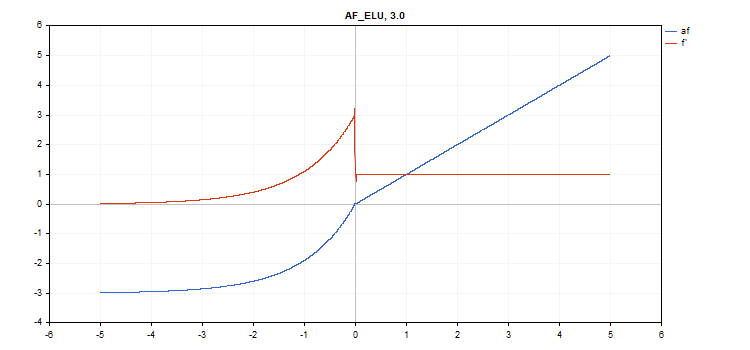
活性化関数は青で表示され、関数の導関数は赤で表示されています。

ELU（Exponential Linear Unit、指数線形ユニット）活性化関数

関数計算

   if(x >= 0)
      f = x;
   else
      f = alpha*(exp(x) - 1);

導関数計算

   if(x >= 0)
      d = 1;
   else
      d = alpha*exp(x);

この関数はさらに「alpha」パラメータを取ります。指定がない場合、デフォルト値は1です。

   vector_a.Activation(vector_c,AF_ELU);      // call with the default parameter

   vector_a.Activation(vector_c,AF_ELU,3.0);  // call with alpha=3.0

指数活性化関数

関数計算

   f = exp(x);

同じexp関数がexp関数の導関数として機能します。

計算式を見ればわかるように、指数活性化関数には追加のパラメーターはありません。

vector_a.Activation(vector_c,AF_EXP);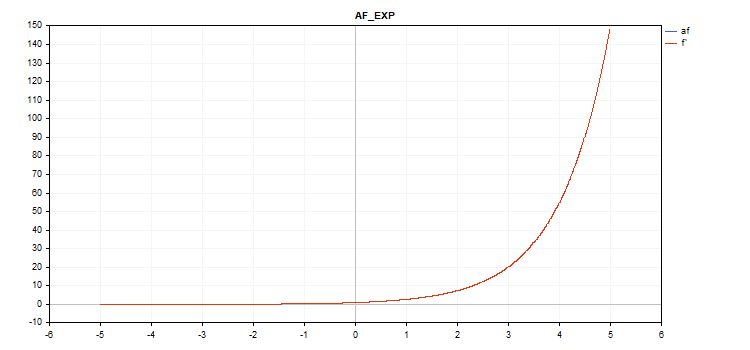

GELU（Gaussian Error Linear Unit、ガウス誤差線形ユニット）活性化関数

関数計算

   f = 0.5*x*(1 + tanh(sqrt(M_2_PI)*(x+0.044715*pow(x,3)));

導関数計算

   double x_3 = pow(x,3);
   double tmp = cosh(0.0356074*x + 0.797885*x);
   d = 0.5*tanh(0.0356774*x_3 + 0.398942*x)+(0.535161*x_3 + 0.398942*x)/(tmp*tmp) + 0.5;

追加パラメータ：なし

vector_a.Activation(vector_c,AF_GELU);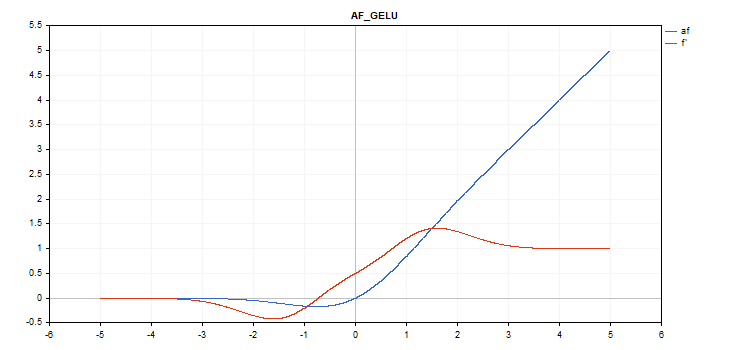

Hard Sigmoid（ハードシグモイド）活性化関数

関数計算

   if(x < -2.5)
      f = 0;
   else
     {
      if(x > 2.5)
         f = 1;
      else
         f = 0.2*x + 0.5;
     }

導関数計算

   if(x < -2.5)
      d = 0;
   else
     {
      if(x > 2.5)
         d = 0;
      else
         d = 0.2;
     }

追加パラメータ：なし

vector_a.Activation(vector_c,AF_HARD_SIGMOID);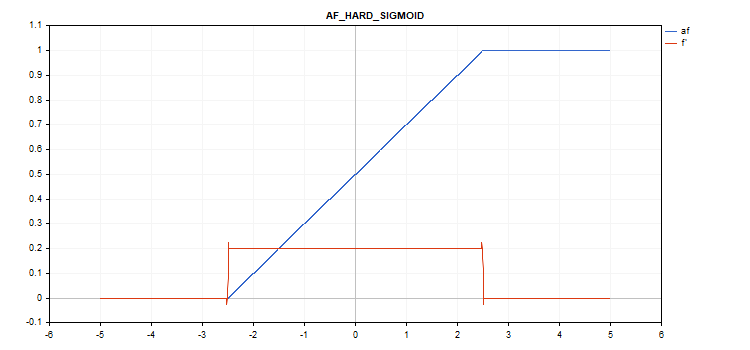

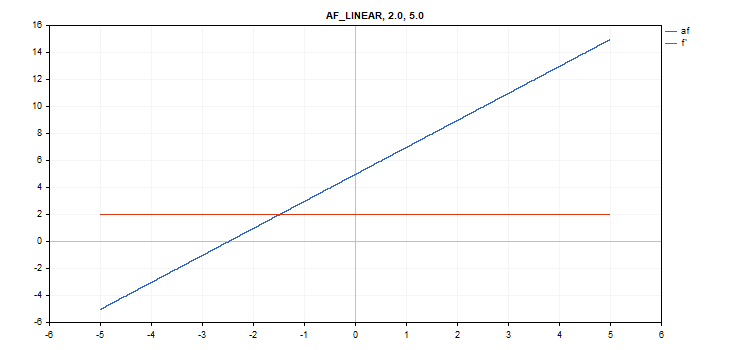
線形活性化関数

関数計算

   f = alpha*x + beta

導関数計算

   d = alpha

追加パラメータ：alpha = 1.0およびbeta = 0.0

vector_a.Activation(vector_c,AF_LINEAR);         // call with default parameters

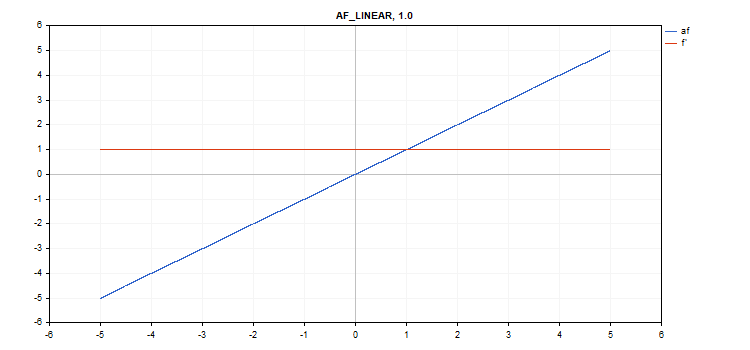
vector_a.Activation(vector_c,AF_LINEAR,2.0,5.0);  // call with alpha=2.0 and beta=5.0

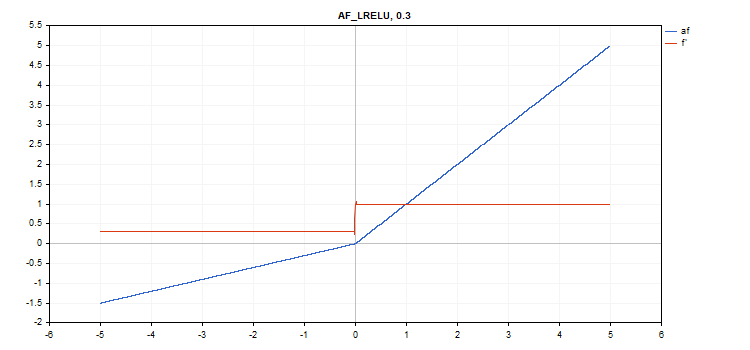
LReLU(Leaky Rectified Linear Unit)活性化関数

関数計算

   if(x >= 0)
      f = x;
   else
      f = alpha * x;

導関数計算

   if(x >= 0)
      d = 1;
   else
      d = alpha;

この関数はさらに「alpha」パラメータを取ります。指定がない場合、デフォルト値は0. 3です。

   vector_a.Activation(vector_c,AF_LRELU);      // call with the default parameter

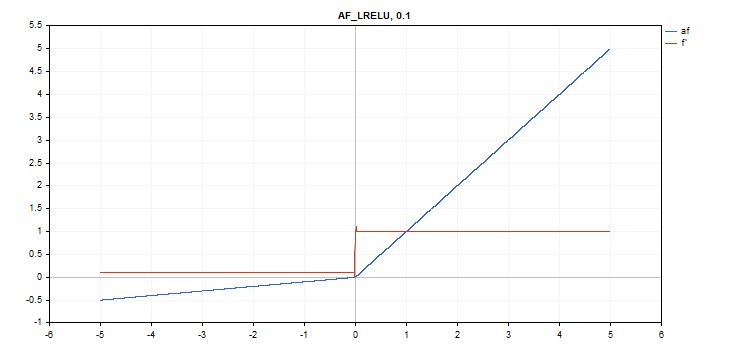
vector_a.Activation(vector_c,AF_LRELU,0.1);  // call with alpha=0.1

ReLU（Rectified Linear Unit、整流線形ユニット）活性化関数

関数計算

   if(alpha==0)
     {
      if(x > 0)
         f = x;
      else
         f = 0;
     }
   else
     {
      if(x >= max_value)
         f = x;
      else
         f = alpha * (x - treshold);
     }

導関数計算

   if(alpha==0)
     {
      if(x > 0)
         d = 1;
      else
         d = 0;
     }
   else
     {
      if(x >= max_value)
         d = 1;
      else
         d = alpha;
     }

追加パラメータ：alpha=0、max_value=0、treshold=0。

vector_a.Activation(vector_c,AF_RELU);         // call with default parameters

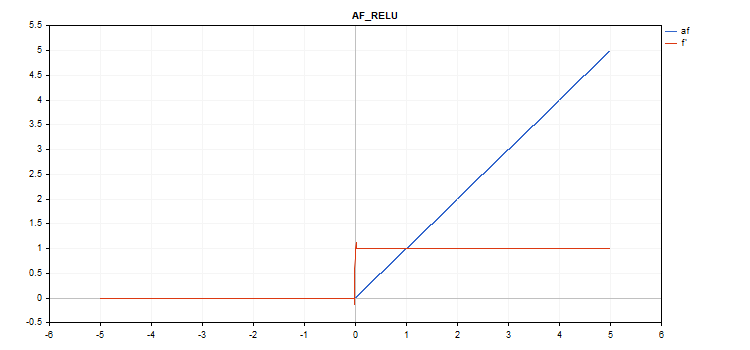
vector_a.Activation(vector_c,AF_RELU,2.0,0.5);      // call with alpha=2.0 and max_value=0.5

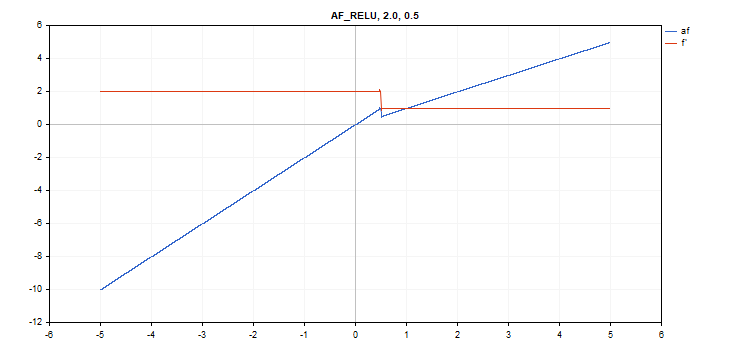
vector_a.Activation(vector_c,AF_RELU,2.0,0.5,1.0);  // call with alpha=2.0, max_value=0.5 and treshold=1.0

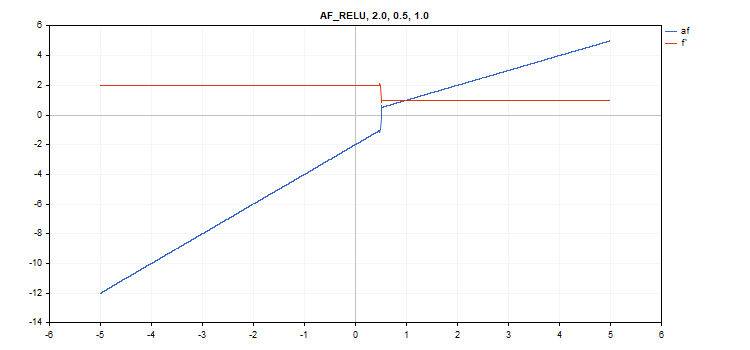
SELU（Scaled Exponential Linear Unit、尺度化指数線形単位）活性化関数

関数計算

   if(x >= 0)
      f = scale * x;
   else
      f = scale * alpha * (exp(x) - 1);

where scale = 1.05070098, alpha = 1.67326324

導関数計算

   if(x >= 0)
      d = scale;
   else
      d = scale * alpha * exp(x);

追加パラメータ：なし

vector_a.Activation(vector_c,AF_SELU);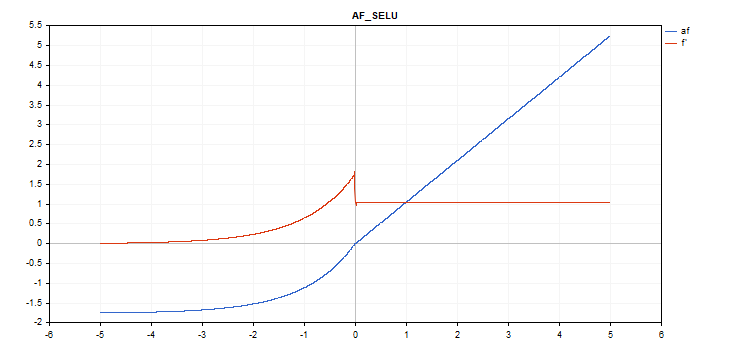

Sigmoid（シグモイド）活性化関数

関数計算

   f = 1 / (1 + exp(-x));

導関数計算

   d = exp(x) / pow(exp(x) + 1, 2);

追加パラメータ：なし

vector_a.Activation(vector_c,AF_SIGMOID);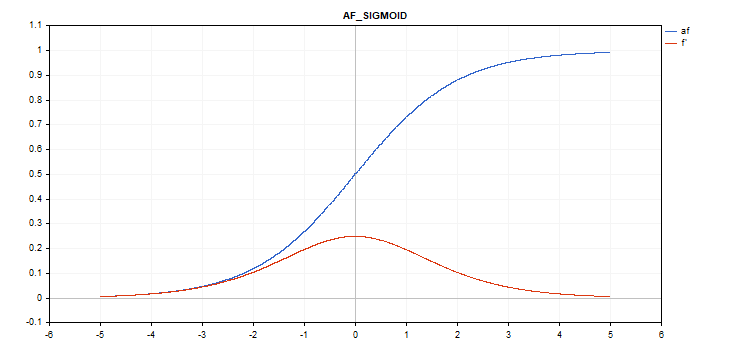

Softplus（ソフトプラス）活性化関数

関数計算

   f = log(exp(x) + 1);

導関数計算

   d = exp(x) / (exp(x) + 1);

追加パラメータ：なし

vector_a.Activation(vector_c,AF_SOFTPLUS);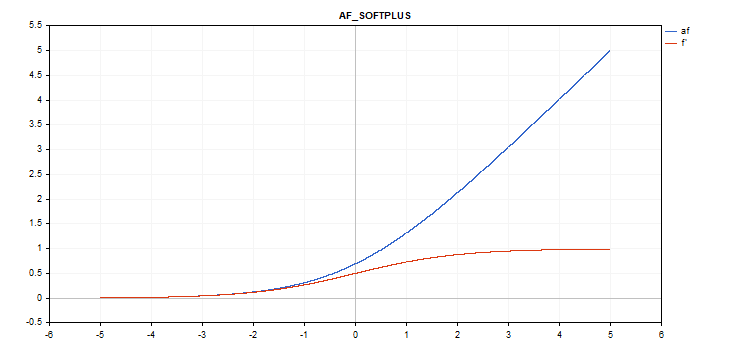

Softsign（ソフトサイン）活性化関数

関数計算

   f = x / (|x| + 1)

導関数計算

   d = 1 / (|x| + 1)^2

追加パラメータ：なし

vector_a.Activation(vector_c,AF_SOFTSIGN);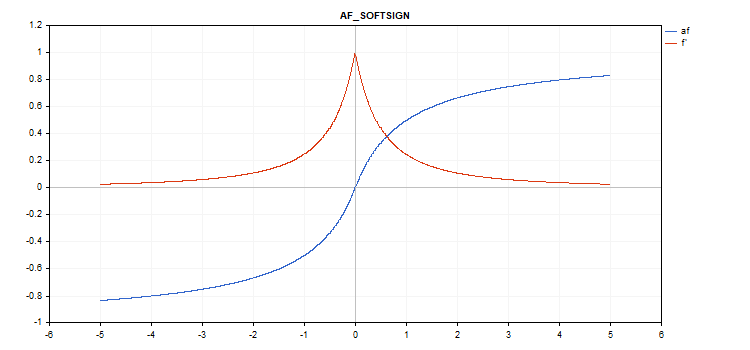

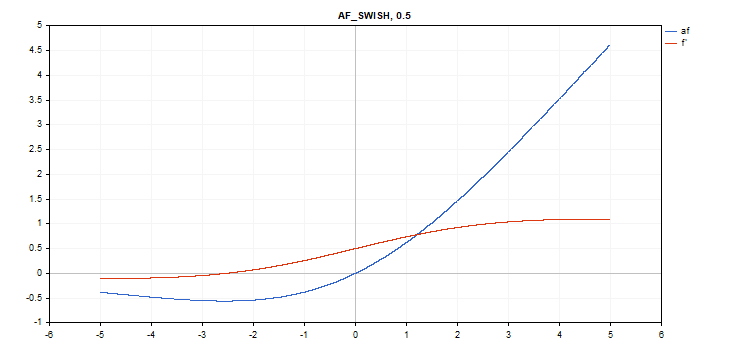
Swish（スウィッシュ）活性化関数

関数計算

   f = x / (1 + exp(-x*beta));

導関数計算

   double tmp = exp(beta*x);
   d = tmp*(beta*x + tmp + 1) / pow(tmp+1, 2);

追加パラメータ：beta = 1

vector_a.Activation(vector_c,AF_SWISH);         // call with the default parameter

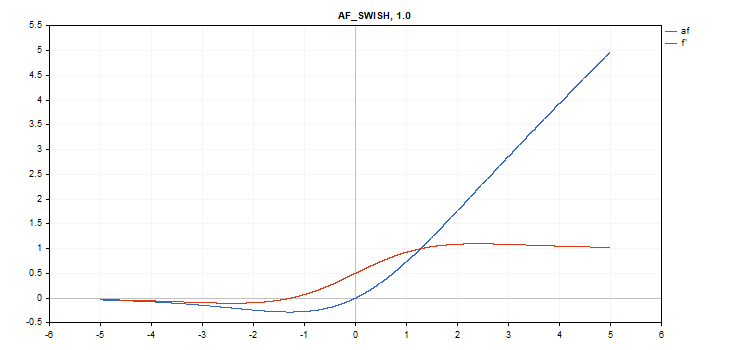
vector_a.Activation(vector_c,AF_SWISH,2.0);     // call with beta = 2.0

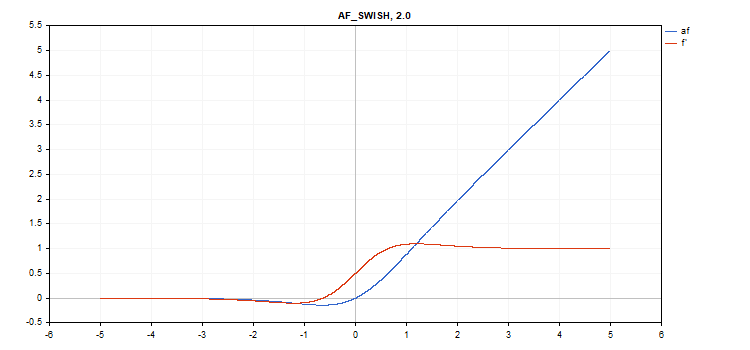
vector_a.Activation(vector_c,AF_SWISH,0.5);   // call with beta=0.5

TanH（双曲線タンジェント）活性化関数

関数計算

   f = tanh(x);

導関数計算

   d = 1 / pow(cosh(x),2);

追加パラメータ：なし

vector_a.Activation(vector_c,AF_TANH);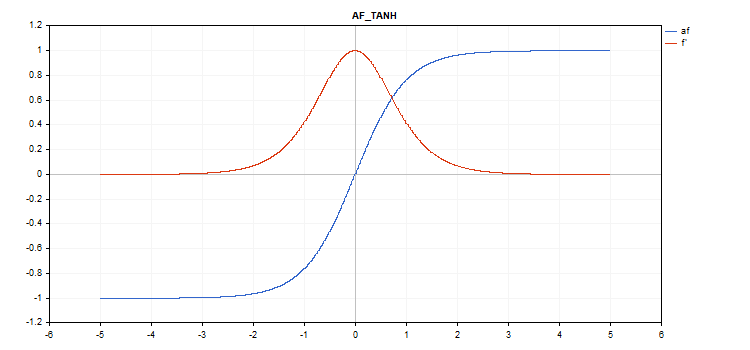

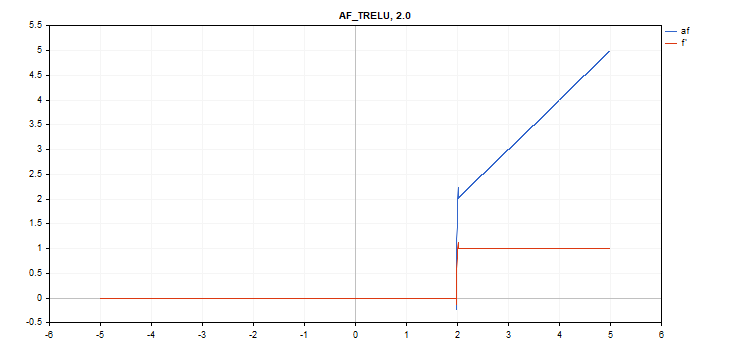
TReLU（Thresholded Rectifiedl Linear Unit、閾値整流線形ユニット）活性化関数

関数計算

   if(x > theta)
      f = x;
   else
      f = 0;

導関数計算

   if(x > theta)
      d = 1;
   else
      d = 0;

追加パラメータ：theta = 1

vector_a.Activation(vector_c,AF_TRELU);         // call with default parameter

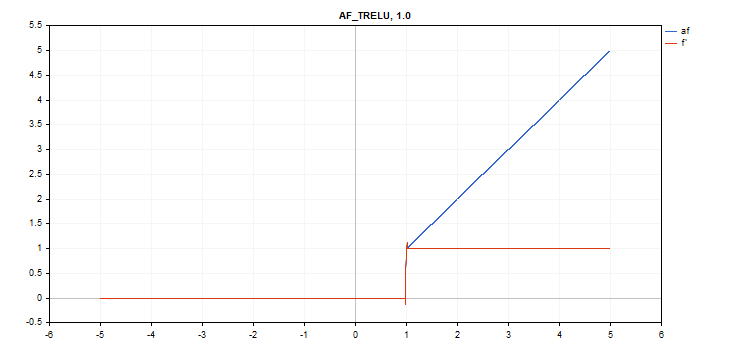
vector_a.Activation(vector_c,AF_TRELU,0.0);     // call with theta = 0.0

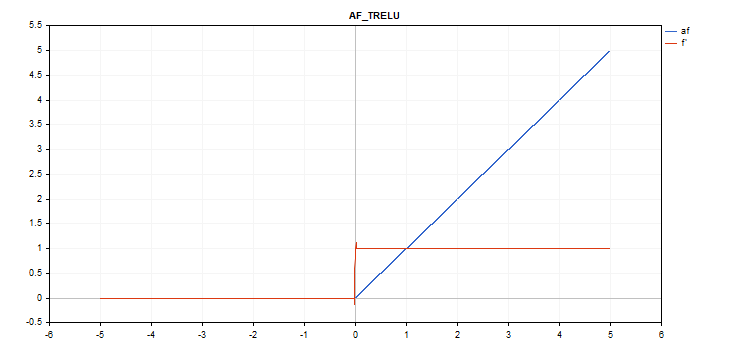
vector_a.Activation(vector_c,AF_TRELU,2.0);      // call with theta = 2.0

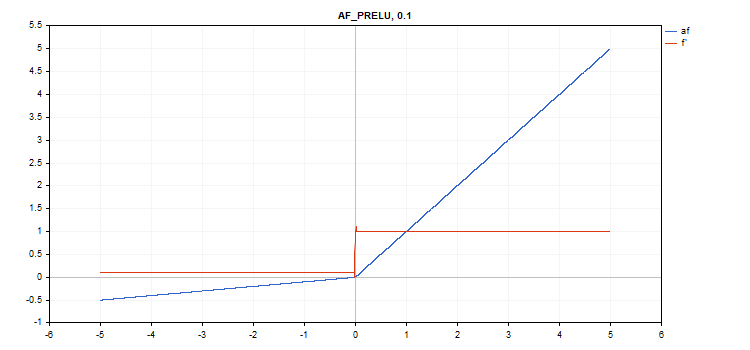
PReLU（Parametric Rectifiedl Linear Unit、パラメトリック整流線形ユニット）活性化関数

関数計算

   if(x[i] >= 0)
      f[i] = x[i];
   else
      f[i] = alpha[i]*x[i];

導関数計算

   if(x[i] >= 0)
      d[i] = 1;
   else
      d[i] = alpha[i];

追加パラメータ：alpha係数ベクトル

vector alpha=vector::Full(vector_a.Size(),0.1);
vector_a.Activation(vector_c,AF_PRELU,alpha);

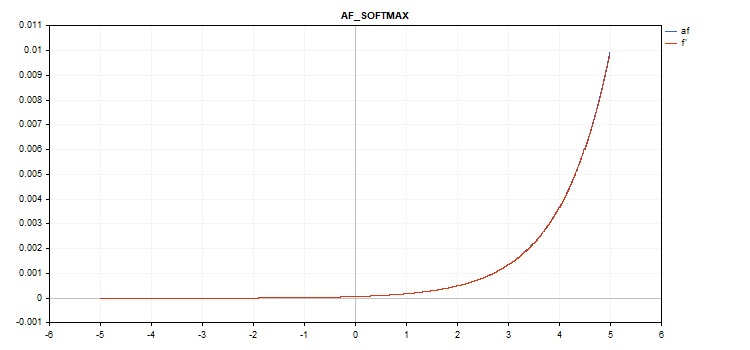
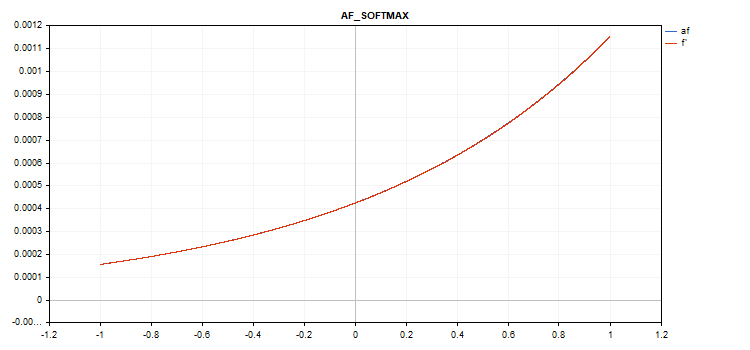
特別なソフトマックス関数

ソフトマックス活性化関数の計算結果は、特定の値だけでなく、すべてのベクトル値に依存します。

   sum_exp = Sum(exp(vector_a))
   f = exp(x) / sum_exp

導関数計算

   d = f*(1 - f)

したがって、すべての活性化されたベクトル値の合計は1になる。したがって、ソフトマックス活性化関数は、分類モデルの最後の層によく使われる。

ベクトル活性化関数のグラフ（値は-5～5）

-1から1までの値を持つベクトル活性化関数グラフ

活性化関数がない場合(AF_NONE)

活性化関数がない場合は、入力ベクトルの値がそのまま出力ベクトルに変換されます。実際、これはα=1、β=0の線形活性化関数です。

結論

以下に添付したActivationFunction.mqhにある活性化関数とその派生関数のソースコードをご自由にご覧ください。