Rを使って高速化したMQL5の統計分布
Rで実装されている基本的な統計分布を操作する関数を考えてみましょう。
コーシー、ワイブル、正規、対数正規、ロジスティック、指数、均一、ガンマ分布、カイ 2 乗、中央と非心 beta スチューデントの t 分布、F 分布フィッシャーの離散二項および否定的な二項分布、幾何学、幾何とポアソン分布。さらに、実際の分布の適合性の程度を評価できるように、分布の理論的モーメントを計算するための関数があります。
Rからの多数の数学関数によって補われた MQL5 を標準ライブラリは、Rの初期バージョンと比較して、3 〜 7 倍の操作速度の増加を実現しています。同時にある関数の実装でエラーが発見されています。
コンテンツ
- 配列の要素の統計的特性を計算するための関数
- 統計分布を操作するための関数
2.1. 正規分布
- 2.1.1. MathProbabilityDensityNormal()
- 2.1.2. MathCumulativeDistributionNormal()
- 2.1.3. MathQuantileNormal()
- 2.1.4. MathRandomNormal()
- 2.1.5. MathMomentsNormal()
2.2. 対数正規分布
- 2.2.1. MathProbabilityDensityLognormal()
- 2.2.2. MathCumulativeDistributionLognormal()
- 2.2.3. MathQuantileLognormal()
- 2.2.4. MathRandomLognormal()
- 2.2.5. MathMomentsLognormal()
2.3. ベータ分布
- 2.3.1. MathProbabilityDensityBeta()
- 2.3.2. MathCumulativeDistributionBeta()
- 2.3.3. MathQuantileBeta()
- 2.3.4. MathRandomBeta()
- 2.3.5. MathMomentsBeta()
2.4. 非心ベータ分布
- 2.4.1. MathProbabilityDensityNoncentralBeta()
- 2.4.2. MathCumulativeDistributionNoncentralBeta()
- 2.4.3. MathQuantileNoncentralBeta()
- 2.4.4. MathRandomNoncentralBeta()
- 2.4.5. MathMomentsNoncentralBeta()
2.5. ガンマ分布
- 2.5.1. MathProbabilityDensityGamma()
- 2.5.2. MathCumulativeDistributionGamma()
- 2.5.3. MathQuantileGamma()
- 2.5.4. MathRandomGamma()
- 2.5.5. MathMomentsGamma()
2.6. カイ 2 乗分布
- 2.6.1. MathProbabilityDensityChiSquare()
- 2.6.2. MathCumulativeDistributionChiSquare()
- 2.6.3. MathQuantileChiSquare()
- 2.6.4. MathRandomChiSquare()
- 2.6.5. MathMomentsChiSquare()
2.7. 非心カイ二乗分布
- 2.7.1. MathProbabilityDensityNoncentralChiSquare()
- 2.7.2. MathCumulativeDistributionNoncentralChiSquare()
- 2.7.3. MathQuantileNoncentralChiSquare()
- 2.7.4. MathRandomNoncentralChiSquare()
- 2.7.5. MathMomentsNoncentralChiSquare()
2.8. 指数分布- 2.8.1. MathProbabilityDensityExponential()
- 2.8.2. MathCumulativeDistributionExponential()
- 2.8.3. MathQuantileExponential()
- 2.8.4. MathRandomExponential()
- 2.8.5. MathMomentsExponential()
2.9. F分布- 2.9.1. MathProbabilityDensityF()
- 2.9.2. MathCumulativeDistributionF()
- 2.9.3. MathQuantileF()
- 2.9.4. MathRandomF()
- 2.9.5. MathMomentsF()
2.10. 非心 F 分布
- 2.10.1. MathProbabilityDensityNoncentralF()
- 2.10.2. MathCumulativeDistributionNoncentralF()
- 2.10.3. MathQuantileNoncentralF()
- 2.10.4. MathRandomNoncentralF()
- 2.10.5. MathMomentsNoncentralF()
2.11. t分布
- 2.11.1. MathProbabilityDensityT()
- 2.11.2. MathCumulativeDistributionT()
- 2.11.3. MathQuantileT()
- 2.11.4. MathRandomT()
- 2.11.5. MathMomentsT()
2.12非心 t 分布
- 2.12.1. MathProbabilityDensityNoncentralT()
- 2.12.2. MathCumulativeDistributionNoncentralT()
- 2.12.3. MathQuantileNoncentralT()
- 2.12.4. MathRandomNoncentralT()
- 2.12.5. MathMomentsNoncentralT()
2.13. ロジスティック分布
- 2.13.1. MathProbabilityDensityLogistic()
- 2.13.2. MathCumulativeDistributionLogistic()
- 2.13.3. MathQuantileLogistic()
- 2.13.4. MathRandomLogistic()
- 2.13.5. MathMomentsLogistic()
2.14. コーシー分布
- 2.14.1. MathProbabilityDensityCauchy()
- 2.14.2. MathCumulativeDistributionCauchy()
- 2.14.3. MathQuantileCauchy()
- 2.14.4. MathRandomCauchy()
- 2.14.5. MathMomentsCauchy()
2.15. 一様分布
- 2.15.1. MathProbabilityDensityUniform()
- 2.15.2. MathCumulativeDistributionUniform()
- 2.15.3. MathQuantileUniform()
- 2.15.4. MathRandomUniform()
- 2.15.5. MathMomentsUniform()
2.16. ワイブル分布
- 2.16.1. MathProbabilityDensityWeibull()
- 2.16.2. MathCumulativeDistributionWeibull()
- 2.16.3. MathQuantileWeibull()
- 2.16.4. MathRandomWeibull()
- 2.16.5. MathMomentsWeibull()
2.17. 二項分布
- 2.17.1. MathProbabilityDensityBinomial()
- 2.17.2. MathCumulativeDistributionBinomial()
- 2.17.3. MathQuantileBinomial()
- 2.17.4. MathRandomBinomial()
- 2.17.5. MathMomentsBinomial()
2.18. 負の二項分布
- 2.18.1. MathProbabilityDensityNegativeBinomial()
- 2.18.2. MathCumulativeDistributionNegativeBinomial()
- 2.18.3. MathQuantileNegativeBinomial()
- 2.18.4. MathRandomNegativeBinomial()
- 2.18.5. MathMomentsNegativeBinomial()
2.19. 幾何分布
- 2.19.1. MathProbabilityDensityGeometric()
- 2.19.2. MathCumulativeDistributionGeometric()
- 2.19.3. MathQuantileGeometric()
- 2.19.4. MathRandomGeometric()
- 2.19.5. MathMomentsGeometric()
2.20. 超幾何分布
- 2.20.1. MathProbabilityDensityHypergeometric()
- 2.20.2. MathCumulativeDistributionHypergeometric()
- 2.20.3. MathQuantileHypergeometric()
- 2.20.4. MathRandomHypergeometric()
- 2.20.5. MathMomentsHypergeometric()
2.21. ポアソン分布
- 2.21.1. MathProbabilityDensityPoisson()
- 2.21.2. MathCumulativeDistributionPoisson()
- 2.21.3. MathQuantilePoisson()
- 2.21.4. MathRandomPoisson()
- 2.21.5. MathMomentsPoisson()
- R の統計関数への対応表
- 関数の使用例
- 計算速度の比較
- R で検出された計算エラー
- レファレンス
イントロダクション
R言語は、統計処理のツールであり、データの分析ソフトのひとつです。
複数の統計的な分布のサポートのおかげで解析と各種データの処理が可能です。確率論と数理統計学の装置を使用して、金融市場データの取引戦略を作成する新しい機会を得られます。統計ライブラリと、これらすべての関数は、MQL5 で利用できます。
統計ライブラリには統計分布を操作するための関数と同様に、データの統計的特性を計算するための関数が含まれます。
この記事では、ライブラリとその活用の例の主な関数を扱います。
1. 配列の要素の統計的特性を計算するための関数
このグループの関数には、配列要素の標準的な特性 (平均、分散、歪み度、尖度、中央値、平均平方根と標準偏差) を計算します。
1.1. MathMean
この関数は、配列の要素の平均 (最初モーメント) を計算します。エラーの場合は、 NaN (非数) を返します。Rでのmean()のアナログ
double MathMean( const double &array[] //[in]データを持つ配列 );
1.2. MathVariance
この関数は、配列要素の差異 (2 次モーメント) を計算します。エラーの場合は、 NaNが返されます。Rでのvar()のアナログ
double MathVariance( const double &array[] //データの配列 );
1.3. MathSkewness
この関数は、配列要素の歪み (3 モーメント) を計算します。エラーの場合は、 NaNが返されます。Rでの (e1071 ライブラリ) skewness()のアナログ。
double MathSkewness( const double &array[] //データの配列 );
1.4. MathKurtosis
この関数は、配列の要素の尖度 (4 モーメント) を計算します。エラーの場合は、 NaNが返されます。R (e1071 ライブラリ) でkurtosis()のアナログ。
double MathKurtosis( const double &array[] //データの配列 );
1.5. MathMoments
この関数は、配列要素の最初 4 のモーメント (平均、分散、歪み度、尖度) を計算します。Returns true if the moments have been calculated successfully, otherwise false.
bool MathMoments( const double &array[], //[in] データを持つ配列 double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 const int start=0, //[in] 計算の初期インデックス const int count=WHOLE_ARRAY //[in] 計算の要素の数 );
1.6. MathMedian
この関数は、配列の要素の平均値を計算します。エラーの場合は、 NaNが返されます。Rでのmedian()のアナログ
double MathMedian( double &array[] //[in]データを持つ配列 );
1.7. MathStandardDeviation
関数は、配列の要素の標準偏差を計算します。エラーの場合は、 NaNが返されます。Rでのsd()のアナログ
double MathStandardDeviation( const double &array[] //[in]データを持つ配列 );
1.8. MathAverageDeviation
この関数は、配列の要素の平均絶対偏差を計算します。エラーの場合は、 NaNが返されます。Rでのaad()のアナログ
double MathAverageDeviation( const double &array[] //[in]データを持つ配列 );
尖度を計算するすべての関数を使用して、正規分布の周りの余分な尖度 (余分な尖度 = 尖度 3)、すなわち正規分布の尖度超過はゼロです。
予想される値の分布のピークが鋭い場合、正で、フラットな場合、負です。
2. 統計分布
統計ライブラリには統計分布を操作するための 5 つの関数が含まれています。
- 確率密度 (MathProbabilityDensityX() 関数) の計算
- 確率の計算 (MathCumulativeDistributionX() 関数);
確率分布関数の範囲内の確率変数に等しい (-inf; x]). - 分布の分位数 (MathQuantileX() 関数) の計算
分位数の範囲内のランダムな値に対応する分布の x (-inf、x] 与えられた分布パラメーターの指定した確率
。 - 指定した分布 (MathRandomX() 関数) 乱数を生成します。
- (MathMomentsX() 関数) 分布の理論的モーメントの計算
2.1. 正規分布
2.1.1. MathProbabilityDensityNormal
この関数は、ランダムな変数x の mu および sigma のパラメーターと正規分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。double MathProbabilityDensityNormal( const double x, //[in] ランダム変数の値 const double mu, //分布の平均値 (期待値) パラメーター const double sigma, //シグマ (二乗) 分布のパラメーター constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます int &error_code //[out]エラー コードの変数 );
この関数は、ランダムな変数x の mu および sigma のパラメーターと正規分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNormal( const double x, //[in] ランダム変数の値 const double mu, //分布の平均値 (期待値) パラメーター const double sigma, //シグマ (二乗) 分布のパラメーター int &error_code // [out] エラー コードの変数 );
この関数には、mu および sigma の確率変数 x[] 配列パラメーターの正規分布の確率密度関数の値が計算されます。エラーの場合falseを返します。Rでのdnorm()のアナログ
bool MathProbabilityDensityNormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, //分布の平均値 (期待値) パラメーター const double sigma, //シグマ (二乗) 分布のパラメーター const bool log_mode, //[in] log_mode = true の場合、確率密度の自然対数の計算 double &result[] // [out] 確率密度関数の値の配列 );
この関数には、mu および sigma の確率変数 x[] 配列パラメーターの正規分布の確率密度関数の値が計算されます。エラーの場合falseを返します。
bool MathProbabilityDensityNormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, //分布の平均値 (期待値) パラメーター const double sigma, //シグマ (二乗) 分布のパラメーター double &result[] // [out] 確率密度関数の値の配列 );
2.1.2. MathCumulativeDistributionNormal
この関数は、ランダムな変数 x の mu および sigma のパラメーターを持つ正規分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNormal( const double x, //[in] ランダム変数の値 const double mu, // [in] 予期される値 const double sigma, //[in] 二乗平均平方根の偏差 const bool tail, //[in] ランダムな変数が x の確率を計算し、true の場合、フラグの計算 const bool log_mode, // [in] log_mode = true の場合、確率の自然対数の計算 int &error_code // [out] エラー コードの変数 );
この関数は、ランダムな変数 x の mu および sigma のパラメーターを持つ正規分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNormal( const double x, //[in] ランダム変数の値 const double mu, // [in] 予期される値 const double sigma, //[in] 二乗平均平方根の偏差 int &error_code // [out] エラー コードの変数 );この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つ正規分布関数の値を計算します。エラーの場合はfalseを返します。Rでのpnorm()のアナログ
bool MathCumulativeDistributionNormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in] 予期される値 const double sigma, //[in] 二乗平均平方根の偏差 const bool tail, //[in] ランダムな変数が x の確率を計算し、true の場合、フラグの計算 const bool log_mode, // [in] log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値の配列 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つ正規分布関数の値を計算します。エラーの場合はfalseを返します。
bool MathCumulativeDistributionNormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in] 予期される値 const double sigma, //[in] 二乗平均平方根の偏差 double &result[] //[out]確率関数の値の配列 );
2.1.3. MathQuantileNormal
指定された確率関数は mu および sigma パラメーターを持つ逆正規分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNormal( const double probability, // [in] 確率変数の確率値 const double mu, // [in] 期待値 const double sigma, // [in] 二乗平均平方根の偏差 const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code // [out] エラー コードの変数 );
指定された確率関数は mu および sigma パラメーターを持つ逆正規分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNormal( const double probability, // [in] 確率変数の確率値 const double mu, // [in] 期待値 const double sigma, // [in] 二乗平均平方根の偏差 int &error_code // [out] エラー コードの変数 );指定された '確率' 配列関数確率値の mu および sigma のパラメーターを持つ逆正規分布関数の値を計算します。エラーの場合falseを返します。Rでのqnorm()のアナログ
bool MathQuantileNormal( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double mu, // [in] 期待値 const double sigma, // [in] 二乗平均平方根の偏差 const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数確率値の mu および sigma のパラメーターを持つ逆正規分布関数の値を計算します。エラーの場合はfalseを返します。
bool MathQuantileNormal( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double mu, // [in] 期待値 const double sigma, // [in] 平均平方根の偏差 double &result[] // [out] 分位数の値を持つ配列 );
2.1.4. MathRandomNormal
この関数は、mu および sigma パラメーターを持つ普通のルールに従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomNormal( const double mu, // [in] 予期される値 const double sigma, // [in] 二乗平均平方根の偏差 int &error_code // [out] エラー コードの変数 );
この関数は、mu および sigma パラメーターを持つ普通のルールに従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrnorm()のアナログ
boolMathRandomNormal( const double mu, // [in] 予期される値 const double sigma, // [in] 二乗平均平方根の偏差 const int data_count, //[in] 必要なデータの量 double &result[] // [out] 疑似変数の値を持つ配列 );
2.1.5. MathMomentsNormal
この関数は、正規分布の最初の4つのモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsNormal( const double mu, // [in] 予期される値 const double sigma, // [in] 二乗平均平方根の偏差 double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code // [out] エラー コードの変数 );
2.2. 対数正規分布
2.2.1. MathProbabilityDensityLognormal
この関数は、ランダムな変数 x の mu および sigma のパラメーターの対数正規分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityLognormal( const double x, //[in] ランダム変数の値 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, //[in] 二乗平均平方根の偏差の対数 (ログ標準偏差) constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます int &error_code // [out] エラー コードの変数 );
この関数は、ランダムな変数 x の mu および sigma のパラメーターの対数正規分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityLognormal( const double x, //[in] ランダム変数の値 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, //[in] 二乗平均平方根の偏差の対数 (ログ標準偏差) int &error_code // [out] エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つ対数正規分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。Rでのdlnorm()のアナログ
bool MathProbabilityDensityLognormal( const double &x[], // [in] 確率変数の値を持つ配列 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, //[in] 二乗平均平方根の偏差の対数 (ログ標準偏差) const bool log_mode, //[in] log_mode = true の場合、確率密度の自然対数の計算 double &result[] // [out] 確率密度関数の値の配列 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つ対数正規分布の確率密度関数の値を計算します。エラーの場合falseを返します。
bool MathProbabilityDensityLognormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, //[in] 二乗平均平方根の偏差の対数 (ログ標準偏差) double &result[] // [out] 確率密度関数の値の配列 );
2.2.2. MathCumulativeDistributionLognormal
この関数は、ランダムな変数 x の mu および sigma のパラメーターを持つ対数正規分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionLognormal( const double x, //[in] ランダム変数の値 const double mu, // [in]期待値 (平均ログ) の対数 const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) const bool tail, //[in] true の場合、ランダムな変数が x の確率を計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 int &error_code // [out] エラー コードの変数 );
この関数は、ランダムな変数 x の mu および sigma のパラメーターを持つ対数正規分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionLognormal( const double x, //[in] ランダム変数の値 const double mu, // [in]期待値 (平均ログ) の対数 const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) int &error_code // [out] エラー コードの変数 );
この関数は、mu および sigma の確率変数 x[] 配列パラメーターを対数正規分布関数の値を計算します。エラーの場合falseを返します。Rでのplnorm()のアナログ
bool MathCumulativeDistributionLognormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in]期待値 (平均ログ) の対数 const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) const bool tail, //[in] true の場合、ランダムな変数が x の確率を計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値の配列 );
この関数は、mu および sigma の確率変数 x[] 配列パラメーターを対数正規分布関数の値を計算します。エラーの場合はfalseを返します。
bool MathCumulativeDistributionLognormal( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in]期待値 (平均ログ) の対数 const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) double &result[] //[out]確率関数の値の配列 );
2.2.3. MathQuantileLognormal
この関数は、指定された確率の mu および sigma のパラメーターを持つ対数正規分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileLognormal( const double probability, //[in] 確率変数の発生の確率値 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code // [out] エラー コードの変数 );
この関数は、指定された確率の mu および sigma のパラメーターを持つ対数正規分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileLognormal( const double probability, //[in] 確率変数の発生の確率値 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) int &error_code // [out] エラー コードの変数 );
指定された '確率' 配列関数確率値の mu および sigma のパラメーターの対数正規分布の逆関数の値を計算します。エラーの場合falseを返します。Rでのqlnorm()のアナログ
bool MathQuantileLognormal( const double &probability[], // [in] ランダム変数の確率値を持つ配列 const double mu, // [in] 期待値 (ログの平均の対数) const double sigma, //平均平方根の偏差の対数の (ログ標準偏差) const bool tail, // [in] 1.0 確率の計算を実行し、false の場合は、フラグの計算 const bool tail, //[in] 計算が実行された場合、フラグの計算 double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数確率値の mu および sigma のパラメーターの対数正規分布の逆関数の値を計算します。エラーの場合falseを返します。
bool MathQuantileLognormal( const double &probability[], // [in] ランダム変数の確率値を持つ配列 const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, // [in] Logarithm of the 二乗平均平方根の偏差 (log standard deviation) double &result[] // [out] 分位数の値を持つ配列 );
2.2.4. MathRandomLognormal
この関数は、mu シグマ パラメーターを使用して対数正規のルールに従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomLognormal( const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, // [in] 対数平均平方根の偏差 (ログ標準偏差) int &error_code // [out] エラー コードの変数 );
この関数は、mu および sigma パラメーターを持つログ通常ルールに従って分散擬似変数を生成します。エラーの場合はfalseを返します。Rでのrlnorm()のアナログ
bool MathRandomLognormal( const double mu, // [in] 期待値 (平均ログ) の対数 const double sigma, // [in] 対数平均平方根の偏差 (ログ標準偏差) const int data_count, //[in] 必要なデータの量 double &result[] // [out] 疑似変数の値を持つ配列 );
2.2.5. MathMomentsLognormal
この関数は、対数正規分布の最初の 4つのの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsLognormal( const double mu, // [in]期待値 (平均ログ) の対数 const double sigma, // [in] 二乗平均平方根の偏差の対数 (ログ標準偏差) double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code // [out] エラー コードの変数 );
2.3. ベータ分布
2.3.1. MathProbabilityDensityBeta
この関数は、ランダムな変数 x の b パラメーター、ベータ分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityBeta( const double x, //[in] ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます int &error_code // [out] エラー コードの変数 );
この関数は、ランダムな変数 x の b パラメーター、ベータ分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityBeta( const double x, //[in] ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
この関数は、a と b の確率変数 x[] 配列のパラメーターのベータ分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdbeta()のアナログ
bool MathProbabilityDensityBeta( const double &x[], //[in] ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const bool log_mode, //[in] log_mode = true の場合、確率密度の自然対数の計算 double &result[] // [out] 確率密度関数の値の配列 );
この関数は、a と b の確率変数 x[] 配列のパラメーターのベータ分布の確率密度関数の値を計算します。エラーの場合はfalseを返します。
bool MathProbabilityDensityBeta( const double &x[], //[in] ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター double &result[] // [out] 確率密度関数の値の配列 );
2.3.2. MathCumulativeDistributionlBeta
この関数は、ベータ分布の分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionBeta( const double x, //ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const bool tail, //[in] true の場合、ランダムな変数が x の確率を計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 int &error_code // [out] エラー コードの変数 );
この関数は、ベータ分布の分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionBeta( const double x, //ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
ベータ分布の分布関数の値を計算します。エラーの場合falseを返します。Rでのpbeta()のアナログ
bool MathCumulativeDistributionBeta( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const bool tail, //[in] true の場合、ランダムな変数が x の確率を計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値の配列 );
ベータ分布の分布関数の値を計算します。エラーの場合はfalseを返します。
bool MathCumulativeDistributionBeta( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター double &result[] //[out]確率関数の値の配列 );
2.3.3. MathQuantileBeta
指定された確率関数と逆 β 分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileBeta( const double probability, //ランダム変数の発生の確率の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます int &error_code // [out] エラー コードの変数 );
指定された確率関数と逆 β 分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileBeta( const double probability, //ランダム変数の発生の確率の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
指定された '確率' 配列関数、確率値の逆 β 分布関数の値を計算します。エラーの場合falseを返します。Rでのqbeta()のアナログ
bool MathQuantileBeta( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数、確率値の逆 β 分布関数の値を計算します。エラーの場合falseを返します
bool MathQuantileBeta( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape1) の最初のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.3.4. MathRandomBeta
この関数は、ベータ分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomBeta( const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
この関数は、ベータ分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrbeta()のアナログ
bool MathRandomBeta( const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] // [out] 疑似変数の値を持つ配列 );
2.3.5. MathMomentsBeta
この関数は、ベータ分布の最初の4つのモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsBeta( const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code // [out] エラー コードの変数 );
2.4. 非心ベータ分布
2.4.1. MathProbabilityDensityNoncentralBeta
非心 beta 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。double MathProbabilityDensityNoncentralBeta( const double x, //ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます int &error_code // [out] エラー コードの変数 );
非心 beta 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralBeta( const double x, //ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター int &error_code // [out] エラー コードの変数 );
非心 beta 分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdbeta()のアナログ
bool MathProbabilityDensityNoncentralBeta( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます double &result[] // [out] 確率密度関数の値の配列 );
非心 beta 分布の確率密度関数の値を計算します。エラーの場合はfalseを返します。
bool MathProbabilityDensityNoncentralBeta( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター double &result[] // [out] 確率密度関数の値の配列 );
2.4.2. MathCumulativeDistributionNoncentralBeta
非心 beta 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralBeta( const double x, //ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター const bool tail, //[in] true の場合、ランダムな変数が x の確率を計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 int &error_code // [out] エラー コードの変数 );
非心 beta 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralBeta( const double x, //ランダム変数の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター int &error_code // [out] エラー コードの変数 );
非心 beta 分布の確率分布関数の値を計算します。エラーの場合はfalseを返します。Rでのpbeta()のアナログ
bool MathCumulativeDistributionNoncentralBeta( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター const bool tail, //[in] true の場合、ランダムな変数が x の確率を計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値の配列 );
非心 beta 分布の確率分布関数の値を計算します。エラーの場合falseを返します。
bool MathCumulativeDistributionNoncentralBeta( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター double &result[] //[out]確率関数の値の配列 );
2.4.3. MathQuantileNoncentralBeta
非心 beta 分布の確率分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralBeta( const double probability, // [in] 確率変数の発生の確率の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます int &error_code // [out] エラー コードの変数 );
非心 beta 分布の確率分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralBeta( const double probability, // [in] 確率変数の発生の確率の値 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数パラメーター int &error_code // [out] エラー コードの変数 );
指定された '確率' 配列関数確率値の非心 beta 分布の確率分布の逆関数の値を計算します。エラーの場合falseを返します。Rでのqbeta()のアナログ
bool MathQuantileNoncentralBeta( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数パラメーター const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数確率値の非心 beta 分布の確率分布の逆関数の値を計算します。エラーの場合falseを返します。
bool MathQuantileNoncentralBeta( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in]ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.4.4. MathRandomNoncentralBeta
この関数は、非心ベータ分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomNoncentralBeta( const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター int &error_code // [out] エラー コードの変数 );
この関数は、非心ベータ分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrbeta()のアナログ
bool MathRandomNoncentralBeta( const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] // [out] 疑似変数の値を持つ配列 );
2.4.5. MathMomentsNoncentralBeta
この関数は、非心 beta 分布の最初 4 モーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
double MathMomentsNoncentralBeta( const double a, // [in] ベータ分布 (shape1) の最初のパラメーター const double b, // [in] ベータ分布 (shape2) の 2 番目のパラメーター const double lambda, // [in] 非心母数のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code // [out] エラー コードの変数 );
2.5. ガンマ分布
2.5.1. MathProbabilityDensityGamma
この関数は、ガンマ分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。double MathProbabilityDensityGamma( const double x, //ランダム変数の値 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター const bool log_mode, // [in] log_mode = true の場合、確率密度の自然対数の計算 int &error_code // [out] エラー コードの変数 );
この関数は、ガンマ分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityGamma( const double x, //ランダム変数の値 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
ガンマ分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdgamma()のアナログ
bool MathProbabilityDensityGamma( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター const bool log_mode, // [in] log_mode = true の場合、確率密度の自然対数の計算 double &result[] // [out] 確率密度関数の値の配列 );
ガンマ分布の確率密度関数の値を計算します。エラーの場合falseを返します。
bool MathProbabilityDensityGamma( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター double &result[] // [out] 確率密度関数の値の配列 );
2.5.2. MathCumulativeDistributionGamma
ガンマ分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionGamma( const double x, //ランダム変数の値 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター const bool tail, //[in] ランダムな変数が x の確率を計算し、true の場合、フラグの計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 int &error_code // [out] エラー コードの変数 );
ガンマ分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionGamma( const double x, //ランダム変数の値 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
ガンマ分布関数の値を計算します。エラーの場合falseを返します。Rでのpgamma()のアナログ
bool MathCumulativeDistributionGamma( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター const bool tail, //[in] ランダムな変数が x の確率を計算し、true の場合、フラグの計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値の配列 );
ガンマ分布関数の値を計算します。エラーの場合falseを返します。
bool MathCumulativeDistributionGamma( const double &x[], //[in] 確率変数の値を持つ配列 const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター double &result[] //[out]確率関数の値の配列 );
2.5.3. MathQuantileGamma
指定された確率関数と逆ガンマ分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileGamma( const double probability, // [in] 確率変数の発生の確率の値 const double a, // [in] 最初分布 (形状) のパラメーター const double a, //分布 (形状) の最初のパラメーター const bool tail, // [in] 1.0の確率の計算を実行し、false の場合は、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます int &error_code // [out] エラー コードの変数 );
指定された確率関数と逆ガンマ分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileGamma( const double probability, // [in] 確率変数の発生の確率の値 const double a, // [in] 最初分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
指定された '確率' 配列関数、確率値の逆ガンマ分布関数の値を計算します。エラーの場合falseを返します。Rでのqgamma()のアナログ
bool MathQuantileGamma( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double a, // [in] 最初分布 (形状) のパラメーター const double a, //分布 (形状) の最初のパラメーター const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, // [in] log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数、確率値の逆ガンマ分布関数の値を計算します。エラーの場合falseを返します。
bool MathQuantileGamma( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double a, // [in] 最初分布 (形状) のパラメーター const double a, //分布 (形状) の最初のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.5.4. MathRandomGamma
この関数は、ガンマ分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomGamma( const double a, // [in] 最初分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター int &error_code // [out] エラー コードの変数 );
この関数は、ガンマ分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrgamma()のアナログ
bool MathRandomGamma( const double a, // [in] 最初分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] // [out] 疑似変数の値を持つ配列 );
2.5.5. MathMomentsGamma
この関数は、ガンマ分布の最初 4つのモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsGamma( const double a, // [in] 最初の分布 (形状) のパラメーター const double b, // [in] 分布 (スケール) の 2 番目のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code // [out] エラー コードの変数 );
2.6. カイ 2 乗分布
2.6.1. MathProbabilityDensityChiSquare
この関数は、ランダムな変数 x の nu パラメーターを持つカイ 2 乗分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityChiSquare( const double x, //ランダム変数の値 const double nu, // [in] 分布 (自由度の数) のパラメーター constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます int &error_code // [out] エラー コードの変数 );この関数は、ランダムな変数 x の nu パラメーターを持つカイ 2 乗分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityChiSquare( const double x, //ランダム変数の値 const double nu, // [in] 分布 (自由度の数のパラメーター) int &error_code // [out] エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の nu パラメーターを持つカイ 2 乗分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdchisq()のアナログ
bool MathProbabilityDensityChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, // [in] 分布 (自由度の数のパラメーター) constbool log_mode //フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます double &result[] // [out] 確率密度関数の値の配列 );
この関数は、ランダム変数 x[] 配列の nu パラメーターを持つカイ 2 乗分布の確率密度関数の値を計算します。エラーの場合はfalseを返します。
bool MathProbabilityDensityChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, // [in] 分布 (自由度の数のパラメーター) double &result[] // [out] 確率密度関数の値の配列 );
2.6.2. MathCumulativeDistributionChiSquare
この関数は、ランダムな変数 x の nu パラメーターを持つカイ 2 乗分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionChiSquare( const double x, //ランダム変数の値 const double nu, // [in] 分布 (自由度の数) のパラメーター const bool tail, //[in] ランダムな変数が x の確率を計算し、true の場合、フラグの計算 const bool log_mode, // [in] log_mode = true の場合、確率の自然対数の計算 int &error_code // [out] エラー コードの変数 );
この関数は、ランダムな変数 x の nu パラメーターを持つカイ 2 乗分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionChiSquare( const double x, //ランダム変数の値 const double nu, // [in] 分布 (自由度の数) のパラメーター int &error_code // [out] エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の nu パラメーターを持つカイ 2 乗分布の確率分布関数の値を計算します。エラーの場合falseを返します。Rでのpchisq()のアナログ
bool MathCumulativeDistributionChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, // [in] 分布 (自由度の数) のパラメーター const bool tail, //[in] ランダムな変数が x の確率を計算し、true の場合、フラグの計算 const bool log_mode, //[in] log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値の配列 );
この関数は、ランダム変数 x[] 配列の nu パラメーターを持つカイ 2 乗分布の確率分布関数の値を計算します。エラーの場合はfalseを返します。
bool MathCumulativeDistributionChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, // [in] 分布 (自由度の数) のパラメーター double &result[] //[out]確率関数の値の配列 );
2.6.3. MathQuantileChiSquare
指定された確率関数カイ 2 乗分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileChiSquare( const double probability, // [in] 確率変数の発生の確率の値 const double nu, // [in] 分布 (自由度の数) のパラメーター const bool tail, // [in] 1.0の確率の計算を実行し、false の場合は、フラグの計算 const bool log_mode, // [in] log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code // [out] エラー コードの変数 );
指定された確率関数カイ 2 乗分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileChiSquare( const double probability, // [in] 確率変数の発生の確率の値 const double nu, // [in] 分布 (自由度の数) のパラメーター int &error_code // [out] エラー コードの変数 );
指定された '確率' 配列関数、確率値のカイ 2 乗分布の逆関数の値を計算します。エラーの場合falseを返します。Rでのqchisq()のアナログ
bool MathQuantileChiSquare( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, // [in] 分布 (自由度の数) のパラメーター const bool tail, //[in] 1.0 確率の偽なら計算が実行された場合、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数、確率値のカイ 2 乗分布の逆関数の値を計算します。エラーの場合falseを返します。
bool MathQuantileChiSquare( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, // [in] 分布 (自由度の数) のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.6.4. MathRandomChiSquare
この関数は、nu パラメーターを持つカイ 2 乗分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomChiSquare( const double nu, // [in] 分布 (自由度の数) のパラメーター int &error_code // [out] エラー コードの変数 );
この関数は、nu パラメーターを持つカイ 2 乗分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrchisq()のアナログ
bool MathRandomChiSquare( const double nu, // [in] 分布 (自由度の数) のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] // [out] 疑似変数の値を持つ配列 );
2.6.5. MathMomentsChiSquare
この関数は、nu パラメーターと χ の最初 4つの のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsChiSquare( const double nu, // [in] 分布 (自由度の数) のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code // [out] エラー コードの変数 );
2.7. 非心カイ二乗分布
2.7.1. MathProbabilityDensityNoncentralChiSquare
この関数は、ランダム変数 x の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralChiSquare( const double x, //ランダム変数の値 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, // 非心母数のパラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralChiSquare( const double x, //ランダム変数の値 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, // 非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdchisq()のアナログ
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, // 非心母数のパラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 double &result[] //[out]確率密度関数の値に配列 );
この関数は、ランダム変数 x[] 配列の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率密度関数の値を計算します。エラーの場合falseを返します。
bool MathProbabilityDensityNoncentralChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, // 非心母数のパラメーター double &result[] //[out]確率密度関数の値に配列 );
2.7.2. MathCumulativeDistributionNoncentralChiSquare
この関数は、ランダム変数 x の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralChiSquare( const double x, //ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code // エラー コードの変数 );
この関数は、ランダム変数 x の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralChiSquare( const double x, //ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター int &error_code // エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率分布関数の値を計算します。エラーの場合 false を返します。 Rでのpchisq()のアナログ
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、ランダム変数 x[] 配列の nu とシグマのパラメーターを持つ非心カイ 2 乗分布の確率分布関数の値を計算します。エラーの場合 false を返します。
bool MathCumulativeDistributionNoncentralChiSquare( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター double &result[] //[out]確率関数の値に配列 );
2.7.3. MathQuantileNoncentralChiSquare
指定された確率関数は ν とシグマのパラメーターと逆の非心カイ 2 乗分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralChiSquare( const double probability, // ランダム変数の発生の確率の値 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code // エラー コードの変数 );
指定された確率関数は ν とシグマのパラメーターと逆の非心カイ 2 乗分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralChiSquare( const double probability, // ランダム変数の発生の確率の値 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター int &error_code // エラー コードの変数 );
指定された '確率' 配列関数確率値の nu とシグマのパラメーターと逆の非心カイ 2 乗分布関数の値を計算します。エラーの場合falseを返します。Rでのqchisq()のアナログ
bool MathQuantileNoncentralChiSquare( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数確率値の nu とシグマのパラメーターと逆の非心カイ 2 乗分布関数の値を計算します。エラーの場合はfalse を返します
。
bool MathQuantileNoncentralChiSquare( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, // 分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.7.4. MathRandomNoncentralChiSquare
この関数は、nu とシグマのパラメーターを持つ非心カイ 2 乗分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomNoncentralChiSquare( const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、nu とシグマのパラメーターを持つ非心カイ 2 乗分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrchisq()のアナログ
bool MathRandomNoncentralChiSquare( const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] //疑似変数の値を持つ配列 );
2.7.5. MathMomentsNoncentralChiSquare
この関数は、nu とシグマのパラメーターを持つ非心カイ 2 乗分布の最初 4 のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsNoncentralChiSquare( const double nu, //分布 (自由度の数) のパラメーター const double sigma, //非心母数のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 );
2.8. 指数分布
2.8.1. MathProbabilityDensityExponential
この関数は、ランダム変数 x の mu パラメーターを持つ指数分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityExponential( const double x, //ランダム変数の値 const double mu, //分布のパラメーター (期待値) const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率密度の自然対数が返されます int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の mu パラメーターを持つ指数分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityExponential( const double x, //ランダム変数の値 const double mu, //分布のパラメーター (期待値) int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の mu パラメーターを持つ指数分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdexp()のアナログ
bool MathProbabilityDensityExponential( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, //分布のパラメーター (期待値) const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率密度の自然対数の計算 double &result[] //[out]確率密度関数の値に配列 );
この関数は、ランダム変数 x[] 配列の mu パラメーターを持つ指数分布の確率密度関数の値を計算します。エラーの場合falseを返します。
bool MathProbabilityDensityExponential( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, //分布のパラメーター (期待値) double &result[] //[out]確率密度関数の値に配列 );
2.8.2. MathCumulativeDistributionExponential
この関数は、確率、ランダム変数 x で mu パラメーターの指数分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionExponential( const double x, //ランダム変数の値 const double mu, //分布のパラメーター (期待値) const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code //エラー コードの変数 );
この関数は、確率、ランダム変数 x で mu パラメーターの指数分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionExponential( const double x, //ランダム変数の値 const double mu, //分布のパラメーター (期待値) int &error_code //エラー コードの変数 );
この関数は、確率、ランダム変数 x で mu パラメーターの指数分布関数の値を計算します。エラーの場合falseを返します。Rでのpexp()のアナログ
bool MathCumulativeDistributionExponential( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, //分布のパラメーター (期待値) const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、確率、ランダム変数 x で mu パラメーターの指数分布関数の値を計算します。エラーの場合 false を返します。
bool MathCumulativeDistributionExponential( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, //分布のパラメーター (期待値) double &result[] //[out]確率関数の値に配列 );
2.8.3. MathQuantileExponential
指定された確率関数は mu パラメーターを持つ指数分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileExponential( const double probability, //ランダム変数の発生の確率の値 const double mu, //分布のパラメーター (期待値) const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code // エラー コードの変数 );
指定された確率関数は mu パラメーターを持つ指数分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileExponential( const double probability, //ランダム変数の発生の確率の値 const double mu, //分布のパラメーター (期待値) int &error_code // エラー コードの変数 );
指定された '確率' 配列関数、確率値の mu パラメーターを持つ指数分布関数の値を計算します。エラーの場合falseを返します。Rでのqexp()のアナログ
bool MathQuantileExponential( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double mu, //分布のパラメーター (期待値) const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列関数、確率値の mu パラメーターを持つ指数分布関数の値を計算します。エラーの場合 false を返します。
bool MathQuantileExponential( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double mu, //分布のパラメーター (期待値) double &result[] // [out] 分位数の値を持つ配列 );
2.8.4. MathRandomExponential
この関数は、mu パラメーターを持つ指数分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomExponential( const double mu, //分布のパラメーター (期待値) int &error_code //エラー コードの変数 );
この関数は、mu パラメーターを持つ指数分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrexp()のアナログ
bool MathRandomExponential( const double mu, //分布のパラメーター (期待値) const int data_count, //[in] 必要なデータの量 double &result[] //疑似変数の値を持つ配列 );
2.8.5. MathMomentsExponential
この関数は、mu パラメーターを持つ指数分布の最初 4つ のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsExponential( const double mu, //分布のパラメーター (期待値) double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 );
2.9. F-分布
2.9.1. MathProbabilityDensityF
この関数は、ランダム変数 x の nu1 と nu2 パラメーターを持つフィッシャー F 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityF( const double x, //ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu1 と nu2 パラメーターを持つフィッシャー F 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityF( const double x, //ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列 nu1 と nu2 パラメーターをフィッシャー F 分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdf()のアナログ
bool MathProbabilityDensityF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 double &result[] //[out]確率密度関数の値に配列 );
この関数は、ランダム変数 x[] 配列 nu1 と nu2 パラメーターをフィッシャー F 分布の確率密度関数の値を計算します。エラーの場合falseを返します。
bool MathProbabilityDensityF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター double &result[] //[out]確率密度関数の値に配列 );
2.9.2. MathCumulativeDistributionF
この関数は、ランダム変数 x の nu1 と nu2 パラメーターを持つフィッシャー F 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionF( const double x, //ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu1 と nu2 パラメーターを持つフィッシャー F 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionF( const double x, // ランダム変数の値 const double nu1, // 分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列 nu1 と nu2 パラメーターをフィッシャー F 分布の確率分布関数の値を計算します。エラーの場合falseを返します。Rでのpf()のアナログ
bool MathCumulativeDistributionF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、ランダム変数 x[] 配列 nu1 と nu2 パラメーターをフィッシャー F 分布の確率分布関数の値を計算します。エラーの場合falseを返します。
bool MathCumulativeDistributionF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, // 分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター double &result[] //[out]確率関数の値に配列 );
2.9.3. MathQuantileF
指定された確率関数はフィッシャー F 分布関数の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileF( const double probability, //ランダム変数の発生の確率の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code //エラー コードの変数 );
指定された確率関数はフィッシャー F 分布関数の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileF( const double probability, //ランダム変数の発生の確率の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター int &error_code //エラー コードの変数 );
指定された確率関数はフィッシャー F 分布関数の逆関数の値を計算します。エラーの場合falseを返します。Rでのqf()のアナログ
bool MathQuantileF( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] //[out]分位数の値を持つ配列 );
指定された確率関数はフィッシャー F 分布関数の逆関数の値を計算します。エラーの場合falseを返します。
bool MathQuantileF( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター double &result[] //[out]分位数の値を持つ配列 );
2.9.4. MathRandomF
この関数は、nu1 と nu2 パラメーターを持つフィッシャー F 分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomF( const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター int &error_code //エラー コードの変数 );
この関数は、nu1 と nu2 パラメーターを持つフィッシャー F 分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrf()のアナログ
bool MathRandomF( const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] //疑似変数の値を持つ配列 );
2.9.5. MathMomentsF
この関数は、nu1 と nu2 パラメーターとフィッシャーの F 分布の最初 4 のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsF( const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 );
2.10. 非心 F 分布
2.10.1. MathProbabilityDensityNoncentralF
この関数は、ランダム変数 x のシグマ、nu2 nu1 パラメーターを持つ非心フィッシャー F 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralF( const double x, // ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, // 非心母数のパラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x のシグマ、nu2 nu1 パラメーターを持つ非心フィッシャー F 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralF( const double x, // ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, // 非心母数パラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列シグマ、nu2 nu1 パラメーターを非心フィッシャー F 分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdf()のアナログ
double MathProbabilityDensityNoncentralF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, // 非心母数パラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 double &result[] //[out]確率密度関数の値に配列 );
この関数は、ランダム変数 x[] 配列シグマ、nu2 nu1 パラメーターを非心フィッシャー F 分布の確率密度関数の値を計算します。エラーの場合 false を返します。
double MathProbabilityDensityNoncentralF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, // 非心母数パラメーター double &result[] //[out]確率密度関数の値に配列 );
2.10.2. MathCumulativeDistributionlNoncentralF
この関数は、ランダム変数 x のシグマ、nu2 nu1 パラメーターを持つ非心フィッシャー F 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralF( const double x, //ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x のシグマ、nu2 nu1 パラメーターを持つ非心フィッシャー F 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralF( const double x, //ランダム変数の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x のシグマ、nu2 nu1 パラメーターを持つ非心フィッシャー F 分布の確率分布関数の値を計算します。エラーの場合falseを返します。Rでのpf()のアナログ
bool MathCumulativeDistributionNoncentralF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、ランダム変数 x のシグマ、nu2 nu1 パラメーターを持つ非心フィッシャー F 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
bool MathCumulativeDistributionNoncentralF( const double &x[], //[in] 確率変数の値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, //分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター double &result[] //[out]確率関数の値に配列 );
2.10.3. MathQuantileNoncentralF
指定された確率関数は逆関数の値を計算します。 nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布関数。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralF( const double probability, //ランダム変数の発生の確率の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code //エラー コードの変数 );
指定された確率関数は逆関数の値を計算します。 nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布関数。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralF( const double probability, //ランダム変数の発生の確率の値 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター int &error_code //エラー コードの変数 );
指定された確率関数は逆関数の値を計算します。 nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布関数。エラーの場合falseを返します。Rでのqf()のアナログ
bool MathQuantileNoncentralF( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された確率関数は逆関数の値を計算します。 nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布関数。エラーの場合falseを返します。
bool MathQuantileNoncentralF( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.10.4. MathRandomNoncentralF
この関数は、nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomNoncentralF( const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // [in] 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrf()のアナログ
bool MathRandomNoncentralF( const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // [in] 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.10.5. MathMomentsNoncentralF
この関数は、最初 4 モーメント nu1、nu2 とシグマのパラメーターを持つ非心フィッシャー F 分布の理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsNoncentralF( const double nu1, //分布 (自由度の数) の最初のパラメーター const double nu2, // [in] 分布 (自由度の数) の 2 番目のパラメーター const double sigma, //非心母数のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 e.)
2.11. t-分布
2.11.1. MathProbabilityDensityT
この関数は、ランダム変数 x の nu パラメーターとスチューデントの t 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityT( const double x, // ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const bool log_mode, //[in] フラグ値の対数を計算する log_mode、確率密度の自然対数が返されます。 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu パラメーターとスチューデントの t 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityT( const double x, // ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター int &error_code //エラー コードの変数 );
この関数は、確率変数 x[] 配列で nu パラメーター スチューデントの t 分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdt()のアナログ
bool MathProbabilityDensityT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率密度の自然対数の計算 double &result[] //[out]確率密度関数の値に配列 );
この関数は、確率変数 x[] 配列で nu パラメーター スチューデントの t 分布の確率密度関数の値を計算します。エラーの場合 false を返します。
bool MathProbabilityDensityT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター double &result[] //[out]確率密度関数の値に配列 );
2.11.2. MathCumulativeDistributionT
この関数は、ランダム変数 x の nu パラメーターとスチューデント t 分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionT( const double x, //ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu パラメーターとスチューデント t 分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionT( const double x, //ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター int &error_code //エラー コードの変数 );
この関数は、スチューデント t 分布関数の確率変数 x[] 配列の nu パラメーターの値を計算します。エラーの場合falseを返します。Rでのpt()のアナログ
bool MathCumulativeDistributionT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、スチューデント t 分布関数の確率変数 x[] 配列の nu パラメーターの値を計算します。エラーの場合falseを返します。
bool MathCumulativeDistributionT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター double &result[] //[out]確率関数の値に配列 );
2.11.3. MathQuantileT
指定された確率関数はnu パラメーターとスチューデント t 分布関数の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileT( const double probability, //ランダム変数の発生の確率の値 const double nu, //分布 (自由度の数) のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code // エラー コードの変数 );
指定された確率関数はnu パラメーターとスチューデント t 分布関数の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileT( const double probability, //ランダム変数の発生の確率の値 const double nu, //分布 (自由度の数) のパラメーター int &error_code // エラー コードの変数 );
指定された '確率' 配列確率値の関数はnu パラメーターとスチューデント t 分布関数の逆関数の値を計算します。 エラーの場合falseを返します。Rでのqt()のアナログ
bool MathQuantileT( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
指定された '確率' 配列確率値の関数はnu パラメーターとスチューデント t 分布関数の逆関数の値を計算します。 エラーの場合 false を返します。
bool MathQuantileT( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.11.4. MathRandomT
この関数は、nu パラメーターとスチューデントの t 分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomT( const double nu, //分布 (自由度の数) のパラメーター int &error_code //エラー コードの変数 );
この関数は、nu パラメーターとスチューデントの t 分布の法則に従って分散擬似変数を生成します。エラーの場合 false を返します。Rでのrt()のアナログ
bool MathRandomT( const double nu, //分布 (自由度の数) のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] //疑似変数の値を持つ配列 );
2.11.5. MathMomentsT
この関数は、nu パラメーターとスチューデントの t 分布の最初 の4つ のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
double MathMomentsT( const double nu, //分布 (自由度の数) のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 );
2.12. 非心 t 分布
2.12.1. MathProbabilityDensityNoncentralT
この関数は、ランダム変数 x の nu パラメーターの非心スチューデント t 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralT( const double x, //ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu パラメーターの非心スチューデント t 分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityNoncentralT( const double x, //ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の nu パラメーターの非心スチューデント t 分布の確率密度関数の値を計算します。エラーの場合falseを返します。Rでのdt()のアナログ
bool MathProbabilityDensityNoncentralT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率密度の自然対数の計算 double &result[] //[out]確率密度関数の値に配列 );
この関数は、ランダム変数 x[] 配列の nu パラメーターの非心スチューデント t 分布の確率密度関数の値を計算します。エラーの場合falseを返します。
bool MathProbabilityDensityNoncentralT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター double &result[] //[out]確率密度関数の値に配列 );
2.12.2. MathCumulativeDistributionlNoncentralT
この関数は、ランダム変数 x の nu とデルタのパラメーターを持つ非心スチューデント t 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralT( const double x, // ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const double delta, // 非心母数のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の nu とデルタのパラメーターを持つ非心スチューデント t 分布の確率分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionNoncentralT( const double x, // ランダム変数の値 const double nu, //分布 (自由度の数) のパラメーター const double delta, // 非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の nu とデルタのパラメーターを持つ非心スチューデント t 分布の確率分布関数の値を計算します。エラーの場合falseを返します。Rでのpt()のアナログ
bool MathCumulativeDistributionNoncentralT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const double delta, // 非心母数のパラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、ランダム変数 x[] 配列の nu とデルタのパラメーターを持つ非心スチューデント t 分布の確率分布関数の値を計算します。エラーの場合 false を返します。
bool MathCumulativeDistributionNoncentralT( const double &x[], //[in] 確率変数の値を持つ配列 const double nu, //分布 (自由度の数) のパラメーター const double delta, // 非心母数のパラメーター double &result[] //[out]確率関数の値に配列 );
2.12.3. MathQuantileNoncentralT
この関数は、指定した確率のデルタのパラメーターを持つ非心スチューデント t 分布関数の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralT( const double probability, // ランダム変数の発生の確率の値 const double nu, // 分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code //エラー コードの変数 );
この関数は、指定した確率のデルタのパラメーターを持つ非心スチューデント t 分布関数の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileNoncentralT( const double probability, // ランダム変数の発生の確率の値 const double nu, // 分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数はデルタのパラメーターを持つ非心スチューデント t 分布関数の逆関数の値を計算します。エラーの場合falseを返します。Rでのqt()のアナログ
bool MathQuantileNoncentralT( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, // 分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
この関数はデルタのパラメーターを持つ非心スチューデント t 分布関数の逆関数の値を計算します。エラーの場合 false を返します。
bool MathQuantileNoncentralT( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double nu, // 分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.12.4. MathRandomNoncentralT
この関数は、nu とデルタのパラメーターを持つ非心スチューデント t 分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomNoncentralT( const double nu, // 分布 (自由度の数) のパラメーター const double delta, // 非心母数のパラメーター int &error_code //エラー コードの変数 );
この関数は、nu とデルタのパラメーターを持つ非心スチューデント t 分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrt()のアナログ
bool MathRandomNoncentralT( const double nu, // 分布 (自由度の数) のパラメーター const double delta, // 非心母数のパラメーター const int data_count, //[in] 必要なデータの量 double &result[] //疑似変数の値を持つ配列 );
2.12.5. MathMomentsNoncentralT
この関数は、nu とデルタのパラメーターを持つ非心スチューデント t 分布の最初 の4つ のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
double MathMomentsNoncentralT( const double nu, //分布 (自由度の数) のパラメーター const double delta, //非心母数のパラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 );
2.13. ロジスティック分布
2.13.1. MathProbabilityDensityLogistic
この関数は、ランダム変数 x の mu および sigma のパラメーターを持つロジスティック分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityLogistic( const double x, //ランダム変数の値 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター const bool log_mode, //[in] log_mode=trueの場合、確率密度の自然対数が返されます。 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の mu および sigma のパラメーターを持つロジスティック分布の確率密度関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathProbabilityDensityLogistic( const double x, //ランダム変数の値 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つロジスティック分布の確率密度関数の値を計算します。エラーの場合 false を返します。Rでのdlogis()のアナログ
bool MathProbabilityDensityLogistic( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率密度の自然対数の計算 double &result[] //[out]確率密度関数の値に配列 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つロジスティック分布の確率密度関数の値を計算します。エラーの場合 false を返します。
bool MathProbabilityDensityLogistic( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター double &result[] //[out]確率密度関数の値に配列 );
2.13.2. MathCumulativeDistributionlLogistic
この関数は、ランダム変数 x の mu および sigma のパラメーターを持つロジスティック分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionLogistic( const double x, //ランダム変数の値 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x の mu および sigma のパラメーターを持つロジスティック分布関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathCumulativeDistributionLogistic( const double x, //ランダム変数の値 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター int &error_code //エラー コードの変数 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つロジスティック分布関数の値を計算します。エラーの場合falseを返します。Rでのplogis()のアナログ
bool MathCumulativeDistributionLogistic( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター const bool tail, //[in] ランダム変数が x の確率を計算し、true の場合は、フラグの計算 const bool log_mode, //[in] フラグ値の対数を計算する log_mode = true の場合、確率の自然対数の計算 double &result[] //[out]確率関数の値に配列 );
この関数は、ランダム変数 x[] 配列の mu および sigma のパラメーターを持つロジスティック分布関数の値を計算します。エラーの場合falseを返します。Rでのplogis()のアナログ
bool MathCumulativeDistributionLogistic( const double &x[], //[in] 確率変数の値を持つ配列 const double mu, // [in]分布のパラメーターの平均 const double sigma, //分布のスケール ・ パラメーター double &result[] //[out]確率関数の値に配列 );
2.13.3. MathQuantileLogistic
mu および sigma パラメーターを持つロジスティック分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileLogistic( const double probability, // ランダム変数の発生の確率の値 const double mu, // [in]パラメーター分布の平均 const double sigma, //分布のスケール ・ パラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます int &error_code //エラー コードの変数 );
mu および sigma パラメーターを持つロジスティック分布の逆関数の値を計算します。エラーの場合は、 NaNが返されます。
double MathQuantileLogistic( const double probability, // ランダム変数の発生の確率の値 const double mu, // [in]パラメーター分布の平均 const double sigma, //分布のスケール ・ パラメーター int &error_code //エラー コードの変数 );
mu および sigma のパラメーターを持つロジスティック分布の逆関数の値を計算します。エラーの場合falseを返します。Rでのqlogis()のアナログ
bool MathQuantileLogistic( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double mu, // [in]パラメーター分布の平均 const double sigma, //分布のスケール ・ パラメーター const bool tail, //[in] 1.0の確率の計算が実行された場合、false、フラグの計算 const bool log_mode, //[in] フラグの計算 log_mode = true の場合、計算は Exp(probability) に対して実行されます double &result[] // [out] 分位数の値を持つ配列 );
mu および sigma のパラメーターを持つロジスティック分布の逆関数の値を計算します。エラーの場合 false を返します。
bool MathQuantileLogistic( const double &probability[],//[in] ランダム変数の確率値を持つ配列 const double mu, // [in]パラメーター分布の平均 const double sigma, //分布のスケール ・ パラメーター double &result[] // [out] 分位数の値を持つ配列 );
2.13.4. MathRandomLogistic
この関数は、mu および sigma パラメーターを持つロジスティック分布の法則に従って分散擬似変数を生成します。エラーの場合は、 NaNが返されます。
double MathRandomLogistic( const double mu, // [in]分布のパラメーターの平均 const double sigma, // 分布のスケール ・ パラメーター int &error_code //エラー コードの変数 );
この関数は、mu および sigma パラメーターを持つロジスティック分布の法則に従って分散擬似変数を生成します。エラーの場合falseを返します。Rでのrlogis()のアナログ
bool MathRandomLogistic( const double mu, // [in]分布のパラメーターの平均 const double sigma, // 分布のスケール ・ パラメーター const int data_count, //[in] 必要なデータの量 double &result[] //疑似変数の値を持つ配列 );
2.13.5. MathMomentsLogistic
この関数は、mu および sigma パラメーターを持つロジスティック分布の最初 4 のモーメントの理論的数値を計算します。モーメントの計算が成功した場合は、true を返します。
bool MathMomentsLogistic( const double mu, // [in]パラメーター分布の平均 const double sigma, //分布のスケール ・ パラメーター double &mean, //[out]平均 (第 1 時) の可変 double &variance, //[out]分散 (第 2 モーメント) の可変 double &skewness, //[out]歪み度 (3 時) の可変 double &kurtosis, //[out]尖度 (第 4 のモーメント) の可変 int &error_code //[out]エラー コードの変数 );
3. R の統計関数の対応表
便宜上、テーブル 1-2 には、統計ライブラリの関数、R 言語に対応する関数が含まれています。
| No. | 計算値 | MQL5関数 | R関数 |
|---|---|---|---|
| 1 | Mean | MathMean | mean |
| 2 | Variance | MathVariance | var |
| 3 | Skewness | MathSkewness | skewness |
| 60 | Kurtosis | MathKurtosis | kurtosis |
| 5 | 中央値 | MathMedian | median |
| 6 | 標準偏差 | MathStandardDeviation | sd |
| 7 | 平均絶対偏差 | MathAverageDeviation | aad |
表 1。配列データの統計的特性を計算するための関数
| No. | Distribution | 密度関数 | MQL5関数 | R関数 |
|---|---|---|---|---|
| 1 | Normal | 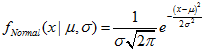 | MathProbabilityDensityNormal MathCumulativeDistributionNormal MathQuantileNormal MathRandomNormal | dnorm pnorm qnorm rnorm |
| 2 | Beta | | MathProbabilityDensityBeta MathCumulativeDistributionBeta MathQuantileBeta MathRandomBeta | dbeta pbeta qbeta rbeta |
| 3 | Binomial | | MathProbabilityDensityBinomial MathCumulativeDistributionBinomial MathQuantileBinomial MathRandomBinomial | dbinom pbinom qbinom rbinom |
| 60 | Cauchy | 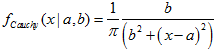 | MathProbabilityDensityCauchy MathCumulativeDistributionCauchy MathQuantileCauchy MathRandomCauchy | dcauchy pcauchy qcauchy rcauchy |
| 5 | Chi-squared | 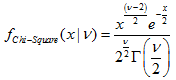 | MathProbabilityDensityChiSquare MathCumulativeDistributionChiSquare MathQuantileChiSquare MathRandomChiSquare | dchisq pchisq qchisq rchisq |
| 6 | Exponential | | MathProbabilityDensityExponential MathCumulativeDistributionExponential MathQuantileExponential MathRandomExponential | dexp pexp qexp rexp |
| 7 | F分布 | 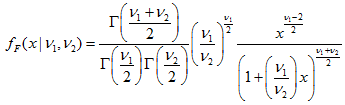 | MathProbabilityDensityF MathCumulativeDistributionF MathQuantileF MathRandomF | df pf qf rf |
| 8 | Gamma | | MathProbabilityDensityGamma MathCumulativeDistributionGamma MathQuantileGamma MathRandomGamma | dgamma pgamma qgamma rgamma |
| 9 | Geometric | | MathProbabilityDensityGeometric MathCumulativeDistributionGeometric MathQuantileGeometric MathRandomGeometric | dgeom pgeom qgeom rgeom |
| 10 | Hypergeometric | 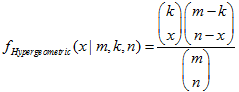 | MathProbabilityDensityHypergeometric MathCumulativeDistributionHypergeometric MathQuantileHypergeometric MathRandomHypergeometric | dhyper phyper qhyper rhyper |
| 11 | Logistic | 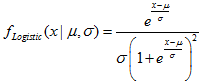 | MathProbabilityDensityLogistic MathCumulativeDistributionLogistic MathQuantileLogistic MathRandomLogistic | dlogis plogis qlogis rlogis |
| 12 | Log-normal | | MathProbabilityDensityLognormal MathCumulativeDistributionLognormal MathQuantileLognormal MathRandomLognormal | dlnorm plnorm qlnorm rlnorm |
| 13 | 負の二項 | | MathProbabilityDensityNegativeBinomial MathCumulativeDistributionNegativeBinomial MathQuantileNegativeBinomial MathRandomNegativeBinomial | dnbinom pnbinom qnbinom rnbinom |
| 14 | 非心 beta | 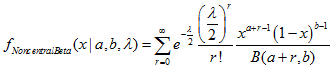 | MathProbabilityDensityNoncentralBeta MathCumulativeDistributionNoncentralBeta MathQuantileNoncentralBeta MathRandomNoncentralBeta | dbeta pbeta qbeta rbeta |
| 15 | 非心カイ 2 乗 | 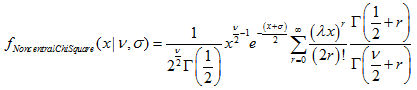 | MathProbabilityDensityNoncentralChiSquare MathCumulativeDistributionNoncentralChiSquare MathQuantileNoncentralChiSquare MathRandomNoncentralChiSquare | dchisq pchisq qchisq rchisq |
| 16 | 非心 F 分布 | 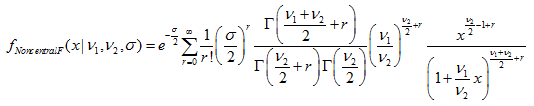 | MathProbabilityDensityNoncentralF() MathCumulativeDistributionNoncentralF() MathQuantileNoncentralF() MathRandomNoncentralF() | df pf qf rf |
| 17 | 非心 t 分布 | 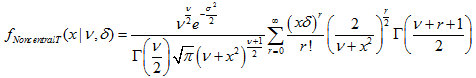 | MathProbabilityDensityNoncentralT MathCumulativeDistributionNoncentralT MathQuantileNoncentralT MathRandomNoncentralT | dt pt qt rt |
| 18 | Poisson | | MathProbabilityDensityPoisson MathCumulativeDistributionPoisson MathQuantilePoisson MathRandomPoisson | dpois ppois qpois rpois |
| 19 | t分布 | 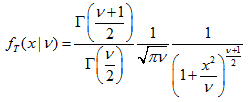 | MathProbabilityDensityT MathCumulativeDistributionT MathQuantileT MathRandomT | dt pt qt rt |
| 20 | Uniform | | MathProbabilityDensityUniform MathCumulativeDistributionUniform MathQuantileUniform MathRandomUniform | dunif punif qunif runif |
| 21 | Weibull | 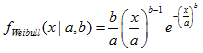 | MathProbabilityDensityWeibull MathCumulativeDistributionWeibull MathQuantileWeibull MathRandomWeibull | dweibull pweibull qweibull rweibull |
表2。統計分布を操作するための関数
数学関数を計算するための関数を提供します。 MQL5 を統計ライブラリは、以下の表 3 に記載されています。
| 詳細 | MQL5 | R |
|---|---|---|
| 値のシーケンスを生成します | bool MathSequence(const double from,const double to,const double step,double &result[]) bool MathSequenceByCount(const double from,const double to,const int count,double &result[]) bool MathSequence(const int from,const int to,const int step,int &result[]) bool MathSequenceByCount(const int from,const int to,const int count,int &result[]) | seq() |
| 繰り返しシーケンスを生成します | bool MathReplicate(const double &array[],const int count,double &result[]) bool MathReplicate(const int &array[],const int count,int &result[]) | rep() |
| 要素の逆の順序で配列を生成します。 | bool MathReverse(const double &array[],double &result[]) bool MathReverse(const int &array[],int &result[]) | rev(x) |
| 配列を比較し、すべての要素に一致する場合は true を返します | bool MathIdentical(const double &array1[],const double &array2[]) bool MathIdentical(const int &array1[],const int &array2[]) | identical() |
| 固有の値のみを持つ配列を生成します。 | bool MathUnique(const double &array[],double &result[]) bool MathUnique(const int &array[],int &result[]) | unique() |
| ソート後の配列の要素の順序に従って順列を持つ整数の配列を生成します。 | bool MathOrder(const double &array[],int &result[]) bool MathOrder(const int &array[],int &result[]) | order() |
| 配列の要素からランダム サンプルを生成します。置換後の文字列 = true 引数が元のシーケンスに置換要素のランダム サンプリングを実行することができます。確率配列は、サンプリングの確率を定義します。 | bool MathSample(const double &array[],const int count,double &result[]) bool MathSample(const double &array[],const int count,const bool replace,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,const bool replace,double &result[]) bool MathSample(const int &array[],const int count,int &result[]) bool MathSample(const int &array[],const int count,const bool replace,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,const bool replace,int &result[]) | sample() |
| 配列の要素の合計を返します | double MathSum(const double &array[]) | sum() |
| 配列要素の積を返します | double MathProduct(const double &array[]) | prod() |
| 累積合計を持つ配列を生成します。 | bool MathCumulativeSum(const double &array[],double &result[]) bool MathCumulativeSum(double &array[]) | cumsum() |
| 累積配列を生成します。 | bool MathCumulativeProduct(const double &array[],double &result[]) bool MathCumulativeProduct(double &array[]) | cumprod() |
| 累積最小値を持つ配列を生成します。 | bool MathCumulativeMin(const double &array[],double &result[]) bool MathCumulativeMin(double &array[]) | cummin() |
| 累積最大値を持つ配列を生成します。 | bool MathCumulativeMax(const double &array[],double &result[]) bool MathCumulativeMax(double &array[]) | cummax() |
| 要素の違いと配列が生成されますy[i]=x[i+lag]-x[i] | bool MathDifference(const double &array[],const int lag,double &result[]) bool MathDifference(const double &array[],const int lag,const int differences,double &result[]) bool MathDifference(const int &array[],const int lag,int &result[]) bool MathDifference(const int &array[],const int lag,const int differences,int &result[]) | diff() |
| 配列要素の最小値を返します | double MathMin(const double &array[]) | min() |
| 配列要素の最大値を返します | double MathMax(const double &array[]) | max() |
| 配列要素の最大値を計算します | bool MathRange(const double &array[],double &min,double &max) | range() |
| 配列の要素の平均値を計算します | double MathMean(const double &array[]) | mean() |
| 配列の要素の標準偏差を計算します | double MathStandardDeviation(const double &array[]) | sd() |
| 配列の要素の平均値を計算します | double MathMedian(double &array[]) | median() |
| 配列要素のランクを計算します | bool MathRank(const int &array[],double &rank[]) bool MathRank(const double &array[],double &rank[]) | rank() |
| ピアソンのスピアマンのケンドールの相関係数を計算します。 | bool MathCorrelationPearson(const double &array1[],const double &array2[],double &r) bool MathCorrelationPearson(const int &array1[],const int &array2[],double &r) bool MathCorrelationSpearman(const double &array1[],const double &array2[],double &r) bool MathCorrelationSpearman(const int &array1[],const int &array2[],double &r) bool MathCorrelationKendall(const double &array1[],const double &array2[],double &tau) bool MathCorrelationKendall(const int &array1[],const int &array2[],double &tau) | corr() |
| 指定された確率に対応する標本を計算します | bool MathQuantile(const double &array[],const double &probs[],double &quantile[]) | qunatile() |
| Tukey の 5要約 (最小、下部ヒンジ、中央、上部ヒンジ、最大) 配列要素を計算します | bool MathTukeySummary(const double &array[],const bool removeNAN,double &minimum,double &lower_hinge,double &median,double &upper_hinge,double &maximum) | fivenum() |
| 配列要素 (自然と与えられたベース) の対数を計算します | bool MathLog(const double &array[],double &result[]) bool MathLog(const double &array[],const double base,double &result[]) bool MathLog(double &array[]) bool MathLog(double &array[],const double base) | log() |
| 2 を基に配列要素の対数を計算します | bool MathLog2(const double &array[],double &result[]) bool MathLog2(double &array[]) | log2() |
| 10 を基準に配列要素の対数を計算します | bool MathLog10(const double &array[],double &result[]) bool MathLog10(double &array[]) | log10() |
| 配列要素の log(1+x) 関数の値を計算します | bool MathLog1p(const double &array[], double &result[]) bool MathLog1p(double &array[]) | log1p() |
| 配列要素の経験 (x) 関数の値を計算します | bool MathExp(const double &array[], double &result[]) bool MathExp(double &array[]) | exp() |
| Exp (x)-1 による配列の要素の値を計算します | bool MathExpm1(const double &array[], double &result[]) bool MathExpm1(double &array[]) | expm1() |
| 配列要素の sin (x) 関数の値を計算します | bool MathSin(const double &array[], double &result[]) bool MathSin(double &array[]) | sin() |
| 配列要素の cos(x) 関数の値を計算します | bool MathCos(const double &array[], double &result[]) bool MathCos(double &array[]) | cos() |
| 配列要素の tan(x) 関数の値を計算します | bool MathTan(const double &array[], double &result[]) bool MathTan(double &array[]) | tan() |
| 配列要素の arcsin(x) 関数の値を計算します | bool MathArcsin(const double &array[], double &result[]) bool MathArcsin(double &array[]) | arcsin() |
| 配列要素の arccos(x) 関数の値を計算します | bool MathArccos(const double &array[], double &result[]) bool MathArccos(double &array[]) | arccos() |
| 配列要素の arctan(x) 関数の値を計算します | bool MathArctan(const double &array[], double &result[]) bool MathArctan(double &array[]) | arctan() |
| 配列要素の arctan(y/x) 関数の値を計算します | bool MathArctan2(const double &array1[], const double &array2[], double &result[]) | arctan2() |
| 配列要素の sin(pi*x) 関数の値を計算します | bool MathSinPi(const double &array[], double &result[]) bool MathSinPi(double &array[]) | sinpi() |
| 配列要素の cos(pi*x) 関数の値を計算します | bool MathCosPi(const double &array[], double &result[]) bool MathCosPi(const double &array[]) | cospi() |
| 配列要素の tan(pi*x) 関数の値を計算します | bool MathTanPi(const double &array[], double &result[]) bool MathTanPi(double &array[]) | tanpi() |
| 配列の要素の絶対値を計算します | bool MathAbs(const double &array[], double &result[]) bool MathAbs(double &array[]) | abs() |
| 配列要素の平方根を計算します | bool MathSqrt(const double &array[], double &result[]) bool MathSqrt(double &array[]) | sqrt() |
| 配列の要素の最も近い大きい整数を返します | bool MathCeil(const double &array[], double &result[]) bool MathCeil(double &array[]) | ceil() |
| 配列の要素の最も近い小さい整数を返します | bool MathFloor(const double &array[], double &result[]) bool MathFloor(double &array[]) | floor() |
| 配列要素の整数部を計算します。 | bool MathTrunc(const double &array[], const int digits, double &result[]) bool MathTrunc(double &array[]) | trunc() |
| 配列の要素のラウンドの値を計算します。 | bool MathRound(const double &array[], const int digits, double &result[]) bool MathRound(double &array[],int digits) | round() |
| 配列の要素に、仮数部の桁数に丸め値を計算します。 | bool MathSignif(const double &array[], const int digits, double &result[]) bool MathSignif(double &array[], const int digits) | signinf() |
| 配列要素のハイパボリック サイン関数の値を計算します | bool MathSinh(const double &array[],double &result[]) bool MathSinh(double &array[]) | sinh() |
| 配列要素のハイパボリック コサイン関数の値を計算します | bool MathCosh(const double &array[],double &result[]) bool MathCosh(double &array[]) | cosh() |
| 配列要素の tanh(x) 関数の値を計算します | bool MathTanh(const double &array[],double &result[]) bool MathTanh(double &array[]) | tanh() |
| 配列要素の arcsinh(x) 関数の値を計算します | bool MathArcsinh(const double &array[],double &result[]) bool MathArcsinh(double &array[]) | asinh() |
| 配列要素の arccosh(x) 関数の値を計算します | bool MathArccosh(const double &array[],double &result[]) bool MathArccosh(double &array[]) | acosh() |
| 配列要素の arctanh(x) 関数の値を計算します | bool MathArctanh(const double &array[],double &result[]) bool MathArctanh(double &array[]) | atanh() |
| ビットごとの否定の結果を計算する配列要素の操作 | bool MathBitwiseNot(const int &array[],int &result[]) bool MathBitwiseNot(int &array[]) | bitwNot() |
| 指定した配列のビットごとの AND 演算の結果を計算します。 | bool MathBitwiseAnd(const int &array1[],const int &array2[],int &result[]) | bitwAnd() |
| 指定した配列のビットごとの OR 演算の結果を計算します。 | bool MathBitwiseOr(const int &array1[],const int &array2[],int &result[]) | bitwOr() |
| 指定した配列のビットごとの XOR 演算の結果を計算します。 | bool MathBitwiseXor(const int &array1[],const int &array2[],int &result[]) | bitwXor() |
| 配列要素の SHL 演算の結果を計算します。 | bool MathBitwiseShiftL(const int &array[],const int n,int &result[]) bool MathBitwiseShiftL(int &array[],const int n) | bitwShiftL() |
| 配列要素の SHR 演算の結果を計算します。 | bool MathBitwiseShiftR(const int &array[],const int n,int &result[]) bool MathBitwiseShiftR(int &array[],const int n) | bitwShiftR() |
表3。配列内の値を計算するための数学関数
4. 関数の使用例
正規分布の例で統計関数の実用的なアプリケーションを考えてみましょう。
次の問題を解決する必要があるとします。
- [Mu シグマ、mu + シグマ] の範囲内の mu および sigma のパラメーターを持つ普通のルールに従って分散確率変数の確率を計算します。
- Mu および sigma パラメーター mu に対称的でり、確率の 95% に対応する通常ルールに従って分散ランダム変数 x の値の範囲を検索します。
- Mu および sigma パラメーターを持つ普通のルールに従って分散 1000000 の乱数を生成し、最初 4 モーメント、得られた値のヒストグラムを計算し、理論値と比較します。
NormalExample スクリプトでソリューションの例:
//+------------------------------------------------------------------+ //| NormalExample.mq5 | //| Copyright 2016, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" //---正規分布を計算するための関数を含める #include <Math\Stat\Normal.mqh> //+------------------------------------------------------------------+ //| CalculateHistogram | //+------------------------------------------------------------------+ void CalculateHistogram(double &data[],const int ncells=200,const string filename="normal.csv") { if(ArraySize(data)<=0) return; int n=ArraySize(data); //---'データ' 配列の最小および最大のデータ値を検索 double minv,maxv,range; minv=data[0]; maxv=data[0]; for(int i=1; i<n; i++) { minv=MathMin(minv,data[i]); maxv=MathMax(maxv,data[i]); } //---範囲を計算 range=maxv-minv; // Print("Min=",minv," Max=",maxv," range=",range," size=",n); if(range==0) return; //---ヒストグラム計算のためのアレイ double x[]; double y[]; //---ヒストグラムの値を設定 ArrayResize(x,ncells); ArrayResize(y,ncells); for(int i=0; i<ncells; i++) { x[i]=minv+i*range/(ncells-1); y[i]=0; } //---ヒストグラムを計算 for(int i=0; i<n; i++) { double v=(maxv-data[i])/range; int ind=int((v*(ncells-1))); y[ind]++; } //---ファイル名を確認 if(filename=="") return; //---書き込み用にファイルを開く ResetLastError(); int filehandle=FileOpen(filename,FILE_WRITE|FILE_TXT|FILE_ANSI); //---ファイルにデータを書き込む if(filehandle!=INVALID_HANDLE) { for(int i=0; i<ncells; i++) { string str=StringFormat("%6.20f;%6.20f",x[i],y[i]); FileWrite(filehandle,str); } FileClose(filehandle); PrintFormat("Histogram saved to file %s",filename); } else PrintFormat("Error calling FileOpen, error code=%d",GetLastError()); } //+------------------------------------------------------------------+ //|プログラム開始関数をスクリプト | //+------------------------------------------------------------------+ void OnStart() { //--- 1. ランダム変数の確率を計算します。 //---[mu シグマ、mu + シグマ] の範囲内の mu および sigma のパラメーターを持つ普通のルールに従って分散 //---分布パラメーターを設定 double mu=5.0; double sigma=1.0; //---間隔を設定 double x1=mu-sigma; double x2=mu+sigma; //---確率の計算用の変数 double cdf1,cdf2,probability; //---エラー コードの変数 int error_code1,error_code2; //---分布関数の値を計算します。 cdf1=MathCumulativeDistributionNormal(x1,mu,sigma,error_code1); cdf2=MathCumulativeDistributionNormal(x2,mu,sigma,error_code2); //---エラー コードをチェック if(error_code1==ERR_OK && error_code2==ERR_OK) { //---確率を計算 probability=cdf2-cdf1; //---結果を出力 PrintFormat("x1=%5.8f, x2=%5.8f, Probability=%5.8f",x1,x2,probability); } //--- 2. Mu および sigma パラメーターを持つ普通のルールに従って分散ランダム変数 x の値の範囲を検索します。 //---mu と 95% の信頼確率に対応する対称です。 //---確率を設定 probability=0.95; //---間隔の境界で確率を設定 double p1=(1.0-probability)*0.5; double p2=probability+(1.0-probability)*0.5; //---間隔の範囲を計算します。 x1=MathQuantileNormal(p1,mu,sigma,error_code1); x2=MathQuantileNormal(p2,mu,sigma,error_code2); //---エラー コードをチェック if(error_code1==ERR_OK && error_code2==ERR_OK) { //---結果を出力 PrintFormat("x1=%5.8f, x2=%5.8f",x1,x2); } //--- 3. Mu および sigma パラメーターを持つ普通のルールに従って分散 1000000 の乱数を生成します。 //---4つの最初のモーメント、得られた値のヒストグラムを計算し、理論値と比較 //---値の数に設定し、配列を準備 int data_count=1000000; double data[]; ArrayResize(data,data_count); //---ランダムな値を生成し、配列に格納 for(int i=0; i<data_count; i++) { data[i]=MathRandomNormal(mu,sigma,error_code1); } //---初期値の計算のためのデータのインデックス設定 int start=0; int count=data_count; //---生成された値の最初の4 のモーメントを計算 double mean=MathMean(data,start,count); double variance=MathVariance(data,start,count); double skewness=MathSkewness(data,start,count); double kurtosis=MathKurtosis(data,start,count); //---理論的なモーメントのための変数 double normal_mean=0; double normal_variance=0; double normal_skewness=0; double normal_kurtosis=0; //---計算されるモーメントの値を表示 PrintFormat(" mean=%.10f, variance=%.10f skewness=%.10f kurtosis=%.10f",mean,variance,skewness,kurtosis); //---モーメントの理論値を計算し、得られた値との比較 if(MathMomentsNormal(mu,sigma,normal_mean,normal_variance,normal_skewness,normal_kurtosis,error_code1)) { PrintFormat("Normal mean=%.10f, Normal variance=%.10f Normal skewness=%.10f Normal kurtosis=%.10f",normal_mean,normal_variance,normal_skewness,normal_kurtosis); PrintFormat("delta mean=%.4f, delta variance=%.4f delta skewness=%.4f delta kurtosis=%.4f",mean-normal_mean,variance-normal_variance,skewness-normal_skewness,kurtosis-normal_kurtosis); } //---分布ヒストグラムを計算し、それを normal.csv ファイルに保存 int ncells=50; CalculateHistogram(data,ncells,"normal.csv"); }
スクリプトの実行結果:
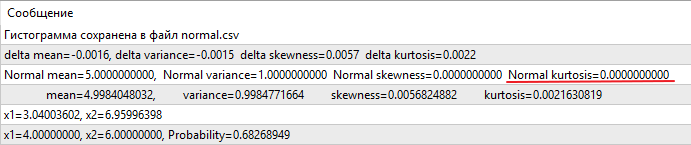
図1TestNormal.mq5 スクリプト操作の結果
注、'尖度' パラメーターの計算をすべて値の使用"kurtosis=kurtosis-3"、すなわち正規分布それが 0 に等しい。
計算されたヒストグラムは normal.csv ファイル (図 2) に保存されます。
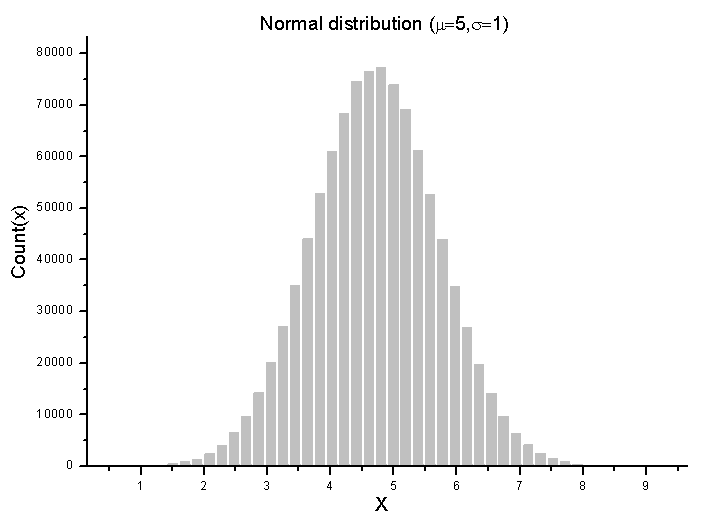
図 2。正規分布に従って生成される乱数の分布ヒストグラム mu = 5 とシグマ = 1
5. 計算速度の比較
統計関数の計算速度を比較するには、確率密度関数 (pdf)、累積分布関数 (cdf)、等量の計算関数と擬似ランダム番号生成関数の計算時間を測定するためのスクリプトがあります。
51 値の配列の計算を行いました。0 から 1 の範囲で連続分布関数値の計算が実行され、離散分布 - 0 から 50 までです。R 言語の統計関数の計算時間は、マイクロ ベンチ マークのライブラリを使用して行われています。MQL5 を関数の計算時間は、 GetMicrosecondCount()関数で測定されています。TestStatBenchmark.mq5 計算スクリプトは、terminal_data_folder\MQL5\Scripts\UnitTests\Statにあります。付録は、R と計算速度の測定の結果のスクリプトです。
この計算は、インテル Core i7-4790、CPU 3.6 Ghz、16 GB の RAM、10 Windows x64 で行われています。
測定結果 (単位 μ s (マイクロ秒))、表 3 に示す計算時間の結果。
| No. | Distribution | MQL5 時間計算 the PDF (µs) | 計算するための R の時間 the PDF (µs) | PDF R/MQL5 を | MQL5 時間計算 the CDF (µs) | 計算するための R の時間 the CDF (µs) | CDF R/MQL5 | MQL5 を時間計算 the quantiles (µs) | 計算するための R の時間 the quantiles (µs) | Quantile R/MQL5 | MQL5 を生成 random numbers (µs) | 生成するための R の時間 random numbers (µs) | Random R/MQL5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Binomial | 4.39 | 11.663 | 2.657 | 13.65 | 25.316 | 1.855 | 50.18 | 66.845 | 1.332 | 318.73 | 1816.463 | 5.699 |
| 2 | Beta | 1.74 | 17.352 | 9.972 | 4.76 | 15.076 | 3.167 | 48.72 | 129.992 | 2.668 | 688.81 | 1723.45 | 2.502 |
| 3 | Gamma | 1.31 | 8.251 | 6.347 | 8.09 | 14.792 | 1.828 | 50.83 | 64.286 | 1.265 | 142.84 | 1281.707 | 8.973 |
| 60 | Cauchy | 0.45 | 1.423 | 3.162 | 1.33 | 15.078 | 11.34 | 1.37 | 2.845 | 2.077 | 224.19 | 588.517 | 2.625 |
| 5 | Exponential | 0.85 | 3.13 | 3.682 | 0.77 | 2.845 | 3.695 | 0.53 | 2.276 | 4.294 | 143.18 | 389.406 | 2.72 |
| 6 | Uniform | 0.42 | 2.561 | 6.098 | 0.45 | 1.423 | 3.162 | 0.18 | 2.846 | 15.81 | 40.3 | 247.467 | 6.141 |
| 7 | Geometric | 2.3 | 5.121 | 2.227 | 2.12 | 4.552 | 2.147 | 0.81 | 5.407 | 6.675 | 278 | 1078.045 | 3.879 |
| 8 | Hypergeometric | 1.85 | 11.095 | 5.997 | 0.9 | 8.819 | 9.799 | 0.75 | 9.957 | 13.28 | 302.55 | 880.356 | 2.91 |
| 9 | Logistic | 1.27 | 4.267 | 3.36 | 1.11 | 4.267 | 3.844 | 0.71 | 3.13 | 4.408 | 178.65 | 626.632 | 3.508 |
| 10 | Weibull | 2.99 | 5.69 | 1.903 | 2.74 | 4.268 | 1.558 | 2.64 | 6.828 | 2.586 | 536.37 | 1558.472 | 2.906 |
| 11 | Poisson | 2.91 | 5.974 | 2.053 | 6.26 | 8.534 | 1.363 | 3.43 | 13.085 | 3.815 | 153.59 | 303.219 | 1.974 |
| 12 | F | 3.86 | 10.241 | 2.653 | 9.94 | 22.472 | 2.261 | 65.47 | 135.396 | 2.068 | 1249.22 | 1801.955 | 1.442 |
| 13 | カイ二乗 | 2.47 | 5.974 | 2.419 | 7.71 | 13.37 | 1.734 | 44.11 | 61.725 | 1.399 | 210.24 | 1235.059 | 5.875 |
| 14 | 非心カイ二乗 | 8.05 | 14.223 | 1.767 | 45.61 | 209.068 | 4.584 | 220.66 | 10342.96 | 46.873 | 744.45 | 1997.653 | 2.683 |
| 15 | 非心 F | 19.1 | 28.446 | 1.489 | 14.67 | 46.935 | 3.199 | 212.21 | 2561.991 | 12.073 | 1848.9 | 2912.141 | 1.575 |
| 16 | 非心 Beta | 16.3 | 26.739 | 1.64 | 10.48 | 43.237 | 4.126 | 153.66 | 2290.915 | 14.909 | 2686.82 | 2839.893 | 1.057 |
| 17 | 負の二項 | 6.13 | 11.094 | 1.81 | 12.21 | 19.627 | 1.607 | 14.05 | 60.019 | 4.272 | 1130.39 | 1936.498 | 1.713 |
| 18 | Normal | 1.15 | 4.267 | 3.71 | 0.81 | 3.983 | 4.917 | 0.7 | 2.277 | 3.253 | 293.7 | 696.321 | 2.371 |
| 19 | Lognormal | 1.99 | 5.406 | 2.717 | 3.19 | 8.819 | 2.765 | 3.18 | 6.259 | 1.968 | 479.75 | 1269.761 | 2.647 |
| 20 | T | 2.32 | 11.663 | 5.027 | 8.01 | 19.059 | 2.379 | 50.23 | 58.596 | 1.167 | 951.58 | 1425.92 | 1.498 |
| 21 | 非心 T | 38.47 | 86.757 | 2.255 | 27.75 | 39.823 | 1.435 | 1339.51 | 1930.524 | 1.441 | 1550.27 | 1699.84 | 1.096 |
| < MQL5 PDF R/> | 3.474 | < MQL5 CDF R/> | 3.465 | <Quantile R/MQL5> | 7.03 | <Random R/MQL5> | 3.13 |
表4。R と MQL5 の統計関数のミリ秒単位の計算時間
R の最小時間の値を取られ、MQL5 を平均値 (pdf_mean、cdf_mean、quantile_mean、random_mean) が行われました。
表3 に示すような条件下でも、MQL5 を統計ライブラリ関数の計算が実行されること数回 r. のそれらより速く平均して、MQL5 は R関数の比較バージョンと比較して、C++ で書かれていることを考慮しても 3 〜 7 倍速く計算します。
実際、C++ の実装よりも速いことが判明し、 MQL5 をコンパイラの質の高さを示しています。速度の大幅な向上を与えることができ、サードパーティ製の DLL を使用する必要はなくなります。
6. R で検出された計算エラー
R のテスト中に非心 t 分布の分位数の計算でエラーが検出されました。
例えば:
> n <- 10 > k <- seq(0,1,by=1/n) > nt_pdf<-dt(k, 10,8, log = FALSE) > nt_cdf<-pt(k, 10,8, log = FALSE) > nt_quantile<-qt(nt_cdf, 10,8, log = FALSE) > nt_pdf [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e-13 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11 > nt_cdf [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12 > k [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 > nt_quantile [1] -Inf -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 [7] -1.340781e + 154 7.000000e-01 8.000000e-01 9.000000e-01 1.000000e + 00
スチューデントの t 分布を計算するには、R 言語は、レンス [6] によって提案されたAS 243アルゴリズムを使用します。この方法の利点は、不完全なベータ関数を持つ無限級数メンバーの高速逐次計算です。しかし、系列メンバーの総和中精度評価を間違えて、このアルゴリズムが非心母数のデルタ パラメーターの値が大きいため特にエラー (記事 [7] で表 2) につながること、記事 [7] を示しました。[7] 著者は、非心 t 分布の確率の再帰的な計算の修正アルゴリズムを提案しました.
MQL5 を統計ライブラリは、正確な結果を提供する記事 [7] で提案されている確率を計算するための正しいアルゴリズムを使用します。
注意すべきポイントは、ガンマ、カイ 2乗、非心カイ二乗分布の確率密度の定義 R 言語で x = 0 につながる無限の表現です。
> dgamma(0,0.5,1) [1] Inf > dchisq(0,df=0.5,ncp=1) [1] Inf > dchisq(0,df=0.5,ncp=0) [1] Inf
したがって、R 言語の制限値の時点で確率密度の定義に x = 0が使用されます。無限にもかかわらず x = 0、統合、および密度の積分の中に、divergencies は発生しません。
確率を計算する場合 (たとえば、x = 0.1)、Wolfram Alpha (ガンマとカイ二乗、 NoncentralChiSquare) からの値が一致します。
> pgamma(0.1,0.5,1) [1] 0.3452792 > pchisq(0.1,df=0.5,ncp=0) [1] 0.5165553 > pchisq(0.1,df=0.5,ncp=1) [1] 0.3194965
x = 0でWolfram Alpha (Mathematica) と Matlab を作る点で密度の異なる定義の使用。
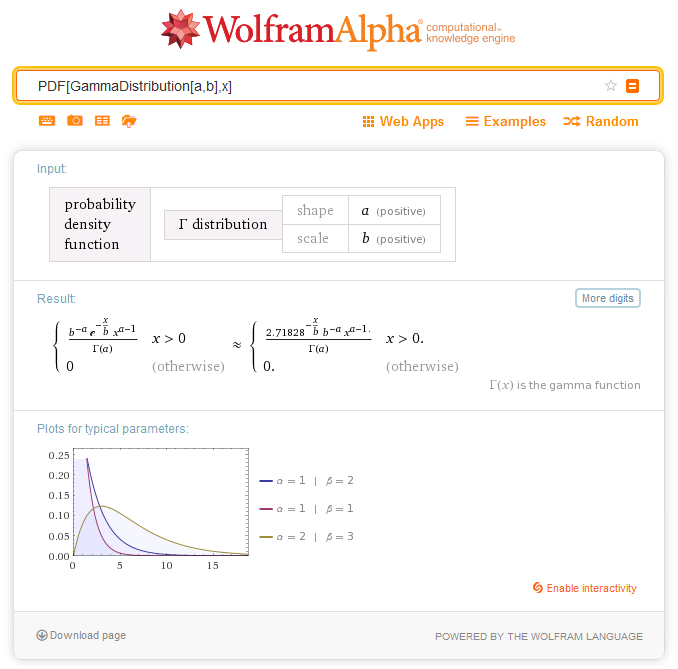
図3。ウルフラムアルファのガンマ分布の確率密度の定義
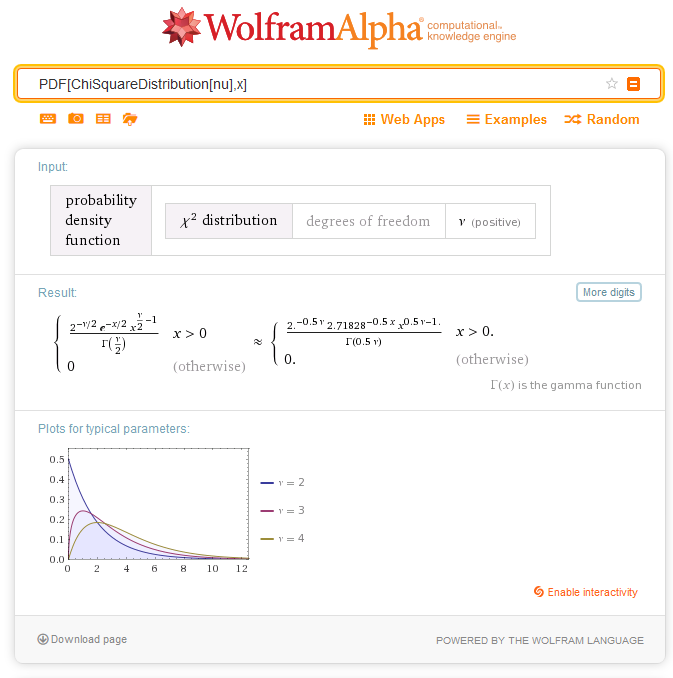
図4。ウルフラムアルファのカイ二乗分布の確率密度の定義
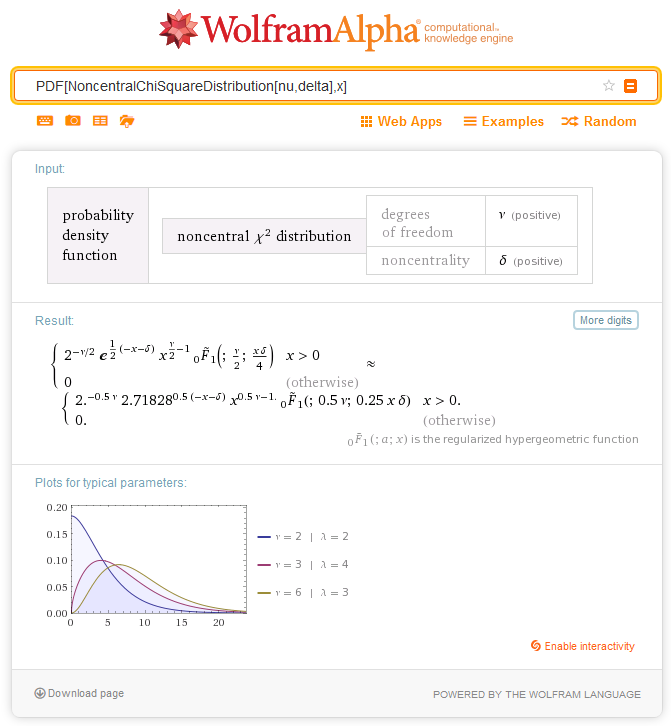
図 5。ウルフラムアルファの非心カイ二乗分布の確率密度の定義
MQL5 を統計ライブラリの時点でこれらの分布の密度で x = 0 は定義上ゼロに等しいと見なされます。
計算精度を確保し、ライブラリの品質をテストするサード パーティの開発者を許可するには、複数の単体テスト スクリプトが標準付属品に含まれます。/Scripts/UnitTests/Stat フォルダーにあります。
結論
この記事では、MQL5 を統計ライブラリの主な関数を扱いました。
データの統計的特性の計算を実行して、R言語で実装されている基本的な統計分布で動作するようにしました。また、ライブラリには、実際の分布の適合性の程度を評価できるように分布の理論的モーメントを計算する関数も含まれます。
MQL5 の新しい 64 ビット コンパイラのパフォーマンスが高いため、大幅に研究のプロセスを容易にし、速く実行されます。
レファレンス
- 統計的コンピューティング R.
- N. Balakrishnan, N. L. Johnson, S. Kotz "Continuous Univariate Distributions: Volume 1." Wiley-Interscience, 1994.
- N. Balakrishnan, N. L. Johnson, S. Kotz "Continuous Univariate Distributions: Volume 2." Wiley-Interscience, 2000.
- N. L. Johnson, S. Kotz, A. W. Kemp "Univariate Discrete Distributions", Wiley-Interscience, 2005.
- Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions", 4th Edition, John Wiley and Sons, 2011.
- Lenth, R.V., "Cumulative distribution function of the noncentral t distribution", Appled Statistics, vol. 38 (1989), 185–189.
- D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient", Computational Statistics & Data Analysis, 43, (2003), 249-267
アペンディクス統計関数の計算時間の測定結果
R とその操作結果による統計関数の計算時間を評価するスクリプトは、TestStatBenchmark.mq5 スクリプト操作の結果と同様に、付録にあります。
Rスクリプト:
n <- 50
k <- seq(0,n,by=1)
binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
print(binomial_pdf)
print(binomial_cdf)
print(binomial_quantile)
print(binomial_random)
n <- 50
k <- seq(0,1,by=1/n)
beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
print(beta_pdf)
print(beta_cdf)
print(beta_quantile)
print(beta_random)
n <- 50
k <- seq(0,1,by=1/n)
gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
print(gamma_pdf)
print(gamma_cdf)
print(gamma_quantile)
print(gamma_random)
n <- 50
k <- seq(0,1,by=1/n)
cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
print(cauchy_pdf)
print(cauchy_cdf)
print(cauchy_quantile)
print(cauchy_random)
n <- 50
k <- seq(0,1,by=1/n)
exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
exponential_random <- microbenchmark(random<-rexp(10000, 2))
print(exponential_pdf)
print(exponential_cdf)
print(exponential_quantile)
print(exponential_random)
n <- 50
k <- seq(0,1,by=1/n)
uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
print(uniform_pdf)
print(uniform_cdf)
print(uniform_quantile)
print(uniform_random)
n <- 50
k <- seq(0,n,by=1)
geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
print(geometric_pdf)
print(geometric_cdf)
print(geometric_quantile)
print(geometric_random)
n <- 50
k <- seq(0,n,by=1)
hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
print(hypergeometric_pdf)
print(hypergeometric_cdf)
print(hypergeometric_quantile)
print(hypergeometric_random)
n <- 50
k <- seq(0,1,by=1/n)
logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
print(logistic_pdf)
print(logistic_cdf)
print(logistic_quantile)
print(logistic_random)
n <- 50
k <- seq(0,1,by=1/n)
weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
print(weibull_pdf)
print(weibull_cdf)
print(weibull_quantile)
print(weibull_random)
n <- 50
k <- seq(0,n,by=1)
poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
poisson_random <- microbenchmark(random<-rpois(10000, 1))
print(poisson_pdf)
print(poisson_cdf)
print(poisson_quantile)
print(poisson_random)
n <- 50
k <- seq(0,1,by=1/n)
f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
f_random <- microbenchmark(random<-rf(10000, 10,20))
print(f_pdf)
print(f_cdf)
print(f_quantile)
print(f_random)
n <- 50
k <- seq(0,1,by=1/n)
chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
print(chisquare_pdf)
print(chisquare_cdf)
print(chisquare_quantile)
print(chisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
print(nchisquare_pdf)
print(nchisquare_cdf)
print(nchisquare_quantile)
print(nchisquare_random)
n <- 50
k <- seq(0,1,by=1/n)
nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
print(nf_pdf)
print(nf_cdf)
print(nf_quantile)
print(nf_random)
n <- 50
k <- seq(0,1,by=1/n)
nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
print(nbeta_pdf)
print(nbeta_cdf)
print(nbeta_quantile)
print(nbeta_random)
n <- 50
k <- seq(0,n,by=1)
nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
print(nbinom_pdf)
print(nbinom_cdf)
print(nbinom_quantile)
print(nbinom_random)
n <- 50
k <- seq(0,1,by=1/n)
normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
print(normal_pdf)
print(normal_cdf)
print(normal_quantile)
print(normal_random)
n <- 50
k <- seq(0,1,by=1/n)
lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
print(lognormal_pdf)
print(lognormal_cdf)
print(lognormal_quantile)
print(lognormal_random)
n <- 50
k <- seq(0,1,by=1/n)
t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
t_random <- microbenchmark(random<-rt(10000, 8))
print(t_pdf)
print(t_cdf)
print(t_quantile)
print(t_random)
n <- 50
k <- seq(0,1,by=1/n)
nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
nt_random <- microbenchmark(random<-rt(10000, 10,1))
print(nt_pdf)
print(nt_cdf)
print(nt_quantile)
print(nt_random)
Result:
R version 3.2.5 (2016-04-14) -- "Very, Very Secure Dishes" Copyright (C) 2016 The R Foundation for Statistical Computing Platform: x86_64-w64-mingw32/x64 (64-bit) R is free software and comes with ABSOLUTELY NO WARRANTY. You are welcome to redistribute it under certain conditions. Type 'license()' or 'licence()' for distribution details. R is a collaborative project with many contributors. Type 'contributors()' for more information and 'citation()' on how to cite R or R packages in publications. Type 'demo()' for some demos, 'help()' for on-line help, or 'help.start()' for an HTML browser interface to help. Type 'q()' to quit R. [Workspace loaded from ~/Test/111/.RData] > library(microbenchmark) > n <- 50 > k <- seq(0,n,by=1) > binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE)) > binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE)) > binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE)) > binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6)) > print(binomial_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbinom(k, 50, 0.6, log = FALSE) 11.663 11.948 13.37888 12.233 12.233 47.503 100 > print(binomial_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbinom(k, 50, 0.6, log = FALSE) 25.316 25.602 29.63195 25.886 35.557 93.868 100 > print(binomial_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbinom(cdf, 50, 0.6, log = FALSE) 66.845 67.13 72.09098 67.699 73.672 130.276 100 > print(binomial_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbinom(10000, 50, 0.6) 1.816463 1.89056 1.948185 1.929814 1.989262 2.308835 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE)) > beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE)) > beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE)) > beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,)) > print(beta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, log = FALSE) 17.352 17.637 19.99512 17.638 18.206 109.797 100 > print(beta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, log = FALSE) 15.076 15.361 16.83489 15.646 15.9295 75.379 100 > print(beta_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, log = FALSE) 129.992 130.277 140.8325 131.4145 143.93 201.672 100 > print(beta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, ) 1.72345 1.794132 1.862292 1.836515 1.901226 2.823963 100 > > n <- 50 > k <- seq(0,1,by=1/n) > gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE)) > gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE)) > gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE)) > gamma_random <- microbenchmark(random<-rgamma(10000, 1,1)) > print(gamma_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgamma(k, 1, 1, log = FALSE) 8.251 8.8195 10.92684 9.104 9.389 122.312 100 > print(gamma_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 1, 1, log = FALSE) 14.792 15.646 20.43306 20.055 21.334 106.099 100 > print(gamma_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgamma(cdf, 1, 1, log = FALSE) 64.286 64.854 70.09419 65.139 67.13 162.988 100 > print(gamma_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgamma(10000, 1, 1) 1.281707 1.330347 1.410961 1.362631 1.421226 2.322204 100 > > n <- 50 > k <- seq(0,1,by=1/n) > cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE)) > cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE)) > cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE)) > cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1)) > print(cauchy_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dcauchy(k, 2, 1, log = FALSE) 1.423 1.708 2.8431 1.709 2.278 67.415 100 > print(cauchy_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgamma(k, 2, 1, log = FALSE) 15.078 15.646 16.51914 15.93 16.215 33.281 100 > print(cauchy_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qcauchy(cdf, 2, 1, log = FALSE) 2.845 3.13 3.8044 3.131 3.415 56.606 100 > print(cauchy_random) Unit: microseconds expr min lq mean median uq max neval random <- rcauchy(10000, 2, 1) 588.517 615.823 663.8658 637.7255 674.845 1520.356 100 > > n <- 50 > k <- seq(0,1,by=1/n) > exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE)) > exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE)) > exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE)) > exponential_random <- microbenchmark(random<-rexp(10000, 2)) > print(exponential_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dexp(k, 2, log = FALSE) 3.13 3.414 4.08887 3.415 3.415 67.699 100 > print(exponential_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pexp(k, 2, log = FALSE) 2.845 3.13 4.38756 3.414 3.5565 58.597 100 > print(exponential_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qexp(cdf, 2, log = FALSE) 2.276 2.561 3.80729 2.5615 2.846 44.659 100 > print(exponential_random) Unit: microseconds expr min lq mean median uq max neval random <- rexp(10000, 2) 389.406 408.8895 440.9583 418.4185 444.8715 1371.875 100 > > > n <- 50 > k <- seq(0,1,by=1/n) > uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE)) > uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE)) > uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE)) > uniform_random <- microbenchmark(random<-runif(10000, 0, 10)) > print(uniform_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dunif(k, 0, 10, log = FALSE) 2.561 2.846 3.78734 3.13 3.131 66.277 100 > print(uniform_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- punif(k, 0, 10, log = FALSE) 1.423 1.708 2.41635 1.992 1.993 53.477 100 > print(uniform_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qunif(cdf, 0, 10, log = FALSE) 2.846 3.131 5.13561 3.415 3.6995 82.774 100 > print(uniform_random) Unit: microseconds expr min lq mean median uq max neval random <- runif(10000, 0, 10) 247.467 258.7035 317.1567 279.6095 357.2635 1267.769 100 > > > n <- 50 > k <- seq(0,n,by=1) > geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE)) > geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE)) > geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE)) > geometric_random <- microbenchmark(random<-rgeom(10000, 0.3)) > print(geometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dgeom(k, 0.3, log = FALSE) 5.121 5.122 6.14258 5.406 5.406 60.304 100 > print(geometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pgeom(k, 0.3, log = FALSE) 4.552 4.836 5.50548 4.837 5.1215 46.081 100 > print(geometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qgeom(cdf, 0.3, log = FALSE) 5.407 5.974 7.12107 5.975 6.259 71.681 100 > print(geometric_random) Unit: milliseconds expr min lq mean median uq max neval random <- rgeom(10000, 0.3) 1.078045 1.127681 1.192608 1.156125 1.199361 1.604267 100 > > n <- 50 > k <- seq(0,n,by=1) > hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE)) > hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE)) > hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE)) > hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11)) > print(hypergeometric_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dhyper(k, 12, 38, 11, log = FALSE) 11.095 13.939 17.07667 14.224 14.935 101.548 100 > print(hypergeometric_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- phyper(k, 12, 38, 11, log = FALSE) 8.819 9.387 12.60515 9.672 12.517 62.01 100 > print(hypergeometric_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qhyper(cdf, 12, 38, 11, log = FALSE) 9.957 10.3835 13.00618 10.81 11.948 64.286 100 > print(hypergeometric_random) Unit: microseconds expr min lq mean median uq max neval random <- rhyper(10000, 12, 38, 11) 880.356 938.9515 993.8324 963.9835 996.8365 1375.289 100 > > n <- 50 > k <- seq(0,1,by=1/n) > logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE)) > logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE)) > logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE)) > logistic_random <- microbenchmark(random<-rlogis(10000, 1,2)) > print(logistic_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlogis(k, 1, 2, log = FALSE) 4.267 4.552 5.94354 4.553 4.837 53.477 100 > print(logistic_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plogis(k, 1, 2, log = FALSE) 4.267 4.552 5.96056 4.837 4.837 96.428 100 > print(logistic_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlogis(cdf, 1, 2, log = FALSE) 3.13 3.415 4.1742 3.415 3.699 56.036 100 > print(logistic_random) Unit: microseconds expr min lq mean median uq max neval random <- rlogis(10000, 1, 2) 626.632 649.956 696.2128 675.2725 715.805 1589.191 100 > > n <- 50 > k <- seq(0,1,by=1/n) > weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE)) > weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE)) > weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE)) > weibull_random <- microbenchmark(random<-rweibull(10000, 5,1)) > print(weibull_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dweibull(k, 5, 1, log = FALSE) 5.69 5.974 7.21775 5.975 6.259 85.619 100 > print(weibull_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pweibull(k, 5, 1, log = FALSE) 4.268 4.552 7.83782 4.8365 7.966 90.455 100 > print(weibull_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qweibull(cdf, 5, 1, log = FALSE) 6.828 7.112 7.96587 7.113 7.397 48.641 100 > print(weibull_random) Unit: milliseconds expr min lq mean median uq max neval random <- rweibull(10000, 5, 1) 1.558472 1.59744 1.659753 1.632853 1.679502 2.616603 100 > > n <- 50 > k <- seq(0,n,by=1) > poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE)) > poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE)) > poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE)) > poisson_random <- microbenchmark(random<-rpois(10000, 1)) > print(poisson_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dpois(k, 1, log = FALSE) 5.974 6.543 7.30316 6.544 6.828 54.046 100 > print(poisson_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- ppois(k, 1, log = FALSE) 8.534 8.819 10.25846 9.104 9.388 64.286 100 > print(poisson_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qpois(cdf, 1, log = FALSE) 13.085 13.086 14.37438 13.37 13.654 61.157 100 > print(poisson_random) Unit: microseconds expr min lq mean median uq max neval random <- rpois(10000, 1) 303.219 314.8815 327.5787 324.552 341.335 373.477 100 > > n <- 50 > k <- seq(0,1,by=1/n) > f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE)) > f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE)) > f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE)) > f_random <- microbenchmark(random<-rf(10000, 10,20)) > print(f_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, log = FALSE) 10.241 10.81 12.43159 10.811 11.095 71.112 100 > print(f_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, log = FALSE) 22.472 22.757 25.66972 23.041 23.3265 86.189 100 > print(f_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, log = FALSE) 135.396 136.25 166.7057 157.7255 186.171 255.717 100 > print(f_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20) 1.801955 1.889706 1.947645 1.929528 1.98272 2.725546 100 > > n <- 50 > k <- seq(0,1,by=1/n) > chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE)) > chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE)) > chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE)) > chisquare_random <- microbenchmark(random<-rchisq(10000, 2)) > print(chisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, log = FALSE) 5.974 6.259 7.06416 6.4015 6.544 52.339 100 > print(chisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, log = FALSE) 13.37 13.655 15.46392 13.655 13.94 99.841 100 > print(chisquare_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, log = FALSE) 61.725 62.2945 68.40176 62.7215 72.25 132.553 100 > print(chisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2) 1.235059 1.29408 1.38993 1.333903 1.401743 2.205582 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE)) > nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE)) > nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE)) > nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1)) > print(nchisquare_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dchisq(k, 2, 1, log = FALSE) 14.223 14.509 17.3866 14.793 15.6455 37.548 100 > print(nchisquare_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pchisq(k, 2, 1, log = FALSE) 209.068 210.49 231.6357 223.1475 240.499 309.193 100 > print(nchisquare_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qchisq(cdf, 2, 1, log = FALSE) 10.34296 10.65955 10.90239 10.83733 11.02563 12.31558 100 > print(nchisquare_random) Unit: milliseconds expr min lq mean median uq max neval random <- rchisq(10000, 2, 1) 1.997653 2.073457 2.187417 2.114845 2.183111 3.134576 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE)) > nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE)) > nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE)) > nf_random <- microbenchmark(random<-rf(10000, 10,20,2)) > print(nf_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- df(k, 10, 20, 2, log = FALSE) 28.446 30.153 34.12338 30.438 31.291 68.836 100 > print(nf_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pf(k, 10, 20, 2, log = FALSE) 46.935 61.8685 64.53899 63.433 65.708 106.953 100 > print(nf_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qf(cdf, 10, 20, 2, log = FALSE) 2.561991 2.640355 2.719223 2.68999 2.744461 3.737598 100 > print(nf_random) Unit: milliseconds expr min lq mean median uq max neval random <- rf(10000, 10, 20, 2) 2.912141 2.989225 3.100073 3.035163 3.110825 4.062433 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE)) > nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE)) > nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE)) > nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1)) > print(nbeta_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dbeta(k, 2, 4, 1, log = FALSE) 26.739 27.308 31.31301 27.592 30.5795 56.891 100 > print(nbeta_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pbeta(k, 2, 4, 1, log = FALSE) 43.237 43.806 55.11814 56.321 57.7435 167.255 100 > print(nbeta_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qbeta(cdf, 2, 4, 1, log = FALSE) 2.290915 2.375111 2.440959 2.431146 2.49927 2.644764 100 > print(nbeta_random) Unit: milliseconds expr min lq mean median uq max neval random <- rbeta(10000, 2, 4, 1) 2.839893 3.002737 3.143906 3.073848 3.150932 4.302789 100 > > n <- 50 > k <- seq(0,n,by=1) > nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE)) > nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE)) > nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE)) > nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5)) > print(nbinom_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnbinom(k, 2, 0.5, log = FALSE) 11.094 11.379 13.37031 11.664 11.948 78.508 100 > print(nbinom_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnbinom(k, 2, 0.5, log = FALSE) 19.627 19.913 22.94469 20.197 20.482 130.277 100 > print(nbinom_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnbinom(cdf, 2, 0.5, log = FALSE) 60.019 60.588 69.73866 61.442 74.099 122.028 100 > print(nbinom_random) Unit: milliseconds expr min lq mean median uq max neval random <- rnbinom(10000, 2, 0.5) 1.936498 2.029226 2.086237 2.072035 2.125084 2.354061 100 > > n <- 50 > k <- seq(0,1,by=1/n) > normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE)) > normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE)) > normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE)) > normal_random <- microbenchmark(random<-rnorm(10000, 1,1)) > print(normal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dnorm(k, 1, 1, log = FALSE) 4.267 4.552 5.7927 4.553 4.837 75.663 100 > print(normal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pnorm(k, 1, 1, log = FALSE) 3.983 4.269 5.94911 4.553 4.979 50.632 100 > print(normal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qnorm(cdf, 1, 1, log = FALSE) 2.277 2.561 3.42042 2.845 2.846 45.227 100 > print(normal_random) Unit: microseconds expr min lq mean median uq max neval random <- rnorm(10000, 1, 1) 696.321 728.747 779.1994 749.7965 778.3835 1541.12 100 > > n <- 50 > k <- seq(0,1,by=1/n) > lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE)) > lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE)) > lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE)) > lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6)) > print(lognormal_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dlnorm(k, 0.5, 0.6, log = FALSE) 5.406 5.69 6.89638 5.975 6.259 50.917 100 > print(lognormal_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- plnorm(k, 0.5, 0.6, log = FALSE) 8.819 9.387 12.3463 9.3885 12.6595 71.681 100 > print(lognormal_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qlnorm(cdf, 0.5, 0.6, log = FALSE) 6.259 6.544 7.38277 6.544 6.828 58.881 100 > print(lognormal_random) Unit: milliseconds expr min lq mean median uq max neval random <- rlnorm(10000, 0.5, 0.6) 1.269761 1.329209 1.380386 1.362632 1.401743 2.247395 100 > > n <- 50 > k <- seq(0,1,by=1/n) > t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE)) > t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE)) > t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE)) > t_random <- microbenchmark(random<-rt(10000, 8)) > print(t_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 8, log = FALSE) 11.663 12.233 15.71413 12.517 16.0725 76.517 100 > print(t_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 8, log = FALSE) 19.059 20.6235 23.23485 21.05 21.619 127.717 100 > print(t_quantile) Unit: microseconds expr min lq mean median uq max neval quantile <- qt(cdf, 8, log = FALSE) 58.596 58.882 64.84339 59.166 62.01 151.611 100 > print(t_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 8) 1.42592 1.480676 1.553132 1.51424 1.569565 2.44679 100 > > n <- 50 > k <- seq(0,1,by=1/n) > nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE)) > nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE)) > nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE)) > nt_random <- microbenchmark(random<-rt(10000, 10,1)) > print(nt_pdf) Unit: microseconds expr min lq mean median uq max neval pdf <- dt(k, 10, 1, log = FALSE) 86.757 88.037 92.88671 89.317 91.4505 130.276 100 > print(nt_cdf) Unit: microseconds expr min lq mean median uq max neval cdf <- pt(k, 10, 1, log = FALSE) 39.823 40.2505 44.51695 40.6765 49.352 70.829 100 > print(nt_quantile) Unit: milliseconds expr min lq mean median uq max neval quantile <- qt(cdf, 10, 1, log = FALSE) 1.930524 1.981866 2.038755 2.0224 2.079715 2.594987 100 > print(nt_random) Unit: milliseconds expr min lq mean median uq max neval random <- rt(10000, 10, 1) 1.69984 1.764693 1.867469 1.814044 1.893263 2.856959 100
Result of the TestStatBenchmark.mq5 operation script:
PP 0 13:06:15.252 TestStatBenchmark (EURUSD,H1)
KJ 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): pdf_mean=4.39, pdf_median=4.00, pdf_min=3.00, pdf_max=40.00, pdf_stddev=2.21, pdf_avgdev=0.95
MS 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): cdf_mean=13.65, cdf_median=12.00, cdf_min=11.00, cdf_max=54.00, cdf_stddev=4.09, cdf_avgdev=2.37
GF 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): quantile_mean=50.18, quantile_median=45.00, quantile_min=43.00, quantile_max=108.00, quantile_stddev=9.97, quantile_avgdev=7.41
QO 0 13:06:15.639 TestStatBenchmark (EURUSD,H1) Binomial time (microseconds): random_mean=318.73, random_median=312.00, random_min=284.00, random_max=478.00, random_stddev=28.74, random_avgdev=22.22
LP 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): pdf_mean=1.74, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.07, pdf_avgdev=0.53
EI 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): cdf_mean=4.76, cdf_median=4.00, cdf_min=3.00, cdf_max=68.00, cdf_stddev=3.07, cdf_avgdev=1.19
LM 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): quantile_mean=48.72, quantile_median=44.00, quantile_min=43.00, quantile_max=111.00, quantile_stddev=10.21, quantile_avgdev=6.96
QG 0 13:06:16.384 TestStatBenchmark (EURUSD,H1) Beta time (microseconds): random_mean=688.81, random_median=680.00, random_min=625.00, random_max=976.00, random_stddev=43.92, random_avgdev=31.81
HE 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): pdf_mean=1.31, pdf_median=1.00, pdf_min=1.00, pdf_max=13.00, pdf_stddev=0.82, pdf_avgdev=0.47
GL 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): cdf_mean=8.09, cdf_median=7.00, cdf_min=7.00, cdf_max=92.00, cdf_stddev=3.67, cdf_avgdev=1.40
CF 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): quantile_mean=50.83, quantile_median=46.00, quantile_min=45.00, quantile_max=106.00, quantile_stddev=9.27, quantile_avgdev=6.72
GR 0 13:06:16.587 TestStatBenchmark (EURUSD,H1) Gamma time (microseconds): random_mean=142.84, random_median=132.00, random_min=128.00, random_max=260.00, random_stddev=19.73, random_avgdev=15.32
QD 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): pdf_mean=0.45, pdf_median=0.00, pdf_min=0.00, pdf_max=11.00, pdf_stddev=0.85, pdf_avgdev=0.54
QK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): cdf_mean=1.33, cdf_median=1.00, cdf_min=1.00, cdf_max=12.00, cdf_stddev=0.81, cdf_avgdev=0.48
MR 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): quantile_mean=1.37, quantile_median=1.00, quantile_min=1.00, quantile_max=14.00, quantile_stddev=0.89, quantile_avgdev=0.51
IK 0 13:06:16.815 TestStatBenchmark (EURUSD,H1) Cauchy time (microseconds): random_mean=224.19, random_median=215.00, random_min=200.00, random_max=352.00, random_stddev=26.86, random_avgdev=20.34
PQ 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): pdf_mean=0.85, pdf_median=1.00, pdf_min=0.00, pdf_max=18.00, pdf_stddev=1.40, pdf_avgdev=0.54
GK 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): cdf_mean=0.77, cdf_median=1.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.94, cdf_avgdev=0.47
HE 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): quantile_mean=0.53, quantile_median=0.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.78, quantile_avgdev=0.54
HL 0 13:06:16.960 TestStatBenchmark (EURUSD,H1) Exponential time (microseconds): random_mean=143.18, random_median=130.00, random_min=128.00, random_max=272.00, random_stddev=21.58, random_avgdev=16.98
LK 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): pdf_mean=0.42, pdf_median=0.00, pdf_min=0.00, pdf_max=12.00, pdf_stddev=0.82, pdf_avgdev=0.52
CE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): cdf_mean=0.45, cdf_median=0.00, cdf_min=0.00, cdf_max=16.00, cdf_stddev=0.96, cdf_avgdev=0.55
LO 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): quantile_mean=0.18, quantile_median=0.00, quantile_min=0.00, quantile_max=1.00, quantile_stddev=0.38, quantile_avgdev=0.29
GE 0 13:06:17.002 TestStatBenchmark (EURUSD,H1) Uniform time (microseconds): random_mean=40.30, random_median=36.00, random_min=35.00, random_max=83.00, random_stddev=7.61, random_avgdev=5.41
OP 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): pdf_mean=2.30, pdf_median=2.00, pdf_min=1.00, pdf_max=14.00, pdf_stddev=1.30, pdf_avgdev=0.52
DK 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): cdf_mean=2.12, cdf_median=2.00, cdf_min=1.00, cdf_max=18.00, cdf_stddev=1.69, cdf_avgdev=0.53
NE 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): quantile_mean=0.81, quantile_median=1.00, quantile_min=0.00, quantile_max=10.00, quantile_stddev=0.68, quantile_avgdev=0.39
IL 0 13:06:17.286 TestStatBenchmark (EURUSD,H1) Geometric time (microseconds): random_mean=278.00, random_median=271.00, random_min=251.00, random_max=429.00, random_stddev=28.23, random_avgdev=21.62
PG 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): pdf_mean=1.85, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.07, pdf_avgdev=0.48
CM 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): cdf_mean=0.90, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=0.85, cdf_avgdev=0.32
NP 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): quantile_mean=0.75, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.96, quantile_avgdev=0.48
FE 0 13:06:17.592 TestStatBenchmark (EURUSD,H1) Hypergeometric time (microseconds): random_mean=302.55, random_median=295.00, random_min=272.00, random_max=466.00, random_stddev=30.20, random_avgdev=22.99
ML 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): pdf_mean=1.27, pdf_median=1.00, pdf_min=0.00, pdf_max=91.00, pdf_stddev=3.04, pdf_avgdev=0.56
DR 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): cdf_mean=1.11, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.34, cdf_avgdev=0.40
IH 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): quantile_mean=0.71, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00, quantile_stddev=0.79, quantile_avgdev=0.47
GL 0 13:06:17.774 TestStatBenchmark (EURUSD,H1) Logistic time (microseconds): random_mean=178.65, random_median=164.00, random_min=162.00, random_max=309.00, random_stddev=24.09, random_avgdev=17.94
MJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): pdf_mean=2.99, pdf_median=3.00, pdf_min=2.00, pdf_max=17.00, pdf_stddev=1.63, pdf_avgdev=0.57
GD 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): cdf_mean=2.74, cdf_median=3.00, cdf_min=2.00, cdf_max=19.00, cdf_stddev=1.23, cdf_avgdev=0.58
FO 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): quantile_mean=2.64, quantile_median=2.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.64, quantile_avgdev=0.76
DJ 0 13:06:18.319 TestStatBenchmark (EURUSD,H1) Weibull time (microseconds): random_mean=536.37, random_median=526.00, random_min=483.00, random_max=759.00, random_stddev=46.99, random_avgdev=34.40
HR 0 13:06:18.485 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): pdf_mean=2.91, pdf_median=3.00, pdf_min=2.00, pdf_max=15.00, pdf_stddev=1.40, pdf_avgdev=0.58
IL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): cdf_mean=6.26, cdf_median=6.00, cdf_min=5.00, cdf_max=23.00, cdf_stddev=2.38, cdf_avgdev=1.07
HE 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): quantile_mean=3.43, quantile_median=3.00, quantile_min=2.00, quantile_max=20.00, quantile_stddev=1.48, quantile_avgdev=0.68
DL 0 13:06:18.486 TestStatBenchmark (EURUSD,H1) Poisson time (microseconds): random_mean=153.59, random_median=144.00, random_min=138.00, random_max=265.00, random_stddev=18.57, random_avgdev=13.99
IH 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): pdf_mean=3.86, pdf_median=4.00, pdf_min=3.00, pdf_max=21.00, pdf_stddev=1.78, pdf_avgdev=0.76
GS 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): cdf_mean=9.94, cdf_median=9.00, cdf_min=7.00, cdf_max=36.00, cdf_stddev=3.82, cdf_avgdev=2.15
OI 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): quantile_mean=65.47, quantile_median=59.00, quantile_min=57.00, quantile_max=147.00, quantile_stddev=12.99, quantile_avgdev=9.64
DE 0 13:06:19.814 TestStatBenchmark (EURUSD,H1) F time (microseconds): random_mean=1249.22, random_median=1213.00, random_min=1127.00, random_max=1968.00, random_stddev=117.69, random_avgdev=72.17
EL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): pdf_mean=2.47, pdf_median=2.00, pdf_min=2.00, pdf_max=13.00, pdf_stddev=1.32, pdf_avgdev=0.65
JK 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): cdf_mean=7.71, cdf_median=7.00, cdf_min=7.00, cdf_max=23.00, cdf_stddev=1.91, cdf_avgdev=0.88
KQ 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): quantile_mean=44.11, quantile_median=41.00, quantile_min=40.00, quantile_max=120.00, quantile_stddev=8.17, quantile_avgdev=5.38
CL 0 13:06:20.079 TestStatBenchmark (EURUSD,H1) ChiSquare time (microseconds): random_mean=210.24, random_median=196.00, random_min=190.00, random_max=437.00, random_stddev=29.14, random_avgdev=21.00
HD 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): pdf_mean=8.05, pdf_median=8.00, pdf_min=7.00, pdf_max=24.00, pdf_stddev=2.41, pdf_avgdev=1.09
MR 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): cdf_mean=45.61, cdf_median=42.00, cdf_min=41.00, cdf_max=97.00, cdf_stddev=8.25, cdf_avgdev=5.70
FN 0 13:06:21.098 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): quantile_mean=220.66, quantile_median=211.50, quantile_min=196.00, quantile_max=362.00, quantile_stddev=24.71, quantile_avgdev=19.45
LI 0 13:06:21.099 TestStatBenchmark (EURUSD,H1) Noncentral ChiSquare time (microseconds): random_mean=744.45, random_median=728.00, random_min=672.00, random_max=1082.00, random_stddev=62.42, random_avgdev=43.24
RE 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): pdf_mean=19.10, pdf_median=18.00, pdf_min=16.00, pdf_max=50.00, pdf_stddev=4.67, pdf_avgdev=2.64
FS 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): cdf_mean=14.67, cdf_median=13.00, cdf_min=12.00, cdf_max=39.00, cdf_stddev=3.94, cdf_avgdev=2.44
EN 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): quantile_mean=212.21, quantile_median=203.00, quantile_min=189.00, quantile_max=347.00, quantile_stddev=24.37, quantile_avgdev=19.30
EF 0 13:06:23.194 TestStatBenchmark (EURUSD,H1) Noncentral F time (microseconds): random_mean=1848.90, random_median=1819.00, random_min=1704.00, random_max=2556.00, random_stddev=118.75, random_avgdev=78.66
EN 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): pdf_mean=16.30, pdf_median=15.00, pdf_min=14.00, pdf_max=43.00, pdf_stddev=4.32, pdf_avgdev=2.43
EP 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): cdf_mean=10.48, cdf_median=10.00, cdf_min=8.00, cdf_max=32.00, cdf_stddev=3.02, cdf_avgdev=1.72
ME 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): quantile_mean=153.66, quantile_median=141.00, quantile_min=135.00, quantile_max=283.00, quantile_stddev=20.83, quantile_avgdev=16.16
QJ 0 13:06:26.061 TestStatBenchmark (EURUSD,H1) Noncentral Beta time (microseconds): random_mean=2686.82, random_median=2649.00, random_min=2457.00, random_max=3753.00, random_stddev=150.32, random_avgdev=98.23
OO 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): pdf_mean=6.13, pdf_median=6.00, pdf_min=5.00, pdf_max=24.00, pdf_stddev=2.38, pdf_avgdev=1.22
DG 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): cdf_mean=12.21, cdf_median=11.00, cdf_min=11.00, cdf_max=33.00, cdf_stddev=3.07, cdf_avgdev=1.58
LJ 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): quantile_mean=14.05, quantile_median=13.00, quantile_min=12.00, quantile_max=82.00, quantile_stddev=4.81, quantile_avgdev=2.28
EM 0 13:06:27.225 TestStatBenchmark (EURUSD,H1) Negative Binomial time (microseconds): random_mean=1130.39, random_median=1108.00, random_min=1039.00, random_max=1454.00, random_stddev=69.41, random_avgdev=51.70
GP 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): pdf_mean=1.15, pdf_median=1.00, pdf_min=0.00, pdf_max=19.00, pdf_stddev=1.34, pdf_avgdev=0.45
OI 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): cdf_mean=0.81, cdf_median=1.00, cdf_min=0.00, cdf_max=17.00, cdf_stddev=1.16, cdf_avgdev=0.49
CN 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): quantile_mean=0.70, quantile_median=1.00, quantile_min=0.00, quantile_max=13.00, quantile_stddev=0.82, quantile_avgdev=0.49
EG 0 13:06:27.521 TestStatBenchmark (EURUSD,H1) Normal time (microseconds): random_mean=293.70, random_median=281.00, random_min=256.00, random_max=537.00, random_stddev=43.28, random_avgdev=31.62
FD 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): pdf_mean=1.99, pdf_median=2.00, pdf_min=1.00, pdf_max=18.00, pdf_stddev=1.48, pdf_avgdev=0.48
PN 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): cdf_mean=3.19, cdf_median=3.00, cdf_min=2.00, cdf_max=17.00, cdf_stddev=1.61, cdf_avgdev=0.64
DH 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): quantile_mean=3.18, quantile_median=3.00, quantile_min=2.00, quantile_max=19.00, quantile_stddev=1.77, quantile_avgdev=0.64
NR 0 13:06:28.010 TestStatBenchmark (EURUSD,H1) Lognormal time (microseconds): random_mean=479.75, random_median=468.00, random_min=428.00, random_max=754.00, random_stddev=48.26, random_avgdev=34.30
FL 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): pdf_mean=2.32, pdf_median=2.00, pdf_min=1.00, pdf_max=15.00, pdf_stddev=1.29, pdf_avgdev=0.54
QE 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): cdf_mean=8.01, cdf_median=7.00, cdf_min=6.00, cdf_max=39.00, cdf_stddev=3.13, cdf_avgdev=1.73
MM 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): quantile_mean=50.23, quantile_median=45.00, quantile_min=44.00, quantile_max=113.00, quantile_stddev=10.28, quantile_avgdev=7.73
KG 0 13:06:29.022 TestStatBenchmark (EURUSD,H1) T time (microseconds): random_mean=951.58, random_median=931.00, random_min=859.00, random_max=1439.00, random_stddev=78.14, random_avgdev=49.72
CQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): pdf_mean=38.47, pdf_median=35.00, pdf_min=32.00, pdf_max=164.00, pdf_stddev=9.66, pdf_avgdev=6.38
OO 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): cdf_mean=27.75, cdf_median=25.00, cdf_min=24.00, cdf_max=80.00, cdf_stddev=7.02, cdf_avgdev=4.63
PF 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): quantile_mean=1339.51, quantile_median=1306.00, quantile_min=1206.00, quantile_max=2262.00, quantile_stddev=128.18, quantile_avgdev=74.83
OR 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) Noncentral T time (microseconds): random_mean=1550.27, random_median=1520.00, random_min=1418.00, random_max=2317.00, random_stddev=112.08, random_avgdev=73.74
LQ 0 13:06:31.979 TestStatBenchmark (EURUSD,H1)
GH 0 13:06:31.979 TestStatBenchmark (EURUSD,H1) 21 of 21 passed
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/2742
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
 ニューラル ネットワーク: EAの自己最適化
ニューラル ネットワーク: EAの自己最適化
 外国為替相場での通貨バスケット
外国為替相場での通貨バスケット
 グラフィカルインタフェースX: Easy And Fast (簡単で手早い)ライブラリの更新(ビルド3)
グラフィカルインタフェースX: Easy And Fast (簡単で手早い)ライブラリの更新(ビルド3)
 シグナルのクイック評価:トレーディング、ドローダウン/ロードとMFE/ MAE配信チャート
シグナルのクイック評価:トレーディング、ドローダウン/ロードとMFE/ MAE配信チャート
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
ドキュメントの 数式:
ウィキペディアの類語:
コードを見てみた。
MathRandomNoncentralBeta() 関数にはこのような行がある:
同じウィキペディアにはこうある:
The noncentral beta distribution (Type I) is the distribution of the ratio
ここで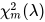 は自由度 m と 非心 パラメータ ↪Ll_1D706 を持つ非心カイ2乗 確率 変数で 𝜒 𝑛 2 は 、 𝜒 2 ( ↪Ll_1D712 ) から独立な自由度 n を持つ 中心カイ2乗 確率 変数 です。
は自由度 m と 非心 パラメータ ↪Ll_1D706 を持つ非心カイ2乗 確率 変数で 𝜒 𝑛 2 は 、 𝜒 2 ( ↪Ll_1D712 ) から独立な自由度 n を持つ 中心カイ2乗 確率 変数 です。
つまり、2つの確率変数が取られ、1つ目は非心カイ2乗分布から、2つ目は中心分布から 取られます。おそらく、このコードは修正可能であろう:
例のグラフを修正したものが以下になります。
これがその結果だ。
どちらもあまりよくないが...。一般的に、非集中ベータ分布での作業は、むしろ非自明なタスクに属する。我々はオープンソースのコードからブーストを 見ることができた。そしてそれは、今SBにあるものよりも複雑になるだろう。
同じウィキペディアにこうある:
つまり、2つの確率変数が取られ、1つ目は非心カイ2乗分布から、2つ目は中心分布から 取られる。おそらくコードはこのように修正できるだろう:
例のグラフを修正したものが以下になります。
ありがとうございます、その通りです、この式で計算する必要があります、しかしもう一つ間違いがありました、ラムダ非中心性パラメータは乗数2なしにすべきです。
テストスクリプト
結果
非心ベータ分布の CFD関数もチェックした。
疑わしい結果もある:
別の情報源では,ASA310アルゴリズムが使われています.
例えば,Wolfram Mathematicaの結果の一部.
これは多かれ少なかれ真実に近い...